| Удельное электрическое сопротивление | |
|---|---|
 |
|
| Размерность |
СИ:L3MT-3I-2 СГС:T |
| Единицы измерения | |
| СИ | Ом·метр |
| СГС | с |
Уде́льное электри́ческое сопротивле́ние (удельное сопротивление) — физическая величина, характеризующая способность материала препятствовать прохождению электрического тока, выражается в Ом·метр. Удельное электрическое сопротивление принято обозначать греческой буквой ρ. Значение удельного сопротивления зависит от температуры в различных материалах по-разному: в проводниках, удельное электрическое сопротивление с повышением температуры возрастает, а в полупроводниках и диэлектриках — наоборот, уменьшается. Величина, учитывающая изменение электрического сопротивления от температуры называется температурный коэффициент удельного сопротивления. Величина, обратная удельному сопротивлению, называется удельной проводимостью (удельной электропроводностью). В отличие от электрического сопротивления, являющегося свойством проводника и зависящего от его материала, формы и размеров, удельное электрическое сопротивление является свойством только вещества.
Электрическое сопротивление однородного проводника с удельным сопротивлением ρ, длиной l и площадью поперечного сечения S может быть рассчитано по формуле 

Из последней формулы следует: физический смысл удельного сопротивления вещества заключается в том, что оно представляет собой сопротивление изготовленного из этого вещества однородного проводника единичной длины и с единичной площадью поперечного сечения.
Единицы измерения[править | править код]
Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м[1]. Из соотношения 
В технике также применяется устаревшая внесистемная единица Ом·мм²/м, равная 10−6 от 1 Ом·м[1]. Данная единица равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 мм², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление какого-либо вещества, выраженное в этих единицах, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 мм².
Зависимость от температуры[править | править код]
В проводниках удельное электрическое сопротивление увеличивается с увеличением температуры. Это объясняется тем, что с ростом температуры увеличивается интенсивность колебания атомов в узлах кристаллической решетки проводника, что препятствует движению свободных электронов[3].
В полупроводниках и диэлектриках удельное электрическое сопротивление уменьшается. Это объясняется тем, что с увеличением температуры увеличивается концентрация основных носителей заряда.
Величина, учитывающая изменение удельного электрического сопротивление от температуры называют температурным коэффициентом удельного сопротивления.
Обобщение понятия удельного сопротивления[править | править код]
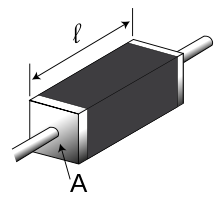
Кусок резистивного материала с электрическими контактами на обоих концах
Удельное сопротивление можно определить также для неоднородного материала, свойства которого меняются от точки к точке. В этом случае оно является не константой, а скалярной функцией координат — коэффициентом, связывающим напряжённость электрического поля 


Эта формула справедлива для неоднородного, но изотропного вещества. Вещество может быть и анизотропно (большинство кристаллов, намагниченная плазма и т. д.), то есть его свойства могут зависеть от направления. В этом случае удельное сопротивление является зависящим от координат тензором второго ранга, содержащим девять компонент 
В анизотропном, но однородном веществе тензор 
Тензор 



Как и для всякого симметричного тензора, для 
ортогональную систему декартовых координат, в которых матрица 






Величины 
Связь с удельной проводимостью[править | править код]
В изотропных материалах связь между удельным сопротивлением 

В случае анизотропных материалов связь между компонентами тензора удельного сопротивления 

Из этого равенства и приведённого ранее соотношения для 
где 

Удельное электрическое сопротивление некоторых веществ[править | править код]
Металлические монокристаллы[править | править код]
В таблице приведены главные значения тензора удельного сопротивления монокристаллов при температуре 20 °C[5].
| Кристалл | ρ1=ρ2, 10−8 Ом·м | ρ3, 10−8 Ом·м |
|---|---|---|
| Олово | 9,9 | 14,3 |
| Висмут | 109 | 138 |
| Кадмий | 6,8 | 8,3 |
| Цинк | 5,91 | 6,13 |
| Теллур | 2,90·109 | 5,9·109 |
Металлы и сплавы, применяемые в электротехнике[править | править код]
Разброс значений обусловлен разной химической чистотой металлов, способов изготовления образцов, изученных разными учеными и непостоянством состава сплавов.
|
|
Значения даны при температуре t = 20 °C. Сопротивления сплавов зависят от их химического состава и могут варьироваться. Для чистых веществ колебания численных значений удельного сопротивления обусловлены различными методами механической и термической обработки, например, отжигом проволоки после волочения.
Другие вещества[править | править код]
| Вещество | ρ, Ом·мм²/м |
|---|---|
| Сжиженные углеводородные газы | 0,84⋅1010 |
Тонкие плёнки[править | править код]
Сопротивление тонких плоских плёнок (когда её толщина много меньше расстояния между контактами) принято называть «удельным сопротивлением на квадрат», 

См. также[править | править код]
- Электрическое сопротивление
- Сверхпроводимость
- Закон Ома
- Удельная проводимость
- Отрицательное сопротивление
- Импеданс
- Температурный коэффициент электрического сопротивления
Примечания[править | править код]
- ↑ 1 2 Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 93. — 240 с. — ISBN 5-7050-0118-5.
- ↑ 1 2 Чертов А. Г. Единицы физических величин. — М.: «Высшая школа», 1977. — 287 с.
- ↑ Никулин Н. В., Назаров А. С. Радиоматериалы и радиокомпоненты. — 3-е изд. — М.: Высшая школа, 1986. — 208 с.
- ↑ Давыдов А. С. Теория твёрдого тела. — М.: «Наука», 1976. — С. 191—192. — 646 с.
- ↑ Шувалов Л. А. и др. Физические свойства кристаллов // Современная кристаллография / Гл. ред. Б. К. Вайнштейн. — М.: «Наука», 1981. — Т. 4. — С. 317.
Литература[править | править код]
- Никулин Н. В., Назаров А. С. Радиоматериалы и радиокомпоненты. — 3-е изд., переработанное и дополненное. — М.: Высшая школа, 1986. — С. 6—7. — 208 с.
Удельное сопротивление
Содержание:
- Что такое удельное сопротивление
- Как образуется в материале проводимость
- Единицы измерения
- Формула расчета удельного сопротивления
-
От чего зависит сопротивление
- Связь с удельной проводимостью
- Удельное сопротивление различных материалов
Что такое удельное сопротивление
Удельное сопротивление (УС) — это свойство вещества оказывать сопротивление электротоку в момент прохождения через него.
Все вещества по способности проводить электрический ток делятся на:
- Проводники. Проводниками называют вещества, в которых находится большое количество свободных заряженных частиц — электронов. Благодаря наличию таких заряженных частиц, свободно перемещающихся по всему металлическому проводнику, электрическое поле внутри таких веществ отсутствует. Отличными проводниками, например, являются металлы.
- Полупроводники. Полупроводниками называют такие вещества, которые способны изменять удельное сопротивление в широких пределах и быстро уменьшать его значение с повышением температуры.
Как образуется в материале проводимость
Причина того, что вещества оказывают сопротивление электрическому току, кроется в том, что движению электрического тока, представляющему собой направленное движение электрических зарядов, мешают ионы кристаллической решетки вещества, движущиеся беспорядочно. Это препятствие или сопротивление электротоку влияет на его скорость — она уменьшается.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Единицы измерения
В физике символом р принято обозначать удельную проводимость вещества. Она характеризует то вещество, из которого выполнен проводник. Ее значение равняется сопротивлению проводника, длина которого составляет 1 метр, а площадь сечения — 1 (м^2.)
Единицами УС вещества в международной системе принято считать 10(м*1) (м^2 /1 м).
Так как площадь поперечного сечения часто измеряют в (мм^2), поэтому в учебниках по физике для удельного сопротивления можно встретить два варианта единиц измерения: (Ом*м) и (Ом*мм^2/м).
Формула расчета удельного сопротивления
Удельное сопротивление рассчитывается по формуле:
(p=frac{Rtimes S}l)
Где R — сопротивление проводника, S — площадь его поперечного сечения, l — его длина.
От чего зависит сопротивление
УС зависит от температуры в различных материалах. Но меняется оно по-разному:
- В проводниках p с повышением температуры увеличивается.
- В полупроводниках и диэлектриках p с повышением температуры уменьшается.
Температурный коэффициент электрического сопротивления — величина, которая учитывает изменение электрического сопротивления от температуры.
Связь с удельной проводимостью
Удельной электропроводностью называют величину, обратную удельному сопротивлению. Она обозначается символом k и измеряется в сименс/м.
Взаимосвязь двух величин выражает формула:
(p=frac1k)
Электрическое сопротивление является свойством проводника и зависит от материала, размеров и формы вещества.
Удельное электрическое сопротивление — это свойство только вещества.
Удельное сопротивление различных материалов
В таблице приведены значения УС некоторых веществ:
Опытным путём было установлено, что у металлов удельное сопротивление с повышением температуры увеличивается. Из всех металлов наименьшим удельным сопротивлением обладают серебро и медь. Следовательно, серебро и медь — лучшие проводники электричества.
Стекло и дерево имеют такое большое удельное сопротивление, что почти совсем не проводят электрический ток и являются изоляторами.
Насколько полезной была для вас статья?
Рейтинг: 2.00 (Голосов: 7)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Удельное сопротивление


4.4
Средняя оценка: 4.4
Всего получено оценок: 185.
4.4
Средняя оценка: 4.4
Всего получено оценок: 185.
Электрический ток — это перемещение электронов в одном направлении, которое возникает когда к концам металлического проводника прикладывается разность потенциалов (напряжение). Величина тока имеет определенную, конечную величину. Это связано с тем, что все вещества “сопротивляются” приложенному извне электрическому полю.
Почему возникает сопротивление
Электроны, сталкиваясь с заряженными атомами (ионами), из которых стоит кристаллическая решетка проводника, теряют скорость. Масса атома значительно превосходит массу электрона, поэтому их столкновение приводит к потере скорости (“торможению”) и изменению направления движения электрона. Таким образом возникает сопротивление протеканию (нарастанию) тока. Значит сопротивление — это физическая величина.
Как вычислить сопротивление
Величину сопротивления можно определить по формуле закона Ома:
$$R={U over I}$$
где:
R — сопротивление, единица измерения Ом;
U — напряжение в вольтах, В;
I — сила тока в амперах, А.
Напряжение и ток измеряются приборами — вольтметром и амперметром.

Единицы для обозначения напряжения, тока и сопротивления получили свое название в честь итальянского физиолога Алессандро Вольты, французского физика Андре Ампера и немецкого ученого Георга Ома. Поэтому сокращенное написание этих единиц полагается писать с заглавных букв В, А, Ом.
Удельное сопротивление
Экспериментально было обнаружено, что значение сопротивления любого проводника прямо пропорционально его длине и обратно пропорционально площади поперечного сечения. Другими словами — сопротивление провода тем больше, чем он длиннее и меньше его толщина. В виде формулы это выглядит так:
$$R= ρ *{L over S}$$
где:
L — длина, измеряется в метрах, м;
S — площадь поперечного сечения в метрах квадратных, м2;
ρ — удельное сопротивление, .
Как вычислить?
Значение коэффициента можно определить из последнего уравнения. Таким образом мы получаем формулу удельного сопротивления: $ρ=R*{S over L}$.
Каждое вещество характеризуется с помощью своего, индивидуального, значения . Поэтому, например, два совершенно одинаковых по длине и толщине (сечению) провода, но из разных металлов, будут иметь значительно отличающиеся сопротивления. Это связано с тем, что атомы различных веществ отличаются друг от друга массой, которая зависит от количества, протонов, нейтронов и электронов.
В каких единицах измеряют ?
Из последней формулы видно, что если R = 1 Ом, S = 1 м2, а L = 1 м, то = 1 .
Это и есть единица измерения удельного сопротивления. Но на практике оказалось, что у реальных проводов площади сечений гораздо меньше 1 м2. Поэтому было решено при вычислении использовать значение площади S в мм2, чтобы итоговое значение имело компактный вид. Тогда получаются более удобные (меньше нулей после запятой) для восприятия числовые значения удельного сопротивления:
$$[ ρ ]={ [Ом]×[мм2] over [м]}$$
Например, медь имеет одно из самых низких значений ρ — 0,017 . Поэтому медные провода имеют небольшое сопротивление и по ним можно пропускать большие токи. Тогда становится понятно, почему большинство электротехнических устройств (трансформаторы, электродвигатели и т.д.) изготавливаются с применением этого провода.
Надо ли каждый раз измерять удельное сопротивление?
Нет, не надо. Эта работа давно проделана физиками-экспериментаторами и сведена в таблицы для разных веществ, которые можно найти в технических справочниках или в их интернет-версиях. Для примера ниже приведена таблица для некоторых веществ:
Удельное сопротивление металлов, Ом*мм2/м
(при Т = 200С)
|
Серебро |
0,016 |
Бронза (сплав) |
0,1 |
|
Медь |
0,017 |
Олово |
0,12 |
|
Золото |
0,024 |
Сталь (сплав) |
0,12 |
|
Алюминий |
0,028 |
Свинец |
0,21 |
|
Иридий |
0,047 |
Никелин (сплав) |
0,42 |
|
Молибден |
0,054 |
Манганин (сплав) |
0,45 |
|
Вольфрам |
0,055 |
Константан (сплав) |
0,48 |
|
Цинк |
0,06 |
Титан |
0,58 |
|
Латунь (сплав) |
0,071 |
Ртуть |
0,958 |
|
Никель |
0,087 |
Нихром (сплав) |
1,1 |
|
Платина |
0,1 |
Висмут |
1,2 |
Надо иметь в виду, что в этих таблицах значения удельного сопротивления приводятся, как правило, при комнатной температуре, которая в среднем равна . Более подробные исследования показали, что зависит от температуры. Но это уже тема для другого занятия.

Что мы узнали?
Итак, мы узнали, что такое удельное сопротивление. Зная эту величину и геометрические размеры образца (например, провода), можно вычислить его сопротивление. Если же нет табличных (справочных) данных, то можно определить с помощью закона Ома и формулы: $ρ=R*{S over L}$.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.4
Средняя оценка: 4.4
Всего получено оценок: 185.
А какая ваша оценка?
Удельное электрическое сопротивление проводника
Под удельным сопротивлением проводника понимают его сопротивление при длине, равной 1 метру, и площади поперечного сечения 1мм2.
Значение удельного сопротивления проводника применяется при расчете электрического сопротивления проводника, которое находится по формуле: R=p (l/S), где:
R– сопротивление, Ом ;
p– удельное сопротивление,
Ом*мм І /м;
l-длина проводника, метров;
S – площадь поперечного сечения проводника, мм І .
Отсюда значение удельного сопротивления проводника может быть найдено по формуле p=(R*S)/l. При нормальных условиях электрическое сопротивление меньше у того материала, у которого меньше значение удельного сопротивления. Резисторы – электронные элементы, обладающие определенным электрическим сопротивлением. Бывают постоянные и переменные, проволочные и непроволочные. В электронных схемах применяются в качестве нагрузок и делителей напряжения.
Основные параметры:
- 1.Номинальное сопротивление
- 2.%
- 3.Номинальная мощность рассеивания
- 4.ТКС
- 5.Уровень собственных шумов
- 6.Надежность
Рабочие температуры:(-60…+200С).
Выпускаются: общего применения,переменные,подстроеч-
ные,специальные (варисторы-R при изм.U; терморезисторы-R при изм.TC; фоторезисторы-R при освещ-ти; магниторезисторы- R от напряженности магнитного поля).
Некоторые вещества в природе (как металлы, так и неметаллы) являются проводниками электрического тока. При движении тока в них тока, вещества оказывают сопротивление его прохождению. Физическая величина, которая определяет способность материала препятствовать прохождению через него электрического тока называется удельным сопротивлением.
Металл с небольшим значением этого параметра – медь. Низкое значение сопротивления движению тока [left(0,017 frac{O м * мм^{2}}{м}right)] позволяет использовать медь в качестве проводника.
Описанная величина обозначается греческой буквой «ро» – ρ.
Формула удельного сопротивления
Для расчета данного параметра немецким физиком Георгом Омом была выведена формула удельного сопротивления:
[boldsymbol{R=frac{rho * l}{S}}]
Эта формула записана относительно сопротивления. Для того чтобы вывести значение данной физической величины, необходимо преобразовать исходную формулу:
[frac{rho * l}{S}=R]
сперва нужно умножить обе части уравнения на S:
[frac{rho}{S}=frac{R}{l}]
затем l переносится в правую часть:
[rho=frac{R * S}{l}]
Исходя из полученного выражения, можно сформулировать понятие удельного сопротивления: препятствие данного вещества единичной длины и единичной площади поперечного сечения движению тока.
Получившаяся формула используется для нахождения значения исследуемого параметра. Кроме искомой величины, в формуле фигурируют ещё три члена:
- R – сопротивление, измеряемое в Ом;
- l – длина проводника, в метрах;
- S – площадь поперечного сечения, мм².
В общепринятой международной системе (СИ) единицей измерения удельного сопротивления является Ом*м. При решении практических задач, полученные значения чаще всего выражают в [frac{O_{mathrm{м} * mathrm{мм}^{2}}}{mathrm{м}}].
Для большинства часто применяемых металлов этот параметр уже рассчитан. Ниже представлена таблица 1, в которой собраны значения величины для некоторых металлов.
| Металл | Числовое значение удельного сопротивления при температуре [20C^{circ}], [frac{O_{м * м м^{2}}}{м}] |
| Медь | 0,017 |
| Серебро | 0,016 |
| Вольфрам | 0,055 |
| Золото | 0,024 |
| Алюминий | 0,028 |
| Железо | 0,1 |
| Свинец | 0,21 |
Зависимость удельного сопротивления от температуры
В приведенной таблице отмечено, что указанные значения приводятся при температуре [20C^{circ}]. Действительно, удельное сопротивление зависит от температуры. Но для каждого материала влияние температуры внешней среды будет разным. Такое явление обусловливается температурным коэффициентом [(alpha)]. Он учитывается при расчете параметра по формуле: [rho_{t}=rho_{0} *left[1+alpha *left(t_{1}-t_{o}right)right]].
В этом выражении представлены значения:
- [rho_{0}] – удельного сопротивления металла при температуре окружающей среды [20 C^{o}];
- α – температурного коэффициента;
- t1 – t0 – разница температур (Δt).
Данная формула устанавливает зависимость удельного сопротивления от температуры.
В таблице 2 приведены числовые значения температурного коэффициента для некоторых металлов.
| Металл | Температурный коэффицент сопротивления [alpha, K^{-1}] |
| Алюминий | 0,0049 |
| Вольфрам | 0,0045 |
| Медь | 0,0039 |
| Никель | 0,0050 |
| Олово | 0,0042 |
| Ртуть | 0,0009 |
| Серебро | 0,0036 |
Примеры расчета удельного сопротивления
Используя приведенную формулу, можно рассчитать значения удельного электрического сопротивления с учетом температурного коэффициента.
Пример
Необходимо рассчитать числовое значение исследуемой величины для вольфрама при температурах 50 и -50 градусов Цельсия.
Применяем полученную формулу для расчетов при 50-ти градусах:
[begin{gathered}
rho_{t}=rho_{0} *left[1+alpha *left(t_{1}-t_{0}right)right]=0,055 *[1+0,0045 *(50-20)]=0,0624 .
end{gathered}]
По этой же формуле произведем расчет при температуре -50 градусов:
[begin{gathered}
rho_{t}=rho_{0} *left[1+alpha *left(t_{1}-t_{0}right)right]=0,055 *[1+0,0045 *(-50-20)]=0,0376 .
end{gathered}]
Исходя из примеров расчета удельного сопротивления, можно сделать вывод, что с увеличением температуры внешней среды растет удельное сопротивление.
На рисунке представлен график зависимости удельного сопротивления от температуры.
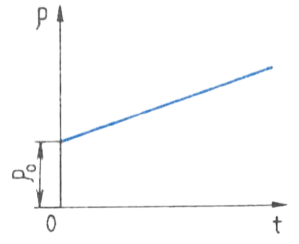
График наглядно показывает рост этой физической величины в процессе повышения температуры.
Применение формул на практике
На практике часто приходится производить расчет по той причине, что материал изделия неизвестен. Это обстоятельство лишает возможности обратиться к справочной литературе за необходимыми данными.
При расчете искомого параметра понадобятся не только теоретические формулы, но и специальные приборы: мультиметр и микрометр.
Дан пруток, имеющий длину 5 метров. При помощи штангенциркуля определим диаметр сечения. Полученное значение составило 0,42 мм.
Площадь сечения определяется по формуле:
[boldsymbol{S=frac{pi * d^{2}}{4}}]
Затем необходимо измерить электрическое сопротивление материала. Мультиметр показывает 45 Ом.
Подставим площадь в исходную формулу для расчета искомой величины:
[begin{gathered}
rho=frac{R * S}{l} \
rho=frac{R * pi * d^{2}}{4 * l}
end{gathered}]
Далее подставим полученные значения в формулу и рассчитаем искомый параметр:
[rho=frac{45 * 3,14 * 0,42^{2}}{4 * 5}=1,24 frac{O м * cdot мм^{2}}{м}]
Полученное значение необходимо сверить со справочником. Учитывая несовершенство приборов, и возникшие в процессе непосредственного измерения размеров изделия погрешности, можно сделать вывод, что пруток изготовлен из нихрома.
Нет времени решать самому?
Наши эксперты помогут!
Понятие проводимости
Физическая величина, которая характеризует возможность материала проводить электрический ток, называется проводимостью (электропроводностью). Единицей измерения этой величины в системе СИ служит Сименс (См).
Проводимость является величиной, обратной к электрическому сопротивлению.
Соотношение между удельным сопротивлением и удельной электропроводностью можно представить в виде:[sigma=frac{1}{rho}]
Электропроводность материала определяется способностью заряженных частиц (ионов и электронов) свободно перемещаться в пределах данной среды. Из этого можно сделать вывод, что проводимость зависит от нескольких характеристик материала:
- строения вещества;
- химического состава;
- агрегатного состояния.
Кроме того, поскольку удельное сопротивление зависит от температуры, то и проводимость тоже будет зависеть от этого фактора.
Ниже представлена таблица 3, в которой показаны значения проводимости для основных металлов.
| Металл | Значение проводимости *107, См/м |
| Серебро | 6,2 |
| Медь | 5,8 |
| Золото | 4,52 |
| Алюминий | 3,77 |
| Вольфрам | 1,9 |
| Латунь | 1,55 |
| Железо | 0,99 |
Стоит отметить, что указанные в данной таблице значения реальны только при температуре 25 градусов Цельсия. С изменение температуры, электропроводность материалов будет изменяться. На основании приведенной выше зависимости удельного сопротивления от температуры и, руководствуясь формулой для расчета проводимости, можно сделать вывод, что с увеличением температуры окружающей среды значение проводимости будет снижаться.
Проводимость серебра выше проводимости меди. Однако серебро не получило широкого промышленного распространения в качестве проводника электричества, поскольку имеет высокую стоимость.





![rho _{{11}}={frac {1}{det(sigma )}}[sigma _{{22}}sigma _{{33}}-sigma _{{23}}sigma _{{32}}],](https://wikimedia.org/api/rest_v1/media/math/render/svg/08befe7409fd1685d379b9d3045f8b7d88b62e44)
![rho _{{12}}={frac {1}{det(sigma )}}[sigma _{{33}}sigma _{{12}}-sigma _{{13}}sigma _{{32}}],](https://wikimedia.org/api/rest_v1/media/math/render/svg/023c28c36a33abc59ec81a040eeeee5d6040e007)

