Как найти удельную энергию связи ядра атома

Энергия связи атомных ядер

Важнейшую роль во всей ядерной физике играет понятие энергии связи ядра. Энергия связи позволяет объяснить устойчивость ядер, выяснить, какие процессы ведут к выделению ядерной энергии. Нуклоны в ядре прочно удерживаются ядерными силами. Для того чтобы удалить нуклон из ядра, надо совершить довольно большую работу, т. е. сообщить ядру значительную энергию.

Под энергией связи ядра понимают ту энергию, которая необходима для полного расщепления ядра на отдельные нуклоны. На основе закона сохранения энергии можно также утверждать, что энергия связи ядра равна той энергии, которая выделяется при образовании ядра из отдельных частиц.

Энергия связи атомных ядер очень велика. Но как ее определить?

В настоящее время рассчитать энергию связи теоретически, подобно тому как это можно сделать для электронов в атоме, не удается. Выполнить соответствующие расчеты можно, лишь применяя соотношение Эйнштейна между массой и энергией:

Точнейшие измерения масс ядер показывают, что масса покоя ядра Мя всегда меньше суммы масс входящих в его состав протонов и нейтронов:

Существует, как говорят, дефект масс: разность масс

положительна. В частности, для гелия масса ядра на 0,75% меньше суммы масс двух протонов и двух нейтронов. Соответственно для гелия в количестве вещества один моль ΔM = 0,03 г.

Уменьшение массы при образовании ядра из нуклонов означает, что при этом уменьшается энергия этой системы нуклонов на значение энергии связи Есв:

Но куда при этом исчезают энергия Есв и масса ΔM?

При образовании ядра из частиц последние за счет действия ядерных сил на малых расстояниях устремляются с огромным ускорением друг к другу. Излучаемые при этом γ-кванты как раз обладают энергией Есв и массой

Энергия связи — это энергия, которая выделяется при образовании ядра из отдельных частиц, и соответственно это та энергия, которая необходима для расщепления ядра на составляющие его частицы.

О том, как велика энергия связи, можно судить по такому примеру: образование 4 г гелия сопровождается выделением такой же энергии, что и при сгорании 1,5—2 вагонов каменного угля.

Важную информацию о свойствах ядер содержит зависимость удельной энергии связи от массового числа А.

Удельной энергией связи называют энергию связи, приходящуюся на один нуклон ядра. Ее определяют экспериментально. Из рисунка 13.11 хорошо видно, что, не считая самых легких ядер, удельная энергия связи примерно постоянна и равна 8 МэВ/нуклон. Отметим, что энергия связи электрона и ядра в атоме водорода, равная энергии ионизации, почти в миллион раз меньше этого значения. Кривая на рисунке 13.11 имеет слабо выраженный максимум. Максимальную удельную энергию связи (8,6 МэВ/нуклон) имеют элементы с массовыми числами от 50 до 60, т. е. железо и близкие к нему по порядковому номеру элементы. Ядра этих элементов наиболее устойчивы.

У тяжелых ядер удельная энергия связи уменьшается за счет возрастающей с увеличением Z кулоновской энергии отталкивания протонов. Кулоновские силы стремятся разорвать ядро.

Частицы в ядре сильно связаны друг с другом. Энергия связи частиц определяется по дефекту масс.

Ядерные реакции

Атомные ядра при взаимодействиях испытывают превращения. Эти превращения сопровождаются увеличением или уменьшением кинетической энергии участвующих в них частиц.

Ядерными реакциями называют изменения атомных ядер при взаимодействии их с элементарными частицами или друг с другом. С примерами ядерных реакций вы уже ознакомились в § 103. Ядерные реакции происходят, когда частицы вплотную приближаются к ядру и попадают в сферу действия ядерных сил. Одноименно заряженные частицы отталкиваются друг от друга. Поэтому сближение положительно заряженных частиц с ядрами (или ядер друг с другом) возможно, если этим частицам (или ядрам) сообщена достаточно большая кинетическая энергия. Эта энергия сообщается протонам, ядрам дейтерия — дейтронам, α-частицам и другим более тяжелым ядрам с помощью ускорителей.

Для осуществления ядерных реакций такой метод гораздо эффективнее, чем использование ядер гелия, испускаемых радиоактивными элементами. Во-первых, с помощью ускорителей частицам может быть сообщена энергия порядка 105 МэВ, т. е. гораздо большая той, которую имеют α-частицы (максимально 9 МэВ). Во-вторых, можно использовать протоны, которые в процессе радиоактивного распада не появляются (это целесообразно потому, что заряд протонов вдвое меньше заряда α-частиц, и поэтому действующая на них сила отталкивания со стороны ядер тоже в 2 раза меньше). В-третьих, можно ускорить ядра более тяжелые, чем ядра гелия.

Первая ядерная реакция на быстрых протонах была осуществлена в 1932 г. Удалось расщепить литий на две α-частицы:

Как видно из фотографии треков в камере Вильсона (рис. 13.12), ядра гелия разлетаются в разные стороны вдоль одной прямой согласно закону сохранения импульса (импульс протона много меньше импульса возникающих α-частиц; на фотографии треки протонов не видны).

Энергетический выход ядерных реакций. В описанной выше ядерной реакции кинетическая энергия двух образующихся ядер гелия оказалась больше кинетической энергии вступившего в реакцию протона на 7,3 МэВ. Превращение ядер сопровождается изменением их внутренней энергии (энергия связи). В рассмотренной реакции удельная энергия связи в ядрах гелия больше удельной энергии связи в ядре лития. Поэтому часть внутренней энергии ядра лития превращается в кинетическую энергию разлетающихся α-частиц.

Изменение энергии связи ядер означает, что суммарная энергия покоя участвующих в реакциях ядер и частиц не остается неизменной. Ведь энергия покоя ядра Мя*с2 согласно формуле (13.5) непосредственно выражается через энергию связи. В соответствии с законом сохранения энергии изменение кинетической энергии в процессе ядерной реакции равно изменению энергии покоя участвующих в реакции ядер и частиц.

Энергетическим выходом ядерной реакции называется разность энергий покоя ядер и частиц до реакции и после реакции. Согласно вышесказанному энергетический выход ядерной реакции равен также изменению кинетической энергии частиц, участвующих в реакции.

Если суммарная кинетическая энергия ядер и частиц после реакции больше, чем до реакции, то говорят о выделении энергии. В противном случае реакция идет с поглощением энергии.

Выделяющаяся при ядерных реакциях энергия может быть огромной. Но использовать ее при столкновениях ускоренных частиц (или ядер) с неподвижными ядрами мишени практически нельзя. Ведь бо́льшая часть ускоренных частиц пролетает мимо ядер мишени, не вызывая реакцию.

Ядерные реакции на нейтронах. Открытие нейтрона было поворотным пунктом в исследовании ядерных реакций. Так как нейтроны не имеют заряда, то они беспрепятственно проникают в атомные ядра и вызывают их изменения. Например, наблюдается следующая реакция:

Великий итальянский физик Энрико Ферми первым начал изучать реакции, вызываемые нейтронами. Он обнаружил, что ядерные превращения обусловлены не только быстрыми, но и медленными нейтронами. Причем эти медленные нейтроны оказываются в большинстве случаев даже гораздо более эффективными, чем быстрые. Поэтому быстрые нейтроны целесообразно предварительно замедлять. Замедление нейтронов до тепловых скоростей происходит в обыкновенной воде. Этот эффект объясняется тем, что в воде содержится большое число ядер водорода — протонов, масса которых почти равна массе нейтронов. Следовательно, нейтроны после соударений движутся со скоростью теплового движения. При центральном соударении нейтрона с покоящимся протоном он целиком передает протону свою кинетическую энергию.

Реакции, в которые вступают атомные ядра, очень разнообразны. Нейтроны не отталкиваются ядрами и поэтому особенно эффективно вызывают превращения ядер.

Тест

Примеры решения задач

Задача
1.
Вычислить
дефект массы и энергию связи ядра
.

Дано:
Решение

Дефект
массы ядра равен

А
= 11 т
= Z
m_p
+ (A
– Z)
m_n
– M_ядра.

(1)

Z
= 5
Выразим массу ядра
через массу атома и массу всех

N
= A
– Z
= 6
электронов:

а.е.м.
М_ат
= М_яд
+ Z
m_e;

т_п
= 1,00867 а.е.м. М_яд
=
М_ат
– Z
m_e;
(т_р
+ т_е)
=
.

т_в
= 11,00930 а.е.м. Тогда

т
– ? Е
– ?
;

.
(2)

Формула
(2) является расчетной формулой дефекта
массы. По формуле (1) определить дефект
массы нельзя, так как в существующих
таблицах даны не массы ядер, а массы
нейтральных атомов (см. табл. 1 приложения).

После подстановки
численных значений, получим:

т
= 5 ^.
1,00783
+ 6 ^.
1,00867
– 11,00930 = 0,08186 а.е.м.

Энергия связи

Е
= 
т
с²,

или
Е
=
0,08186 ^.
931,5
= 76 МэВ.

Ответ:
т
= 0,08186 а.е.м.; Е
= 76 МэВ.

Задача
2.
Определить энергию, необходимую для
отделения одного нейтрона от ядра
.

Дано:Решение

Энергия
отделения от ядра одного нейтрона

а.е.м
численно равна энергии связи нейтрона
с

а.е.м.
ядром.

а.е.м
Е_п
= т
с²;

Е_п
– ? т
= т_п
+
,

Подставим численные значения масс,
взятые из табл. 1 приложения:

т
= 1,00867 + 21,99440 – 22,98977 = 0,01334 а.е.м.;

Е_п
= т
^.
с²
= 931,5 ^.
0,01334
= 12,4 МэВ.

Ответ:
Е_п
= 12,4 МэВ.

Задача
3.
Какую наименьшую энергию нужно затратить,
чтобы отделить один протон от ядра
?

Дано:

Решение

В
результате отделения одного протона
от ядра

а.е.м.

получается новое ядрои протон.

т_р
= 1,00728 а.е.м. Изменение массы

а.е.м.

Е_р
– ? Энергия связи протона
в ядре

.

Подставим числовые значения

МэВ.

Ответ:
Е_р
= 7,04 МэВ.

Задача
4.
Определить удельную энергию связи ядра
.

Дано:

Решение

М_U
= 238,05076 а.е.м. Удельной энергией связи
называется средняя

А
= 238
энергия связи, приходящаяся
на один нуклон в ядре,

Z
= 92 т. е.
;

A
– Z
=
146
.

 –
?

или

Ответ:

Задача
5.
Какую наименьшую энергию нужно затратить,
чтобы разделить ядро
на
две одинаковые части.

Дано:
Решение

В
результате деления ядра
на две одинаковые

а.е.м.
части получается два ядра дейтерия
.
Сумма масс

а.е.м.
образовавшихся ядер больше массы ядра
:

Е
– ?

;

МэВ.

Ответ:
Е
= 23,85 МэВ.

Задача
6.
Сколько энергии выделится при образовании
1 г
из протонов и нейтронов?

Дано:

Решение

М
= 4,00260 а.е.м. При образовании одного
ядра
из протонов и

а.е.м.
нейтронов выделится энергия, равная
численно

т_п
= 1,00867 а.е.м. энергии связи ядра
.

Q
– ? Определим энергию
связи ядра:

;

МэВ.

В
1 г
содержитсяN
атомов (ядер):

,

где

– молярная масса
:
4 ^.
10^-3
кг/моль;
N_A
– число Авогадро.

Тогда
полная энергия Q,
выделившаяся при образовании 1 г гелия,
равна

МэВ;

1
МэВ = 1,6 ^.
10^-13
Дж.

Q
= 26 ^.
10¹⁰
Дж.

Ответ:
При синтезе 1 г

выделяется энергия

Q
= 42 ^.
10²³
МэВ=26Дж.

Задача
7.
Энергия связи ядра
равна 139,8 МэВ; ядраМэВ. Определить минимальную энергию,
необходимую для отделения одного протона
от ядра.

Дано:Решение

Е₁
= 139,8 МэВ Схема отделения протона

Е₂
= 147,8 МэВ

А₁
= 18 Энергия связи протона в
ядре
:

А₂
= 19
(1)

Z₁
= 8 Энергия связи ядра
:;

Z₂
= 9 Энергия связи ядра
:;

N₁
= N₂
= 10 Вычтем Е₁
из формулы
.
Получим

Е_р
– ?

.
(2)

Сравним
выражение (2) с выражением (1):
.

Вычисляя,
получим: Е_р
= 147,8 – 139,8 = 8 МэВ.

Ответ:
Е_р
= 8 МэВ.

Задача
8.
Какую наименьшую энергию нужно затратить,
чтобы разделить на отдельные нуклоны
изобарные ядра
и?

Дано:Решение

Е₁
= 931,5 ^.
(3 ^.
1,00783
+ 4 ^.
1,00867
– 7,01601) =

А
= 7 А
= 7 = 931,5 ^.
0,4216
= 39,2 МэВ;

Z
= 3
Z
= 4 Е₂
= 931,5 ^.
(4 ^.
1,00783
+ 3 ^.
1,00867
– 7,01693) =

N
= 4
N
= 3 = 931,5 ^.
0,04040
= 37,6 МэВ.

а.е.м.

а.е.м.

Е₁
– ? Е₂
– ?

Ответ:
Е_Li
= 39,2 МэВ; Е_Ве
= 37,6 МэВ.

Задача
9.
Найти энергию связи ядер
и.
Какое из этих ядер наиболее устойчиво?

Дано:
Решение

МэВ
=

=
(1,00783 + 2 ^.
1,00867
–

Е₁
– ? – 3,01605) ^.
931,5
МэВ = 8,5 МэВ;

Е₂
– ? Е₂
= (1,00783 ^.
2
+ 1,00867 – 3,01603) ^.
931,5
МэВ =

=
6,8 МэВ;

Оба
ядра содержат одинаковое количество
нуклонов, но ядро
более устойчиво, чем ядро,
так как в состав(в отличие от)
входит 2 протона, между которыми существуют
силы кулоновского отталкивания, что
уменьшает энергию связи ядра.

Задача
10.
Используя формулу Вайцзеккера, определить
массу ядра тяжелого водорода
.

Дано:Решение

т_р
= 1,00728 а.е.м. Энергия связи ядра

т_п
= 1,00867 а.е.м.
.

 =
15,75 МэВ Найдем массу ядра

 =
17,8 МэВ
.

 =
0,71
МэВ Запишем полуэмпирическую
формулу Вайцзеккера,

 =
94,8 МэВ позволяющую определить
энергию связи ядра:


=
34 МэВ

т_я
– ?

,

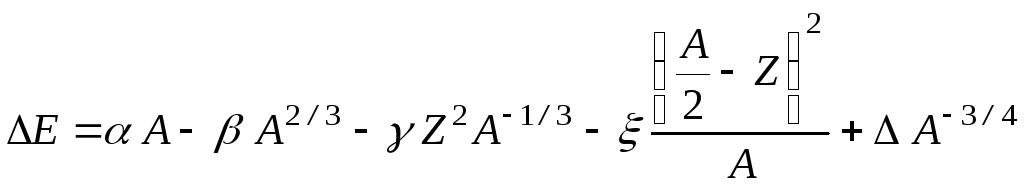где
А
– массовое число; Z
– зарядовое число; ,
,
,
,

– поправочные коэффициенты, с помощью
которых учитываются силы кулоновского
отталкивания протонов, энергия
поверхностного натяжения ядра-капли,
соотношение между числом протонов и
нейтронов в ядре, четность или нечетность
ядер. Масса ядра с учетом формулы
Вайцзеккера для тяжелого водорода:

.

Ядро нечетно-нечетное.

.

Ответ:

а.е.м.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #