| Энтальпия | |
|---|---|
 |
|
| Размерность |
 |
| Единицы измерения | |
| СИ | Дж |
| СГС | эрг |
| Примечания | |
| Внесистемные единицы: калория, британская тепловая единица |
Энтальпи́я (от др.-греч. ενθαλπω — «нагреваю», также теплова́я фу́нкция[1][2], теплова́я фу́нкция Гиббса[3], теплосодержа́ние[1][3] и изобарно-изоэнтропийный потенциал[4]) — функция состояния 



(Определение энтальпии)
Из уравнения для дифференциала внутренней энергии[9][10]:
(Дифференциал внутренней энергии)
где 

(Дифференциал энтальпии)
которое является полным дифференциалом функции 
Понятие энтальпии существенно дополняет математический аппарат термодинамики[⇨] и гидродинамики[⇨].
Важно, что в изобарном процессе при постоянном 
равное сумме изменения внутренней энергии 


Отношение малого количества теплоты, 

Это экспериментально измеримая величина, и из её измерений находят температурную зависимость энтальпии[⇨].
Энтальпия — экстенсивная величина: для составной системы она равна сумме энтальпий её независимых частей. Как и внутренняя энергия, энтальпия определяется с точностью до произвольного постоянного слагаемого.
Первое упоминание об использовании термина «энтальпия» в его современном значении[21]
История вопроса[править | править код]
Понятие энтальпии было введено и развито Дж. В. Гиббсом[22][23][24] в 1875 году в классической работе «О равновесии гетерогенных веществ». Для обозначения этого понятия Гиббс использовал термин «тепловая функция при постоянном давлении»[25][26].
Автором термина «энтальпия» в его современном значении считают Х. Камерлинг-Оннеса. Впервые о его авторстве упоминает работа 1909 года[27][28] в связи с обсуждением сохранения энтальпии в эффекте Джоуля — Томсона[⇨], хотя в печатных публикациях самого Камерлинг-Оннеса это слово не встречается[29]. Что же касается буквенного обозначения 

Энтальпия как термодинамический потенциал[править | править код]
Поскольку внутренняя энергия является термодинамическим потенциалом относительно энтропии и объёма[30],
определение энтальпии можно рассматривать как преобразование Лежандра для перехода от потенциала относительно переменных 


Из выражения для дифференциала энтальпии получаются ещё два уравнения состояния, непосредственно выражающие температуру и объём через энтальпию и давление[32]:
Если известна энтальпия, другие термодинамические потенциалы — внутренняя энергия 


Из равных друг другу смешанных производных энтальпии выводятся две термодинамические производные, связанные третьим соотношением Максвелла[33]:
Через вторые производные энтальпии выражаются ещё две термодинамические производные:
Первая из этих производных характеризует теплоёмкость при постоянном давлении 
Метод якобианов позволяет получить тождества, аналогичные соотношениям Бриджмена, для выражения любых термодинамических производных через приведённые производные энтальпии.
Зависимость энтальпии от числа частиц[править | править код]
Для состоящей из одинаковых частиц открытой системы число частиц 
где 





Схема контрольного объёма. За малый интервал времени 
В англоязычной литературе, особенно технической, понятие открытой системы обычно отождествляют с понятием «контрольного объёма» (англ. control volume)[39], который ограничен воображаемой неподвижной контрольной[40] поверхностью, проницаемой для вещества, но оставляющей неизменной заключённый в ней объём. В то же время закрытую систему называют «контрольной массой» (англ. control mass). Последнее название подчеркивает постоянство массы (





Энергия контрольного объёма)
Если в системе присутствуют несколько различных веществ характеризующихся массами 

Удельная энтальпия[править | править код]
| Удельная энтальпия | |
|---|---|
 |
|
| Размерность |
 |
| Единицы измерения | |
| СИ | Дж/кг |
| СГС | эрг/г |
| Примечания | |
| Внесистемные единицы: кал/г, кал/кг |
| Молярная (мольная) энтальпия | |
|---|---|
 |
|
| Размерность |
 |
| Единицы измерения | |
| СИ |
Дж/моль ( кг/моль) кг/моль) |
| СГС |
эрг/моль ( 1 г/моль) 1 г/моль) |
| Примечания | |
| Внесистемная единица: кал/моль |
| Плотность энтальпии | |
|---|---|
 |
|
| Размерность |
 |
| Единицы измерения | |
| СИ | Дж/м3 |
| СГС | эрг/см3 |
Вместо экстенсивной величины энтальпии часто используют её отношение 

Соотношение для полного дифференциала удельной энтальпии можно получить, разделив уравнение для дифференциала энтальпии на 
(Дифференциал удельной энтальпии)
Удельную энтальпию можно представлять графически в виде 


Вводят также молярную (мольную) энтальпию 



Плотности внутренней энергии и энтальпии (на единицу объёма) вводят как отношение этих величин к объёму. Отдельные обозначения для этих величин здесь не вводятся, их можно выразить через удельные величины и массовую плотность:
Деление уравнения для дифференциала энергии контрольного объёма на величину контрольного объёма даёт соотношение[47]:
(Дифференциал плотности энергии)
Плотность энергии и энтальпии идеального газа[править | править код]
Для идеального газа с постоянной теплоёмкостью плотность внутренней энергии и энтальпии простым образом выражается через давление[48]:
где 


Энтальпия сложных термодинамических систем[править | править код]
Для термодинамических систем сложного типа, в которых термодинамическая работа[50] не сводится к работе внешних сил давления 
где 






Обобщенная энтальпии сохраняет смысл эквивалента теплоты для изобарного процесса[54][55], если не только давление, но и все остальные обобщённые силы поддерживаются постоянными: 
Энтальпия образования[править | править код]
Для приложений к химии в общем случае открытых систем для полного дифференциала энтальпии получаем:
Выражение для 
где 


Подставив это выражение в соотношение (***), получаем дифференциальную версию фундаментального уравнения Гиббса для энтальпии:
Все химические реакции сопровождаются выделением (экзотермические) или поглощением (эндотермические) тепла. Одно из приложений энтальпии основано на том, что множество химических процессов в реальных или лабораторных условиях реализуются именно при постоянном (атмосферном) давлении. Поэтому мерой теплового эффекта реакции служит изменение энтальпии ΔН в ходе химической реакции, в результате которой исходные вещества исчезают и образуются продукты реакции. В случае экзотермических реакций система теряет тепло и ΔН — величина отрицательная. В случае эндотермических реакций система поглощает тепло и ΔН — величина положительная. В частности, энтальпия образования — это количество теплоты, которое поглощается (если энтальпия образования положительна) или выделяется (если энтальпия образования отрицательна) при образовании сложного вещества из простых веществ.
Значение энтальпии образования и другие термодинамические свойства веществ приведены в справочниках[58][59].
Зависимость энтальпии от температуры[править | править код]
Во многих приложениях (но только не в качестве термодинамического потенциала!) энтальпию системы удобно представлять в виде функции 




Температурная производная энтропии выражается через (измеримую) теплоёмкость при постоянном давлении 


Для идеального газа в силу закона Гей-Люссака
(Энтальпия идеального газа)
где 


Для реальных систем изменение энтальпии при изменении температуры в изобарическом процессе практически удобно рассчитывать, если известна теплоёмкость при постоянном давлении 


Поскольку разности энтальпий продуктов химической реакции и исходных веществ определяет тепловой эффект химической реакции[⇨], разность теплоёмкостей продуктов реакции и исходных веществ определяет зависимость теплового эффекта реакции от температуры (термохимический закон Кирхгофа).
Сохранение энтальпии в эффекте Джоуля — Томсона[править | править код]
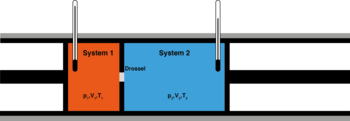
Рис. 2 — Сохранение энтальпии в эффекте Джоуля — Томсона. Изменение энергии газа в ходе этого процесса равно работе: 

Сохранение энтальпии в процессе Джоуля — Томсона привлекается для количественного описания эффекта. Схема процесса представлена на рисунке 2. Левый поршень, вытесняя газ под давлением 








Из уравнения для дифференциала энтальпии выводится выражение для коэффициента Джоуля — Томсона 

![{displaystyle C_{P}mathrm {d} T+left[V-Tleft({frac {partial V}{partial T}}right)_{P}right]mathrm {d} P=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10e30be2110fa951c716fb887b72bb50a0fe82b4)
а выражение для дифференциала энтальпии в переменных 
В процессе Джоуля — Томсона давление всегда убывает, следовательно, энтропия возрастает.
Полная энергия и полная энтальпия[править | править код]
| Полная энтальпия (удельная) (энтальпия торможения) |
|
|---|---|
 |
|
| Размерность |
 |
| Единицы измерения | |
| СИ | Дж/кг |
| СГС | эрг/г |
| Примечания | |
| Зависит от выбора системы отсчёта |
Для движущихся тел помимо внутренней энергии, включающей кинетическую энергию теплового движения составляющих тело частиц (измеренную в системе координат, в которой тело как целое покоится), вводят также его полную энергию в системе координат, относительно которой тело движется со скоростью 

(Дифференциал полной энергии)
где 



Обобщение дифференциала плотности энергии для полной энергии принимает вид[47]:
(Дифференциал плотности полной энергии)
Релятивистская энтальпия[править | править код]
| Полная энтальпия (инвариантная релятивистская) |
|
|---|---|
 |
|
| Размерность |
 |
| Единицы измерения | |
| СИ | Дж |
| СГС | эрг |
| Примечания | |
| Лоренц-инвариант |
| Полная энтальпия (релятивистская) |
|
|---|---|
 |
|
| Размерность |
 |
| Единицы измерения | |
| СИ | Дж |
| СГС | эрг |
| Примечания | |
Образует 4-вектор вместе с импульсом  |
Если скорость тела 


Релятивистская полная энергия 




В неподвижной системе отсчета энтальпия и импульс движущегося тела[68][67]
образуют 4-вектор, а инвариантная энтальпии в движущейся с телом системы отсчёта даётся инвариантной функцией этого 4-вектора:
Именно полная энтальпия (а не энергия) релятивистского тела оказывается аналогом энергии релятивистской частицы. Давление 

является следствием Лоренцева сокращения. Уравнение релятивистской термодинамики даётся выражением[68]:
Оно позволяет решить любой вопрос термодинамики движущихся систем, если известна функция 


Энтальпия в гидродинамике[править | править код]
| Механика сплошных сред |
|---|
 |
| Сплошная среда |
|
Классическая механика Закон сохранения массы · Закон сохранения импульса |
|
Теория упругости Напряжение · Тензор · Твёрдые тела · Упругость · Пластичность · Закон Гука · Реология · Вязкоупругость |
|
Гидродинамика Жидкость · Гидростатика · Гидродинамика · Вязкость · Ньютоновская жидкость · Неньютоновская жидкость · Поверхностное натяжение |
|
Основные уравнения Уравнение непрерывности · Уравнение Эйлера · Уравнение Громеки — Лэмба · Уравнение Бернулли · Уравнения Навье — Стокса · Уравнение вихря · Уравнение диффузии · Закон Гука |
| См. также: Портал:Физика |
Энтальпия играет большую роль в гидродинамике, науке о движениях жидкостей и газов (в гидродинамике газы тоже называют жидкостями). Течения идеальной жидкости (то есть без вязкости и теплопроводности) описываются следующими уравнениями в частных производных[69]:
(Уравнение непрерывности)
(Уравнение Эйлера)
где 








(Уравнение Эйлера, выраженное через энтальпию)
Такое представление обладает значительными преимуществами, поскольку в силу «адабатичности» течения идеальной жидкости, задаваемого уравнением сохранения энтропии:
член в уравнении Эйлера, связанный с градиентом энтропии, во многих случаях не даёт вклада в рассчитываемые эффекты.
Поток энергии[править | править код]
Выражение для дифференциала плотности полной энергии позволяет получить скорость изменения последней[47]:
Интеграл Бернулли[править | править код]
Из приведённых здесь термодинамических соотношений для энтальпии следует простой вывод интеграла Бернулли и в наиболее общей его форме. Закон утверждает, что вдоль линии тока для стационарного течения идеальной жидкости[70] сохраняется следующая величина:
где 



Вывод закона Бернулли из уравнения Эйлера и термодинамических соотношений
1. В уравнении Эйлера для стационарного (


2. Скалярное произведение этого уравнения на единичный вектор 
так как произведение градиента на единичный вектор даёт производную по направлению 
3. Выражение для Дифференциала удельной энтальпии даёт:
так что
В стационарном течении идеальной жидкости все частицы, движущиеся вдоль данной линии тока, имеют одинаковую энтропию[71] (
См. также[править | править код]
- Тепловой эффект химической реакции
- Удельная теплота плавления
Комментарии[править | править код]
- ↑ В России определение энтальпии
как суммы
закреплено действующими стандартами[7][8].
- ↑ Это соотношение носит название дифференциальной формы фундаментального уравнения Гиббса для энтальпии закрытой термодеформационной системы[12][13][14].
- ↑ Энтальпию, заданную в виде функции её естественных независимых переменных, называют интегральной формой фундаментального уравнения Гиббса[15][16][17] для энтальпии закрытой термодеформационной системы[12][18][19].
- ↑ В термодинамике при написании частных производных внизу справа указывают переменные, который при вычислении производной считают постоянным. Причина в том, что в термодинамике для одной и той же функции используют различные наборы независимых переменных, которые, во избежание неопределённости, приходится перечислять.
- ↑ Число частиц в закрытой системе тоже может быть переменным, например числе фотонов равновесного излучения в полости с абсолютно чёрными стенками[34].
- ↑ Использование масс независимых компонентов, а не масс составляющих систему веществ, позволяет учитывать химические превращения в системе без явного рассмотрения протекающих в ней химических реакций (см. статью Химическая термодинамика).
- ↑ Энергия
включает в себя энергию химической связи и вносит значительный вклад в энтальпию образования[⇨] газообразных сложных веществ
Примечания[править | править код]
- ↑ 1 2 3 Энтальпия // Большая российская энциклопедия. Том 35. Москва, 2017, стр. 396.
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, §14. Тепловая функция.
- ↑ 1 2 3 Зубарев Д. Н., Энтальпия, 1992.
- ↑ Горшков В. И., Кузнецов И. А., Основы физической химии, 2009, с. 111.
- ↑ Enthalpy, H // IUPAC Gold Book.
- ↑ Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин, 1984, с. 13.
- ↑ §113-04-21. Энтальпия (Н)//ГОСТ IEC 60050-113-2015 (2015). Дата обращения: 1 декабря 2018.
- ↑ §54. Энтальпия(теплосодержание)//ГОСТ Р 57700.4-2017 (2017). Дата обращения: 1 декабря 2018.
- ↑ Зубарев Д. Н., Термодинамика, 1992.
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (12.3).
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (16.3).
- ↑ 1 2 Белов Г. В., Термодинамика, ч. 1, 2017, с. 155.
- ↑ Степановских Е. И. и др., Химическая термодинамика в вопросах и ответах, 2014, с. 37.
- ↑ Мечковский Л. А., Блохин А. В., Химическая термодинамика, ч. 1, 2012, с. 124.
- ↑ Борщевский А. Я., Физическая химия, т. 1, 2017, с. 312.
- ↑ Воронин Г. Ф., Основы термодинамики, 1987, с. 76.
- ↑ Мюнстер А., Химическая термодинамика, 2002, с. 90—91.
- ↑ Белов Г. В., Термодинамика, ч. 2, 2016, с. 23.
- ↑ Зарубин Д. П., Физическая химия, 2017, с. 45.
- ↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, с. 67.
- ↑ Dalton, 1909.
- ↑ Гиббс Дж. В., Термодинамические работы, 1950, Примечание 3, с. 448.
- ↑ 1 2 Howard, 2002, с. 697.
- ↑ Ахметов Б. В. и др. Физическая и коллоидная химия, 1986, с. 64.
- ↑ Гиббс Дж. В., Термодинамика. Статистическая механика, 1982, с. 96, 510.
- ↑ Henderson, Douglas; Eyring, Henry; Jost, Wilhelm. Physical Chemistry: An Advanced Treatise (неопр.). — Academic Press, 1967. — С. 29.
- ↑ Dalton, 1909, с. 863.
- ↑ Laidler (англ.) (рус.; Keith. The World of Physical Chemistry (англ.). — Oxford University Press, 1995. — P. 110.
- ↑ Van Ness, 2003, с. 486.
- ↑ Зубарев Д. Н., Потенциал термодинамический, 1994, с. 89.
- ↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, §45. Термодинамические функции.
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (14.4).
- ↑ Беляев Н. М., Термодинамика, 1987, с. 126.
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, §63. Чёрное излучение.
- ↑ 1 2 Зубарев Д. Н., Термодинамика, 1992.
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнения (24.5–7).
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (15.7).
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (24.11).
- ↑ Automotive Encyclopedia, 2015, §1.1.2.2. Open dynamic system, с. 27.
- ↑ Белов Г. В., Термодинамика, ч. 1, 2017, с. 11.
- ↑ Automotive Encyclopedia, 2015, Уравнение (15), с. 28.
- ↑ Мюнстер А., Химическая термодинамика, 2002, с. 103.
- ↑ Кубо Р., Термодинамика, 1970, с. 24—25.
- ↑ Поль Р. В., Механика, акустика и учение о теплоте, 2013, с. 446.
- ↑ Поль Р. В., Механика, акустика и учение о теплоте, 2013, с. 449–451.
- ↑ Quantities, Units and Symbols in Physical Chemistry (англ.). IUPAC (2015). Дата обращения: 7 декабря 2018. Архивировано из оригинала 11 февраля 2014 года.
- ↑ 1 2 3 Ландау Л. Д., Лифшиц Е. М. Гидродинамика, 2015, §6. Поток энергии.
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнения (42.5), (43.2) и (43.4).
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, §63.
- ↑ Зубарев Д. Н., Работа в термодинамике, 1994.
- ↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, §12.
- ↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, Уравнение (45.21).
- ↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, Уравнение (45.25).
- ↑ Борщевский А. Я., Физическая химия, т. 1, 2017, с. 121.
- ↑ Базаров И. П., Термодинамика, 2010, с. 113.
- ↑ Артемов А. В., Физическая химия, 2013, с. 23.
- ↑ Ипполитов Е. Г. и др., Физическая химия, 2005, с. 35.
- ↑ Search for Species Data by Chemical Formula (англ.). Дата обращения: 3 декабря 2018.
- ↑ Термодинамические свойства. Дата обращения: 3 декабря 2018.
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (43.4).
- ↑ Пригожин И., Дефэй Р., Химическая термодинамика, 2009, с. 51.
- ↑ Алабовский А. Н., Недужий И. А., Техническая термодинамика и теплопередача, 1990, с. 25—26.
- ↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, Уравнение (19.3).
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (18.1).
- ↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, Уравнение (46.1).
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (18.2).
- ↑ 1 2 3 4 Зубарев Д. Н., Релятивистская термодинамика, 1994.
- ↑ 1 2 3 Каллен Г., Горвиц Дж., Релятивистская термодинамика, 1972.
- ↑ 1 2 Ландау Л. Д., Лифшиц Е. М. Гидродинамика, 2015, Уравнение (2.4).
- ↑ Вишневецкий С. Л., Бернулли уравнение, 1988, с. 187.
- ↑ Седов Л. И. Механика сплошной среды, 1970, Глава VII. §2. Функция давления.
Литература[править | править код]
- Алабовский А. Н., Недужий И. А. Техническая термодинамика и теплопередача. — 3-е изд., пераб. и доп. — Киев: Выща школа, 1990. — 256 с. — ISBN 5-11-001997-5.
- Ансельм А. И. Основы статистической физики и термодинамики. — 2-е изд., стереотип. — СПб.: Лань, 2007. — 427 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-0756-9.
- Артемов А. В. Физическая химия. — М.: Академия, 2013. — 288 с. — (Бакалавриат). — ISBN 978-5-7695-9550-9.
- Ахметов Б. В., Новиченко Ю. П., Чапурин В. И. Физическая и коллоидная химия. — Л.: Химия, 1986. — 320 с.
- Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.—Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
- Белов Г. В. Термодинамика. Часть 1. — 2-е изд., испр. и доп. — М.: Юрайт, 2017. — 265 с. — (Бакалавр. Академический курс). — ISBN 978-5-534-02731-0.
- Белов Г. В. Термодинамика. Часть 2. — М.: Юрайт, 2016. — 249 с. — (Бакалавриат). — ISBN 978-5-9916-7252-8.
- Беляев Н. М. Термодинамика. — Киев: Вища школа, 1987. — 344 с.
- Болгарский А. В., Мухачев Г. А., Щукин В. К. Термодинамика и теплопередача. — 2-е изд., перераб. и доп. — М.: Высшая школа, 1975. — 496 с.
- Борщевский А. Я. Физическая химия. Том 1 online. Общая и химическая термодинамика. — М.: Инфра-М, 2017. — 868 с. — (Высшее образование: Бакалавриат). — ISBN 978-5-16-104227-4.
- Буданов В. В., Максимов А. И. Химическая термодинамика / Под ред. О. И. Койфмана. — 3-е изд., стер. — СПб.: Лань, 2017. — 320 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-2271-5.
- Вишневецкий С. Л. Бернулли уравнение // Физическая энциклопедия. — Большая Российская энциклопедия, 1988. — Т. 5: Стробоскопические приборы — Яркость. — С. 187.
- Воронин Г. Ф. Основы термодинамики. — М.: Изд-во Моск. ун-та, 1987. — 192 с.
- Гамбург Ю. Д. Химическая термодинамика. — М.: Лаборатория знаний, 2016. — 237 с. — (Учебник для высшей школы). — ISBN 978-5-906828-74-3.
- Герасимов Я. И., Древинг В. П., Еремин Е. Н. и др. Курс физической химии / Под общ. ред. Я. И. Герасимова. — 2-е изд., испр. — М.: Химия, 1970. — Т. 1. — 592 с.
- Гиббс Дж. В. Термодинамические работы / Пер. с англ. под ред. проф. В. К. Семенченко. — М. — Л.: Гостехиздат, 1950. — 492 с. — (Классики естествознания).
- Гиббс Дж. В. Термодинамика. Статистическая механика / Отв. ред. Д. Н. Зубарев. — М.: Наука, 1982. — 584 с. — (Классики науки).
- Горшков В. И., Кузнецов И. А. Основы физической химии. — 3-е изд. — М.: Бином. Лаборатория знаний, 2009. — 408 с. — ISBN 978-5-94774-375-3.
- Еремин В. В., Каргов С. И., Успенская И. А. и др. Основы физической химии. Теория и задачи. — М.: Экзамен, 2005. — 481 с. — (Классический университетский учебник). — ISBN 5-472-00834-4.
- Зарубин Д. П. Физическая химия. — М.: Инфра-М, 2017. — 474 с.
- Зубарев, Д. Н. Потенциал термодинамический // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга-Робертсона эффект — Стримеры. — С. 89—91. — 704 с. — ISBN 5-85270-087-8.
- Зубарев, Д. Н. Работа в термодинамике // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга-Робертсона эффект — Стримеры. — С. 193. — 704 с. — ISBN 5-85270-087-8.
- Зубарев, Д. Н. Релятивистская термодинамика // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга-Робертсона эффект — Стримеры. — С. 333—334. — 704 с. — ISBN 5-85270-087-8.
- Зубарев Д. Н. Термодинамика // Физическая энциклопедия / Ред.А. М. Прохоров. — М.: Большая Советская Энциклопедия, 1992. — Т. 5. — С. 83—87.
- Зубарев Д. Н. Энтальпия // Физическая энциклопедия / Ред. А. М. Прохоров. — М.: Большая Советская Энциклопедия, 1992. — Т. 5. — С. 616.
- Ипполитов Е. Г., Артемов А. В., Батраков В.В. Физическая химия / Под ред. Е. Г. Ипполитова. — М.: Академия, 2005. — 448 с. — (Высшее профессиональное образование). — ISBN 978-5-7695-1456-6.
- Каллен Г., Горвиц Дж. Релятивистская термодинамика // Успехи Физических Наук : журнал. — 1972. — Т. 107, вып. 7. — С. 489—502. — doi:10.3367/UFNr.0107.197207g.0489.
- Колесников И. М., Винокуров В. А. Термодинамика физико-химических процессов. — 2-е, перераб. и доп. — М.: Нефть и газ, 2005. — 480 с. — ISBN 5-7246-0351-9.
- Кубо Р. Термодинамика. — М.: Мир, 1970. — 304 с.
- Ландау Л. Д., Лифшиц Е. М. Гидродинамика. — Издание 6-е, исправленное. — М.: Физматлит, 2015. — 728 с. — («Теоретическая физика», том VI). — ISBN 978-5-9221-1625-1.
- Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1. — Издание 5-е. — М.: Физматлит, 2002. — 616 с. — («Теоретическая физика», том V). — ISBN 5-9221-0054-8.
- Мечковский Л. А., Блохин А. В. Химическая термодинамика. В двух частях. Часть 1. Феноменологическая термодинамика. Основные понятия, фазовые равновесия. — Минск: Издательство БГУ, 2012. — 141 с. — ISBN 978-985-518-635-0.
- Мюнстер А. Химическая термодинамика / Пер. с нем. под. ред. чл.-корр. АН СССР Я. И. Герасимова. — 2-е изд., стереотип. — М.: УРСС, 2002. — 296 с. — ISBN 5-354-00217-6.
- Новиков И. И. Термодинамика. — 2-е изд., испр. — СПб.: Лань, 2009. — 592 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-0987-7.
- Поль Р. В. Механика, акустика и учение о теплоте. — Рипол Классик, 2013. — 490 с. — ISBN 5458431251, 9785458431255.
- Пригожин И., Дефэй Р. Химическая термодинамика / Пер. с англ. под ред. В. А. Михайлова. — 2-е изд.. — М.: Бином. Лаборатория знаний, 2009. — 533 с. — (Классика и современность. Естествознание). — ISBN 978-5-9963-0201-7.
- Савельев И. В. Курс общей физики. — М.: КноРус, 2012. — Т. 1. Механика. Молекулярная физика и термодинамика. — 528 с. — ISBN 9785406025888.
- Свиридов В. В., Свиридов А. В. Физическая химия. — СПб.: Лань, 2016. — 597 с. — ISBN 978-5-8114-2262-3.
- Седов Л. И. Механика сплошной среды. — М.: Наука, 1970. — Т. 2. — 568 с.
- Сивухин Д. В. Общий курс физики. — Издание 5-е, исправленное. — М.: Физматлит, 2005. — Т. II. Термодинамика и молекулярная физика. — 544 с. — ISBN 5-9221-0601-5.
- Степановских Е. И., Брусницына Л. А., Маскаева Л. Н. Химическая термодинамика в вопросах и ответах. — Екатеринбург: Уральский издательско-полиграфический центр, 2014. — 221 с. — ISBN 978-5-4430-0061-9.
- Сычёв В. В. Сложные термодинамические системы. — 5-е изд., перераб. и доп. — М.: Издательский дом МЭИ, 2009. — 296 с. — ISBN 978-5-383-00418-0.
- Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин / Отв. ред. И. И. Новиков. — АН СССР. Комитет научно-технической терминологии. Сборник определений. Вып. 103. — М.: Наука, 1984. — 40 с.
- Хаазе Р. Термодинамика необратимых процессов / Пер. с нем. под ред. А. В. Лыкова. — М.: Мир, 1967. — 544 с.
- Хачкурузов Г. А. Основы общей и химической термодинамики. — М.: Высшая школа, 1979. — 268 с.
- Dalton J. P. Researches on the Joule-Kelvin effect, especially at low temperatures. I. Calculations for hydrogen // KNAW Proceedings. — 1909. — Т. 11. — С. 863—873.
- Howard Irmgard K. H Is for Enthalpy, Thanks to Heike Kamerlingh Onnes and Alfred W. Porter (англ.) // Journal of Chemical Education : журнал. — 2002. — Vol. 79, iss. 6. — P. 697—698. — ISSN 0021-9584. — doi:10.1021/ed079p697.
- Van Ness Hendrick C. H Is for Enthalpy (англ.) // Journal of Chemical Education : журнал. — 2003. — Vol. 80, iss. 5. — P. 486. — ISSN 0021-9584. — doi:10.1021/ed080p486.1.
- Part 1 : Engines — Fundamentals // Encyclopedia of Automitive Engineering / Editors-in-Chief : David Crolla, David E. Foster, Toshio Kobayashi, Nicolas Vaughan. — John Wiley & Sons, 2015. — Т. 1. — 607 с. — ISBN 978-0-470-97402-5.
Энтальпия. Этому элементу I–d диаграммы я посвятил отдельную тему, потому как для меня этот элемент являлся наименее понятным среди остальных (температуры, влагосодержания и относительной влажности) и требующим разбора других попутных понятий.
Продублирую рисунок из прошлой статьи http://mrcynognathus.livejournal.com/7641.html:
Не буду глубоко вдаваться в терминологию, скажу лишь, что я понимаю энтальпию воздуха, как энергию, которую хранит в себе определенный объем воздуха. Эта энергия является потенциальной, то есть в условии равновесия воздух не тратит эту энергию и не поглощает её из других источников.
Не буду даже приводить пример для разъяснения своего определения (хотя хотел), потому как, по моему мнению, это запутает и уведет в сторону.
Сразу к делу – что главное мы можем взять из энтальпии? – отвечаю – энергию (или количество теплоты), которую нужно передать воздуху, чтобы нагреть его или отнять, чтобы его охладить (или осушить).
Например, у нас есть задача – посчитать какой мощности нам нужен калорифер, чтобы осенью или весной подать в помещение 1200 м3/ч нагретого до температуры плюс 20 градусов наружного воздуха. Расчетная температура наружного воздуха в переходный период – плюс 10 градусов при энтальпии 26,5 кДж/кг (по СП 60.13330.2012).
Задача решается легко. Для того чтобы решить такую простую задачку используя и-д диаграмму, нам необходимо ввести в уровень понимания единицы измерения некоторых физических величин:
1) Энтальпия – килоДжоуль/килограмм . То есть количество потенциальной энергии в одном килограмме воздуха. Здесь все просто – если энтальпия равна 20, то это означает, что в одном килограмме данного воздуха находится 20 килоджоулей потенциальной теплоты или 20000 джоулей.
2) Мощность калорифера – Ватты, но в то же время ватты можно разложить на Джоуль/секунда. То есть, сколько может выдать калорифер энергии за одну секунду. Чем больше энергии нам сможет выдать калорифер за секунду, тем он мощнее. И тут все просто.
Итак, берем I–d диаграмму и ставим на ней точку наружного воздуха. После, проводим прямую линию вверх (идет нагрев воздуха без изменения влагосодержания).
Мы получаем точку на j–d диаграмме с температурой плюс 20 градусов и энтальпией 36,5 кДж/кг. Возникает вопрос – что, же, черт возьми, нам дальше делать с этой гребанной информацией?! 🙂
Во первых, обратим внимание на то, что мы производили все операции с одним килограммом воздуха (это косвенно видно по единице измерения энтальпии кДж/кг).
Во вторых, у нас был килограмм воздуха с 26,5 кДж, а стал с 36,5 кДж потенциальной энергии. То есть килограмму воздуха сообщили 10 кДж для того чтобы его температура поднялась с плюс 10 градусов до плюс двадцати.
Дальше мы переведем 1200 м3/ч в кг/с(килограммы/секунда, т.к. на I–d диаграмме используются эти единицы измерения), умножив 1200 на 1,25 кг/м3 (один метр кубический десятиградусного воздуха весит 1,25 килограмма), что даст нам 1500 кг/ч, а затем разделив на 3600 (обратите внимание на логику перевода между системами – делим мы на 3600 не потому что мы так зазубрили или запомнили, а потому что за секунду у нас воздуха пройдет меньше чем за час, меньше в 3600 раз) получаем итог 0,417 кг/с.
Идем дальше. Мы получили, что за одну секунду проходит 0,417 кг воздуха. И мы знаем, что каждому килограмму необходимо передать (сообщить) 10 кДж для того, чтобы нагреть его до температуры плюс 20 градусов. Сообщаем, умножая 0,417 кг/с на 10 кДж/кг, и получая 4,17 кДж/с (килограммы сократились) или 4170 Дж/с, что равно 4170 Вт (определено нами ранее по тексту). Вот мы и получили мощность нашего калорифера.
Кондиционирование
Охлаждение происходит по тому же принципу, но только немного сложнее из-за выделения влаги из воздуха.
Выделение влаги (конденсата) из воздуха происходит тогда, когда температура воздуха при охлаждении достигает точки росы на линии относительной влажности 100%. В предыдущей статье я описал этот процесс: http://mrcynognathus.livejournal.com/7641.html
Вроде бы, нет ничего сложного – охлаждаем воздух с температурой плюс 20 градусов и относительной влажностью 50% до плюс 12 градусов (как это обычно происходит в сплит-системах), проводя прямую вертикально вниз из точки 20-ти градусного воздуха до точки 12-ти градусного воздуха.
И что мы видим – никаких влаговыделений. Влагосодержание осталось на прежнем уровне – 8 г/кг. Но мы то знаем, что при работе кондиционера идет обильное влаговыделение (конденсат активно капает из дренажной трубки, выведенной на фасад здания) – этот факт подтверждается неоднократным наблюдением гуляющего по летним улицам.
Возникает вопрос – откуда же влага? Ответ: дело в том, что через внутренний блок кондиционера проходят медные трубки, которые охлаждаются хладагентом до температур, которые ниже плюс 12 градусов, и в связи с этим охлаждаемый воздух делится на слои с различной температурой, примерно как на рисунке ниже (предположим, что трубки охлаждаются до плюс 5 градусов). Сразу скажу, что это далекий от действительности, но показывающий общий смысл вышесказанных мною слов рисунок (прошу меня за него не ругать)
Поэтому из того воздуха, который соприкасается с трубками(и оребрением) и выпадает влага. А тот воздух, что не успел охладиться до точки росы, или успел, но избежал контакта с охлажденной поверхностью, минует процесс влаговыделения и несет в себе столько же влаги, сколько он нес в себе до охлаждения (по сути).
Для того чтобы провести правильную прямую процесса охлаждения воздуха в таком охладителе (где температура хладагента ниже температуры точки росы), нам необходимо учесть каждый воздушный поток с различными тепловлажностными параметрами воздуха и найти на графике точки смешения всех этих потоков – что по моему мнению – не реально (у меня просто не хватит мозгов на это)! Но…
…Я пришел к вот такому решению (скорее всего не я такой один) – у нас есть температура входящего воздуха, есть температура хладагента и есть температура получаемого воздуха, и я считаю, что нам достаточно провести линию процесса охлаждения части воздуха до плюс 5 градусов и найти точку смешения 5-ти градусного воздуха и 20-ти градусного воздуха. То есть, я предполагаю, что проходя через внутренний блок кондиционера, воздух делится на два потока – тот, который охлаждается до плюс пяти градусов и выдает нам наибольшее количество влаги, и тот который вообще не охлаждается, а на выходе эти два потока смешиваются и образуют поток воздуха с температурой плюс 12 градусов и определенным влагосодержанием.
Я считаю, что для достижения тех целей, которые я преследую, результата, полученного при таком упрощении, вполне достаточно. А какие же цели я преследую?
Первая цель – это определение максимального влаговыделения для того, чтобы рассчитать систему конденсатоотвода (особенно актуально это при системах кондиционирования, в составе которых две и более охлаждающих установок)
Вторая цель – учесть количество холода, идущего на перевод воды из газообразного состояния в жидкое (на конденсацию влаги; так назывемая скрытая холодопроизводительность). Особенно актуально это при охлаждении (отведении тепла) во влажных помещениях. Например, нам необходимо отвести от определенного насоса 2 кВт тепла, которые он выделяет в помещение. Если мы не учтем, что помещение влажное (влажное, по каким либо причинам) и установим в помещение сплит-систему мощностью 2,5 кВт, то мы можем получить (при определенных условиях), что сплит-система тратит 1 кВт лишь для того, чтобы перевести пар во влагу, а на удаление теплоизбытков тратит оставшиеся 1,5 кВт, что меньше на 500 Вт необходимого, и что может привести к перегреву насоса и скорого его выхода из строя.
Итак, делим поток на два потока, один из которых охлаждаем до плюс пяти – отрезок 1-2, а другой оставляем не тронутым – точка 1.
Смешиваем эти два потока, объединяя получившиеся точки прямой 1-3-2, и находим нашу 12-ти градусную точку на получившейся прямой.
Оставляем прямую 1-3 как линию процесса охлаждения воздуха в сухом охладителе с температуры плюс 20 градусов до плюс 12 градусов с выделением конденсата.
Для того чтобы узнать количество конденсата, выпавшего на оребрении и трубках охладителя нам необходимо вычесть влагосодержание получившегося воздуха из влагосодержания необработанного воздуха 7,3 г/кг – 6,3 г/кг. В итоге мы получим, что из каждого килограмма прошедшего через охладитель воздуха выделится 1 грамм конденсата. Чтобы узнать расход конденсата, нам необходимо узнать, сколько килограммов воздуха проходит через теплообменник за определенное время. Например, если нам необходимо охладить 1400 м3/ч воздуха с температуры плюс 20 градусов с относительной влажностью 50% до температуры плюс 12 градусов, то мы переведем 1400 м3/ч в 1680 кг/ч и получим, что за час обработки воздуха выделится 1680 грамм конденсата (по одному грамму на каждый килограмм воздуха), что равно 0,47 г/с (грамм/секунда) и 0,47 * 10-3 кг/с.
Полная холодопроизводительность находится так же, как мы искали теплопроизводительность калорифера ранее. Берем энтальпию начальной точки 28 кДж/кг, вычитаем из нее энтальпию конечной точки 38,5 кДж/кг, получая отрицательное число 10,5 кДж/кг (минус указывает на то, что энергия отдается хладагенту). Переводим 1680 кг/ч в килограмм/секунда, что будет равняться 0,47 кг/с. В итоге получаем 4,935 кДж/с, что равно 4,935 кВт мощности.
Подпишись на мой YouTube-канал FAN-tastiK – канал о проектировании Вентиляции, Кондиционирования и Отопления
Если есть необходимость определить скрытую холодопроизводительность , можно найти её, отталкиваясь от количества выделенного конденсата, используя удельную теплоту парообразования:
Теплота, требуемая для конденсации влаги, находится по формуле: Q = L * m,
где L – удельная теплота парообразования; m – масса влаги.
L воды равно: 2260 кДж/кг.
Для того, чтобы перевести 0,47 грамма воды из газообразного состояния в жидкое состояние за секунду нам требуется 2260 Дж * 103 * 0,47 кг/с * 10-3 = 1063 Дж/с, что равно 1063 Вт.
Итак скрытая холодопроизводительность данного процесса равна 1063 Вт.
Это Все
Собственно, это все, что я хотел рассмотреть в данной статье. Прошу не бранить меня за наивную упрощенность описанного мною – я постарался объяснить в первую очередь себе – что такое энтальпия и как ей пользоваться. Надеюсь Вам было интересно и полезно. Спасибо за внимание.
P.S. Эта статья не в коем случае не является учебным пособием. Она лишь мое субъективное видение вопроса. Я бы даже сказал – каждое слово, написанное в этой статье, является ошибочным. Информацию, достойную носить звание “Научная истина” ищите в учебниках.
P.P.S Предыдущая статья, в которой я описывал собственное видение таких элементов I-d диаграммы (диаграммы Рамзина) как температура, влагосодержание, относительная влажность находится здесь:
http://mrcynognathus.livejournal.com/7641.html
Знать Удельная энтальпия По сравнению с энтальпией системы необходимо знать общее теплосодержание системы, а также массу системы.
Этальпия системы определяется как сумма ее внутренней энергии и произведения давления и объема системы, где удельная энтальпия определяется как энтальпия на единицу массы.
Энтальпия системы определяется как
Н = Э + ПВ,
Где,
H = энтальпия
E = внутренняя энергия
PV = выполненная работа по объему давления
В приведенном выше выражении для всех практических целей значение PV незначительно или довольно мало, а энтальпия состоит в основном из содержания внутренней энергии.
Трудно рассчитать внутреннюю энергию в абсолютном выражении, и для инженерных расчетов первостепенное значение имеет изменение энтальпии или удельной энтальпии, и они учитываются.
Eнтальпия изменения часто используются в химии для расчета теплоты реакций. Для экзотермической реакции, протекающей с выделением тепла, изменение энтальпии считают положительным.
Для эндотермической реакции, протекающей с поглощением тепла, изменение энтальпии считают отрицательным. Теплоту реакции можно рассчитать по изменению энтальпии между реагентами и их продуктами при стандартных состояниях (25°C и давление 1 атмосфера).
Энтальпия является экстенсивным свойством, что означает, что энтальпия зависит от размера или массы системы, тогда как удельная энтальпия является интенсивная недвижимость что означает, что оно зависит от типа системы или вещества и не зависит от его размера.
Удельная энтальпия против энтальпии:
Сравнительный анализ удельной энтальпии и энтальпии показан ниже:
| энтальпия | Удельная энтальпия |
| Энтальпия есть сумма ее внутренняя энергия и выполненная работа по объему давления | Удельная энтальпия – это энтальпия на единицу массы. |
| Энтальпия является экстенсивным свойством, т.е. ее значение зависит от размера вещества. | Удельная энтальпия является интенсивным свойством, т.е. ее значение не зависит от размера или массы системы или вещества, а только от его вида. |
| Энтальпия определяется в джоулях или килоджоулях в единицах СИ. | Удельная энтальпия определяется как джоули/кг или килоджоули/кг. |
Удельная энтальпия пароводяной системы
Eнтальпия является свойством системы и специфично для определенной температуры или давления. Например, удельная энтальпия парообразования воды при атмосферном давлении составляет 2257 кДж/кг.
Точно так же для насыщенной воды удельная энтальпия составляет 419 кДж/кг при атмосферном давлении. Таким образом, для насыщенный пар при атмосферном давлении удельная энтальпия равна
hs = 2676 кДж/кг = hw + he
hw = Sp энтальпия насыщенной воды
he = Sp энтальпия испарения воды
hs = Sp энтальпия насыщенного пара
Это значение удельной энтальпии увеличивается с увеличением давления в системе.
Для перегретого пара при определенной степени перегрева удельная энтальпия определяется по формуле:
hss = чs + сps (tss – тf), Где,
hss = энтальпия пересыщенного пара
hs = энтальпия насыщенного пара
Cps = Sp теплота пара при постоянном давлении
tss = температура перегретого пара
tf = температура насыщения
Молярная энтальпия против удельной энтальпии
Молярная энтальпия обозначает энтальпию на моль вещества, а удельная энтальпия обозначает энтальпию на единицу массы вещества.
| Молярная энтальпия | Удельная энтальпия |
| Молярная энтальпия – это энтальпия на единицу молей вещества. | Массовая энтальпия – это энтальпия на единицу массы вещества. |
| Молярная энтальпия обычно используется для расчета изменения энтальпии на единицу молей реагента в реакции. Расчет основан на стехиометрическом соотношении числа молей, необходимого для завершения реакции, и общей энтальпии, необходимой для завершения реакции.Конкретный Энтальпия обычно используется в технике для расчета теплового баланса в промышленных установках, где скорости потока рассчитываются по массе. Следовательно, зная удельную энтальпию, можно составить тепловой баланс системы. | |
| Единицей молярной энтальпии является кДж/моль в системе СИ. | Единицей удельной энтальпии является кДж/кг в единицах СИ. |
| Чтобы рассчитать общую энтальпию изменения, количество молей вещества, претерпевающего физическое изменение, умножается на молярную энтальпию. | Чтобы рассчитать общую энтальпию изменения, массу вещества, подвергающегося физическому/изменению, умножают на удельную энтальпию. |
Различные типы изменения энтальпии
Изменение энтальпии происходит, когда материя претерпевает физическое превращение или химическое изменение. Различные изменения энтальпии описаны ниже:
Энтальпия реакции: Энтальпия изменяется в том месте, когда один моль реагента превращается в продукт.
Энтальпия сгорания: изменение энтальпии, которое происходит, когда один моль вещества реагирует с кислородом и полностью сгорает.
Энтальпия образования: изменение энтальпии, которое происходит, когда один моль соединения образуется из его основных составляющих элементов.
Энтальпия нейтрализации: изменение энтальпии, происходящее при образовании одного моля воды после реакции кислоты с основанием.
Энтальпия раствора: изменение энтальпии, которое происходит, когда один моль растворенного вещества полностью растворяется в растворителе, избытке которого образуется раствор.
Энтальпия плавления: изменение энтальпии, необходимое для полного перехода одного моля вещества из твердого состояния в жидкое.
Энтальпия сублимации: изменение энтальпии, необходимое для полного перехода одного моля вещества из твердого состояния в газообразное.
Энтальпия испарения: изменение энтальпии, необходимое для полного перехода одного моля вещества из жидкого состояния в газообразное.
Энтальпия смешения: изменение энтальпии при смешивании двух химических веществ без какой-либо химической реакции между ними.
Что такое благоприятная энтальпия?
По законам природы благоприятное изменение энтальпии отрицательно..
Это означает, что реакция предпочтительнее, если изменение энтальпии отрицательно или реакция является экзотермической. Однако спонтанность реакции или благоприятность реакции также должны зависеть от того, каково изменение энтропии.
Когда идет реакция, всегда благоприятно, если система теряет энергию или изменение энтальпии отрицательно. С другой стороны, законом природы является увеличение энтропии системы. Следовательно, реакция благоприятна, если она приводит к увеличению энтропии системы.
Если происходит реакция, которая приводит к увеличению энтропии, но также и к увеличению энтальпии, то благоприятность реакции зависит от вклада каждого компонента.
Этот ответ в данном случае количественно обеспечивается другим выражением, называемым свободной энергией Гиббса, как показано ниже:
ΔG = ΔH –TΔS
Где,
ΔG = изменение свободной энергии Гиббса
ΔH = изменение энтальпии
ΔS = изменение энтропии
T = температура в Кельвинах
В приведенном выше уравнении реакция благоприятна, если свободная энергия Гиббса отрицательна. Фактически реакция протекает самопроизвольно. С другой стороны, реакция не может протекать самопроизвольно, если свободная энергия Гиббса положительна.
Мера энергии в термодинамической системе
Энтальпия (послушать ) термодинамической системы определяемым как сумма внутренней энергии системы и произведения ее давления и объема. Это удобная функция состояния , предпочтительная во время измеренийх в химических, биологических и физических системах при постоянном давлении. Термин «давление-объем» выражает работу, для физических размеров системы, для освобождения места для нее перемещением ее окружения. Функция состояния энтальпия зависит только от окончательной конфигурации внутренней энергии, давления и объема, а не от пути выбора ее достижений.
Единицей измерения энтальпии в Международной системе единиц (СИ) является джоуль. Другие исторические условные единицы, которые еще используются, включая британские тепловые единицы (БТЕ) и калорий.
. Полная энтальпия системы не может быть измерена напрямую, поскольку внутренняя энергия содержит компоненты, которые неизвестны., труднодоступны или не интереса для термодинамики. Практическое изменение энтальпии (ΔH) является предпочтительным методом измерения для измерения при постоянном давлении, поскольку оно упрощает описание передачи энергии. Когда переносится в систему, предотвращается изменение энтальпии равно энергии, передаваемой с окружающей средой за счет тепла. Для калибровки изменений энтальпии устанавливается конкретная и удобная точка отсчета. Энтальпии химических веществ при постоянном давлении обычно состояние к стандартному состоянию : чаще всего давление 1 бар (100 кПа). Стандартное состояние не определяет температуру строго, но выражения для обычно стандартной энтальпии образования при 25 ° C (298 K). Для эндотермических изменений ΔH является положительным и отрицательным в экзотермических (выделяющих тепло) процессов.
Энтальпия идеального газа не зависит от его давления и зависит только от его температуры, которая коррелирует с его внутренней энергией. Реальные газы при обычных температурах и давлениях часто очень близки к этому поведению, что упрощает практическое термодинамическое проектирование и анализ.
Содержание
- 1
- 2 Другие выражения
- 2.1 Кардинальные функции
- 3 Физическая интерпретация
- 4 Отношение к теплу
- 5 Приложения
- 5.1 Теплота реакции
- 5.2 Удельная энтальпия
- 5.3 Изменения энтальпии
- 5.4 Открытые системы
- 6 Диаграммы
- 6.1 Некоторые базовые приложения
- 6.2 Дросселирование
- 6.3 Компрессоры
- 7 История
- 8 См. Также
- 9 Примечания
- 10 Ссылки
- 11 Библиография
- 12 Внешние ссылки
Определение
Энтальпия H термодинамической системы определяется как сумма ее внутренней энергии U и работы, необходимой для достижения своего давления и объема:
- H = U + pV,
, где p – давление, а V – объем системы.
Энтальпия – это обширное свойство ; он пропорционален размеру системы (для однородных систем). В качестве интенсивных свойств, удельная энтальпия h = H / м относится к единице массы м системы, а молярная энтальпия H m – H / n, где n – количество молей. Для неоднородных систем энтальпия – это сумма энтальпий составляющих подсистем:
- H = ∑ k H k, { displaystyle H = sum _ {k} H_ {k},}
где
- H – полная энтальпия всех подсистема,
- относится к различным подсистемам,
- Hkотносится к энтальпии каждой подсистемы.
Замкнутая система может находиться в термодинамическом равновесии в статике гравитационное поле, так что его давление p непрерывно изменяется с высотой, в то время как из-за требований равновесия его температура T инвариантна с высотой. (Соответственно, плотность гравитационной потенциальной энергии система также изменяется с высотой.) Суммирование энтальпий становится интегралом :
- H = ∫ (ρ h) d V, { displaystyle H = int ( rho h) , dV,}
где
- ρ (“rho “) – плотность (масса на единицу объема),
- h – удельная энтальпия (на единицу массы),
- (ρh) представляет собой плотность энтальпии (энтальпия на единицу массы),
- dV означает бесконечно Элемент объема в системе, например, объем бесконечно тонкого горизонтального слоя,
- интеграл, следовательно, представляет собой сумму энтальпий всех элементов объема.
Энтальпия замкнутой однородной системы – это ее кардинальная функция состояния энергии H (S, p), с переменными состояниями естественного, ее энтропия S [p] и ее давление p. Дифференциальное соотношение для него можно вывести следующим образом. Мы начнем с первого закона термодинамики для замкнутых систем для бесконечно малого процесса:
- d U = δ Q – δ W, { displaystyle dU = delta Q- delta W,}
где
- ΔQ – небольшое количество тепла, добавляемого к системе,
- ΔW – небольшое количество работы, выполняемой системой.
В гомогенной системе, в которой только обратимо, или квазистатические процессы, второй закон термодинамики дает ΔQ = T dS, где T – абсолютная температура, а dS – бесконечно малое изменение энтропии S системы. Кроме того, если выполняется только работа pV, ΔW = p dV. В результате
- d U = T d S – pd V. { displaystyle dU = T , dS-p , dV.}
Добавление d (pV) к обеим сторонам этого выражения дает
- d U + d (п V) знак равно T d S – пд V + d (п V), { displaystyle dU + d (pV) = T , dS-p , dV + d (pV),}
или
- d (U + p V) = T d S + V дп. { displaystyle d (U + pV) = T , dS + V , dp.}
Итак,
- d H (S, p) = T d S + V d p. { displaystyle dH (S, p) = T , dS + V , dp.}
Другие выражения
Приведенное выше выражение dH в терминах энтропии и давления может быть незнакомо некоторым читателям. Однако есть выражения для более привычных чисел, таких как температура и давление:
- d H = C p d T + V (1 – α T) d p. { displaystyle dH = C_ {p} , dT + V (1- alpha T) , dp.}
Здесь C p – теплоемкость при постоянном давлении и α – коэффициент (кубического) теплового расширения :
- α = 1 V (∂ V ∂ T) p. { displaystyle alpha = { frac {1} {V}} left ({ frac { partial V} { partial T}} right) _ {p}.}
С помощью этого выражения можно, в принципе, определить энтальпию, если C p и V известны как функции p и T.
Обратите внимание, что для идеального газа, αT = 1, так что
- d H = C pd T. { displaystyle dH = C_ {p} , dT.}
В более общей форме первой законной внутренней компетенции дополнительными, включающими химический потенциал и количество различных типов. Тогда отличное выражение для dH становится
- d H = T d S + V dp + ∑ i μ id N i, { displaystyle dH = T , dS + V , dp + sum _ {i} mu _ {i} , dN_ {i},}
где μ i – химический потенциал на частицу для частиц i-типа, а N i – количество таких частиц. Последний член также может быть записан как μ idni(с dn i количество молей компонента i, добавленных в систему, и, в этом случае, μ i молярный химический потенциал) или как μ idmi(при dm i масса компонента i, добавленного в систему, и, в этом случае, μ i удельный химический потенциал).
Кардинальные функции
Энтальпия H (S [p], p, {N i }) выражает термодинамику в системе энергетического представлении. Как функция состояния, ее аргументы включают в себя как одну интенсивную, так и несколько расширенных число состояний. Переменные состояния S [p], p и {N i } называются переменными естественного состояния в этом представлении. Они подходят для описания, в котором они экспериментально контролируются. Например, в идеализированном процессе S [p] и p можно контролировать, предотвращает процесс переноса тепла и вещества, заключенную систему в диатермическую и проницаемую для вещества стенку, и делает бесконечно медленным и изменяя только внешнее давление на поршень, регулирующее объем системы. Это основа так называемого адиабатического приближения, которое используется в метеорологии.
Наряду с энтальпией, с этими аргументами, другая кардинальная функция состояния термодинамической системы ее энтропия, как функция S [p] (H, p, {N i }) того же списка состояний, за исключением того, что энтропия, S [p], заменяется в списке на энтальпия, H. Она выражает представление энтропии. Переменные состояния H, p и {N i } называются переменными естественного состояния в этом представлении. Они подходят для описания, в котором они экспериментально контролируются. Например, H и p можно регулировать, допуская теплопередачу и изменяя только внешнее давление на поршень, которое задает объем системы.
Физическая интерпретация
Термин U может интерпретироваться как энергия, необходимая для создания системы, а термин pV как работа, которая потребовалась бы, чтобы «освободить место» для системы, если давление окружающей среды оставалось постоянным. Когда система, например, n моль газа объем V при давлении p и температуре T, создается или создается действие в его текущем состоянии. от абсолютного нуля, необходимо подавать энергию, равную его внутреннюю энергию U плюс pV, где pV – работа, совершенная при отталкивании от окружного (атмосферного) давления.
В программе физика и статистической механике может быть более интересным изучением внутренних свойств системы, и поэтому используется внутренняя энергия. В данном химии эксперименты часто используются при постоянном атмосферном давлении, а работа «давление-объем» представляет собой энергией с атмосферой, к которой нельзя получить доступ или нельзя контролировать, так что ΔH – это выражение, выбранное для теплоты реакции.
Для теплового двигателя изменение его внутренней представляет собой разницу подводимой и теплотой работой объема давления, выполненной рабочим веществом, а изменение его энтальпии – это разница между тепловложением и работой, выполненной двигателем:
- d H = δ Q – δ W { displaystyle dH = delta Q- delta W}
где работа W, выполняемая двигателем, равно:
- W = – ∮ pd V { displaystyle W = – oint pdV}
Отношение к теплу
Чтобы обсудить связь между вызывающими энтальпии и подвода тепла, мы возвращаемся к первому закону для замкнутых систем с условным обозначением физических знаков : dU = δQ – δW, где тепло δQ передает ся за счет теп лопроводности, излучения и излучения Джоуля нагреватель. Применим его к частному случаю с постоянным давлением на поверхности. В этом случае рабочий член можно разделить на два вклада, так называемую работу pV, определяемую как p dV (где p – давление на поверхности, dV – увеличение объема системы), и так называемая работа pV. – так называемая изохорная механическая работа δW ‘, такая как перемешивание валом с лопастями или внешним магнитным полем, действующим на внутренний ротор. Случаи дальнодействующего электромагнитного взаимодействия требует состояний в своей формулировке и здесь не исследуется. Итак, мы пишем δW = p dV + δW ′. В этом случае первый закон гласит:
- d U = δ Q – p d V – δ W ′. { displaystyle dU = delta Q-p , dV- delta W ‘.}
Итак,
- d H = d U + d (p V). { Displaystyle dH = dU + d (pV).}
Итак,
- d H = δ Q + V dp + pd V – pd V – δ W ′ { displaystyle dH = delta Q + V , dp + p , dV-p , dV- delta W ‘}
- = δ Q + V dp – δ W ′. { displaystyle , , = delta Q + V , dp- delta W ‘.}
- = δ Q + V dp – δ W ′. { displaystyle , , = delta Q + V , dp- delta W ‘.}
Согласно физическому соглашению о знаках, δW’ < 0, because изохорическая работа, выполняемая система на Систему системы координат энергии и может действовать как фактически добавляющая тепло. Единственная термодинамическая механическая работа, выполняемая система, – это работа расширения, p dV.
Система находится под постоянным давлением (dp = 0). Следовательно, увеличение энтальпии системы равно добавленному и виртуальному теплу:
- d H = δ Q – δ W ‘. { displaystyle dH = delta Q- delta W ‘.}
Вот почему в 19 веке использовался устаревший термин теплосодержание.
Приложения
В термодинамике можно вычислить энтальпию, определив требования для создания системы из «ничего»; Требуется механическая работа, pV, различается в зависимости от условий, которые возникают при создании термодинамической системы.
Энергия должна подаваться для удаления частиц из окружающей среды, чтобы освободить место для создания системы, предполагая, что давление p остается постоянным; это термин pV. Подаваемая энергия должна также обеспечивать изменение внутренней энергии U, которое включает в себя активацию энергии ионизации, химические связи и так далее. Вместе они составляют изменение энтальпии U + pV. Для систем с постоянным давлением внешняя работа не выполняется, кроме работы pV, изменение энтальпии – это тепло, получаемое системой.
Для простой системы с постоянным числом частиц разница в энтальпии представляет собой максимальное количество тепловой энергии, получаемой в результате давления термодинамического процесса, в котором поддерживается постоянным давлением.
Теплота реакция
Полная энтальпия системы не может быть измерена напрямую; вместо этого измените изменение энтальпии системы системы. Изменение энтальпии определяется следующим уравнением:
- Δ H = H f – H i, { displaystyle Delta H = H _ { mathrm {f}} -H _ { mathrm {i}},}
где
- ΔH – «изменение энтальпии»,
- Hf- конечная энтальпия системы (химическая – энтальпия продуктов),
- Hi- начальная энтальпия (в системе химической реакции, энтальпия реагентов).
Для экзотермической энергии реакции при постоянном давлении изменение энтальпии системы равно, выделяемой энергии, включая энергию, остающуюся в системе и потеря из-за расширения против своего окружения. Аналогичным образом для эндотермической реакции изменение энтальпии системы равно энергии, поглощенной в реакции, включая энергию, потерянную систему и полученную при нагрузке из окружающей среды. Если ΔH положительно, реакция эндотермическая, то есть тепло поглощается системой из-за продуктов, имеющей большую энтальпию, чем реагенты. С другой стороны, если ΔH отрицательное, реакция экзотермической, то есть общее снижение энтальпии за счет выделения тепла.
Из определения энтальпии как H = U + pV энтальпия изменение при постоянном давлении ΔH = ΔU + p ΔV. Однако для правительства используется более подходящий член p ΔV намного меньше, чем изменение внутренней энергии ΔU, как показано на ΔH. Например, для сжигания окиси углерода 2 CO (г) + O 2 (г) → 2 CO 2 (г), ΔH = −566,0 кДж и ΔU = – 563, 5 кДж. Различия между малы, энтальпии часто в общих чертах описываются как энергия и анализируются в терминах энергий связи.
Удельная энтальпия
Удельная энтальпия однородной системы определяется как h = H / м, где m – масса системы. Единица СИ для удельной энтальпии – джоуль на килограмм. Это может быть выражено в других величинах, как h = u + pv, где u – удельная внутренняя энергия, p – давление, а который v – удельный объем, равенство 1 / ρ, где ρ – плотность.
Изменения энтальпии
Изменение энтальпии изменение составления, наблюдаемое в части термодинамической системы, когда они подвергаются превращению или реакции. Это разница между энтальпией после завершения процесса, то есть энтальпией продуктов, и начальной энтальпией системы, а именно реагентов. Эти процессы обратимы, и энтальпия обратного процесса отрицательной величиной прямого изменения.
Обычным стандартным изменением энтальпии является энтальпия образования, которая была определена для большого количества веществ. Изменения энтальпии обычно измеряются и собираются в справочниках по химическим и физическим веществам, например в Справочнике по химии и физике CRC. Ниже представлена подборка изменений энтальпии, общепризнанных в термодинамике.
При использовании в этих признанных терминах квалификатора обычно опускается, и свойство просто называют энтальпией «процесса». Эти свойства часто используются в качестве эталонных значений, очень часто их цитируют для стандартизованного набора параметров окружающей среды или стандартных условий, включая:
- A температуру 25 ° C или 298,15 K, <479.>давление одной атмосферы (1 атм или 101,325 кПа),
- A содержание 1,0 М, когда элемент или соединение присутствует в растворе,
- Элементы или соединения в их нормальных физических состояниях, то есть стандартное состояние.
Для таких стандартизованных значений название энтальпии обычно предваряется термином «стандарт», например стандартная энтальпия образования.
Химические свойства:
- Энтальпия реакции, определяемая как изменение энтальпии, наблюдаемое в компоненте термодинамической системы, когда один моль вещества вступает в реакцию полностью.
- Энтальпия образования, определяет, как изменяется энтальпии, наблюдаемое в составном элементе термодинамической системы, когда один моль соединения образуется из его элементарных предшественников.
- Энтальпия сгорания, определяемая как изменение энтальпии, наблюдаемое в составной части термодинамической системы, когда один моль вещества полностью сгорает с кислородом.
- Энтальпия гидрирования, определяемая как изменение энтальпии, наблюдаемое в компоненте термодинамической системы, когда один моль ненасыщенного соединения полностью реагирует с избытком водорода с образованием насыщенное соединение.
- Энтальпия распыления, необходимая для изменения энтальпии, необходимое для полного распыления одного моля соединения.
- Энтальпия нейтрализации, определяемая как изменение энтальпии, наблюдаемое в компоненте термодинамической системы, когда при взаимодействии и основания образует один моль воды.
- Стандарт Энтальпия раствор, определяемая как изменение энтальпии, наблюдаемое в компоненте терментеодинамической системы, когда один моль раствор вещества полностью растворяется в избытке растворителя, так что раствор находится в состоянии бесконечного разбавления.
- Стандартная энтальпия денатурации (биохимия), определяемая как изменение энтальпии, для необходимого денатурировать один моль соединения.
- Энтальпия гидратации, определяемая как изменение энтальпии, наблюдаемое, когда один моль газообразных благоприятных условий полностью растворяется в воде, образуя один моль водных видов.
Физические свойства:
- Энтальпия плавления, определяемое как изменение энтальпии, необходимое для полного изменения состояния одного моля вещества между твердым и жидким состояниями.
- Энтальпия испарения, важная как изменение энтальпии, необходимое для полного изменения состояния один моль вещества жидкостью и газомом.
- Энтальпия сублимации, важная как изменение энтальпии, необходимое для полного изменения состояния одного моля вещества твердым и газообразным состояниями.
- Энтальпия решетки, определяемая как энергия, необходимая для разделения моль ионного соединения на отдельные газообразные ионы на бесконечное расстояние друг от друга (что означает отсутствие силы притяжения).
- Энтальпия смешения, определяемая как изменение энтальпии при смешивании (не реагирующих) химических веществ.
Открытые системы
В термодинамических открытых систем масса (вещества) может вливаться и выходить за границы. Первый закон термодинамики для открытого системного гласит: увеличение внутренней энергии системы как количество энергии, добавленной к системе за счет втекающей массы и нагревания, за вычет количества, теряемого за счет истечения массы и в форме работы, выполненной системой:
- d U = δ Q + d U вход – d U выход – δ W, { displaystyle dU = delta Q + dU _ { text {in}} – dU _ { text {out}} – delta W,}
где U in – средняя внутренняя энергия, поступающая в систему, а U out – средняя внутренняя энергия, выходящая из системы.

Область, ограниченная границами Открытая система обычно называется контрольным объемом, она может соответствовать или не соответствовать физическим стенам. Если бы поток массы в системе работал, то если бы он приводил в движение поршневую жидкость, то система работала бы над потоком массы в системе. Таким образом, выполняются два типа работы: описанная выше работа потока выполняется с жидкостью (это также называется работой pV), и работа вала, которая может на каком-либо механическом устройстве.
Эти два типа работы выражены в уравнении
- δ W = d (p out V out) – d (p in V in) + δ W вал. { displaystyle delta W = d (p _ { text {out}} V _ { text {out}}) – d (p _ { text {in}} V _ { text {in}}) + delta W_ { text {вал}}.}
Подстановка контрольного объема (cv) в приведенном выше уравнении дает:
- d U cv = δ Q + d U in + d (p in V in) – d U out – d (p out V out) – δ Ш вал. { displaystyle dU _ { text {cv}} = delta Q + dU _ { text {in}} + d (p _ { text {in}} V _ { text {in}}) – dU _ { text {out}} – d (p _ { text {out}} V _ { text {out}}) – delta W _ { text {вал}}.}
Определение энтальпии, H, позволяет нам использовать этот термодинамический потенциал для учета внутренней энергии и pV работы в жидкостях для открытых систем:
- d U cv = δ Q + d H in – d H out – δ W вал. { displaystyle dU _ { text {cv}} = delta Q + dH _ { text {in}} – dH _ { text {out}} – delta W _ { text {вал}}.}
Если мы позволяем также границы перемещаться (например, из-за движущихся поршней), мы получаем довольно общую форму первого закона для открытых систем. В терминах производных по времени он выглядит так:
- d U dt = ∑ k Q ˙ k + ∑ k H ˙ k – ∑ kpkd V kdt – P, { displaystyle { frac {dU} {dt}} = сумма _ {k} { dot {Q}} _ {k} + sum _ {k} { dot {H}} _ {k} – sum _ {k} p_ {k} { frac {dV_ {k}} {dt}} – P,}
с суммой по различным местам k, где подается тепло, потоки массы в систему и перемещение границ. Члены Ḣ k представляют потоки энтальпии, которые можно записать как
- H ˙ k = hkm ˙ k = H mn ˙ k, { displaystyle { dot {H}} _ {k} = h_ { k} { dot {m}} _ {k} = H _ { mathrm {m}} { dot {n}} _ {k},}
с ṁ k массовый расход и k молярный расход в положении k соответственно. Член dV k / dt представляет скорость изменения объема системы в позиции k, которая приводит к мощности pV, создаваемой системой. Параметр P представляет все другие формы мощности, производимой системой, такие как мощность на валу, но это также может быть, например, электроэнергия, производимая электростанцией.
Обратите внимание, что предыдущее выражение верно, только если скорость потока кинетической энергии сохраняется между входом и выходом системы. В противном случае его необходимо включить в баланс энтальпии. Во время установившейся работы устройства (см. турбина, насос и двигатель ) может быть установлено среднее значение dU / dt равно нулю. Это дает полезное выражение для средней выработки для этих устройств в отсутствие химических факторов:
- P = ∑ k ⟨Q ˙ k⟩ + ∑ k ⟨H ˙ k⟩ – ∑ k ⟨pkd V kdt⟩, { displaystyle P = sum _ {k} left langle { dot {Q}} _ {k} right rangle + sum _ {k} left langle { dot {H}} _ {k} right rangle – sum _ {k} left langle p_ {k} { frac {dV_ {k}} {dt}} right rangle,}
где угловые скобки обозначают средние по времени. Техническое значение энтальпии связано с ее присутствием в первом законе для открытого, изложенного выше.
Диаграммы

Значения энтальпии важных веществ могут быть получены с использованием коммерческого программного обеспечения. Практически все соответствующие материалы можно получить в табличной или графической форме. Существует много типов диаграмм, которые показывают различные функции температуры для различных давлений, и диаграммы h – p, которые показывают различные функции для T. Одна из наиболее распространенных диаграмм – температурно-удельная энтропийная диаграмма (T – s диаграмма). Он дает кривую плавления и значения насыщенной жидкости и пара вместе с изобарами и изентальпами. Эти диаграммы являются мощным инструментом инженера-теплотехника.
Некоторые базовые приложения
Точки с a по h на рисунке играют роль в обсуждении в этом разделе.
-
Точка T (K) p (бар) s (кДж / (кг · K)) h (кДж / кг) a 300 1 6,85 461 b 380 2 6,85 530 c 300 200 5,16 430 d 270 1 6.79 430 e 108 13 3.55 100 f 77,2 1 3.75 100 g 77.2 1 2.83 28 h 77.2 1 5.41 230
Точки e и g – насыщенные жидкости, а точка h – насыщенный газ.
Дросселирование
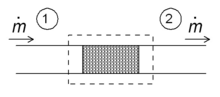
Одним из простых приложений концепции энтальпии является так называемый процесс дросселирования, также известный как <Расширение Джоуля-Томсона. Это касается адиабатического потока жидкости через сопротивление потоку (клапан, пористую пробку или другой тип сопротивления потока), как показано на рисунке. Этот процесс очень важен, поскольку он основан на основе бытовых холодильников, где он отвечает за перепад температур между температурой окружающей среды и внутренней частью холодильника. Это также заключительный этап во многих типах.
Для установившегося режима потока энтальпия системы (пунктирный прямоугольник) должна быть постоянной. Следовательно,
- 0 = mh 1 – m ˙ h 2. { displaystyle 0 = { dot {m}} h_ {1} – { dot {m}} h_ {2}.}
Временный массовый расход постоянен, удельные энтальпии на двух сторонах потока сопротивления одинаковы:
- h 1 = h 2, { displaystyle h_ {1} = h_ {2},}
то есть энтальпия на единицу массы не изменяется во время дросселирования. Следствия этого отношения можно использовать с помощью приведенной выше диаграммы T – s. Точка c находится при 200 бар и комнатная температура (300 К). Расширение Джоуля-Томсона от 200 бар до 1 барана постоянной постоянной энтальпии 425 кДж / кг (не показано на диаграмме), лежащей между изентальпами 400 и 450 кДж / кг, и заканчивается в точке d, который находится при температуре около 270 К. Следовательно, расширение от 200 бар до 1 бар охлаждает азот с 300 К до 270 К. В клапане существует большое трение и создается много энтропии, но все же конечная температура ниже начального значения.
Точка e выбрана так, чтобы она находилась на линии насыщенной жидкости с h = 100 кДж / кг. Это примерно соответствует p = 13 бар и T = 108 K. Дросселирование от точки до давления 1 бар заканчивается в этой двухфазной области (точка f ). Это означает, что смесь газа и жидкости покидает дроссельный клапан. Максимальная энтальпия в f(hf), точная энтальпия в g(hg), умноженная на жидкую долю в f(xf), плюс энтальпию в h(hh), умноженную на долю газа в f . (1 – х f). Итак,
- h f = x f h g + (1 – x f) h h. { displaystyle h _ { mathbf {f}} = x _ { mathbf {f}} h _ { mathbf {g}} + (1-x _ { mathbf {f}}) h _ { mathbf {час}}. }
С числами: 100 = x f× 28 + (1 – x f) × 230, поэтому x f= 0,64. Это означает, что массовая доля жидкости в газожидкостной смеси, покидающая дроссельный клапан, составляет 64%.
Компрессоры

. как электрическая мощность. Если сжатие адиабатическое, температура газа повышается. В обратимом случае это будет при постоянной энтропии, что соответствует вертикальной линии на диаграмме T – s. Например, сокращение выбросов азота от 1 бара (точка a ) до 2 бар (точка b ) приведет к повышению температуры с 300 K до 380 K. Выход газа при температуре окружающей среды T a, теплообмен, например охлаждающей водой, необходимо. В идеальном случае воздействия изотермическое. Средний тепловой поток в обществе составляет Q̇. Система находится в установившемся состоянии, первый закон дает
- 0 = – Q ˙ + m ˙ h 1 – m ˙ h 2 + P. { displaystyle 0 = – { dot {Q}} + { dot {m }} h_ {1} – { dot {m}} h_ {2} + P.}
Минимальная мощность, необходимая для реагирования реализуется, если сжатие обратимое. В этом случае второй закон термодинамики для открытых систем дает
- 0 = – Q ˙ T a + m ˙ s 1 – m ˙ s 2. { displaystyle 0 = – { frac { dot { Q}} {T _ { mathrm {a}}}} + { dot {m}} s_ {1} – { dot {m}} s_ {2}.}
Исключение Q̇ дает для минимальной мощности
- P min m ˙ = h 2 – h 1 – T a (s 2 – s 1). { displaystyle { frac {P _ { text {min}}} { dot {m}}} = h_ {2} -h_ {1} -T _ { mathrm {a}} (s_ {2} -s_ {1}).}
Например, сжатие 1 кг азота от 1 до 200 бар стоит не менее (h c- h a) – T a(sc- s a). По данным, полученным с помощью диаграммы T – s, находим значение (430 – 461) – 300 × (5,16 – 6,85) = 476 кДж / кг.
Соотношение мощности можно дополнительно упростить, записав его как
- P min m ˙ = ∫ 1 2 (d h – T a d s). { displaystyle { frac {P _ { text {min}}} { dot {m}}} = int _ {1} ^ {2} (dh-T _ { mathrm {a}} , ds).}
При dh = T ds + v dp это приводит к окончательному соотношению
- P min m ˙ = ∫ 1 2 vdp. { displaystyle { frac {P _ { text {min}}} { dot {m}}} = int _ {1} ^ {2} v , dp.}
История
Термин энтальпия был введен относительно поздно в истории термодинамики, в начале 20 века. Энергия была представлена в современном понимании Томасом Янгом в 1802 году, а энтропия была придумана Рудольфом Клаузиусом в 1865 году. корень греческого слова ἔργον (эргон), означающего «работа», чтобы выразить идею способности выполнять работу. В энтропии используется греческое слово τροπή (тропе), означающее преобразование. В энтальпии используется корень греческого слова θάλπος (thalpos) «тепло, тепло»
Термин выражает устаревшую концепцию теплосодержания, поскольку dH относится к количеству тепла, полученному в процессе только при постоянном давлении, но не в общем случае, когда давление является переменным. Джозайя Уиллард Гиббс для ясности использовал термин «тепловая функция для постоянного давления».
Введение понятия «теплосодержание» H связан с Бенуа Полем Эмилем Клапейроном и Рудольфом Клаузиусом (соотношение Клаузиуса-Клапейрона, 1850).
Термин энтальпия впервые появился в печати в 1909 году. Его приписывают Хайке Камерлинг-Оннес, которая, скорее всего, представила его устно годом ранее, на первом заседании Института холода в г. Париж. Он получил распространение только в 1920-х годах, в частности с Таблицами и диаграммами пара Молье, опубликованными в 1927 году.
До 1920-х годов символ H использовался несколько непоследовательно для обозначения «тепла». в общем. Определение H как строго ограниченного энтальпией или «теплосодержанием при постоянном давлении» было официально предложено Альфредом У. Портером в 1922 году.
См. Также
- Стандартное изменение энтальпии образования (таблица данных)
- Калориметрия
- Калориметр
- Функция отклонения
- Закон Гесса
- Изентальпический процесс
- Законы термодинамики
- Энтальпия застоя
- Термодинамические базы данных для чистых веществ
Примечания
Ссылки
Библиография
- Dalton, JP (1909). «Исследования эффекта Джоуля – Кельвина, особенно при низких температурах. I. Расчеты для водорода» (PDF). KNAW Proceedings. 11 : 863–873. Bibcode : 1908KNAB… 11..863D.
- Haase, R. (1971). Йост, W. (ред.). Физическая химия: расширенный трактат. Нью-Йорк: Академ. п. 29.
- Гиббс, Дж. У. Собрание сочинений Дж. Уилларда Гиббса, Vol. I (изд. 1948 г.). Нью-Хейвен, Коннектикут: Издательство Йельского университета. п. 88.
- Ховард И. К. (2002). «H для энтальпии, спасибо Хайке Камерлинг-Оннес и Альфреду В. Портеру». Дж. Chem. Образов. 79(6): 697–698. Bibcode : 2002JChEd..79..697H. doi : 10.1021 / ed079p697.
- Лэйдлер, К. (1995). Мир физической химии. Оксфорд: Издательство Оксфордского университета. п. 110.
- Киттель, С.; Кремер, Х. (1980). Теплофизика. Нью-Йорк: S. R. Furphy Co., стр. 246.
- ДеХофф Р. (2006). Термодинамика в материаловедении. CRC Press. ISBN 9780849340659 .
Внешние ссылки
- Энтальпия – Мир физики Эрика Вайсштейна
- Энтальпия – Государственный университет Джорджии
- Пример расчета энтальпии – Химический факультет Техасского университета AM
Как читать таблицы водяного пара
Если вы едете по неизвестной местности, вам понадобится карта или навигатор, если вы летите на самолете, вам не обойтись без расписания полётов. Так и таблицы водяного пара необходимы всем пользователям в индустрии пара. В этой статье мы познакомимся с таблицами пара, рассмотрим их виды и немного поговорим о присутствующих в них элементах.
Таблицы насыщенного водяного пара
Таблицы насыщенного водяного пара — необходимый инструмент для любого инженера, работающего с паром. Обычно их используют для определения зависимости температуры насыщенного пара от парового давления или, наоборот, давления от температуры насыщенного пара. Кроме этих параметров, таблицы обычно включают и другие показатели, такие как удельная энтальпия (h) и удельный объём (v).
Данные таблиц насыщенного водяного пара всегда отображают информацию о конкретной точке насыщения известной как точка кипения. Это точка, в которой вода (жидкость) и пар (газ) могут сосуществовать при одинаковых температуре и давлении. Так как H2O может быть и в жидком, и в газообразном состоянии, нам будут необходимы две подборки данных: данные о насыщенной воде (жидкости), которые обычно обозначаются подстрочной буквой f, и данные о насыщенном паре (газе), которые обозначают подстрочной буквой g.
Пример таблицы насыщенного пара
Обозначения:
- P = Давление пара/воды
- T = Точка насыщения пара/воды (точка кипения)
- vf = Удельный объём насыщенной воды (жидкости)
- vg = Удельный объём насыщенного пара (газа)
- hf = Удельная энтальпия насыщенной воды (энергия, необходимая для подогрева воды от 0 °C до точки кипения)
- hfg = Скрытое тепло испарения (энергия, необходимая для трансформации насыщенной воды в насыщенный пар)
- hg = Удельная энтальпия насыщенного пара (энергия, необходимая для получения пара из воды с температурой 0 °C)
* Источник: 1999 таблицы пара Японского общества инженеров-механиков
При нагреве обычно используется скрытое тепло испарения (Hfg). Как видно из таблицы, это скрытое тепло испарения будет выше при более низком давлении. По мере увеличения парового давления скрытое тепло постепенно снижается и достигает 0 при суперкритическом давлении, например, 22.06 МПа.
Полезно знать
Два формата: на основе давления и температуры
Так как давление и температура насыщенного пара напрямую связаны друг с другом, таблицы пара обычно доступны в двух форматах: на основе давления и температуры. В обоих содержится одинаковая информация, но классифицирована она по-разному.
Таблица насыщенного водяного пара, основанная на давлении
| Давл. (изб.) | Темп. | Удельный объём | Удельная энтальпия | |||
|---|---|---|---|---|---|---|
| кПа изб. | °C | м3/кг | кДж/кг | |||
| P | T | Vf | Vg | Hf | Hfg | Hg |
| 0 | 99.97 | 0.0010434 | 1.673 | 419.0 | 2257 | 2676 |
| 20 | 105.10 | 0.0010475 | 1.414 | 440.6 | 2243 | 2684 |
| 50 | 111.61 | 0.0010529 | 1.150 | 468.2 | 2225 | 2694 |
| 100 | 120.42 | 0.0010607 | 0.8803 | 505.6 | 2201 | 2707 |
Таблица насыщенного водяного пара, основанная на температуре
| Темп. | Давл. (изб.) | Удельный объём | Удельная энтальпия | |||
|---|---|---|---|---|---|---|
| °C | кПа изб. | м3/кг | кДж/кг | |||
| T | P | Vf | Vg | Hf | Hfg | Hg |
| 100 | 0.093 | 0.0010435 | 1.672 | 419.1 | 2256 | 2676 |
| 110 | 42.051 | 0.0010516 | 1.209 | 461.4 | 2230 | 2691 |
| 120 | 97.340 | 0.0010603 | 0.8913 | 503.8 | 2202 | 2706 |
| 130 | 168.93 | 0.0010697 | 0.6681 | 546.4 | 2174 | 2720 |
| 140 | 260.18 | 0.0010798 | 0.5085 | 589.2 | 2144 | 2733 |
| 150 | 374.78 | 0.0010905 | 0.39250 | 632.3 | 2114 | 2746 |
Разные единицы измерения: избыточное и абсолютное давление
Таблицы насыщенного пара также используют два различных вида давления: абсолютное и манометрическое (избыточное).
- Абсолютное давление — это нулевая точка по отношению к абсолютному вакууму.
- Манометрическое давление — это нулевая точка по отношению к атмосферному давлению (101.3 кПа).
Таблица насыщенного пара с абсолютным давлением
| Давл. (абс.) | Темп. | Удельный объём | Удельная энтальпия | |||
|---|---|---|---|---|---|---|
| кПа | °C | м3/кг | кДж/кг | |||
| P | T | Vf | Vg | Hf | Hfg | Hg |
| 0 | — | — | — | — | — | — |
| 20 | 60.06 | 0.0010103 | 7.648 | 251.4 | 2358 | 2609 |
| 50 | 81.32 | 0.0010299 | 3.240 | 340.5 | 2305 | 2645 |
| 100 | 99.61 | 0.0010432 | 1.694 | 417.4 | 2258 | 2675 |
Таблица насыщенного пара с избыточным давлением
| Давл. (изб.) | Темп. | Удельный объём | Удельная энтальпия | |||
|---|---|---|---|---|---|---|
| кПа изб. | °C | м3/кг | кДж/кг | |||
| P | T | Vf | Vg | Hf | Hfg | Hg |
| 0 | 99.97 | 0.0010434 | 1.673 | 419.0 | 2257 | 2676 |
| 20 | 105.10 | 0.0010475 | 1.414 | 440.6 | 2243 | 2684 |
| 50 | 111.61 | 0.0010529 | 1.150 | 468.2 | 2225 | 2694 |
| 100 | 120.42 | 0.0010607 | 0.8803 | 505.6 | 2201 | 2707 |
Избыточное давление было придумано для простоты измерения давления по отношению к тому, которое мы обычно испытываем.
В таблицах пара, составленных на основе манометрического давления, атмосферное давление определяется как 0, а в таблицах с абсолютным давлением — 101.3 кПа. А для того чтобы отличать избыточное давление от абсолютного в конце добавляют “изб.”, например, кПа изб. или фт/кв. дюйм изб..
Перевести показатели избыточного давления в показатели абсолютного
Для единиц СИ
Давление пара [кПа изб.] = Давление пара [кПа изб.] + 101.3 кПа
Важное замечание: Проблемы могут возникнуть в том случае, если перепутать абсолютное и манометрическое давление, именно поэтому надо быть особенно внимательными с единицами давления, указанными в таблице.
Сводная таблица
Избыточное давление
- Нулевая точка отсчёта при атмосферном давлении*
- Нулевое давление = Атмосферное давление
Абсолютное давление:
- Нулевая точка отсчёта при атмосферном давлении
- Нулевое давление = Абсолютный вакуум
*Атмосферное давление — 101.3 кПа
Таблицы перенасыщенного пара
Информацию о перенасыщенном паре нельзя получить из обычных таблиц насыщенного пара, для этого существуют специальные таблицы перенасыщенного пара. Происходит это потому, что температура перенасыщенного пара в отличии от температуры насыщенного может существенно меняться при одном и том же давлении.
В действительности, количество возможных комбинаций температуры и давления настолько велико, что даже теоретически не представляется возможным собрать их в одной таблице. В результате для перегретого пара используется общая сводная таблица данных о температуре и давлении.
Пример таблицы перенасыщенного пара
В приведенной выше таблице есть данные об удельном объёме (Vg), удельной энтальпии (Hg) и удельном тепле (Sg) при типичных значениях давления и температуры.

















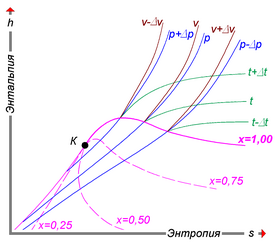











![{displaystyle quad mathrm {d} H=C_{P}mathrm {d} T+left[V-Tleft({frac {partial V}{partial T}}right)_{P}right]mathrm {d} P.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db8b72626dbc316bfcff5dcbb2aae49c93912304)