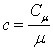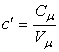Как найти удельную массовую теплоемкость

  Теплоёмкость тел – способность поглощать определённое количество тепла при нагревании, или отдавать при охлаждении. Теплоёмкость тела, это отношение бесконечно малого количества теплоты, полученного телом, к соответствующему приращению его температуры. Измеряется эта величина в Дж/К. Для практического же применения применяют Удельную теплоёмкость. Удельной теплоёмкостью называется теплоёмкость, отнесённая к единичному количеству вещества. Количество этого вещества, в свою очередь, может быть измерено в кубометрах, килограммах или в молях. В зависимости от того, к какой количественной единице относится теплоёмкость, различают объёмную, массовую и молярную теплоёмкость. В строительстве вряд-ли нам придётся встречаться с молярными измерениями, потому молярную теплоёмкость я оставлю физикам.

     Массовая удельная теплоёмкость (обозначается буквой С), также называемая просто удельной теплоёмкостью – это количество теплоты, которое необходимо подвести к единице массы вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на килограмм на кельвин – Дж/(кг·К).

   Объёмная теплоёмкость (С`) – это количество теплоты, которое необходимо подвести соответственно к единице объёма вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на кубический метр на кельвин Дж/(м³·К).  В строительных справочниках обычно приводят массовую удельную теплоёмкость – её и будем рассматривать.

  На значение удельной теплоёмкости влияет температура вещества, давление и другие термодинамические параметры. С ростом температуры вещества его удельная теплоёмкость, как правило, возрастает, но некоторые вещества имеют совсем нелинейную кривую этой зависимости.  К примеру, с повышением температуры от 0°С до 37°С удельная теплоёмкость воды снижается, а после 37°С до 100°С возрастает (см. картинку слева). Кроме того, удельная теплоёмкость зависит от того, каким образом позволено изменяться термодинамическим параметрам вещества (давлению, объёму и т. д.); например, удельная теплоёмкость при постоянном давлении и при постоянном объёме различны.

   Формула расчёта удельной теплоёмкости:  С=Q/(m·ΔT), где Q – количество теплоты, полученное веществом при нагреве (или выделившееся при охлаждении), m – масса вещества, ΔT – разность конечной и начальной температур вещества.  Значения теплоёмкости многих стротиельных материалов представлены в таблице ниже.

   Что же даёт нам эта характеристика материалов на практике? 

Теплоёмкие материалы используют при возведении теплоустойчивых стен. Это важно для домов с периодическим отоплением, например, печным. Теплоёмкие материалы и стены из них хорошо аккумулируют тепло. Запасают его в период работы отопительной системы (печи) и постепенно отдают после выключения отопительной системы, позволяя тем самым поддерживать комфортную температуру в течение суток. Чем больше может быть запасено тепла в теплоёмкой конструкции, тем стабильней будет температура в помещении. Интересно заметить, что традиционный в домостроении кирпич и бетон имеют значительно меньшую теплоёмкость, чем например, пенополистирол, а эковата и вовсе в три(!) раза более теплоёмкая, чем бетон.  Однако, в формуле теплоёмкости не зря задействована масса. Именно огромная масса бетона или кирпича в сравнении с той же эковатой позволяет в каменных стенах домов аккумулировать значительные количества тепла и сглаживать суточные колебания температур. И именно ничтожная масса утеплителя в каркасных домах, не смотря на бОльшую теплоёмкость, является слабым местом всех каркасных технологий. 

 Для решения описанной проблемы в каркасных домах устанавливают массивные теплоаккумуляторы – конструктивные элементы, имеющие высокую массу при достаточно высоком значении теплоёмкости. Это могут быть и какие-то внутренние стены из кирпича, массивная печь или камин, бетонные стяжки. Мебель в доме тоже является хорошим теплоаккумулятором, поскольку фанера, ДСП и любое дерево почти втрое больше может запасать тепла на килограмм веса, чем тот же кирпич. Недостаток такого подхода в том, что теплоаккумулятор необходимо проектировать ещё на стадии проектирования каркасного дома. В силу огромного его веса требуется заранее проектировать фундамент, представлять, как этот объект будет интегрирован в интерьер. Стоит отметить, что масса – это всё же не единственный критерий, нужно оценивать именно обе характеристики: массу и теплоёмкость. Даже золото со своим невероятным весом под 20 тонн на кубометр в качестве теплоаккумулятора будет работать лишь на 23% лучше, чем бетонный куб весом 2,5 тонны.

    Но самым лучшим веществом для теплоаккумулятора является вовсе не бетон и даже не кирпич! Хороша медь, бронза и железо, но они уж чрезмерно тяжелы. Вода! Вода имеет огромную теплоёмкость, наибольшую среди доступных веществ. Ещё бОльшую теплоёмкость имеют газы Гелий (5190 Дж/(кг·К) и Водород (14300 Дж/(кг·К), но их немножко проблематично использовать…  

      Я посчитал количество запасённой тепловой энергии в 1 м³ и 1 тонне материала при ΔT=1 °С.           Q=C·m·ΔT

   Как видно из графического представления данных – с водой не может соперничать ни один материал по параметру количества запасённого тепла! Для того, чтобы запастись 1МДж теплоты нам понадобится 240 литров воды или почти 8 тонн золота! Вода в 2,6 раза больше накапливает тепла, чем кирпич (при одинаковом объёме). На практике это означает, что в качестве очень эффективного теплоаккумулятора лучше всего использовать ёмкости с водой. Реализация тёплого водяного пола так же поможет улучшить стабильность температурного режима. 

     Однако, эти рассуждения применимы для температур не выше 100°С. После закипания вода переходит в иное фазовое состояние и резко меняет свою теплоёмкость. 

Математические упражнения

  Для расчёта теплопотерь и системы отопления своего будущего дома я использовал специализированный программный продукт по расчёту элементов инженерных систем “VALTEC” от некоего ООО “Веста-Трейдинг”. Программа VALTEC.PRG находится в открытом доступе и дает возможность рассчитать водяное радиаторное, напольное и настенное отопление, определить теплопотребность помещений, необходимые расходы холодной, горячей воды, объем канализационных стоков, получить гидравлические расчеты внутренних сетей тепло- и водоснабжения объекта. Так вот, используя эту чудесную бесплатную программку я высчитал, что теплопотери моего дома площадью в 152 квадратных метра составляют чуть менее 5 кВт тепловой энергии. В сутки выходит 120 кВт·ч или 432 МДж теплоты. Если допустить, что я буду использовать водяной теплоаккумулятор, который каким-либо источником тепла один раз в сутки разогреется до 85°С и будет постепенно отдавать тепло в систему тёплых полов до температуры 25°С  (ΔT=60 °С), то для накопления 432 МДж теплоты мне потребуется ёмкость m=Q/(C·ΔT),    432/(4,184·60)=1,7 м³.  

      А что было бы, если бы я установил в доме кирпичную печь, например. Разогретый в топке до 500°С кирпич весом в 1 тонну полностью компенсирует теплопотери моего дома в течение суток. При этом объём кирпича будет около 0,5 кубометра. 

    Особенностью моего проекта дома (в общем-то ничего особенного) является отопление тёплым водяным полом. Труба теплоносителя будет заложена в 7-и сантиметровый слой бетонной стяжки под всей площадю пола (152 м²) – это 10,64 м³ бетона! Под бетонной стяжкой планируется деревянное перекрытие по балкам с 25-ю сантиметрами пенополистирольного утеплителя – можно сказать, что через такой пирог утепления 1 м² пола будет терять тепла около 4 Вт, чем, конечно, можно смело пренебреч. Какова же будет теплоёмкость пола? При температуре теплоносителя 27°С бетонная стяжка впитает в себя 580 МДж теплоты, что эквивалентно 161 кВт·ч энергии и с лихвой перекрывает суточную потребность в тепле. Иными словами, зимой при -20°С (именно на такие температуры делался расчёт теплопотерь дома) мне нужно будет раз в два дня подогревать до 27°С пол, а если установить дополнительный водяной теплоаккумулятор на 1000 литров – то и вовсе раза два в неделю будет работать котёл! 

      Вот такая она, теплоёмкость при очень поверхностном рассмотрении. 

Теплоусвоение

  Коэффициент теплоусвоения (англ. U-value) отражает способность материала воспринимать теплоту при колебании температуры на его поверхности или, иными словами, этот коэффициент S показывает способность поверхности материала площадью в 1 м² усваивать теплоту в течение 1 с при температурном перепаде в 1 °С. Как это можно понять из повседневной жизни? Если приложить одновременно обе руки к двум поверхностям из бетона и пенопласта, имеющим одинаковую температуру, то первая будет восприниматься как более холодная – эксперимент ещё со школьных уроков физики. Это ощущение вызывается тем, что бетонная поверхность более интенсивно отбирает (усваивает) тепло от руки, чем пенопластовая, так как бетон имеет больший коэффициент теплоусвоения (Sбетона=18 Вт/(м²·°С), Seps=0,41 Вт/(м²·°С)), не смотря на то, что удельная теплоёмкость пенопласта в полтора раза больше, чем бетона.

   Величина коэффициента теплоусвоения S материалов при периоде колебания теплового потока 24 ч пропорциональна коэффициенту теплопроводности λ, Вт/(м·K), удельной теплоёмкости с, Дж/(кг·K), и плотности материала ρ, кг/м³, и обратно пропорциональна периоду тепловых колебаний T, с (формула слева). Но в строительной практике используются формулы, учитывающие действие массового отношения влаги в материале и климатические условия эксплуатации. Дабы не загромождать вас ненужной инфой, предлагаю использовать уже вычисленные табличные данные из СНиП II-3-79 “Строительная теплотехника”. Наиболее интересные я собрал в небольшую табличку.

      Теплоизоляционные материалы высокой эффективности (меньшим коэффициентом теплопроводности) обладают весьма низким коэффициентом теплоусвоения, т.е. при изменении температуры поверхности отнимают меньшее количество тепла и поэтому активно применяются для изоляции сооружений и аппаратов с резко переменным режимом работы.

      Колебания температуры на наружной поверхности материала вызывают в свою очередь и колебания температуры в самом материале, причём они будут постепенно затухать в толще материала.

   О теплоусвоении материалов я в процессе стройки ещё не слышал ни от одного строителя – может сложиться впечатление, что это некий теоретический и не очень важный параметр. Однако это не так – теплоусвоение материалов внутренней отделки, например полов, напрямую влияет на ощущение комфорта. Сможете ли вы комфортно ходить по полу босиком, или весь год придётся носить тапочки? Для полов существуют нормы по предельному коэффициенту теплоусвоения. Нормативная величина теплоусвоения покрытия для полов жилых зданий, больничных учреждений, диспансеров, поликлиник, общеобразовательных и детских школ, детских садов – не более 12 Вт/(м2-°С); для полов общественных зданий, кроме вышеуказанных, вспомогательных зданий и помещений промышленных предприятий, участков с постоянными рабочими местами в отапливаемых производственных зданиях, где выполняются легкие физические работы (категория I) – не более 14 Вт/(м2-°С); для полов в отапливаемых помещениях производственных зданий, где выполняются физические работы средней тяжести (категория II) – не более 17 Вт/(м2-°С). 

  Показатель теплоусвоения не нормируется: в помещениях с температурой поверхности пола выше 23 °С; в отапливаемых производственных помещениях, где выполняются тяжелые физические работы (категория III); в производственных зданиях, если на участки пола постоянных рабочих мест укладывают деревянные щиты или теплоизолирующие коврики; в общественных зданиях, эксплуатация которых не связана с постоянным пребыванием в них людей (залы музеев и выставок, фойе театров и киноте” атров и т. п.).

Тепловая инерция    

    Тепловая инерция, это способность ограждающей конструкции сопротивляться изменению температурного поля при перемененных тепловых воздействиях. Она определяет количество волн температурных колебаний, располагающихся (затухающих) в толще ограждения.

  Параметр теплоусвоения неразрывно связан с тепловой инерцией материалов. На рисунке, иллюстрирующем прохождение температурных волн в толще материала можно видеть длину волны, обозначенную как l. Число таких волн, располагающихся в толще ограждения, является показателем тепловой инерции ограждения. Численная величина этого показателя имеет название “массивности ограждения” и обозначается D. Она равна для однородного ограждения произведению его термического сопротивления R на коэффициент теплоусвоения материала S:    D=RS.

D – величина безразмерная. В ограждении, имеющем D=8.5, располагается около одной целой температурной волны. При D < 8,5 в ограждении распологается неполная волна (т.е. запаздывание колебаний на внутренней поверхности по отношению к колебаниям на наружней поверхности менее одного периода; при Т=24 часа запаздывание менее суток), а при D > 8,5 – в толще распологается более одной температурной волны.

      Для многослойных ограждений его массивность определяется как сумма массивности отдельных слоёв:

D=R1S1+R2S2+….RnSn,      где

R1, R2, Rn – термическое сопротивление отдельных слоёв, 

S1, S2, Sn – расчётные коэффициенты теплоусвоения материала отдельных слоёв конструкции.

Ограждение считается:

• Безынерционным при D < 1,5;

• “Лёгким” при  D от 1,5 до 4;

• “Средней массивности” при D от 4 до 7;

• “Массивным” при D > 7.

     Интересно сравнить “массивность” D ограждения из, например, 20 см пенополистирола ПСБ-25 и глиняного кирпича:

D eps=R (0.2/0.035) * S (0.41)=2.34    (похолодание на улице скажется на температуре внутри примерно через 6,6 часов)

D кирпич=R (0.2/0.7) * S (9.2)=2.63  (похолодание на улице скажется на температуре внутри примерно через 7,5 часов)

Видим, что кирпичная кладка “массивнее” пенопласта лишь на 12% !  Интересный результат, но нужно отметить, что в реальности обычно используют более тонкую теплоизоляцию из пенопласта (стандартная СИП-панель – 15см EPS), а из кирпича делают более толстые стены. Так, при толщине кирпичной стены в 60 см параметр D=7.9 а это уже “массивное” строение во всех смыслах этого термина, температурная волна через такую стену будет проходить около 22 часов.

     Тепловая инерция – безусловно, любопытное явление, но как его учитывать при подборе утеплителя? Мы можем представлять себе физический процесс прохождения тепловой волны через наш утеплитель, но если посмотрим на температуру внутренней поверхности (Tse), её амплитуду (A) и потери тепла (Q), то становится несколько не понятно, как этот параметр (D) может влиять на выбор. Например, возьмём толщину 30см:

– кирпичная стена D=3.35, A=2°C, Tse=15°C, Q=31;

– пенополистирол D=3.2, A=0.1°C, Tse=19,7°C Q=2.4;

       Очевидно, что при почти равной тепловой инерции с пенопластом будет заметно теплее! Однако, тепловая инерция оказывает влияние на так называемую теплоустойчивость зданий. Согласно “Строительной теплотехнике” при расчётах тебуемых сопротивлений теплопередаче расчётная зимняя температура наружного воздуха зависит именно от тепловой инерции! Чем выше тепловая инерция, тем меньшее влияние оказывает резкое изменение температуры наружнего воздуха на стабильность внутренней температуры. Эта зависимость имеет следующий вид:

• D <=1,5 : Расчётная зимняя температура tн равна температуре наиболее холодных суток обеспеченностью 98%;

• 1.5 < D < 4 : tн равна температуре наиболее холодных суток обеспеченностью 92%;

• 4 < D < 7 : tн равна средней температуре наиболее холодных ТРЁХ суток;

• D >7 : tн равна средней температуре наиболее холодных ПЯТИ дней обеспеченностью 92%. 

Как ни странно, но в этом же документе нету средней температуры наболее холодных трёх суток, но в СНиПе 23-01-99 есть пункт “температура наиболее холодной пятидневки обеспеченностью 98%, я думаю, её вполне можно использовать для расчёта. Табличка слева (как всегда, есть расхождения в документах). Поясню на примере:

• Мы строим каркасный дом в Бресте, и утепляем его 15 см минваты. Тепловая инерционность конструкции D=1,3. Это значит, что во всех расчётах температуру наружного воздуха нам стоит принимать -31°С. 

• Мы строим дом в Бресте из газобетона толщиной 30 см. D=3,9. Температурные расчёты теперь мы можем проводить для -25°С. 

• Напоследок мы строим в Бресте дом из пущанского бруса диаметром 30 см. D=9,13. Его инерционность позволяет производить тепловые расчёты для температур не ниже -21°С.

    Массивные теплоемкие стены летом могут выполнять функцию пассивного регулятора температуры в помещениях за счет суточной разницы температур. Остывшие за ночь стены охлаждают днем поступающий с улицы жаркий воздух, и наоборот. Такая регуляция полезна, когда среднесуточная температура воздуха комфортна для человека. Но если ночью не слишком прохладно, а днем очень жарко, то без кондиционера в каменном доме уже не обойтись.     Зимой массивные наружные стены в качестве регулятора климата абсолютно бесполезны. Зимой холодно днем и ночью. Если дом отапливается не постоянно, а периодически, например, дровами, то в качестве аккумулятора тепла нужна массивная каменная печь, а не кирпичные наружные стены. Чтобы зимой наружные стены стали аккумулятором тепла их нужно хорошо утеплить снаружи! Но тогда летом эти стены уже не смогут быстро охладиться за ночь. Это будет тот же каркасный дом с утеплителем, но с внутренним аккумулятором тепла.

    Для наглядной визуализации термических процессов, происходящих в толще однородного материала, я сделал интерактивную флешку, в которой можно подёргать входную и выходную температуры, поменять толщину материала в некоторых пределах и выбрать (из небольшого списка самых интересных с моей точки зрения) сам материал. Часть математики во флешке построена на формулах из СНиП II-3-79 “Строительная теплотехника”, и может немного расходится с другими моими же примерами в силу чрезвычайно разнообразных данных по характеристикам одного и того же материала, по разнообразным требованиям к микроклимату от источника к источнику (СНиПы, КТП), и даже с расчётами во всяких методичках в силу произвольного округления как в методичках, так и с моей стороны=) Все расчёты, так сказать, ознакомительные.

Как найти удельную теплоемкость компонентов смеси ( жидких) может знает кто формулу

Ксения Пыталь

Ученик

(26),
закрыт

3 года назад

٭هSky ا Neт ا

Высший разум

(108399)


7 лет назад

Можно найти теплоемкость смеси, зная удельную теплоемкость компонентов.
Массовая теплоемкость смеси жидкостей рассчитывается по уравнению:
C(смеси) = C₁ χ₁ + C₂ χ₂ + .+Ci χi
Сi – теплоемкость i-го компонента, χi – его массовая доля.
Аддитивность соблюдается, если компоненты между собой не вступают в физико-химическое взаимодействие.
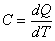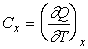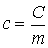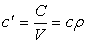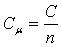