Почему медь проводит электричество лучше, чем вода? Прочитав эту статью, вы больше не будете задавать себе больше этот вопрос. Далее мы обсудим электропроводность и рассмотрим формулы, которые описывают это понятие. Наконец, вы можете проверить свои знания на двух примерах.
Простое объяснение.
Электропроводность — это физическая величина, которая описывает насколько хорошо определенный материал проводит электричество.
Формулы
Существует три различных формульных обозначения удельной электропроводности σ (греч. сигма), k (каппа) и γ (гамма). В дальнейшем мы будем использовать σ. Формула электропроводности, также называемой удельной электропроводностью, описывается формулой:
σ = 1 / ρ .
Здесь ρ называется удельным сопротивлением. Вы можете рассчитать электрическое сопротивление R проводника с учетом его параметров следующим образом: R = ( ρ * l ) / S .
Таким образом, сопротивление R равно удельному сопротивлению ρ , умноженному на длину проводника l, деленному на площадь поперечного сечения S. Если теперь вы хотите выразить эту формулу через удельную электропроводность σ = 1 / ρ , полезно знать, что электрическая проводимость G проводника выражается следующим образом: G = 1 / R .
Если в верхнюю формулу подставить удельную электропроводность σ и электрическую проводимость G, то получится следующее: 1 / G = ( 1 / σ ) * ( l / S ) .
Путем дальнейшего преобразования можно получить выражение: G = σ * S / l .
С помощью электропроводности можно также описать важную зависимость между плотностью электрического тока и напряженностью электрического поля с помощью выражения: J = σ * E .
Единица измерения
Единицей удельной электропроводности σ в СИ является: [ σ ] = 1 См/м ( Сименс на метр ).
Эти единицы определяются по формуле G = σ * S / l . Если решить эту формулу в соответствии с σ, то получим σ = G * l / S .
Единица измерения электрической проводимости G задается как: [ G ] = 1 / σ = 1 См ( Сименс, международное обозначение: S ).
Если теперь ввести в формулу все единицы измерения, то получится:
[ σ ] = 1 См * 1 м / м2 = 1 См / м .
Вы также будете чаще использовать единицы измерения См / см , м / Ом * мм2 или См * м / мм2 . Вы можете преобразовать отдельные измеряемые переменные так: См / см = См / 10-2 м и так: м / Ом * мм2 = См * м / мм2 = См * м / 10-3 м * 10-3 м = 106 См / м .
Электропроводность металлов
В зависимости от количества свободно перемещающихся электронов один материал проводит лучше, чем другой. В принципе, любой материал является проводящим, но в изоляторах, например, протекающий электрический ток ничтожно мал, поэтому здесь мы говорим о непроводниках.
В металлических связях валентные электроны, т.е. крайние электроны в атоме, свободно подвижны. Они расположены в так называемой полосе проводимости. Находящиеся там электроны образуют так называемый электронный газ. Соответственно, металлы являются сравнительно хорошими проводниками. Если теперь подать электрическое напряжение на металл, валентные электроны медленно движутся к положительному полюсу, потому что он их притягивает.

На рисунке 1 видно, что некоторые электроны не могут быть притянуты непосредственно к положительному полюсу, потому что на пути стоит, так сказать, твердое атомное ядро. Там они замедляются и в некоторой степени отклоняются. Именно поэтому электроны не могут ускоряться в металле бесконечно, и именно так возникает удельное сопротивление или электропроводность.
Теперь вы также можете измерить удельную электропроводность в металле с помощью следующей формулы: σ = ( n * e2 * τ ) / m .
В этой формуле n означает число электронов, e — заряд электрона, m — массу электрона, а τ — среднее время полета электрона между двумя столкновениями.
Таблица удельной электропроводности
Для большинства веществ уже известны значения удельной электропроводности. Некоторые из них вы можете найти в следующей таблице ниже. Все значения в этой таблице действительны для комнатной температуры, т.е. 25°C.
| Вещество | Удельная электропроводность в См / м |
| Серебро | 62 · 106 |
| Медь | 58 · 106 |
| Золото | 45,2 · 106 |
| Алюминий | 37,7 · 106 |
| Вольфрам | 19 · 106 |
| Латунь | 15,5 · 106 |
| Железо | 9,93 · 106 |
| Нержавеющая сталь (WNr. 1,4301) | 1,36 · 106 |
| Германий (легирование <10-9) | 2 |
| Кремний (легирование <10-12) | 0,5 · 10-3 |
| Морская вода | примерно 5 |
| Водопроводная вода | примерно 0,05 |
| Дистиллированная вода | 5 · 10-6 |
| Изолятор | обычно <10-8 |
Удельная электропроводность сильно зависит от температуры, поэтому указанные значения применимы только при 25°C. При повышении температуры вибрация решетки в веществе становится выше. Это нарушает поток электронов, и поэтому электропроводность уменьшается с ростом температуры.
Из таблицы видно, что медь имеет вторую по величине электропроводность, поэтому медные кабели очень часто используются в электротехнике. Серебро обладает еще более высокой проводимостью, но стоит намного дороже меди.
Интересно также сравнение между морской и дистиллированной водой. Здесь электропроводность возникает благодаря растворенным в воде ионам. Морская вода имеет очень высокую долю соли, которая растворяется в воде. Эти ионы передают электрический ток. В дистиллированной воде нет растворенных ионов, поэтому в ней практически не может протекать электрический ток. Поэтому электропроводность морской воды намного выше, чем дистиллированной.
Примеры задач
Для более детального рассмотрения приведём два примера расчетов.
Задача 1.
В первой задаче представьте, что у вас есть провод длиной 2 м с поперечным сечением 0,5 мм2. Электрическое сопротивление провода при комнатной температуре составляет 106 мОм. Из какого материала изготовлен провод?
Решение.
Решение данной задачи можно найти с помощью формулы: R = ( 1 / σ ) * ( l / S ). Из этой формулы найдём σ = l / ( S * R ) .
Теперь вы можете вставить заданные значения, убедившись, что вы перевели сечение в м2.
σ = l / ( S * R ) = 2 м / ( ( 0,5 * 10-6 м2 ) * ( 1 / 106 * 10-3 Ом ) ) = 37, 7 * 106 См / м .
Наконец, вы ищите в таблице, какой материал имеет удельную электропроводность σ = 37, 7 * 106 См / м и приходите к выводу, что провод сделан из алюминия.
Задача 2.
В задаче 2 вам дано только удельное сопротивление образца с 735 * 10-9 Ом * м. Из какого материла изготовлен образец?
Решение.
Вы можете использовать формулу σ = 1 / ρ для расчёта удельной электропроводности. После подстановки значений в эту формулу вы получите: σ = 1 / ρ = 1 / 735 * 10-9 Ом * м = 1,36 * 106 См / м .
Если вы снова заглянете в таблицу, то обнаружите, что образец должен быть изготовлен из нержавеющей стали.
Электрическая
проводимость
– это способность веществ проводить
электрический ток под действием внешнего
электрического поля. Электрическая
проводимость – величина, обратная
электрическому сопротивлению L
= 1/R.
![]() [См],
[См],
где ρ
– удельное
сопротивление, Ом·м;
![]() – удельная электрическая проводимость,
– удельная электрическая проводимость,
См/м (сименс/метр);S
– поперечное сечение, м2;
l
– длина
проводника, м) (в электрохимии
удельная электрическая проводимость
(![]() )
)
читается – каппа).
Единица измерения
L
– сименс (См), 1 См = 1 Ом-1.
Удельная
электрическая проводимость
раствора характеризует проводимость
объема раствора, заключенного между
двумя параллельными электродами,
имеющими площадь по 1 м2
и расположенными на расстоянии 1 м друг
от друга. Единица измерения в системе
СИ – См·м-1.
Удельная проводимость
раствора электролита определяется
количеством ионов, переносящих
электричество и скоростью их миграции:
![]() ,
,
(2.5)
где α
– степень диссоциации электролита; С
– молярная концентрация эквивалента,
моль/м3;
F
– число
Фарадея, 96485 Кл/моль;
![]() – абсолютные скорости движения катиона
– абсолютные скорости движения катиона
и аниона (скорости при градиенте
потенциала поля, равном 1 В/м); единица
измерения скорости – м2В-1с-1.
Из уравнения (2.5)
следует, что
![]() зависит от концентрации как для сильных
зависит от концентрации как для сильных
так и для слабых электролитов (рисунок
2.1):
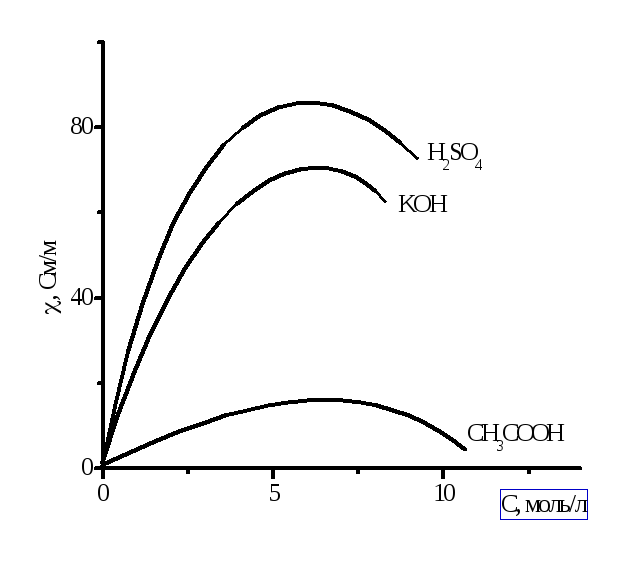
Рисунок 2.1 –
Зависимость удельной электрической
проводимости от концентрации электролитов
в водных растворах
В разбавленных
растворах при С → 0
![]() стремится к удельной электропроводности
стремится к удельной электропроводности
воды, которая составляет около 10-6
См/м и обусловлена присутствием ионов
Н3О+
и
ОН–.
С ростом концентрации электролита,
![]() вначале увеличивается, что отвечает
вначале увеличивается, что отвечает
увеличению числа ионов в растворе.
Однако, чем больше ионов в растворе
сильных электролитов, тем сильнее
проявляется ионное взаимодействие,
приводящее к уменьшению скорости
движения ионов. У слабых электролитов
в концентрированных растворах заметно
снижается степень диссоциации и,
следовательно, количество ионов,
переносящих электричество. Поэтому,
почти всегда, зависимость удельной
электрической проводимости от концентрации
электролита проходит через максимум.
2.1.3 Молярная и эквивалентная электрические проводимости
Чтобы выделить
эффекты ионного взаимодействия, удельную
электрическую проводимость
![]() делят на молярную концентрацию
делят на молярную концентрацию
(С, моль/м3),
и получают молярную
электрическую проводимость
![]() ;
;
или делят на молярную концентрацию
эквивалента и получаютэквивалентную
проводимость.
![]() .
.
(2.6)
Единицей измерения
![]() является м2См/моль.
является м2См/моль.
Физический смысл эквивалентной
проводимости состоит в следующем:
эквивалентная проводимость численно
равна электрической проводимости
раствора, заключенного между двумя
параллельными электродами, расположенными
на расстоянии 1 м и имеющими такую
площадь, что объем раствора между
электродами содержит один моль эквивалента
растворенного вещества (в случае молярной
электрической проводимости – один моль
растворенного вещества). Таким образом,
в случае эквивалентной электрической
проводимости в этом объеме будет NА
положительных и NА
отрицательных зарядов для раствора
любого электролита при условии его
полной диссоциации (NА
– число Авогадро). Поэтому, если бы ионы
не взаимодействовали друг с другом, то
![]() сохранялась бы постоянной при всех
сохранялась бы постоянной при всех
концентрациях. В реальных системах![]() зависит от концентрации (рисунок 2.2).
зависит от концентрации (рисунок 2.2).
При С → 0,![]() → 1, величина
→ 1, величина![]() стремится к
стремится к![]() ,
,
отвечающей отсутствию ионного
взаимодействия. Из уравнений (2.5 и 2.6)
следует:
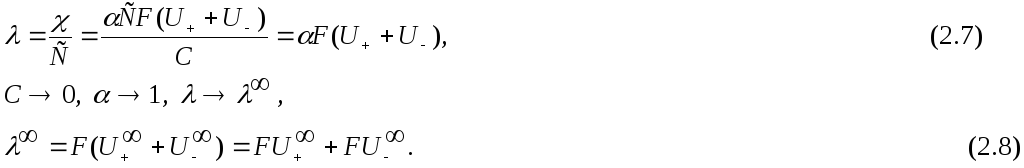
Произведение
![]() называютпредельной
называютпредельной
эквивалентной электрической проводимостью
ионов, или
предельной
подвижностью
ионов:
![]() .
.
(2.9)
Соотношение (2.9)
установлено Кольраушем и называется
законом
независимого движения ионов.
Предельная подвижность является
специфической величиной для данного
вида ионов и зависит только от природы
растворителя и температуры. Уравнение
для молярной электрической проводимости
принимает вид (2.10):
![]() ,
,
(2.10)
где
![]() – число эквивалентов катионов и анионов,
– число эквивалентов катионов и анионов,
необходимых для образования 1 моль соли.
Пример:
![]()
В случае одновалентного
электролита, например, HCl,
![]() ,
,
то есть молярная и эквивалентная
электрические проводимости совпадают.
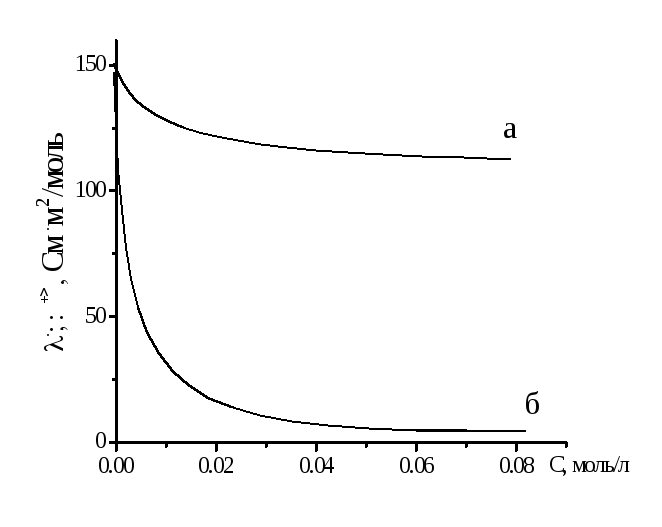
Рисунок 2.2 –
Зависимость эквивалентной электропроводности
от концентрации для сильных (а) и слабых
(б) электролитов
Для растворов
слабых электролитов эквивалентная
электрическая проводимость остается
небольшой вплоть до очень низких
концентраций, по достижении которых
она резко поднимается до значений,
сравнимых с
![]() сильных электролитов. Это происходит
сильных электролитов. Это происходит
за счет увеличения степени диссоциации,
которая, согласно классической теории
электролитической диссоциации, растет
с разбавлением и, в пределе, стремится
к единице.
Степень диссоциации
можно выразить, разделив уравнение
(2.7) на (2.8):
![]() .
.
С увеличением
концентрации
![]() растворов сильных электролитов
растворов сильных электролитов
уменьшается, но незначительно. Кольрауш
показал, что![]() таких растворов при невысоких концентрациях
таких растворов при невысоких концентрациях
подчиняется уравнению:
![]() ,
,
(2.11)
где А
– постоянная, зависящая от природы
растворителя, температуры и валентного
типа электролита.
По теории Дебая –
Онзагера снижение эквивалентной
электрической проводимости растворов
сильных электролитов связано с уменьшением
скоростей движения ионов за счет двух
эффектов торможения движения ионов,
возникающих из-за электростатистического
взаимодействия между ионом и его ионной
атмосферой. Каждый ион стремится окружить
себя ионами противоположного заряда.
Облако заряда называют ионной
атмосферой,
в среднем оно сферически симметрично.
Первый эффект –
эффект электрофоретического
торможения.
При наложении электрического поля ион
движется в одну сторону, а его ионная
атмосфера – в противоположную. Но с
ионной атмосферой за счет гидратации
ионов атмосферы увлекается часть
растворителя, и центральный ион при
движении встречает поток растворителя,
движущегося в противоположном направлении,
что создает дополнительное вязкостное
торможение иона.
Второй эффект –
релаксационного
торможения.
При движении иона во внешнем поле
атмосфера должна исчезать позади иона
и образовываться впереди него. Оба эти
процесса происходят не мгновенно.
Поэтому впереди иона количество ионов
противоположного знака меньше, чем
позади, то есть облако становится
несимметричным, центр заряда атмосферы
смещается назад, и поскольку заряды
иона и атмосферы противоположны, движение
иона замедляется. Силы релаксационного
и электрофоретического торможения
определяются ионной силой раствора,
природой растворителя и температурой.
Для одного и того же электролита, при
прочих постоянных условиях, эти силы
возрастают с увеличением концентрации
раствора.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определить удельную проводимость материала проводника, если сила тока в цепи 3 ампера, разность потенциалов приложенных к проводнику 12 вольт, длина проводника 12 метров, поперечное сечение проводника 4 мм2.
Дано: l=12 м; S=4×10-6 м2; U=12 В; I=3 A
Найти: σ-?
Решение:
Удельная проводимость материала проводника

Сопротивление проводника определяем по закону Ома
 ,
,
Тогда

Определяем удельную проводимость материала проводника
 ом-1·м-1
ом-1·м-1
σ=7.5×105 ом-1·м-1
Ответ: удельная проводимость материала данного проводника равна 7.5×105 ом-1·м-1
| Классическая электродинамика |
|---|
 |
| Электричество · Магнетизм |
|
Электростатика Закон Кулона |
|
Магнитостатика Закон Био — Савара — Лапласа |
|
Электродинамика Векторный потенциал |
|
Электрическая цепь Закон Ома |
|
Ковариантная формулировка Тензор электромагнитного поля |
| См. также: Портал:Физика |
Электропрово́дность (электри́ческая проводи́мость, проводимость) — способность тела (среды) проводить электрический ток, свойство тела или среды, определяющее возникновение в них электрического тока под воздействием электрического поля. Также физическая величина, характеризующая эту способность и обратная электрическому сопротивлению[1].
В Международной системе единиц (СИ) единицей измерения электрической проводимости является сименс (русское обозначение: См; международное: S), определяемый как 1 См = 1 Ом−1, то есть как электрическая проводимость участка электрической цепи сопротивлением 1 Ом[2].
Также термин электропроводность (электропроводность среды, вещества) применяется для обозначения удельной электропроводности (см. ниже).
Под электропроводностью подразумевается способность проводить прежде всего постоянный ток (под воздействием постоянного поля), в отличие от способности диэлектриков откликаться на переменное электрическое поле колебаниями связанных зарядов (переменной поляризацией), создающими переменный ток. Ток проводимости практически не зависит от частоты приложенного поля (до определённых пределов, в области низких частот).
Электропроводность среды (вещества) связана со способностью заряженных частиц (электронов, ионов), содержащихся в этой среде, достаточно свободно перемещаться в ней. Величина электропроводности и её механизм зависят от природы (строения) данного вещества, его химического состава, агрегатного состояния, а также от физических условий, прежде всего таких, как температура.
Удельная электропроводность[править | править код]
Удельной электропроводностью (удельной проводимостью) называют меру способности вещества проводить электрический ток. Согласно закону Ома в линейном изотропном веществе удельная проводимость является коэффициентом пропорциональности между плотностью возникающего тока и величиной электрического поля в среде:
- где
— удельная проводимость,
— вектор плотности тока,
— вектор напряжённости электрического поля.
- Электрическая проводимость G однородного проводника длиной L с постоянным поперечным сечением площадью S может быть выражена через удельную проводимость вещества, из которого сделан проводник:
- В системе СИ удельная электропроводность измеряется в сименсах на метр (См/м) или в Ом−1·м−1. В СГСЭ единицей удельной электропроводности является обратная секунда (с−1).
В неоднородной среде σ может зависеть (и в общем случае зависит) от координат, то есть не совпадает в различных точках проводника.
Удельная проводимость анизотропных (в отличие от изотропных) сред является, вообще говоря, не скаляром, а тензором (симметричным тензором ранга 2), и умножение на него сводится к матричному умножению:
при этом векторы плотности тока и напряжённости поля в общем случае не коллинеарны.
Для любой линейной среды можно выбрать локально (а если среда однородная, то и глобально) т. н. собственный базис — ортогональную систему декартовых координат, в которых матрица 






Величины 
Величина, обратная удельной проводимости, называется удельным сопротивлением.
Вообще говоря, линейное соотношение, написанное выше (как скалярное, так и тензорное), верно в лучшем случае[4] приближённо, причём приближение это хорошо только для сравнительно малых величин E. Впрочем, и при таких величинах E, когда отклонения от линейности заметны, удельная электропроводность может сохранять свою роль в качестве коэффициента при линейном члене разложения, тогда как другие, старшие, члены разложения дадут поправки, обеспечивающие хорошую точность.
Также в случае нелинейной зависимости J от E (то есть в общем случае) может явно вводиться дифференциальная удельная электропроводность, зависящая от E:
(для анизотропных сред:
).
Электропроводность и носители тока[править | править код]
Электропроводность всех веществ связана с наличием в них носителей тока (носителей заряда) — подвижных заряженных частиц (электронов, ионов) или квазичастиц (например, дырок в полупроводнике), способных перемещаться в данном веществе на большое расстояние. Упрощённо можно сказать, что такая частица или квазичастица должна быть способна пройти в данном веществе неограниченно большое, по крайней мере макроскопическое, расстояние, хотя в некоторых частных случаях носители могут меняться, рождаясь и уничтожаясь, и переносить ток, сменяя друг друга (возможно, и через очень небольшое расстояние)[5].
Поскольку плотность тока определяется для одного типа носителей формулой:
- где
— заряд одного носителя,
— концентрация носителей,
— средняя скорость их движения,
или 

- где
— коэффициент пропорциональности, называемый подвижностью и зависящий от вида носителя тока в данной конкретной среде[6].
Отсюда следует, что для электропроводности справедливо выражение:
или:
— для более чем одного вида носителей.
Механизмы электропроводности и электропроводность различных классов веществ[править | править код]
Электронная проводимость[править | править код]
Подробнее по теме «Электронная проводимость» см. Электронный газ
Дырочная проводимость[править | править код]
Ионная проводимость[править | править код]
Подробнее по теме «Ионная проводимость» см. Электролит
Ионной проводимостью обладают газы, некоторые твердые соединения (ионные кристаллы и стёкла), расплавленные индивидуальные соли и растворы соединений в воде, неводных растворителях и расплавах. Значения удельной проводимости проводников второго рода разных классов колеблются в очень широких пределах.
Электропроводность металлов[править | править код]
Ещё до открытия электронов было обнаружено, что протекание тока в металлах, в отличие от тока в жидких электролитах, не обусловлено переносом вещества металла. Эксперимент, который выполнил немецкий физик Карл Виктор Эдуард Рикке (Riecke Carl Viktor Eduard) в 1901 году, состоял в том, что через контакты различных металлов, — двух медных и одного алюминиевого цилиндра с тщательно отшлифованными торцами, поставленными один на другой, в течение года пропускался постоянный электрический ток. Затем исследовался состав материала вблизи контактов. Оказалось, что переноса вещества металла через границу не происходит и вещество по разные стороны границы раздела имеет тот же состав, что и до пропускания тока. Таким образом было показано, что перенос электрического тока осуществляется не атомами и молекулами металлов, а другими частицами. Однако эти опыты не дали ответа на вопрос о природе носителей заряда в металлах[7].
Связь с коэффициентом теплопроводности[править | править код]
Закон Видемана — Франца, выполняющийся для металлов при высоких температурах, устанавливает однозначную связь удельной электрической проводимости 
- где k — постоянная Больцмана,
- e — элементарный заряд.
Эта связь основана на том факте, что как электропроводность, так и теплопроводность в металлах обусловлены движением свободных электронов проводимости.
Электропроводность растворов[править | править код]
Скорость движения ионов зависит от напряженности электрического поля, температуры, вязкости раствора, радиуса и заряда иона и межионного взаимодействия.
У растворов сильных электролитов наблюдается характер концентрационной зависимости электрической проводимости объясняется действием двух взаимно противоположных эффектов. С одной стороны, с ростом разбавления уменьшается число ионов в единице объёма раствора. С другой стороны, возрастает их скорость за счет ослабления торможения ионами противоположного знака.
Для растворов слабых электролитов наблюдается характер концентрационной зависимости электрической проводимости можно объяснить тем, что рост разбавления ведёт, с одной стороны, к уменьшению концентрации молекул электролита. В то же время возрастает число ионов за счёт роста степени ионизации.
В отличие от металлов (проводники 1-го рода) электрическая проводимость растворов как слабых, так и сильных электролитов (проводники 2-го рода) при повышении температуры возрастает. Этот факт можно объяснить увеличением подвижности в результате понижения вязкости раствора и ослаблением межъионного взаимодействия
Электрофоретический эффект — возникновение торможения носителей вследствие того, что ионы противоположного знака под действием электрического поля двигаются в направлении, обратном направлению движения рассматриваемого иона
Релаксационный эффект — торможение носителей в связи с тем, что ионы при движении расположены асимметрично по отношению к их ионным атмосферам. Накопление зарядов противоположного знака в пространстве за ионом приводит к торможению его движения.
При больших напряжениях электрического поля скорость движения ионов настолько велика, что ионная атмосфера не успевает образоваться. В результате электрофоретическое и релаксационное торможение не проявляется.
Удельная электропроводность некоторых веществ (таблица)[править | править код]
Удельная проводимость приведена при температуре +20 °C[8]:
| Вещество | См/м | Вещество | См/м | Вещество | См/м | Вещество | См/м | Вещество | См/м |
|---|---|---|---|---|---|---|---|---|---|
| серебро | 62 500 000 | молибден | 18 500 000 | олово | 8 330 000 | ртуть | 1 040 000 | мрамор | 10−8 |
| медь | 59 500 000[9] | вольфрам | 18 200 000 | сталь литая | 7 690 000 | нихром | 893 000 | стекло | 10−11 |
| золото | 45 500 000 | цинк | 16 900 000 | свинец | 4 810 000 | графит | 125 000 | фарфор | 10−14 |
| алюминий | 38 000 000[9] | никель | 11 500 000 | нейзильбер | 3 030 000 | вода морская | 4 | кварцевое стекло | 10−16 |
| магний | 22 700 000 | железо чистое | 10 000 000 | константан | 2 000 000 | земля влажная | 10−2 | янтарь | 10−18 |
| иридий | 21 100 000 | платина | 9 350 000 | манганин | 2 330 000 | вода дистилл. | 10−4 |
См. также[править | править код]
- Адмиттанс
- Зонная теория
- Эффект Холла
- Сверхпроводимость
- Отрицательная абсолютная проводимость
Примечания[править | править код]
- ↑ Электропроводность (физич.) // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978. (см. копию на bse.sci-lib.com/article126142.html)
- ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 105. — 240 с. — ISBN 5-7050-0118-5.
- ↑ В случае совпадения двух из трех собственных чисел
, есть произвол в выборе такой системы координат (собственных осей тензора
), а именно довольно очевидно, что можно произвольно повернуть её относительно оси с отличающимся собственным числом, и выражение не изменится. Однако это не слишком меняет картину. В случае же совпадения всех трех собственных чисел мы имеем дело с изотропной проводимостью, и, как легко видеть, умножение на такой тензор сводится к умножению на скаляр.
- ↑ Для многих сред линейное приближение является достаточно хорошим или даже очень хорошим для достаточно широкого диапазона величин электрического поля, однако существуют среды, для которых это совсем не так уже при весьма малых E.
- ↑ Впрочем, если речь идет об однородном веществе, как правило, если что-то подобное имеет место, проще описать коллективное возмущение как квазичастицу.
- ↑ Здесь мы для простоты не рассматриваем анизотропных кристаллов с тензорной подвижностью, считая μ скаляром; впрочем, при желании можно считать его тензором, понимая произведение
в матричном смысле.
- ↑ Элементарный учебник физики / Под ред. Г. С. Ландсберга. — М.: Наука, 1985. — Т. II. Электричество и магнетизм. — С. 194. — 479 с.
- ↑ Кухлинг Х. Справочник по физике. Пер. с нем., М.: Мир, 1982, стр. 475 (табл. 39); значения удельной проводимости вычислены из удельного сопротивления и округлены до 3 значащих цифр.
- ↑ 1 2 Герасимов В. Г., Грудинский П. Г., Жуков Л. А. Электротехнический справочник. В 3-х томах. Т.1 Общие вопросы. Электротехнические материалы / Под общей редакцией профессоров МЭИ. — 6-е изд.. — Москва: Энергия, 1980. — С. 353. — 520 с. — ISBN ББК 31.2.
Литература[править | править код]
- Матвеев А. Н. Электричество и магнетизм. (Первое изд. М.: Высшая школа, 1983. 463 с.)
- Ершов Ю. А., Попков В. А., Берлянд А. С. и др. Общая химия. Биофизическая химия. Химия биогенных элементов. — Изд. 8-е, стереотипное. — М.: Высшая школа, 2010. — 559 с. — ISBN 978-5-06-006180-2.
- Блатт Ф. Физика электронной проводимости в твердых телах. — М.: Мир, 1971. — 470 с.
Мера способности вещества сопротивляться или проводить электрический ток
Удельное электрическое сопротивление (также называемое удельное электрическое сопротивление или объемное удельное сопротивление ) и его обратная, электрическая проводимость, является фундаментальным свойством материала, которое количественно определяет, насколько сильно он сопротивляется или проводит электрический ток. Низкое удельное сопротивление указывает на материал, который легко пропускает электрический ток. Удельное сопротивление обычно обозначается греческой буквой ρ (rho ). Единица измерения удельного электрического сопротивления SI – это Ом – метр (Ом⋅м). Например, если твердый куб материала размером 1 м × 1 м × 1 м имеет контакты листов на двух противоположных гранях, а сопротивление между этими контактами составляет 1 Ом, то удельное сопротивление материала составляет 1 Ом · м.
Электропроводность или удельная проводимость обратно пропорциональна удельному электрическому сопротивлению. Он представляет собой способность материала проводить электрический ток. Обычно обозначается греческой буквой σ (сигма ), но иногда используются κ (каппа ) (особенно в электротехнике) и γ (гамма ).. Единица измерения электрической проводимости в системе СИ – сименс на метр (См / м).
Содержание
- 1 Определение
- 1.1 Идеальный случай
- 1.2 Общие скалярные величины
- 1.3 Тензорное удельное сопротивление
- 2 Проводимость и носители тока
- 2.1 Связь между плотностью тока и скоростью электрического тока
- 3 Причины проводимости
- 3.1 Упрощение зонной теории
- 3.2 В металлах
- 3.3 В полупроводниках и изоляторах
- 3.4 В ионных жидкостях / электролитах
- 3.5 Сверхпроводимость
- 3.6 Плазма
- 4 Удельное сопротивление и проводимость различных материалов
- 5 Температурная зависимость
- 5.1 Линейное приближение
- 5.2 Металлы
- 5.2.1 Закон Видемана-Франца
- 5.3 Полупроводники
- 6 Комплексное удельное сопротивление и проводимость
- 7 Сопротивление по сравнению с удельным сопротивлением в сложных геометрических формах
- 8 Произведение удельного сопротивления
- 9 См. также
- 10 Примечания
- 11 Ссылки
- 12 Дополнительная литература
- 13 Внешние ссылки
Определение
Идеальный случай
 Кусок резистивного материала с электрическими контактами на обоих концах.
Кусок резистивного материала с электрическими контактами на обоих концах.
В идеальном случае поперечное сечение и физический состав части исследуемого материала однородны по всему образцу, а электрическое поле и плотность тока везде параллельны и постоянны. Многие резисторы и проводники на самом деле имеют однородное поперечное сечение с равномерным течением электрического тока и изготовлены из одного материала, так что это хорошая модель. (См. Диаграмму рядом.) В этом случае удельное электрическое сопротивление ρ (греч.: rho ) можно рассчитать следующим образом:
- ρ = RA ℓ, { displaystyle rho = R { frac {A} { ell}}, , !}
где
- R { displaystyle R}
– электрическое сопротивление однородного образца материал
- ℓ { displaystyle ell}
– это длина образца
- A { displaystyle A}
– крест -площадь сечения образца
Как сопротивление, так и удельное сопротивление описывают, насколько сложно заставить электрический ток течь через материал, но, в отличие от сопротивления, удельное сопротивление является внутренним свойством. Это означает, что все провода из чистой меди (которые не подвергались искажению своей кристаллической структуры и т. Д.), Независимо от их формы и размера, имеют одинаковое удельное сопротивление, но длинный тонкий медный провод имеет гораздо большее сопротивление, чем толстый, провод медный короткий. Каждый материал имеет свое собственное удельное сопротивление. Например, резина имеет гораздо большее удельное сопротивление, чем медь.
В гидравлической аналогии, прохождение тока через материал с высоким удельным сопротивлением похоже на проталкивание воды через трубу, полную песка, а пропускание тока через материал с низким удельным сопротивлением – как проталкивание воды через пустая труба. Если трубы одинакового размера и формы, у трубы, заполненной песком, будет более высокое сопротивление потоку. Однако сопротивление определяется не только наличием или отсутствием песка. Это также зависит от длины и ширины трубы: короткие или широкие трубы имеют меньшее сопротивление, чем узкие или длинные.
Приведенное выше уравнение можно транспонировать, чтобы получить закон Пуйе (названный в честь Клода Пуйе ):
- R = ρ ℓ A. { displaystyle R = rho { frac { ell} {A}}. , !}
Сопротивление данного материала пропорционально длине, но обратно пропорционально площади поперечного сечения. Таким образом, удельное сопротивление может быть выражено с помощью единицы SI «ом метр » (Ом⋅м) – то есть омы, разделенные на метры (для длины), а затем умноженные на квадратные метры (по площади поперечного сечения).
Например, если A = 1 м, ℓ { displaystyle ell}
Проводимость σ является обратной величиной удельного сопротивления:
- σ = 1 ρ. { displaystyle sigma = { frac {1} { rho}}. , !}
В единицах системы СИ сименс на метр (См / м).
Общие скалярные величины
Для менее идеальных случаев, таких как более сложная геометрия, или когда ток и электрическое поле изменяются в разных частях материала, необходимо использовать более общее выражение в котором удельное сопротивление в конкретной точке определяется как отношение электрического поля к плотности тока, который он создает в этой точке:
- ρ = EJ, { displaystyle rho = { frac {E} {J}}, , !}
где
- ρ { displaystyle rho}
– удельное сопротивление материала проводника,
- E { displaystyle E}
– величина электрического поля,
- J { displaystyle J}
– величина плотность тока,
, в которой E { displaystyle E}

Электропроводность – это величина, обратная (обратной) величине удельного сопротивления. Здесь это определяется как:
- σ = 1 ρ = J E. { displaystyle sigma = { frac {1} { rho}} = { frac {J} {E}}. , !}
Например, резина – это материал с большим ρ и малым σ – потому что даже очень большое электрическое поле в резине почти не пропускает ток. С другой стороны, медь – это материал с малым ρ и большим σ, потому что даже небольшое электрическое поле пропускает через него большой ток.
Как показано ниже, это выражение упрощается до одного числа, когда электрическое поле и плотность тока в материале постоянны.
-
Вывод из общего определения удельного сопротивления Здесь необходимо объединить три уравнения. Первый – это удельное сопротивление для параллельного тока и электрического поля: - ρ = EJ, { displaystyle rho = { frac {E} {J}}, , !}
Если электрическое поле постоянно, электрическое поле определяется как полное напряжение V на проводнике, деленное на длину ℓ проводника:
- E = V ℓ { displaystyle E = { frac {V} { ell}}}
Если плотность тока постоянна, она равна полному току, деленному на площадь поперечного сечения:
- J = IA { displaystyle J = { frac {I} {A}}}
Подсоединение значений E и J в первое выражение, мы получаем:
- ρ = VAI ℓ { displaystyle rho = { frac {VA} {I ell}}}
Наконец, мы применяем закон Ома, V / I = R.
- ρ = RA ℓ { displaystyle rho = R { frac {A} { ell}}}
- ρ = EJ, { displaystyle rho = { frac {E} {J}}, , !}
Тензорное удельное сопротивление
Когда удельное сопротивление материала имеет направленную составляющую, необходимо использовать самое общее определение удельного сопротивления. Он начинается с тензорно-векторной формы закона Ома, который связывает электрическое поле внутри материала с потоком электрического тока. Это уравнение является полностью общим, то есть справедливо во всех случаях, включая упомянутые выше. Однако это определение является наиболее сложным, поэтому оно напрямую используется только в анизотропных случаях, когда более простые определения не могут применяться. Если материал не является анизотропным, можно проигнорировать определение вектора тензора и вместо этого использовать более простое выражение.
Здесь анизотропный означает, что материал имеет разные свойства в разных направлениях. Например, кристалл графита микроскопически состоит из стопки листов, и ток очень легко течет через каждый лист, но гораздо труднее от одного листа к соседнему. В таких случаях ток не течет точно в том же направлении, что и электрическое поле. Таким образом, соответствующие уравнения обобщаются до трехмерной тензорной формы:
- J = σ E ⇌ E = ρ J { displaystyle mathbf {J} = { boldsymbol { sigma}} mathbf {E} , , rightleftharpoons , , mathbf {E} = { boldsymbol { rho}} mathbf {J} , !}
, где проводимость σ и удельное сопротивление ρ – тензоры ранга 2, а электрическое поле E и плотность тока J – векторы. Эти тензоры могут быть представлены матрицами 3 × 3, векторами с матрицами 3 × 1, с умножением матриц , используемым в правой части этих уравнений. В матричной форме соотношение удельных сопротивлений определяется следующим образом:
- [E x E y E z] = [ρ xx ρ xy ρ xz ρ yx ρ yy ρ yz ρ zx ρ zy ρ zz] [J x J y J z ] { displaystyle { begin {bmatrix} E_ {x} \ E_ {y} \ E_ {z} end {bmatrix}} = { begin {bmatrix} rho _ {xx} rho _ { xy} rho _ {xz} \ rho _ {yx} rho _ {yy} rho _ {yz} \ rho _ {zx} rho _ {zy} rho _ {zz} end {bmatrix}} { begin {bmatrix} J_ {x} \ J_ {y} \ J_ {z} end {bmatrix}}}
где
- E { displaystyle mathbf {E}}
– вектор электрического поля с компонентами (E x, E y, E z).
- ρ { displaystyle { boldsymbol { rho}}}
– тензор удельного сопротивления, обычно матрица три на три.
- J { displaystyle mathbf {J}}
– вектор плотности электрического тока, с компонентами (J x, J y, J z)
Эквивалентно, удельное сопротивление может быть задано в более компактной нотации Эйнштейна :
- E i = ρ ij J j { displaystyle mathbf {E} _ {i} = { boldsymbol { rho}} _ {ij} mathbf {J} _ {j}}
В любом случае результат Значение сопротивления для каждой компоненты электрического поля составляет:
- E x = ρ x x J x + ρ x y J y + ρ x z J z. { Displaystyle E_ {x} = rho _ {xx} J_ {x} + rho _ {xy} J_ {y} + rho _ {xz} J_ {z}.}
- E y = ρ yx J x + ρ yy J y + ρ yz J z. { Displaystyle E_ {y} = rho _ {yx} J_ {x} + rho _ {yy} J_ {y} + rho _ {yz} J_ {z}.}
- E z = ρ zx J x + ρ zy J y + ρ zz J z. { displaystyle E_ {z} = rho _ {zx} J_ {x} + rho _ {zy} J_ {y} + rho _ {zz} J_ {z}.}
Поскольку выбор система координат свободна, обычное соглашение состоит в том, чтобы упростить выражение, выбрав ось x, параллельную текущему направлению, поэтому J y = J z = 0. Это оставляет:
- ρ xx = E x J x, ρ yx = E y J x и ρ zx = E z J x. { displaystyle rho _ {xx} = { frac {E_ {x}} {J_ {x}}}, quad rho _ {yx} = { frac {E_ {y}} {J_ {x} }}, { text {and}} rho _ {zx} = { frac {E_ {z}} {J_ {x}}}.}
Проводимость определяется аналогично:
- [J x J Y J Z] знак равно [σ xx σ xy σ xz σ yx σ yy σ yz σ zx σ zy σ zz] [E x E y E z] { displaystyle { begin {bmatrix} J_ {x} \ J_ { y} \ J_ {z} end {bmatrix}} = { begin {bmatrix} sigma _ {xx} sigma _ {xy} sigma _ {xz} \ sigma _ {yx} sigma _ {yy} sigma _ {yz} \ sigma _ {zx} sigma _ {zy} sigma _ {zz} end {bmatrix}} { begin {bmatrix} E_ {x } \ E_ {y} \ E_ {z} end {bmatrix}}}
или
- J i = σ ij E j { displaystyle mathbf {J} _ {i} = { boldsymbol { sigma}} _ {ij} mathbf {E} _ {j}}
Оба результата дают:
- J x = σ xx E x + σ xy E y + σ xz E z { displaystyle J_ {x} = sigma _ {xx} E_ {x} + sigma _ {xy} E_ {y} + sigma _ {xz} E_ {z}}
- J y = σ yx E x + σ yy E y + σ yz E Z { displaystyle J_ {y} = sigma _ {yx} E_ {x} + sigma _ {yy} E_ {y} + sigma _ {yz} E_ {z}}
- J Z знак равно σ zx E Икс + σ zy E Y + σ zz E Z { Displaystyle J_ {z} = sigma _ {zx} E_ {x} + sig ma _ {zy} E_ {y} + sigma _ {zz} E_ {z}}
Глядя на два выражения, ρ { displaystyle { boldsymbol { rho}}}




- σ xx = ρ xx ρ xx 2 + ρ xy 2, σ xy = – ρ xy ρ xx 2 + ρ xy 2 { displaystyle sigma _ {xx} = { frac { rho _ {xx}} { rho _ {xx} ^ { 2} + rho _ {xy} ^ {2}}}, quad sigma _ {xy} = { frac {- rho _ {xy}} { rho _ {xx} ^ {2} + rho _ {xy} ^ {2}}}}
Если электрическое поле параллельно приложенному току, ρ xy { displaystyle rho _ {xy}}



Проводимость и носители тока
Связь между плотностью тока и скоростью электрического тока
Электрический ток – это упорядоченное движение электрических зарядов. Эти расходы называются носителями тока. В металлах и полупроводниках, электроны являются носителями тока; в электролитах и ионизированных газах, положительных и отрицательных ионах. В общем случае плотность тока одного носителя определяется по формуле:
- j → = qn υ → a { displaystyle { vec {j}} = qn { vec { upsilon}} _ {a }}
,
где 𝑛 – плотность носителей заряда (количество носителей в единице объема), 𝑞 – заряд одного носителя, υ → a { displaystyle { vec { upsilon}} _ {a}}
- j → = ∑ jji { displaystyle { vec {j}} = sum _ {j} j_ {i}}
.
, где ji { displaystyle j_ {i}}

Причины проводимости
Упрощенная зонная теория
 Заполнение электронных состояний в различных типах материалов при равновесии. Здесь высота – это энергия, а ширина – это плотность доступных состояний для определенной энергии в перечисленном материале. Оттенок соответствует распределению Ферми – Дирака (черный = все состояния заполнены, белые = состояния не заполнены). В металлах и полуметаллах уровень Ферми EFнаходится внутри по крайней мере одной зоны. В изоляторах и полупроводниках уровень Ферми находится внутри запрещенной зоны ; однако в полупроводниках зоны достаточно близки к уровню Ферми, чтобы быть термически заселенными электронами или дырками.
Заполнение электронных состояний в различных типах материалов при равновесии. Здесь высота – это энергия, а ширина – это плотность доступных состояний для определенной энергии в перечисленном материале. Оттенок соответствует распределению Ферми – Дирака (черный = все состояния заполнены, белые = состояния не заполнены). В металлах и полуметаллах уровень Ферми EFнаходится внутри по крайней мере одной зоны. В изоляторах и полупроводниках уровень Ферми находится внутри запрещенной зоны ; однако в полупроводниках зоны достаточно близки к уровню Ферми, чтобы быть термически заселенными электронами или дырками.
Согласно элементарной квантовой механике, электрон в атоме или кристалл может иметь только определенные точные уровни энергии; энергии между этими уровнями невозможны. Когда большое количество таких разрешенных уровней имеют близкорасположенные значения энергии, то есть имеют энергии, которые отличаются лишь незначительно, эти близкие энергетические уровни в комбинации называются «энергетической зоной». В материале может быть много таких энергетических зон, в зависимости от атомного номера составляющих атомов и их распределения в кристалле.
Электроны материала стремятся минимизировать общую энергию в материале за счет перехода в низкоэнергетические состояния; однако принцип исключения Паули означает, что только один может существовать в каждом таком состоянии. Таким образом, электроны «заполняют» зонную структуру, начиная снизу. Характерный уровень энергии, до которого заполнились электроны, называется уровнем Ферми . Положение уровня Ферми по отношению к зонной структуре очень важно для электропроводности: только электроны на энергетических уровнях около или выше уровня Ферми могут свободно перемещаться в более широкой структуре материала, поскольку электроны могут легко перепрыгивать между частично занятыми государствами в этом регионе. Напротив, состояния с низкой энергией полностью заполнены с фиксированным пределом на количество электронов в любое время, а состояния с высокой энергией всегда пусты от электронов.
Электрический ток состоит из потока электронов. В металлах есть много уровней энергии электронов вблизи уровня Ферми, поэтому существует много электронов, которые могут двигаться. Это причина высокой электронной проводимости металлов.
Важной частью теории зон является то, что могут существовать запрещенные зоны энергии: интервалы энергии, которые не содержат уровней энергии. В изоляторах и полупроводниках количество электронов является правильным, чтобы заполнить определенное целое число низкоэнергетических зон точно до границы. В этом случае уровень Ферми попадает в запрещенную зону. Поскольку вблизи уровня Ферми нет доступных состояний, а электроны не могут свободно перемещаться, электронная проводимость очень мала.
В металлах
 Подобно шарам в колыбели Ньютона, электроны в металле быстро передают энергию от одного вывода к другому, несмотря на их собственное незначительное движение.
Подобно шарам в колыбели Ньютона, электроны в металле быстро передают энергию от одного вывода к другому, несмотря на их собственное незначительное движение.
A металл состоит из решетки из атомов, каждый из которых имеет внешнюю оболочку из электронов, которые свободно отделяются от своих родительских атомов и проходят через решетку. Это также известно как положительная ионная решетка. Это «море» диссоциируемых электронов позволяет металлу проводить электрический ток. Когда к металлу прикладывается разность электрических потенциалов (напряжение ), возникающее электрическое поле заставляет электроны дрейфовать к положительному выводу. Фактическая скорость дрейфа электронов обычно мала, порядка метров в час. Однако из-за огромного количества движущихся электронов даже низкая скорость дрейфа приводит к большой плотности тока. Механизм аналогичен передаче количества движения шарикам в колыбели Ньютона, но быстрое распространение электрической энергии по проводу происходит не из-за механических сил, а из-за распространения несущего энергию электромагнитного поля. по проводам.
Большинство металлов обладают электрическим сопротивлением. В более простых моделях (неквантово-механических моделях) это можно объяснить заменой электронов и кристаллической решетки волнообразной структурой. Когда электронная волна проходит через решетку, волны интерферируют, что вызывает сопротивление. Чем более правильная решетка, тем меньше возмущений и, следовательно, меньше сопротивления. Таким образом, сопротивление в основном обусловлено двумя факторами. Во-первых, это вызвано температурой и, следовательно, количеством колебаний кристаллической решетки. Более высокие температуры вызывают более сильные вибрации, которые действуют как неровности решетки. Во-вторых, важна чистота металла, поскольку смесь различных ионов также является неоднородностью. Небольшое уменьшение проводимости при плавлении чистых металлов связано с потерей дальнего кристаллического порядка. Сохраняется ближний порядок, и сильная корреляция между положениями ионов приводит к когерентности между волнами, дифрагированными на соседних ионах.
В полупроводниках и изоляторах
В металлах уровень Ферми находится в зоне проводимости (см. Теорию зон выше), что приводит к свободному электроны проводимости. Однако в полупроводниках положение уровня Ферми находится внутри запрещенной зоны, примерно на полпути между минимумом зоны проводимости (нижняя часть первой зоны незаполненных электронных уровней энергии) и максимумом валентной зоны (верхняя часть зоны ниже зоны проводимости заполненных уровней энергии электронов). Это применимо к собственным (нелегированным) полупроводникам. Это означает, что при абсолютном нуле температуры не было бы свободных электронов проводимости, а сопротивление бесконечно. Однако сопротивление уменьшается по мере увеличения плотности носителей заряда (то есть, без дополнительных осложнений, плотности электронов) в зоне проводимости. В примесных (легированных) полупроводниках легирующие атомы увеличивают концентрацию основных носителей заряда, отдавая электроны зоне проводимости или создавая дырки в валентной зоне. («Дырка» – это положение, в котором отсутствует электрон; такие дырки могут вести себя аналогично электронам.) Для обоих типов донорных и акцепторных атомов увеличение плотности примеси снижает сопротивление. Следовательно, высоколегированные полупроводники ведут себя металлически. При очень высоких температурах вклад термически генерируемых носителей преобладает над вкладом атомов примеси, а сопротивление экспоненциально уменьшается с температурой.
В ионных жидкостях / электролитах
В электролитах электрическая проводимость осуществляется не зонными электронами или дырками, а полностью атомарными частицами (ионами ) путешествующие, каждый из которых несет электрический заряд. Удельное сопротивление ионных растворов (электролитов) сильно зависит от концентрации – в то время как дистиллированная вода является почти изолятором, соленая вода является разумным проводником электричества. Проводимость в ионных жидкостях также контролируется движением ионов, но здесь мы говорим о расплавленных солях, а не о сольватированных ионах. В биологических мембранах токи переносятся ионными солями. Небольшие отверстия в клеточных мембранах, называемые ионными каналами, избирательны по отношению к определенным ионам и определяют сопротивление мембраны.
Концентрация ионов в жидкости (например, в водном растворе) зависит от степени диссоциации растворенного вещества, характеризующейся коэффициентом диссоциации α { displaystyle alpha}


- N = α N 0 { displaystyle N = alpha N_ {0}}
.
Удельная электрическая проводимость (σ { displaystyle sigma}
- σ = q (b + + b -) α N 0 { displaystyle sigma = q left (b ^ {+} + b ^ {-} right) alpha N_ {0}}
,
где q { displaystyle q}




Сверхпроводимость
Удельное электрическое сопротивление металлического проводника постепенно уменьшается при понижении температуры. В обычных проводниках, таких как медь или серебро, это уменьшение ограничено примесями и другими дефектами. Даже около абсолютного нуля реальный образец нормального проводника показывает некоторое сопротивление. В сверхпроводнике сопротивление резко падает до нуля, когда материал охлаждается ниже критической температуры. Электрический ток, протекающий в петле из сверхпроводящего провода, может сохраняться бесконечно без источника питания.
В 1986 году исследователи обнаружили, что некоторые купрат – перовскит керамические материалы имеют гораздо более высокие критические температуры, и в 1987 году был произведен один материал с критической температурой выше 90 К (-183 ° C). Такая высокая температура перехода теоретически невозможна для обычного сверхпроводника , поэтому исследователи назвали эти проводники высокотемпературными сверхпроводниками. Жидкий азот кипит при 77 К, достаточно холодном, чтобы активировать высокотемпературные сверхпроводники, но не достаточно холодном для обычных сверхпроводников. В обычных сверхпроводниках электроны удерживаются вместе парами за счет притяжения, связанного с решеточными фононами. Лучшая доступная модель высокотемпературной сверхпроводимости все еще остается грубой. Существует гипотеза, что спаривание электронов в высокотемпературных сверхпроводниках обеспечивается короткодействующими спиновыми волнами, известными как парамагноны.
Плазма
 Молния – пример плазмы, присутствующей на поверхности Земли. Обычно молния разряжает 30 000 ампер при напряжении до 100 миллионов вольт и излучает свет, радиоволны и рентгеновские лучи. Температура плазмы при молнии может приближаться к 30 000 кельвинов (29 727 ° C) (53 540 ° F), что в пять раз выше, чем температура на поверхности Солнца, а плотность электронов может превышать 10 м.
Молния – пример плазмы, присутствующей на поверхности Земли. Обычно молния разряжает 30 000 ампер при напряжении до 100 миллионов вольт и излучает свет, радиоволны и рентгеновские лучи. Температура плазмы при молнии может приближаться к 30 000 кельвинов (29 727 ° C) (53 540 ° F), что в пять раз выше, чем температура на поверхности Солнца, а плотность электронов может превышать 10 м.
Плазма – очень хорошие проводники и электрические потенциалы. играть важную роль.
Потенциал, существующий в среднем в пространстве между заряженными частицами, независимо от того, как его можно измерить, называется потенциалом плазмы или космическим потенциалом. Если электрод вставлен в плазму, его потенциал обычно значительно ниже потенциала плазмы из-за того, что называется оболочкой Дебая. Хорошая электропроводность плазмы делает ее электрические поля очень маленькими. Это приводит к важной концепции квазинейтральности, согласно которой плотность отрицательных зарядов примерно равна плотности положительных зарядов в больших объемах плазмы (n e = ⟨Z⟩>n i), но на шкале длины Дебая может быть дисбаланс заряда. В особом случае, когда образуются двойные слои , разделение зарядов может увеличиваться на несколько десятков длин Дебая.
Величина потенциалов и электрических полей должна определяться другими способами, кроме простого нахождения чистой плотности заряда. Типичным примером является предположение, что электроны удовлетворяют соотношению Больцмана :
- n e ∝ e e Φ / k B T e. { displaystyle n _ { text {e}} propto e ^ {e Phi / k _ { text {B}} T _ { text {e}}}.}
Дифференциация этого отношения дает средства для вычисления электрическое поле от плотности:
- E = – k BT ee ∇ nene. { displaystyle mathbf {E} = – { frac {k _ { text {B}} T _ { text {e}}} {e}} { frac { nabla n _ { text {e}}} {n _ { text {e}}}}.}
(∇ – оператор векторного градиента; дополнительную информацию см. в символе набла и gradient.)
Возможно создание не квазинейтральной плазмы. Электронный луч, например, имеет только отрицательные заряды. Плотность ненейтральной плазмы обычно должна быть очень низкой или очень маленькой. В противном случае отталкивающая электростатическая сила рассеивает его.
В астрофизической плазме экранирование Дебая предотвращает непосредственное воздействие электрических полей на плазму на больших расстояниях, то есть больше, чем длина Дебая. Однако наличие заряженных частиц заставляет плазму генерировать магнитные поля и воздействовать на них. Это может вызвать и вызывает чрезвычайно сложное поведение, такое как образование двойных слоев плазмы, объекта, который разделяет заряд на несколько десятков длин Дебая. Динамика взаимодействия плазмы с внешними и самогенерируемыми магнитными полями изучается в академической дисциплине магнитогидродинамика.
Плазму часто называют четвертым состоянием вещества после твердого тела, жидкостей и газов. Оно отличается от этих и других низкоэнергетических состояний материи. Хотя он тесно связан с газовой фазой в том смысле, что он также не имеет определенной формы или объема, он отличается по ряду причин, включая следующее:
| Свойство | Газ | Плазма |
|---|---|---|
| Электропроводность | Очень низкая: воздух является отличным изолятором, пока не распадется на плазму при напряженности электрического поля выше 30 киловольт на сантиметр. | Обычно очень высокая: для многих целей проводимость плазмы можно считать бесконечной. |
| Независимо действующие частицы | Один: все частицы газа ведут себя одинаково, под влиянием гравитации и столкновений друг с другом. | Два или три: электроны, ионы, протоны и нейтроны можно различить по знаку и значению их заряжают, так что они ведут себя независимо во многих обстоятельствах, с разными объемными скоростями и температурами, что допускает такие явления, как новые типы волн и нестабильности. |
| Распределение скоростей | Максвелловский : столкновения обычно приводят к максвелловскому распределению скоростей всех частиц газа с очень небольшим количеством относительно быстрых частиц. | Часто не максвелловские: столкновительные взаимодействия часто бывают слабыми в горячей плазме, и внешнее воздействие может увести плазму далеко от локального равновесия и привести к значительной популяции необычно быстрых частиц. |
| Взаимодействия | Двоичные: столкновения двух частиц – правило, столкновения трех тел – крайне редко. | Коллективный: волны или организованное движение плазмы очень важны, потому что частицы могут взаимодействовать на больших расстояниях посредством электрических и магнитных сил. |
Удельное сопротивление и проводимость различных материалов
- Проводник, такой как металл, имеет высокую проводимость и низкое удельное сопротивление.
- Изолятор , такой как стекло, имеет низкое проводимость и высокое удельное сопротивление.
- Электропроводность полупроводника обычно является промежуточной, но сильно варьируется в различных условиях, таких как воздействие на материал электрических полей или определенных частот свет, и, что наиболее важно, с температурой и составом полупроводникового материала.
Степень легирования полупроводников имеет большое значение для проводимости. В некотором смысле, большее количество легирования приводит к более высокой проводимости. Электропроводность раствора воды воды в значительной степени зависит от его концентрации растворенных солей и других химических веществ, которые ионизируют в растворе. Электропроводность образцов воды используется как индикатор того, насколько образец не содержит соли, ионов или примесей; чем чище вода, тем ниже проводимость (тем выше удельное сопротивление). Измерения проводимости воды часто выражаются как удельная проводимость по отношению к проводимости чистой воды при 25 ° C. EC-метр обычно используется для измерения проводимости в растворе. Приблизительное резюме выглядит следующим образом:
| Материал | Удельное сопротивление, ρ (Ом · м) |
|---|---|
| Сверхпроводники | 0 |
| Металлы | 10 |
| Полупроводники | Переменная |
| Электролиты | Переменная |
| Изоляторы | 10 |
| Суперизоляторы | ∞ |
В этой таблице показаны удельное сопротивление (ρ), проводимость и температурный коэффициент различных материалов при 20 ° C (68 ° F, 293 K )
| Материал | Удельное сопротивление, ρ,. при 20 ° C (Ом · м) | Проводимость, σ,. при 20 ° C (S / m) | Temperature. coefficient (K) | Reference |
|---|---|---|---|---|
| Silver | 1.59×10 | 6.30×10 | 0.00380 | |
| Copper | 1.68×10 | 5.96×10 | 0.00404 | |
| Annealed copper | 1.72×10 | 5.80× 10 | 0.00393 | |
| Gold | 2.44×10 | 4.11×10 | 0.00340 | |
| Aluminium | 2.65×10 | 3.77×10 | 0.00390 | |
| Calcium | 3.36×10 | 2.98×10 | 0.00410 | |
| Tungsten | 5.60×10 | 1.79×10 | 0.00450 | |
| Zinc | 5.90×10 | 1.69×10 | 0. 00370 | |
| Cobalt | 6.24×10 | 1.60×10 | 0.007 | |
| Nickel | 6.99×10 | 1.43×10 | 0.006 | |
| Ruthenium | 7.10×10 | 1.41×10 | ||
| Lithium | 9.28×10 | 1.08×10 | 0.006 | |
| Iron | 9.70×10 | 10 | 0.005 | |
| Platinum | 1.06×10 | 9.43×10 | 0.00392 | |
| Tin | 1.09×10 | 9.17×10 | 0.00450 | |
| Gallium | 1.40×10 | 7.10×10 | 0.004 | |
| Niobium | 1.40×10 | 7.00×10 | ||
| Carbon steel (1010) | 1.43×10 | 6.99×10 | ||
| Lead | 2.20×10 | 4.55×10 | 0.0039 | |
| Galinstan | 2.89×10 | 3.46×10 | ||
| Titanium | 4.20×10 | 2.38×10 | 0.0038 | |
| Grain oriented electrical steel | 4.60×10 | 2.17×10 | ||
| Manganin | 4.82×10 | 2.07×10 | 0.000002 | |
| Constantan | 4.90×10 | 2.04×10 | 0.000008 | |
| Stainless steel | 6.90×10 | 1.45×10 | 0.00094 | |
| Mercury | 9.80×10 | 1.02×10 | 0.00090 | |
| Mangane se | 1.44×10 | 6.94×10 | ||
| Nichrome | 1.10×10 | 6.70×10. | 0.0004 | |
| Carbon (amorphous) | 5×10 to 8×10 | 1.25×10 to 2.00×10 | −0.0005 | |
| Carbon (graphite). parallel to. basal plane | 2.5×10 to 5.0×10 | 2×10 to 3×10. | ||
| Carbon (graphite). perpendicular to. basal plane | 3×10 | 3.3×10 | ||
| GaAs | 10 to 10 | 10 to 10 | ||
| Germanium | 4.6×10 | 2.17 | −0.048 | |
| Sea water | 2.0×10 | 4.8 | ||
| Swimming pool water | 3.3×10 to 4.0×10 | 0.25 to 0.30 | ||
| Drinking water | 2×10 to 2×10 | 5×10 to 5×10 | ||
| Silicon | 2.3×10 | 4.35×10 | −0.075 | |
| Wood (damp) | 10 to 10 | 10 to 10 | ||
| Deionized water | 1.8×10 | 5. 5 × 10 | ||
| Стекло | от 10 до 10 | от 10 до 10 | ? | |
| Углерод (алмаз) | 10 | ~ 10 | ||
| Твердая резина | 10 | 10 | ? | |
| Воздух | от 10 до 10 | ~ 10 до 10 | ||
| Древесина (высушенная в печи) | 10-10 | 10-10 | ||
| Сера | 10 | 10 | ? | |
| плавленый кварц | 7,5 × 10 | 1,3 × 10 | ? | |
| ПЭТ | 10 | 10 | ? | |
| Тефлон | от 10 до 10 | от 10 до 10 | ? |
Эффективный температурный коэффициент зависит от температуры и уровня чистоты материала. Значение 20 ° C является приблизительным при использовании при других температурах. Например, для меди коэффициент становится ниже при более высоких температурах, и значение 0,00427 обычно указывается при 0 ° C.
Чрезвычайно низкое удельное сопротивление (высокая проводимость) серебра характерно для металлов. Джордж Гамов аккуратно резюмировал природу взаимодействия металлов с электронами в своей научно-популярной книге «Один, два, три… бесконечность» (1947):
Металлические вещества отличаются от всех других материалов тем, что тот факт, что внешние оболочки их атомов связаны довольно слабо и часто позволяют одному из своих электронов уйти на свободу. Таким образом, внутренняя часть металла заполнена большим количеством непривязанных электронов, которые бесцельно путешествуют, как толпа перемещенных лиц. Когда на металлическую проволоку действует электрическая сила, приложенная к ее противоположным концам, эти свободные электроны устремляются в направлении силы, образуя так называемый электрический ток.
С технической точки зрения, модель свободных электронов дает базовое описание электронного потока в металлах.
Древесина широко считается чрезвычайно хорошим изолятором, но ее удельное сопротивление сильно зависит от содержания влаги, при этом влажная древесина как минимум в 10 раз хуже изолирует, чем высушенная в печи. В любом случае достаточно высокое напряжение – например, при ударах молнии или в некоторых высоковольтных линиях электропередачи – может привести к риску пробоя изоляции электрического тока даже для явно сухой древесины.
Температурная зависимость
Линейное приближение
Удельное электрическое сопротивление материала изменяется в зависимости от температуры. Если температура T не меняется слишком сильно, обычно используется линейное приближение :
- ρ (T) = ρ 0 [1 + α (T – T 0)] { displaystyle rho (T) = rho _ {0} [1+ alpha (T-T_ {0})]}
где α { displaystyle alpha}







Металлы
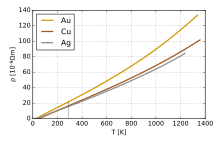 Температурная зависимость удельного сопротивления золота, меди и серебра.
Температурная зависимость удельного сопротивления золота, меди и серебра.
В общем, удельное электрическое сопротивление металлов увеличивается с температурой. Взаимодействия – фонон могут играть ключевую роль. При высоких температурах сопротивления металла линейно увеличивается с температурой. При понижении температуры металла температурная зависимость удельного сопротивления подчиняется степенной функции температуры. Математически температурная зависимость удельного сопротивления металла ρ определяетсялой Блоха – Грюнайзена:
- ρ (T) = ρ (0) + A (T Θ R) n ∫ 0 Θ RT xn (ex – 1) (1 – е – Икс) dx { Displaystyle rho (T) = rho (0) + A left ({ frac {T} { Theta _ {R}}} right) ^ {n} int _ {0} ^ { frac { Theta _ {R}} {T}} { frac {x ^ {n}} { left (e ^ {x} -1 right) left (1- e ^ {- x} right)}} , dx}
где ρ (0) { displaystyle rho (0)}

- n = 5 означает, что сопротивление вызвано рассеянием электронов на фононах (как в случае простых металлов).
- n = 3 означает, что сопротивление возникает из-за sd-рассеяния электронов (как в случае с переходными металлами)
- n = 2 означает, что сопротивление вызывает электрон-электронным взаимодействием.
. значение n.
Температура металла достаточно снижена (чтобы «заморозить» все фононы), удельное сопротивление обычно постоянное значение, известное как остаточное сопротивление . Это значение не только от типа металла, но и от его чистоты и термической истории. Величина остаточного сопротивления металла определяется концентрацией его примесей. Некоторые материалы теряют все электрическое сопротивление при достаточно низких температурах из-за эффекта, известного как сверхпроводимость.
Исследование низкотемпературного сопротивления металлов было мотивацией для экспериментов Хайке Камерлинг-Оннес что привело в 1911 году к открытию сверхпроводимости. Подробнее см. История сверхпроводимости.
Закон Видемана – Франца
Закон Видемана – Франца гласит, что коэффициент электропроводности металлов при нормальных температурах обратно пропорционален температура:
- σ ∼ 1 T { displaystyle sigma Thicksim {1 over T}}
.
При высоких температурах металла закон Видемана-Франца выполнен:
- K σ = π 2 3 (ke) 2 T { Displaystyle {K over sigma} = { pi ^ {2} over 3} left ({ frac {k} {e}} right) ^ {2} T}
,
где K { displaystyle K}




Полупроводники
В общем, собственное удельное сопротивление полупроводника уменьшается с повышением температуры. Электроны попадают в зону энергии проводимости тепловая энергия, где они свободно текут, и при этом оставляют после себя дырки в валентной зоне, которая также течь свободно. Электрическое сопротивление типичного собственного (нелегированного) полупроводника уменьшается экспоненциально с температурой:
- ρ = ρ 0 e – a T { displaystyle rho = rho _ {0} e ^ {- aT} ,}
Еще лучшее приближение температурной зависимости удельного сопротивления полупроводника дается уравнением Стейнхарта – Харта :
- 1 T Знак равно A + В пер ρ + С (пер ρ) 3 { Displaystyle { гидроразрыва {1} {T}} = A + B ln rho + C ( ln rho) ^ {3} ,}
где A, B и C – так называемые коэффициенты Стейнхарта – Харта .
Это уравнение используется для калибровки термисторов.
Внешние (легированные) полупроводники имеют намного больше сложный температурный профиль. При повышении температуры, начиная с абсолютного нуля, их сопротивление сначала резко падает, поскольку носители покидают доноры или акцепторы. После большинства доноров или акцепторов потеряли своих носителей сопротивление снова начинает немного увеличиваться из-за уменьшения подвижности носителей (как в металле). При более высоких температурах они ведут себя как собственные полупроводники, поскольку носители от доноров / акцепторов становятся незначительными по сравнению с термически генерируемыми носителями.
В некристаллических полупроводниках проводимость может происходить за счет зарядов квантовое туннелирование с одного локализованного сайта на другой. Это известно как скачкообразное изменение диапазона и имеет характерную форму
- ρ = A exp (T – 1 n), { displaystyle rho = A exp left (T ^ {- { frac {1} {n}}} right),}
где n = 2, 3, 4, в зависимости от размерности системы.
Комплексное сопротивление и проводимость
При реакции материалов на переменные электрические поля (электрический спектроскопия ) в таких приложениях, как томография электрического импеданса, удобно заменить удельное сопротивление на комплексную определяемую импедансом (по аналогии с электрическим импедансом ). Импедивность – это сумма реальной составляющей, удельного сопротивления и мнимой составляющей, реактивности (по аналогии с реактивным сопротивлением ). Величина импеданса – это квадратный корень из суммы квадратов значений удельного сопротивления и реактивности.
И наоборот, в таких случаях проводимость должна быть выражена в виде комплексного числа (или даже в виде матрицы комплексных чисел в случае анизотропных материалов), называемых допустимость. Адмиттивная способность – сумма проводимой составляющей, называемой способностию, и мнимой составляющей, называемой восприимчивостью.
. В альтернативном описании реакции на переменные токи используется реальная (но частотно-зависимая) проводимость, а также реальная диэлектрическая проницаемость. Чем больше проводимость, тем быстрее сигнал переменного тока поглощается (т.е. тем более непрозрачным является материалом). Подробнее см. Математическое описание непрозрачности.
Сопротивление в зависимости от формы сопротивления в геометрических формах
Даже если сопротивление материала известно, расчет сопротивления чего-либо, сделанного из него, в некоторых случаях может быть значительным. сложнее, чем формула R = ρ ℓ / A { displaystyle R = rho ell / A}
В подобных случаях формулы
- J = σ E ⇌ E = ρ J { displaystyle J = sigma E , , rightleftharpoons , , E = rho J , !}
необходимо заменить на
- J (r) = σ (r) E (r) ⇌ E (r) = ρ (r) J (r), { displaystyle mathbf {J} ( mathbf {r }) = sigma ( mathbf {r}) mathbf {E} ( mathbf {r}) , , rightleftharpoons , , mathbf {E} ( mathbf {r}) = rho ( mathbf {r}) mathbf {J} ( mathbf {r}), , !}
где E и J теперь присутствует поля. Это уравнение, вместе с уравнением неразрывности для J и уравнением Пуассона для E, образуют набор частных производных уравнений. “В особых точных или приближенных решениях” таких как анализ конечных элементов.
Произведение удельного сопротивления на плотность
В некоторых приложениях, где вес объекта очень важен, произведение удельного сопротивления и плотности более важно, чем абсолютно низкое удельное сопротивление – часто можно сделать проводник толще, чтобы компенсировать более высокое удельное сопротивление; и тогда желателен продукт с низким удельным сопротивлением и плотностью (или, что эквивалентно, с высоким отношением к плотности). Например, для междугородных воздушных линий электропередачи часто используется алюминий, а не медь (Cu), поскольку он легче при той же проводимости.
Серебро, хотя и является наименования резистивным из известных металлов, высокая плотность и по своим характеристикам аналогично меди, но намного дороже. Кальций и щелочные металлы используют лучшие произведения удельного сопротивления, но редко используются для проводников из-за их высокой реакционной способности с водой и кислородом (и прочности физической). Алюминий гораздо более устойчиво. Токсичность исключает выбор бериллия. (Чистый бериллий также является хрупким.) Таким образом, алюминий обычно является предпочтительным металлом, когда решающим фактором является вес или стоимость проводника.
| Материал | Удельное сопротивление. (нОм · м) | Плотность. (г / см) | Удельное сопротивление × плотность | …, Относительно Cu, что дает. такую же проводимость | Приблизительная цена, на. 9 декабря 2018 г. | |||
|---|---|---|---|---|---|---|---|---|
| (г · мОм / м) | Относительно. к Cu | Объем | Масса | (долл. США за кг) | относительно Cu | |||
| натрия | 47,7 | 0,97 | 46 | 31% | 2,843 | 0,31 | ||
| Литий | 92,8 | 0,53 | 49 | 33% | 5,531 | 0,33 | ||
| Кальций | 33,6 | 1,55 | 52 | 35% | 2,002 | 0,35 | ||
| Калий | 72,0 | 0,89 | 64 | 43% | 4,291 | 0,43 | ||
| Бериллий | 35,6 | 1,85 | 66 | 44% | 2,122 | 0,44 | ||
| Алюминий | 26,50 | 2,70 | 72 | 48% | 1,5792 | 0,48 | 2,0 | 0,16 |
| Магний | 43,90 | 1,74 | 7 6 | 51% | 2,616 | 0,51 | ||
| Медь | 16,78 | 8,96 | 150 | 100% | 1 | 1 | 6,0 | 1 |
| Серебро | 15,87 | 10,49 | 166 | 111% | 0, 946 | 1,11 | 456 | 84 |
| Золото | 22,14 | 19,30 | 427 | 285% | 1,319 | 2,85 | 39000 | 19000 |
| Железо | 96,1 | 7,874 | 757 | 505% | 5,727 | 5,05 |
См.
Примечания
Ссылки
Дополнительная литература
- Типлер (2004). Физика для ученых и инженеров: электричество, магнетизм, свет и элементарная современная физика (5-е изд.). В. Х. Фриман. ISBN 978-0-7167-0810-0.
- Измерение удельного электрического сопротивления и проводимости
































![{ displaystyle rho (T) = rho _ {0} [1+ альфа (T-T_ {0})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f0d28efd73ce74b1399b50c01300a171066e9be)






