Для того чтобы нагреть на определённую величину тела, взятые при одинаковой температуре, изготовленные из различных веществ, но имеющие одинаковую массу, требуется разное количество теплоты.
Пример:
для нагревания (1) кг воды на (1°C) требуется количество теплоты, равное (4200) Дж. А если нагревать (1) кг цинка на (1°C), то потребуется всего (400) Дж.
Удельная теплоёмкость вещества — физическая величина, численно равная количеству теплоты, которое необходимо передать веществу массой (1) кг для того, чтобы его температура изменилась на (1~°C).
([c]=1frac{Дж}{кг cdot °C}).
Пример:
по таблице удельной теплоёмкости твёрдых веществ находим, что удельная теплоёмкость алюминия составляет (c(Al)=920 frac{Дж}{кг cdot °C}). Поэтому при охлаждении (1) килограмма алюминия на (1) градус Цельсия ((°C)) выделяется (920) джоулей энергии. Столько же необходимо для нагревания (1) килограмма на алюминия на (1) градус Цельсия ((°C)).
Ниже представлены значения удельной теплоёмкости для некоторых веществ.
Твёрдые вещества
|
Вещество |
(c), Дж/(кг·°C) |
| Алюминий |
(920) |
| Бетон |
(880) |
| Дерево |
(2700) |
|
Железо, сталь |
(460) |
| Золото |
(130) |
| Кирпич |
(750) |
| Латунь |
(380) |
| Лёд |
(2100) |
| Медь |
(380) |
| Нафталин |
(1300) |
| Олово |
(230) |
| Парафин |
(3200) |
| Песок |
(970) |
| Платина |
(130) |
| Свинец |
(120) |
| Серебро |
(240) |
| Стекло |
(840) |
| Цемент |
(800) |
| Цинк |
(400) |
| Чугун |
(550) |
| Сера |
(710) |
Жидкости
|
Вещество |
(c), Дж/(кг·°C) |
| Вода |
(4200) |
| Глицерин |
(2400) |
| Керосин |
(2140) |
|
Масло подсолнечное |
(1700) |
|
Масло трансформаторное |
(2000) |
| Ртуть |
(120) |
|
Спирт этиловый |
(2400) |
|
Эфир серный |
(2300) |
Газы (при постоянном давлении и температуре (20°C))
|
Вещество |
(c), Дж/(кг·°C) |
| Азот |
(1000) |
| Аммиак |
(2100) |
| Водород |
(14300) |
|
Водяной пар |
(2200) |
| Воздух |
(1000) |
| Гелий |
(5200) |
| Кислород |
(920) |
|
Углекислый газ |
(830) |
Удельная теплоёмкость реальных газов, в отличие от идеальных газов, зависит от давления и температуры. И если зависимостью удельной теплоёмкости реальных газов от давления в практических задачах можно пренебречь, то зависимость удельной теплоёмкости газов от температуры необходимо учитывать, поскольку она очень существенна.
Обрати внимание!
Удельная теплоёмкость вещества, находящегося в различных агрегатных состояниях, различна.
Пример:
вода в жидком состоянии имеет удельную теплоёмкость, равную (4200) Дж/(кг·°C), в твёрдом состоянии (лёд) — (2100) Дж/(кг·°C), в газообразном состоянии (водяной пар) — (2200) Дж/(кг·°C).
Вода — вещество особенное, обладающее самой высокой среди жидкостей удельной теплоёмкостью. Но самое интересное, что теплоёмкость воды снижается при температуре от (0°C) до (37°C) и снова растёт при дальнейшем нагревании (рис. (1)).

Рис. (1). График удельной теплоёмкости воды
В связи с этим вода в морях и океанах, нагреваясь летом, поглощает из окружающей среды огромное количество теплоты. А зимой вода остывает и отдаёт в окружающую среду большое количество теплоты. Это явление оказывает влияние на климат данного региона. Летом здесь нет изнуряющей жары, а зимой — лютых морозов.
Высокая удельная теплоёмкость воды нашла широкое применение в различных областях: от медицинских грелок до систем отопления и охлаждения.
Задумывались ли вы, почему воду используют при тушении пожаров? Из-за большой теплоёмкости. При соприкосновении с горящим предметом вода забирает у него большое количество теплоты. Оно значительно больше, чем при использовании такого же количества любой другой жидкости.
Помимо непосредственного отвода тепла, вода гасит пламя ещё и косвенным образом. Водяной пар, образующийся при контакте с огнём, окутывает горящее тело, предотвращая поступление кислорода, без которого горение невозможно.
Какой водой эффективнее тушить огонь: горячей или холодной? Горячая вода тушит огонь быстрее, чем холодная. Дело в том, что нагретая вода скорее превратится в пар, а значит, и отсечёт поступление воздуха к горящему объекту.
Источники:
Рис. 1. Автор: Epop — собственная работа. Общественное достояние, https://commons.wikimedia.org/w/index.php?curid=10750129.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 13 января 2022 года; проверки требуют 7 правок.

Молекулы имеют внутреннюю структуру, образованную атомами, которые могут совершать колебания внутри молекул. Кинетическая энергия, запасённая в этих колебаниях, отвечает не только за температуру вещества, но и за его теплоёмкость
Уде́льная теплоёмкость — это отношение теплоёмкости к массе, теплоёмкость единичной массы вещества (разная для различных веществ); физическая величина, численно равная количеству теплоты, которое необходимо передать единичной массе данного вещества для того, чтобы его температура изменилась на единицу[1].
В Международной системе единиц (СИ) удельная теплоёмкость измеряется в джоулях на килограмм на кельвин, Дж/(кг·К)[2]. Иногда используются и внесистемные единицы: калория/(кг·°C) и т. д.
Удельная теплоёмкость обычно обозначается буквами c или С, часто с индексами.
На значение удельной теплоёмкости влияет температура вещества и другие термодинамические параметры. К примеру, измерение удельной теплоёмкости воды даст разные результаты при 20 °C и 60 °C. Кроме того, удельная теплоёмкость зависит от того, каким образом позволено изменяться термодинамическим параметрам вещества (давлению, объёму и т. д.); например, удельная теплоёмкость при постоянном давлении (CP) и при постоянном объёме (CV), вообще говоря, различны.
Формула расчёта удельной теплоёмкости:
где
- c — удельная теплоёмкость(от лат. capacite – емкость, вместимость),
- Q — количество теплоты, полученное веществом при нагреве (или выделившееся при охлаждении),
- m — масса нагреваемого (охлаждающегося) вещества,
- ΔT — разность конечной и начальной температур вещества.
Удельная теплоёмкость зависит от температуры, поэтому более корректной является следующая формула с малыми (формально бесконечно малыми) 

Значения удельной теплоёмкости некоторых веществ[править | править код]
Приведены значения удельной теплоёмкости при постоянном давлении (Cp).
| Вещество | Агрегатное состояние |
Удельная теплоёмкость, кДж/(кг·K) |
|---|---|---|
| Водород | газ | 14,304[3] |
| Аммиак | газ | 4,359—5,475 |
| Гелий | газ | 5,193[3] |
| Вода (300 К, 27 °C) | жидкость | 4,1806[4] |
| Литий | твёрдое тело | 3,582[3] |
| Этанол | жидкость | 2,438[5] |
| Лёд (273 К, 0 °C) | твёрдое тело | 2,11[6] |
| Водяной пар (373 К, 100 °C) | газ | 2,0784[4] |
| Нефтяные масла | жидкость | 1,670—2,010 |
| Бериллий | твёрдое тело | 1,825[3] |
| Азот | газ | 1,040[3] |
| Воздух (100 % влажность) | газ | 1,030 |
| Воздух (сухой, 300 К, 27 °C) | газ | 1,007[7] |
| Кислород (O2) | газ | 0,918[3] |
| Алюминий | твёрдое тело | 0,897[3] |
| Графит | твёрдое тело | 0,709[3] |
| Стекло кварцевое | твёрдое тело | 0,703 |
| Чугун | твёрдое тело | 0,554[8] |
| Алмаз | твёрдое тело | 0,502 |
| Сталь | твёрдое тело | 0,468[8] |
| Железо | твёрдое тело | 0,449[3] |
| Медь | твёрдое тело | 0,385[3] |
| Латунь | твёрдое тело | |
| Молибден | твёрдое тело | 0,251[3] |
| Олово (белое) | твёрдое тело | 0,227[3] |
| Ртуть | жидкость | 0,140[3] |
| Вольфрам | твёрдое тело | 0,132[3] |
| Свинец | твёрдое тело | 0,130[3] |
| Золото | твёрдое тело | 0,129[3] |
| Значения приведены для стандартных условий (T = +25 °C, P = 100 кПа), если это не оговорено особо. |
| Вещество | Удельная теплоёмкость кДж/(кг·K) |
|---|---|
| Древесина | 1,700 |
| Гипс | 1,090 |
| Асфальт | 0,920 |
| Талькохлорит | 0,980 |
| Бетон | 0,880 |
| Мрамор, слюда | 0,880 |
| Стекло оконное | 0,840 |
| Кирпич керамический красный | 0,840—0,880[10] |
| Кирпич силикатный | 0,750—0,840[10] |
| Песок | 0,835 |
| Почва | 0,800 |
| Гранит | 0,790 |
| Стекло кронглас | 0,670 |
| Стекло флинт | 0,503 |
| Сталь | 0,470 |
См. также[править | править код]
- Теплоёмкость
- Объёмная теплоёмкость
- Молярная теплоёмкость
- Теплоёмкость идеального газа
Примечания[править | править код]
- ↑ Для неоднородного (по химическому составу) образца удельная теплоемкость является дифференциальной характеристикой
, меняющейся от точки к точке. Зависит она в принципе и от температуры (хотя во многих случаях изменяется достаточно слабо при достаточно больших изменениях температуры), при этом строго говоря определяется — вслед за теплоёмкостью — как дифференциальная величина и по температурной оси, то есть строго говоря следует рассматривать изменение температуры в определении удельной теплоёмкости не на один градус (тем более не на какую-то более крупную единицу температуры), а на малое
с соответствующим количеством переданной теплоты
. (См. далее основной текст.)
- ↑ Кельвины (К) здесь можно заменять на градусы Цельсия (°C), поскольку эти температурные шкалы (абсолютная и шкала Цельсия) отличаются друг от друга лишь начальной точкой, но не величиной единицы измерения.
- ↑ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 CRC Handbook of Chemistry and Physics / D. R. Lide (Ed.). — 90th edition. — CRC Press; Taylor and Francis, 2009. — P. 4-135. — 2828 p. — ISBN 1420090844.
- ↑ 1 2 CRC Handbook of Chemistry and Physics / D. R. Lide (Ed.). — 90th edition. — CRC Press; Taylor and Francis, 2009. — P. 6-2. — 2828 p. — ISBN 1420090844.
- ↑ CRC Handbook of Chemistry and Physics / D. R. Lide (Ed.). — 90th edition. — CRC Press; Taylor and Francis, 2009. — P. 15-17. — 2828 p. — ISBN 1420090844.
- ↑ CRC Handbook of Chemistry and Physics / D. R. Lide (Ed.). — 90th edition. — CRC Press; Taylor and Francis, 2009. — P. 6-12. — 2828 p. — ISBN 1420090844.
- ↑ CRC Handbook of Chemistry and Physics / D. R. Lide (Ed.). — 90th edition. — CRC Press; Taylor and Francis, 2009. — P. 6-17. — 2828 p. — ISBN 1420090844.
- ↑ 1 2 3 Paul Evans. Specific heat capacity of materials (англ.). The Engineering Mindset (16 октября 2016). Дата обращения: 14 июля 2019. Архивировано 14 июля 2019 года.
- ↑ Spezifische_Wärmekapazität. www.chemie.de. Дата обращения: 29 июня 2021. Архивировано 29 июня 2021 года.
- ↑ 1 2 Плотность и удельная теплоемкость кирпича: таблица значений Архивная копия от 22 марта 2019 на Wayback Machine.
Литература[править | править код]
- Таблицы физических величин. Справочник, под ред. И. К. Кикоина, М., 1976.
- Сивухин Д. В. Общий курс физики. — Т. II. Термодинамика и молекулярная физика.
- Лифшиц E. М. Теплоёмкость // под. ред. А. М. Прохорова Физическая энциклопедия. — М.: «Советская энциклопедия», 1998. — Т. 2.
Вы познакомились с понятиями количества теплоты и удельной теплоемкости. В уроке «Расчет количества теплоты, необходимого для нагревании тела или выделяемого им при охлаждении» вы познакомились с основной формулой, которую мы будем использовать и в этом уроке:
$Q = cm(t_2 — t_1)$
В данном уроке мы рассмотрим задачи на нахождение различных величин, связанных с нагреванием и охлаждением тел. При их решении вам может понадобиться таблица значений удельной теплоемкости различных веществ из прошлого урока.
Задача №1 на расчет количества теплоты
Рассчитайте количество теплоты, необходимое для нагрева $15 space кг$ меди на $80 degree C$.
Дано:
$m = 15 space кг$
$c = 400 frac{Дж}{кг cdot degree C}$
$Delta t = 80 degree C$
$Q — ?$
Показать решение и ответ
Скрыть
Решение:
Для решения этой задачи мы будем использовать формулу для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
В данном случае нам не известны начальная и конечная температуры тела ($t_2$ и $t_1$). Нам известно изменение этой температуры: $Delta t = t_2 — t_1$. Тогда формула для расчета количества теплоты примет вид:
$Q = cm Delta t$.
Подставим значения всех величин и рассчитаем количество теплоты:
$Q = 400 frac{Дж}{кг cdot degree C} cdot 15 space кг cdot 80 degree C = 480 space 000 space Дж = 480 space кДж$.
Ответ: $Q = 480 space кДж$.
Задача №2 на расчет количества теплоты
Рассчитайте количество теплоты, необходимое, чтобы нагреть бассейн объемом $300 space м^3$ на $10 degree C$.
В задаче идет речь о бассейне, а значит, о пресной воде. Она имеет плотность, равную $1000 frac{кг}{м^3}$. Запишем условия задачи и решим ее.
Дано:
$V = 300 space м^3$
$Delta t = 10 degree C$
$c = 4200 frac{Дж}{кг cdot degree C}$
$rho = 1000 frac{кг}{м^3}$
$c = 4200 frac{Дж}{кг cdot degree C}$
$Q — ?$
Показать решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Нам неизвестна масса воды в бассейне, но известен ее объем и плотность. Плотность по определению:
$rho = frac{m}{V}$.
Тогда масса будет равна:
$m = rho V$.
Также нам неизвестны начальная и конечная температуры тела ($t_2$ и $t_1$). Нам известно изменение этой температуры: $Delta t = t_2 — t_1$. Тогда формула для расчета количества теплоты примет вид:
$Q = c rho V Delta t$.
Рассчитаем количество теплоты:
$Q = 4200 frac{Дж}{кг cdot degree C} cdot 1000 frac{кг}{м^3} cdot 300 space м^3 cdot 10 degree C = 12.6 cdot 10^9 space Дж = 12.6 space ГДж$.
Ответ: $Q = 12.6 space ГДж$.
Задача №3 на расчет массы
Найдите массу глицерина, если при нагревании от $10 degree C$ до $15 degree C$ он поглотил $12 space кДж$ теплоты. Удельная теплоемкость глицерина равна $2430 frac{Дж}{кг cdot degree C}$.
Дано:
$Q = 12 space кДж$
$t_1 = 10 degree C$
$t_2 = 15 degree C$
$c = 2430 frac{Дж}{кг cdot degree C}$
СИ:
$Q = 12 cdot 10^3 space Дж$
$m — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Выразим отсюда массу глицерина:
$m = frac{Q}{c(t_2 — t_1)}$.
Рассчитаем:
$m = frac{12 cdot 10^3 space Дж}{2430 frac{Дж}{кг cdot degree C} cdot (15 degree C — 10 degree C)} approx 1 space кг$.
Ответ: $m approx 1 space кг$.
Задача №4 на расчет плотности
Определите плотность машинного масла объемом $1 space л$, если известно, что для увеличения температуры на $30 degree C$ ему требуется передать $45 space кДж$ теплоты. Удельная теплоемкость масла равна $1.67 frac{кДж}{кг cdot degree C}$.
Дано:
$V = 1 space л$
$Q = 45 space кДж$
$c = 1.67 frac{кДж}{кг cdot degree C}$
$Delta t = 30 degree C$
СИ:
$V = 10^{-3} space м^3$
$Q = 45 cdot 10^3 space Дж$
$c = 1.67 cdot 10^3 frac{Дж}{кг cdot degree C}$
$rho — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Нам известны изменение температуры ($Delta t = t_2 — t_1$), количество теплоты и удельная теплоемкость машинного масла. Выразим массу и рассчитаем ее:
$m = frac{Q}{c Delta t} = frac{45 cdot 10^3 space Дж}{1.67 cdot 10^3 frac{Дж}{кг cdot degree C} cdot 30 degree C} approx 0.9 space кг$.
По определению плотности:
$rho = frac{m}{V}$.
Рассчитаем плотность машинного масла:
$rho = frac{0.9 space кг}{10^{-3} space м^3} = 0.9 cdot 10^3 frac{кг}{м^3} = 900 frac{кг}{м^3}$.
Ответ: $rho = 900 frac{кг}{м^3}$.
Задача №5 на расчет удельной теплоемкости
В калориметр было налито $450 space г$ воды, температура которой $20 degree C$. Когда в эту воду погрузили $200 space г$ железных опилок, нагретых до $100 degree C$, температура воды стала равна $24 degree C$. Определите удельную теплоемкость опилок.
Записывая условия задачи, используем индекс “в” для обозначения величин, связанных с водой, и индекс “ж” для обозначения величин, связанных с железными опилками.
Дано:
$m_в = 450 space г$
$m_ж = 200 space г$
$t_{в1} = 20 degree C$
$t_{в2} = 24 degree C$
$c_в = 4200 frac{Дж}{кг cdot degree C}$
$t_{ж1} = 100 degree C$
СИ:
$m_в = 0.45 space кг$
$m_ж = 0.2 space кг$
$с_ж — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела и выделяемого при его охлаждении:
$Q = cm(t_2 — t_1)$.
Запишем эту формулу для воды:
$Q_в = c_в m_в (t_{в2} — t_{в1})$.
Запишем формулу количества теплоты для железных опилок:
$Q_ж = c_ж m_ж (t_{ж2} — t_{ж1})$.
Нагретые железные опилки помещают в воду для их охлаждения. Значит, вода будет нагреваться и поглотит некоторое количество теплоты, а опилки будут охлаждаться и выделят некоторое количество теплоты. Т.е., между этими телами будет происходить теплообмен, для которого действует уже известное вам правило:
Если между телами происходит теплообмен, то внутренняя энергия всех нагревающихся тел увеличивается на столько, на сколько уменьшается внутренняя энергия остывающих тел.
Это значит, что количество теплоты $Q_в$, полученное водой, будет равно количеству теплоту $Q_ж$, которое выделится при охлаждении железных опилок, но с обратным знаком: $Q_в = — Q_ж$.
Подставим выражения, которые дает формула для расчета количества теплоты:
$c_в m_в (t_{в2} — t_{в1}) = — c_ж m_ж (t_{ж2} — t_{ж1})$.
После завершения теплообмена температура воды и температура железных опилок будут равны друг другу: $t_в2 = t_ж2 = t_2$.
Подставим в наше равенство и выразим $c_ж$:
$c_ж = — frac{c_в m_в (t_2 — t_{в1})}{m_ж (t_2 — t_{ж1})}$.
Рассчитаем удельную теплоемкость железных опилок:
$c_ж = — frac{4200 frac{Дж}{кг cdot degree C} cdot 0.45 space кг cdot (24 degree C — 20 degree C)}{0.2 space кг cdot (24 degree C — 100 degree C)} = — frac{7560 space Дж}{- 15.2 space кг cdot degree C} approx 497 frac{Дж}{кг cdot degree C} approx 0.5 frac{кДж}{кг cdot degree C}$.
Ответ: $c_ж approx 0.5 frac{кДж}{кг cdot degree C}$.
Задача №6 на использование графика
Используя график зависимости температуры керосина от сообщенного ему количества теплоты (рисунок 1), определите массу керосина.
Для начала нам нужно записать условия задачи. Из графика мы видим, что начальная температура керосина $t_1$ была равна $0 degree C$. Теперь выберем удобную нам точку на графике. Например, когда керосину сообщили количество теплоты $Q$, равное $2 space кДж$, его температура $t_2$ стала равной $10 degree C$. Теперь мы можем записать условия задачи и решить ее. Удельная теплоемкость керосина известна нам из таблицы.
Дано:
$Q = 2 space кДж$
$t_1 = 0 degree C$
$t_2 = 10 degree C$
$c = 2100 frac{Дж}{кг cdot degree C}$
СИ:
$Q = 2 cdot 10^3 space Дж$
$m — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Выразим отсюда массу:
$m = frac{Q}{c (t_2 — t_1)}$.
Рассчитаем ее:
$m = frac{2 cdot 10^3 space Дж}{2100 frac{Дж}{кг cdot degree C} cdot (10 degree C — 0 degree C)} approx 0.095 space кг approx 100 space г$.
Ответ: $m approx 100 space г$.
Задача №7 на расчет температуры нагрева
Стальной резец массой $2 space кг$ был нагрет до температуры $800 degree C$ и затем опущен в сосуд, содержащий $15 space л$ воды при температуре $10 degree C$. До какой температуры нагреется вода в сосуде?
Записывая условия задачи, используем индекс “в” для обозначения величин, связанных с водой, и индекс “р” для обозначения величин, связанных со стальным резцом.
Дано:
$V_в = 15 space л$
$m_р = 2 space кг$
$t_{р1} = 800 degree C$
$c_р = 500 frac{Дж}{кг cdot degree C}$
$rho_в = 1000 frac{кг}{м^3}$
$c_в = 4200 frac{Дж}{кг cdot degree C}$
$t_{в1} = 10 degree C$
СИ:
$V_в = 15 cdot 10^3 м^3$
$t_{в2} — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Когда нагретый резец опускают в холодную воду, между этими двумя телами происходит теплообмен. Резец остывает и выделяет энергию, а вода получает эту энергию и нагревается. Соответственно, количество теплоты, которое выделится при остывании стального резца, численно будет равно количеству теплоту, которое получит вода.
Когда теплообмен завершится,температуры стального резца и воды будут одинаковы: $t_{в2} = t_{р2} = t_2$.
Запишем формулу для расчета количества теплоты, которое выделится при остывании резца:
$Q_р = с_р m_р (t_2 — t_{р1})$.
Запишем формулу для расчета количества теплоты, которое получила вода:
$Q_в = с_в m_в (t_2 — t_{в1})$.
Приравняем правые части этих уравнений, не забыв про знак “минус”, которые указывает на выделение энергии при охлаждении тела:
$с_р m_р (t_2 — t_{р1}) = — с_в m_в (t_2 — t_{в1})$.
Раскроем скобки:
$с_р m_р t_2 — с_р m_р t_{р1} = — с_в m_в t_2 + с_в m_в t_{в1}$.
Перенесем множители с $t_2$ на одну сторону уравнения и выразим эту температуру, до которой нагреется вода:
$с_р m_р t_2 + с_в m_в t_2 = с_в m_в t_{в1} + с_р m_р t_{р1}$,
$t_2 (с_р m_р + с_в m_в) = с_в m_в t_{в1} + с_р m_р t_{р1}$,
$t_2 = frac{с_в m_в t_{в1} + с_р m_р t_{р1}}{с_р m_р + с_в m_в}$.
Нам неизвестна масса воды, но известны ее плотность и объем. Выразим и рассчитаем массу через эти величины:
$m_в = rho_в V_в = 1000 frac{кг}{м^3} cdot 15 cdot 10^3 м^3 = 15 space кг$.
Теперь мы можем рассчитать температуру $t_2$:
$t_2 = frac{4200 frac{Дж}{кг cdot degree C} cdot 15 space кг cdot 10 degree C + 500 frac{Дж}{кг cdot degree C} cdot 2 space кг cdot 800 degree C}{500 frac{Дж}{кг cdot degree C} cdot 2 space кг + 4200 frac{Дж}{кг cdot degree C} cdot 15 space кг} = frac{630 cdot 10^3 space Дж + 800 cdot 10^3 space Дж}{1 cdot 10^3 frac{Дж}{degree C} + 63 cdot 10^3 frac{Дж}{degree C}} = frac{1430 cdot 10^3 space Дж}{64 cdot 10^3 frac{Дж}{degree C}} approx 22.3 degree C$.
Ответ: $t_2 approx 22.3 degree C$.
Какой температуры получится вода, если смешать $0.02 space кг$ воды при $15 degree C$, $0.03 space кг$ воды при $25 degree C$ и $0.01 space кг$ воды при $60 degree C$?
Дано:
$m_1 = 0.02 space кг$
$t_1 = 15 degree C$
$m_2 = 0.03 space кг$
$t_2 = 25 degree C$
$m_3 = 0.01 space кг$
$t_3 = 60 degree C$
$t — ?$
Посмотреть решение и ответ
Скрыть
Решение:
При смешивании жидкостей разных температур, мы знаем, что внутренняя энергия всех нагревающихся тел увеличивается на столько, на сколько уменьшается внутренняя энергия остывающих тел.
Для смешивания двух жидкостей мы можем записать, что $Q_1 = — Q_2$ или $Q_1 + Q_2 = 0$.
Сначала рассмотрим смешивание первых двух порций воды. Первая порция с температурой $15 degree C$ будет нагреваться (получать энергию), а вторая порция с температурой $25 degree C$ будет охлаждаться (выделять энергию). Эти энергии будут численно равны друг другу, но противоположны по знаку:
$cm_1(t_{1+2} — t_1) = — cm_2(t_{1+2} — t_2)$.
Найдем конечную температуру этой смеси:
$m_1(t_{1+2} — t_1) = — m_2 (t_{1+2} — t_2)$,
$m_1 t_{1+2} — m_1 t_1 = -m_2 t_{1+2} + m_2 t_2$,
$t_{1+2} (m_1 + m_2) = m_1 t_1 + m_2 t_2$,
$t_{1+2} = frac{m_1 t_1 + m_2 t_2}{m_1 + m_2} = frac{0.02 space кг cdot 15 degree C + 0.03 space кг cdot 25 degree }{0.02 space кг + 0.03 space кг} = frac{0.3 space кг cdot degree + 0.75 space кг cdot degree C}{0.05 space кг} = 21 degree C$.
Так мы получили смесь первой и второй порций воды массой $m_{1+2} = 0.05 space кг$ и температурой $t_{1+2} = 21 degree C$.
Теперь добавим третью порцию воды в полученную смесь. Смесь будет нагреваться (получать энергию), а третья порция воды будет охлаждаться (выделять энергию):
$Q_{1+2} = — Q_3$.
$cm_{1+2} (t — t_{1+2}) = — cm_3 (t — t_3)$,
$m_{1+2} (t — t_{1+2}) = — m_3 (t — t_3)$.
Выразим отсюда конечную температуру смеси из трех порций воды $t$:
$m_{1+2} t — m_{1+2} t_{1+2} = -m_3 t + m_3 t_3$,
$t (m_{1+2} + m_3) = m_{1+2} t_{1+2} + m_3 t_3$,
$t = frac{m_{1+2} t_{1+2} + m_3 t_3}{m_{1+2} + m_3}$.
Рассчитаем ее:
$t = frac{0.05 space кг cdot 21 degree C + 0.01 space кг cdot 60 degree}{0.05 space кг + 0.01 space кг} = frac{1.05 space кг cdot degree C + 0.6 space кг cdot degree C}{0.06 space кг} = 27.5 degree C$.
Ответ: $t = 27.5 degree C$.
Задача №9 на расчет количества теплоты, рассеиваемого в окружающую среду
Электрочайник с водой нагревается от температуры $70 degree C$ до температуры $80 degree C$ за $3 space мин$, а остывает от температуры $80 degree C$ до температуры $70 degree C$ за $9 space мин$. Какая часть количества теплоты, выделяемой спиралью чайника при нагревании воды, рассеивается в окружающую среду? Тепловые потери считать постоянными.
Внесем необходимые пояснения. Спираль чайника передает воде определенное количество теплоты $Q_2$. Часть ее ($Q_1$) рассеивается в окружающую среду. Т.е., количество теплоты $Q_2$, выделяемое спиралью, больше количества теплоты $Q$, необходимого для нагрева воды.
Дано:
$t_1 = 70 degree C$
$t_2 = 80 degree C$
$T_1 = 3 space мин$
$T_2 = 9 space мин$
$frac{Q_1}{Q_2} — ?$
Показать решение и ответ
Скрыть
Решение:
Сначала рассчитаем количество теплоты, которое необходимо сообщить воде в чайнике, чтобы ее температура увеличилась с $70 degree C$ до $80 degree C$:
$Q = cm(t_2 — t_1)$.
Масса воды в чайнике нам неизвестна, поэтому примем ее, равной $1 space кг$. Тогда,
$Q = 4200 frac{Дж}{кг cdot degree C} cdot 1 space кг cdot (80 degree C — 70 degree C) = 42 space 000 space Дж = 42 space кДж$.
Когда вода в чайнике остывает с температуры $80 degree C$ до температуры $70 degree C$, она выделяет в окружающую среду точно такое же количество энергии $Q$. Остывание происходит за $9 space мин$. Значит, количество теплоты, которое выделяется в окружающую среду за $1 space мин$ будет равно:
$Q_0 = frac{42 space кДж}{9 space мин} approx 4.7 frac{кДж}{мин}$.
В условиях задачи сказано, что тепловые потери постоянны. Это означает, что вода массой $1 space кг$ отдает $4.7 space кДж$ каждую минуту, в том числе, и при ее нагревании.
Нагревается вода за 3 минуты. За это время она отдает в окружающую среду следующее количество теплоты:
$Q_1 = 4.7 space кДж cdot 3 = 14.1 space кДж$.
Тем не менее, чайник нагрел воду до нужной температуры. Значит, он сообщил воде количество энергии, равное $Q_2 = Q + Q_1$.
$Q_2 = 42 space кДж + 14.1 space кДж = 56.1 space кДж$.
Теперь мы можем рассчитать отношение $frac{Q_1}{Q_2}$, и узнать какая часть теплоты, выделяемая спиралью чайника, рассеивается в окружающую среду:
$frac{Q_1}{Q_2} = frac{14.1 space кДж}{56.1 space кДж} approx 0.25$.
Т.е., в окружающую среду рассеивается $frac{1}{4}$ часть энергии, сообщаемая воде в чайнике.
Можно доказать, что это соотношение останется постоянным для воды любой массы в этой задаче. Чем больше будет масса воды, тем больше энергии ей будет нужно, чтобы нагреться до определенной температуры. Больше будут и тепловые потери. Искомое соотношение же останется неизменным.
Ответ: $frac{Q_1}{Q_2} approx 0.25$.
Удельная теплоёмкость — это энергия, которая требуется для увеличения температуры 1 грамма чистого вещества на 1°. Параметр зависит от его химического состава и агрегатного состояния: газообразное, жидкое или твёрдое тело. После его открытия начался новый виток развития термодинамики, науки о переходных процессах энергии, которые касаются теплоты и функционирования системы.
Как правило, удельная теплоёмкость и основы термодинамики используются при изготовлении радиаторов и систем, предназначенных для охлаждения автомобилей, а также в химии, ядерной инженерии и аэродинамике. Если вы хотите узнать, как рассчитывается удельная теплоёмкость, то ознакомьтесь с предложенной статьёй.
Содержание:
- Формула
- Инструкция по расчёту параметра
- Расчёт
- Как рассчитать теплоемкость продуктов питания
- Полезные советы
- Видео
Формула
Перед тем, как приступить к непосредственному расчёту параметра следует ознакомиться с формулой и её компонентами.
Формула для расчёта удельной теплоёмкости имеет следующий вид:
- с = Q/(m*∆T)
Знание величин и их символических обозначений, использующихся при расчёте, крайне важно. Однако необходимо не только знать их визуальный вид, но и чётко представлять значение каждого из них. Расчёт удельной теплоёмкости вещества представлен следующими компонентами:
ΔT – символ, означающий постепенное изменение температуры вещества. Символ «Δ» произносится как дельта.
ΔT можно рассчитать по формуле:
ΔT = t2–t1, где
- t1 – первичная температура;
- t2 – конечная температура после изменения.
m – масса вещества используемого при нагреве (гр).
Q – количество теплоты (Дж/J)
На основании Цр можно вывести и другие уравнения:
- Q = m*цp*ΔT – количество теплоты ;
- m = Q/цр*(t2 – t1) – массы вещества;
- t1 = t2–(Q/цp*m) – первичной температуры;
- t2 = t1+(Q/цp*m) – конечной температуры.
Инструкция по расчёту параметра
Рассчитать с вещества достаточно просто и чтобы это сделать нужно, выполнить следующие шаги:
- Взять расчётную формулу: Теплоемкость = Q/(m*∆T)
- Выписать исходные данные.
- Подставить их в формулу.
- Провести расчёт и получим результат.
В качестве примера произведём расчёт неизвестного вещества массой 480 грамм обладающего температурой 15ºC, которая в результате нагрева (подвода 35 тыс. Дж) увеличилась до 250º.
Согласно инструкции приведённой выше производим следующие действия:
Выписываем исходные данные:
- Q = 35 тыс. Дж;
- m = 480 г;
- ΔT = t2–t1 =250–15 = 235 ºC.
Берём формулу, подставляем значения и решаем:
с=Q/(m*∆T)=35тыс.Дж/(480 г*235º)=35тыс.Дж/(112800 г*º)=0,31 Дж/г*º.

Расчёт
Выполним расчёт CP воды и олова при следующих условиях:
- m = 500 грамм;
- t1 =24ºC и t2 = 80ºC – для воды;
- t1 =20ºC и t2 =180ºC – для олова;
- Q = 28 тыс. Дж.
Для начала определяем ΔT для воды и олова соответственно:
- ΔТв = t2–t1 = 80–24 = 56ºC
- ΔТо = t2–t1 = 180–20 =160ºC
Затем находим удельную теплоёмкость:
- с=Q/(m*ΔТв)= 28 тыс. Дж/(500 г *56ºC) = 28 тыс.Дж/(28 тыс.г*ºC) = 1 Дж/г*ºC.
- с=Q/(m*ΔТо)=28тыс.Дж/(500 гр*160ºC)=28 тыс.Дж/(80 тыс.г*ºC)=0,35 Дж/г*ºC.
Таким образом, удельная теплоемкость воды составила 1 Дж/г *ºC, а олова 0,35 Дж/г*ºC. Отсюда можно сделать вывод о том, что при равном значении подводимого тепла в 28 тыс. Дж олово нагрется быстрее воды, поскольку его теплоёмкость меньше.
Теплоёмкостью обладают не только газы, жидкости и твёрдые тела, но и продукты питания.
Как рассчитать теплоемкость продуктов питания
При расчёте емкости питания уравнение примет следующий вид:
с=(4.180*w)+(1.711*p)+(1.928*f)+(1.547*c)+(0.908 *a), где:
- w – количество воды в продукте;
- p – количество белков в продукте;
- f – процентное содержание жиров;
- c – процентное содержание углеводов;
- a – процентное содержание неорганических компонентов.
Определим теплоемкость плавленого сливочного сыра Viola. Для этого выписываем нужные значения из состава продукта (масса 140 грамм):
- вода – 35 г;
- белки – 12,9 г;
- жиры – 25,8 г;
- углеводы – 6,96 г;
- неорганические компоненты – 21 г.
Затем находим с:
- с=(4.180*w)+(1.711*p)+(1.928*f)+(1.547*c)+(0.908*a)=(4.180*35)+(1.711*12,9)+(1.928*25,8) + (1.547*6,96)+(0.908*21)=146,3+22,1+49,7+10,8+19,1=248 кДж /кг*ºC.

Полезные советы
Всегда помните, что:
- процесс нагревания металла проходит быстрее, чем у воды, так как он обладает CP в 2,5 раза меньше;
- по возможности преобразуйте полученные результаты в более высокий порядок, если позволяют условия;
- в целях проверки результатов можно воспользоваться интернетом и посмотреть с для расчётного вещества;
- при равных экспериментальных условиях более значительные температурные изменения будут наблюдаться у материалов с низкой удельной теплоёмкостью.
Видео
Разобраться в этой теме вам поможет видео урок.
Привет
Измерение удельной теплоемкости твердого тела
Цель работы: определить удельную теплоемкость металлического цилиндра.
Приборы и материалы: стакан с водой, калориметр, термометр, весы, гири, металлический цилиндр на нити, сосуд с горячей водой.
Ход работы:
1. Нальем в калориметр воду массой 0,120 кг и измерим ее температуру (20°С).
2. Нагреем цилиндр в сосуде с горячей водой. Измерим температуру воды (70°С), и опустим цилиндр в колориметр с холодной водой.
3. Немного подождем и измерим температуру воды в калориметре (ЗО0С).
4. Вытащим цилиндр из калориметра, обсушим его и измерим его массу на весах (0,140 кг).
5. Все результаты измерений занесем в таблицу и рассчитаем удельную теплоемкость металлического цилиндра.
Результаты: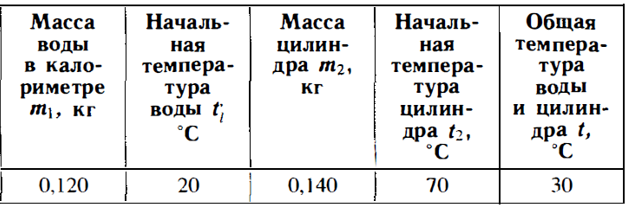
Вычислим удельную теплоемкость металлического цилиндра по формуле с2 =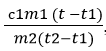 где с2 – удельная теплоемкость металлического цилиндра; с1 = 4200
где с2 – удельная теплоемкость металлического цилиндра; с1 = 4200 ![]() – удельная теплоемкость воды; m1 – масса воды в калорифере; t – температура нагретой цилиндром воды в калорифере; t1 – температура холодной воды; t2 – масса металлического цилиндра; t2 – температура нагретого металлического цилиндра.
– удельная теплоемкость воды; m1 – масса воды в калорифере; t – температура нагретой цилиндром воды в калорифере; t1 – температура холодной воды; t2 – масса металлического цилиндра; t2 – температура нагретого металлического цилиндра.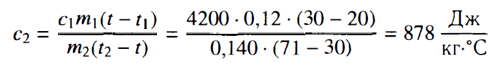
Выводы: Удельная теплоемкость металлического цилиндра равна 878 ![]() , что близко к значению удельной теплоемкости для алюминия. Полученное значение несколько меньше табличного, что связано с невысокой точностью приборов и наличием теплообмена.
, что близко к значению удельной теплоемкости для алюминия. Полученное значение несколько меньше табличного, что связано с невысокой точностью приборов и наличием теплообмена.


