Как найти удельную теплоемкость при постоянном объеме

Как найти удельную теплоемкость при постоянном объеме

При введении
понятия теплоемкости мы не обращали
внимание на одно существенное
обстоятельство: теплоемкости зависят
не только от свойств вещества, но и от
процесса, при котором осуществляется
теплопередача.

Если нагревать
тело при постоянном давлении, то оно
будет расширяться и совершать работу.
Для нагревания тела на 1 К при постоянном
давлении ему нужно передать большее
количество теплоты, чем при таком же
нагревании при постоянном объеме.

Жидкие и твердые
тела расширяются при нагревании
незначительно, и их теплоемкости при
постоянном объеме и постоянном давлении
мало различаются. Но для газов это
различие существенно. С помощью первого
закона термодинамики можно найти связь
между теплоемкостями газа при постоянном
объеме и постоянном давлении.

Теплоемкость газа при постоянном объеме Найдем молярную теплоемкость газа при постоянном объеме. Согласно определению теплоемкости

где
ΔT
—
изменение температуры. Если процесс
происходит при постоянном объеме, то
эту теплоемкость обозначим через Cv.
Тогда

(5.6.1)

При постоянном
объеме работа не совершается. Поэтому
первый закон термодинамики запишется
так:


(5.6.2)

Изменение
энергии одного моля достаточно
разреженного (идеального) одноатомного
газа равно:

(см.
§ 4.8).

Следовательно,
молярная теплоемкость при постоянном
объеме одноатомного газа равна:


(5.6.3)

Теплоемкость газа при постоянном давлении

Согласно
определению теплоемкости при постоянном
давлении Ср


(5.6.4)

Работа, которую
совершит 1 моль идеального газа,
расширяющегося при постоянном давлении,
равна:


(5.6.5)

* Из формулы (5.6.5)
видно, что универсальная газовая
постоянная численно равна работе,
которую совершает 1 моль идеального
газа при постоянном давлении, если
температура его увеличивается на 1К.

Это
следует из выражения для работы газа
при постоянном давлении А’
= pΔV
и
уравнения состояния (для одного моля)
идеального газа pV
=
RT.

Внутренняя
энергия идеального газа от объема не
зависит. Поэтому и при постоянном
давлении изменение внутренней энергии
ΔU
= CVΔT,
как
и при постоянном объеме. Применяя первый
закон термодинамики, получим:


(5.6.6)

Следовательно,
молярные теплоемкости идеального газа
связаны соотношением


(5.6.7)

Впервые эта формула
была получена Р. Майером и носит его
имя.

В случае идеального
одноатомного газа


(5.6.8)

Теплоемкость идеального газа при изотермическом процессе

Можно формально
ввести понятие теплоемкости и при
изотермическом процессе. Так как при
этом процессе внутренняя энергия
идеального газа не меняется, какое бы
количество теплоты ему ни было передано,
то теплоемкость бесконечна.

Молярная
теплоемкость идеального газа при
постоянном давлении больше теплоемкости
при постоянном объеме на величину
универсальной газовой постоянной R.

§ 5.7. Адиабатный процесс

Мы
рассмотрели изотермический, изобарный
и изохорный процессы. После ознакомления
с первым законом термодинамики появляется
возможность изучить еще один процесс,
—
это
процесс, протекающий в системе при
отсутствии теплообмена с окружающими
телами. (Но работу над окружающими телами
система может совершать.)

Процесс в
теплоизолированной системе называют
адиабатным.

При
адиабатном процессе Q
=
0 и согласно закону (5.5.3) изменение
внутренней энергии происходит только
за счет совершения работы:


(5.7.1)

Конечно, нельзя
окружить систему оболочкой, абсолютно
исключающей теплообмен. Но в ряде случаев
реальные процессы очень близки к
адиабатным. Существуют оболочки,
обладающие малой теплопроводностью,
например двойные стенки с вакуумом
между ними. Так изготовляются термосы.

Процесс можно
считать адиабатным даже без теплоизолирующей
оболочки, если он происходит достаточно
быстро, т. е. так, чтобы за время процесса
не происходило заметного теплообмена
между системой и окружающими телами.

Согласно
выражению (5.7.1) при совершении над
системой положительной работы, например
при сжатии газа, внутренняя энергия его
увеличивается; газ нагревается. Наоборот,
при расширении газ сам совершает
положительную работу (А’ > 0), но А
< 0
и внутренняя энергия его уменьшается;
газ охлаждается.

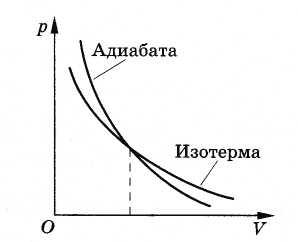
Зависимость
давления газа от его объема при адиабатном
процессе изображается кривой, называемой
адиабатой
(рис. 5.9). Адиабата обязательно идет круче
изотермы. Ведь при адиабатном процессе
давление газа уменьшается не только за
счет увеличения объема, как при
изотермическом процессе, но и за счет
уменьшения его температуры.

Рис. 5.9

Адиабатные процессы
широко используются в технике. Они
играют немалую роль в природе.

Нагревание воздуха
при быстром сжатии нашло применение в
двигателях Дизеля. В этих двигателях
отсутствуют системы приготовления и
зажигания горючей смеси, необходимые
для обычных бензиновых двигателей
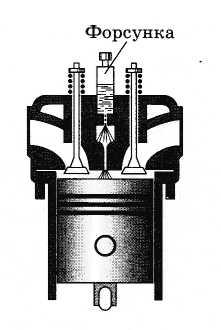
внутреннего сгорания. В цилиндр
засасывается не горючая смесь, а
атмосферный воздух. К концу такта сжатия
в цилиндр с помощью специальной форсунки
впрыскивается жидкое топливо (рис.
5.10). К этому моменту температура сжатого
воздуха так велика, что горючее
воспламеняется.

Рис. 5.10

Так как в двигателе
Дизеля сжимается не горючая смесь, а
воздух, то степень сжатия у этого
двигателя больше, а значит, коэффициент
полезного действия (КПД) двигателей
Дизеля выше, чем у обычных двигателей
внутреннего сгорания. Кроме того, они
могут работать на более дешевом
низкосортном топливе. Есть, однако, у
двигателя Дизеля и недостатки:
необходимость высоких степеней сжатия
и большое рабочее давление делают эти
двигатели массивными и вследствие этого
более инерционными — они медленнее
набирают мощность. Двигатели Дизеля
более сложны в изготовлении и эксплуатации,
тем не менее они постепенно вытесняют
обычные бензиновые двигатели, используемые
в автомобилях.

Охлаждение газа
при адиабатном расширении происходит
в грандиозных масштабах в атмосфере
Земли. Нагретый воздух поднимается
вверх и расширяется, так как атмосферное
давление падает с высотой. Это расширение
сопровождается значительным охлаждением.
В результате водяные пары конденсируются
и образуются облака.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Теплоемкости при постоянном давлении и постоянном объеме

При сообщении телу некоторого количества теплоты изменяется его температура (за исключением агрегатных превращений и вообще изотермических процессов). Характеристиками такого изменения являются различные теплоемкости: теплоемкость тела CT, удельная теплоемкость вещества c, молярная теплоемкость C.

Понятия теплоемкости тела и удельной теплоемкости рассмотрены тут.

Молярная теплоемкость C — величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К:

(~C = frac{Q}{nu Delta T} . qquad (1))

Единицей молярной теплоемкости в СИ является джоуль на моль-Кельвин (Дж/моль·К).

Удельная теплоемкость связана с молярной соотношением

(~C = cM. )

В отличие от такой, например, характеристики вещества, как его молекулярная масса Mr удельная теплоемкость вещества не является неизменным параметром. Удельная теплоемкость может резко изменяться при переходе вещества из одного агрегатного состояния в другое. Так, вода в газообразном состоянии имеет удельную теплоемкость 2,2·103 Дж/кг·К а в жидком 4,19·103 Дж/кг·К .

Теплоемкость зависит и от условий, при которых происходит передача теплоты телу. Последнее особенно относится к газам. Например, при изотермическом расширении газа ему передается некоторое количество теплоты Q > 0, а ΔΤ = 0. Следовательно, удельная теплоемкость газа при изотермическом процессе

(~c = frac{Q}{m Delta T} to infty .)

При адиабатном сжатии (расширении) газ не получает теплоты и не передает ее окружающим телам (Q = 0), а температура газа изменяется (ΔΤ ≠ 0). Следовательно, удельная теплоемкость газа при адиабатном процессе

(~c = frac{Q}{m Delta T} = 0 .)

Наибольший интерес представляет теплоемкость для случаев, когда нагревание происходит при постоянном объеме или при постоянном давлении. В первом случае теплоемкость называется теплоемкостью при постоянном объеме или изохорной теплоемкостью (cV, CV), во втором — теплоемкостью при постоянном давлении или изобарной теплоемкостью (cp, Cp).

Если объем не изменяется (ΔV = 0), то работа, совершенная газом, так же равна нулю (А = 0). Согласно первому закону термодинамики

(~Q = Delta U) и (~C_{TV} = frac{Delta U}{Delta T},)

Откуда

(~Delta U = C_{TV} cdot Delta T = c_V m Delta T . qquad (2))

Следовательно, теплоемкость при постоянном объеме равна изменению внутренней энергии газа при изменении температуры на 1 К.

Если газ идеальный, то в формуле (2)

(~Delta U = frac i2 frac mM R Delta T .)

Тогда молярная теплоемкость при постоянном объеме (~C_V = frac{Delta U_M}{Delta T}), где (~Delta U_M = frac i2 R Delta T) — изменение внутренней энергии 1 моль газа. Из этих равенств теплоемкость газа при постоянном объеме — (~C_{TV} = frac i2 frac mM R); молярная теплоемкость газа при постоянном объеме — (~C_V = frac i2 R).

Если газ нагревается при постоянном давлении, то согласно первому закону термодинамики

(~Q = Delta U + A,)

где (~A = p Delta V = frac mM R Delta T).

Тогда теплоемкость газа при постоянном давлении

(~C_{Tp} = frac{Q}{Delta T} = frac{Delta U}{Delta T} + frac mM R = C_{TV} + frac mM R = frac{i + 2}{i} frac mM R .)

Молярная теплоемкость при постоянном давлении:

(~C_p = C_V + R) — уравнение Майера;

(~C_p = frac i2 R + R = frac{i + 2}{i} R .)

Таким образом, теплоемкость при постоянном давлении всегда больше теплоемкости при постоянном объеме. Их отношение равно

(~gamma = frac{C_p}{C_V} = frac{i + 2}{i} .)

где γ — показатель адиабаты (коэффициент Пуассона).

Из-за малости величины коэффициента объемного расширения твердых и жидких тел работой, совершаемой ими при нагревании при постоянном давлении, можно пренебречь и считать, что теплоемкости при постоянном объеме и постоянном давлении практически совпадают. Поэтому теплоемкость твердых и жидких тел при заданной температуре может считаться вполне определенной величиной.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 159-161.

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 ноября 2020 года; проверки требует 1 правка.

Теплоёмкость определяется суммой поступательных, вращательных и удвоенным числом колебательных степеней свободы.

Теплоёмкость идеального газа — отношение количества теплоты, сообщённой газу delta Q, к изменению температуры dT, которое при этом произошло {displaystyle C={frac {delta Q}{dT}}} [1].

Удельная и молярная теплоёмкость[править | править код]

Молярная теплоёмкость — теплоёмкость 1 моля вещества [2]:

{displaystyle C_{M}={frac {C}{nu }}={frac {1}{nu }}{frac {delta Q}{Delta T}},}

где {displaystyle nu =m/M,} m — масса, M — молярная масса вещества.

Теплоёмкость единичной массы вещества называется удельной теплоёмкостью и, в системе СИ, измеряется в Дж/(кг·К)[1].

Формула расчёта удельной теплоёмкости[1][2]:

{displaystyle c={frac {C_{M}}{M}}={frac {delta Q}{mdT}},}

где c — удельная теплоёмкость, m — масса нагреваемого (охлаждающегося) вещества.

Теплоёмкость идеального газа в изопроцессах[править | править код]

Адиабатический[править | править код]

В адиабатическом процессе теплообмена с окружающей средой не происходит, то есть {displaystyle dQ=0}. Однако, объём, давление и температура меняются, то есть {displaystyle dTneq 0}[3].

Следовательно, теплоёмкость идеального газа в адиабатическом процессе равна нулю: C = {0 over dT} = 0.

Изотермический[править | править код]

В изотермическом процессе постоянна температура, то есть {displaystyle dT=0}. При изменении объёма газу передаётся (или отбирается) некоторое количество тепла[3]. Следовательно, теплоёмкость идеального газа равна плюс-минус бесконечности: {displaystyle Cto pm infty }

Изохорный[править | править код]

В изохорном процессе постоянен объём, то есть {displaystyle delta V=0} и, следовательно газ не совершает работы. Первое Начало Термодинамики для изохорного процесса имеет вид[1]:

{displaystyle dU=delta Q=nu C_{V}dT.qquad (1)}

А для идеального газа

{displaystyle dU={frac {i}{2}}nu RDelta T.}

Таким образом,

C_V=frac i2 R,

где i — число степеней свободы частиц газа.

Другая формула:

{displaystyle C_{V}={frac {R}{gamma -1}},}

где gamma  — показатель адиабаты, R — газовая постоянная газа.

Изобарный[править | править код]

Молярная теплоёмкость при постоянном давлении обозначается как C_p. В идеальном газе она связана с теплоёмкостью при постоянном объёме соотношением Майера C_p = C_v + R[1].
Уравнение Майера вытекает из первого начала термодинамики[4]:

{displaystyle delta Q=mathrm {d} U+delta A,qquad (2)}.

В рассматриваемом случае, согласно определению теплоёмкости:

{displaystyle delta Q=C_{p}mathrm {d} T,}

Учитываем, что работа газа равна [4]:

{displaystyle delta A=mathrm {d} (pV)=nRmathrm {d} Tqquad =pmathrm {d} Vqquad +Vmathrm {d} pqquad =pmathrm {d} Vqquad ,(Vmathrm {d} pqquad =0)(3)}

Согласно уравнению Менделеева-Клапейрона для одного моля газа[1]:

{displaystyle pmathrm {d} V=Rmathrm {d} T.qquad (4)}

Подставляя уравнение (4) в (3) получаем:

{displaystyle delta A=Rmathrm {d} Tqquad (5)}

Так как энергия одной молекулы равна {displaystyle <e>={frac {i}{2}}kT} (6)[Комм 1][5], то и внутренняя энергия в целом и при изобарном процессе будет определяться по соотношению (1). Следовательно, подставляя уравнения (1) и (5) в (2) получаем соотношение Майера.

Молекулярно-кинетическая теория позволяет вычислить значения молярной теплоёмкости для классического идеального газа газов через значение универсальной газовой постоянной исходя из уравнения (6) и предположения, что молекулы газа не взаимодействуют между собой[5]:

Теплоёмкости можно также определить исходя из уравнения Майера, если известен показатель адиабаты, который можно измерить экспериментально (например, с помощью измерения скорости звука в газе или используя метод Клемана — Дезорма).

Теплоёмкость реального газа может значительно отклонятся от теплоёмкости идеального газа. Так при температуре в 25 °С и атмосферном давлении атомарный водород имеет теплоёмкость 2,50R , а атомарный кислород — 2,63R. Также теплоёмкость реального газа зависит от температуры[5].

См. также[править | править код]

  • Идеальный газ
  • Первое начало термодинамики
  • Теплоёмкость

Комментарии[править | править код]

  1. ↑ i — сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы
  2. ↑ 1 2 При жёсткой связи между атомами, то есть колебательные степени свободы исключены из рассмотрения. Примером трёхатомной линейной молекулы служит цианистый водород HCN.

Примечания[править | править код]

  1. ↑ 1 2 3 4 5 6 Савельев, 2001, с. 26—30.
  2. ↑ 1 2 Базаров И. П., Термодинамика, 2010, с. 41.
  3. ↑ 1 2 Савельев, 2001, с. 30—31.
  4. ↑ 1 2 Савельев, 2001, с. 18-20.
  5. ↑ 1 2 3 Савельев, 2001, с. 61-63.

Литература[править | править код]

  • Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.— Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
  • Белоконь Н. И. Основные принципы термодинамики. — М.: Недра, 1968. — 110 с.
  • Савельев И. В. Курс общей физики:Молекулярная физика и термодинамика. — М.: Астрель, 2001. — Т. 3. — 208 с. — 7000 экз. — ISBN 5-17-004585-9.
Источник

Добавить комментарий