Удельный объем газа
Количество вещества n характеризует число структурных элементов содержащихся в данной системе.
Это могут быть атомы, молекулы, а также ионы, электроны и другие частицы.
Единица количества вещества n является одной из основных единиц СИ.
Единица СИ количества вещества:
[ [n] = (моль) enspace основная enspace единица ]
Один моль – это такое количества вещества , в котором содержится столько же структурных элементов,
сколько атомов в 12 грамм изотопа углерода-12. В количестве вещества, равном один моль, содержится
6.022 × 1023 структурных элементов.
Часто бывает удобно относить объем и массу газа к количеству вещества.
Если
| m | масса газа, | кг |
|---|---|---|
| ρ | плотность газа, | кг/м3 |
| V | объем газа, | м3 |
| n | количество вещества (газа), | кмоль |
| M | молярная масса (отнесенная к количеству вещества), | кг/кмоль |
| Vm | молярный объем (отнесенный к количеству вещества), | м3/кмоль |
| υ | удельный объем газа, | м3/кг |
то
[ υ = frac{V}{m} ]
[ M = frac{m}{n} ]
[ V_m = frac{V}{n} ]
[ υ = frac{V_m}{M} = frac{V}{m} = frac{1}{ρ} ]
Вычислить, найти удельный объем газа по формуле (5)
Удельный объем газа |
стр. 531 |
|---|
Объем, масса, плотность, удельный объем. Приведение к нормальным и стандартным условиям и пересчет
Приведение к нормальным и стандартным условиям
Единицей измерения объема газа является кубический метр (м³). Измеренный объем приводится к нормальным физическим условиям.
Нормальные физические условия: давление 101 325 Па, температура 273,16 К (0 °С).
Стандартные условия: давление 101 325 Па, температура 293,16 К (+20 °С).
В настоящее время эти обозначения выходят из употребления. Поэтому в дальнейшем следует указывать те условия, к которым относятся объемы и другие параметры газа. Если эти условия не указываются, то это значит, что параметры газа даны при 0 °С (273,16 °К) и 760 мм рт. ст. (1,033 кгс/см²). Иногда объем газа (особенно в иностранной литературе и нормах) при пользовании системой СИ приводится к 288,16 °К (+15 °С) и давлению 1 бар (105 Па).
Если известен объем газа при одних условиях, то пересчитать его в объемы при других условиях можно с помощью коэффициентов, приведенных следующей таблице.
Коэффициенты для пересчета объемов газа из одних условий в другие
| Температура и даление газа | 0 °С и 760 мм рт. ст. | 15 °С и 760 мм рт. ст. | 20 °С и 760 мм рт. ст. | 15 °С (288,16 °К) и 1 бар |
| 0 °С и 760 мм рт. ст. (норм. условия) | 1 | 1,055 | 1,073 | 1,069 |
| 15 °С и 760 мм рт. ст. (в зар. литературе) | 0,948 | 1 | 1,019 | 1,013 |
| 20 °С и 760 мм рт. ст. (ст. условия) | 0,932 | 0,983 | 1 | 0,966 |
| 15 °С (288,16 °К) и 1 бар (СИ) | 0,936 | 0,987 | 1,003 | 1 |
Для приведения объемов газа к 0 °С (273,16 °К) и 760 мм рт. ст. (1,033 кгс/см²), а также к 20 °С (293,16 °К) и 760 мм рт. ст. (1,033 кгс/см²) могут быть применены следующие формулы:

где V0 °С и 760 мм рт. ст. — объем газа при 0 °С и 760 мм рт. ст., м³;
V20° С и 760 мм рт. ст. — объем газа при 20 °С и 760 мм рт. ст., м³;
VP — объем газа в рабочих условиях, м³;
р — абсолютное давление газа в рабочих условиях, мм рт. ст.;
Т — абсолютная температура газа в рабочих условиях, °К.
Пересчет объемов газа, приведенных к 0 °С и 760 мм рт. ст., а также к 20 °С и 760 мм рт. ст., в объемы при других (рабочих) условиях можно производить по формулам:

Любой газ способен расширяться. Следовательно, знание объема, который занимает газ, недостаточно для определения его массы, так как в любом объеме, целиком заполненном газом, его масса может быть различной.
Масса — это мера вещества какого-либо тела (жидкости, газа) в состоянии покоя; скалярная величина, характеризующая инерционные и гравитационные свойства тела. Единицы массы в СИ — килограмм (кг).
Плотность, или масса единицы объема, обозначаемая буквой p, — это отношение массы тела m, кг, к его объему, V, м³:
p = m/V
или с учетом химической формулы газа:
p = M/VМ = M/22,4,
где M — молекулярная масса,
VМ — молярный объем.
Единица плотности в СИ — килограмм на кубический метр (кг/м³).
Зная состав газовой смеси и плотность ее компонентов, определяем по правилу смешения среднюю плотность смеси:
pсм = (p1V1 + p2V2 + … + pnVn)/100,
где p1, p2, …, pn — плотность компонентов газового топлива, кг/м³;
V1, V2, …, Vn — содержание компонента, об. %.
Величину, обратную плотности, называют удельным, или массовым, объемом (ν) и измеряют в кубических метрах на килограмм (м³/кг).
Как правило, на практике, чтобы показать, на сколько 1 м³ газа легче или тяжелее 1 м³ воздуха, используют понятие относительная плотность d, которая представляет собой отношение плотности газа к плотности воздуха:
d = p/1,293
и
d = M/(22,4×1,293).
Удельный объём υ
– объём занимаемый 1 кг рабочего тела
(газа) и определяется по формуле:
υ
= V/m,
м3/кг,
(1.6)
где V
– объём занимаемый газом м3;
m
– масса газа, кг.
Плотностью ρ
называется количество газа, заключённое
в единице объёма. Следовательно, если
m
кг занимают объём V
м3,
то плотность его определяется по формуле
ρ
= m/V,
кг/м3.
(1.7)
Из данных определений
видно, что плотность газа ρ
это величина обратная удельному объёму
υ,
т.е.
ρ·υ
= 1. (1.8)
1.4. Уравнение состояния идеального и реального газов
1.4.1. Уравнение состояния идеального газа
Основные параметры
рабочего тела независимо от его
агрегатного состояния связаны между
собой уравнением, называемым уравнением
состояния, которое может быть представлено
так:
f
(p,
υ,
T)
= 0.
(1.9)
Уравнение
(1.9) в пространстве отображает поверхность,
которая характеризует всевозможные
равновесные состояния химически
однородной термодинамической системы
(газ, жидкость). При отсутствии внешних
полей (гравитационного, электрического,
магнитного) число независимых параметров,
однозначно определяющих равновесное
состояние системы, будет равно двум из
трех (p,
υ,
T),
так как любой из этих трех параметров
является однозначной функцией двух
заданных.
Например,
если принять за независимые переменные
υ
и T,
то
p
можно выразить как функцию υ
и Т,
т.е. р
= р
(Т,
υ);
если же за независимые переменные
принять р
и Т,
то удельный объём можно выразить как
функцию р
и Т,
т.е. υ
= υ (р,
Т).
Таким
образом, уравнение состояния устанавливает
связь между давлением, температурой и
удельным объёмом однородной
термодинамической системы.
Наиболее
простой вид уравнение состояния имеет
для идеальных газов. Свойства идеальных
газов, как известно, основаны на
экспериментальных законах. (Законы
Бойля – Мариотта, Гей – Люсака и Шарля).
Эти
законы можно объединить в один, который
формируется так: для данного газа
произведение давления на объём в любом
состоянии пропорционально его массе и
абсолютной температуре.
Математическая
запись этого закона выражается уравнением
Клапейрона (1834 г.).
p·V
= m·R·T
(1.10)
Для одного кг газа
уравнение (1.10) принимает вид:
p·υ
= R·T
(1.11)
В
уравнениях (1.10), (1.11) коэффициент R
имеет размерность Дж/(кг·K)
и называется газовой постоянной, которая
зависит от молекулярной массы газа μ.
Уравнению
Клапейрона можно придать универсальную
форму, если отнести газовую постоянную
к одному киломолю газа.
Киломолем (кмоль)
или килограммолекулой называется
количество килограммов вещества,
численно равное его молекулярной массе.
Обе
части уравнения (1.11) умножим на массу
одного киломоля μ,
г/кмоль.
p·υ·μ
= R·T·μ
, (1.12)
где
υ·μ
= Vμ
,
![]()
–
объём
одного киломоля газа;
μ·R
= Rμ
, Дж/(кмоль·К) – универсальная
газовая постоянная.
Известно,
что идеальные газы подчиняются закону
Авогадро (1811 г.), который гласит, что при
одинаковых температурах и давлениях
объёмы, занимаемые одним киломолем
любого идеального газа, одинаковы.
Измерения показали, что при нормальных
атмосферных условиях (pо
= 101325 Па; То
= 273,15 К) один киломоль идеального газа
занимает Vμ
= 22,4136 м3,
отсюда можно получить, что
μ·R
= Rμ
=
![]()
Rμ
= Rун
.
Таким
образом, для одного киломоля идеального
газа уравнение состояния будет одинаковым
для всех газов:
p·Vμ
= Rμ·T
(1.13)
Это
уравнение носит название уравнение
Клапейрона – Менделеева.
С помощью формулы
R
=
![]()
(1.14)
можно
определить газовую постоянную R
для любого газа.
Масса одного
киломоля сухого воздуха находится по
уравнению:
μвозд
=
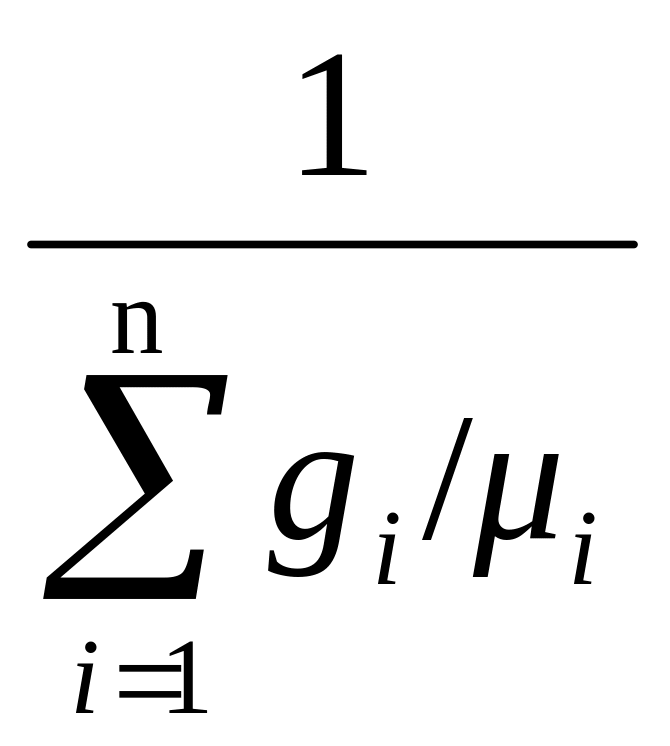
, (1.15)
где
gi
=
mi
/mсм
– массовая доля газа или отношение
массы газа к общей массе смеси;
μi
– молекулярная масса одного киломоля
i-го
газа в составе смеси, кг/кмоль.
Пользуясь
таблицей 1.1., получаем
μвозд
= 1/(0,78084/28,0134 + 0,209476/31,9968 + 0,934/39,3440 +
+
0,0314/44,0079
+ и т.д.) = 28,966 кг/кмоль.
Таким
образом, газовая постоянная сухого
воздуха равна
Rвозд
=
![]()
= 287 Дж/(кг·К).
Рассуждая
аналогичным образом можно вычислить
газовую постоянную для продуктов
сгорания для газотурбинных двигателей
(ГТД), она получается равной
Rг
= 288 Дж/(кг·К).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
| Удельный объём | |
|---|---|
 |
|
| Размерность | L3M−1 |
| Единицы измерения | |
| СИ | м³/кг |
| СГС | см³/г |
| Примечания | |
| скалярная величина |
Уде́льный объём — объём, занимаемый единицей массы вещества.
Скалярная физическая величина, обычно обозначаемая 

- где
— объём;
— масса.
В СИ имеет размерность м3/кг, в СГС — см3/г.
Связь с молярным объёмом[править | править код]
Молярный объём 
- где
— число молей вещества в объёме
Отсюда следует:
- где
— молекулярная масса вещества.
Удельный объем идеального газа[править | править код]
Удельный объем идеального газа связан с газовой постоянной 



Плотности и удельные объёмы[править | править код]
В таблице приведены плотности и удельные объёмы для некоторых веществ и объектов. Значения указаны для стандартных температуре и давлении: 0°С (273,15 К) и 1 атм (101,325 кПа или 760 мм рт. ст.).
| Название вещества | Плотность,
кг/м3 |
Удельный объём | Название вещества | Плотность,
кг/м3 |
Удельный объём | ||
|---|---|---|---|---|---|---|---|
| м3/кг | л/кг | м3/кг | л/кг | ||||
| Воздух | 1.225 | 0,816 | 816 | Двуокись углерода | 1,977 | 0,506 | 506 |
| Водяной лёд | 916,7 | 0,00109 | 1,09 | Хлор | 2,994 | 0,334 | 334 |
| Морская вода | 1030 | 0,00097 | 0,97 | Метан | 0,717 | 1,39 | 1390 |
| Ртуть | 13546 | 0,00007 | 0,07 | Азот | 1,25 | 0,799 | 799 |
| Фреон R-22* | 3,66 | 0,273 | 273 | Водяной пар* | 0,804 | 1,24 | 1240 |
| Аммиак | 0,769 | 1,30 | 1300 | Водород | 0,0899 | 11,12 | 11120 |
| Жидкая вода | 1000 | 0,001 | 1 | Человек | 940—980 (вдох)
1010—1070 (выдох) |
0,00104
0,00096 |
1,04
0,96 |
| Солнце | 1410 | 0,0007 | 0,7 | Земля | 5510 | 0,00018 | 0,18 |
| * — значения указаны для нестандартных температуры и давления |
См. также[править | править код]
- Плотность вещества (Удельная масса)
- Удельный вес
- Пикнометр
- Ареометр
Примечания[править | править код]
- ↑ Зеленцов Д. В., Техническая термодинамика, 2012, с. 4.
- ↑ Новиков И. И., Термодинамика, 2009, с. 13.
- ↑ Карминский В. Д., Техническая термодинамика и теплопередача, 2005, с. 8.
- ↑ Мурзаков В. В., Основы технической термодинамики, 1973, с. 13.
- ↑ Вукалович М. П., Новиков И. И., Термодинамика, 1972, с. 13.
Литература[править | править код]
- Вукалович М. П., Новиков И. И. Термодинамика. — М.: Машиностроение, 1972. — 671 с.
- Зеленцов Д. В. Техническая термодинамика. — Самара: Самарский гос. архитект.-строит. ун-т, 2012. — 140 с. — ISBN 978-5-9585-0456-5.
- Карминский В. Д. Техническая термодинамика и теплопередача. — М.: Маршрут, 2005. — 224 с. — ISBN 5-89035-202-4.
- Мурзаков В. В. Основы технической термодинамики. — М.: Энергия, 1973. — 304 с.
- Новиков И. И. Термодинамика. — 2-е изд., испр. — СПб.: Лань, 2009. — 590 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-0987-7.
Ссылки[править | править код]
- Объем удельный // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907. Статья Коновалова Д. П.
- Удельный объем
- скалярная физическая величина равная объёму, занимаемому единицей массы вещества.
Общие сведения.
Для обозначения удельного объема обычно используется греческая буква υ. Удельный объем равен обратной плотности вещества.
Перевод единиц измерения удельного объема онлайн:
Калькулятор удельного объема. Перевод единиц измерения удельного объема (см3/г, м3/кг и т.д.)
Введите удельного объема (vud)
Результат перевода единиц измерения удельного объема (vud)
Результаты работы калькулятора удельного объема при переводе в другие единицы измерения удельного объема:
Примеры результатов работы калькулятора удельного объема:
Поделится ссылкой на расчет:
Единицы измерения удельного объема:
-
- кубический сантиметр на грамм — единица измерения в СГС. Обозначение в России: см3 /г международное: cm3/g. Данная единица измерения широко применяется при инженерных расчетах, в современной справочной литературе;
- кубический метр на килограмм— единица измерения в СИ. Обозначение в России: м3/кг; международное: m3/kg. Данная единица измерения широко применяется при инженерных расчетах, в справочной литературе.
Калькуляторы удельного объема:
Удельный объем твердых тел и жидкостей при известной массе и объеме.
Результат расчета удельного объема тела/жидкости (u1)
Формула расчета удельного объема тела/жидкости:
Скачать результат расчета удельного объема тела/жидкости:

Поделится ссылкой на расчет удельного объема:
Удельный объем веществ (тел) при известной плотности.
Введите плотность тела/вещества (pl)
Скачать полный вариант расчета:
В разработке!
Поделится ссылкой на полный вариант расчета:
Результат расчета удельного объема тела/жидкости (u2)
Формула расчета удельного объема тела/жидкости:
Скачать результат расчета удельного объема тела/жидкости:

Поделится ссылкой на расчет удельного объема:
Удельный объем идеального газа.
Результат расчета удельного объема газа (u3)
Формула расчета удельного объема газа:
Скачать результат расчета удельного объема газа:

Поделится ссылкой на расчет удельного объема:








