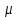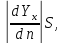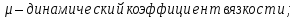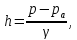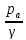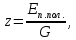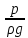Как найти удельный объем жидкости

К основным физическим свойствам жидкости, которые рассматриваются в гидродинамике, относятся плотность, удельный вес, удельный объем, температурное расширение, сжимаемость и вязкость.

Плотность — это отношение массы вещества к его объему:

р = m/V

На плотность жидкости влияют температура и давление. Значения плотности некоторых жидкостей приведены ниже:

• Жидкость: р, кг/м3
• Вода: 1000
• Антифриз: 1070
• Бензин: 750
• Керосин: 800
• Дизельное топливо: 860
• Масло МГ- 15-Б: 850
• МГ-22-А: 880
• ТМ-5-18: 900
• Нефть: 900
• Ацетон: 700
• Спирт: 800
• Глицерин: 1260

Удельный вес — это отношение веса жидкости к занимаемому объему:

у = mg/V = pg.

Удельный объем жидкости — объем единицы массы этой жидкости:

v = У/m = 1/р.

Температурное расширение — свойство жидкости изменять свой объем при изменении температуры. С ростом температуры объем жидкости увеличивается и наоборот. Различные жидкости при увеличении температуры на одну и ту же величину увеличиваются в объеме по разному. Поэтому свойство жидкости увеличиваться в объеме с увеличением температуры характеризуется коэффициентом температурного расширения Bт, который показывает изменение единицы объема данной жидкости при изменении ее температуры на 1 К.

• Жидкость — Bт (10^-4, К^-1)
• Вода: 2
• Антифриз: 5
• Нефть: 8
• Ртуть: 1,8

Увеличение объема при нагревании рассчитывается по уравнению:

дельта V= Bт*V0*дельта Т

где V0 начальный объем жидкости; дельта Т— изменение температуры.

В расчетах ДВС коэффициент температурного расширения считают постоянным, хотя на самом деле он зависит от условий нагревания или охлаждения, давления и начальной температуры.

Сжимаемость — свойство жидкости изменять объем при изменении давления.

дельта V = Bр*V0*дельта р,

где дельта V— изменение объема; дельта р — изменение давления; Вр — коэффициент объемного сжатия.

Коэффициент объемного сжатия показывает изменение единицы объема жидкости при изменении давления на 1 Па. Он зависит от условий сжатия, температуры и начального давления. При расчетах эта зависимость не учитывается.

Коэффициент объемного сжатия для воды равен 5 * 10^-4 1/Па, для нефтепродуктов — 7*10^-4 1/Па, для ртути — 0,3*10^-4 1/Па.

Ввиду незначительных величин жидкости считаются несжимаемыми.

Вязкость — свойство жидкости оказывать сопротивление перемещению одной ее части относительно другой.

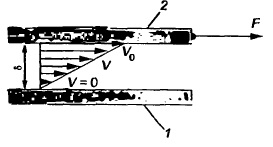
Рис. Схема изменения скорости жидкости, заключенной между неподвижной (1) и подвижной (2) пластинами

Если плоскость 2, находящаяся на расстоянии б от плоскости 1, под действием силы F перемещается со скоростью V0, то слои жидкости, находящиеся между плоскостями, перемещаются с разными скоростями. При этом максимальная скорость V0 в точках контакта с плоскостью 2, минимальная (вплоть до нуля) в точках контакта с плоскостью 1.

Если слои жидкости при движении не перемешиваются, то скорость в потоке изменяется по линейному закону, и отношение V0/б представляет собой градиент скорости.

При скольжении слоев жидкости между ними возникают силы внутреннего трения, которые сопротивляются движению. На преодоление этих сил и расходуется внешняя сила F:

F = nSV0/б

где n — динамический коэффициент вязкости или динамическая вязкость; S — площадь трения (жидкости о пластину).

Динамическая вязкость учитывает свойства жидкости, от которых зависит ее внутреннее трение. В технике и в частности в гидравлике часто используется кинематическая вязкость v, которая равна отношению динамической вязкости жидкости к ее плотности:

v = n/p

Для упрощения решения гидродинамических задач считают, что рассматриваемые жидкости не обладают температурным расширением, сжимаемостью и вязкостью. Такие жидкости в отличие от реальных называются идеальными.

Удельный объём
Размерность	L3M−1
Единицы измерения
СИ	м³/кг
СГС	см³/г
Примечания
скалярная величина

Уде́льный объём — объём, занимаемый единицей массы вещества.

Скалярная физическая величина, обычно обозначаемая обратная плотности вещества ^{[1][2][3][4][5]}:

где  — объём;

 — масса.

В СИ имеет размерность м³/кг, в СГС — см³/г.

Связь с молярным объёмом[править | править код]

Молярный объём по определению:

где  — число молей вещества в объёме

Отсюда следует:

где  — молекулярная масса вещества.

Удельный объем идеального газа[править | править код]

Удельный объем идеального газа связан с газовой постоянной абсолютной температурой давлением и молекулярной массой через уравнение состояния идеального газа:

Плотности и удельные объёмы[править | править код]

В таблице приведены плотности и удельные объёмы для некоторых веществ и объектов. Значения указаны для стандартных температуре и давлении: 0°С (273,15 К) и 1 атм (101,325 кПа или 760 мм рт. ст.).

Название вещества	Плотность, кг/м3	Удельный объём		Название вещества	Плотность, кг/м3	Удельный объём
м3/кг	л/кг	м3/кг	л/кг
Воздух	1.225	0,816	816	Двуокись углерода	1,977	0,506	506
Водяной лёд	916,7	0,00109	1,09	Хлор	2,994	0,334	334
Морская вода	1030	0,00097	0,97	Метан	0,717	1,39	1390
Ртуть	13546	0,00007	0,07	Азот	1,25	0,799	799
Фреон R-22*	3,66	0,273	273	Водяной пар*	0,804	1,24	1240
Аммиак	0,769	1,30	1300	Водород	0,0899	11,12	11120
Жидкая вода	1000	0,001	1	Человек	940—980 (вдох) 1010—1070 (выдох)	0,00104 0,00096	1,04 0,96
Солнце	1410	0,0007	0,7	Земля	5510	0,00018	0,18
* — значения указаны для нестандартных температуры и давления

См. также[править | править код]

• Плотность вещества (Удельная масса)
• Удельный вес
• Пикнометр
• Ареометр

Примечания[править | править код]

Литература[править | править код]

• Вукалович М. П., Новиков И. И. Термодинамика. — М.: Машиностроение, 1972. — 671 с.
• Зеленцов Д. В. Техническая термодинамика. — Самара: Самарский гос. архитект.-строит. ун-т, 2012. — 140 с. — ISBN 978-5-9585-0456-5.
• Карминский В. Д. Техническая термодинамика и теплопередача. — М.: Маршрут, 2005. — 224 с. — ISBN 5-89035-202-4.
• Мурзаков В. В. Основы технической термодинамики. — М.: Энергия, 1973. — 304 с.
• Новиков И. И. Термодинамика. — 2-е изд., испр. — СПб.: Лань, 2009. — 590 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-0987-7.

Ссылки[править | править код]

• Объем удельный // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907. Статья Коновалова Д. П.

Удельный объем

Удельный
объем – физическая величина, равная
отношению объема тела к его массе:

=V/
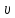
m,

где

–
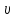
удельный объем, м³/кг;

V
– объем,
м³;

m
– масса,
кг.

Плотность

Плотность
– физическая величина, равная отношению
массы тела к его объему:

ρ
= m/V,

где
ρ – плотность, кг/м³.

m
– масса,
кг;

V
– объем,
м³.

Удельный вес

Удельный
вес – вес единицы объема тела:

=
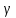
G/V
= ρ
g,

где
γ – удельный вес, Н/м³;

G
– вес тела в объеме V,
Н;

g
– ускорение свободного падения, g
= 9,81 м/с².

В
отличие от плотности ρ удельный вес
не является физической характеристикой
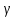
тела, так как зависит от места измерения.

Энергия

Энергия
– это общая количественная мера движения
и взаимодействия всех видов материи.

Энергия
независимо от конкретных форм
проявления обозначается Е.
За единицу энергии в СИ принят д ж о у
л ь (Дж). Джоуль – это энергия, затраченная
системой при перемещении точки вследствие
приложения силы 1 Н на расстояние 1 м в
направлении действия силы, то есть 1 Дж
= 1 Н ٠
1
м. Вычислить абсолютное значение энергии
невозможно, так как нет ноля отсчета
энергии. Такое положение не играет
существенной роли для практики, потому
что при исследовании энергообмена важна
не абсолютная величина энергии, а ее
изменение.

Часть I. Гидравлика

Г
и д р а в л и к о й называют
прикладную науку о законах равновесия
и движения жидкостей и способах приложения
этих законов к решению задач инженерной
практики.

Жидкость

Жидкостью
называется
физическое тело, обладающее свойством
текучести, то есть способностью изменять
форму под действием сколь угодно малых
сил.

Понятие
«жидкость»
включает в себя как капельные жидкости,
так и газы. В небольших количествах вне
сосуда жидкость (в обычном понимании)
принимает форму капли, что и определило
ее название. При силовом взаимодействии
капельные жидкости почти не изменяют
свой объем (то есть почти не сжимаются),
но легко изменяют свою форму. Газы могут
менять свой объем и форму под действием
внешних и внутренних сил.

Жидкая частица

Жидкая
частица – это физически бесконечно
малый объем, в котором параметры сплошной
среды сохраняют постоянные значения и
не зависят от изменения объема.

Масса
жидкой частицы неизменна, а объем и
форма могут меняться.

Внешние
и внутренние силы

Внешние
силы – это силы, приложенные к частицам
рассматриваемого объема жидкости со
стороны жидкости, окружающей этот объем.

Внутренние
силы – это силы, возникающие внутри
жидкости в результате воздействия на
нее внешних сил.

Массовые
силы

Под
массовыми понимают силы, непрерывно
распределенные по массе (объему) жидкости
и пропорциональные массе жидкости.

Примерами
массовых сил являются сила тяжести и
сила инерции.

Поверхностные
силы

Под
поверхностными понимают силы, которые
непрерывно распределены по поверхностям
и пропорциональны величинам площадей
поверхностей, которые ограничивают
объемы жидкости, а также мысленно
выделены внутри объемов.

В
общем случае поверхностная сила имеет
две составляющие: нормальную силу
давления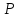и касательную силу внутреннего трения
Т.

Свободная
поверхность

Свободная
поверхность – это поверхность раздела
между капельной жидкостью и внешней
газообразной средой.

Сжимаемость
жидкостей

Под
сжимаемостью понимают свойство жидкости
изменять свой объем (и плотность) при
изменении давления.

Вязкость

Вязкость
(или внутреннее трение) – свойство
капельных жидкостей и газов оказывать
сопротивление перемещению одной их
части относительно другой.

Закон
внутреннего трения Ньютона

Законом
внутреннего трения Ньютона называют
выражение вида:
T
=

где
T
– cила
внутреннего трения, возникающая между
слоями жидкости, движущимися с разными
скоростями;

dY_x
– изменение скорости течения при
удалении на расстояние dn
от поверхности слоя в перпендикулярном
к нему направлении;

–модуль
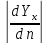
градиента скорости;

S
– площадь поверхности слоя жидкости.

Ньютоновские
и неньютоновские жидкости

Ньютоновскими
принято называть жидкости, которые при
своем течении строго подчиняются закону
внутреннего трения Ньютона. Все иные
жидкости относят к неньютоновским.

Именно
ньютоновские жидкости являются объектом
исследования в гидравлике. Поведение
неньютоновских жидкостей рассматриваются
в науке, которая называется р
е о л о г и е й.

1.
Гидростатика

Гидростатика
– раздел гидравлики, в котором изучаются
условия и

закономерности
равновесия жидкостей под действием
приложенных к ним сил, а так же воздействие
покоящихся жидкостей на погруженные в
них твердые тела и стенки сосудов.

Абсолютный
покой жидкости

Под
абсолютным покоем понимают неподвижность
жидкости относительно содержащего ее
сосуда, когда сам сосуд не движется
относительно земли.

Относительный
покой жидкости

Под
относительным покоем понимают
неподвижность жидкости относительно
содержащего ее сосуд, в то время, когда
сам сосуд находиться в движении
относительно земли.

Внешнее
поверхностное давление

Давление
на свободной поверхности жидкости
называют внешним поверхностным давлением.
Его обозначают р₀
.

Сила
гидростатического давления

Сила
гидростатического давления (абсолютного
или избыточного), действующая на плоскую
твердую стенку – это равнодействующая
элементарных сил соответствующего
гидростатического давления, действующих
на эту стенку.

Она
равна величине гидростатического
давления в центре смоченной поверхности
стенки, умноженной на площадь этой
поверхности. Силу гидростатического
давления обозначают Р
и выражают
в ньютонах (Н).

Центр
давления

Центр
давления – это точка пересечения линии
действия силы абсолютного гидростатического
давления с плоскостью, в которой лежит
воспринимающая эту силу стенка.

Эпюра
гидростатического давления

Эпюра
гидростатического давления (абсолютного
или избыточного), действующего на
смоченную поверхность стенки – это
объемная фигура, отражающая характер
распределения соответствующего давления
на рассматриваемой поверхности.

Объем
эпюры гидростатического давления равен
силе гидростатического давления.

Открытый
пьезометр

Открытый
пьезометр – это прозрачная трубка
небольшого диаметра, один конец которой
открыт и сообщается с атмосферой, а
второй конец присоединён к точке сосуда
с капельной жидкостью, в которой
измеряется избыточное давление.

Пьезометрическая
высота

Высота
столба жидкости в открытом пьезометре,
который своим весом способен создать
давление, равное избыточному давлению
в рассматриваемой точке.

Обозначают
пьезометрическую
высоту h,
а находят как

где
p
– абсолютное
гидростатическое давление в точке;

p_a
– атмосферное давление;

–удельный
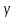
вес жидкости.

Закрытый
пьезометр

Прозрачная
трубка с запаянным одним концом, из
которой откачали воздух, а другим концом
подсоединили к точке сосуда с капельной
жидкостью, в которой измеряют абсолютное
гидростатическое давление.

Абсолютная
пьезометрическая высота

Высота
такого столба жидкости в закрытом
пьезометре, который своим весом способен
создать давление, равное абсолютному
гидростатическому давлению в
рассматриваемой точке.

Абсолютная
пьезометрическая высота h_а
=

.

Геометрически
напор

Геометрический
напор (геометрическая высота или удельная
потенциальная энергия положения) – это
потенциальная энергия положения жидкой
частицы, отнесенная к единице ее веса.

Обозначают
геометрический напор
,
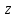
выражают в
метрах (м). Из определения следует:

где
Е_п.пол
– потенциальная
энергия положения жидкой частицы;

G
– вес жидкой частицы.

Абсолютный
пьезометрический напор

Абсолютный
пьезометрический напор – это потенциальная
энергия давления жидкой частицы,
приходящаяся на единицу ее веса.

Обозначают
абсолютный пьезометрический напор
,
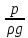
выражают в

метрах
(м). Из определения следует:

=,

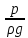
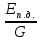
где
p
– абсолютно
давление;

=– удельный вес жидкости;

–потенциальная
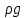
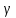
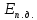
энергия давления жидкой частицы;

G
– вес жидкой частицы.

Полный
гидростатический напор

Полный
гидростатический напор – это полная
потенциальная энергия, отнесенная к
единице веса жидкости.

Обозначают
полный гидростатический напор через
Н_ст
и вычисляют как
Н_ст
= z+
.

Основные
уравнения гидростатики

Основное
уравнение гидростатики выражает закон
сохранения и превращения энергии для
случая абсолютного покоя несжимаемой
жидкости в гравитационном поле при
неизменной величине ускорения свободного
падении.

Форма
записи: z
+= const
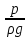
и p
= p₀
+,

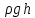
где
p₀
– внешнее поверхностное давление

весовое
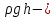
давление;

h
– глубина
погружения рассматриваемой точки под
свободную по- верхность жидкости.

Основное
уравнение гидростатики выражает
зависимость гидростатического давления
p
в любой
точке неподвижной несжимаемой капельной
жидкости от внешнего поверхностного
давления р₀
и глубины
погружения в том случае, когда из массовых
сил на нее действует одна сила тяжести.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Удельный объем

скалярная физическая величина равная объёму, занимаемому единицей массы вещества.

Общие сведения.

Для обозначения удельного объема обычно используется греческая буква υ. Удельный объем равен обратной плотности вещества.

Перевод единиц измерения удельного объема онлайн:

Единицы измерения удельного объема:

• • кубический сантиметр на грамм — единица измерения в СГС. Обозначение в России: см³ /г международное: cm³/g. Данная единица измерения широко применяется при инженерных расчетах, в современной справочной литературе;
  • кубический метр на килограмм— единица измерения в СИ. Обозначение в России: м³/кг; международное: m³/kg. Данная единица измерения широко применяется при инженерных расчетах, в справочной литературе.

Калькуляторы удельного объема:

Удельный объем твердых тел и жидкостей при известной массе и объеме.

Удельный объем веществ (тел) при известной плотности.

Удельный объем  идеального газа.

Поделиться ссылкой:

Модуль
4.  

Тема
4.1    Гидродинамика

Виды
движения (течения) жидкости

Гидродинамика — это
раздел гидравлики, изучающий законы механического движения жидкости и ее
взаимодействия с неподвижными и подвижными поверхностями. Основная задача гидродинамики:
определение гидродинамических характеристик потока, таких как гидродинамическое
давление, скорость движения жидкости, сопротивление движению жидкости, а также
изучение их взаимосвязи.

Общие сведения.

Кинематика жидкости обычно в гидравлике
рассматривается совместно с динамикой и отличается от нее изучением видов и
кинематических характеристик движения жидкости без учета сил, под действием
которых происходит движение, тогда как динамика жидкости изучает законы
движения жидкости в зависимости от приложенных к ней сил.

Жидкость в гидравлике рассматривается как
непрерывная среда, сплошь заполняющая некоторое пространство без образования
пустот. Причины, вызывающие ее движение, — внешние силы, такие, как сила
тяжести, внешнее давление и т. д. Обычно при решении задач гидродинамики этими
силами задаются. Неизвестные факторы, характеризующие движение жидкости, — это
внутреннее гидродинамическое давление (по аналогии с гидростатическим давлением
в гидростатике) и скорость течения жидкости в каждой точке некоторого
пространства. Причем гидродинамическое давление в каждой точке — функция не
только координат данной точки, как это было с гидростатическим давлением, но и
функция времени t, т. е. может изменяться и со временем.

Основной задачей этого раздела гидравлики
является определение следующих зависимостей скорости u и давления P в каждой
точке потока жидкости, которые являются соответствующими функциями времени t и
координат x,y,z:

.

Трудность изучения законов движения
жидкости обусловливается самой природой жидкости и особенно сложностью учета
касательных напряжений, возникающих вследствие наличия сил трения между
частицами. Поэтому изучение гидродинамики, по предложению Л. Эйлера, удобнее
начинать с рассмотрения невязкой (идеальной) жидкости, т. е. без учета сил
трения, внося затем уточнения в полученные уравнения для учета сил трения
реальных жидкостей.

Существует два метода изучения движения
жидкости: метод Ж. Лагранжа и метод Л. Эйлера.

Метод Лагранжа заключается в рассмотрении
движения каждой частицы жидкости, т. е. траектории их движения. Из-за
значительной трудоемкости этот метод не получил широкого распространения.

Метод Эйлера заключается в рассмотрении
всей картины движения жидкости в различных точках пространства в данный момент
времени. Этот метод позволяет определить скорость движения жидкости в любой
точке пространства в любой момент времени, т. е. характеризуется построением
поля скоростей и поэтому широко применяется при изучении движения жидкости.
Недостаток метода Эйлера в том, что при рассмотрении поля скоростей не
изучается траектория отдельных частиц жидкости.

При перемещении жидкости силу давления,
отнесенную к единице площади, рассматривают как напряжение гидродинамического
давления, подобно напряжению гидростатического давления при равновесии
жидкости. Как и в гидростатике, вместо термина «напряжение давления» используют
выражение «гидродинамическое давление», или просто «давление».

По характеру изменения скоростей во времени
движение жидкости бывает установившееся и неустановившееся.

Виды движения (течения) жидкости

Течение жидкости
вообще может быть неустановившимся (нестационарным) или установившимся
(стационарным).

гидродинамика движение жидкость трубопровод

Неустановившееся движение – такое, при
котором в любой точке потока скорость движения и давление с течением времени
изменяются, т.е. u и P зависят не только от координат точки в потоке, но и от
момента времени, в который определяются характеристики движения т.е.:

ADVERTISEMENT

и .

Примером неустановившегося движения может
являться вытекание жидкости из опорожняющегося сосуда, при котором уровень
жидкости в сосуде постепенно меняется (уменьшается) по мере вытекания жидкости.

Установившееся движение – такое, при
котором в любой точке потока скорость движения и давление с течением времени не
изменяются, т.е. u и P зависят только от координат точки в потоке, но не
зависят от момента времени, в который определяются характеристики движения:

и ,

и, следовательно,

    

, ,,.

Пример установившегося движения – вытекание
жидкости из сосуда с постоянным уровнем, который не меняется (остаётся
постоянным) по мере вытекания жидкости.

В случае установившегося течения в процессе
движения любая частица, попадая в заданное, относительно твёрдых стенок, место
потока, всегда имеет одинаковые параметры движения. Следовательно, каждая
частица движется по определённой траектории.

Траекторией называется путь, проходимый
данной частицей жидкости в пространстве за определенный промежуток времени.

При установившемся движении форма
траекторий не изменяется во время движения. В случае неустановившегося движения
величины направления и скорости движения любой частицы жидкости непрерывно
изменяются, следовательно, и траектории движения частиц в этом случае также
постоянно изменяются во времени.

Поэтому для рассмотрения картины движения,
образующейся в каждый момент времени, применяется понятие линии тока.

Линия тока – это кривая, проведенная в
движущейся жидкости в данный момент времени так, что в каждой точке векторы
скорости ui совпадают с касательными к этой кривой.

Нужно различать траекторию и линию тока.
Траектория характеризует путь, проходимый одной определенной частицей, а линия
тока направление движения в данный момент времени каждой частицы жидкости,
лежащей на ней.

При установившемся движении линии тока
совпадают с траекториями частиц жидкости. При неустановившемся движении они не
совпадают, и каждая частица жидкости лишь один момент времени находится на
линии тока, которая сама существует лишь в это мгновение. В следующий момент
возникают другие линии тока, на которых будут располагаться другие частицы. Еще
через мгновение картина опять меняется.

Если выделить в движущейся жидкости
элементарный замкнутый контур площадью dщ и через все точки этого контура
провести линии тока, то получится трубчатая поверхность, которую называют
трубкой тока. Часть потока, ограниченная поверхностью трубки тока, называется
элементарной струйкой жидкости. Таким образом, элементарная струйка жидкости
заполняет трубку тока и ограничена линиями тока, проходящими через точки
выделенного контура с площадью dщ. Если dщ устремить к 0, то элементарная
струйка превратится в линию тока.

Из приведённых выше определений вытекает,
что в любом месте поверхности каждой элементарной струйки (трубки тока) в любой
момент времени вектора скоростей направлены по касательной (и, следовательно,
нормальные составляющие отсутствуют). Это означает, что ни одна частица
жидкости не может проникнуть внутрь струйки или выйти наружу.

При установившемся движении элементарные
струйки жидкости обладают рядом свойств:

·        
· площадь поперечного сечения струйки и ее форма с течением
времени не изменяются, так как не изменяются линии тока;

·        
· проникновение частиц жидкости через боковую поверхность
элементарной струйки не происходит;

·        
· во всех точках поперечного сечения элементарной струйки
скорости движения одинаковы вследствие малой площади поперечного сечения;

·        
· форма, площадь поперечного сечения элементарной струйки и
скорости в различных поперечных сечениях струйки могут изменяться.

Трубка тока является как бы непроницаемой
для частиц жидкости, а элементарная струйка представляет собой элементарный поток
жидкости.

При неустановившемся движении форма и
местоположение элементарных струек непрерывно изменяются.

Кроме того, установившееся движение
подразделяется на равномерное и неравномерное.

Равномерное движение характеризуется тем,
что скорости, форма и площадь сечения потока не изменяются по длине потока.

Неравномерное движение отличается
изменением скоростей, глубин, площадей сечений потока по длине
потока.

Среди неравномерно движущихся потоков
следует отметить плавно изменяющиеся движения, характеризующееся тем, что:

·        
· линии тока искривляются мало;

·        
· линии тока почти параллельны, и живое сечение можно считать
плоским;

·        
· давления в живом сечении потока зависят от глубины.

Физические свойства жидкости

К основным физическим свойствам жидкости, которые
рассматриваются в гидродинамике, относятся плотность, удельный вес, удельный
объем, температурное расширение, сжимаемость и вязкость.

Плотность —
это отношение массы вещества к его объему:

р = m/V

На плотность жидкости влияют температура и давление. Значения
плотности некоторых жидкостей приведены ниже:

§  Жидкость:
р, кг/м3

§  Вода:
1000

§  Антифриз:
1070

§  Бензин:
750

§  Керосин:
800

§  Дизельное
топливо: 860

§  Масло
МГ- 15-Б: 850

§  МГ-22-А:
880

§  ТМ-5-18:
900

§  Нефть:
900

§  Ацетон:
700

§  Спирт:
800

§  Глицерин:
1260

Удельный
вес — это отношение веса жидкости к занимаемому объему:

у = mg/V = pg.

Удельный
объем жидкости — объем единицы массы этой жидкости:

v = У/m = 1/р.

Температурное
расширение — свойство жидкости изменять свой объем при изменении
температуры. С ростом температуры объем жидкости увеличивается и наоборот.
Различные жидкости при увеличении температуры на одну и ту же величину
увеличиваются в объеме по разному. Поэтому свойство жидкости увеличиваться в
объеме с увеличением температуры характеризуется коэффициентом температурного
расширения Bт, который показывает изменение единицы объема данной жидкости при
изменении ее температуры на 1 К.

§  Жидкость
— Bт (10^-4, К^-1)

§  Вода:
2

§  Антифриз:
5

§  Нефть:
8

§  Ртуть:
1,8

Увеличение объема при нагревании рассчитывается по уравнению:

дельта
V= Bт*V0*дельта Т

где V0 начальный объем жидкости; дельта Т— изменение
температуры.

В расчетах ДВС коэффициент температурного расширения считают
постоянным, хотя на самом деле он зависит от условий нагревания или охлаждения,
давления и начальной температуры.

Сжимаемость —
свойство жидкости изменять объем при изменении давления.

дельта
V = Bр*V0*дельта р,

где дельта V— изменение объема; дельта р — изменение давления;
Вр — коэффициент объемного сжатия.

Коэффициент объемного сжатия показывает изменение единицы объема
жидкости при изменении давления на 1 Па. Он зависит от условий сжатия,
температуры и начального давления. При расчетах эта зависимость не учитывается.

Коэффициент объемного сжатия для воды равен 5 * 10^-4 1/Па, для
нефтепродуктов — 7*10^-4 1/Па, для ртути — 0,3*10^-4 1/Па.

Ввиду незначительных величин жидкости считаются несжимаемыми.

Вязкость —
свойство жидкости оказывать сопротивление перемещению одной ее части
относительно другой.

Рис. Схема изменения скорости жидкости, заключенной между
неподвижной (1) и подвижной (2) пластинами

Если плоскость 2, находящаяся на расстоянии б от плоскости 1,
под действием силы F перемещается со скоростью V0, то слои жидкости,
находящиеся между плоскостями, перемещаются с разными скоростями. При этом
максимальная скорость V0 в точках контакта с плоскостью 2, минимальная (вплоть
до нуля) в точках контакта с плоскостью 1.

Если слои жидкости при движении не перемешиваются, то скорость в
потоке изменяется по линейному закону, и отношение V0/б представляет собой
градиент скорости.

При скольжении слоев жидкости между ними возникают силы
внутреннего трения, которые сопротивляются движению. На преодоление этих сил и
расходуется внешняя сила F:

F =
nSV0/б

где n — динамический коэффициент вязкости или динамическая
вязкость; S — площадь трения (жидкости о пластину).

Динамическая вязкость учитывает свойства жидкости, от которых
зависит ее внутреннее трение. В технике и в частности в гидравлике часто
используется кинематическая вязкость v, которая равна отношению динамической
вязкости жидкости к ее плотности:

v = n/p

Для упрощения решения гидродинамических задач считают, что
рассматриваемые жидкости не обладают температурным расширением, сжимаемостью и
вязкостью. Такие жидкости в отличие от реальных называются идеальными.