Задачи на силу Архимеда с решениями
Формулы, используемые на уроках «Задачи на силу Архимеда», «Сообщающиеся сосуды».
Название величины |
Обозначение |
Единица измерения |
Формула |
Объем тела |
V |
м3 |
Vт = FA / pg |
Плотность жидкости |
p |
кг/м3 |
pж = FA / (Vg) |
Сила Архимеда |
FA |
Н |
FA = pж Vт g |
Постоянная |
g ≈ 10 Н/кг |
Н/кг |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Тело объемом 2 м3 погружено в воду. Найдите архимедову силу, действующую на тело.

Задача № 2.
Определить выталкивающую силу, действующую на деревянный плот объемом 12 м3, погруженный в воду на половину своего объема.

Задача № 3.
Каков объем железобетонной плиты, если в воде на нее действует выталкивающая сила 8000 Н?

Задача № 4.
Какую силу надо приложить, чтобы удержать под водой бетонную плиту, масса которой 720 кг?

Задача № 5.
Какую высоту должен иметь столб нефти, чтобы уравновесить в сообщающихся сосудах столб ртути высотой 16 см?

Задача № 6.
Вес тела в воздухе равен 26 кН, а в воде — 16 кН. Каков объем тела?

Задача № 7.
Какую силу нужно приложить, чтобы удержать в воде кусок гранита объемом 40 дм3?
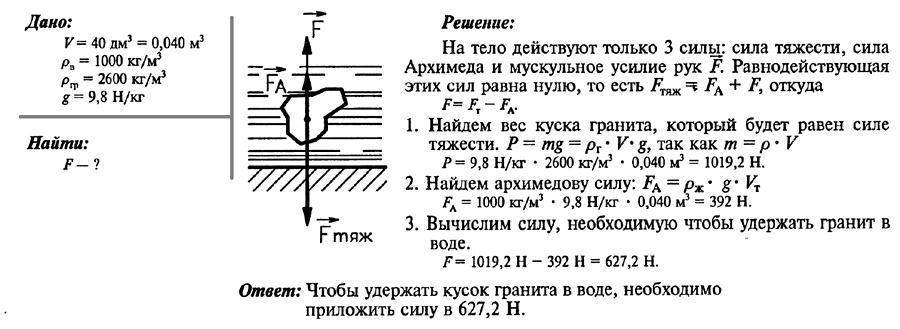
Задача № 8.
Определите объем куска меди, который при погружении в керосин выталкивается силой 160 Н.
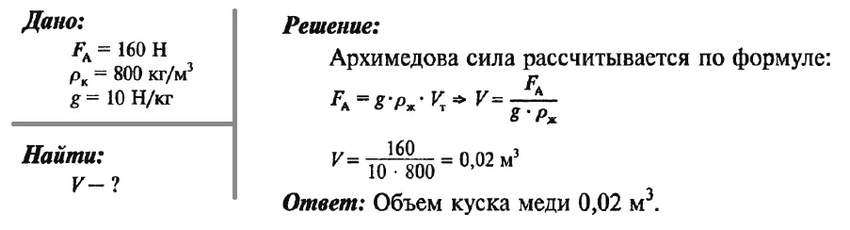
Задача № 9 (повышенной сложности).
Медный шар в воздухе весит 1,96 Н, а в воде 1,47 Н. Сплошной этот шар или полый?

Задача № 10 (повышенной сложности).
Рассчитайте, какой груз сможет поднять шар объемом 1 м3, наполненный водородом. Какой примерно объем должен иметь шар с водородом, чтобы поднять человека массой 70 кг? (Вес оболочки не учитывать.)

Задача № 11.
Деревянный цилиндр плавает на поверхности воды так, что он погружен в воду на 90%. Какая часть цилиндра будет погружена в воду, если поверх воды налить слой масла, полностью закрывающий цилиндр? Плотность масла 800 кг/м3.
Дано: V – объем цилиндра (V = Sh); h – высота цилиндра; S – площадь основания цилиндра; V1 – объем цилиндра, погруженного в масло (V1 = V – V2 = Sh1); h1 – высота части цилиндра, погруженной в масло; V2 – объем цилиндра, погруженного в воду после добавления масла; рв – плотность воды (1000 кг/м3); рм – плотность масла (800 кг/м3)
Найти: (h – h1) / h — ?
Решение. F – сила, выталкивающая цилиндр из воды до добавления масла F = 0,9pвgV
F1 – сила, выталкивающая цилиндр из масла F1 = pмgV1
F2 – сила, выталкивающая цилиндр из воды после добавления масла F2 = pвgV2
Баланс сил: F – F1 = F2
0,9pвgV – pмgV1 = pвgV2 V1 = V – V2 ⇒ 0,9pвV – pм(V – V2) = pвV2
V(0,9pв – pм) = V2(pв – pм) V = Sh; V1 = Sh1 ⇒

Ответ: 1/2 часть цилиндра будет погружена в воду (50%).
Задача № 12.
Плоская льдина плавает в воде, выступая над уровнем воды на 3 см. Человек массой 70 кг зашел на льдину. В результате, высота выступающей части над льдиной уменьшилась в 3 раза. Найти площадь льдины.
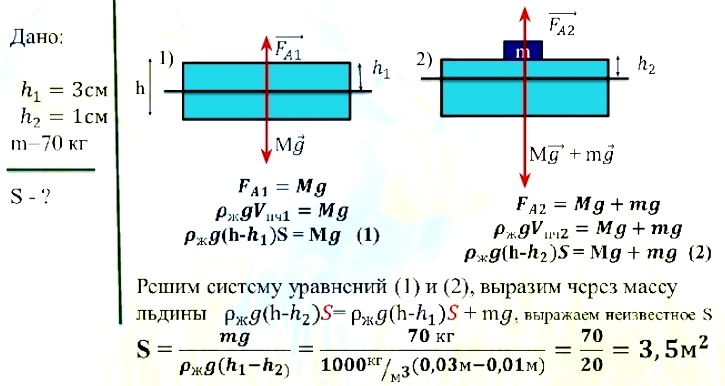
Ответ: 3,5 м3.
Теория для решения задач.
Давление жидкости на покоящееся в ней тело называют гидростатическим давлением. Гидростатическое давление на глубине h равно р = ратм + p*g*h
Закон Паскаля. Жидкость и газ передают оказываемое на них давление во всех направлениях одинаково.

Конспект урока «Задачи на силу Архимеда с решениями».
Следующая тема: «Задачи на механическую работу».
Сила Архимеда
Вместе с преподавателем физики разбираемся, в чем измеряется и от чего зависит сила Архимеда. А в конце статьи вспомним известную легенду о том, как был открыт закон Архимеда, и узнаем, действует ли он в условиях невесомости

Как объяснить, почему плавают огромные корабли из стали, которая тяжелее воды? Да еще и перевозят тонны грузов. Это происходит благодаря открытию, сделанному за два с лишним столетия до нашей эры изобретателем и ученым Архимедом.
История сохранила нам немного имен ученых-практиков, чьи изобретения изменили мир. Навсегда забыт гений, который придумал колесо. Но любой современный школьник назовет Архимеда, даже если знает о нем только легенду про мокрого голого философа, бежавшего по улице Сиракуз с криком: «Эврика!», то есть «Нашел!». А ведь ученый заслужил вечную благодарную память человечества благодаря многим изобретениям и открытиям:
- Теория рычага и способы его расчета. На этой основе построены боевые машины для метания тяжелых камней и «коготь Архимеда» — машина для переворачивания римских трирем;
- Шкив и многоступенчатый блок, полиспаст;
- Червячная передача;
- Архимедов винт и насосы, работающие на его принципе;
- Одометр, машина для измерения пройденного пути;
- «Архимедово число»: отношение длины окружности к ее диаметру

- Фокусировка световых лучей при помощи зеркал. По легенде, так были сожжены римские корабли, осаждавшие Сиракузы. Недавно энтузиасты провели экспериментальную проверку и удалось поджечь деревянный баркас.
Однако самое знаменитое открытие — закон Архимеда, основа гидростатики. Удивительно, что он был почти забыт, пока корабли строили из дерева. И только когда они стали железными, а потом стальными, инженеры осознали важность силы Архимеда и стали применять ее формулу при расчетах водных и воздушных судов.
Определение закона Архимеда простыми словами
На тело, погруженное в жидкость или газ, действует подъемная, она же выталкивающая сила (сила Архимеда), равная весу вытесненного объема жидкости или газа.
Вектор силы Архимеда направлен против направления действия силы тяжести. Следствия закона Архимеда:
- В невесомости закон Архимеда не действует.
- Если сила Архимеда меньше силы тяжести, то тело утонет.
- Если силы одинаковы по величине, тело «повисает» в окружающей среде.
- Если сила Архимеда больше силы тяжести, то тело всплывает, пока они не уравновесятся. В воде этот момент наступит на поверхности.

Формула силы Архимеда
Предыдущая формулировка годится только для участка цепи, где отсутствует сам источник электродвижущей силы. В реальности ток течет по замкнутому контуру, где обязательно есть батарея или генератор, имеющий собственное внутреннее сопротивление. Поэтому формула закона Ома для полной цепи выглядит несколько сложнее

Где: FA — сила Архимеда;
ρ — плотность жидкости или газа, в которое погружают тело;
g — ускорение свободного падения, которое зависит от того, на какой планете или спутнике мы находимся. Для поверхности Земли, например, ускорение примерно равно 9,8 м/с2;
V — объем погруженной в среду части тела.
Закон Паскаля
Объяснение закона простыми словами и его формула
подробнее

В чем измеряется сила Архимеда
Единица измерения силы Архимеда в системе СИ — ньютон (Н).
1Н = 1 кг·м/с2
Архимед и наше время
В перечне военных трофеев, взятых римлянами в Сиракузах, есть некий «Планетарий Архимеда» — механическая модель движения планет. Он не сохранился, но есть подозрение, что загадочное устройство, случайно обнаруженное в затонувшем корабле у острова Антикитера, тоже сделано золотыми руками Архимеда. Прямых доказательств этого факта нет, но уже выяснено, что время изготовления приблизительно соответствует годам жизни гениального инженера.
Популярные вопросы и ответы
Отвечает Николай Герасимов, старший преподаватель по физике Домашней школы «ИнтернетУрок».
От чего зависит сила Архимеда?
Например, для определения выталкивающей силы, действующей на камень, лежащий на дне озера, нужно брать весь его объем. Если же определяем силу Архимеда, действующую на мяч, плавающий по этому озеру, то нужно брать лишь объем той части, которая находится под водой. Зависимость выталкивающей силы от ускорения свободного падения позволяет сделать интересный вывод о том, что в невесомости силы Архимеда нет.
Зная, что сила Архимеда зависит от плотности жидкости, можно объяснить следующее явление: куриное яйцо, помещенное в обычную воду, утонет и будет лежать на дне банки. Но стоит добавить в эту банку насыщенный раствор поваренной соли и тем самым изменить плотность воды — и яйцо начинает всплывать.
Как был открыт закон Архимеда?
Открытие закона Архимеда связано с интересной легендой. Древнегреческий царь Герон II приказал ювелирам изготовить золотую корону, что и было вскоре выполнено. Царь заподозрил, что ювелиры его обманули и сделали корону из электрона, сплава золота и серебра. Отличить подделку на глаз не удалось. Для проверки пригласили ученого из Сиракуз по имени Архимед. Достаточно было сравнить объем короны с объемом куска золота такой же массы.
Сложность состояла в определении объема короны, так как она была сложной формы, и вычислить объем по математическим формулам было невозможно. Долгие размышления не увенчались успехом, и Архимед решил сходить отдохнуть в баню. Именно там ученому пришла гениальная идея: погружаясь в воду, тело вытесняет ее в объеме, который равен объему погруженной части тела. «Эврика!» («Нашел!») — закричал Архимед и побежал к царю.
Сравнив объемы воды, вытесненной короной и куском золота такой же массы, он уличил ювелиров в нечестности и алчности. Так Архимедом был открыт закон, который позволяет нам объяснить, почему ходят по морям и океанам огромные корабли, изготовленные из железа, а маленькая металлическая гайка тонет.
Какой буквой обозначают силу Архимеда?
Как и большинство сил, сила Архимеда обозначается буквой F. Это первая буква английского слова force – сила. В индексе пишут букву А или В, которые позволяют отличить силу Архимеда FA или выталкивающую силу FВ от других сил в природе.
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,653 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,912 -
разное
16,901
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
На прошлом уроке мы доказали с помощью опытов существование силы, действующей на тела, погруженные в жидкость или газ — выталкивающей силы. Также мы теперь знаем, что ее можно рассчитать по формуле: $F_{выт} = gm_ж = P_ж$. Но какое еще есть значение у этой силы? На этом уроке мы более подробно рассмотрим выталкивающую силу.
Выталкивающая сила и вес тела
Как можно на опыте определить, с какой силой тело, погруженное целиком в жидкость, выталкивается из жидкости?
Давайте познакомимся с таким опытом. Он представлен на рисунке 1.
Подвесим на пружину небольшую емкость для жидкости и тело цилиндрической формы ниже. На конце пружины у нас расположена стрелка-указатель. Она отмечает растяжение пружины на штативе (рисунок 1, а). Таким образом, мы видим вес тела в воздухе.
Теперь опустим наше тело в большой сосуд. Сосуд имеет трубку для слива и наполнен жидкостью до уровня этой трубки (рисунок 1, б).
Когда мы полностью опустим тело в сосуд, часть жидкости из него выльется через трубку для слива в стакан. Объем этой жидкости будет равен объему тела. Мы уже знаем, что на тело действует выталкивающая сила: пружина сокращается, стрелка-указатель поднимается, вес тела в жидкости становится меньше.
А теперь возьмем жидкость, которая вылилась в стакан. Зальем ее в емкость, которая также подвешена к пружине (рисунок 1, в). Теперь стрелка-указатель вернулась к своему изначальному положению.
Так чему равна эта сила? Сделаем вывод из данного опыта.
Сила, выталкивающая целиком погруженное в жидкость тело, равна весу жидкости в объеме этого тела.
Если провести подобный опыт с газом, а не с жидкостью, то мы получим, что сила, выталкивающая тело из газа, равна весу газа, взятого в объеме тела.
Сила Архимеда
Как называют силу, которая выталкивает тела, погруженные в жидкости и газы?
Теперь мы добавим, что эту выталкивающую силу называют архимедовой силой. Архимед (рисунок 2) — древнегреческий ученый и инженер, сделавший множество открытий и в математике, и в физике. Именно он первый обнаружил наличие выталкивающей силы и рассчитал ее значение.
Как подсчитать архимедову силу?
В прошлом уроке мы получили формулу $F_{выт} = P_ж = g m_ж$. Теперь мы будем называть эту силу архимедовой $F_A$.
Из выше рассмотренных опытов мы можем выразить массу вытесненной жидкости через ее плотность и объем тела, который эту жидкость вытеснил (они одинаковы): $m_ж = rho_ж cdot V_т$. Получим формулу для архимедовой силы.
$F_A = g rho_ж V_т$.
От чего зависит архимедова сила?
Взгляните еще раз на формулу: $F_A = g rho_ж V_т$.
Ясно видно, что архимедова сила зависит только от плотности жидкости и от объема тела, которое мы погружаем в эту жидкость.
Если мы будем погружать в одну и ту же жидкость тела разной плотности и разной формы (рисунок 3), то значение силы меняться не будет (при условии, что эти тела будут обладать одинаковым объемом).
Определение веса тела, погруженного в жидкость или газ
На тело, погруженное в жидкость (или в газ), действуют две силы: сила тяжести и архимедова сила. Направлены они в противоположные стороны. Вес тела в жидкости $P_1$ будет меньше веса тела в вакууме $P$ на архимедову силу $F_A$. То есть:
$P_1 = P space − space F_A = gm space − space gm_ж$.
Если тело погружено в жидкость или газ, то его вес уменьшается на вес вытесненной им жидкости или газа.
Пример задачи
Определите выталкивающую силу, которая будет действовать на камень объемом $2.6 space м^3$, лежащий на морском дне.
Дано:
$V_т = 2.6 space м^3$
$rho_ж = 1030 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$F_A — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Сила Архимеда рассчитывается по формуле:
$F_A = g rho_ж V_т$.
Подставим численные значения величин и рассчитаем эту силу:
$F_A = 9.8 frac {Н}{кг} cdot 1030 frac{кг}{ м^3} cdot 2.6 space м^3 approx 26 244 space Н approx 26.2 space кН$.
Ответ: $F_A approx 26,2 space кН$.
Забавное дополнение: легенда об Архимеде
Архимед, великий изобретатель, шокировал своих современников гениальными открытиями. Его имя упоминается во множестве легенд, но одна из них стала наиболее известной: легенда о том, как Архимед пришел к открытию выталкивающей силы.
Царь Гиерон поручил Архимеду проверить работу мастера, который изготовил для него золотую корону.
Долгое время ученый не мог найти ответ: как определить количество некачественных примесей? Проблема заключалась в том, что определить ее объем — сложная задача. По легенде озарение настигло Архимеда, когда он принимал ванну.
Ученый заметил, что из ванны вылилась вода, когда он залез в нее. И здесь его посетила гениальная мысль. Все вы слышали его известную цитату: «Эврика! Эврика!» (в переводе означает: «Нашел! Нашел!»).
Так Архимед победно выкрикивал свою фразу, потрясенный своим открытием, что она дошла в виде легенды и до наших времен.
Упражнения
Упражнение №1
К коромыслу весов подвешены два цилиндра одинаковой массы: свинцовый и алюминиевый (рисунок 4). Весы находятся в равновесии. Нарушится ли равновесие весов, если оба цилиндра одновременно погрузить в воду; в спирт? Ответ обоснуйте. Проверьте его на опыте. Как зависит выталкивающая сила от объема тела?
Посмотреть ответ
Скрыть
Ответ:
Когда мы погрузим цилиндры в жидкость, на каждый их них будет действовать сила Архимеда. Если эти силы будут равны, то весы останутся в равновесии.
Запишем формулы архимедовой силы для каждого цилиндра.
Для свинцового цилиндра:
$F_{A1} = g rho_ж V_1$.
Для алюминиевого цилиндра:
$F_{A2} = g rho_ж V_2$.
Мы видим, что равенство этих сил зависит от объемов цилиндров. Они равны? Нет, они имеют одинаковые массы, но разные плотности. Цилиндр из алюминия будет обладать большим объемом, чем свинцовый цилиндр ($V = frac{m}{rho}$). Значит, на алюминиевый цилиндр будет действовать большая выталкивающая сила, чем на свинцовый.
Если мы проверим это на опыте, то увидим подтверждение нашим выводам (рисунок 5).
При этом весы выйдут из равновесия в случае и с водой (рисунок 5, а), и со спиртом (рисунок 5, б). Так как мы опускаем цилиндры одновременно в один и тот же тип жидкости, значение архимедовой силы, действующей на цилиндры, будет различаться только в зависимости от объемов этих цилиндров — свинцовый перевесит алюминиевый в любой жидкости.
Заметим, что в случае погружения в воду, архимедова сила будет больше, чем в случае погружения в спирт. Это объясняется тем, что вода имеет большую плотность, чем спирт.
Упражнение №2
К коромыслу весов подвешены два алюминиевых цилиндра одинакового объема. Нарушится ли равновесие весов, если один цилиндр погрузить в воду, а другой — в спирт? Ответ обоснуйте. Зависит ли выталкивающая сила от плотности жидкости?
Посмотреть ответ
Скрыть
Ответ:
Если один цилиндр погрузить в воду, а другой — в спирт, то равновесие весов нарушится (рисунок 6). На цилиндр, находящийся в воде, будет действовать большая архимедова сила.
Так происходит, потому что архимедова сила зависит от объема погруженного тела (а они у нас одинаковые: $V_1 = V_2 = V$) и от плотности жидкости:
$F_А = g rho_ж V$.
Плотность спирта ($800 frac{кг}{м^3}$) меньше плотности воды ($1000 frac{кг}{м^3}$). Значит, на цилиндр, погруженный в воду, будет действовать большая архимедова сила, чем на тот, что погружен в спирт.
Упражнение №3
Объем куска железа равен $0.1 space дм^3$. Какая выталкивающая сила будет на него действовать при полном его погружении в воду; в керосин?
Дано:
$V = 0.1 space дм^3$
$g = 9.8 frac{Н}{кг}$
$rho_1 = 1000 frac{кг}{м^3}$
$rho_2 = 800 frac{кг}{м^3}$
СИ:
$V = 0.1 cdot 10^{-3} space м^3$
$F_{А1} — ?$
$F_{А2} — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Рассчитаем архимедову силу, которая будет действовать на кусок железа в воде:
$F_{А1} = g rho_1 V$,
$F_{А1} = 9.8 frac{Н}{кг} cdot 1000 frac{кг}{м^3} cdot 0.1 cdot 10^{-3} space м^3 = 0.98 space Н approx 1 space Н$.
Теперь рассчитаем архимедову силу, которая будет действовать на кусок железа в керосине:
$F_{А2} = g rho_2 V$,
$F_{А2} = 9.8 frac{Н}{кг} cdot 800 frac{кг}{м^3} cdot 0.1 cdot 10^{-3} space м^3 = 0.784 space Н approx 0.8 space Н$.
Ответ: $F_{А1} approx 1 space Н$, $F_{А2} approx 0.8 space Н$.
Упражнение №4
Бетонная плита объемом $2 space м^3$ погружена в воду. Какую силу необходимо приложить, чтобы удержать ее в воде; в воздухе?
Дано:
$V = 2 space м^3$
$g = 9.8 frac{Н}{кг}$
$rho_1 = 1000 frac{кг}{м^3}$
$rho_2 = 1.29 frac{кг}{м^3}$
$rho_б = 2300 frac{кг}{м^3}$
$F_1 — ?$
$F_2 — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Бетонная плита находится в воде. На нее действует сила тяжести и архимедова сила. Они направлены противоположно друг другу и будут иметь разные величины. Разность этих сил — и будет искомая сила $F_1$, которую нужно приложить, чтобы удержать бетонную плиту в воде (чтобы она не опускалась на дно и не всплывала):
$F_1 = F_{тяж} space − space F_{А1}$.
Сила тяжести рассчитывается по формуле:
$F_{тяж} = gm$.
Массу бетонной плиты мы можем выразить через ее плотность и объем:
$m = rho_б V$,
$F_{тяж} = g rho_б V$.
Архимедова сила, действующая на бетонную плиту в воде:
$F_{А1} = g rho_1 V$.
Подставим силу тяжести и архимедову силу в формулу и рассчитаем $F_1$:
$F_1 = F_{тяж} space − space F_{А1} = g rho_б V space − space g rho_1 V = gV cdot (rho_б space − space rho_1)$,
$F_1 = 9.8 frac {Н}{кг} cdot 2 space м^3 cdot (2300 frac{кг}{м^3} space − space 1000 frac{кг}{м^3}) = 25 space 480 space Н approx 25 space кН$.
Используем ту же формулу для того, чтобы рассчитать силу $F_2$, которую нужно приложить, чтобы удержать бетонную плиту в воздухе:
$F_2 = gV cdot (rho_б space − space rho_2)$,
$F_2 = 9.8 frac {Н}{кг} cdot 2 space м^3 cdot (2300 frac{кг}{м^3} space − space 1.29 frac{кг}{м^3}) approx 45 space 054 space Н approx 45 space кН$.
Ответ: $F_1 approx 25 space кН$, $F_2 approx 45 space Н$.
Упражнение №5
Предположив, что корона царя Гиерона в воздухе весит $20 space Н$, а в воде — $18.75 space Н$, вычислите плотность вещества короны. Полагая, что к золоту было подмешано только серебро, определите, сколько в короне было золота и сколько серебра. При решении задачи плотность золота считайте равной $20 space 000 frac{кг}{м^3}$, плотность серебра — $10 space 000 frac{кг}{м^3}$. Каков был бы объем короны из чистого золота?
Дано:
$P_1 = 20 space Н$
$P_2 = 18.75 space Н$
$rho_з = 20 space 000 frac{кг}{м^3}$
$rho_с = 10 space 000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$rho_1 = 1.29 frac{кг}{м^3}$
$rho_2 = 1000 frac{кг}{м^3}$
$rho — ?$
$m_з — ?$
$m_с — ?$
$V_1 — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Вес короны в воздухе $P_1$ будет меньше веса тела в вакууме $P$ на архимедову силу $F_{A1}$. То есть:
$P_1 = P space − space F_{A1}$.
Значит, вес короны в вакууме будет равен сумме ее веса в воздухе и архимедовой силы:
$P = P_1 space + space F_{А1}$,
$gm = P_1 space + space g rho_1 V$.
Теперь запишем такое же уравнение для веса короны в воде:
$gm = P_2 space + space g rho_2 V$.
Левые части уравнений у нас равны, поэтому мы можем приравнять правые части друг к другу:
$P_1 space + space g rho_1 V = P_2 space + space g rho_2 V$.
Перенесем элементы, содержащие неизвестный объем вправо:
$P_1 space − space P_2 = g rho_2 V space − space g rho_1 V$,
$P_1 space − space P_2 = gV (rho_2 space − space rho_1)$.
Выразим отсюда объем короны и рассчитаем его:
$V = frac{P_1 space − space P_2}{g (rho_2 space − space rho_1)}$,
$V = frac{20 space Н space − space 18.75 space Н}{9.8 frac{Н}{кг} (1000 frac{кг}{м^3} space − space 1.29 frac{кг}{м^3})} = frac{1.25}{9787} space м^3 = 12.8 cdot 10^{-5} space м^3$.
Используем одно из первых уравнений для веса короны в вакууме и в воздухе:
$gm = P_1 space + space g rho_1 V$.
Выразим отсюда массу короны и рассчитаем ее:
$m = frac{P_1 space + space g rho_1 V}{g}$,
$m = frac{20 space Н space + space 9.8 frac{Н}{кг} cdot 1.29 frac{кг}{м^3} cdot 12.8 cdot 10^{-5} space м^3}{9.8 frac{Н}{кг}} approx 2.04 space кг$.
Теперь мы знаем массу и объем короны. Рассчитаем ее плотность:
$rho = frac{m}{V}$,
$rho = frac{2.04 space кг}{12.8 cdot 10^{-5} space м^3} approx 16 space 000 frac{кг}{м^3}$.
Корона состоит из серебра и золота. Это означает, что ее общий объем мы можем записать в виде суммы объемов серебра и золота, ее составляющих:
$V = V_с space + space V_з$.
То же самое с общей массой короны:
$m = m_с space + space m_з$.
Запишем объемы через массы и плотности (а также выразим массу золота через общую массу короны и массу серебра):
$V_с = frac{m_с}{rho_с}$,
$V_з = frac{m_з}{rho_з} = frac{m space − space m_с}{rho_з}$.
Подставим эти объемы в формулу для общего объема короны и выразим из нее массу серебра:
$V = frac{m_с}{rho_с} space + space frac{m space − space m_с}{rho_з} = frac{m_с (rho_з space − space rho_с) space + space rho_с m}{rho_с rho_з} = m_с cdot frac{rho_з space − space rho_с}{rho_с rho_з} space + space frac{m}{rho_з}$,
$m_с = frac{V space − space frac{m}{rho_з}}{frac{rho_з space − space rho_с}{rho_с rho_з}} = frac{rho_с (V rho_з space − space m)}{rho_з space − space rho_с}$.
Рассчитаем массу серебра, содержащегося в короне:
$m_с = frac{10 space 000 frac{кг}{м^3} (12.8 cdot 10^{-5} space м^3 cdot 20 space 000 frac{кг}{м^3} space − space 2.04 space кг)}{20 space 000 frac{кг}{м^3} space − space 10 space 000 frac{кг}{м^3}} = frac{5200 frac{кг^2}{м^3}}{10 space 000 frac{кг}{м^3}} = 0.52 space кг$.
Теперь мы можем вычислить и количество золота в короне:
$m_з = m space − space m_с$,
$m_з = 2.04 space кг space − space 0.52 space кг = 1.52 space кг$.
Если бы вся корона была из золота, то ее объем был бы равен:
$V_1 = frac{m}{rho_з}$,
$V_1 = frac{2.04 space кг}{20 space 000 frac{кг}{м^3}} = 10.2 cdot 10^{-5} space м^3$.
Ответ: $rho approx 16 space 000 frac{кг}{м^3}$, $m_з = 1.52 space кг$, $m_с = 0.52 space кг$, $V_1 = 10.2 cdot 10^{-5} space м^3$.
Упражнение №6
По мелким камешкам ходить босыми ногами больно. Почему человек не испытывает боли, если ходит по таким же камням в воде?
Посмотреть ответ
Скрыть
Ответ:
Что означает фраза «ходить по камням»? Со стороны физики, когда мы наступаем на камни, мы давим на них своим весом: $p = frac{F}{S} = frac{P}{S}$.
Когда мы оказываемся в воде, наш вес уменьшается. Это следствие действия на нас архимедовой силы. Уменьшается вес — уменьшается и давление наших стоп на камни.
Содержание:
Выталкивающая сила:
Наблюдение. Почему тяжело погрузить мяч в воду, и почему, как только мы его отпустим, он выпрыгивает из воды? Почему в море легче плавать, чем в озере? Почему в воде мы можем поднять камень, а в воздухе — нет?
Опыт 1. Подвесим к пружине тело (рис. 138). В связи с тем, что на тело действует сила тяжести 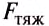
Газы во многом подобны жидкостям. На тела, помещённые в газ, также действует выталкивающая сила. Именно под действием этой силы воздушные шары, метеорологические зонды, детские шарики, наполненные водородом, поднимаются вверх.
А от чего зависит выталкивающая сила ?
Опыт 2. Два тела разного объёма, но одинаковой массы, погрузим полностью в одну и ту же жидкость (воду). Мы видим, что тело большего объёма выталкивается из жидкости (воды) с большей силой (рис. 139).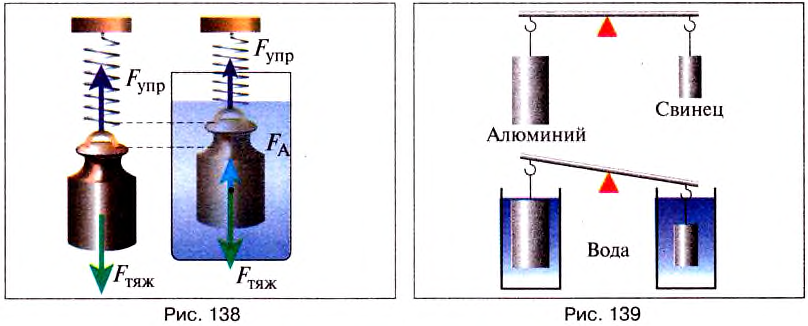
Выталкивающая сила зависит от объёма погружённого в жидкость тела. Чем больше объём тела, тем большая выталкивающая сила действует на него.
Опыт 3. Погрузим полностью два тела одинакового объёма и массы в разные жидкости, например воду и керосин (рис. 140). Нарушение равновесия в этом случае свидетельствует, что в воде на тело действует большая выталкивающая сила, это можно связать с тем, что плотность воды больше, чем плотность керосина.
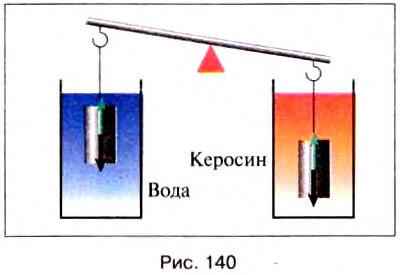
Выталкивающая сила зависит от плотности жидкости, в которую погружено тело. Чем больше плотность жидкости, тем большая выталкивающая сила действует на погружённое в неё тело.
Обобщая результаты наблюдений и опытов можно сделать такой вывод.
На тело, погружённое в жидкость (газ), действует выталкивающая сила, равная по значению весу жидкости (газа), вытесненной этим телом.
Это утверждение называют законом Архимеда, древнегреческого учёного, который его открыл и, по легенде, успешно применил для решения практической задачи: определил, содержится ли в золотой короне царя Гиерона примесь серебра. Силу, которая выталкивает тело из жидкости или газа, называют еще архимедовой силой.
На основе закона Архимеда можно сразу написать формулу для определения выталкивающей силы, но чтобы лучше понять, вследствие чего она возникает, выполним простые расчёты. Для этого рассмотрим тело в форме прямоугольного бруска, погружённого в жидкость таким образом, чтобы его верхняя и нижняя фан и располагались параллельно поверхности жидкости (рис. 141). 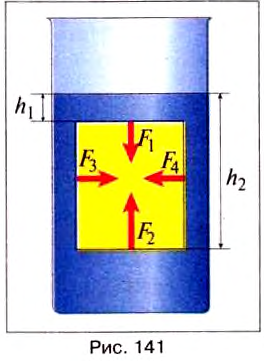
Посмотрим, каким будет результат действия сил давления на поверхность этого тела.
Согласно закону Паскаля горизонтальные силы 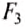 и
и 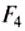 действующие на симметричные боковые грани бруска, попарно равны по значению и противоположно направлены. Они не выталкивают брусок вверх, а только сжимают его с боков. Рассмотрим силы гидростатического давления на верхнюю и нижнюю грани бруска.
действующие на симметричные боковые грани бруска, попарно равны по значению и противоположно направлены. Они не выталкивают брусок вверх, а только сжимают его с боков. Рассмотрим силы гидростатического давления на верхнюю и нижнюю грани бруска.
Пусть верхняя грань площадью S расположена на глубине 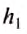 тогда сила давления
тогда сила давления 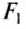 , на неё будет равна:
, на неё будет равна: 
где 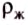 — плотность жидкости.
— плотность жидкости.
Нижняя грань бруска площадью S расположена на большей глубине 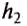 , поэтому сила давления
, поэтому сила давления 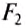 на неё будет также больше, чем
на неё будет также больше, чем 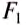 :
: 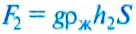
Обе силы давления 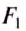 , и
, и 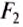 действуют вдоль вертикали, их равнодействующая и будет силой Архимеда
действуют вдоль вертикали, их равнодействующая и будет силой Архимеда 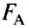 , направленной вверх в сторону большей силы
, направленной вверх в сторону большей силы 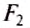 , а её значение будет равно разности сил
, а её значение будет равно разности сил
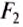 и
и 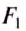 :
:  .
.
Поскольку разность 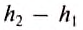 является высотой бруска, то произведение
является высотой бруска, то произведение 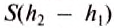 равно объёму тела
равно объёму тела 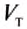 , и мы окончательно получаем формулу,
, и мы окончательно получаем формулу,
являющуюся математическим выражением закона Архимеда:
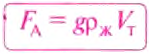
Действительно, поскольку жидкость не сжимается, то объём вытесненной телом жидкости равен объёму этого тела, и произведение 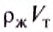 равно массе жидкости
равно массе жидкости 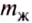 в объёме тела
в объёме тела 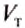 . В свою очередь, произведение
. В свою очередь, произведение 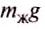 является весом этой жидкости.
является весом этой жидкости.
Из приведённого расчета наглядно видно, что выталкивающая (архимедова) сила возникает вследствие того, что значения гидростатического давления на разных глубинах неодинаковы и возрастают с глубиной.
Архимедовую силу можно определить экспериментально.
Опыт 4. Подвесим тело к динамометру (рис. 142). На тело действует сила тяжести почти 10 Н. Погрузим тело в жидкость (рис. 143).
 Динамометр показывает 6 Н. Определим разность показаний динамометра. Она равняется 4 Н.
Динамометр показывает 6 Н. Определим разность показаний динамометра. Она равняется 4 Н.
Кстати:
Однажды у императора Цао-Цао, который правил в Китае свыше 2000 лет тому назад, возникла мысль взвесить слона. Как ни суетились сановники, никто из них не мог ничего придумать, ведь нигде не было таких гигантских весов, чтобы на них можно было взвесить слона. Когда все сановники признали свою беспомощность, пришёл человек по имени Чао Чун и сказал, что он может взвесить слона. Он попросил: «Прикажите поставить слона в большую лодку, после чего обозначьте уровень погружения лодки в воду. Снимите слона, а лодку загрузите камнями так, чтобы она погрузилась до отметки. Вес камней будет равен весу слона”. Талантливый самородок, на много лет опередивший великого Архимеда, получил за своё предложение «щедрое» вознаграждение – благосклонный кивок императора Цао-Цао.
Выталкивающая сила и закон Архимеда
При взаимодействии твердых неподвижных тел, действуя друг на друга, они только деформируются. И действие каждого из этих тел на другое характеризуется силой.
Как взаимодействуют твердое тело и жидкость
Если твердое тело взаимодействует с жидкостью, то оно проникает в жидкость. Что происходит в таком случае? Ответ на этот вопрос получим из опыта.
К резиновой нити прицепим груз и измерим длину нити, которая растягивается весом груза. Если же груз после этого опустить в воду, то станет заметным сокращение длины нити. Таким образом, вес тела в воде уменьшился. Это возможно только потому, что в жидкости на погруженное тело действует выталкивающая сила. Направление этой силы противоположно направлению действия силы тяжести.
Как рассчитать значение выталкивающей силы
Опыты показывают, что значение выталкивающей силы зависит как от характеристик погруженного тела, так и от свойств жидкости.
Возьмем металлический цилиндр и стакан, объем которого равен объему цилиндра. Прицепим их к крючку динамометра и определим вес цилиндра и стакана (рис. 110). Теперь полностью погрузим цилиндр в воду. Динамометр покажет уменьшение веса. Но если стакан полностью заполнить водой, то показания динамометра восстановятся. Таким образом, выталкивающая сила равна весу воды, объем которой равен объему тела. Если воду заменить насыщенным раствором соли в воде, то выталкивающая сила будет большей, так как большим будет вес воды, объем которой равен объему тела.

Если учесть, что вес жидкости 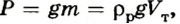 то для расчета выталкивающей силы можно использовать формулу
то для расчета выталкивающей силы можно использовать формулу
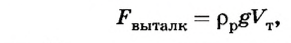
где 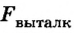 – выталкивающая сила;
– выталкивающая сила; 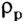 – плотность жидкости;
– плотность жидкости; 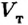 – объем погруженного в жидкость тела или его части.
– объем погруженного в жидкость тела или его части.
Зависимость, выраженная формулой для выталкивающей силы, называется законом Архимеда, сама выталкивающая сила — силой Архимеда.
От чего зависит сила Архимеда
Почему действует сила Архимеда в жидкости? Представим себе, что в жидкость погружено тело в виде прямоугольного бруска (рис. 111).
На тело, погруженное в жидкость, действует выталкивающая сила, которая равна весу жидкости в объеме погруженного тела или его погруженной части.
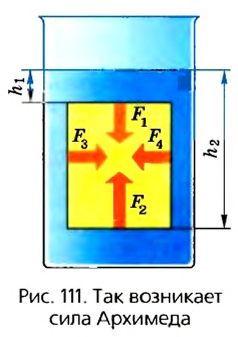
В результате действия силы тяжести в жидкости существует давление, которое согласно закону Паскаля действует во всех направлениях. В связи с этим на верхнюю грань бруска будет действовать сила 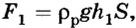 направленная вниз.
направленная вниз.
На нижнюю грань будет действовать сила 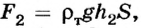 направленная вверх. Так как
направленная вверх. Так как 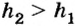 , то и
, то и 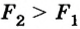 . Равнодействующая этих сил направлена вверх. Это и будет сила Архимеда.
. Равнодействующая этих сил направлена вверх. Это и будет сила Архимеда.
Действует сила Архимеда и в газах, так как в них давление тоже изменяется с высотой.
Окончательно закон Архимеда можно сформулировать так: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу жидкости или газа в объеме погруженной части тела.
В газах сила Архимеда значительно меньше, чем в жидкостях, поскольку плотность газа намного меньше плотности жидкости.
Выталкивающая сила в жидкостях и газах
Почему мяч, если его погрузить в воду и отпустить, выпрыгивает над поверхностью воды? Почему тяжелый камень, который на суше нельзя сдвинуть с места, можно легко поднять под водой? Почему корабль, севший на мель, самостоятельно не может всплыть? Попробуем разобраться.
Существование выталкивающей силы:
Подвесим к коромыслу весов два одинаковых шара. Массы шаров равны, значит, весы будут уравновешены (рис. 27.1, а). Подставим под правый шар пустой сосуд (рис. 27.1, б). Затем нальем в сосуд воду и увидим, что равновесие весов нарушится (рис. 27.1, в), — некая сила пытается вытолкнуть шар из воды.
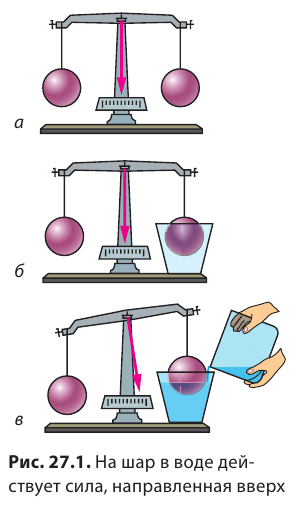
Откуда берется эта сила? Чтобы разобраться, рассмотрим погруженный в жидкость кубик. На него со всех сторон действуют силы гидростатического давления жидкости (рис. 27.2). Силы гидростатического давления 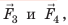 действующие на боковые грани кубика, противоположны по направлению и равны по значению, так как площади боковых граней одинаковы и эти грани расположены на одинаковой глубине. Такие силы уравновешивают друг друга. А вот силы гидростатического давления
действующие на боковые грани кубика, противоположны по направлению и равны по значению, так как площади боковых граней одинаковы и эти грани расположены на одинаковой глубине. Такие силы уравновешивают друг друга. А вот силы гидростатического давления 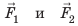 , соответственно действующие на верхнюю и нижнюю грани кубика, друг друга не уравновешивают. На верхнюю грань кубика действует сила давления
, соответственно действующие на верхнюю и нижнюю грани кубика, друг друга не уравновешивают. На верхнюю грань кубика действует сила давления 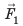 :
: 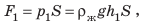 где
где 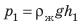 — гидростатическое давление жидкости; S — площадь грани. Аналогично на нижнюю грань кубика действует сила давления
— гидростатическое давление жидкости; S — площадь грани. Аналогично на нижнюю грань кубика действует сила давления 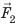 :
: 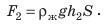 Нижняя грань находится на большей глубине, чем верхняя
Нижняя грань находится на большей глубине, чем верхняя 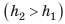 поэтому сила давления
поэтому сила давления 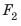 больше силы давления
больше силы давления 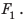
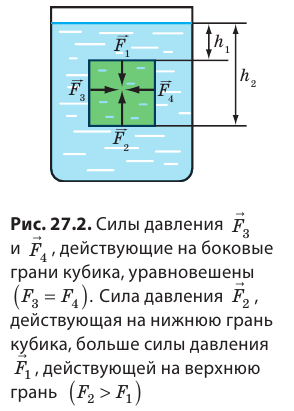
Равнодействующая этих сил равна разности значений сил 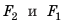 и направлена в сторону действия большей силы, то есть вертикально вверх. По вертикали вверх на кубик, погруженный в жидкость, действует сила, обусловленная разностью давлений на его нижнюю и верхнюю грани, — выталкивающая сила:
и направлена в сторону действия большей силы, то есть вертикально вверх. По вертикали вверх на кубик, погруженный в жидкость, действует сила, обусловленная разностью давлений на его нижнюю и верхнюю грани, — выталкивающая сила: 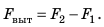 На тело, помещенное в газ, тоже действует выталкивающая сила, но она значительно меньше выталкивающей силы, действующей на то же тело в жидкости, поскольку плотность газа намного меньше плотности жидкости. Выталкивающую силу, которая действует на тело в жидкости или газе, называют также архимедовой силой (в честь древнегреческого ученого Архимеда (рис. 27.3), который первым указал на существование этой силы и вычислил ее значение).
На тело, помещенное в газ, тоже действует выталкивающая сила, но она значительно меньше выталкивающей силы, действующей на то же тело в жидкости, поскольку плотность газа намного меньше плотности жидкости. Выталкивающую силу, которая действует на тело в жидкости или газе, называют также архимедовой силой (в честь древнегреческого ученого Архимеда (рис. 27.3), который первым указал на существование этой силы и вычислил ее значение).

Расчет и вычисление силы Архимеда
Вычислим значение архимедовой (выталкивающей) силы для кубика, погруженного в жидкость (см. рис. 27.2). Вы уже знаете, что архимедова сила равна разности сил давлений жидкости на нижнюю и верхнюю грани кубика: 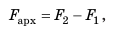 где
где 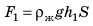 — сила давления жидкости на верхнюю грань кубика;
— сила давления жидкости на верхнюю грань кубика; 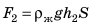 — сила давления жидкости на нижнюю грань кубика. Зная
— сила давления жидкости на нижнюю грань кубика. Зная 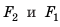 , найдем выталкивающую силу:
, найдем выталкивающую силу: 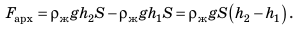 Разность глубин
Разность глубин 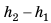 , на которых находятся нижняя и верхняя грани кубика, — это высота h кубика, следовательно,
, на которых находятся нижняя и верхняя грани кубика, — это высота h кубика, следовательно, 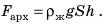 . Произведение площади S основания кубика на его высоту h — это объем V кубика: V= Sh, значит, формула для расчета архимедовой силы:
. Произведение площади S основания кубика на его высоту h — это объем V кубика: V= Sh, значит, формула для расчета архимедовой силы: 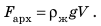 Здесь
Здесь 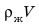 — это масса жидкости в объеме кубика, то есть масса жидкости, объем которой равен объему кубика. Так как
— это масса жидкости в объеме кубика, то есть масса жидкости, объем которой равен объему кубика. Так как 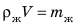 , то
, то 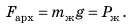 Архимедова сила равна весу жидкости в объеме кубика:
Архимедова сила равна весу жидкости в объеме кубика: 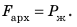
Мы рассмотрели случай с кубиком, полностью погруженным в жидкость. Однако полученный результат выполняется для тела любой формы, а также в случаях, когда тело погружено в жидкость частично (для расчетов следует брать объем погруженной в жидкость части тела). Кроме того, результат справедлив и для газов. А теперь сформулируем закон Архимеда: На тело, погруженное в жидкость или газ, действует выталкивающая сила, которая равна весу жидкости или газа в объеме погруженной части тела: 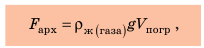 где
где 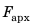 — архимедова сила;
— архимедова сила; 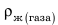 — плотность жидкости или газа;
— плотность жидкости или газа; 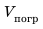 — объем погруженной части тела. Архимедова сила приложена к центру погруженной части тела и направлена вертикально вверх (рис. 27.4).
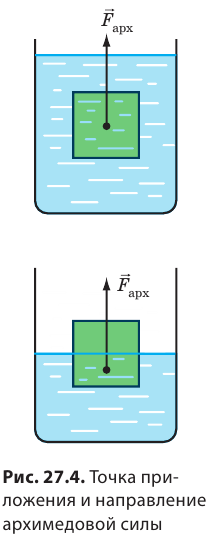
— объем погруженной части тела. Архимедова сила приложена к центру погруженной части тела и направлена вертикально вверх (рис. 27.4).
Выясняем, всегда ли на тело, погруженное в жидкость, действует архимедова сила:
Подвесим к динамометру камешек на нити. Динамометр покажет вес камешка. Подставим стакан с водой так, чтобы камешек оказался полностью погруженным в воду. Показание динамометра уменьшится. Кажется, что камешек «потерял» часть своего веса. Но никакой потери веса тела в жидкости не происходит: вес перераспределяется между подвесом (нитью) и опорой (жидкостью). Даже если архимедова сила, действующая на тело, достаточна, чтобы его удержать, и подвес не будет растянут, тело все равно не находится в состоянии невесомости, ведь оно давит на опору — жидкость. Следует отметить: когда тело плавает, его вес распределяется на воду, окружающую всю поверхность тела. Поэтому во время плавания нам кажется, что мы потеряли вес. Такие комфортные условия поддержания тяжелого тела обусловили то, что в результате эволюции самые массивные существа на Земле живут в океане (рис. 27.5).
Именно архимедова сила помогает нам поднимать в воде тяжелые камни или другие предметы, ведь часть силы тяжести, действующей на эти тела, уравновешивается не силой наших рук, а выталкивающей силой.

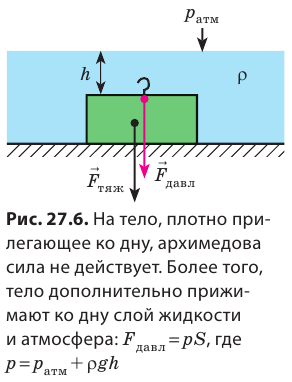
Однако случается, что вода не помогает поднять тело, а наоборот — препятствует этому. Это происходит, если тело лежит на дне и плотно к нему прилегает. Вода не может попасть под нижнюю поверхность тела и помочь своим давлением поднять его. В таком случае, чтобы оторвать тело от дна, нужно преодолеть не только силу тяжести, действующую на тело, но и силу давления воды на верхнюю поверхность тела (рис. 27.6). Данное явление может стать причиной трагедии: если подводная лодка опустится на глинистое дно и вытеснит из под себя воду, всплыть сама она не сможет.
Пример №1
Однородный алюминиевый брусок массой 540 г полностью погружен в воду и не касается дна и стенок сосуда. Определите архимедову силу, действующую на брусок. Анализ физической проблемы. Для вычисления архимедовой силы нужно знать плотность воды и объем бруска. Объем бруска определим по его массе и плотности. Плотности воды и алюминия узнаем из таблиц плотностей (с. 249). Задачу будем решать в единицах СИ.
Дано:
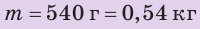 ,
,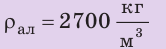 ,
,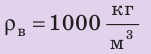 ,
,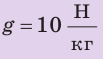
Найти:
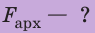
Решение:
По закону Архимеда: 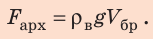 По определению плотности:
По определению плотности: 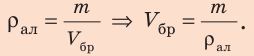
Подставим выражение для объема бруска в формулу для расчетов архимедовой силы: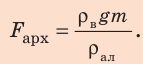
Проверим единицу, найдем значение искомой величины:
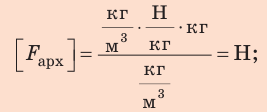

Ответ: 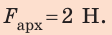
Итоги:
На тело, находящееся в жидкости или газе, действует выталкивающая (архимедова) сила. Причина ее появления в том, что давление, которое оказывает жидкость или газ на верхнюю поверхность тела, отличается от давления, оказываемого на нижнюю поверхность тела. Закон Архимеда: на тело, погруженное в жидкость или газ, действует выталкивающая сила, которая направлена вертикально вверх и равна весу жидкости или газа в объеме погруженной части тела: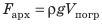
Условия плавания тел
При приготовлении раствора соли определенной плотности хозяйки погружают в него сырое яйцо: если плотность раствора недостаточна, яйцо тонет, если достаточна — всплывает. аналогично определяют плотность сахарного сиропа при консервации.
Вы наверняка можете привести множество примеров плавания тел. Плавают корабли и лодки, деревянные игрушки и воздушные шарики, плавают рыбы, дельфины, другие существа. А от чего зависит способность тела плавать? Проведем опыт. Возьмем небольшой сосуд с водой и несколько шариков, изготовленных из разных материалов. Будем поочередно погружать тела в воду, а потом отпускать их без начальной скорости. Далее в зависимости от плотности тела возможны разные варианты (см. таблицу).
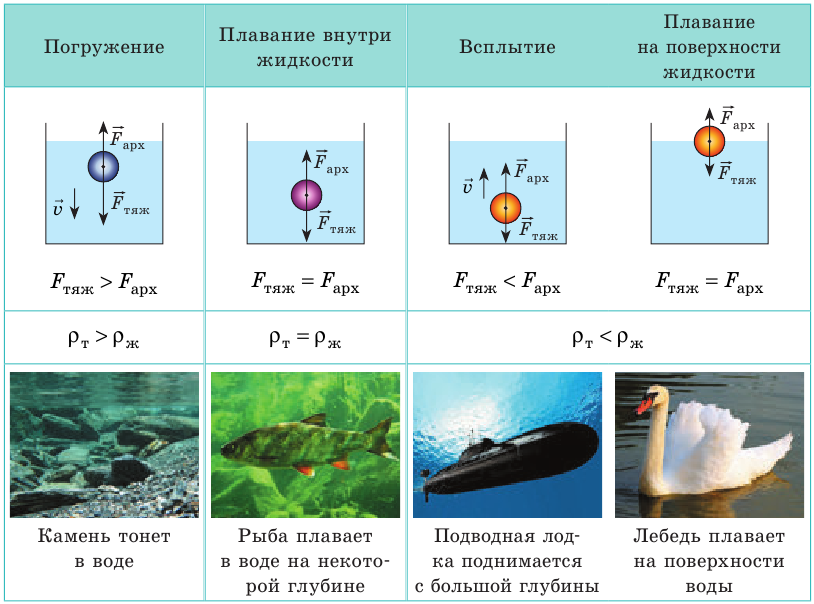
Погружение
Тело начинает тонуть и в конце концов опускается на дно сосуда. Выясним, почему это происходит. На тело действуют две силы: 1) сила тяжести 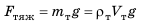 (поскольку
(поскольку 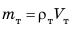 ), направленная вертикально вниз; 2) выталкивающая сила
), направленная вертикально вниз; 2) выталкивающая сила 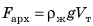 направленная вертикально вверх. Тело погружается, а это значит, что сила, направленная вниз, больше:
направленная вертикально вверх. Тело погружается, а это значит, что сила, направленная вниз, больше: 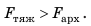 Поскольку
Поскольку 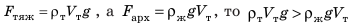 . После сокращения на
. После сокращения на 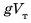 имеем:
имеем:
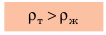 тело тонет в жидкости или газе, если плотность тела больше, чем плотность жидкости или газа. Вариант 2. Плавание внутри жидкости. Тело не тонет и не всплывает, а остается плавать внутри жидкости. Попробуйте доказать, что в данном случае плотность тела равна плотности жидкости:
тело тонет в жидкости или газе, если плотность тела больше, чем плотность жидкости или газа. Вариант 2. Плавание внутри жидкости. Тело не тонет и не всплывает, а остается плавать внутри жидкости. Попробуйте доказать, что в данном случае плотность тела равна плотности жидкости:
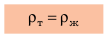
тело плавает внутри жидкости или газа, если плотность тела равна плотности жидкости или газа. Вариант 3. Всплытие. Тело начинает всплывать и в конце концов останавливается на поверхности жидкости, погрузившись в жидкость частично. Пока тело всплывает, архимедова сила больше силы тяжести: 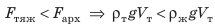 или:
или: 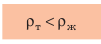 Остановка тела на поверхности жидкости означает, что архимедова сила и сила тяжести уравновешены:
Остановка тела на поверхности жидкости означает, что архимедова сила и сила тяжести уравновешены: 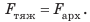 тело всплывает в жидкости или газе либо плавает на поверхности жидкости, если плотность тела меньше, чем плотность жидкости или газа.
тело всплывает в жидкости или газе либо плавает на поверхности жидкости, если плотность тела меньше, чем плотность жидкости или газа.
Плавание тел в живой природе
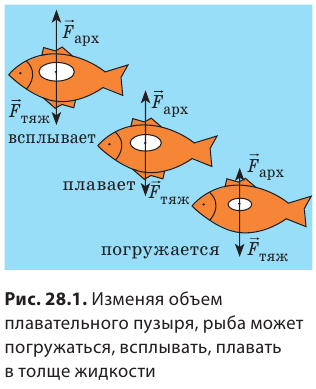
Тела обитателей морей и рек содержат в своем составе много воды, поэтому их средняя плотность близка к плотности воды. Чтобы свободно двигаться в жидкости, они должны «управлять» средней плотностью своего тела. Приведем примеры. У рыб с плавательным пузырем такое управление происходит за счет изменения объема пузыря (рис. 28.1). Моллюск наутилус (рис. 28.2), обитающий в тропических морях, может быстро всплывать и снова опускаться на дно благодаря тому, что может менять объем внутренних полостей в организме (моллюск живет в закрученной спиралью раковине). Распространенный в Европе водяной паук (рис. 28.3) несет с собой в глубину воздушную оболочку на брюшке — именно она дает ему запас плавучести и помогает вернуться на поверхность.


Пример №2
Медный шар массой 445 г имеет внутри полость объемом 450 см3. Будет ли этот шар плавать в воде? Анализ физической проблемы. Чтобы ответить на вопрос, как поведет себя шар в воде, нужно плотность шара 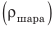 сравнить с плотностью воды
сравнить с плотностью воды  Для вычисления плотности шара следует определить его объем и массу. Масса воздуха в шаре незначительна по сравнению с массой меди, поэтому
Для вычисления плотности шара следует определить его объем и массу. Масса воздуха в шаре незначительна по сравнению с массой меди, поэтому 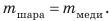 Объем шара — это объем медной оболочки
Объем шара — это объем медной оболочки 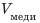 и объем полости
и объем полости 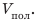 Объем медной оболочки можно определить, зная массу и плотность меди. О плотностях меди и воды узнаем из таблиц плотностей (с. 249). Задачу целесообразно решать в представленных единицах.
Объем медной оболочки можно определить, зная массу и плотность меди. О плотностях меди и воды узнаем из таблиц плотностей (с. 249). Задачу целесообразно решать в представленных единицах.
Дано:
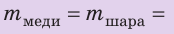
 ,
,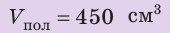 ,
,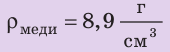 ,
,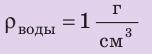
Найти:
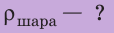
Решение:
По определению плотности: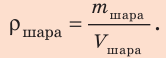
Объем шара:  — объем медной оболочки.
— объем медной оболочки.
Таким образом, 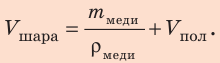
Решим задачу по действиям. 1. Определим объем шара:
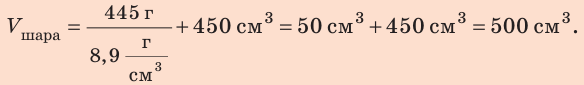
2. Зная объем и массу шара, определим его плотность:
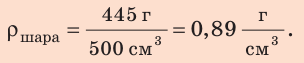
Анализ результата: плотность шара меньше плотности воды, поэтому шар будет плавать на поверхности воды.
Ответ: да, шар будет плавать на поверхности воды.
- Заказать решение задач по физике
Итоги:
Тело тонет в жидкости или газе, если плотность тела больше, чем плотность жидкости или газа 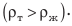 плавает внутри жидкости или газа, если плотность тела равна плотности жидкости или газа
плавает внутри жидкости или газа, если плотность тела равна плотности жидкости или газа 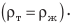 Тело всплывает в жидкости или газе либо плавает на поверхности жидкости, если плотность тела меньше плотности жидкости или газа
Тело всплывает в жидкости или газе либо плавает на поверхности жидкости, если плотность тела меньше плотности жидкости или газа 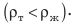
Судоходство и воздухоплавание
Стальной брусок в воде тонет, а стальные корабли плавают. Нейлоновая ткань падает в воздухе, а воздушные шары, изготовленные из этой ткани, поднимаются вверх сами и поднимают гондолы с пассажирами. Почему же стальные корабли плавают в воде, а воздушные шары называют аппаратами, которые легче воздуха? Получить ответы на эти вопросы вам помогут знания об основах судоходства и воздухоплавания.

Почему плавают суда
На первый взгляд, сталь непригодна для изготовления плавучего средства: плотность стали намного больше плотности воды, поэтому стальная пластинка в воде тонет. Но если из пластинки сделать кораблик и опустить его на поверхность воды, кораблик будет плавать (рис. 29.1). Почему? Дело в том, что погруженная в воду часть кораблика вытесняет воды достаточно, чтобы архимедова сила уравновесила силу тяжести, действующую на кораблик. Другими словами, средняя плотность кораблика за счет воздуха внутри него намного меньше плотности воды. Именно поэтому кораблик плавает на поверхности воды лишь немного в нее погружаясь.
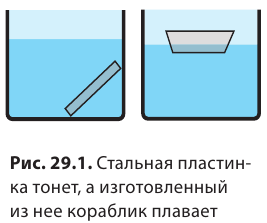
Этот принцип лежит в основе конструкции всех судов. Средняя плотность судов намного меньше плотности воды, поэтому суда плавают на ее поверхности, погружаясь на относительно небольшую часть своего объема.
Характеристики судов:
Когда новое судно спускают на воду, оно начинает погружаться. Нижняя часть судна начинает вытеснять воду, вследствие чего возникает архимедова сила. Когда архимедова сила уравновешивает силу тяжести, действующую на судно, оно прекращает погружение. Глубину, на которую погружается судно, называют осадкой. Осадка судна изменяется в зависимости от загруженности судна и от того, в речной или морской воде оно находится. Разумеется, судно нельзя перегружать.
На корпус судна нанесена ватерлиния — линия, указывающая максимально допустимую осадку судна, при которой оно может безопасно плавать (рис. 29.2). Когда судно полностью нагружено, оно находится в воде вровень с ватерлинией.

Вес воды, которую вытесняет судно, погруженное в воду до ватерлинии, то есть архимедова сила, действующая на полностью нагруженное судно, называется полным водоизмещением судна. Напомним: поскольку нагруженное судно плавает на поверхности воды, то архимедова сила, которая действует на него, по значению равна силе тяжести, действующей на судно с грузом: 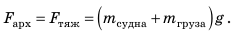 Самые большие суда — танкеры для нефти — имеют полное водоизмещение до 5 млн кН, то есть их масса вместе с грузом достигает 500 000 т. Если из полного водоизмещения исключить вес самого судна, то получим максимальный вес груза, который может взять на борт данное судно, то есть определим грузоподъемность судна. грузоподъемность судна — максимальный вес груза, который судно может взять на борт, — это разность между полным водоизмещением судна и его весом. Украина — морское государство. В стране есть морской и речной флот, а также порты, имеющие большое экономическое значение: Одесский, Ильичевский, Южный, Николаевский, Херсонский, Бердянский, Мариупольский.
Самые большие суда — танкеры для нефти — имеют полное водоизмещение до 5 млн кН, то есть их масса вместе с грузом достигает 500 000 т. Если из полного водоизмещения исключить вес самого судна, то получим максимальный вес груза, который может взять на борт данное судно, то есть определим грузоподъемность судна. грузоподъемность судна — максимальный вес груза, который судно может взять на борт, — это разность между полным водоизмещением судна и его весом. Украина — морское государство. В стране есть морской и речной флот, а также порты, имеющие большое экономическое значение: Одесский, Ильичевский, Южный, Николаевский, Херсонский, Бердянский, Мариупольский.
Как осуществилась мечта человека летать
Люди уже давно используют воздушные шары (аэростаты), поднимающиеся в воздух благодаря заполнению их оболочки горячим воздухом или легким газом. На воздушный шар в воздухе действует выталкивающая сила. Средняя плотность воздушного шара меньше плотности воздуха, поэтому выталкивающая сила больше силы тяжести и шар поднимается вверх. Разность между выталкивающей (архимедовой) силой и силой тяжести представляет собой подъемную силу воздушного шара. Сейчас воздушные шары используют для метеорологических и других исследований, соревнований, перевозок пассажиров, туристических и познавательных путешествий. Воздушные шары, наполненные легким газом (в основном гелием), называют шарльерами. В последнее время распространены воздушные шары, наполненные горячим воздухом, — современные монгольфьеры (рис. 29.3). Высокую температуру воздуха внутри шара поддерживают газовые горелки, установленные в его горловине. Поскольку плотность воздуха с высотой уменьшается, воздушные шары не могут подняться на какую угодно высоту. Воздушные шары поднимаются только до той высоты, где плотность воздуха равна средней плотности шара вместе с грузом.

Пример №3
В речном порту судно взяло на борт 100 т груза. В результате осадка судна увеличилась на 0,2 м и достигла максимально допустимой. Какова площадь сечения судна на уровне ватерлинии? Анализ физической проблемы. Когда на судно взяли груз, оно увеличило осадку и дополнительно вытеснило некоторый объем воды. По закону Архимеда, вес груза равен весу дополнительно вытесненной воды: 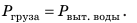 Осадка судна увеличилась всего на 20 см, значит, площадь сечения судна на уровне поверхности воды изменилась незначительно. Поэтому объем дополнительно вытесненной воды равен
Осадка судна увеличилась всего на 20 см, значит, площадь сечения судна на уровне поверхности воды изменилась незначительно. Поэтому объем дополнительно вытесненной воды равен 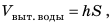 где h — увеличение осадки; S — площадь сечения судна на уровне ватерлинии (по условию судно достигло максимальной осадки). Порт речной, поэтому плотность воды равна
где h — увеличение осадки; S — площадь сечения судна на уровне ватерлинии (по условию судно достигло максимальной осадки). Порт речной, поэтому плотность воды равна 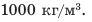 Задачу следует решать в единицах СИ.
Задачу следует решать в единицах СИ.
Дано:
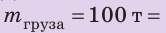
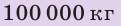 ,
,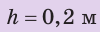 ,
,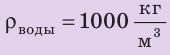
Найти:

Решение:
1. Определим массу дополнительно вытесненной воды. По закону Архимеда: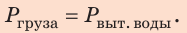
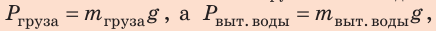 поэтому
поэтому 
2. Определим объем дополнительно вытесненной воды:
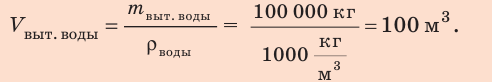
3. Площадь S сечения судна на уровне ватерлинии найдем через объем вытесненной воды:
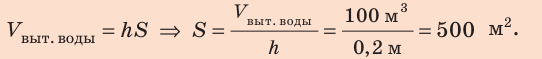
Ответ: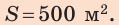
Мы решили задачу 1 по действиям. Решите эту задачу в общем виде (получите общую формулу, найдите значение искомой величины).
Пример №4
Объем воздушного шара равен 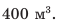 Шар натягивает трос, которым прикреплен к причалу, с силой 800 Н. После освобождения троса шар смог подняться на некоторую высоту. Какова плотность воздуха на этой высоте, если плотность воздуха у причала
Шар натягивает трос, которым прикреплен к причалу, с силой 800 Н. После освобождения троса шар смог подняться на некоторую высоту. Какова плотность воздуха на этой высоте, если плотность воздуха у причала 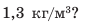
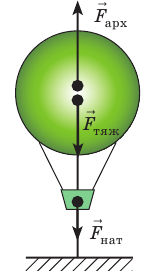
Анализ физической проблемы. Шар прекратил подъем потому, что на этой высоте его средняя плотность равна плотности воздуха 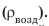 . Чтобы определить среднюю плотность шара, следует найти его массу. Массу шара найдем по силе тяжести, действующей на шар. Для определения силы тяжести выполним пояснительный рисунок и покажем все силы, действовавшие на шар на причале:
. Чтобы определить среднюю плотность шара, следует найти его массу. Массу шара найдем по силе тяжести, действующей на шар. Для определения силы тяжести выполним пояснительный рисунок и покажем все силы, действовавшие на шар на причале: 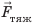 — сила тяжести;
— сила тяжести; 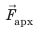 — архимедова сила,
— архимедова сила, 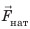 — сила натяжения троса. Шар на причале не двигался, поэтому силы, действовавшие на него, были скомпенсированы. Задачу будем решать по действиям в единицах СИ.
— сила натяжения троса. Шар на причале не двигался, поэтому силы, действовавшие на него, были скомпенсированы. Задачу будем решать по действиям в единицах СИ.
Дано:
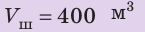 ,
,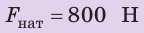 ,
,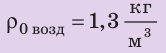 ,
,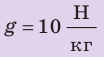
Найти:
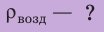
Решение:
Силы, действовавшие на прикрепленный к причалу шар, были скомпенсированы, следовательно:
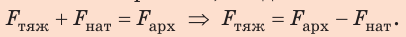
1. Найдем архимедову силу, которая действовала на прикрепленный к причалу шар:
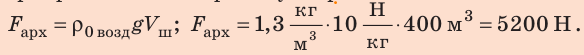
2. Найдем силу тяжести, действующую на шар:
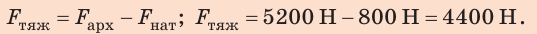
3. Определим массу шара: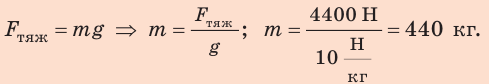
4. По известным массе и объему шара вычислим его среднюю плотность:
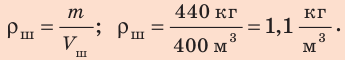
5. Плотность воздуха на высоте максимального подъема шара равна средней плотности шара, потому на этой высоте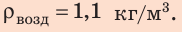
Ответ: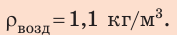
Итоги:
Взаимодействие тел:
Вы узнали, что причиной изменения скорости движения тел и причиной изменения формы и объема тел является взаимодействие.
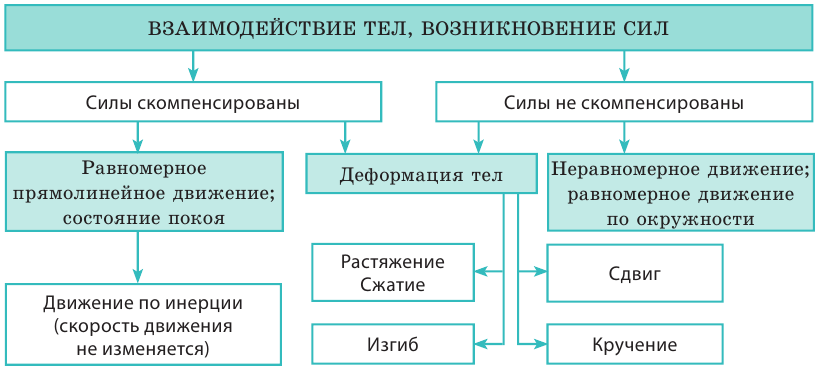
Вы ознакомились с разными силами в механике.
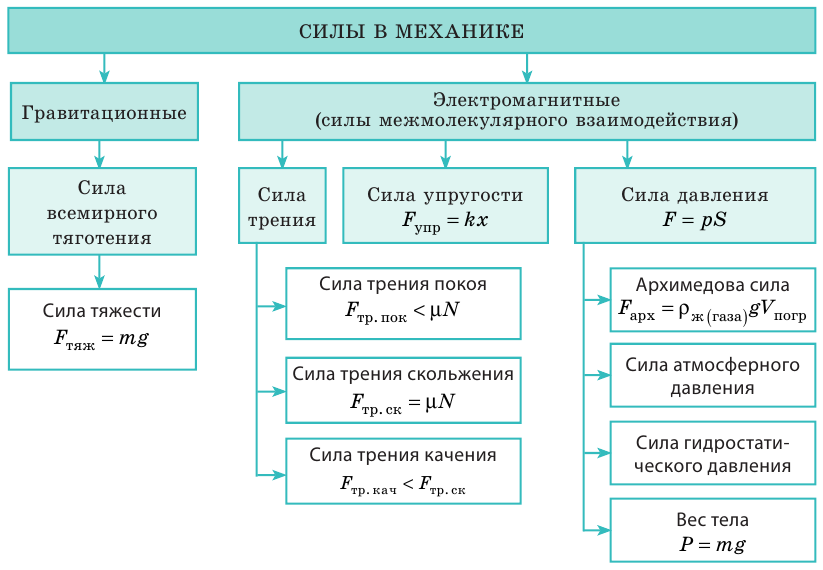
Вы продолжили знакомство с физическими телами и веществами и узнали о физических величинах, характеризующих тело, вещество, взаимодействие.
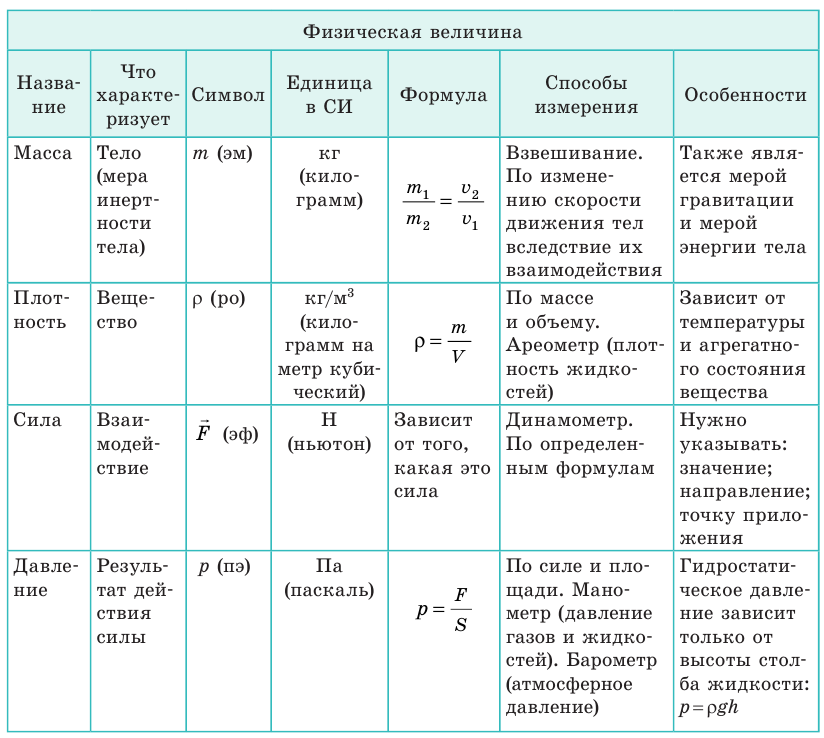
Вы узнали о давлении жидкостей и газов, ознакомились с законом Паскаля, законом Архимеда, доказали наличие атмосферного давления.
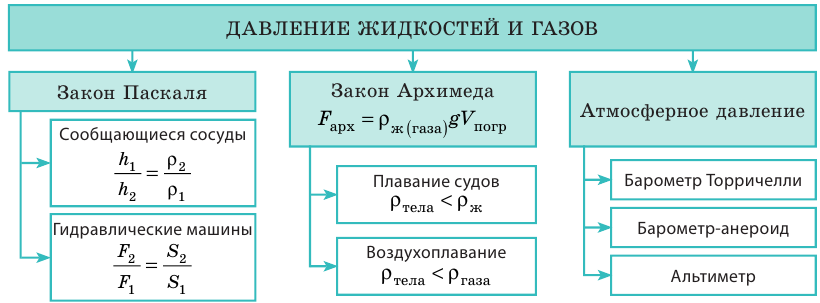
- Условия плавания тел в физике
- Гидростатическое взвешивание в физике
- Воздухоплавание в физике
- Машины и механизмы в физике
- Атмосферное давление в физике и его измерение
- Манометры в физике
- Барометры в физике
- Жидкостные насосы в физике
