Бетонная плита объёмом 2
м
3
погружена в воду. Какую силу необходимо приложить, чтобы удержать её в воде; в воздухе?

reshalka.com
ГДЗ учебник по физике 7 класс Перышкин. §51. Упражнение 26. Номер №4
Решение
Дано:
V = 2
м
3
;
ρ
в
= 1000 кг/
м
3
;;
ρ
б
= 2300 кг/
м
3
;
Найти:
F
1
−?
F
2
−?
Решение:
В этой задаче столкнёмся со взаимодействием двух сил: силой тяжести, силой архимеда.
На плиту в воздухе действует сила тяжести. Чтобы удержать плиту, нужно приложить силу, равную силе тяжести.
F
2
=
F
т
я
ж
=
g
m
− сила тяжести.
m
=
ρ
б
V
;
F
2
=
g
ρ
б
V
;
g = 9,8 Н/кг;
F
2
=
9
,
8
∗
2300
∗
2
=
45080
Н
.
Рассчитаем какую силу нужно приложить, чтобы удерживать плиту в воде.
F
1
=
F
2
−
F
А
;
F
А
=
g
ρ
ж
V
т
;
F
1
=
45080
−
(
9
,
8
∗
1000
∗
2
)
= 25480 Н.
Ответ. 45080 Н, 25480 Н.
На прошлом уроке мы доказали с помощью опытов существование силы, действующей на тела, погруженные в жидкость или газ — выталкивающей силы. Также мы теперь знаем, что ее можно рассчитать по формуле: $F_{выт} = gm_ж = P_ж$. Но какое еще есть значение у этой силы? На этом уроке мы более подробно рассмотрим выталкивающую силу.
Выталкивающая сила и вес тела
Как можно на опыте определить, с какой силой тело, погруженное целиком в жидкость, выталкивается из жидкости?
Давайте познакомимся с таким опытом. Он представлен на рисунке 1.
Подвесим на пружину небольшую емкость для жидкости и тело цилиндрической формы ниже. На конце пружины у нас расположена стрелка-указатель. Она отмечает растяжение пружины на штативе (рисунок 1, а). Таким образом, мы видим вес тела в воздухе.
Теперь опустим наше тело в большой сосуд. Сосуд имеет трубку для слива и наполнен жидкостью до уровня этой трубки (рисунок 1, б).
Когда мы полностью опустим тело в сосуд, часть жидкости из него выльется через трубку для слива в стакан. Объем этой жидкости будет равен объему тела. Мы уже знаем, что на тело действует выталкивающая сила: пружина сокращается, стрелка-указатель поднимается, вес тела в жидкости становится меньше.
А теперь возьмем жидкость, которая вылилась в стакан. Зальем ее в емкость, которая также подвешена к пружине (рисунок 1, в). Теперь стрелка-указатель вернулась к своему изначальному положению.
Так чему равна эта сила? Сделаем вывод из данного опыта.
Сила, выталкивающая целиком погруженное в жидкость тело, равна весу жидкости в объеме этого тела.
Если провести подобный опыт с газом, а не с жидкостью, то мы получим, что сила, выталкивающая тело из газа, равна весу газа, взятого в объеме тела.
Сила Архимеда
Как называют силу, которая выталкивает тела, погруженные в жидкости и газы?
Теперь мы добавим, что эту выталкивающую силу называют архимедовой силой. Архимед (рисунок 2) — древнегреческий ученый и инженер, сделавший множество открытий и в математике, и в физике. Именно он первый обнаружил наличие выталкивающей силы и рассчитал ее значение.
Как подсчитать архимедову силу?
В прошлом уроке мы получили формулу $F_{выт} = P_ж = g m_ж$. Теперь мы будем называть эту силу архимедовой $F_A$.
Из выше рассмотренных опытов мы можем выразить массу вытесненной жидкости через ее плотность и объем тела, который эту жидкость вытеснил (они одинаковы): $m_ж = rho_ж cdot V_т$. Получим формулу для архимедовой силы.
$F_A = g rho_ж V_т$.
От чего зависит архимедова сила?
Взгляните еще раз на формулу: $F_A = g rho_ж V_т$.
Ясно видно, что архимедова сила зависит только от плотности жидкости и от объема тела, которое мы погружаем в эту жидкость.
Если мы будем погружать в одну и ту же жидкость тела разной плотности и разной формы (рисунок 3), то значение силы меняться не будет (при условии, что эти тела будут обладать одинаковым объемом).
Определение веса тела, погруженного в жидкость или газ
На тело, погруженное в жидкость (или в газ), действуют две силы: сила тяжести и архимедова сила. Направлены они в противоположные стороны. Вес тела в жидкости $P_1$ будет меньше веса тела в вакууме $P$ на архимедову силу $F_A$. То есть:
$P_1 = P space − space F_A = gm space − space gm_ж$.
Если тело погружено в жидкость или газ, то его вес уменьшается на вес вытесненной им жидкости или газа.
Пример задачи
Определите выталкивающую силу, которая будет действовать на камень объемом $2.6 space м^3$, лежащий на морском дне.
Дано:
$V_т = 2.6 space м^3$
$rho_ж = 1030 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$F_A — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Сила Архимеда рассчитывается по формуле:
$F_A = g rho_ж V_т$.
Подставим численные значения величин и рассчитаем эту силу:
$F_A = 9.8 frac {Н}{кг} cdot 1030 frac{кг}{ м^3} cdot 2.6 space м^3 approx 26 244 space Н approx 26.2 space кН$.
Ответ: $F_A approx 26,2 space кН$.
Забавное дополнение: легенда об Архимеде
Архимед, великий изобретатель, шокировал своих современников гениальными открытиями. Его имя упоминается во множестве легенд, но одна из них стала наиболее известной: легенда о том, как Архимед пришел к открытию выталкивающей силы.
Царь Гиерон поручил Архимеду проверить работу мастера, который изготовил для него золотую корону.
Долгое время ученый не мог найти ответ: как определить количество некачественных примесей? Проблема заключалась в том, что определить ее объем — сложная задача. По легенде озарение настигло Архимеда, когда он принимал ванну.
Ученый заметил, что из ванны вылилась вода, когда он залез в нее. И здесь его посетила гениальная мысль. Все вы слышали его известную цитату: «Эврика! Эврика!» (в переводе означает: «Нашел! Нашел!»).
Так Архимед победно выкрикивал свою фразу, потрясенный своим открытием, что она дошла в виде легенды и до наших времен.
Упражнения
Упражнение №1
К коромыслу весов подвешены два цилиндра одинаковой массы: свинцовый и алюминиевый (рисунок 4). Весы находятся в равновесии. Нарушится ли равновесие весов, если оба цилиндра одновременно погрузить в воду; в спирт? Ответ обоснуйте. Проверьте его на опыте. Как зависит выталкивающая сила от объема тела?
Посмотреть ответ
Скрыть
Ответ:
Когда мы погрузим цилиндры в жидкость, на каждый их них будет действовать сила Архимеда. Если эти силы будут равны, то весы останутся в равновесии.
Запишем формулы архимедовой силы для каждого цилиндра.
Для свинцового цилиндра:
$F_{A1} = g rho_ж V_1$.
Для алюминиевого цилиндра:
$F_{A2} = g rho_ж V_2$.
Мы видим, что равенство этих сил зависит от объемов цилиндров. Они равны? Нет, они имеют одинаковые массы, но разные плотности. Цилиндр из алюминия будет обладать большим объемом, чем свинцовый цилиндр ($V = frac{m}{rho}$). Значит, на алюминиевый цилиндр будет действовать большая выталкивающая сила, чем на свинцовый.
Если мы проверим это на опыте, то увидим подтверждение нашим выводам (рисунок 5).
При этом весы выйдут из равновесия в случае и с водой (рисунок 5, а), и со спиртом (рисунок 5, б). Так как мы опускаем цилиндры одновременно в один и тот же тип жидкости, значение архимедовой силы, действующей на цилиндры, будет различаться только в зависимости от объемов этих цилиндров — свинцовый перевесит алюминиевый в любой жидкости.
Заметим, что в случае погружения в воду, архимедова сила будет больше, чем в случае погружения в спирт. Это объясняется тем, что вода имеет большую плотность, чем спирт.
Упражнение №2
К коромыслу весов подвешены два алюминиевых цилиндра одинакового объема. Нарушится ли равновесие весов, если один цилиндр погрузить в воду, а другой — в спирт? Ответ обоснуйте. Зависит ли выталкивающая сила от плотности жидкости?
Посмотреть ответ
Скрыть
Ответ:
Если один цилиндр погрузить в воду, а другой — в спирт, то равновесие весов нарушится (рисунок 6). На цилиндр, находящийся в воде, будет действовать большая архимедова сила.
Так происходит, потому что архимедова сила зависит от объема погруженного тела (а они у нас одинаковые: $V_1 = V_2 = V$) и от плотности жидкости:
$F_А = g rho_ж V$.
Плотность спирта ($800 frac{кг}{м^3}$) меньше плотности воды ($1000 frac{кг}{м^3}$). Значит, на цилиндр, погруженный в воду, будет действовать большая архимедова сила, чем на тот, что погружен в спирт.
Упражнение №3
Объем куска железа равен $0.1 space дм^3$. Какая выталкивающая сила будет на него действовать при полном его погружении в воду; в керосин?
Дано:
$V = 0.1 space дм^3$
$g = 9.8 frac{Н}{кг}$
$rho_1 = 1000 frac{кг}{м^3}$
$rho_2 = 800 frac{кг}{м^3}$
СИ:
$V = 0.1 cdot 10^{-3} space м^3$
$F_{А1} — ?$
$F_{А2} — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Рассчитаем архимедову силу, которая будет действовать на кусок железа в воде:
$F_{А1} = g rho_1 V$,
$F_{А1} = 9.8 frac{Н}{кг} cdot 1000 frac{кг}{м^3} cdot 0.1 cdot 10^{-3} space м^3 = 0.98 space Н approx 1 space Н$.
Теперь рассчитаем архимедову силу, которая будет действовать на кусок железа в керосине:
$F_{А2} = g rho_2 V$,
$F_{А2} = 9.8 frac{Н}{кг} cdot 800 frac{кг}{м^3} cdot 0.1 cdot 10^{-3} space м^3 = 0.784 space Н approx 0.8 space Н$.
Ответ: $F_{А1} approx 1 space Н$, $F_{А2} approx 0.8 space Н$.
Упражнение №4
Бетонная плита объемом $2 space м^3$ погружена в воду. Какую силу необходимо приложить, чтобы удержать ее в воде; в воздухе?
Дано:
$V = 2 space м^3$
$g = 9.8 frac{Н}{кг}$
$rho_1 = 1000 frac{кг}{м^3}$
$rho_2 = 1.29 frac{кг}{м^3}$
$rho_б = 2300 frac{кг}{м^3}$
$F_1 — ?$
$F_2 — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Бетонная плита находится в воде. На нее действует сила тяжести и архимедова сила. Они направлены противоположно друг другу и будут иметь разные величины. Разность этих сил — и будет искомая сила $F_1$, которую нужно приложить, чтобы удержать бетонную плиту в воде (чтобы она не опускалась на дно и не всплывала):
$F_1 = F_{тяж} space − space F_{А1}$.
Сила тяжести рассчитывается по формуле:
$F_{тяж} = gm$.
Массу бетонной плиты мы можем выразить через ее плотность и объем:
$m = rho_б V$,
$F_{тяж} = g rho_б V$.
Архимедова сила, действующая на бетонную плиту в воде:
$F_{А1} = g rho_1 V$.
Подставим силу тяжести и архимедову силу в формулу и рассчитаем $F_1$:
$F_1 = F_{тяж} space − space F_{А1} = g rho_б V space − space g rho_1 V = gV cdot (rho_б space − space rho_1)$,
$F_1 = 9.8 frac {Н}{кг} cdot 2 space м^3 cdot (2300 frac{кг}{м^3} space − space 1000 frac{кг}{м^3}) = 25 space 480 space Н approx 25 space кН$.
Используем ту же формулу для того, чтобы рассчитать силу $F_2$, которую нужно приложить, чтобы удержать бетонную плиту в воздухе:
$F_2 = gV cdot (rho_б space − space rho_2)$,
$F_2 = 9.8 frac {Н}{кг} cdot 2 space м^3 cdot (2300 frac{кг}{м^3} space − space 1.29 frac{кг}{м^3}) approx 45 space 054 space Н approx 45 space кН$.
Ответ: $F_1 approx 25 space кН$, $F_2 approx 45 space Н$.
Упражнение №5
Предположив, что корона царя Гиерона в воздухе весит $20 space Н$, а в воде — $18.75 space Н$, вычислите плотность вещества короны. Полагая, что к золоту было подмешано только серебро, определите, сколько в короне было золота и сколько серебра. При решении задачи плотность золота считайте равной $20 space 000 frac{кг}{м^3}$, плотность серебра — $10 space 000 frac{кг}{м^3}$. Каков был бы объем короны из чистого золота?
Дано:
$P_1 = 20 space Н$
$P_2 = 18.75 space Н$
$rho_з = 20 space 000 frac{кг}{м^3}$
$rho_с = 10 space 000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$rho_1 = 1.29 frac{кг}{м^3}$
$rho_2 = 1000 frac{кг}{м^3}$
$rho — ?$
$m_з — ?$
$m_с — ?$
$V_1 — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Вес короны в воздухе $P_1$ будет меньше веса тела в вакууме $P$ на архимедову силу $F_{A1}$. То есть:
$P_1 = P space − space F_{A1}$.
Значит, вес короны в вакууме будет равен сумме ее веса в воздухе и архимедовой силы:
$P = P_1 space + space F_{А1}$,
$gm = P_1 space + space g rho_1 V$.
Теперь запишем такое же уравнение для веса короны в воде:
$gm = P_2 space + space g rho_2 V$.
Левые части уравнений у нас равны, поэтому мы можем приравнять правые части друг к другу:
$P_1 space + space g rho_1 V = P_2 space + space g rho_2 V$.
Перенесем элементы, содержащие неизвестный объем вправо:
$P_1 space − space P_2 = g rho_2 V space − space g rho_1 V$,
$P_1 space − space P_2 = gV (rho_2 space − space rho_1)$.
Выразим отсюда объем короны и рассчитаем его:
$V = frac{P_1 space − space P_2}{g (rho_2 space − space rho_1)}$,
$V = frac{20 space Н space − space 18.75 space Н}{9.8 frac{Н}{кг} (1000 frac{кг}{м^3} space − space 1.29 frac{кг}{м^3})} = frac{1.25}{9787} space м^3 = 12.8 cdot 10^{-5} space м^3$.
Используем одно из первых уравнений для веса короны в вакууме и в воздухе:
$gm = P_1 space + space g rho_1 V$.
Выразим отсюда массу короны и рассчитаем ее:
$m = frac{P_1 space + space g rho_1 V}{g}$,
$m = frac{20 space Н space + space 9.8 frac{Н}{кг} cdot 1.29 frac{кг}{м^3} cdot 12.8 cdot 10^{-5} space м^3}{9.8 frac{Н}{кг}} approx 2.04 space кг$.
Теперь мы знаем массу и объем короны. Рассчитаем ее плотность:
$rho = frac{m}{V}$,
$rho = frac{2.04 space кг}{12.8 cdot 10^{-5} space м^3} approx 16 space 000 frac{кг}{м^3}$.
Корона состоит из серебра и золота. Это означает, что ее общий объем мы можем записать в виде суммы объемов серебра и золота, ее составляющих:
$V = V_с space + space V_з$.
То же самое с общей массой короны:
$m = m_с space + space m_з$.
Запишем объемы через массы и плотности (а также выразим массу золота через общую массу короны и массу серебра):
$V_с = frac{m_с}{rho_с}$,
$V_з = frac{m_з}{rho_з} = frac{m space − space m_с}{rho_з}$.
Подставим эти объемы в формулу для общего объема короны и выразим из нее массу серебра:
$V = frac{m_с}{rho_с} space + space frac{m space − space m_с}{rho_з} = frac{m_с (rho_з space − space rho_с) space + space rho_с m}{rho_с rho_з} = m_с cdot frac{rho_з space − space rho_с}{rho_с rho_з} space + space frac{m}{rho_з}$,
$m_с = frac{V space − space frac{m}{rho_з}}{frac{rho_з space − space rho_с}{rho_с rho_з}} = frac{rho_с (V rho_з space − space m)}{rho_з space − space rho_с}$.
Рассчитаем массу серебра, содержащегося в короне:
$m_с = frac{10 space 000 frac{кг}{м^3} (12.8 cdot 10^{-5} space м^3 cdot 20 space 000 frac{кг}{м^3} space − space 2.04 space кг)}{20 space 000 frac{кг}{м^3} space − space 10 space 000 frac{кг}{м^3}} = frac{5200 frac{кг^2}{м^3}}{10 space 000 frac{кг}{м^3}} = 0.52 space кг$.
Теперь мы можем вычислить и количество золота в короне:
$m_з = m space − space m_с$,
$m_з = 2.04 space кг space − space 0.52 space кг = 1.52 space кг$.
Если бы вся корона была из золота, то ее объем был бы равен:
$V_1 = frac{m}{rho_з}$,
$V_1 = frac{2.04 space кг}{20 space 000 frac{кг}{м^3}} = 10.2 cdot 10^{-5} space м^3$.
Ответ: $rho approx 16 space 000 frac{кг}{м^3}$, $m_з = 1.52 space кг$, $m_с = 0.52 space кг$, $V_1 = 10.2 cdot 10^{-5} space м^3$.
Упражнение №6
По мелким камешкам ходить босыми ногами больно. Почему человек не испытывает боли, если ходит по таким же камням в воде?
Посмотреть ответ
Скрыть
Ответ:
Что означает фраза «ходить по камням»? Со стороны физики, когда мы наступаем на камни, мы давим на них своим весом: $p = frac{F}{S} = frac{P}{S}$.
Когда мы оказываемся в воде, наш вес уменьшается. Это следствие действия на нас архимедовой силы. Уменьшается вес — уменьшается и давление наших стоп на камни.
Изучаете ли вы полет птиц, которые бьют своими крыльями, чтобы подняться в небо, или подъем газа из трубы в атмосферу, вы можете изучить, как объекты поднимаются против силы гравитации, чтобы лучше узнать об этих методах “. рейс.”
Для авиационного оборудования и беспилотников, которые летают в воздухе, полет зависит от преодоления силы тяжести, а также от учета силы воздуха на эти объекты с тех пор, как братья Райт изобрели самолет. Расчет подъемной силы может сказать вам, сколько силы необходимо, чтобы отправить эти объекты в воздух.
Уравнение подъемной силы
Объекты, летящие по воздуху, должны иметь дело с силой воздуха, действующей на себя. Когда объект движется вперед по воздуху, сила сопротивления является частью силы, которая действует параллельно потоку движения. Подъем, напротив, представляет собой часть силы, которая перпендикулярна потоку воздуха или другого газа или жидкости на объект.
Искусственные летательные аппараты, такие как ракеты или самолеты, используют уравнение подъемной силы L = (C L ρ v 2 A) / 2 для подъемной силы L , коэффициента подъемной силы C L , плотности материала вокруг объекта ρ («rho»), скорость v и площадь крыла A. Коэффициент подъемной силы суммирует влияние различных сил на находящийся в воздухе объект, включая вязкость и сжимаемость воздуха и угол наклона тела относительно потока, что значительно упрощает уравнение для расчета подъемной силы.
Ученые и инженеры обычно определяют C L экспериментально, измеряя значения подъемной силы и сравнивая их со скоростью объекта, площадью размаха крыла и плотностью жидкого или газового материала, в который погружен объект. Составление графика зависимости подъема от количество ( ρ v 2 A) / 2 даст вам строку или набор точек данных, которые можно умножить на C L, чтобы определить силу подъема в уравнении силы подъема.
Более продвинутые вычислительные методы могут определять более точные значения коэффициента подъема. Однако существуют теоретические способы определения коэффициента подъема. Чтобы понять эту часть уравнения подъемной силы, вы можете посмотреть на вывод формулы подъемной силы и на то, как рассчитывается коэффициент подъемной силы в результате этих воздушных сил на объекте, испытывающем подъем.
Вывод уравнения лифта
Чтобы учесть множество сил, которые воздействуют на объект, летящий по воздуху, вы можете определить коэффициент подъемной силы C L как C L = L / (qS) для подъемной силы L , площади поверхности S и динамического давления жидкости q , обычно измеряемого в паскаль. Вы можете преобразовать динамическое давление жидкости в его формулу q = ρu 2/2, чтобы получить C L = 2L / ρu 2 S, в которой ρ – плотность жидкости, а u – скорость потока. Из этого уравнения вы можете переставить его для получения уравнения подъемной силы L = C L ρu 2 S / 2.
Это динамическое давление жидкости и площадь поверхности, находящиеся в контакте с воздухом или жидкостью, также сильно зависят от геометрии находящегося в воздухе объекта. Для объекта, который может быть приближен как цилиндр, такой как самолет, сила должна распространяться наружу от тела объекта. Таким образом, площадь поверхности будет равна длине окружности цилиндрического тела, умноженной на высоту или длину объекта, и даст вам S = C xh .
Вы также можете интерпретировать площадь поверхности как произведение толщины на величину площади, деленную на длину t , так что при умножении толщины на высоту или длину объекта вы получите площадь поверхности. В этом случае S = txh .
Соотношение между этими переменными площади поверхности позволяет вам изобразить или экспериментально измерить, как они различаются, чтобы изучить влияние силы вокруг окружности цилиндра или силы, которая зависит от толщины материала. Существуют и другие методы измерения и изучения находящихся в воздухе объектов с использованием коэффициента подъемной силы.
Другие виды использования коэффициента подъема
Есть много других способов аппроксимации коэффициента кривой подъема. Поскольку коэффициент подъемной силы должен включать множество различных факторов, влияющих на полет самолета, вы также можете использовать его для измерения угла, который самолет может взять относительно земли. Этот угол известен как угол атаки (AOA), представленный α («альфа»), и вы можете переписать коэффициент подъема C L = C L0 + C L α α .
С помощью этой меры C L, которая имеет дополнительную зависимость из-за AOA α, вы можете переписать уравнение как α = (C L + C L0) / C L α и, после экспериментального определения подъемной силы для одного конкретного AOA Вы можете рассчитать общий коэффициент подъема C L. Затем вы можете попробовать измерить различные AOA, чтобы определить, какие значения C L0 и CL α будет соответствовать наилучшему соответствию _._ Это уравнение предполагает, что коэффициент подъема изменяется линейно с AOA, поэтому могут быть некоторые обстоятельства, в которых более точное уравнение коэффициента может соответствовать лучше.
Чтобы лучше понять AOA по силе подъема и коэффициенту подъема, инженеры изучили, как AOA изменяет способ полета самолета. Если вы построите график коэффициентов подъема по отношению к AOA, вы можете рассчитать положительное значение наклона, которое известно как двумерный наклон кривой подъема. Тем не менее, исследования показали, что после некоторого значения АОА значение C L уменьшается.
Этот максимальный AOA известен как точка сваливания с соответствующей скоростью сваливания и максимальным значением C L. Исследования толщины и кривизны авиационного материала показали способы расчета этих значений, когда вы знаете геометрию и материал находящегося в воздухе объекта.
Калькулятор уравнения и коэффициента подъема
У НАСА есть онлайн-апплет, чтобы показать, как уравнение подъема влияет на полет самолета. Это основано на калькуляторе коэффициента подъемной силы, и вы можете использовать его для установки различных значений скорости, угла, который воздушный объект принимает относительно земли, и площади поверхности, которую объекты имеют относительно материала, окружающего самолет. Апплет даже позволяет вам использовать исторические самолеты, чтобы показать, как с 1900-х годов развивались инженерные конструкции.
Моделирование не учитывает изменение веса находящегося в воздухе объекта из-за изменений в области крыла. Чтобы определить, какое влияние это окажет, вы можете измерить различные значения площадей поверхности, которые будут влиять на подъемную силу, и рассчитать изменение силы подъема, которое могут вызвать эти площади поверхности. Вы также можете рассчитать гравитационную силу, которую имели бы различные массы, используя W = mg для веса из-за силы тяжести W, массы m и константы гравитационного ускорения g (9, 8 м / с 2).
Вы также можете использовать «зонд», который можно направить вокруг находящихся в воздухе объектов, чтобы показать скорость в различных точках симуляции. Симуляция также ограничена тем, что самолет приближается с использованием плоской пластины для быстрого, грязного расчета. Вы можете использовать это для приблизительного решения уравнения подъемной силы.
Трение между воздухом и другим объектом называется сопротивлением воздуха. Рассмотрим, как определить сопротивление воздуха при падении объекта.
Сопротивление воздуха падающего объекта можно рассчитать, умножив плотность воздуха на коэффициент сопротивления, умноженный на площадь, на два, а затем умножив на скорость.
Сила тяжести и сопротивление воздуха — две силы естественного поля, которые двигают все на Земле. Формула сопротивления воздуха для сферы, доказательство формулы сопротивления воздуха, формула сопротивления воздуха для свободного падения и то, как получить среднее сопротивление воздуха, будут рассмотрены более подробно.
Как рассчитать сопротивление воздуха падающего предмета?
Скорость, площадь и форма объекта, проходящего через воздух, влияют на сопротивление воздуха. Проверим, как оценить сопротивление воздуха падающего предмета.
Чтобы определить, какое сопротивление воздуха будет испытывать падающий предмет, используйте формулу FD = 1 / 2 ρv2CDА. В этом уравнении FD означает перетаскивание, ρ – плотность жидкости, v для относительной скорости объекта относительно жидкости, CD для коэффициента лобового сопротивления и A для площади поперечного сечения.
Задача: Огромный пассажирский самолет летит со скоростью 250.0 метров в секунду. A = 500 квадратных метров крыльев самолета подвергаются ветру. Коэффициент аэродинамического сопротивления CD = 0.024. Плотность воздуха ρ = 0.4500 кг на кубический метр на высоте самолета. Какому сопротивлению воздуха подвергается пассажирский самолет?
Решение: Даны данные,
А = 500 квадратных метров
CD = 0.024
ρ = 0.4500 кг на кубический метр
Сопротивление воздуха падающего предмета определяется выражением
FD = 1/2 ρv2CDA
FD =(0.4500 кг/м3 × 0.025 × 510.0 м2)/2 (250.0 м/с) 2
FD = (0.4500 кг/м3 × 0.025 × 510.0 м2)/2 (62500 м2/s2)
FD = 179296 кг.м/с2
Как рассчитать сопротивление воздуха при движении снаряда?
Объект или частица называется снарядом, а его движение называется движением снаряда. Посмотрим, как можно рассчитать сопротивление воздуха при движении снаряда.
Скорость, ускорение, и перемещение должно быть включено при описании движения снаряда в целом, как описано ниже,
- По осям x и y мы должны расположить их составные части. Предположим, что все силы, кроме силы тяжести, ничтожны.
- Компоненты ускорения тогда чрезвычайно прямолинейны, если положительное направление определено как восходящее, ay = -g = – 0.98 м / с.2 (-32 фут/с2).
- Поскольку гравитация вертикальна,x = 0. аx = 0 указывает, что vx = V0x, или что начальная и конечная скорости в направлении x равны.
- При этих ограничениях на ускорение и скорость кинематическое уравнение x (t) = x0 + (вx) среднийt для движения в униформе гравитационное поле можно записать через уравнение v2y (т) = v2oy + 2аy (г – г0), куда входят и остальные кинематические уравнения движения с ускорением с постоянным ускорением.
- Кинематические уравнения движения в однородном гравитационном поле переходят в кинематические уравнения сy = -г, аx = 0.
- Горизонтальное движение, v0x= Vx, х = х0 + Vxt.
- Вертикальное движение, у = у0 + ½ (в0y + Vy)т; вy = Voy – гт; у = уo + Voyт – ½ гт2, v2y = V2oy – 2г (у – уo).
Задача: Снаряд взлетает в воздух во время фейерверка под углом 75.00 над горизонтом с начальной скоростью 70.0 м/с. Снаряд рассчитан так, что взрыватель сработает именно тогда, когда он будет на максимальной высоте над землей.
- а. Рассчитайте высоту взрыва снаряда.
- б. Через какое время снаряд выстрелит и взорвется?
- в. Что происходит с горизонтальным положением снаряда при его взрыве?
- д. Как далеко в целом продвинулся объект от места запуска до самой высокой точки?
Решение: (а) Под «высотой» мы подразумеваем высоту над начальной точкой или высоту. Когда vy = 0 достигается высшая точка любой траектории, известная как вершина. Мы используем следующее уравнение, чтобы получить y, потому что мы знаем начальное местоположение, начальную и конечную скорости и начальное положение:
v2y = V2oy – 2г (у – у0)
Уравнение упрощается тем, что yo и vy оба равны нулю.
0 = в2oy – 2г.
Вычислив y, мы получаем, y = v2oy/ 2г.
Теперь нам нужно выяснить, какова начальная компонента скорости y, или v0y, является. Его можно рассчитать по формуле v0y=v0sin θ, где v0 обозначает начальную скорость 70.0 м/с и θo=75° обозначает начальный угол. Таким образом-
v0y=v0sin θ = (70.0 м/с) sin750 = 67.6 м/с и-
у = (67.6 м/с)2 / 2(9.80 м/с2)
у = 233 м.
Начальная вертикальная скорость и максимальная высота положительны, потому что вверх положительна, а ускорение, вызванное силой тяжести, отрицательно. Снаряд с начальной вертикальной составляющей скорости 67.6 м/с достигнет максимальной высоты 233 м. Также имейте в виду, что максимальная высота зависит только от вертикальной составляющей начальной скорости (без учета сопротивления воздуха).
(b) Существуют различные способы определить, когда снаряд достигает высшей точки, как и во многих физических задачах. Самый простой подход в этой ситуации — использовать vy=v0y -гт. Это уравнение становится vy= 0 на вершине
0 = в0y− гт
или,
т = voy/g = (67.6 м/с) / (9.80 м/с2)
t = 6.90 с.
Другой способ найти время – использовать y = yo + ½ (в0y + Vy) т.
в) Сопротивление воздуха мало, следовательно, ах и ау равны нулю. И, как упоминалось ранее, горизонтальная скорость постоянна. Как показывают уравнения x=x0+vxт, где х0 равно нулю, горизонтальное перемещение равно горизонтальной скорости, умноженной на время. Таким образом,
х = vxt,
Когда vx – компонент x скорости, определяется выражением
vx = V0cosθ = (70.0 м/с) cos75°=18.1 м/с.
Поскольку оба движения имеют одинаковое время t, x равно
х = (18.1 м/с) × 6.90 с = 125 м.
Без сопротивления воздуха горизонтальное движение имеет постоянную скорость. Горизонтальное смещение, наблюдаемое здесь, может помочь предотвратить травму зрителей от падающих пиротехнических фрагментов. Немалую роль при взрыве снаряда играет сопротивление воздуха, и многие осколки падают сразу внизу.
(d) Нахождение размера и направления смещения в самой высокой точке — это все, что здесь требуется, поскольку горизонтальная и вертикальная составляющие смещения уже рассчитаны:
s→ = 125 см + 233 см; |ŝ|=√ (1252 + 2332) = 264 м; Φ = загар -1 (233/125) = 61.8°
Как рассчитать сопротивление воздуха при конечной скорости?
Сопротивление воздуха по величине эквивалентно весу падающего тела с предельной скоростью. Рассмотрим метод расчета сопротивления воздуха при предельной скорости.
- Используя второй закон Ньютона для падающего объекта в качестве отправной точки, мы можем определить сопротивление воздуха при конечной скорости: Fg + Far = ма.
- Для определения сопротивления воздуха при заданной скорости используются следующие два типа сопротивления воздуха: Far = – bv альтернативно, Far = – бв2.
- Для расчета сопротивления воздуха при конечной скорости используется закон Ньютона для определения сопротивления воздуха при конечной скорости, поскольку ускорение равно нулю. мг – бв = 0; мг – бв2 = 0.
- Чтобы определить сопротивление воздуха при заданной скорости, ответом на задачу о скорости является vT = мг/б. Альтернативой является то, что vT = √(мг/б).
Если m представляет массу в килограммах, g — квадрат ускорения свободного падения, а b — произвольная величина.
Задача: При падении из состояния покоя объект массой 55 кг испытывает силу сопротивления воздуха, определяемую Far = -15В2. Определить конечную скорость объекта.
Решение: используйте формулу vT = √ (мг/б) для определения конечной скорости силы сопротивления вида Far = -bv2. Добавляя к уравнению, получаем,
vT = √(55) × (9.81)/15)
vT = 5.99 м / с
Как рассчитать коэффициент сопротивления воздуха?
Коэффициент сопротивления изменяется как квадратное отношение относительной скорости объекта. Рассмотрим метод расчета коэффициента сопротивления воздуха.
Коэффициент сопротивления воздуха рассчитывается по уравнению с = Fвоздух /v2. В расчете Фвоздух – силовое сопротивление, а c – силовая постоянная в этом уравнении. Жидкости, обычно вода в спортивной среде, также подвержены силе трения, которая не ограничивается только воздухом.
Сопротивление жидкости, сопротивление воздуха и сопротивление — все это относится к одному и тому же.
Проблема: Если объект движется со скоростью 22 мс-1 столкнуться с сопротивлением воздуха 50 Н, какова постоянная силы?
Решение: Даны данные,
v = 22 мс-1
Fвоздух = 50 Н
Формула для коэффициента сопротивления воздуха:
с = Fвоздух /v2
Замените указанные значения в формуле выше. Затем,
с = 50/(22)2
с = 0.103
Как рассчитать аэродинамическое сопротивление парашюта?
Вес пульсирует на шнуре, когда парашют раскрывается. Рассмотрим, как определить аэродинамическое сопротивление парашюта.
- Чтобы определить аэродинамическое сопротивление парашюта. Уравнение для силы сопротивления парашюта, также известной как его сила сопротивления ветру, имеет вид F.D = 1 / 2 ρv2CDА. Где, ФD – сила сопротивления, r – плотность воздуха, Cd — коэффициент лобового сопротивления, A — площадь парашюта, а v — скорость в воздухе.
- Чтобы определить сопротивление воздуха парашюта по квадрату скорости, сопротивление возрастает.
- Чтобы определить сопротивление воздуха парашюта, нет никакой чистой силы, действующей на ракету, когда сопротивление равно весу. F = D – W = 0.
- Cd = 2 Фd / ρв2A = W для определения аэродинамического сопротивления парашюта.
- И, наконец, V = sqrt (2W/Cdρ A) используется для определения аэродинамического сопротивления парашюта.
При сравнении двух предметов те, у которых больший вес, меньший коэффициент лобового сопротивления, меньшая плотность газа или меньшая площадь, движутся с большей скоростью.
Как найти сопротивление воздуха через массу и ускорение?
Единственной силой, воздействующей на людей поначалу, является гравитация, которая толкает их со скоростью -9.8 м/с2. Давайте посмотрим, как можно рассчитать сопротивление воздуха, используя массу и ускорение.
- Чтобы найти сопротивление воздуха с массой и ускорением, мы можем использовать некоторую алгебру, чтобы получить ускорение объекта с точки зрения чистой внешней силы и массы объекта (a = F/m).
- Чистая внешняя сила (F = W – D) равна разнице между силами веса и силы сопротивления. Тогда ускорение объекта определяется выражением a = (W – D) / m.
Задача: Автомобиль массой около 29 кг движется из Калькутты в Раджастхан со скоростью 50 метров в секунду, а гусеница нагружена железом и весит 84 кг. Определить силу сопротивления автомобиля.
Решение: Даны данные,
Ускорение = 50 м/с2
Вес = 84 кг
Масса = 29 кг
Мы знаем, что a = (W – D) / m
50 = (84 – Д)/ 29
1450 = 84 – Д
-Д = 1450 – 84
Д = – 1366 Н
График сопротивления воздуха
Когда частички воздуха сталкиваются с передней частью объекта, он замедляется. Давайте проверим этот график сопротивления воздуха.

За счет уменьшения угла выпуска можно свести к минимуму влияние сопротивления воздуха на горизонтальную составляющую траектории снаряда. Расстояние и скорость, или скорость, обратно пропорциональны.
Как рассчитать сопротивление воздуха по скорости?
Чем больше частиц воздуха воздействует на объект, тем больше его общее сопротивление увеличивается с площадью поверхности. Давайте рассмотрим, как определить сопротивление воздуха на основе скорости.
Формула, используемая для определения сопротивления воздуха по скорости: c = Fv.2. Сила сопротивления воздуха представлена в технике буквой F, постоянная силы представлена буквой c, а скорость объекта представлена буквой v. Существует линейная зависимость между сопротивлением воздуха и величиной сопротивления воздуха. плотность.
Между скоростью и сопротивлением воздуха создается квадратичная зависимость. Площадь передней кромки объекта, движущегося по воздуху, определяет, какое сопротивление воздуха он будет испытывать. Сопротивление воздуха увеличивается с увеличением площади.
Задача: Если сопротивление воздуха тела равно 34 Н, а силовая постоянная равна 0.04, какова его скорость?
Данные приведены, Fвоздух = 34 Н и с = 0.04
Формула сопротивления воздуха:
Fвоздух = резюме2
v2 = 34 / 0.04
v2 = 850
v = 29.15 м / с.
Как рассчитать силу сопротивления воздуха?
Сила сопротивления воздуха измеряется в Ньютонах (Н). Рассмотрим, как определить силу сопротивления воздуха.
Fвоздух = – резюме2 уравнение, используемое для определения силы сопротивления воздуха. Фвоздух – силовое сопротивление, а c – силовая постоянная в этом уравнении. Знак минус показывает, что объект движется в направлении, противоположном направлению сопротивления воздуха.
Задача: силовая постоянная для самолета, движущегося со скоростью 50 мс.-1 составляет 0.05. Определить сопротивление воздуха.
Решение: Даны данные,
Скорость воздуха, v = 50
Силовая постоянная, c = 0.05
Сила воздуха определяется выражением
F = – резюме2
F = (-) 0.05 × 50 × 50
F = – 125 Н.
Формула сопротивления воздуха для шара
Зависимость между силой сопротивления, действующей на тело, и сопротивлением воздуха обратная. Давайте посмотрим на формулу сопротивления воздуха шара.
Коэффициент сопротивления воздуха для сферических материалов можно рассчитать по следующей формуле: Cd = 2 Фd / ρв2A, где для сферических материалов-
- Cd = коэффициент сопротивления воздуха,
- Fd сопротивление воздуха по Ньютону,
- А – площадь формы в плане в квадратных метрах,
- ρ = плотность сферы, выраженная в килограммах на кубический метр,
- А вязкость вещества, выраженная в метрах в секунду, известна как v.
Задача: Плотность воздуха 0.4500 кг/м3, а самолет, летящий на высоте, имеет скорость 250 м/с. 500 м2 Крылья самолета открыты ветру. На самолет действует сила сопротивления воздуха 168750 Н. Выполните расчет коэффициента лобового сопротивления.
Решение: Приведенные данные, Сопротивление воздуха для сферических материалов, Fd = 168750 Н
Плотность, ρ = 0.4500 кг/м3
Площадь поперечного сечения, А = 500 м2
Скорость, v = 250 м/с
Мы знаем, что для сферических материалов
Cd = 2 Фd / ρв2A
Cd = 2 × 168750 / (0.4500 × 2502 × 500)
Cd = 0.025
Как рассчитать среднее сопротивление воздуха?
Сопротивление воздуха — это разновидность жидкостного трения, которое влияет на падающие в воздухе предметы. Давайте посмотрим, как определить среднее сопротивление воздуха.
Умножив плотность воздуха, коэффициент сопротивления, площадь и скорость на два, можно рассчитать среднее сопротивление воздуха, которое будет испытывать падающий объект. Гравитация заставляет объекты двигаться вниз, в отличие от трения воздуха, которое действует противоположным образом и замедляет скорость.
Сопротивление воздуха возрастает по мере увеличения площади поверхности, на которую падают предметы.
Заключение
Сопротивление воздуха – это сила, которую испытывает объект при прохождении через воздух, где, если человек движется быстрее, сила сопротивления воздуха возрастает. Безразмерный коэффициент сопротивления CD, который рассчитывается как CD = ФD/1/2 ρАв2 где ρ — плотность жидкости (в данном случае воздуха). Площадь поперечного сечения объекта A = (1/4) ΠD2, а его скорость v.
Задачи на силу Архимеда с решениями
Формулы, используемые на уроках «Задачи на силу Архимеда», «Сообщающиеся сосуды».
Название величины |
Обозначение |
Единица измерения |
Формула |
Объем тела |
V |
м3 |
Vт = FA / pg |
Плотность жидкости |
p |
кг/м3 |
pж = FA / (Vg) |
Сила Архимеда |
FA |
Н |
FA = pж Vт g |
Постоянная |
g ≈ 10 Н/кг |
Н/кг |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Тело объемом 2 м3 погружено в воду. Найдите архимедову силу, действующую на тело.

Задача № 2.
Определить выталкивающую силу, действующую на деревянный плот объемом 12 м3, погруженный в воду на половину своего объема.

Задача № 3.
Каков объем железобетонной плиты, если в воде на нее действует выталкивающая сила 8000 Н?

Задача № 4.
Какую силу надо приложить, чтобы удержать под водой бетонную плиту, масса которой 720 кг?

Задача № 5.
Какую высоту должен иметь столб нефти, чтобы уравновесить в сообщающихся сосудах столб ртути высотой 16 см?

Задача № 6.
Вес тела в воздухе равен 26 кН, а в воде — 16 кН. Каков объем тела?

Задача № 7.
Какую силу нужно приложить, чтобы удержать в воде кусок гранита объемом 40 дм3?
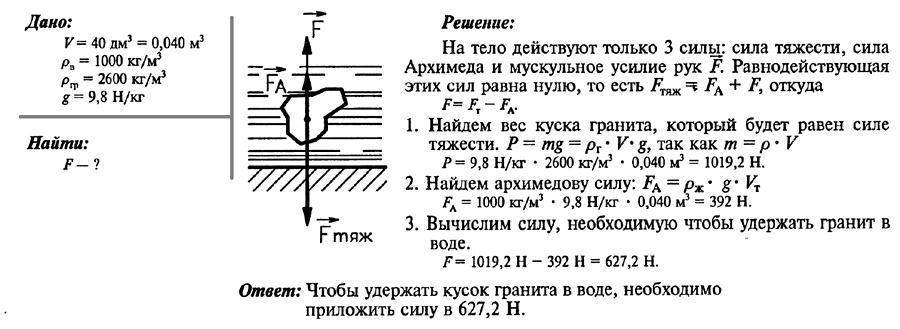
Задача № 8.
Определите объем куска меди, который при погружении в керосин выталкивается силой 160 Н.
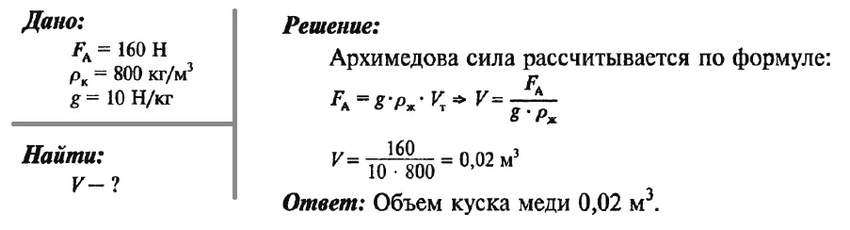
Задача № 9 (повышенной сложности).
Медный шар в воздухе весит 1,96 Н, а в воде 1,47 Н. Сплошной этот шар или полый?

Задача № 10 (повышенной сложности).
Рассчитайте, какой груз сможет поднять шар объемом 1 м3, наполненный водородом. Какой примерно объем должен иметь шар с водородом, чтобы поднять человека массой 70 кг? (Вес оболочки не учитывать.)

Задача № 11.
Деревянный цилиндр плавает на поверхности воды так, что он погружен в воду на 90%. Какая часть цилиндра будет погружена в воду, если поверх воды налить слой масла, полностью закрывающий цилиндр? Плотность масла 800 кг/м3.
Дано: V – объем цилиндра (V = Sh); h – высота цилиндра; S – площадь основания цилиндра; V1 – объем цилиндра, погруженного в масло (V1 = V – V2 = Sh1); h1 – высота части цилиндра, погруженной в масло; V2 – объем цилиндра, погруженного в воду после добавления масла; рв – плотность воды (1000 кг/м3); рм – плотность масла (800 кг/м3)
Найти: (h – h1) / h — ?
Решение. F – сила, выталкивающая цилиндр из воды до добавления масла F = 0,9pвgV
F1 – сила, выталкивающая цилиндр из масла F1 = pмgV1
F2 – сила, выталкивающая цилиндр из воды после добавления масла F2 = pвgV2
Баланс сил: F – F1 = F2
0,9pвgV – pмgV1 = pвgV2 V1 = V – V2 ⇒ 0,9pвV – pм(V – V2) = pвV2
V(0,9pв – pм) = V2(pв – pм) V = Sh; V1 = Sh1 ⇒

Ответ: 1/2 часть цилиндра будет погружена в воду (50%).
Задача № 12.
Плоская льдина плавает в воде, выступая над уровнем воды на 3 см. Человек массой 70 кг зашел на льдину. В результате, высота выступающей части над льдиной уменьшилась в 3 раза. Найти площадь льдины.
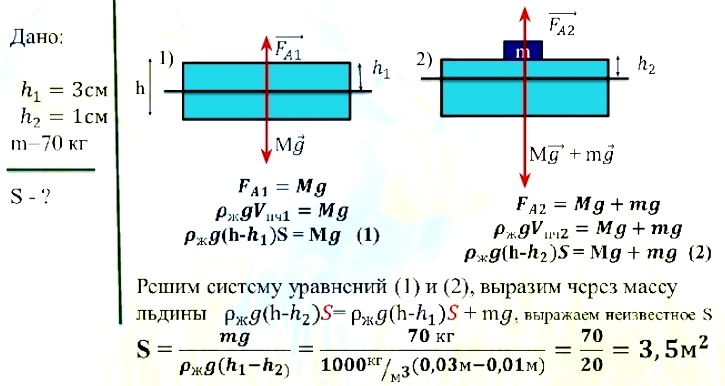
Ответ: 3,5 м3.
Теория для решения задач.
Давление жидкости на покоящееся в ней тело называют гидростатическим давлением. Гидростатическое давление на глубине h равно р = ратм + p*g*h
Закон Паскаля. Жидкость и газ передают оказываемое на них давление во всех направлениях одинаково.

Конспект урока «Задачи на силу Архимеда с решениями».
Следующая тема: «Задачи на механическую работу».
