Как найти удлинение стального бруса

Как найти удлинение стального бруса

Задача

Круглый стальной брус диаметром 2 см, длиной 16 м растягивается силой, равной 36 кН. Найдите удлинение этого бруса.

Решение

Дано

d = 2 см = 0,02 м
l0 = 16 м
F = 36 кН = 36 000 Н = 3,6 ⋅ 104 Н
E = 210 ⋅ 109 Па

Найти

Δl — ?

Решение

Найдем площадь поперечного сечения стального бруса

S = πd2/4

S = 3,14 ⋅ 0,022/4 = 0,000314 м2 = 3,14 ⋅ 10-4 м2

Модуль Юнга — физическая величина, характеризующая способность материала сопротивляться растяжению, сжатию при упругой деформации.

E = F : S/Δl : l = Fl/SΔl

Откуда

Δl = Fl/ES

Δl = 3,6 ⋅ 104 ⋅ 16/210 ⋅ 109 ⋅ 3,14 ⋅ 10-4 = 0,0087 м = 8,7 ⋅ 10-3 м

Ответ:
Δl = 8,7 ⋅ 10-3 м

Опубликовано: 05.11.2019
Обновлено: 05.11.2019

Источник
Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.

поделиться знаниями или
запомнить страничку

  • Все категории
  • экономические
    43,658
  • гуманитарные
    33,653
  • юридические
    17,917
  • школьный раздел
    611,962
  • разное
    16,905

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Источник

На
стальной ступенчатый брус круглого
сечения, схема которого представлена
на рис.7, действует система сил.

Т



Рис.7.

ребуется
построить эпюры продольных сил, подобрать
поперечные сечения всех участков бруса,
определить нормальные напряжения и
осевые перемещения.

Принято
допускаемое напряжение на растяжение
для стали:

МПа.

Решение:

  1. Разобьём
    брус на участки. Границы участков
    определяются сечениями, где изменяются
    поперечные размеры и приложены внешние
    нагрузки (рис.7).

  2. Для
    определения продольных сил воспользуемся
    методом сечений (РОЗУ). Мысленно рассечём
    брус в пределах участка 1 и отбросим
    левую часть бруса. Для уравновешивания
    силы F1
    необходимо,
    чтобы равнодействующая внутренних сил
    (продольная сила

    )
    равнялась этой внешней силе (рис.8):

Аналогично
мысленно рассечём брус в пределах
участка II
и отбросим левую часть бруса. Чтобы
уравновесить внешние силы F1,F2,
равнодействующая внутренних сил
(продольная сила

)
должна равняться алгебраической сумме
внешних сил
F1,F2:

.

Аналогично, для
остальных участков получим:

на
участке III

на
участке IV


;

на
участке V

;

на
участке VI


.

Продольные
силы на IV,V
и VI
участках можно также определить, мысленно
отбросив правую часть бруса и рассматривая
равновесие его левой части. Для этого
необходимо определить реакцию в заделке.

Согласно
знакам продольных сил: брус на участках
I,IV,V,VI
будет растягиваться, а на участках II,
III
– сжиматься.

В
соответствии с полученными результатами
строим эпюру продольных сил (эпюра N,
рис.8).

  1. Определение
    поперечных размеров.

Требуемая
площадь поперечного сечения i-ой
ступени определяется по формуле

откуда диаметр
сечения ступени бруса


.

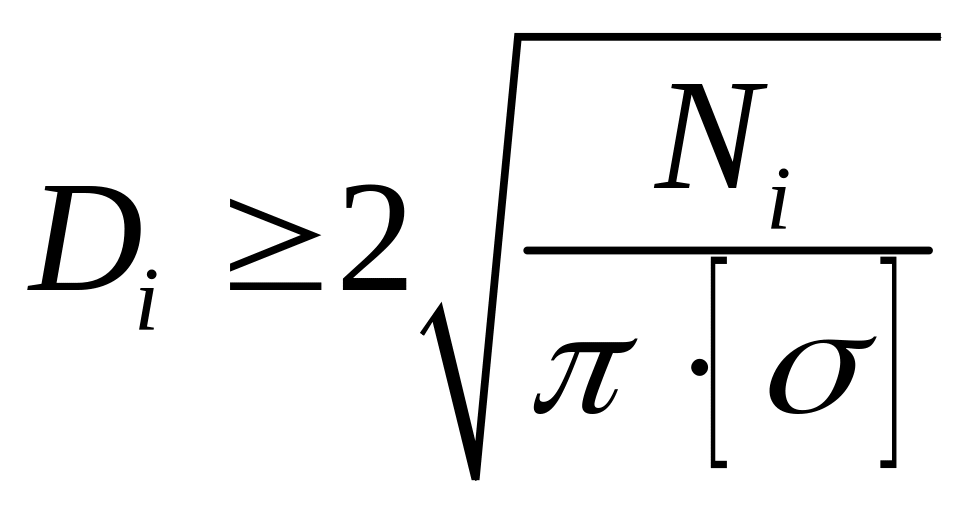
Диаметр
поперечного сечения бруса в пределах
I
и II
участков (первой ступени) рассчитываем
исходя из наибольшей по абсолютной
величине продольной силы N

.

В
соответствии с рядом нормальных линейных
размеров (см. Приложение П.3*)
выбираем для этих участков размер

.

Рис.8.

Площадь
поперечного сечения


2.

Аналогично,

.

Согласно
Приложения П.3 назначаем

.

Площадь
поперечного сечения

.

Для последней
ступени бруса


.

В
соответствии с Приложением П.3 принимаем

.

Площадь
поперечного сечения

.

  1. Вычисление
    нормальных напряжений по участкам
    бруса


,


,


,


,


,


.

В
соответствии с полученными значениями
напряжений строим эпюру нормальных
напряжений (эпюра

рис.8).

  1. Определение
    удлинения бруса.

Полное
абсолютное удлинение бруса равно
алгебраической сумме абсолютных
удлинений его участков:

,


,

или

.

3.1.3. Пример расчета статически неопределимого бруса при нагреве

Н

Рис.9.

а рис.9 представлен составной
ступенчатый брус, защемлённый с двух
концов. Длины участков и их поперечные
сечения взяты по рис.7, а именно:


,

,

.

В
отличие от примера 1 каждый из ступенчатых
участков в данном примере выполнен из
разных материалов: I
участок – из стали, II
– из алюминия, III
– из бронзы.

Необходимые
характеристики материалов ступеней
представлены в таблице:

№
ступени

Материал

Модули упругости

Коэффициенты

линейного расширения

I

сталь

II

алюминий

III

бронза

Требуется:

  1. Определить степень
    статической неопределимости задачи.

  2. Раскрыть статическую
    неопределимость, определив реакции
    опор.

  3. Построить эпюры
    распределения продольной силы, нормальных
    напряжений и перемещений бруса.

Решение:

  1. Определим степень
    статической неопределимости.

При
изменении температуры защемлённого
бруса его общая длина не меняется, а в
защемлениях возникают реакции
,
сжимающие брус. Число реакции nR
=2.

Для
расчетной схемы на рис.10 имеем одно
уравнение статического равновесия
вида:

(nу=1)
или

или

,
где X-
продольная сила. Таким образом, для
определения единственного внутреннего
усилия, действующего в теле бруса,
достаточно найти величину силы X.
Однако решаемая задача является
статически неопределимой, так как из
рассматриваемого уравнения статического
равновесия невозможно найти величину
X.

Степень
статической неопределимости nH=
nR
– nу
= 2-1=1, т.е система один раз статически
неопределима.

Подобные
задачи решаются путём добавления к
уравнениям статики недостающего числа
уравнений, получаемых из рассмотрения
упругих деформаций тела. В данном случае
число таких дополнительных уравнений
равно единице.

Упругие
деформации бруса компенсируют его
удлинение

,
вызванное нагревом, которое имеет
следующий вид:


,

где

– температурное удлинение стального
участка бруса,

– температурное
удлинение алюминиевого участка бруса,

– температурное
удлинение бронзового участка бруса.

Тогда


,


.

Деформация
сжатия бруса, вызванная реакциями опор,
выражается формулой


,

где

– укорочение стального участка от силы
X,

– укорочение
алюминиевого участка от силы X,

– укорочение бронзового участка от
силы X.

Уравнение
совместности деформаций, вызванное
нагревом и реакциями заделок, имеет вид

.

Данное
уравнение позволяет найти продольную
силу X=RD=RA=N

или


.

Расчёт нормальных
напряжений

,


,

.

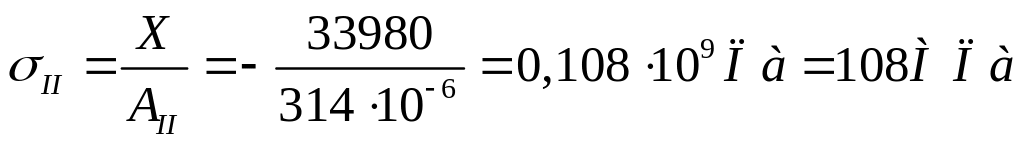
Расчет
перемещений от продольной силы


,


,


.

Результаты
этих вычислений представлены на эпюрах
рис.11.

Рис.11.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

В окружающем нас мире на различные тела действуют множество сил. Вы уже познакомились с несколькими из них: весом тела, силой тяжести и силой упругости.

  • Сила тяжести действует на все тела находящиеся на Земле и всегда направлена вертикально вниз:
    $F_{тяж} = gm$,
    где $m$ — масса тела, $g$ — ускорение свободного падения ($g = 9.8 frac{Н}{кг}$)
  • Вес тела — это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес. Вес тела приложен всегда к опоре или подвесу.
    Если тело и опора/подвес неподвижны или движутся прямолинейно и равномерно, то вес будет численно равен силе тяжести, действующей на это тело:
    $P = F_{тяж}$
  • Сила упругости возникает в теле в результате его деформации и стремится вернуть тело в исходное положение.
    Закон Гука определяет зависимость этой силы от деформации тела:
    $F_{упр} = k Delta l$,
    где $k$ — коэффициент упругости (жесткость тела), $Delta l$ — изменение длины тела

В данном уроке мы рассмотрим задачи и их подробные решения, чтобы вы научились уверенно использовать новые понятия и вычислять изученные силы.

Задача №1

Вычислите силу тяжести, действующую на тело массой: $1.5 space кг$; $500 space г$; $2.5 space т$; $20 space г$.

Дано:
$m_1 = 1.5 space кг$
$m_2 = 500 space г$
$m_3 = 2.5 space т$
$m_4 = 20 space г$
$g = 9.8 frac{Н}{кг}$

СИ:

$m_2 = 0.5 space кг$
$m_3 = 2500 space кг$
$m_4 = 0.02 space кг$

$F_{тяж1}, F_{тяж2}, F_{тяж3}, F_{тяж4} — ?$

Показать решение и ответ

Скрыть

Решение:

Сила тяжести рассчитывается по формуле $F_{тяж} = gm$.

Для того чтобы получить верный ответ при таких простых вычислениях, всегда обращайте внимание на единицы измерения данных величин. Мы уже перевели единицы массы в $кг$. Если бы мы этого не сделали, то получили бы неверные ответы.

Рассчитаем силу тяжести, действующую на каждое тело:

  1. $F_{тяж1} = gm_1$,
    $F_{тяж1} = 9.8 frac{Н}{кг} cdot 1.5 space кг = 14.7 space Н$
  2. $F_{тяж2} = gm_2$,
    $F_{тяж2} = 9.8 frac{Н}{кг} cdot 0.5 space кг = 4.9 space Н$
  3. $F_{тяж3} = gm_3$,
    $F_{тяж3} = 9.8 frac{Н}{кг} cdot 2500 space кг = 24 space 500 space Н = 24.5 space кН$
  4. $F_{тяж4} = gm_4$,
    $F_{тяж4} = 9.8 frac{Н}{кг} cdot 0.02 space кг = 0.196 space Н$

Ответ: $F_{тяж1} = 14.7 space Н$, $F_{тяж2} = 4.9 space Н$, $F_{тяж3} = 24.5 space кН$, $F_{тяж1} = 0.196 space Н$.

Задача №2

Банка объемом $5 space дм^3$ заполнена водой. Какой вес имеет вода?

Дано:
$V = 5 space дм^3$
$rho = 1000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$

СИ:
$V = 5 cdot 10^{-3} space м^3$

Показать решение и ответ

Скрыть

Решение:

У нас в задаче не сказано, что банка каким-либо образом движется, поэтому мы будем считать, что она неподвижна. Если банка неподвижна, то и вода в ней тоже. Тогда вес воды мы можем рассчитать следующим способом:
$P = F_{тяж} = gm$.

Массу воды выразим через ее плотность и объем банки, который она заполняет:
$m = rho V$.

Подставим в нашу формулу и рассчитаем вес воды:
$P = g rho V$,
$P = 9.8 frac{Н}{кг} cdot 1000 frac{кг}{м^3} cdot 5 cdot 10^{-3} space м^3 = 49 space Н$.

Ответ: $P = 49 space Н$.

Задача №3

Два кубика изготовлены из одного материала. Объем первого кубика в 12.2 раза больше, чем второго. На какой кубик действует большая сила тяжести и во сколько раз?

Дано:
$V_1 = 12.2 V_2$
$rho_1 = rho_2 = rho$

$frac{F_{тяж1}}{F_{тяж2}} — ?$

Показать решение и ответ

Скрыть

Решение:

Сила тяжести рассчитывается по формуле:
$F_{тяж} = gm$.

Выразим массу кубиков через их объем и плотность:
$m_1 = rho V_1 = rho 12.2 V_2$,
$m_2 = rho V_2$.

Мы видим, что масса первого кубика в 12.2 раза больше массы второго. Это означает, что и сила тяжести, действующая на него, будет в 12.2 раза больше, чем сила тяжести, действующая на второй кубик:
$frac{F_{тяж1}}{F_{тяж2}} = frac{rho 12.2 V_2}{rho V_2} = 12.2$.

Ответ: на первый, в 12.2 раза.

Задача №4

Какой вес имеет человек, имеющий массу $65 space кг$ и находящийся на Земле?

Дано:
$m = 65 space кг$
$g = 9.8 frac{Н}{кг}$

$P — ?$

Показать решение и ответ

Скрыть

Решение:

Если человек находится на Земле неподвижно или движется равномерно и прямолинейно, то его вес будет равен силе тяжести, действующей на него:
$P = F_{тяж} = gm$,
$P = 9.8 frac{Н}{кг} cdot 65 space кг = 637 space Н$.

Ответ: $P = 637 space Н$.

Задача №5

Стальная проволока удлиняется на $2 space мм$ при действии на нее груза в $320 space Н$. Вычислите коэффициент жесткости проволоки.

Дано:
$Delta l = 2 space мм$
$F_{упр} = 320 space Н$

СИ:
$Delta l = 2 cdot 10^{-3} space м$

$k — ?$

Показать решение и ответ

Скрыть

Решение:

Запишем закон Гука:

$F_{упр} = k Delta l$.

Выразим отсюда коэффициент жесткости проволоки и рассчитаем его:

$k = frac{F_{упр}}{Delta l}$,

$k = frac{320 space Н}{2 cdot 10^{-3} space м} = 160 cdot 10^3 frac{Н}{м} = 160 frac{кН}{м}$.

Ответ: $k = 160 frac{кН}{м}$.

Задача №6

Под действием груза в $200 space Н$ пружина динамометра удлинилась на $0.5 space см$. Каково удлинение пружины под действием груза в $700 space Н$?

Дано:
$Delta l_1 = 0.5 space см$
$F_{упр1} = 200 space Н$
$F_{упр2} = 700 space Н$

$Delta l_2 — ?$

Показать решение и ответ

Скрыть

Решение:

Закон Гука описывает силу упругости, возникающую в пружине при ее удлинении:
$F_{упр1} = k Delta l_1$.

Выразим отсюда жесткость пружины и рассчитаем ее:
$k = frac{F_{упр1}}{Delta l_1}$,
$k = frac{200 space Н}{0.5 space см} = 400 frac{Н}{см}$.

Используя тот же закон Гука рассчитаем удлинение пружины при другой силе упругости, измерений динамометром:
$F_{упр2} = k Delta l_2$,
$Delta l_2 = frac{F_{упр2}}{k}$,
$Delta l_2 = frac{700 space Н}{400 frac{Н}{см}} = 1.75 space см$.

Ответ: $Delta l_2 = 1.75 space см$.

Под действием силы давления вагона $50 space кН$ буферные пружины между вагонами сжимаются на $1 space см$. С какой силой давит вагон, если пружины сжались на $4 space см$?

Дано:
$F_{упр1} = 50 space кН$
$Delta l_1 = 1 space см$
$Delta l_2 = 4 space см$

$F_{упр2} — ?$

Показать решение и ответ

Скрыть

Решение:

Вследствие давления вагона, буферные пружины сжимаются и в них возникает сила упругости, равная $50 space кН$. Найдем жесткость этих пружин:
$F_{упр1} = k Delta l_1$,
$k = frac{F_{упр1}}{Delta l_1}$,
$k = frac{50 space кН}{1 space см} = 50 frac{кН}{см}$.

Рассчитаем силу, с которой давит вагон, (силу упругости, возникающую в пружинах под таким давлением), если изменение длины пружин составило $4 space см$:
$F_{упр2} = k Delta l_2$,
$F_{упр2} = 50 frac{кН}{см} cdot 4 space см = 200 space кН$.

Ответ: $F_{упр2} = 200 space кН$.

Задача №8

Пружина без нагрузки длиной $20 space см$ имеет коэффициент жесткости $20 frac{Н}{м}$. Какой станет длина растянутой пружины под действием силы $2 space Н$?

Дано:
$l = 20 space см$
$k = 20 frac{Н}{м}$
$F_{упр1} = 2 space Н$

СИ:
$l = 0.2 space м$

$F_{упр2} — ?$

Показать решение и ответ

Скрыть

Решение:

Для того чтобы узнать длину растянутой пружины, нам нужно вычислить ее изменение длины — длину, на которую она растянется:
$l_1 = l + Delta l$.

Если бы пружина сжималась под действием силы, то мы бы отнимали удлинение от первоначальной длины.

Рассчитаем удлинение пружины:
$F_{упр} = k Delta l$,
$Delta l = frac{F_{упр}}{k}$,
$Delta l = frac{2 space Н}{20 frac{Н}{м}} = 0.1 space м$.

Теперь рассчитаем длину растянутой пружины:
$l_1 = 0.2 space м + 0.1 space м = 0.3 space м = 30 space см$.

Ответ: $l_1 = 30 space см$.

Задача №9

На рисунке 1 изображен график зависимости модуля силы упругости от удлинения пружины. Найдите жесткость пружины.

Рисунок 1. Зависимость удлинения пружины от силы упругости

Показать решение и ответ

Скрыть

Решение:

Для того чтобы определить коэффициент жесткости нам нужно силу упругости разделить на удлинение пружины:
$k = frac{F_{упр}}{Delta l}$.

Пользуясь графиком, вы можете выбрать любую удобную для вас точку. График демонстрирует линейную зависимость силы упругости от удлинения, коэффициент жесткости при этом — величина постоянная.

Мы выберем точку, в которой сила упругости равна $4 space Н$. Этому значению силы соответствует удлинение пружины, равное $0.4 space м$.

Рассчитаем коэффициент жесткости:
$k = frac{4 space Н}{0.4 space м} = 10 frac{Н}{м}$.

Ответ: $k = 10 frac{Н}{м}$.

Задача №10

Круглый стальной брус диаметром $2 space см$, длиной $16 space м$ растягивается силой, равной $36 space кН$. Найдите удлинение этого бруса.

Дано:
$d = 2 space см$
$l = 16 space м$
$F_{упр} = 36 space кН$
$E = 200 cdot 10^9 space Па$

$Delta l — ?$

Модуль упругости $E$ — это физическая величина, характеризующая способность материала сопротивляться растяжению или сжатию. 

Модуль упругости является характеристикой материала, для стали он равен $200 cdot 10^9 space Па$.
Он связан с коэффициентом упругости $k$:

$k = frac{ES}{l}$,

где $S$ — площадь поперечного сечения,
$l$ — длина.

Показать решение и ответ

Скрыть

Решение:

Запишем закон Гука:
$F_{упр} = k Delta l$.

Выразим отсюда удлинение стального бруса:
$Delta l = frac{F_{упр}}{k}$.

Коэффициент упругости $k$ мы можем выразить через модуль упругости $E$:
$k = frac{ES}{l}$.

Площадь поперечного сечения $S$ выразим через диаметр:
$S = frac{pi d^2}{4}$.

Подставим эти формулы в закон Гука:
$Delta l = frac{F_{упр}}{frac{ES}{l}} = frac{F_{упр} l}{E frac{pi d^2}{4}} = frac{4 F_{упр} l}{E pi d^2}$.

Рассчитаем удлинение бруса:
$Delta l = frac{4 cdot 36 cdot 10^3 space Н cdot 16 space м}{200 cdot 10^9 space Па cdot 3.14 cdot 0.02^2 space м^2} = frac{2304 cdot Н cdot м}{251 space 200 space Н} approx 0.009 space м approx 9 space мм$.

Ответ: $Delta l = 9 space мм$.

Источник

Примеры решения задач по сопротивлению материалов



На этой странице приведен еще один пример решения задачи по Сопромату, где необходимо найти внутренние усилия, напряжения и линейные удлинения на участках и в сечениях бруса, нагруженного продольной силой и собственным весом.

Результаты расчетов оформлены эпюрами продольных сил, напряжений и удлинений бруса.

Студентам технических специальностей ВУЗов в качестве методической помощи предлагаются к скачиванию готовые варианты контрольных работ по сопромату (прикладной механике). Представленные задания и примеры их решения предназначены, в частности, для учащихся Алтайского Государственного технического университета.
Варианты контрольных работ можно скачать в формате Word для ознакомления с порядком решения заданий, или для распечатывания и защиты (при совпадении вариантов).

***

Расчет стержня

Условие задачи:

Стержень, жестко закрепленный одним концом, состоящий из трех участков длиной l1…l3, и площадью А1…А3, находится под действием собственного веса и силы F, приложенной на координате lF (см. рис. 1).
Материал стрежня – сталь Ст.3.

Требуется:

Построить эпюры продольных сил N, нормальных напряжений σ и перемещений δ.

Исходные данные:
  • l1 = 1,1 м;
  • l2 = 1,0 м;
  • l3 = 0,9 м;
  • А1 = 40 см2;
  • А2 = 20 см2;
  • А3 = 25 см2;
  • F = 70 кН;
  • lF = l1 + l2;
  • Опора расположена вверху.
Справочная информация:

Удельный вес стали Ст.3:   γ = (77…79)×103 Н/м3.
Для расчетов принимаем удельный вес равным   γ = 78×103 Н/м3.
Модуль продольной упругости (модуль Юнга) для стали Ст.3:   Е = 2×1011 Н/м2.

Указания:

Собственный вес стержня можно представить в виде распределенной нагрузки q1 = γ×А1.
Ось z, направление силы F и нумерацию участков вести от опоры.

Решение задачи:

1. Вычерчиваем схему стержня в соответствии с исходными данными.

пример решения задачи по сопромату расчет стержня

2. Расчет ведем от свободного конца стержня, т. е. с III-го участка.
Рассекаем стержень на силовом участке и отбрасываем часть стержня, содержащую опору (верхнюю часть).
Составляем уравнения для нахождения продольной силы N, нормального напряжения σ и удлинения стержня ∆l на силовом участке III:

2.1. Поскольку сила F на участке III не действует, то продольная сила на этом участке представлена только весом стержня, который увеличивается по мере удаления от плоскости 3-3. При этом зависимость величины продольной силы F от координаты z3 будет прямо пропорциональной, поскольку изменяется только координата, а площадь сечения А3 и плотность стали γ остается неизменной по всему участку.
Уравнение для продольной силы на участке:

N = q3×z3 = γ×А1×z3,

где
q3 – вес стержня, представленный в виде распределенной нагрузки (Н/м);
z3 – координата рассматриваемого сечения стержня по оси z (м);
А3 – площадь сечения участка III (м2);
γ – удельный вес материала стержня (для стали Ст.3 – γ = 78×103 Н/м3).

Тогда в сечении 3-3 продольная сила будет равна нулю (т. к. и координата и вес равны нулю), а в сечении 2-2 (верхнем сечении участка III) продольная сила определится по формуле:

N3 = q3×z3 = l3× γ×А3 = 0,9×78×103×25×10-4 = 175,5 Н.

2.2. Нормальное напряжение на силовом участке III определяем, как отношение продольной силы к площади участка в каждом рассматриваемом сечении стержня:

σ3 = N3/А3.

Тогда в сечении 3-3 нормальное напряжение будет равно нулю (т. к. продольная сила равна нулю), а в сечении 2-2 (со стороны участка III) определится по формуле:

σ3 = N3/А3 = 175,5/25×10-4 =70222,2 Па   или   σ3 ≈0,07 МПа.

2.3. Удлинение бруса на участке III определяем по закону Гука, с учетом изменяющегося по координате z веса стержня:

∆l3 = ∫[N3/(E×A3)]dz,

где Е – модуль продольной упругости стали;   Е = 2×1011 Н/м2.

Удлинение изменяется по линейной зависимости от нижнего сечения (3-3) до верхнего сечения (2-2) участка, при этом в сечении 3-3 оно будет равно нулю, поскольку продольная сила N3 в этом сечении равна нулю, а в сечении 2-2 удлинение будет равно:

∆l3 = ∫[N3/(E×A3)]dz = ∫[(А3×γ×z3)/(Е×А3)]dz = (γ×l32)/2E =

= 78×103×0,81)/(2×2×1011) ≈ 0,000000158 м или ∆l3 ≈ 0,000158 мм.



3. Проводим расчет продольных сил, нормальных напряжений и удлинений стержня на участках II и I, учитывая, что к сечению 2-2 участка II приложена продольная сила F, которая по отношению к участкам II и I является растягивающей (т. е. положительной).

3.1. Продольная сила на участках II и I будет равна:

В начале участка II:

N21 = F + N3 = 70000 + 175,5 = 70175,5 Н  или  N21 ≈ 70,175 кН.

В конце участка II и в начале участка I:

N22 = N11 = N21 + q2×z2 = N21 + l2× γ×А2 =

= 70175,5 + (1,0×78×103×20×10-4) =70331,5 Н  или  N22 = N11 ≈ 70,33 кН.

В конце участка I:

N12 = N11 + q1×z1 = F + l1× γ×А1 = 70331,5 + (1,1×78×103×40×10-4) =70674,7 Н  или  N12 ≈ 70,67 кН.

3.2. Нормальное напряжение на участках II и I:

В начале участка II:
σ21 = N12 /А2 = 70175/20×10-4 = 35087500 Па  или  σ21 ≈ 35,09 МПа.

В конце участка II:
σ22 = N22/А2 = 70331,5 /20×10-4 = 35 165 750 Па  или  σ22 ≈ 35,16 МПа.

В начале участка I:
σ11 = N11/А1 = 70331,5 /40×10-4 = 17 582 875 Па  или  σ11 ≈ 17,58 МПа.

В конце участка I:
σ12 = N12/А1 = 70674,7 /40×10-4 = 17668675 Па  или  σ12 ≈ 17,7 МПа.

3.3. Удлинение стержня на участках II и I:

∆l2 = (γ×l22)/2E + (N×l2/E×A2) =

= 78×103×1)/(2×2×1011) + (70156×1/2×1011×20×10-4) ≈ 0,00017851 м  или  ∆l2 ≈ 0,1785 мм.

∆l1 = (γ×l12)/2E + (N×l1/E×A1) =

= (78×103×1,21)/(2×2×1011) + (70343×1,1/2×1011×40×10-4) ≈ 0,0000991 м или ∆l1 ≈ 0,0991 мм.

4. Определяем перемещения сечений стержня:

  • δ0-0 = 0 мм;
  • δ1-1 = ∆l1 = 0,0991 мм;
  • δ2-2 = ∆l1 + ∆l2 = 0,0991 + 0,1785 = 0,2776 мм;
  • δ3-3 = ∆l1 + ∆l2 + ∆l3 = 0,0991 + 0,1785 + 0,000158 = 0,2777 мм.

5. Результаты расчетов сводим в Таблицу 1, и строим эпюры продольных сил, нормальных напряжений и перемещений (см. рис. 1).

Таблица 1. Значения продольной силы, нормального напряжения и удлинения стержня по сечениям силовых участков.

Участок

Границы
участка

Продольная
сила,
N, кН

Нормальное напряжение,
σ, МПа

Перемещение
δ, мм

III

      начало

0

0

0,2777
     конец

0,1755

0,07

0,2776

II

      начало

70,175

35,09

0,2776
     конец

70,33

35,16

0,0991

I

      начало

70,33

17,58

0,0991
     конец

70,67

17,70

0

***

Пример расчета вала на скручивание

Контрольная по сопромату для ВУЗов



Источник

Добавить комментарий