Как найти удлинение тела при растяжении - Сайт, где вы сможете решить свои вопросы

Растяжение и сжатие. Удлинения и деформации при растяжении и сжатии

Растяжением будем
называть такое нагружение стержня,
когда в поперечных сечениях возникает
лишь один внутренний силовой фактор –
нормальная сила.

Для того чтобы
возникло растяжение необходимо, чтобы
внешние силы, приложенные по торцам
стержня, были статически эквивалентны
сосредоточенной силе, приложенной по
оси стержня.

Схематизируя силы,
приложенные к стержню, мы используем
принцип Сен-Венана, который в данном
конкретном случае примет следующий
вид: “Способ приложения нагрузки не
сказывается в сечениях достаточно
удаленных от места приложения нагрузки”.

Н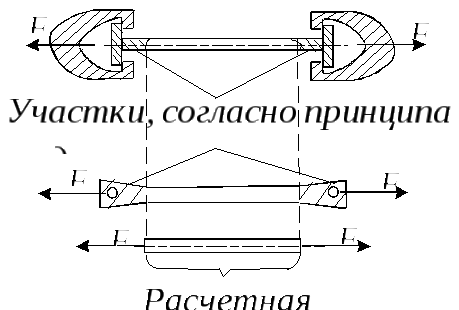апример,
стержень одной и той же длины и сечения
загружается разным образом. В первом
случае имеется закладная головка,
которая помещена в захваты испытательной
машины, во втором случае она представляет
собой равнодействующую давления со
стороны болта или заклепки. Безусловно,
что характер распределения напряжений
в месте передачи нагрузки, совершенно
различный и весьма сложный. Однако, на
расстояниях равных примерно характерному
размеру поперечного сечения,
индивидуальности в передачи нагрузки
не сказываются, и для обоих случаев
может быть принята одна и та же расчетная
схема: Стержень загружен по торцам
сосредоточенными силами, направленными
по оси.

Параллельно с
растяжением мы будем рассматривать и
случай сжатия, отличая его от растяжения
лишь знаком нормальной силы и напряжения.
Но в данной лекции мы будем рассматривать
сжатие коротких стержней, длина которых
не превышает нескольких размеров
поперечного сечения.

13)

Коэффициенты запаса прочности и допускаемые напряжения

Состояния, при
которых происходят коренные изменения
механического состояния материала в
точке, называется предельным.

Различают два
предельных состояния:

1) Переход материала
в пластическое состояние, т.е. появление
значительных остаточных деформаций.

2) Разрушение. Т.е.
рост трещин и распадение на части.

Соответственно
сказанному, оценивая состояние
конструкции, различают два коэффициента
запаса:

а) Коэффициент
запаса по текучестигде

– предел текучести;

– максимальное
напряжение, возникающее в конструкции.

По данному
коэффициенту оцениваются конструкции,
выполненные из достаточно пластичных
материалов.

б) Если материал
конструкции хрупок и обладает
незначительными пластическими свойствами,
то прибегают к коэффициенту запаса по
разрушению

где

– предел прочности
или временное сопротивление.

Иногда коэффициенты
запаса выступают в другом качестве: в
роли нормативных заданных величин, с
помощью которых определяются так
называемые допускаемые напряжения:

Допускаемое
напряжение;

а) для пластичных
материалов определяется

б) Для хрупких
материалов

Расчет по методу
допускаемых напряжений состоит в
обеспечении условия:
,
называется условием прочности.

14)

Закон Гука при растяжении и сжатии

Как уже упоминалось
ранее, между напряжениями и деформациями
существует связь, которая может быть
установлена лишь экспериментальным
путем.

Б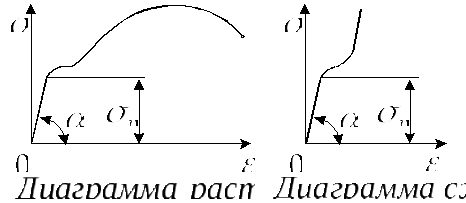ольшинство
твердых тел, при сравнительно небольших
нагрузках, обнаруживают свойство
однозначной зависимости между напряжениями
и деформациями (или между силами и
перемещениями).

Например, если
вспомнить известные нам из курса
лабораторных работ диаграммы растяжения
и сжатия малоуглеродистой стали, то
можно заметить, что вплоть до значений
напряжения равного
–
предела пропорциональности зависимость
между напряжениями и деформациями
близка к линейной.

Подобная картина
наблюдается и у других сталей, а также,
может быть менее отчетливо, у других
материалов. Данный экспериментальный
факт позволяет принять простейший из
упругих законов – закон Гука, т.е. закон
линейной упругости:

Напряжения
пропорциональны деформациям

Коэффициент
пропорциональности между напряжениями
и деформациями

называется модулем упругости первого
рода (модулем Юнга). Модуль упругости

определяется опытным путем и служит
мерой жесткости материала. Геометрический
смысл

– угловой коэффициент прямолинейного
начального участка диаграммы материала.

Модуль упругости
для некоторых, часто применяемых
материалов, имеет приблизительно
следующие значения.

Сталь:;
Медь:
;

Дерево:
;
Каучук:

Отметим еще раз,
что свойство упругости, в частности
линей-

ной упругости,
относительно. Уместно говорить не о
упругих и неупругих материалах, а о
упругом и неупругом состоянии материала.

Если в (3) выразить

по формуле (2) и учесть (1), то получим
закон Гука в форме, позволяющей находить
удлинения.

Величину

называют жесткостью при растяжении-сжатии.
Закон (4) можно сформулировать следующим
образом: удлинение стержня прямо
пропорционально нормальной силе и длине
стержня и обратно пропорционально
жесткости при растяжении-сжатии.

По формуле (4) можно
определять удлинения только в том

случае, если
нормальная сила и поперечное сечение
постоянны по

длине стержня,
т.е. если напряженное состояние однородно.

Если нормальная
сила и поперечное сечение меняются по
длине ступенчато, то стержень надо
разбить на участки, так чтобы в пределах
каждого участка

и

были постоянны, определить удлинение
каждого из участков и тогда полное
удлинение стержня будет равняться
алгебраической сумме, (знак определяется
знаком
)
удлинений участков.

Е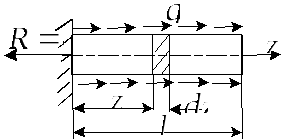сли
же напряженное состояние в стержне
неоднородно, то выделив малый элемент
длиной
определим
его удлинение

,
Здесь

и

рассматривается как функции z.
Полное удлинение стержня будет равно:

15)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Сила упругости широко используется в технике. Эта сила возникает в упругих телах при их деформации. Деформация – это изменение формы тела, под действием приложенных сил.

Виды деформации

Деформация – это изменение формы, или размеров тела.

Есть несколько видов деформации:

сдвиг;
кручение;
изгиб;
сжатие/растяжение;

Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.

Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.

Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.

Рис. 1. пластиковая линейка, деформированная изгибом – а) и кручением – б)

В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.

Растяжение пружины

Рассмотрим подробнее деформацию растяжения на примере пружины.

Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина (L_{0}) пружины.

Рис. 2. Сравнивая длину свободной пружины с длиной нагруженной, можно найти ее удлинение

Подвесим теперь к пружине груз. Пружина будет иметь длину (L), указанную на рисунке справа.

Сравним длину нагруженной пружины с длиной свободно висящей пружины.

[ large L_{0} + Delta L = L ]

Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину (L_{0}).

[ large boxed{ Delta L = L — L_{0} }]

( L_{0} left(text{м} right) ) – начальная длина пружины;

( L left(text{м} right) ) – конечная длина растянутой пружины;

( Delta L left(text{м} right) ) – кусочек длины, на который растянули пружину;

Величину ( Delta L ) называют удлинением пружины.

Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.

Примечание: Отношение – это дробь. Относительное – значит, дробное.

[ large boxed{ frac{Delta L }{ L_{0}} = frac{ L — L_{0}}{L_{0} } = varepsilon } ]

( varepsilon ) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.

Расчет силы упругости

Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.

Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.

Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.

Разноцветная пластмассовая пружина-игрушка растяжению сопротивляется слабо

Закон Гука

Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал ( F_{text{упр}} ) силой упругости.

[ large boxed{ F_{text{упр}} = k cdot Delta L }]

Эту формулу назвали законом упругости Гука.

( F_{text{упр}} left( H right) ) – сила упругости;

( Delta L left(text{м} right) ) – удлинение пружины;

( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости).

Какие деформации называют малыми

Закон Гука применяют для малых удлинений (деформаций).

Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.

Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.

Как рассчитать коэффициент жесткости

Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.

Рис. 4. Вес подвешенного на пружине груза уравновешивается силой упругости

Так как силы взаимно компенсируются, в правой части уравнения находится ноль.

[ large F_{text{упр}} — m cdot g = 0 ]

Подставим в это уравнение выражение для силы упругости

[ large k cdot Delta L — m cdot g = 0 ]

Прибавим к обеим частям вес груза и разделим на измеренное изменение длины (Delta L ) пружины. Получим выражение для коэффициента жесткости:

[ large boxed{ k = frac{ m cdot g }{Delta L} }]

(g) – ускорение свободного падения, оно связано с силой тяжести.

Соединяем две одинаковые пружины

В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.

Параллельное соединение пружин

На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину (Delta L). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.

Рис. 5. Две пружины, соединенные параллельно, деформируются меньше одной такой пружины

Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом (mg).

Одна пружина:

[ large k_{1} cdot Delta L = m cdot g ]

Две параллельные пружины:

[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= m cdot g ]

Так как правые части уравнений совпадают, левые части тоже будут равны:

[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= k_{1} cdot Delta L ]

Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:

[ large k_{text{параллел}} cdot frac{1}{2}= k_{1} ]

Умножим обе части полученного уравнения на число 2:

[ large boxed{ k_{text{параллел}} = 2k_{1} } ]

Коэффициент жесткости (k_{text{параллел}}) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной

Последовательное соединение пружин

Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину (Delta L). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.

Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.

На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину (Delta L).

Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений

Рис. 6. Система, состоящая из двух одинаковых пружин, соединенных последовательно, деформируются больше одной пружины

Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом (mg).

Одна пружина:

[ large k_{1} cdot Delta L = m cdot g ]

Две последовательные пружины:

[ large k_{text{послед}} cdot Delta L cdot 2 = m cdot g ]

Так как правые части уравнений совпадают, левые части тоже будут равны:

[ large k_{text{послед}} cdot Delta L cdot 2 = k_{1} cdot Delta L ]

Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:

[ large k_{text{послед}} cdot 2 = k_{1} ]

Разделим обе части полученного уравнения на число 2:

[ large boxed{ k_{text{послед}} = frac{k_{1}}{2} } ]

Коэффициент жесткости (k_{text{послед}}) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной

Потенциальная энергия сжатой или растянутой пружины

Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину (Delta L ) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.

Рис. 7. Деформированная — сжатая или растянутая пружина обладает потенциальной энергией

Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).

Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:

[ large boxed{ E_{p} = frac{k}{2} cdot left( Delta L right)^{2} }]

( E_{p} left( text{Дж} right)) – потенциальная энергия сжатой или растянутой пружины;

( Delta L left(text{м} right) ) – удлинение пружины;

( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости) пружины.

Выводы

Упругие тела – такие, которые сопротивляются деформации;
Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
Деформация – изменение формы, или размеров тела;
Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
Удлинение пружины – это разность ее конечной и начальной длин;
Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.

Источник

Известно, что на все тела, находящиеся на Земле, действует сила тяжести, обусловленная гравитацией.

Какие ещё силы могут возникнуть? Рассмотрим несколько примеров.

(1). На яблоко в тарелке действует сила притяжения Земли. Фрукт не проваливается сквозь тарелку, а находится в покое.

Значит, существует сила, которая уравновешивает силу тяжести.

(2). Рассмотрим тело, подвешенное на нити. Сила тяжести будет направлена вниз.

Тело не может упасть, потому что силу тяжести компенсирует сила натяжения нити.

(3). Проведём опыт.

Позволим гире опуститься на середину доски на опорах.

Рис. (1). Гиря

Вес гири воздействует на доску и оказывает деформацию изгиба — заставляет сгибаться. Свойство упругости доски вызывает противоположную силу — силу реакции опоры — для того, чтобы вернуться в исходное, недеформированное состояние. Обе силы направлены вдоль одной прямой через центр масс гири, но направления противоположны, поэтому сумма сил равна нулю.

Под весом гири доска прогнулась — изменила свою форму.

Деформацией тела называют изменение размера или формы тела под воздействием внешних сил.

При изменении формы и размера под воздействием деформирующих сил каждое упругое тело пытается вернуться в начальное состояние.

Сила упругости — сила, которая возникает при деформации тела и стремится вернуть его в исходное состояние.

Сила упругости — векторная величина, обозначается (vec{F})(_{упр}).

Чем сильнее давит тело на опору, тем больше деформация и возникающая в ответ на деформацию сила упругости. Деформация опоры прекращается в тот момент, когда действующие по вертикали силы уравновесят друг друга (сила упругости станет равной силе тяжести).

Если исчезнет деформирующая сила, то исчезнет и сила упругости.

В зависимости от приложенных сил различают виды деформации:

деформация растяжения и сжатия;
деформация сдвига;
деформация изгиба;
деформация кручения.

Деформация называется упругой в случае, если тело полностью восстанавливает свою форму и объём после прекращения действия деформирующей силы.

(4). Рассмотрим силы, действующие в опыте с гирей, подвешенной на нити.

Рис. (2). Гиря на штативе

Синей стрелкой обозначен вектор силы тяжести (vec{F_2}), направленной к центру Земли (вертикально вниз). Силе тяжести противодействует сила упругости нити (vec{F_1}), называемая силой натяжения нити. Она обозначена красной стрелкой, направленной вверх.

Гиря не движется, значит, силы компенсируют друг друга, сила тяжести равна силе упругости: (vec{F_1}+vec{F_2}=0), но направлена противоположно.

Подвесом называют нить, на которую подвешивается тело. Обычно имеют в виду нерастяжимую прочную нить.

Подвесом может быть упругое тело: пружина, резина. Значит, оно может растягиваться (деформироваться) под действием силы тяжести тела. При растяжении длина подвеса изменяется на некоторую величину, которую называют удлинением: (Delta l=l-l_0), где (l_0) — начальная длина нити, а (l) — конечная длина.

Закон Гука: изменение длины тела при растяжении (или сжатии) прямо пропорционально модулю силы упругости

(Δl) — удлинение тела (изменение его длины),

(k) — коэффициент пропорциональности, называющийся жёсткостью (пружины), которая зависит от материала.

Закон Гука работает только в случае, если деформация была упругая.

Источники:

Рис. 1. Гиря. © ЯКласс.
Рис. 2. Гиря на штативе. © ЯКласс.

Источник

Подборка формул для расчета элементов и конструкций на растяжение-сжатие и решения задач сопротивления материалов по расчету нормальных напряжений, деформаций и перемещения сечений стержней при продольном нагружении.

Обозначения в формулах:

σ — нормальные напряжения,
N – внутренняя продольная сила,
A – площадь поперечного сечения,
[σ] – допустимые напряжения,
E – модуль продольной упругости,
ε — относительные деформации.

Закон Гука:

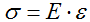
Формула для расчета напряжений в поперечном сечении стержня

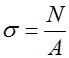
Условие прочности (проверочный расчет) при растяжении-сжатии

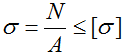
Расчет минимальной площади поперечного сечения бруса

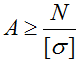
Расчет допустимой величины внешней растягивающей/сжимающей силы (определение грузоподъемности)

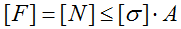
Формула для расчета абсолютных деформаций

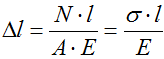
Расчет перемещения сечений

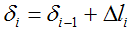
Здесь: δ_i — перемещение рассматриваемого сечения,
δ_i-1 — перемещение предыдущего сечения,
Δl_i — деформация участка между указанными сечениями.

Напряжения в наклонных сечениях

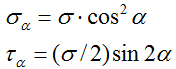
Здесь α — угол отклонения сечения от поперечного.

Другие формулы >
Примеры решения задач >
Краткая теория >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Решение задач и лекции по технической механике, теормеху и сопромату

Источник

Не зная, чему равна сила растяжения пружины, невозможно вычислить коэффициент ее жесткости, поэтому найдите силу растяжения. То есть, Fупр = kx , где k и является коэффициентом жесткости. В этом случае вес груза будет равен силе упругости, действующей на тело, коэффициент жесткости которого нужно найти, например, пружины.

При параллельном соединении жёсткость увеличивается, при последовательном — уменьшается. Физика 7 класс, тема 03. Силы вокруг нас (13+2 ч) Сила и динамометр. Виды сил. Уравновешенные силы и равнодействующая. Физика 7 класс, тема 06. Введение в термодинамику (15+2 ч) Температура и термометры.

Растяжение пружины

Рассмотрим подробнее деформацию растяжения на примере пружины.

Рис. 2. Сравнивая длину свободной пружины с длиной нагруженной, можно найти ее удлинение

Подвесим теперь к пружине груз. Пружина будет иметь длину (L), указанную на рисунке справа.

Сравним длину нагруженной пружины с длиной свободно висящей пружины.

[ large L_{0} + Delta L = L ]

[ large boxed{ Delta L = L — L_{0} }]

( L_{0} left(text{м} right) ) – начальная длина пружины;

( L left(text{м} right) ) – конечная длина растянутой пружины;

( Delta L left(text{м} right) ) – кусочек длины, на который растянули пружину;

Величину ( Delta L ) называют удлинением пружины.

Примечание: Отношение – это дробь. Относительное – значит, дробное.

[ large boxed{ frac{Delta L }{ L_{0}} = frac{ L — L_{0}}{L_{0} } = varepsilon } ]

Определение коэффициента жесткости растяжения

Для определения коэффициента жесткости растяжения производятся следующие расчеты.

Измеряется длина пружины в вертикальном подвесе с одной свободной стороной изделия – L1;
Измеряется длина пружины с подвешенным грузом – L2.Если взять груз массой 100гр., то он будет воздействовать силой в 1Н (Ньютон) – величина F;
Вычисляется разница между последним и первым показателем длины – L;
Рассчитывается коэффициент упругости по формуле: k = F/L.

Определение коэффициента жесткости сжатия производится по этой же формуле. Только вместо подвешивания груз устанавливается на верхнюю часть вертикально установленной пружины.

Подводя итог, делаем вывод, что показатель жесткости пружины является одной из существенных характеристик изделия, которая указывает на качество исходного материала и определяет долговечность использования конечного изделия.

Расчет пружины сжатия из проволоки прямоугольного сечения.

Жесткость пружины из проволоки или прутка прямоугольного сечения при тех же габаритах, что и из круглой проволоки может быть гораздо больше. Соответственно и сила сжатия пружины может быть больше.

Представленная ниже программа является переработанной версией , подробное описание которой вы найдете, перейдя по ссылке. Прочтите эту статью, и вам проще будет разобраться в алгоритме.

Основным отличием в расчете, как вы уже догадались, является определение жесткости витка (C
1)
, задающей жесткость пружины
(C)
в целом.

Далее представлены скриншот программы и формулы для цилиндрической стальной пружины из прямоугольной проволоки, у которой поджаты по ¾ витка с каждого конца и опорные поверхности отшлифованы на ¾ длины окружности.

Внимание!!!

После выполнения расчета по программе выполняйте проверку касательных напряжений!!!

4. I
=(D 1/B )-1
5.

При
1/3
:
Y=5,3942*(H/B) 2 -0,3572*(H /B )+0,5272
При 1

:
Y=5,4962*(H/B) (-1.715)
При 2

H
/B: Y =3 ,9286 *(H / B ) (-1. 2339 )
6.

При
HB : C 1 =(78500* H 4 )/(Y * (D 1 — B ) 3)
При H
>B:C 1=(78500*B4)/(Y *(D 1—B) 3)
8. T nom
=1,25*(F 2/C 1)+H
9. T max
=π*(D 1—B)*tg (10°)
11. S 3
=T—H
12. F 3
=C 1*S 3
14. N
расч=(L 2—H)/(H+F 3/C 1—F 2/C 1)
16. C
=C 1/N
17. L 0
=N*T+H
18. L 3
=N*H+H
19. F 2
=C*L 0—C*L 2
21. F 1
=C*L 0—C*L 1
22. N 1
=N+1,5
23. A
=arctg (T/(π*(D 1—H)))
24. L
разв=π*N 1*(D 1—H)/cos (A)
25. Q
=H *B*L разв*7,85/10 6

Соединяем две одинаковые пружины

Параллельное соединение пружин

Выводы

Упругие тела – такие, которые сопротивляются деформации;
Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
Деформация – изменение формы, или размеров тела;
Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
Удлинение пружины – это разность ее конечной и начальной длин;
Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.