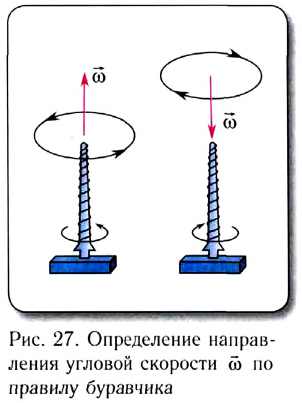
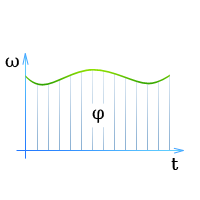
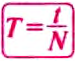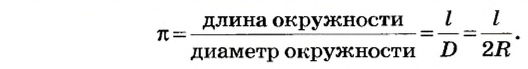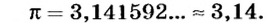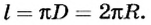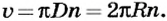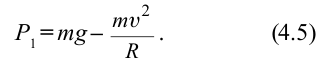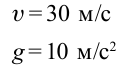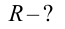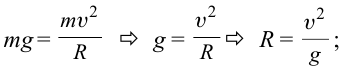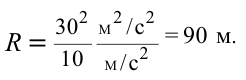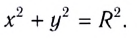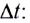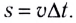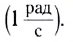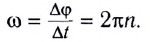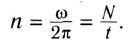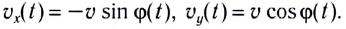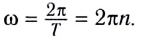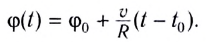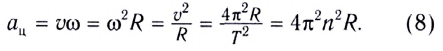Как найти угловое перемещение колеса - Сайт, где вы сможете решить свои вопросы

Угловые перемещения колесной пары

Одной
из причин колебаний вагона является
виляние (извилистое движение). Как
известно, между ребордами колес и
рабочими гранями рельсов существуют
зазоры, за счет которых колесная пара
при своем движении может постепенно
переходить от контактирования гребнем
правого колеса с правым по ходу рельсом
к контактированию гребнем левого колеса
с левым рельсом.

Поскольку
колесная пара при движении непрерывно
перемещается поперек колеи ( в пределах
указанного выше зазора), то ось колесной
пары при конической форме колес совершает
угловые
колебания
вокруг оси х
(угол
φ), и шейки оси то поднимаются, то
опускаются на некоторую величину z.
Эти колебания также передаются затем
другим элементам вагона.

Колебания
вагонов вызываются также действием
сил, возникающих при входе вагона в
кривые участки пути и в стрелочные
кривые, от порывов ветра, аэродинамических
толчков воздуха в боковую поверхность
вагонов при встрече поездов и по некоторым
другим причинам.

Виды колебаний

В
линейных колебательных системах известны
два вида колебаний:

Собственные
колебания
– происходят в изолированных колебательных
системах вследствие какого-либо
начального возмущения; в процессе самих
собственных колебаний никакие внешние
дополнительные возмущения на систему
не действуют.

Системы,
в которых энергия колебаний расходуется
на преодоление сопротивлений среды,
называют диссипативными,
а
системы, у которых энергия в окружающую
среду не рассеивается – консервативными.

Вынужденные
колебания –
в колебательных системах возникают
тогда, когда на систему все время
действуют возмущающие силы.

Полнее
всего изучены, так называемые, гармонические
колебания
систем, которые описываются обычно
уравнением

где
z
– величина
перемещений в колебательном процессе;

А
–

амплитуда колебаний;

ωt
+α
– фаза колебаний;

ω

– угловая частота колебаний;

t

–
время;

α
– начальная фаза колебаний.

Динамические характеристики верхнего строения пути.

Важной
характеристикой верхнего строения пути
(ВСП) является жёсткость. Жёсткость пути
различна в горизонтальном и вертикальном
направлениях, в неодинаковом стыке и
середине рельс.

Вертикальная
жесткость пути определяется отношением
действующей на головку рельса вертикальной
нагрузки к вертикальному перемещению
точки контакта колеса с рельсом.

Приведенная
масса пути – это условная величина,
которая представляет собой коэффициент
пропорциональности в расчетных
уравнениях, связывающих скорость удара
колеса по рельсу с максимальной силой
соударения.

Горизонтальная
жёсткость пути определяется соотношением
горизонтальной поперечной (боковой)
силы приложенной к головке рельса к
вызванному ею отклонению головки рельса
от положения в ненагруженном состоянии.

Отклонения
от сжатия возникают из-за деформации
упругих прокладок между рельсами и
шпалами.

Динамические
свойства пути описывают с помощью
модели, которые учитывают его упругие,
диссипативные и инерционные свойства.

В
основном используются две модели пути:

Дисктретная-
путь представляется в виде сосредоточенной
массы m_п
приведенная к точке контакта колеса и
рельса, пружины жесткостью ж_п
и гидравлического гасителя колебаний
с коэффициентом затухания β_п.

При
выполнении расчетов по этой модели
можно принимать значения параметров
пути в следующих диапазонах:

m_п
= 0,3 – 0,8 т;

ж_п
= 35 – 85 МН/м;

β_п=
0,2 – 0,8 МН*с/м.

Континуальная
– путь как система с распределенными
по его длине параметрами (балка на
упруго-вязком винклеровском основании,
то есть на основании, в котором прогиб
проявляется только в точке приложения
силы).

Геометрические
неровности входящие в эквивалентную
геометрическую неровность пути
подразделяются на три группы:

Рифли
– неровности с длиной волны L_B=
0,03- 0,08 м.
Короткие
– возникают в кривых радиусах менее
600м, вызываются проскальзыванием одного
из колес. L_B=0,08
– 0,3м.
Длинные
– связаны с прокаткой и правкой рельсов,
а также движением разнотипного подвижного
состава. L_B=
0,3 – 3м.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Содержание:

Вращательное движение тела:

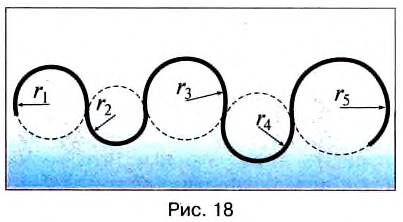
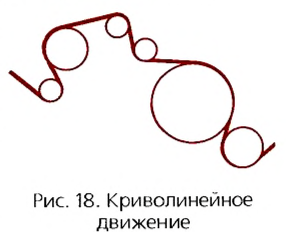
До сих пор мы изучали прямолинейное движение тел, хотя в природе и технике часто совершаются более сложные движения тел — криволинейные, когда траекторией тела является кривая линия. Любую кривую линию всегда можно представить как совокупность дуг окружностей разных радиусов (рис. 18).

Поэтому, изучив движение материальной точки по окружности, сможем в дальнейшем изучать и любые другие криволинейные движения. Кроме того, из всех возможных криволинейных движений в технике широко применяется вращательное движение деталей машин и механизмов, например вращение шестерён машин и станков, деталей, обрабатываемых на токарных станках, валов двигателей, колес машин, фрез, свёрл и т. п. Любая точка этих деталей движется по окружности. Эти две особенности и обусловили обязательное изучение движения по окружности, а именно — равномерное движение тела по окружности.

Движение материальной точки по круговой траектории с постоянной по значению, но изменяющейся по направлению скоростью, называют равномерным движением по окружности.

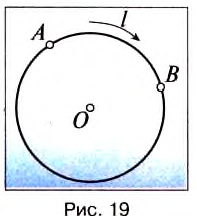
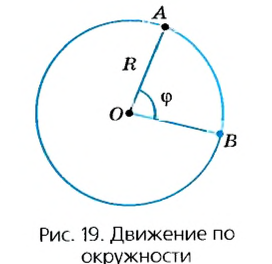
Предположим, что тело равномерно движется по окружности из точки А в точку В (рис. 19). Тогда пройденный им путь — это длина дуги

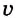
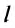
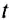
где — скорость движения тела по окружности; — пройденный телом путь (длина дуги); — время движения тела.

Направление скорости проще всего определить на опыте.

Опыт:

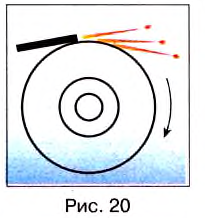
К вращающемуся точильному кругу, прикоснемся железным стержнем. Увидим, что искры из-под стержня летят по касательной к окружности этого круга (рис. 20).

Результат будет таким же в любой точке этого круга. Но каждая искра — это раскалённая частичка, оторвавшаяся от круга и летящая с такой же скоростью, какую она имела в последний момент движения вместе с кругом.

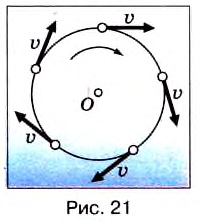
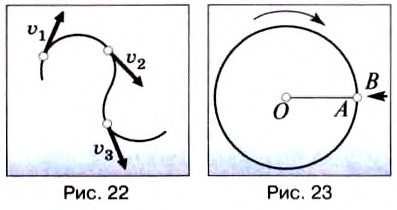
Итак, скорость материальной точки при движении по окружности направлена по касательной к ней в любой точке круга (рис. 21), а с учётом представления кривой на рисунке 18 этот вывод можно распространить на любые криволинейные движения (рис. 22).

Опыт:

Закрепим на горизонтальной оси О фанерный диск (рис. 23), на котором проведен радиус ОА. Напротив точки А поставим указатель В и будем медленно и равномерно вращать диск. Увидим, что точка А с каждым оборотом диска снова появляется напротив указателя В, т. е. совершает движение, повторяющееся через определенный интервал времени.

Движения, при которых определенные положения материальной точки повторяются через одинаковые интервалы времени, называют периодическими движениями.

Равномерное движение по окружности — это периодическое движение. Периодическое движение характеризуют такими величинами, как период обращения и частота обращения.

Период обращения – это интервал времени, в течение которого материальная точка совершает один оборот при равномерном движении по окружности.

Обозначается период обращения большой латинской буквой Т.

Если за время 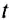материальная точка при равномерном движении по окружности совершает N оборотов, то период обращения определяется формулой:

Единицей периода обращения в СИ является одна секунда (1 с).

Если период обращения равняется 1 с, то материальная точка при равномерном движении по окружности осуществляет один оборот за 1 с.

Частота обращения определяется числом оборотов, которое материальная точка совершает за единицу времени при равномерном движении по окружности

Обозначается частота обращения малой латинской буквой .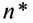

* В научной и учебной литературе частоту обращения еще обозначают малой греческой буквой 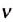(ню).

Если за время материальная точка совершила N оборотов, то, чтобы определить частоту обращения , нужно N поделить на , т. е.:
а так как = ТN , то .
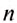
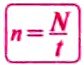
Из последней формулы видно, что частота обращения и период обращения связаны обратно пропорциональной зависимостью, а для определения единицы частоты обращения нужно единицу разделить на единицу периода обращения, т. е. на секунду.

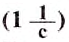
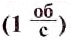
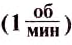
Единицей частоты обращения в СИ является единица, разделённая на секунду . это частота обращения, при котором за 1 с материальная точка совершает 1 полный оборот, двигаясь равномерно по окружности. В технике такую единицу иногда называют одним оборотом в секунду , часто применяют также единицу один оборот в минуту .

Движение точки по окружности

Движения, происходящие в природе и технике, могут отличаться по изменению значения скоростей и по изменению направления скоростей. Так, например, при движении точки вдоль прямой линии в одном направлении направление скорости не меняется, хотя ее значение может быть различным. В этом случае движение считается неравномерным.

Но движения могут быть и криволинейными, например, точки могут двигаться по окружностям. На рисунке 18 изображена траектория движения точек нити или ленты между круглыми барабанами. Такие траектории можно представить в виде отрезков прямых линий и окружностей разных размеров. Понятно, что такие движения могут быть и равномерными, каждая точка все время будет иметь одинаковую скорость по значению, хотя направление скорости от точки к точке траектории может меняться.

Рассмотрим движение материальной точки по окружности, когда это движение равномерно, т. е. значение скорости остается постоянным (рис. 19). Точка, двигаясь по окружности радиуса R, за определенное время 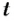переходит из точки А в точку В. При этом отрезок OA поворачивается на угол – угловое перемещение точки. Такое движение можно характеризовать угловой скоростью:

где 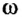(греческая буква «омега») – угловая скорость; (греческая буква «фи») – угловое перемещение.

Угловое перемещение определяется в радианах (рад.). 1 радиан — это такое перемещение, когда траектория движения точки – длина дуги окружности АВ – равна длине радиуса R.

Единицей угловой скорости является радиан в секунду (рад/с).

1 рад/с равен угловой скорости такого равномерного движения по окружности, при котором за 1 с осуществляется угловое перемещение 1 рад.

При определении угловой скорости слово «рад» обычно не пишут, а просто обозначают 1/с (имеется в виду рад/с).

Движение точки по окружности (и вращение твердого тела) характеризуют также такие величины, как период и частота вращения.

Период вращения (Т) – это время, на протяжении которого точка (тело) совершает один полный оборот по окружности. Период вращения:

где t — время вращения, N — количество выполненных оборотов.

Период вращения Т измеряется в секундах. Период равен 1 с, если точка (тело) осуществляет один оборот в секунду. Частота вращения (вращательная частота):

где N — количество совершенных оборотов за время t .

Частота вращения измеряется в оборотах за секунду (об/с).

Частота вращения определяет количество оборотов точки (тела) вокруг центра (оси вращения) за 1 с.

Еще Архимед установил, что для всех окружностей любого радиуса отношение длины окружности к его диаметру является величиной постоянной. это число обозначили греческой буквой 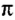(«пи»).

Таким образом, длина окружности

За один оборот материальная точка осуществляет угловое перемещение 2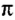 рад.

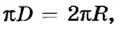
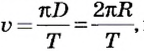
Движение по окружности характеризуется привычным для нас понятием скорости как пути, который проходит точка за единицу времени. В данном случае эта скорость называется линейной. Если учитывать, что за один оборот (время Т) точка проходит путь то линейная скорость равномерного движения точки по окружности или

Вращение твердого тела

Твердые тела состоят из большого количества частичек. Абсолютно твердыми наукой считаются тела, расстояние между точками которых не изменяется во время явлений, которые с ними происходят. Однако следует иметь в виду, что абсолютно твердых тел в природе нет.

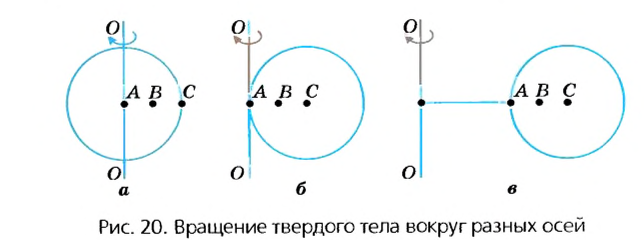
Как упоминалось в § 3, движения твердых тел бывают поступательные и вращательные. Твердые тела могут вращаться вокруг любых осей, в том числе и тех, которые проходят через их центры.

В случае а (рис. 20) ось вращения проходит через центр шара (например, вращаются колеса транспортных средств или Земля в своем суточном вращении вокруг оси). В случае в ось проходит через край шара. В случае в шар находится на определенном расстоянии от оси (например, Земля движется вокруг Солнца или Луна вокруг Земли). В некоторых случаях даже Землю и Луну можно считать материальными точками, а в некоторых случаях это сделать невозможно. Подумайте, в каких?

Что же является наиболее характерным для вращательного движения твердых тел? Очевидно, что при этом все точки этих тел в своем движении описывают окружности, центры которых находятся на осях вращения.

Понятно также, что разные точки тел за одно и то же время проходят по своим траекториям разные расстояния – чем дальше от оси вращения лежат точки, тем больше эти расстояния. Но за одно и то же время угловое перемещение всех точек одинаково. Следовательно, и угловая скорость для всех точек данного тела также будет одинаковой.

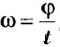
Для характеристики вращательного движения твердых тел используют такие же понятия, что и для движения точки по окружности: период вращения Т – время одного полного вращения; вращательная частота (частота вращения) 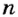— количество полных вращений за единицу времени; угловая скорость со. Кроме основной единицы частоты вращения об/с, используют об/мин, об/ч и т. п.

Период вращения Земли вокруг- Солнца равен в среднем 365 суток, а период вращения Луны вокруг Земли в среднем 28 суток. Изучая физику, астрономию, вы узнаете, что небесные тела, например планеты Солнечной системы, движутся не по окружностям, а по так называемым эллипсам.

Динамика вращательного движения

При просмотре фильмов-боевиков вы могли наблюдать, что при резком вращении руля автомобиля машина опрокидывается. В цирке мотоциклисты катаются по поверхности стен.
Проведем такой опыт. Нальем воду в ведро и раскрутим его в вертикальной плоскости. При определенной скорости вращения вода не выливается из ведра.

Из приведенных выше примеров можно сделать заключение, что существует сила, которая опрокинет машину при резком повороте, удержит мотоциклиста на стене и не даст вылиться воде из ведра при вращении.
Откуда появляется эта сила? От чего зависит ее величина?
Для этого вспомним о возникновении центростремительной силы в теле при равномерном вращательном движении:

По третьему закону Ньютона:

и при вращении появляется также центробежная сила.
Вот эта центробежная сила опрокинет резко разворачивающуюся машину, удержит воду в ведре при вращении и т.д.

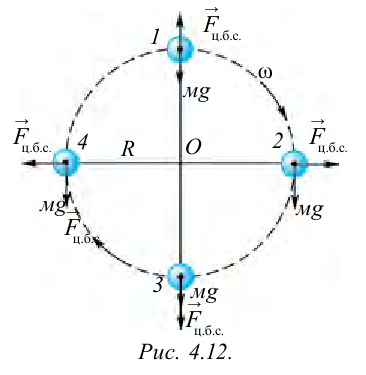
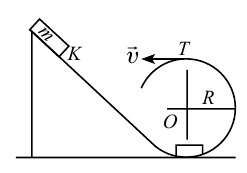
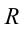
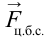
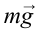
На рисунке 4.12 показаны силы, действующие на тело, которое совершает вращательные движения по кругу радиусом . В точке 1, из-за того что центробежная сила направлена противоположно силе тяжести , вес тела уменьшается:

В точке 3 сила тяжести тела и центробежная сила направлены вниз, т.е. в одном направлении. В этом случае вес тела растет:

Центробежную силу нужно учитывать при вращении тела и в случаях поворота в ходе движения.
Кроме того, на поворотах дороги под воздействием центробежной силы наблюдается отклонение тела от вертикального положения. Чтобы это не приводило к авариям, велосипедисты или мотоциклисты должны двигаться с небольшим уклоном в сторону от центра вращения (рис. 4.13а).
Для уравновешивания этой силы специально для автомобилей на поворотах строят участки дороги с уклоном с одной стороны (рис. 4.13б). Для трамваев и поездов рельсы на поворотах дороги с внешней стороны круга делаются чуть выше.

Заказать решение задач по физике

Пример

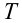
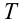
При движении по кругу тело опускается вниз. При каком радиусе круга тело не упадет с точки . Скорость тела в точке равна 30 м/с.
Дано:

Найти:

Решение:

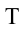
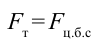
Чтобы тело не упало из точки должно выполняться следующее условие:

Ответ: 90 м.

Кинематика вращательного движения

При криволинейном движении материальной точки ее мгновенная скорость направлена по касательной к траектории в данной точке.
Движение тела (МТ) по окружности является частным случаем криволинейного движения по траектории, лежащей в одной плоскости.

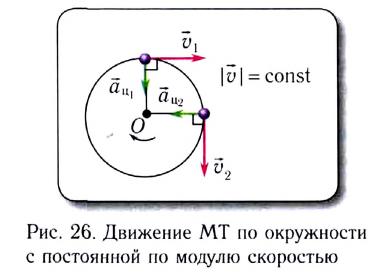
Одним из простейших и широко распространенных видов такого движения является движение по окружности с постоянной по модулю скоростью. Это такое движение, при котором тело (МТ) за любые равные промежутки времени описывает одинаковые дуги. Подчеркнем, что при подобном движении скорость точки постоянно меняет свое направление.

Для описания движения по окружности используется ряд физических величин. Рассмотрим некоторые из них.

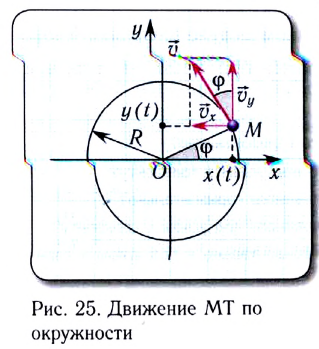
Удобным параметром для определения положения материальной точки М, совершающей движение по окружности радиусом R с центром в начале координат, является угол поворота 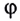(рис. 25)

радиус-вектора точки М. Он отсчитывается от оси Ох против хода часовой стрелки и связан с декартовыми координатами соотношениями:

По теореме Пифагора можно найти, что координаты х и у материальной точки в декартовой системе координат удовлетворяют соотношению

Скорость 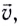с которой материальная точка движется по окружности, называется линейной скоростью (рис. 26).

Проходимый точкой путь s (длина дуги окружности) равен, как и для всякого равномерного движения, произведению модуля скорости v и промежутка времени движения

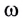
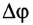
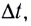
Модуль угловой скорости — это отношение угла поворота к промежутку времени за который этот поворот произошел:

Угловая скорость 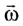со является величиной векторной. Она направлена вдоль оси вращения материальной точки, и ее направление определяется по правилу буравчика, т. е. совпадает с направлением поступательного движения конца буравчика, рукоятка которого вращается в том же направлении, что и тело (рис. 27).

Единица угловой скорости в СИ — радиан в секунду

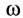
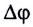
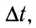
При движении по окружности с постоянной по модулю скоростью v угловая скорость является величиной постоянной и ее модуль равен отношению угла поворота к промежутку времени за который этот поворот произошел:

Здесь n — частота вращения — физическая величина, численно равная числу оборотов N материальной точки в единицу времени:

Единица частоты вращения в СИ — секунда в минус первой степени 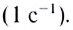Время совершения одного оборота называется периодом вращения Т.

Следовательно,

В СИ период измеряется в секундах (1с).

При совершении полного оборота 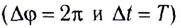период определяется по формуле

Модуль постоянной линейной скорости тела (МТ), движущегося по окружности, вычисляется по формуле

Проекции скорости 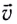(см. рис. 25) с течением времени изменяются по закону

Модуль угловой скорости определяется соотношением

Следовательно, соотношение между модулями линейной и угловой скорости имеет вид

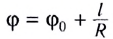
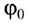
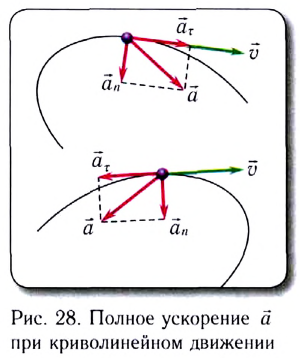
Поскольку (докажите самостоятельно), где — угол поворота радиус-вектора в момент начала движения, то кинематический закон движения МТ но окружности имеет вид

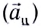
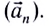
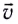
При движении МТ по окружности с постоянной по модулю скоростью ее направление непрерывно изменяется и, следовательно, движение МТ происходит с ускорением, которое называется центростремительным или нормальным Ускорение направлено по радиусу к центру окружности и характеризует быстроту изменения направления скорости с течением (см. рис. 26). Его модуль определяется формулой

Нормальное ускорение 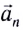в любой момент времени перпендикулярно скорости

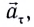
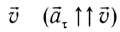
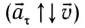
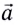
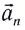
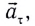
Как и при прямолинейном равноускоренном движении, ускорение называемое тангенциальным (касательным), совпадает с направлением скорости или направлено противоположно ей и поэтому изменяет только модуль скорости. Следовательно, при движении по окружности с непостоянной по модулю скоростью (например, математический маятник) или при любом криволинейном движении полное ускорение 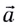можно представить в виде векторной суммы нормального ускорения и тангенциального ускорения направленного по касательной к окружности в данной точке (рис. 28):

Полное ускорение всегда направлено в сторону вогнутости траектории (см. рис. 28).

Модуль полного ускорения находится по теореме Пифагора:

где 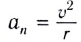– нормальное ускорение, с которым точка двигалась бы по дуге
окружности радиусом r, заменяющей траекторию в окрестности рассматриваемой точки. Этот радиус r называют радиусом кривизны траектории.

Равномерное движение материальной точки по окружности
Колебательное движение
Физический и математический маятники
Пружинные и математические маятники
Поступательное движение
Равномерное и неравномерное движение
Равномерное движение
Неравномерное движение

Источник

Вращательное движение (Движение тела по окружности)

Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:

Если:
перемещение s — угловое перемещение (угол поворота) φ,
скорость u — угловая скорость ω,
ускорение a — угловое ускорение α

Вращательное движение, характеристики

Вращательное движение	Угловая скорость	Угловое ускорение
Равномерное	Постоянная	Равно нулю
Равномерно ускоренное	Изменяется равномерно	Постоянно
Неравномерно ускоренное	Изменяется неравномерно	Переменное

Угол поворота

Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).

Если
φ — угловое перемещение в радианах,
s — длина дуги, заключенной
между сторонами угла поворота,
r — радиус,
то по определению радиана

[
φ = frac{s}{r}
]

Соотношение между единицами угла

[ frac{φ_{рад}}{φ_{°}} = frac{π}{180°} ]

$ 1 enspace рад = 57.3° $

$ 1° = 17.45 enspace мрад $

$ 1´ = 291 enspace мкрад $

Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
(1рад = 1м/ 1м = 1), он не имеет размерности.

Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ω от t).

Поэтому графику можно определить, какой угловой скоростью обладает тело в тот или иной момент времени и на какой угол с момента начала движения оно повернулось (он характеризуется площадью под кривой).

Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость φ от t) и график углового ускорения (зависимость α от t).

Число оборотов

Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.

Единица СИ частоты (или числа оборотов)

[ [n] = [f] = frac{Обороты}{Секунда} = frac{(об)}{с} = frac{1}{c} = Герц ]

В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.

Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.

Если
n — число оборотов,
f — частота,
T — продолжительность одного оборота, период,
φ — угловое перемещение,
N — полное число оборотов,
t — время, продолжительность вращения,
ω — угловая частота,
то

Период

[
T = frac{1}{f} = frac{1}{n}
]

Угловое перемещение

Угловое перемещение равно произведению полного числа оборотов на 2π:

[
φ = 2 π N
]

Угловая скорость

Из формулы для одного оборота следует:

[
ω = 2 π f = frac{2π}{T}
]

Обратите внимание:
• формулы (1)—(6) справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
• вопреки своему названию число оборотов n — это не число, а физическая величина.
• следует различать число оборотов n и полное число оборотов N.

Вращательное движение (движение тела по окружности)	стр. 422

Источник

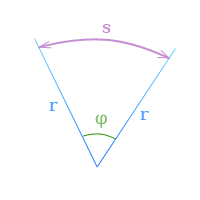
Угловое перемещение (угол поворота) – это угол, на который переместился радиус-вектор при перемещении тела из точки 1 в точку 2.

Δφ=φ-φ₀

Угловое Δφ перемещения при движении тела по окружности.

Единица измерения угла поворота – 1 радиан [1 рад]. Радиан – это угол, опирающийся на дугу окружности, равную ее радиусу.

Длина дуги связана с углом поворота соотношением Δl = RΔφ.

Считая, что в начальный момент времени φ₀=0, угловое перемещение (угол поворота) часто обозначают φ.

Зная угловую скорость и время, за которое был совершен поворот, можно определить угол поворота:

φ=ωt

Обозначения:

Δφ, φ– угловое перемещение (угол поворота)

Δl – длина дуги

R – радиус окружности

ω – угловая скорость

t – время, за которое был совершен поворот

Источник

Для начала давайте выясним, для чего нужно уметь определять полный оборот колеса? Знать полный оборот колеса своего авто нужно по разным причинам. В первую очередь, чтобы выяснить периметр колеса (круга).

Это не что иное, как расстояние, которое оно проходит по плоскости за один оборот. Периметр же зависит от диаметра колеса, и здесь уже возможны варианты.

Многие автолюбители устанавливают на машины колеса большего диаметра, чем рекомендует производитель. Зачем это нужно? Многие рассуждают так: чем больше диаметр, тем выше максимальная скорость и короче время разгона, и наоборот. При этом, колесо имеет значительную инерцию, а двигателю сложней его оборачивать.

Нередко водители устанавливают колеса большего размера и для того, чтобы повысить клиренс и сэкономить на топливе, поскольку чем больше колесо, тем длинней пройденный путь.

Если диаметр колеса отличается от стандартного в большую или меньшую сторону, то данные спидометра будут показывать некорректную скорость движения. Так, при меньшем диаметре она будет больше, чем есть на самом деле.

Еще одной причиной знать полный оборот колеса автомобиля является резонансная частота колебаний. Например, за один оборот колесо прошло 2 метра, сильней всего машину трясет на скорости 90 км/ч или 25 м/ч. При таких исходных данных резонансная частота колебаний составит 12,5 Гц.

Угол поворота

Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).

Если φ — угловое перемещение в радианах, s — длина дуги, заключенной между сторонами угла поворота, r — радиус, то по определению радиана

Соотношение между единицами угла

Обратите внимание:

Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков ( 1 рад = 1 м/ 1 м = 1 ), он не имеет размерности.

Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ω от t). Поэтому графику можно определить, какой угловой скоростью обладает тело в тот или иной момент времени и на какой угол с момента начала движения оно повернулось (он характеризуется площадью под кривой).

Маркировка шин и расшифровка

Ширина шины по маркировке

Ширина шины (Wшины

) указана первым числом в маркировке в миллиметрах:
225
/50 R16