Как найти угловое ускорение автомобиля

Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.

Обозначение угловой скорости: ω (омега).

Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.

С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.

Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:

Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.

Быстрота изменения угла φ (перемещения плоскости П из положения П₁ в положение П₂) – это и есть угловая скорость:

Приняв вектор k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

1. если известно количество оборотов n за единицу времени t:
   
2. если задан угол поворота φ за единицу времени:
   
3. если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:
   

Размерности угловой скорости:

• Количество оборотов за единицу времени [об/мин], [c^-1].
• Угол поворота за единицу времени [рад/с].

Определение угловой скорости

Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.

Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.

Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.

Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.

Другие примеры решения задач >

Угловое ускорение

Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:

Обозначение: ε (Эпсилон)

Единицы измерения углового ускорения: [рад/с²], [с^-2]

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

Расчет углового ускорения

Пример: По заданному значению касательной составляющей полного ускорения a_τ точки B, расположенной на расстоянии r от центра вращения колеса.

Требуется определить величину и направление углового ускорения колеса ε, если a_τ = 10 м/с², r = 50 см.

Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.

Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

ω = 1,5 с^-1 = 9,42 рад/с.

Смотрите также:

• Примеры расчета угловой скорости и ускорения
• Скорости и ускорения точек вращающегося тела

Была ли эта статья полезной?

Физика автомобиля для игр.

Автор: Marco Monster

Введение

Эта статья рассказывает о поведении автомобилей в играх, а именно о физике автомобиля.

Одним из ключевых пунктов в упрощении физики транспортного средства является раздельная обработка продольной и боковой силы. Продольная сила работает в направлении корпуса автомобиля (или же в противоположном направлении). Это сила тяги, тормозящая сила, сила трения и сила сопротивления перемещению (= сопротивление воздуха). Вместе эти силы управляют ускорением или замедлением автомобиля, следовательно, и скоростью автомобиля. Боковые силы позволяют автомобилю поворачиваться. Эти силы вызваны поперечным трением на колесах. Мы также рассмотрим угловой момент скорости автомобиля и момент вращения, вызванные боковыми силами.

Примечание и соглашения

Векторы выделены полужирным текстом, мы будем использовать 2d векторы. Так что примечание a = —b означало бы следующее:

На протяжении все этой статьи я буду предполагать, что задние колеса являются ведущими (для четырех ведущих колес нужно применять необходимую адаптацию)

Все физические величины я буду измерять в единицах СИ (метры, килограммы, Ньютоны и т.д.).

Физика движения по прямой

Сначала рассмотрим автомобиль, двигающийся по прямой линии. Какие силы задействованы здесь? Прежде всего, это сила тяги, то есть сила, которая передается двигателем через задние колеса. Двигатель вращает колеса вперед (на самом деле он передает момент вращения на колеса), колеса «толкают назад» поверхность дороги, в результате поверхность дороги выталкивает колеса в противоположном направлении, то есть вперед. Сейчас мы просто положим, что сила тяги эквивалентна по величине переменной Engineforce, которая управляется непосредственно пользователем.

F_traction = u * Engineforce,
где u — единичный вектор в направлении движения автомобиля.

Если бы это была единственная сила, то автомобиль просто бы ускорился до бесконечной скорости. Ясно, что в реальной жизни дело обстоит совсем не так. Введем силы сопротивления. Первая и обычно наиболее важная — сила воздушного сопротивления, другими словами аэродинамическое сопротивление. Эта сила важна, поскольку она пропорциональна квадрату скорости. Когда мы двигаемся быстро (а какая игра не вовлекает в высокие скорости?) эта сила становится наиболее важной силой сопротивления.

F_drag = — C_drag * v * |v|
где C_drag константа, v — вектор скорости и |v| — модуль вектора v, являющийся длиной вектора v.

Длина вектора скорости обычно известна как скорость. Обратите внимание на различие типа данных: скорость — скаляр, скорость — вектор. Используйте приблизительно следующий код:

Так же, еще есть сопротивление вращения. Это вызвано трением между резиной и дорожной поверхностью, так как колеса прокручиваются, трением на осях и т.д. Мы обозначим это силой, которая пропорциональна скорости, с использованием другой константы.

При низких скоростях трение (F_rr) является основной силой сопротивления, при высоких скоростях F_drag превышает по значению F_rr. Приблизительно при 100 км/час (60 миль в час, 30 м/с) они равны ([Zuvich]). Это означает, что C_rr должен быть равен приблизительно 30-ти C_drag.

Общая продольная сила — это векторная сумма этих трех сил.

Обратите внимание, что если вы двигаетесь по прямой линии, то силы аэродинамического сопротивления и трения будут направлены противоположно силе тяги (F_traction). То есть вы вычитаете силу аэродинамического сопротивления из силы сцепления. И когда автомобиль движется с постоянной скоростью, то силы находятся в равновесии, и F_long равен нулю.

Ускорение (a) автомобиля (в м/с 2 ) определено равнодействующей силой автомобиля (в Ньютонах) и массой автомобиля М (в килограммах) по второму закону Ньютона:

Скорость автомобиля (в метрах в секунду) определяется, как интеграл ускорения через какое-то время (dt). Это звучит слишком сложным, но следующее уравнение поможет нам. Воспользуемся методом Эйлера для численного интегрирования.

v = v + dt * a,
где dt — промежуток времени между предыдущим и текущим вызовами просчета физики.

Позиция автомобиля свою очередь определяется, как интеграл скорости по dt.

Используя эти три силы, мы уже довольно точно можем моделировать ускорение автомобиля. Вместе они также определяют максимальную скорость автомобиля для данной мощности двигателя. То есть, нет необходимости устанавливать максимальную скорость где-нибудь в коде, она автоматически вычисляется из уравнений. Дело в том, что уравнения формируют своего рода цикл отрицательной обратной связи. Если сила тяги (F_traction) превышает все другие силы, то автомобиль ускоряется. Увеличивающаяся скорость, также заставляет увеличиваться силы сопротивления. Равнодействующая сила уменьшается, а следовательно уменьшается и ускорение. В некоторой точке силы сопротивления и сила тяги компенсируют друг друга, и автомобиль достигает своей максимальной скорости для данной мощности двигателя.

На этом графике Ось X обозначает скорость автомобиля в метрах в секунду и значения силы, которая отмечена по Оси Y. Значение силы тяги (темно синий) установлено произвольно, оно не зависит от скорости автомобиля. Трение (пурпурная линия) — линейная функция скорости, и сопротивление (желтая кривая) — квадратичная функция скорости. При низких скоростях трение превышает аэродинамическое сопротивление. При 30 м/с эти две функции пересекаются. При более высоких скоростях аэродинамическое сопротивление является наибольшей силой сопротивления. Сумма из двух сил сопротивления показана светло-синей кривой. При 37 м/с эта кривая пересекает горизонтальную линию силы тяги. Это — максимальная скорость для данной мощности автомобиля (37 м/с = 133 км/час = 83 мили в час).

Формула для вычисления углового ускорения

Угловое ускорение – что это?

Угловое ускорение (varepsilon) – физическая величина, характеризующая изменение угловой скорости при движении тела.

Единица измерения: (lbrackvarepsilonrbrack=frac1<с^2>) или (с^<-2>)

Угловая скорость

Круговым движением точки вокруг оси называют движение, где траектория точки – окружность с центром, который лежит на оси вращения, перпендикулярной плоскости окружности.

Угловая скорость (omega) – векторная физическая величина, характеризующая скорость изменения угла поворота при круговом движении точки или твердого тела.

При движении по окружности (круговом движении) скорость меняет свое направление, значит такое движение не может считаться равномерным, оно ускоренное или равноускоренное (в частных случаях).

Вектор угловой скорости направлен вдоль оси вращения.

Основные формулы для вычисления угловой скорости

Для равномерного вращения (когда за равные отрезки времени тело поворачивается на один и тот же угол):

1. (omega=frac nt) , где (n) – количество оборотов за единицу времени (t) .
2. (omega=fracvarphi t) , где (varphi) – угол поворота, (t) – время, за которое он совершен.
3. (omega=frac<2pi>T) , где (Т) – период обращения (время, за которое тело/точка совершает один оборот).
4. (omega=2pinu) , где (nu) – числом оборотов в единицу времени.

Единица измерения угловой скорости в СИ: (lbrackomegarbrack=frac<рад>с)

Связь между угловой скоростью и нормальным (центростремительным) ускорением

Центростремительное (нормальное) ускорение (a_n) – это составляющая полного ускорения, которая характеризует изменение направления вектора скорости при криволинейном движении. Другим компонентом полного ускорения является тангенциальное ускорение, оно характеризует изменение величины скорости.

Центростремительное ускорение определяется по формуле:

где (V) – скорость движения, (R) – радиус окружности.

Единица измерения в СИ: (lbrack a_nrbrack=frac м<с^2>)

Итак, формула связывающая эти две величины:

Основные формулы для расчета углового ускорения

Значение углового ускорения в определенный момент времени вычисляется как первая производная от угловой скорости или вторая производная от угла поворота по времени.

Угловое ускорение маховика

(varepsilon=fracomega t=frac<2pi n>t) , где (n) – количество оборотов за единицу времени (t) .

Среднее угловое ускорение

Средним угловым ускорением тела называют отношение изменения угловой скорости к отрезку времени, за который оно совершилось.

Тангенциальное ускорение

Тангенциальным (касательным) ускорением (a_tau) называют ту составляющую полного ускорения, которая направлена по касательной к траектории движения в данной точке. Тангенциальное ускорение описывает изменение скорости по модулю при криволинейном движении.

(a_tau=varepsilon r) , где (varepsilon) – угловое ускорение, (r) – радиус кривизны траектории в заданной точке.

Мгновенное угловое ускорение

Мгновенное угловое ускорение (alpha) есть первая производная угловой скорости по времени или вторая производная углового перемещения по времени.

Угловое ускорение колеса автомобиля

Конечно, нельзя, основываясь на школьном курсе физики, обсчитать и описать все поведение автомобиля в меняющихся дорожных условиях. Но некоторые моменты могут быть рассчитаны довольно точно при минимальных упрощениях и допущениях. Просто большинство автолюбителей не задумывается над этим, а если и понимает описанные процессы на интуитивном уровне, то до расчетов у них как правило дело не доходит.

Эта статья — попытка простым языком описать некоторые моменты физики взаимодействия автомобиля с дорогой. А тех, кому на первый взгляд в начале изложении все показалось знакомым и примитивным, стоит все-таки просмотреть статью до конца: здесь есть некоторые неочевидные выводы или, по крайней мере, интересные цифры и ссылки.

Исходные положения и допущения

Приводимые ниже определения вполне сознательно немного упрощены — их нестрогость не повлияет на точность дальнейших рассуждений, но облегчит понимание процессов и закономерностей. Кроме того, будем считать, что в узлах трансмиссии нет трения — оно невелико по сравнению с действующими в них силами. Эти потери будут оценены отдельно.

Радиус колеса R для простоты везде и всегда будем считать равным внешнему радиусу покрышки, допуская, что деформация колеса в зоне контакта с дорогой невелика. При расчете размеров колеса удобно пользоваться шинным калькулятором. Для штатной резины Нивы (175/80R16) радиус колеса R=0,343 м.

Скорость автомобиля V, ускорение a. Еще нам потребуются угловая скорость вращения колес w =V/R и угловое ускорение e =a/R.

Крутящий момент (момент силы) M равен произведению силы F на плечо. В формулах вращательного движения крутящий момент занимает то же место, что и сила при прямолинейном движении. Для нашего случая данного определения вполне достаточно, причем плечо будет равно радиусу колеса R:

Передаточное отношение i в механике определяется, как отношение угловых скоростей входного и выходного валов передачи. Применительно к автомобилю угловые скорости принято считать в оборотах в минуту n:

Здесь действует так называемое «золотое правило механики»: во сколько раз мы проигрываем в скорости и пути, во столько же раз выигрываем в силе, и соотношение крутящих моментов на валах передачи обратно соотношению скоростей:

При нескольких передачах общее передаточное отношение равно произведению передаточных отношений.

Сила трения возникает как реакция при попытке смещения одного тела относительно поверхности другого сдвигающей силой, приложенной параллельно этой поверхности. Рассмотрим процесс трения последовательно — по мере роста сдвигающей силы.

При небольших значениях сдвигающей силы движению тела препятствует сила трения (реакция поверхности). Она равна приложенной силе, но действует в противоположном направлении. В результате тело остается в покое. По мере роста сдвигающей силы будет расти и сила трения. И это будет продолжаться до тех пор, пока сдвигающая сила не превысит порог F_{тр max}, после которого тело начнет двигаться. Величину F_{тр max} определяют через коэффициент трения k_т, равный отношению F_{тр max} к перпендикулярной поверхности прижимающей силе, точнее, равной ей по величине силе реакции N:

Обязательно нужно отметить, что при переходе к скольжению сила трения скачком уменьшается. Это знает каждый автомобилист: тормозной путь с заблокированными колесами больше, чем в случае, когда колеса тормозят, но вращаются со скоростью автомобиля «на пределе». Именно поэтому самый короткий тормозной путь обеспечивает система ABS, контролирующая вращение колес при торможении и не позволяющая им заблокироваться.

Нас будет интересовать только сила трения между колесом и поверхностью дороги. Коэффициент трения сильно зависит от состояния трущихся поверхностей. Для сухого асфальта коэффициент трения доходит до 0,8, а при наличии пленки воды он падает до 0,1. 0,2, на обледеневшей поверхности — еще меньше.

Момент инерции J материальной точки массой m, вращающейся по окружности радиусом r, равен:

Ниже нас будет интересовать только момент инерции колеса J_к. Точно рассчитать момент инерции такого сложного по форме тела затруднительно. На основании приближенного расчета, приведенного в Приложении, будем считать, что момент инерции колеса, складывающийся из моментов инерции покрышки (п) и диска (д), определяется формулой:

Второй закон Ньютона определяет зависимость между приложенной к телу силой F, массой тела m и ускорением a:

Для вращательного движения этот закон имеет вид:

Принцип суперпозиции позволяет отдельно рассматривать и рассчитывать составляющие сложного движения. Применительно к настоящей статье будем рассматривать отдельно поступательное движение автомобиля (включая колеса) и вращательное движение колес. Допущением здесь будет то, что мы будем применять принцип суперпозиции в том числе и при ускоренном движении автомобиля.

Расчет скорости и крутящего момента

Передаточные отношения трансмиссии i_т для ВАЗ-21213/214 с пятиступенчатой коробкой передач, двухступенчатой раздаткой и редукторами 3,9 (точнее, 43/11) сведены в таблицу:

Передача
в раздатке

Чтобы узнать крутящий момент на одном (каждом!) колесе M_к, нужно взять крутящий момент двигателя M_дв, умножить его на значение i_т из таблицы и разделить на количество ведущих колес (для Нивы — на четыре).

Скорость автомобиля V [км/час] по оборотам двигателя n_дв [об/мин] и радиусу колеса R [м] можно рассчитать по формуле:

Коэффициент 0,377 учитывает все остальные параметры, включая размерность. Подчеркну, что допущение об отсутствии деформации колеса на точность расчета скорости не влияет: здесь все определяет длина окружности колеса, которая рассчитывается по радиусу как 2 p R.

Примечание. Участники конференции vasak и Loggy, которых я попросил посмотреть статью до ее публикации, считают, что деформация колеса в зоне контакта влияет на расчет скорости. В частности, vasak считает , что в формулу следует подставлять радиус нагруженного колеса. Решено провести экспериментальную проверку, результаты которой будут опубликованы.

Почему машина едет

Парадоксально, но факт: машину «толкает» дорога. Покажем, почему это так.

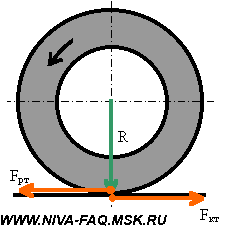
Двигатель создает крутящий момент M_дв. После преобразования трансмиссией этот момент передается на каждое ведущее колесо машины в виде M_к и заставляет колесо вращаться, т. е. создает сдвигающую силу F_кт=M_к/R в точке контакта колеса с дорогой, причем эта сила через колесо приложена к дороге. Поверхность дороги препятствует вращению колеса силой трения F_рт той же величины, но приложенной к колесу и направленной противоположно. Чтобы показать, что силы действуют на разные объекты, точки приложения сил на рисунке условно немного разнесены по вертикали:

Эта сила реакции трения F_рт, умноженная на число ведущих колес, и движет машину. Применительно к Ниве разгоняющим усилием будет величина 4F_рт. Определим эту величину.

Максимальный крутящий момент M_дв=127 Н . м двигатель ВАЗ-21213 развивает при 3200-3400 об/мин (это паспортные данные двигателя 1,7). Значит, на первой передаче в КПП при пониженной в раздатке суммарный крутящий момент на колесах будет равен:

При колесах штатного размера тяговое усилие всех четырех колес составит:

При нормальной передаче в раздатке сила станет в 1,78 раза меньше и будет уменьшаться дальше при повышении передач в КПП. При тех же оборотах двигателя на пятой передаче тяговое усилие составит всего 152 кГ.

В узлах трансмиссии неизбежно существует трение. Согласно «Деталям машин» Д. Н. Решетова КПД закрытой среднескоростной цилиндрической одноступенчатой зубчатой передачи составляет около 98%, конической — около 97%. В коробке передач мы имеет две ступени (от первичного вала к промежуточному и от промежуточного к вторичному). Аналогично — две ступени в раздатке. Все эти передачи — цилиндрические. А в мостах — гипоидные передачи, близкие к коническим. Поэтому КПД трансмиссии будет приблизительно равен:

К этому добавятся еще потери на трение в карданах, ШРУСах и подшипниках. Поэтому из-за трения в узлах трансмиссии реальные значения усилий будут примерно на 10-15% меньше рассчитанных.

Вспомним о силе трения и коэффициенте трения между колесом и поверхностью дороги. Если F_кт=M_к/R меньше максимальной силы трения F_{рт max}, машина будет нормально разгоняться силой 4F_рт. Если же M_к/R>F_{рт max}, то избыток крутящего момента пойдет просто на раскручивание ведущих колес — они начнут буксовать. На заснеженном или обледеневшем асфальте часто можно наблюдать такое у моноприводных машин, иногда они даже не могут тронуться с места. Поскольку у Нивы крутящий момент распределен на четыре колеса, каждая из сил F_рт оказывается вдвое меньше, чем у машин с неполным приводом, а максимальная сила трения примерно такая же. Это дает значительное преимущество Ниве при разгоне на зимней дороге. Но не нужно забывать, что тормозят и моноприводные машины, и Нива — всеми четырьмя колесами.

О силах, противодействующих разгону автомобиля на горизонтальной дороге, можно почитать статьи, скопированные с сайта http://autotheory.by.ru: «Момент сопротивления качению» и «Аэродинамическое сопротивление автомобиля».

Особое внимание обратим на последний фактор — сопротивление воздуха растет пропорционально квадрату скорости и после 100 км/час на горизонтальном участке дороги оно превышает все иные противодействующие движению силы, взятые вместе. В результате именно сопротивление воздуха определяет максимальную скорость автомобиля. Подробнее о максимальной скорости будет сказано в конце статьи.

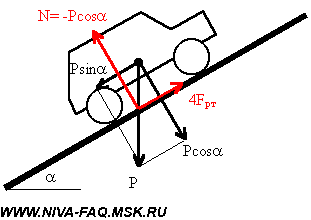
Рассмотрим силы, действующие на автомобиль на наклонной плоскости с углом a к горизонту:

Вес автомобиля P можно разложить на две составляющие. Первая (Psin a ) — скатывающая сила — направлена параллельно поверхности и противодействует подъему автомобиля, ее и должно преодолеть тяговое усилие 4F_рт, чтобы машина взяла подъем. Вторая (Pcos a ), направленная перпендикулярно дороге, прижимает колеса к поверхности и обеспечивает их трение о дорогу и силу реакции N=-Pcos a . На рисунке показаны равнодействующие сил реакции и трения всех четырех колес. Хочу подчеркнуть, что прижимающая сила стала меньше на величину cos a , т. е. по сравнению с горизонтальным участком дороги предельная сила трения стала меньше:

Расчет тягового усилия (максимум 1155 кГ) хорошо согласуется с паспортными данными Нивы о преодолеваемом уклоне 58% (tg30 о =0,58). Разрешенная максимальная масса ВАЗ-21312 равна 1870 кг, sin30 о =0,5, значит, тяговое усилие должно быть не меньше 1870 . 0,5=935 кГ.

Подъем будет взят только в том случае, если сцепление колес с дорогой окажется достаточным для обеспечения такой силы тяги при прижимающем усилии, составляющем 87% веса машины (cos30 o =0,87).

При дальнейшем увеличении крутизны подъема скатывающая сила будет расти, а прижимающая сила и предельная сила трения — уменьшаться.

Важное замечание. Преобразование крутящего момента в трансмиссии сопровождается образованием внутренних реактивных сил в узлах трансмиссии, причем эти силы тем больше, чем бОльший крутящий момент ею передается. Превышение некоторого порога может привести к разрушению элементов трансмиссии, в чем автор имел неосторожность убедиться на собственном опыте.

При попытке штурма довольно крутого подъема в Крылатском машине не хватало сцепления с почвой, и колеса буксовали. Чтобы улучшить сцепление, на колеса передней оси были одеты цепи и включена блокирвка дифференциала в раздатке. Все это привело к существенному возрастанию момента на передних колесах и вывело из строя редуктор переднего моста: подшипник ведущего вала РПМ выдавило вместе с куском стенки картера размером 10х10 см.

Напомню, что при заблокированной раздатке крутящий момент в ней направляется в сторону наибольшего сопротивления вращению (см. статью Привод Нивы), т. е. в сторону переднего моста, где цепи обеспечивали хорошее сцепление с почвой. Цепи — «лесенки», образованные поперечными цепными перемычками с интервалом около 25 см. Поэтому колесо проворачивалось рывками с проскальзыванием в промежутках между цепными перемычками, т. е. возникала ударная нагрузка. Во время одного из рывков реактивная сила, передаваемая подшипником ведущего вала на стенку РПМ, превысила предел прочности стенки.

Разгон и торможение

По второму закону Ньютона суммарная сила F_рт всех ведущих колес разгоняет автомашину массой m_а с ускорением a. Но часть крутящего момента расходуется на раскручивание колес. Рассмотрим этот вопрос подробнее.

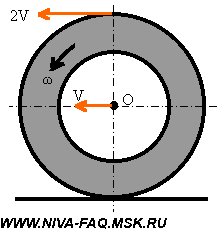
По принципу суперпозиции движение колеса можно рассматривать как сумму двух движений: прямолинейное вместе со всей машиной со скоростью V и вращение вокруг оси:

Если колесо не проскальзывает относительно поверхности (нет заноса), мгновенная скорость в зоне контакта (самой нижней точке колеса) должна быть равна нулю — там прямолинейная скорость движения машины (и оси колеса) V компенсируется такой же по величине, но противоположно направленной скоростью вращения назад. А в самой верхней точке скорость вращения колеса складывается с прямолинейной скоростью и оказывается равной 2V. При таком вращении угловая скорость колеса равна w =V/R.

При равномерном движении ускорение автомобиля a и угловое ускорение колеса e равны нулю. Весь момент 4M_к идет на создание тягового усилия 4F_рт=4M_к/R и преодоление сопротивления движению автомобиля. Но на этапе разгона, когда ускорение a>0, помимо разгона автомобиля массой m_а нужно еще обеспечить колесам с моментом инерции J_к угловое ускорение e =a/R>0 . Поэтому F_рт . R+4J_к . e =m_а . a . R+4J_к . a/R.

Здесь большая часть момента (первое слагаемое) разгоняет автомобиль силой 4F_рт, а второе слагаемое — раскручивает колеса.

Если разделить второй член суммы на первый, мы получим долю момента, приходящуюся на раскручивание колес:

Масса штатного колесного диска 16″ m_д=9,3 кг (данные Nivandy), масса штатной покрышки ВлИ-10 с камерой m_п=12 кг. Тогда:

J_к=0,78m_дR_д 2 +0.85m_пR 2 =0,78 . 9,3 . 0,203 2 +0,85 . 12 . 0,343 2 =0,30+1,20=1,50 кг . м 2 .

Массу Нивы с одним водителем примем равной m_а=1300 кг. Тогда:

Итак, доля крутящего момента, расходуемая на раскрутку колес штатного размера, равна 3,9%. В дальнейшем эта цифра нам пригодится.

Строго говоря, раскрутить нужно не только колеса, но и все вращающиеся элементы трансмиссии. Но доля колес в общем моменте инерции вращающихся деталей на один-два порядка больше, чем у любой другой вращающейся детали трансмиссии. Поэтому их вращением будем пренебрегать.

Процессы при торможении аналогичны разгону, только колеса затормаживаются тормозными колодками, которые создают момент, противодействующий вращению колес. Этот момент тоже делится на две неравные части. На снижение скорости движения автомобиля расходуется та часть момента, за счет которой колеса тормозятся о поверхность дороги. Но часть тормозного момента пойдет на снижение скорости вращения колес. И чем больше момент инерции колес, тем меньшая часть момента пойдет на снижение скорости собственно автомобиля.

Колесо стало больше

Пусть на Ниву вместо колес штатного размера поставили колесо бОльшего диаметра, например, Я-569 (235/75R15). Как это сделать (проставки под шаровые, резка арок и проч.) — не является предметом настоящей статьи. Нас интересует, как изменится динамика машины, и под этим мы будем понимать изменение ускорения при разгоне машины.

Радиус Я-569 0,369 м, т. е. дорожный просвет (клиренс) увеличится на 369-343=26 мм (примерно на дюйм). Посчитаем, чем придется заплатить за это повышение проходимости.

Радиус колеса увеличился относительно штатного размера колеса на 7,6%. Это означает, что при прежнем крутящем моменте на колесе M_к из-за увеличения радиуса R силы F_кт=F_рт=M_к/R будут меньше на 7.6%, т. е. динамика машины будет хуже.

Общая масса автомобиля возросла на величину:

Из-за этого масса автомобиля стала равной m_а=1300+50,8=1350,8 кг, т. е. больше на 50,8/1300=3,9%. Из-за этого при прежней силе F_рт ускорение a=F_рт/m_а уменьшится на те же 3,9%.

А теперь определим влияние момента инерции этих колес. Масса бескамерной покрышки Я-569 20 кг. Масса штампованного диска 15″ от УАЗа около 14 кг (данные Nivandy). Считаем:

J_к=0,78m_дR_д 2 +0,85m_пR 2 =0,78 . 14 . 0,19 2 +0,85 . 20 . 0,369 2 =0,39+2,31=2,70 кг . м 2

Доля крутящего момента, расходуемого на раскрутку колес:

4J_к/m_а . R 2 =4 . 2,70/1350,8 . 0,369 2 =0,059=5,9%.

Вспомним, что при штатных колесах на их раскрутку тратилось 3,9% крутящего момента. Из-за необходимости раскрутить более массивные колеса на разгон автомобиля пойдет часть момента еще на 2,0% меньшая.

Посчитаем общее ухудшение динамики при установке колес большого диаметра:

1,076 . 1,039 . 1,020=1,140.

Итого из-за установки колес Я-569 на дисках от УАЗа динамика ухудшается на 14,0%.

Нива была создана как компромисс между шоссейным автомобилем и вездеходом. Она имеет вполне приличную динамику и скорость, позволяющую ей ехать по шоссе, практически ни в чем не уступая другим легковым автомобилям. И вместе с тем у Нивы вполне приличная проходимость вне асфальта. Колеса большого диаметра нарушают этот компромисс в сторону внедорожности. Впрочем, крутизна преодолеваемого подъема также уменьшится.

Возникает вопрос: как сохранить динамику?

В формуле, связывающей крутящий момент, радиус колеса и силу, мы пока изменили только один член — радиус. Чтобы сохранить динамику прежней, нужно увеличить крутящий момент на колесах. Это означает, что нужно либо поставить двигатель с бОльшим крутящим моментом (дорого, да и выбор мал), либо переделать трансмиссию так, чтобы при том же моменте двигателя момент на колесах стал больше, т. е. изменить ее передаточное отношение.

КПП для Нивы выпускается только с одним набором передаточных отношений, раздатка — тоже. Остается одновременная замена редукторов переднего и заднего моста, и этот выбор не так уж и мал. Производятся серийно и есть в обычных магазинах запчастей передние и задние редукторы с передаточными отношениями 3,9, 4,1 и 4,3 (подробности — в соответствующих статьях FAQ: здесь и здесь). Ранее выпускались редукторы 2102 (передаточное отношение 4,44). Существуют тюнинговые главные пары редукторов с передаточными отношениями 5,25 и др.

Штатно в 21213/214 ставятся редукторы с передаточным отношением 3,9 (точнее, 43/11=3,91). Если поменять их на редукторы 4,1, момент на колесах вырастет на 4,9%, а если на 4,3 — то на 10%. Но даже в последнем случае при резине Я-569 динамика все-таки будет хуже, чем на резине штатного размера.

Немного улучшить положение могут легкосплавные диски с меньшей массой. Но выигрыш не так велик, как хотелось бы. Для иллюстрации по той же методике пересчитаем изменение динамики (относительно штатных колес) для Я-569 на легкосплавных дисках «Эллада» с массой 5,2 кг.

Радиус покрышки тот же, что и в предыдущем расчете, поэтому F_кт=F_рт=M_к/R будут меньше на 7.6%, чем при штатных колесах.

Общая масса машины (опять относительно штатных колес) увеличилась на:

Из-за этого при прежней силе F_рт ускорение a уменьшится на 15,6/1300=1,2%.

Момент инерции колеса:

J_к=0,78m_дR_д 2 +0,85m_пR 2 =0,78 . 5,2 . 0,19 2 +0,85 . 20 . 0,369 2 =0,15+2,31=2,46 кг . м 2 .

Доля крутящего момента, расходуемого на раскрутку колес:

4J_к/m_а . R 2 =4 . 2,46/1315,6 . 0,369 2 =0,055=5,5%.

Относительно 3,9% для штатных колес проигрыш 1,6%.

Общее ухудшение динамики:

1,076 . 1,012 . 1,016=1,106.

Следовательно, при Я-569 на легкосплавных дисках динамика ухудшится на 10,6%.

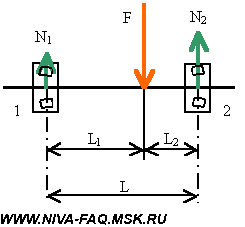
Колеса 14″, вылет и плечо обката

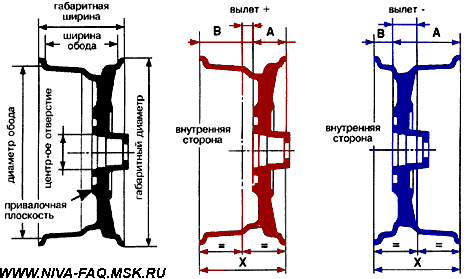
Есть такие любители уродовать Ниву — они ставят на на нее волговские колеса 14 дюймов с нулевым вылетом. Клиренс, разумеется, будет меньше, но динамика машины вырастет: при меньшем радиусе R и прежнем моменте M_к сила F_кт=F_рт=M_к/R станет больше. К тому же уменьшится масса и момент инерции колес. Но в этом параграфе речь будет идти не о динамике, а о влиянии вылета колесных дисков на нагрузку ступичных подшипников и плечо обката.

Взаимодействие ступицы с колесом удобно представить силой, лежащей в плоскости симметрии колеса (т. е. в средней плоскости колеса). Вылет — расстояние между этой плоскостью симметрии и посадочной плоскостью, где диск крепится к ступице. Иллюстрирующий это рисунок взят с сайта http://www.protcar.com:

У штатного диска Нивы положительный вылет колеса, равный 58 мм (ЕТ58), он соответствует среднему рисунку.

Сначала заметим, что устойчивость машины на дороге в значительной степени определяется величиной отношения ширины колеи к колесной базе (расстоянию между осями). Колесные диски с нулевым вылетом расширят колею на 58 . 2= 116 мм, что заметно ухудшит устойчивость Нивы.

А теперь разберемся с нагрузкой на ступичные подшипники. Мнение, что из-за слишком малого вылета волговских дисков подшипники приходится менять буквально на каждом ТО, в конференции существует давно. Обоснуем это утверждение.

Вспомним, как устроена ступица переднего колеса Нивы (посмотреть это можно в иллюстрированном альбоме). Нагрузку F, действующую в плоскости симметрии колеса, принимают на себя два упорных роликовых подшипника, в которых возникают силы реакции N₁ и N₂. Эти силы и определяют степень нагруженности подшипников:

Нагрузка F — это равнодействующая всех сил, действующих на колесо в продольной плоскости, т. е. не только вес машины, приходящийся на колесо, но и всевозможные удары при наезде на препятствия, кочки и выбоины, причем эти удары могут создавать нагрузку, на порядок большую, чем вес.

В зависимости от точки приложения силы F относительно подшипников силы N₁ и N₂ меняются. В принципе, подобный объект — балка на двух опорах — является предметом курса «Сопротивление материалов», но вывод расчетных формул очень прост. Достаточно применить познания из курса элементарной физики и рассматривать балку как рычаг.

Принимаем за точку опоры рычага подшипник 1. Поскольку рычаг неподвижен, моменты сил F и N₂ должны уравновешивать друг друга:

Можно составить такое же уравнение для определения N₁, но удобнее использовать тот факт, что сила F в точности уравновешивается реактивными силами (результат будет тот же):

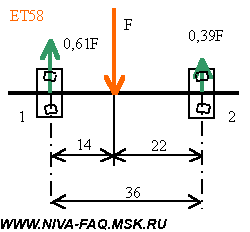
С реальных запчастей были сняты размеры. Оказалось, что расстояние между подшипниками (по серединам) составляет 36 мм, а при штатном диске точка приложения силы F оказывается на 4 мм глубже середины расстояния между подшипниками. При штатном диске нагрузка делится между подшипниками следующим образом:

Для штампованных стальных (ЕТ48) и легкосплавных (ЕТ40) дисков Шеви-Нивы:

Для легкосплавных дисков «Нива» (ВСМПО, ЕТ28) и волговских дисков (ЕТ0):

Обратите внимание, что при вылетах меньше 36 мм нагрузка внутреннего (левого на рисунках) подшипника меняет знак, а на внешнем (правом) становится больше приложенной силы F.

Получается, что при дисках с нулевым вылетом нагрузка внешнего подшипника ступицы в 5,1 раза больше, чем при штатном диске. Если за отправную точку взять нагрузку внутреннего подшипника при штатном диске, это превышение составит 3,3 раза. Отсюда и скорый выход из строя внешнего ступичного подшипника.

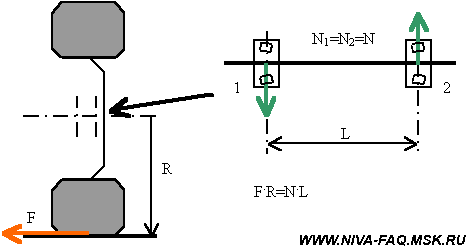
При поворотах автомобиля возникает боковое усилие на колесах, которое порождает крутящий момент в вертикальной плоскости, проходящей через ось оси ступицы. Момент уравновешивается парой сил реакции на ступичных подшипниках:

Величина этих сил определяется соотношением между радиусом колеса R и расстоянием между подшипниками L и от значения вылета не зависит:

F . R=N . L; N=F . R/L.

Для штатного размера колес отношение R/L=343/36=9,53, т. е. нагрузка подшипников в повороте примерно в 10 раз больше бокового усилия на колесе. На крутых поворотах это тонны.

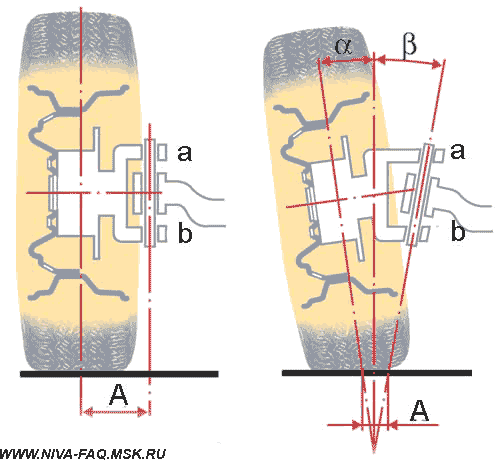
А теперь вспомним, что такое плечо обката. Очень хорошо это иллюстрирует рисунок с сайта журнала «За рулем»:

Центр зоны контакта колеса с дорогой (левые оси на рисунках) смещен относительно оси поворота колеса (правые оси, проходящие через шаровые опоры a и b) на величину плеча обката А. Поэтому для поворота колеса нужно преодолеть момент силы трения M_т=F_т . A. При увеличении плеча обката пропорционально будет расти и этот момент.

Вот данные Сергея Мишина о плече обката Нивы и Шеви-Нивы: