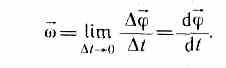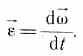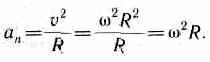Как найти угловое ускорение через ускорение точки - Сайт, где вы сможете решить свои вопросы

Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.

Обозначение угловой скорости: ω (омега).

Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.

С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.

Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:

Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.

Быстрота изменения угла φ (перемещения плоскости П из положения П₁ в положение П₂) – это и есть угловая скорость:

Приняв вектор k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

если известно количество оборотов n за единицу времени t:
если задан угол поворота φ за единицу времени:
если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:

Размерности угловой скорости:

Количество оборотов за единицу времени [об/мин], [c^-1].
Угол поворота за единицу времени [рад/с].

Определение угловой скорости

Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.

Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.

Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.

Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.

Другие примеры решения задач >

Угловое ускорение

Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:

Обозначение: ε (Эпсилон)

Единицы измерения углового ускорения: [рад/с²], [с^-2]

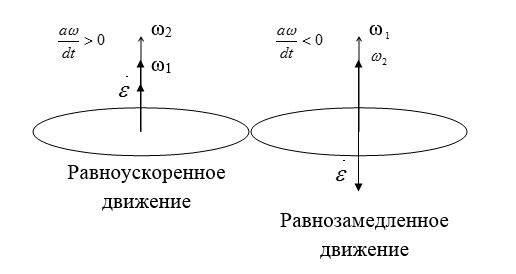
Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

Расчет углового ускорения

Пример: По заданному значению касательной составляющей полного ускорения a_τ точки B, расположенной на расстоянии r от центра вращения колеса.

Требуется определить величину и направление углового ускорения колеса ε, если a_τ = 10 м/с², r = 50 см.

Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.

Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

ω = 1,5 с^-1 = 9,42 рад/с.

Смотрите также:

Примеры расчета угловой скорости и ускорения
Скорости и ускорения точек вращающегося тела

Источник

Угловое ускорение – что это?

Угловое ускорение (varepsilon) – физическая величина, характеризующая изменение угловой скорости при движении тела.

Единица измерения: (lbrackvarepsilonrbrack=frac1{с^2}) или (с^{-2})

Угловая скорость

Круговым движением точки вокруг оси называют движение, где траектория точки – окружность с центром, который лежит на оси вращения, перпендикулярной плоскости окружности.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Угловая скорость (omega) – векторная физическая величина, характеризующая скорость изменения угла поворота при круговом движении точки или твердого тела.

При движении по окружности (круговом движении) скорость меняет свое направление, значит такое движение не может считаться равномерным, оно ускоренное или равноускоренное (в частных случаях).

Вектор угловой скорости направлен вдоль оси вращения.

Основные формулы для вычисления угловой скорости

Для равномерного вращения (когда за равные отрезки времени тело поворачивается на один и тот же угол):

(omega=frac nt), где (n) – количество оборотов за единицу времени (t).
(omega=fracvarphi t), где (varphi) – угол поворота, (t) – время, за которое он совершен.
(omega=frac{2pi}T), где (Т) – период обращения (время, за которое тело/точка совершает один оборот).
(omega=2pinu), где (nu) – числом оборотов в единицу времени.

Единица измерения угловой скорости в СИ: (lbrackomegarbrack=frac{рад}с)

Связь между угловой скоростью и нормальным (центростремительным) ускорением

Центростремительное (нормальное) ускорение (a_n) – это составляющая полного ускорения, которая характеризует изменение направления вектора скорости при криволинейном движении. Другим компонентом полного ускорения является тангенциальное ускорение, оно характеризует изменение величины скорости.

Центростремительное ускорение определяется по формуле:

(a_n=frac{V^2}R),

где (V) – скорость движения, (R) – радиус окружности.

Единица измерения в СИ: (lbrack a_nrbrack=frac м{с^2})

Итак, формула связывающая эти две величины:

(a_n=omega^2R)

Основные формулы для расчета углового ускорения

Значение углового ускорения в определенный момент времени вычисляется как первая производная от угловой скорости или вторая производная от угла поворота по времени.

(varepsilon=lim_{triangle trightarrow0}frac{triangleomega}{triangle t}=frac{domega}{dt}=frac{d^2varphi}{dt}=overset.omega=overset{..}varphi)

Угловое ускорение маховика

(varepsilon=fracomega t=frac{2pi n}t), где (n) – количество оборотов за единицу времени (t).

Среднее угловое ускорение

Средним угловым ускорением тела называют отношение изменения угловой скорости к отрезку времени, за который оно совершилось.

(leftlanglevarepsilonrightrangle=frac{triangleomega}{triangle t})

Тангенциальное ускорение

Тангенциальным (касательным) ускорением (a_tau) называют ту составляющую полного ускорения, которая направлена по касательной к траектории движения в данной точке. Тангенциальное ускорение описывает изменение скорости по модулю при криволинейном движении.

(a_tau=varepsilon r), где (varepsilon) – угловое ускорение, (r) – радиус кривизны траектории в заданной точке.

Мгновенное угловое ускорение

Мгновенное угловое ускорение (alpha) есть первая производная угловой скорости по времени или вторая производная углового перемещения по времени.

(alpha=tg(varepsilon)=frac{;domega}{dt}=frac{d^2phi}{dt^2})

Источник

Нам уже известно понятие ускорения тела. Так именуют величину, характеризующую изменение его скорости. Также нам известно понятие угловой скорости. Для характеристики этого изменения используют величину, называемую угловым ускорением. Рассмотрим его особенности и использование.

Определения углового ускорения тела. Среднее и мгновенное угловое ускорение

Определение 1

Угловым ускорением называется кинематическая величина, характеризующая изменение угловой скорости с течением времени. Обозначают его обычно греческой буквой ε.

Слово «кинематическая» означает, что движение рассматривается без учёта действия на тело сил, независимо от них. Обозначим промежуток времени как Δt. Изменение угловой скорости за этот промежуток обозначим как Δω. Отношение Δω/Δt называют средним угловым ускорением. Среднее угловое ускорение равно угловой скорости за определённый интервал времени. Однако, как она себя вела, например, в самом его начале, середине или конце ничего не скажешь.

Если мы будем выбранный нами интервал времени постоянно уменьшать, изменение скорости получится описывать всё более и более точно. В идеале, чтобы Δt вообще стремился к нулю:

ε = lim (Δt→0)(Δω/Δt) = dω/dt = d²φ /d²t

Так мы перешли ко второму определению углового ускорения, только оно уже не среднее, а, как говорят, мгновенное.

Определение 2

Угловое ускорение тела есть первая производная его угловой скорости по времени или вторая производная его углового перемещения. Ещё раз перепишем формулы, но уже в качестве официального определения.

Угловое ускорение тела равно:

ε = dω/dt = d²φ /d²t

Размерностью величины будет 1/T² (1/время²). Измеряют его обычно в радианах на секунду в квадрате, рад/с² или 1/с² (с^-2).

Обязательно следует отметить, что ε может рассматриваться, в качестве вектора, т. е. ему приписывается направление. Хотя в отличие от направления обычной скорости, воспринимается это несколько сложнее, ведь наглядность отсутствует.

Угловое ускорение через радиус выражается как a = ε*R, где a – ускорение, направленное по касательной траектории.

Определения

Если тело вращается всё быстрее и быстрее, то это значит, что модуль его угловой скорости с течением времени увеличивается. Такое вращение называют ускоренным. При нём вектора угловых скорости и ускорения имеют одно и то же направление.

Если тело вращается всё медленнее и медленнее, то это значит, что модуль его угловой скорости со временем уменьшается. Такое вращение называют замедленным. При нём вектора угловой скорости и углового ускорения направлены противоположно.

Угловое ускорение и формула закона движения при равнопеременном вращении

Определение 5

Равнопеременным вращением называют вращение, при котором угловое ускорение не меняется с течением времени, т. е. является константой [(ε=const)].

Выведем его закон. Пусть в начальный момент времени (t=0) равен φ₀, а его начальная скорость ω_0.

Из определений выше следует

ε = dω/dt следует, что dω = ε dt.

Чтобы найти угловую скорость нам нужно найти первообразную от этого выражения по времени. Получаем

ω = εt + С1.

С1 – некоторая постоянная. В нашем случае, по начальным условиям, она равна начальной угловой скорости тела, ω₀.

Поэтому

ω = εt + ω₀

Напомним, что мгновенная угловая скорость равна: ω = dφ /dt

Отсюда

dφ /dt = εt + ω₀

φ = (εt + ω₀)dt

Находим первообразную по времени

φ = εt²/2 + ω₀t + С2

С2 – некоторая постоянная. Исходя из начальных условий она равна φ₀. Приходим к выражению

φ = εt²/2 + ω₀t + φ₀

Это и есть закон равнопеременного вращательного движения.

Нет времени решать самому?

Наши эксперты помогут!

Примеры

Пример. 1

Колесо стало вращаться с постоянным угловым ускорением и, спустя 10 оборотов от начала вращения, получило скорость 20 рад/с. Чему равно угловое ускорение?

Решение:

Применим к вращению колеса формулу равнопеременного движения, исходя из того, что его начальная угловая скорость ω₀была равна нулю. Формулы, с которыми нам придётся иметь дело:

φ = εt²/2; ω = εt; φ = 2πN

Из первой формулы выражаем ε

ε = (φ/t²)

Из второй формулы выражаем время

t = ω/ε

Подставляем его в формулу выше.

ε = (2*φ)/(ω/ε)² = ( 2* φ * ε²)/ω²

Проводим необходимые сокращения и приходим к формуле углового ускорения:

ε = ω²/2φ

Вместо угла φ подставляем в выражение третью формулу

ε = ω²/2*2πN = ω²/4πN

После подстановки численных значений получим ε = 3,2 рад/c²

Ответ: Угловое ускорение колеса равно 3,2 рад/c².

Пример. 2

Тело вокруг собственной оси вращается по следующему закону:

φ = 10 + 20*t – 2*t²

Нужно найти угловое и полное ускорение точки, находящейся в 109 см. от оси вращения через 4 секунды после начала движения.

Решение:

Формулы, с которыми нам придётся иметь дело:

[a=sqrt{a_{n}^{2}+a_{T}^{2}}]

A_t = dv/dt = Rε

a_n = v²/R = ω²R

Если известен закон движения, то ω и ε не составляет труда выразить через производные. Сначала находим ω.

ω = d(10 + 20t – 2t²)/dt = 20 – 4t

Ускорение находим, дифференцируя последнее полученное выражение:

ε = d(20 — 4t)/dt = (- 4 )рад/с²

Смотрим на формулу нахождения полного a и выражение ε через радиус, после чего делаем соответствующие подстановки.

[a=sqrt{R^{2} varepsilon^{2}+omega^{4} R^{2}}]

После численных подстановок выясняем, что a точки равно 1,65 м/с².

Ответ: Угловое ускорение точки равно (-4) рад/с², а полное её ускорение – 1,65 м/с².

Источник

Угловое ускорение
${boldsymbol varepsilon }={frac {{mathrm d}{boldsymbol omega }}{{mathrm d}t}}={boldsymbol {dot omega }}$
Единицы измерения
СИ	рад/с²
СГС	рад/с²
Примечания
псевдовектор

Угловое ускорение — псевдовекторная физическая величина, равная первой производной от псевдовектора угловой скорости по времени

${displaystyle {vec {varepsilon }}={frac {d{vec {omega }}}{dt}}.}$

Угловое ускорение характеризует интенсивность изменения модуля и направления угловой скорости при движении твёрдого тела.

Как приходят к понятию углового ускорения: ускорение точки твёрдого тела при свободном движении[править | править код]

К понятию углового ускорения можно прийти, рассматривая вычисление ускорения точки твёрдого тела, совершающего свободное движение. Скорость точки тела при свободном движении, согласно формуле Эйлера, равна

${displaystyle {vec {v}}_{B}={vec {v}}_{A}+{vec {omega }}times {vec {AB}},}$

где ${vec v}_{A}$ — скорость точки тела , принятой в качестве полюса; — псевдовектор угловой скорости тела; — вектор, выпущенный из полюса в точку, скорость которой вычисляется. Дифференцируя по времени данное выражение и используя формулу Ривальса^[1], имеем

${displaystyle {vec {a_{B}}}={vec {a_{A}}}+{vec {varepsilon }}times {vec {AB}}+{vec {omega }}times ({vec {omega }}times {vec {AB}})}$

${displaystyle {vec {a_{B}}}={vec {a_{A}}}+{vec {a_{BA}^{rot}}}+{vec {a_{BA}^{axis}}},}$

где ${vec a}_{A}$ — ускорение полюса ; ${vec varepsilon }={frac {d{vec omega }}{dt}}$ — псевдовектор углового ускорения. Составляющая ускорения точки , вычисляемая через угловое ускорение называется вращательным ускорением точки вокруг полюса

${displaystyle {vec {a}}_{BA}^{,rot}={vec {varepsilon }}times {vec {AB}}.}$

Последнее слагаемое в полученной формуле, зависящее от угловой скорости, называют осестремительным ускорением ускорением точки вокруг полюса

${displaystyle {vec {a}}_{BA}^{,axis}={vec {omega }}times left({vec {omega }}times {vec {AB}}right).}$

Геометрический смысл псевдовектора углового ускорения[править | править код]

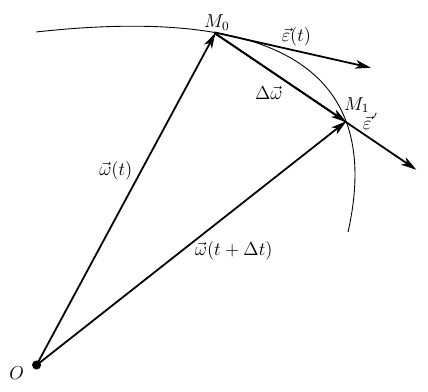
Псевдовектор направлен по касательной к годографу угловой скорости. Действительно, рассмотрим два значения вектора угловой скорости, в момент времени и в момент времени . Оценим изменение угловой скорости за рассматриваемый промежуток времени Delta t

Отнесём это изменение к тому промежутку времени, за которое оно произошло

${displaystyle {frac {Delta {vec {omega }}}{Delta t}}={vec {varepsilon }}^{,,'}.}$

Получившийся вектор называется вектором среднего углового ускорения. Он занимает положение секущей, пересекая годограф вектора угловой скорости в точках $M_{0}$ и $M_{1}$ . Перейдём к пределу при

${displaystyle lim _{Delta tto 0}{frac {Delta {vec {omega }}}{Delta t}}={frac {d{vec {omega }}}{dt}}={vec {varepsilon }}.}$

Вектор среднего углового ускорения перейдёт в вектор мгновенного углового ускорения и займёт положение касательной в точке $M_{0}$ к годографу угловой скорости.

Выражение вектора углового ускорения через параметры конечного поворота[править | править код]

При рассмотрении вращения тела через параметры конечного поворота, вектор углового ускорения можно расписать формулой

${displaystyle {vec {varepsilon }}=left(1-cos varphi right)left({vec {u}}times {frac {d^{2}{vec {u}}}{dt^{2}}}right)+{dot {varphi }}left(1+cos varphi right){frac {d{vec {u}}}{dt}}+{dot {varphi }}sin varphi left({vec {u}}times {frac {d{vec {u}}}{dt}}right)+sin varphi ,{frac {d^{2}{vec {u}}}{dt^{2}}}+{ddot {varphi }},{vec {u}},}$

где vec u — орт, задающий направление оси поворота; varphi — угол, на который совершается поворот вокруг оси vec u .

Угловое ускорение при вращении тела вокруг неподвижной оси[править | править код]

При вращении тела вокруг неподвижной оси, проходящей через неподвижные точки тела $O_{1}$ и $O_{2}$ , производные орта оси вращения равны нулю

${displaystyle {frac {d{vec {u}}}{dt}}={frac {d^{2}{vec {u}}}{dt^{2}}}=0.}$

В этом случае вектор углового ускорения определяется тривиально через вторую производную угла поворота

или

где — алгебраическая величина углового ускорения. В этом случае псевдовектор углового ускорения, как и угловая скорость, направлен вдоль оси вращения тела. Если первая и вторая производные угла поворота имеют одинаковый знак

(),

то вектор углового ускорения и вектор угловой скорости совпадают по направлению (тело вращается ускоренно). В противном случае, при , векторы угловой скорости и углового ускорения направлены в противоположные стороны (тело вращается замедленно).

В курсе теоретической механики традиционным является подход, при котором понятие угловой скорости и углового ускорения вводится при рассмотрении вращения тела вокруг неподвижной оси. При этом в качестве закона движения рассматривается зависимость от времени угла поворота тела

В этом случае закон движения точки тела может быть выражен естественным способом, как длина дуги окружности, пройденная точкой при повороте тела от некоторого начального положения ${displaystyle varphi _{0}=varphi (t_{0}).}$

${displaystyle s(t)=R,left(varphi (t)-varphi _{0}right),}$

где — расстояние от точки до оси вращения (радиус окружности, по которой движется точка). Дифференцируя последнее соотношение по времени получаем алгебраическую скорость точки

${displaystyle {frac {ds}{dt}}=v_{tau }=R,{frac {dvarphi }{dt}}=omega ,R,}$

где ${displaystyle omega ={frac {dvarphi }{dt}}}$ — алгебраическая величина угловой скорости. Ускорение точки тела при вращении может быть представлено как геометрическая сумма тангенциального и нормального ускорения

${displaystyle {vec {a}}_{M}={vec {a}}_{M}^{,tau }+{vec {a}}_{M}^{,n},}$

причём тангенциальное ускорение получается как производная от алгебраической скорости точки

${displaystyle a_{M}^{,tau }={frac {dv_{tau }}{dt}}={frac {d}{dt}}left(omega ,Rright)=R,{frac {domega }{dt}}=varepsilon ,R,}$

где ${displaystyle varepsilon ={frac {domega }{dt}}={frac {d^{2}varphi }{dt^{2}}}}$ — алгебраическая величина углового ускорения. Нормальное ускорение точки тела может быть вычислено по формулам

${displaystyle a_{M}^{,n}={frac {v_{tau }^{2}}{R}}=omega ^{2},R.}$

Выражение псевдовектора углового ускорения через тензор поворота тела[править | править код]

Если поворот твёрдого тела задан тензором ранга (линейным оператором), выраженным, например, через параметры конечного поворота

${displaystyle B_{,m}^{,p}=left(1-cos varphi right),u^{,p},u_{,m}+cos varphi ,delta _{,m}^{,p}+sin varphi ,g^{,pl},epsilon _{,lkm},u^{,k},}$

где ${displaystyle delta _{,m}^{,p}}$ — символ Кронекера; ${displaystyle epsilon _{,lkj}}$ — тензор Леви-Чивиты, то, псевдовектор углового ускорения может быть вычислен по формуле

${displaystyle varepsilon ^{,i}={frac {1}{2}},epsilon ^{ikl},g_{,lp},left(B_{,m}^{',p},{ddot {B}}_{,k}^{,m}+{dot {B}}_{,m}^{',p},{dot {B}}_{,k}^{,m}right),}$

где ${displaystyle B_{,m}^{',p}}$ — тензор обратного преобразования, равный

${displaystyle B_{,m}^{',p}=left(1-cos varphi right),u^{,p},u_{,m}+cos varphi ,delta _{,m}^{,p}-sin varphi ,g^{,pl},epsilon _{,lkm},u^{,k}.}$

Примечания[править | править код]

↑ В.И. Дронг, В.В. Дубинин, М.М. Ильин и др.; под ред. К.С. Колесникова, В.В. Дубинина. Курс теоретической механики: учебник для вузов. — 2017. — С. 101, 111. — 580 с. — ISBN 978-5-7038-4568-4.

Литература[править | править код]

Тарг С. М. Краткий курс теоретической механики — 10-е изд., перераб. и доп. — М.: Высш. шк., 1986 — 416 С.
Погорелов Д. Ю. Введение в моделирование динамики систем тел: Учебное пособие. — Брянск: БГТУ, 1997. — 197 С.

Источник

Рассмотрим
твердое тело, которое вращается
вокруг неподвижной оси. Тогда отдельные
точки этого тела будут описывать
окружности разных радиусов, центры
которых лежат на оси вращения. Пусть
некоторая точка движется по окружности
радиуса R
(рис.6).
Ее положение через промежуток времени
t
зададим
углом .
Элементарные (бесконечно малые) углы
поворота рассматривают как векторы.
Модуль вектора d
равен
углу поворота, а его направление совпадает
с направлением поступательного
движения острия винта, головка которого
вращается в направлении движения
точки по окружности, т. е. подчиняется
правилу
правого, винта (рис.6).
Векторы, направления которых связываются
с направлением вращения, называются
псевдовекторами
или
аксиальными
векторами. Эти
векторы не имеют определенных точек
приложения: они могут откладываться
из любой точки оси вращения.

Угловой
скоростью называется
векторная величина, равная первой
производной угла поворота тела по
времени:

Вектор
«в направлен вдоль оси вращения по
правилу правого винта, т. е. так же, как
и вектор d
(рис. 7). Размерность угловой скорости
dim=T^-1,
a .
ее единица — радиан в секунду (рад/с).

Линейная скорость
точки (см. рис. 6)

В векторном виде
формулу для линейной скорости можно
написать как векторное произведение:

При
этом модуль векторного произведения,
по определению, равен

,
а
направление совпадает с
направлением
поступательного движения правого винта
при его вращении от 
к R.

Если
=const,
то
вращение равномерное и его можно
характеризовать периодом
вращения Т
—
временем, за которое точка совершает
один полный оборот, т. е. поворачивается
на угол 2.
Так как промежутку времени t=T
соответствует =2,
то =
2/Т,
откуда

Число
полных оборотов, совершаемых телом при
равномерном его движении по окружности,
в единицу времени называется частотой
вращения:

Угловым
ускорением называется
векторная величина, равная первой
производной угловой скорости по
времени:

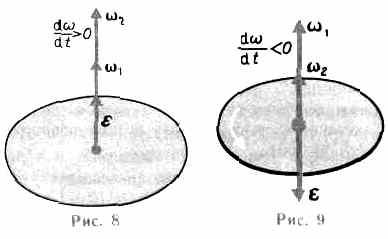
При вращении тела
вокруг неподвижной оси вектор углового
ускорения направлен вдоль оси вращения
в сторону вектора элементарного
приращения угловой скорости. При
ускоренном движении вектор

 сонаправлен
вектору 
(рис.8),
при замедленном.— противонаправлен
ему (рис. 9).

Тангенциальная
составляющая ускорения

Нормальная
составляющая ускорения

Таким
образом, связь между линейными (длина
пути s,
пройденного
точкой по дуге окружности радиуса R,
линейная
скорость v,
тангенциальное
ускорение а_,
нормальное ускорение а_n)
и угловыми величинами (угол поворота
,
угловая скорость (о, угловое ускорение
)
выражается следующими формулами:

В
случае равнопеременного движения точки
по окружности (=const)

где
₀
— начальная угловая скорость.

Контрольные
вопросы

• Что
называется материальной точкой? Почему
в механике вводят такую модель?

• Что
такое система отсчета?

• Что
такое вектор перемещения? Всегда ли
модуль вектора перемещения равен отрезку
пути,

пройденному точкой?

• Какое
движение называется поступательным?
вращательным?

• Дать
определения векторов средней скорости
и среднего ускорения, мгновенной
скорости

и мгновенного
ускорения. Каковы их направления?

• Что
характеризует тангенциальная
составляющая ускорения? нормальная
составляющая

ускорения? Каковы
их модули?

• Возможны
ли движения, при которых отсутствует
нормальное ускорение? тангенциальное

ускорение? Приведите
примеры.

• Что
называется угловой скоростью? угловым
ускорением? Как определяются их
направления?

• Какова
связь между линейными и угловыми
величинами?

Задачи

1.1.
Зависимость
пройденного телом пути от времени
задается уравнением s
= A+Вt+Сt²+Dt³(С
= 0,1 м/с²,
D
= 0,03 м/с³).
Определить: 1) через какое время после
начала движения ускорение а тела будет
равно 2 м/с²;
2) среднее ускорение <а>
тела за этот промежуток времени. [ 1) 10
с; 2) 1,1 м/с²]

1.2.
Пренебрегая сопротивлением воздуха,
определить угол, под которым тело брошено
к горизонту, если максимальная высота
подъема тела равна 1/4 дальности его
полета. [45°]

1.3.
Колесо
радиуса R
=
0,1 м вращается так, что зависимость
угловой скорости от времени задается
уравнением 
= 2At+5Вt⁴
(A=2
рад/с²
и B=1
рад/с⁵).
Определить полное ускорение точек обода
колеса через t=1
с после начала вращения и число оборотов,
сделанных колесом за это время. [а =
8,5 м/с²;
N
= 0,48]

1.4.
Нормальное ускорение точки, движущейся
по окружности радиуса r=4
м,
задается уравнением а_n=А+-Bt+Ct²
(A=1
м/с²,
В=6
м/с³,
С=3
м/с⁴).
Определить: 1) тангенциальное ускорение
точки; 2) путь, пройденный точкой за время
t₁=5
с после начала движения; 3) полное
ускорение для момента времени t₂=1
с. [ 1) 6 м/с²;
2) 85 м; 3) 6,32 м/с²]

1.5.
Частота
вращения колеса при равнозамедленном
движении за t=1
мин
уменьшилась от 300 до 180 мин^-1.
Определить: 1) угловое ускорение колеса;
2) число полных оборотов, сделанных
колесом за это время. [1)
0,21 рад/с²;
2) 360]

1.6.
Диск
радиусом R=10
см вращается вокруг неподвижной оси
так, что зависимость угла поворота
радиуса диска от времени задается
уравнением =A+Bt+Ct²+Dt³
(B
= l рад/с,
С=1
рад/с²,
D=l
рад/с³).
Определить для точек на ободе колеса к
концу второй секунды после начала
движения: 1) тангенциальное ускорение
а_;
2) нормальное ускорение а_n;
3) полное ускорение а. [ 1) 0,14 м/с²;
2) 28,9 м/с²;
3) 28,9 м/с²]

Соседние файлы в папке Трофимова

Источник

Угловая скорость

Формулы угловой скорости

Определение угловой скорости

Угловое ускорение

Расчет углового ускорения

Угловое ускорение – что это?

Угловая скорость

Основные формулы для вычисления угловой скорости

Связь между угловой скоростью и нормальным (центростремительным) ускорением

Основные формулы для расчета углового ускорения

Угловое ускорение маховика

Среднее угловое ускорение

Тангенциальное ускорение

Мгновенное угловое ускорение

Определения углового ускорения тела. Среднее и мгновенное угловое ускорение

Угловое ускорение и формула закона движения при равнопеременном вращении

Примеры

Как приходят к понятию углового ускорения: ускорение точки твёрдого тела при свободном движении[править | править код]

Геометрический смысл псевдовектора углового ускорения[править | править код]

Выражение вектора углового ускорения через параметры конечного поворота[править | править код]

Угловое ускорение при вращении тела вокруг неподвижной оси[править | править код]

Выражение псевдовектора углового ускорения через тензор поворота тела[править | править код]

Примечания[править | править код]

Литература[править | править код]

Вам также может понравиться

Участки вов как найти

Powershell как найти папку

Как найти имя по очеству

Добавить комментарий Отменить ответ