Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.
Угловая скорость
Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.
Обозначение угловой скорости: ω (омега).
Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.
С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.

Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:

Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.
Быстрота изменения угла φ (перемещения плоскости П из положения П1 в положение П2) – это и есть угловая скорость:

Приняв вектор k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.
Формулы угловой скорости
Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:
- если известно количество оборотов n за единицу времени t:

- если задан угол поворота φ за единицу времени:

- если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:

Размерности угловой скорости:
- Количество оборотов за единицу времени [об/мин], [c-1].
- Угол поворота за единицу времени [рад/с].
Определение угловой скорости
Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.

Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.

Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.
Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.
Другие примеры решения задач >
Угловое ускорение
Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:

Обозначение: ε (Эпсилон)
Единицы измерения углового ускорения: [рад/с2], [с-2]
Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.
Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).
Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:
Расчет углового ускорения
Пример: По заданному значению касательной составляющей полного ускорения aτ точки B, расположенной на расстоянии r от центра вращения колеса.

Требуется определить величину и направление углового ускорения колеса ε, если aτ = 10 м/с2, r = 50 см.

Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.
Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.
В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость
ω = 1,5 с-1 = 9,42 рад/с.
Смотрите также:
- Примеры расчета угловой скорости и ускорения
- Скорости и ускорения точек вращающегося тела
Download Article
Different ways to calculate rotation speed
Download Article
Most people have a general understanding of the idea of velocity and acceleration. Velocity is the measure of how fast an object is moving, and acceleration is the measure of how quickly the object’s velocity is changing (i.e., speeding up or slowing down). When the object is moving in a circle, such as a spinning tire or a rotating CD, velocity and acceleration are generally measured by the angle of rotation. They are then called angular velocity and angular acceleration. If you know the object’s velocity over some period of time, you can calculate its average angular acceleration. Alternatively, you may have a function to calculate the object’s position. With this information, you can calculate its angular acceleration at any chosen instant.
-

1
Determine the function for angular position. In some cases, you may be provided with a function or formula that predicts or assigns the position of an object with respect to time. In other cases, you may derive the function from repeated experiments or observations. For this article, we assume that the function has been provided or previously calculated.[1]
-

2
Find the function for angular velocity. Velocity is the measure of how fast an object changes its position. In layman’s terms, we think of this as its speed. In mathematical terms, the change of position over time can be found by finding the derivative of the position function. The symbol for angular velocity is
. Angular velocity is generally measured in units of radians divided by time (radians per minute, radians per second, etc.).[2]
Advertisement
-

3
Find the function for angular acceleration. Acceleration is the measure of how fast an object’s velocity is changing over time. You can mathematically calculate the angular acceleration by finding the derivative of the function for angular velocity. Angular acceleration is generally symbolized with
, the Greek letter alpha. Angular acceleration is reported in units of velocity per time, or generally radians divided by time squared (radians per second squared, radians per minute squared, etc.).[3]
-

4
Apply the data to find instantaneous acceleration. Once you have derived the function for instantaneous acceleration as the derivative of velocity, which in turn is the derivative of position, you are ready to calculate the instantaneous angular acceleration of the object at any chosen time.[4]
Advertisement
-

1
-

2
Measure final angular velocity. The second piece of information that you need is the angular velocity of the spinning or rotating object at the end of the time period that you want to measure. This is to be called the “final” velocity.[6]
- A compact disc plays in the machine by rotating at an angular velocity of 160 radians per second.
- The roller coaster, after applying its brakes to the spinning wheels, ultimately reaches an angular velocity of zero when it stops. This will be its final angular velocity.
-

3
Measure the elapsed time. To calculate the average angular velocity of the spinning or rotating object, you need to know the amount of time that passes during your observation. This can be found by direct observation and measurement, or the information can be provided for a given problem.[7]
- The owner’s manual for the CD player provides the information that the CD reaches its playing speed in 4.0 seconds.
- From observations of roller coasters being tested, it has been found that they can come to a complete stop within 2.2 seconds from when the brakes are initially applied.
-

4
Calculate the average angular acceleration. If you know the initial angular velocity, the final angular velocity, and the elapsed time, fill that data into the equation and find the average angular acceleration.[8]
Advertisement
-

1
Understand the concept of angular motion. When people think of the speed of an object, they often consider linear motion – that is, objects traveling mostly in a straight line. This would include a car, a plane, a ball that is thrown or any number of other objects. However, angular motion describes objects that spin or rotate. Think of the earth spinning on its axis. The position or speed of the earth can be measured with angular quantities. A spinning compact disc (or record player, if you’re old enough), electrons on their axes, or the wheels of a car on the axle are other examples of rotating objects that can be measured through angular motion.[9]
-

2
Visualize angular position. When you measure the position of a moving vehicle, for example, you can measure the distance traveled in a straight line from the starting point. With a rotating object, the measurement is generally done in terms of the angle around a circle. By convention, the starting or “zero” point is generally a horizontal radius from the center to the right side of the circle. The distance traveled is measured by the size of the angle
, measured from that horizontal radius.[10]
- The angle that is being measured is commonly represented by
, the Greek letter theta.
- Positive motion is measured in a counterclockwise direction. Negative motion is measured in a clockwise direction.
- The angle that is being measured is commonly represented by
-

3
Measure angular motion in radians. Linear travel is generally measured in some unit of distance, such as miles, meters, inches or some other unit of length. Rotational or angular motion is generally measured in units called radian. A radian is a fraction of the circle. For standard reference, mathematicians use the “unit circle,” which has a standard radius of 1 unit.[11]
-

4
Understand the concept of angular acceleration. Angular acceleration is the measurement of how fast or slow a rotating object is changing its velocity. In other words, is the spinning speeding up or slowing down? If you know the angular velocity at a starting time and then at a later ending time, you can calculate the average angular acceleration over that time interval. If you know the function for the object’s position, you can use calculus to derive the instantaneous angular acceleration at any chosen time.[12]
- People often use the word “acceleration” to mean speeding up, and “deceleration” to mean slowing down. In mathematical and physical terms, however, only the word “acceleration” is used. If the object is speeding up, the acceleration is positive. If it is slowing down, the acceleration is negative.
Advertisement
Add New Question
-
Question
What are the formulas to find the initial acceleration of an object?

Initial acceleration generally has to be given as a condition of the problem or the experiment.
-
Question
What is the direction of radial and tangential acceleration and how do they affect each other?

Angular (or radial) measurements are generally counterclockwise. Tangential acceleration means the straight line direction of the tangent at some measured point along the circle. The tangent is a line that is perpendicular to the radius at that point.
-
Question
How can you find angular acceleration in revolutions per second squared?

This article shows how to find acceleration in radians per second squared. To convert the number of radians to the number of revolutions, recall that 1 full circle (or 1 revolution) is equal to 2pi radians. This is roughly equivalent to 6.28 radians per revolution. If you know the acceleration in radians per second squared, divide that answer by 6.28 to get revolutions per second squared.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Remember to express final results with the proper units. Angular position is usually expressed in radians. Angular velocity is expressed in radians per time. Angular acceleration is expressed in units of radians per time squared.
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Article SummaryX
To calculate instantaneous angular acceleration, start by determining the function for angular position, or the position of the object with respect to time. Next, find the angular velocity, which is the measure of how fast the object changes its position. Then, find the derivative of the function for angular velocity in order to determine the function for angular acceleration. Finally, plug in the data to find the instantaneous acceleration of the object at any chosen time. To learn more, including how to calculate average angular acceleration, read on.
Did this summary help you?
Thanks to all authors for creating a page that has been read 90,962 times.
Did this article help you?
В этой статье мы увидим различные примеры углового ускорения с подробным пониманием.
Объект, демонстрирующий круговое движение, связывает угловое ускорение. Ниже приведен список примеров углового ускорения:
электродвигатели
Электродвигатель работает по принципу электромагнетизма. При подаче электрического тока катушка в двигателе создает магнитное поле, которое испытывает крутящий момент, и двигатель вращается. Он помогает преобразовывать электрическую энергию в механическую энергию. Скорость двигателя рассчитывается как число оборотов в минуту (об/мин).
Карусель
Человек, сидящий на карусели, испытывает центростремительная сила действующая по направлению к точке в центре, а центробежная сила направлена наружу. Обе силы уравновешиваются, что удерживает тело на сиденье и в направлении движения.

Изображение Фото: Pixabay
Происходит изменение угловой скорости карусели при ускорении и замедлении колеса. Направление радиальной скорости человека продолжает изменяться, что пропорционально угловой скорости и расстоянию стула, на котором сидит человек, от центра карусели.
колесо обозрения
Колесо парома ускоряется с постоянная скорость, а его скорость меняется только в начале пути и в конце замедляется. Так как происходит изменение угловой скорости паромного колеса, при ускорении вверх или вниз оно связано с угловым ускорением; в противном случае он имеет постоянное угловое ускорение.

Изображение Фото: Pixabay
Мы можем написать кинематическое уравнение для угловой скорости колеса парома как

![]()
Интегрируя приведенное выше уравнение,

![]()
![]()
![]()
![]()

![]()
![]()
Квадрат уравнения (1) с обеих сторон
![]()

Из уравнения (2)

Используя это в приведенном выше уравнении, мы получаем третье кинематическое уравнение.
![]()
Смеситель
Из-за вращения вала, прикрепленного к лопастям, используемым в миксере, лопасти вращаются, чтобы измельчить миксер. Скорость двигателя регулируется мощностью, подаваемой на машину, которая увеличивает или уменьшает количество оборотов в секунду соединителей двигателя. Поскольку угловая скорость муфты двигателя изменяется, соответственно изменяется и скорость углового ускорения.
Шлифовальный станок
Вал на машине вращается при подаче электрического тока, что приводит к ускорению роторов, прикрепленных к валам. Один оборот ротора сместит внешний сосуд, заполненный смесью, на длину окружности ротора.
Компания угловая скорость шлифовальной машины изменяется при смене питания при запуске станка и при отключении от сети.
Gravitron
Угловая скорость гравитрона постепенно и постоянно возрастает до тех пор, пока центробежная сила, действующая на тело, не достигнет эпической точки, при которой даже после удаления пластины под ногой стоящего в гравитроне человека не падает вниз под действием силы тяжести.
Это захватывающая вещь, чтобы испытать в парке развлечений. Скорость гравитрона постоянно меняется и, следовательно, существует угловое ускорение гравитрона. Центробежная сила отвечает за то, чтобы тело оставалось прикрепленным к стенке гравитрона и не позволяло человеку упасть под него.
Колесо автомобиля
Угловая скорость колеса зависит от скорости автомобиля. Угловое ускорение колеса равно изменению угловой скорости колеса.

Расстояние, проходимое за один оборот колеса автомобиля, равно длине окружности колеса. Чем больше диаметр колеса, тем меньше будет его угловая скорость и, следовательно, меньше будет угловое ускорение за рулем.
Поклонники
При подаче питания на вентилятор пропеллеры сначала вращаются из-за накопленная энергия в конденсаторе вентилятора, а затем постепенно увеличивайте скорость по мере того, как двигатель вентилятора испытывает крутящий момент из-за электромагнитного поля.

Изображение Фото: Pixabay
Скорость вращения винта регулируется регулятором и изменяется переключением вилки на разные диапазоны мощности. Мы видим вариации в угловая скорость вентилятора, следовательно, является примером углового ускорения.
Ветряные мельницы
Ветряная мельница преобразует энергию ветра в электрическую энергия. Чтобы пропеллеры ветряной мельницы вращались, вал соединяется с пропеллерами, а затем соединяется с двигателем, чтобы увеличить количество вращений пропеллера для производства большого количества энергии. Произведенная электрическая энергия накапливается в генераторе.

Изображение Фото: Pixabay
Вырабатываемая энергия зависит от числа оборотов пропеллера, которое определяется угловой скоростью, которая продолжает изменяться в зависимости от скорости ветра. Следовательно, скорость ускорения гребных винтов меняется.
Шкив
Шкив — это колесо, которое предназначено для легкого перемещения или подъема объектов, чтобы свести к минимуму использование мышечная сила путем изменения направления приложенной силы.

Угловое ускорение шкива зависит от угловой скорости шкива, изменяющейся во времени. Блок ускоряется за счет растяжения струны, прикрепленной к блоку.
Маятник в простом гармоническом движении
Маятник в гармоническом движении колеблется с угловая скорость образуя угол между начальной и конечной самой высокой точкой, который со временем уменьшается. Скорость маятника также уменьшается за счет возвращающей силы и сопротивления воздуха.
Происходит непрерывное изменение в угловая скорость маятника, уменьшающаяся со временем; отсюда и угловое ускорение маятника в простом гармоническом движении отрицательна.
Подробнее о Как найти постоянное угловое ускорение: задачи и примеры.
Часто задаваемые вопросы
Q1. Колесо парома, находящееся в состоянии покоя, начинает ускоряться с угловой скоростью 4 м/с за 8 с. Чему равно угловое ускорение колеса парома?
Данный:
ωf = 4 м / с
ωi = 0
т = 8 с
ωf = шi + α t
4= 0+ α * 8
α = 4/8 = 0.5 м/с2]
Q2. Рассмотрим объект, совершающий вращательное движение. Угловое смещение объекта определяется уравнением θ = 3πt2 + πt + 6π + 2 Найдите угловую скорость и угловое ускорение тела.
Данный:
![]()
![]()
Угловая скорость определяется выражением

![]()
Компания угловое ускорение объекта


![]()
Что такое орбитальное угловое ускорение?
Объект, движущийся по орбите с фокусом в центре, образующим угол θ при смещении.
Изменение угловой скорости объекта, находящегося в орбитальном движении, за счет изменения углов относительно времени называется орбитальным угловым ускорением.
Нажмите, чтобы узнать больше о 16+ примеров изменения ускорения.
В этой статье речь пойдет о физических величинах, которые характеризуют вращательное движение тела: угловая скорость, угловое перемещение, угловое ускорение, момент сил.
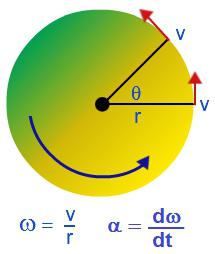
Твердым телом называют совокупность жестко связанных материальных точек. Когда твердое тело производит вращение относительно какой-либо оси, отдельные материальные точки, из которых оно складывается, двигаются по окружностям разных радиусов.
За определенный промежуток времени, например, за которое тело совершит один оборот, отдельные материальные точки, из которых состоит твердое тело, пройдут разные пути, следовательно, отдельные точки будут иметь разные линейные скорости. Описывать вращение твердого тела с помощью линейных скоростей отдельных материальных точек – сложно.
Угловое перемещение
Однако, анализируя движение отдельных материальных точек, можно установить, что за одинаковый промежуток времени все они поворачиваются вокруг оси на одинаковый угол. То есть для описания вращения твердого тела удобно пользоваться такой физической величиной, как угловое перемещение:
φ = φ(t).
Угловая скорость и угловое ускорение
Вращательное движение можно охарактеризовать угловой скоростью: ω = ∆φ/∆t.
Угловая скорость характеризует скорость вращения тела и равняется отношению изменения угла поворота ко времени, за которое оно произошло. Измеряется в радианах за секунду: [ω] = рад/с.
Угловая скорость вращения связана с линейной скоростью следующим соотношением: v = Rω, где R – радиус окружности, по которой двигается тело.
Вращательное движение тела характеризуется еще одной физической величиной – угловым ускорением, которое равно отношению изменения угловой скорости ко времени, за которое оно произошло: ε = ∆ω/∆t. Единица измерения углового ускорения: [ε] = рад/с2.
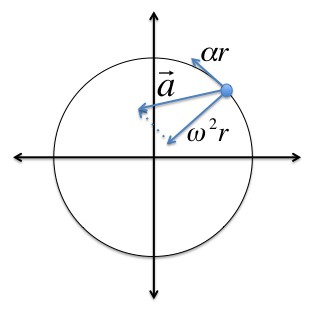
Угловая скорость и угловое ускорение являются псевдовекторами, направление которых зависит от направления вращения. Его можно определить по правилу правого винта.
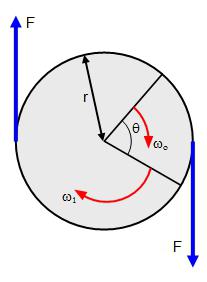
Равномерное вращательное движение
Равномерное вращательное движение осуществляется с постоянной угловой скоростью и описывается такими уравнениями: ε = 0, ω = const, φ = φ0 + ωt, где φ0 – начальное значение угла поворота.
Равноускоренное вращательное движение
Равноускоренное вращательное движение происходит с постоянным угловым ускорением и описывается такими уравнениями: ε = const, ω = ω0+ εt, φ = φ0 + ω0t + εt2/2.
Во время вращения твердого тела центростремительное ускорение каждой точки этого тела можно найти так: ɑц = v2/R = (ωR)2/R = ω2R.
Когда вращение твердого тела ускоренное, можно найти тангенциальное ускорение его точек по формуле: ɑt = ∆v/∆t= ∆(ωR)/∆t= R(∆ω/∆t) = Rε.
Момент сил
Если, рассматривая физическую проблему, мы имеем дело не с материальной точкой, а с твердым телом, то действие нескольких сил на него, приложенных к различным точкам этого тела, нельзя свести к действию одной силы. В этом случае рассматривают момент сил.
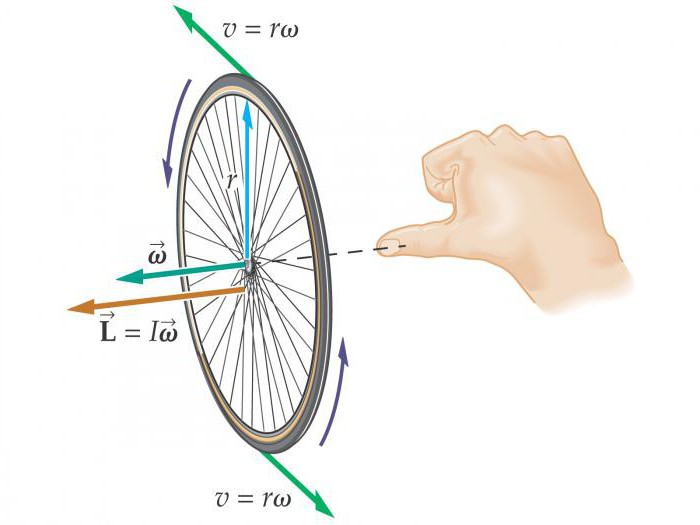
Моментом силы называют произведение силы на плечо. Это векторная величина, и ее находят по формуле: M = RFsinα, где α – угол между векторами R и F. Если на тело действует несколько моментов сил, то их действие можно заменить их равнодействующей, векторной суммой этих моментов: M = M1 + M2 + …+ Mn.
Эксперименты и опыт показывают, что под действием момента силы угловая скорость тела меняется, то есть тело имеет угловое ускорение. Выясним, как зависит угловое ускорение материальной точки (совокупности материальных точек) от приложенного момента сил: F = mɑ, RF = Rma = R2mβ, β= M/mR2 = M/I, где I = mR2 – момент инерции материальной точки. Заметим, что момент инерции тела имеет зависимость как от массы тела, так и от расположения этой массы относительно оси вращения.
Примеры решения задач
Задача 1. Ротор центрифуги делает 2•104 об/мин. После того как выключили двигатель, его вращение прекращается через 8 мин. Найдите угловое ускорение, а также число оборотов, которое совершает ротор с момента выключения двигателя до его полной остановки, считая, что движение ротора равноускоренное.
Решение
Найдем угловое ускорение, учитывая, что угловая скорость при равноускоренном движении описывается уравнением: ω(t) = ω0 – εt.
Отсюда, учитывая, что в конце движения скорость равна нулю, найдем: ε = ω0/t = 2πn/t.
Переведя данные задачи в систему единиц СИ (n = 333 об/с; t = 480 с), получим: ε = 2π333/480 = 4,36(рад/с2).
Угол поворота ротора центрифуги за время t будет: φ(t)= φ0 + ω0t + εt2/2. Учитывая выражение для углового ускорения и то, что φ0 = 0, находим: φ(t)= ω0t/2 = πnt.
Количество оборотов ротора за это время будет: N = φ(t)/2π = πnt/2π = nt = 8•104 (об.).
Ответ: угловое ускорение равно 4,36 рад/с2; количество оборотов, сделанное ротором с момента выключения двигателя до его полной остановки, равно 8•104 об.
Задача 2. Диск, имеющий массу 1 кг и радиус 20 см, вращается с частотой 120 об. в минуту. Под действием тормозного устройства на край диска начала действовать сила трения 10 Н. Найдите время остановки диска, после того как на него стала действовать сила трения.
Решение
Найдем тормозной момент сил, действующий на диск: M = RF.
Найдем угловое ускорение диска: ε = M/I = FR/mR2 = F/mR.
Найдем время, за которое диск остановится: t = ω0/ε, где ω0 – начальная угловая скорость диска, которая равна 2πv.
Сделаем вычисления: t = 2πv/ ε = 2πvmR/F = 6,28•2•1•0,2/10 = 2,5 (с).
Ответ: время остановки равно 2,5 с.
Загрузить PDF
Загрузить PDF
Угловое ускорение, обозначаемое α, характеризует быстроту изменения угловой скорости тела. Чтобы вычислить угловое ускорение, вы должны знать определения угла поворота и угловой скорости. Угол поворота, обозначаемый Θ, характеризует вращение тела вокруг центра вращения; угловая скорость, обозначаемая ω, характеризует скорость вращения тела вокруг центра вращения.
Шаги
-

1
Проверьте вращающееся тело. Перед любыми расчетами убедитесь, что рассматриваемое тело движется по идеальной окружности вокруг центра вращения (или оси вращения).
- Для понимания этой концепции представьте камень, привязанный к концу веревки. Теперь возьмите другой конец веревки и покрутите камень. Линия, проходящая через вашу руку, является осью вращения; камень, привязанный к веревке, является вращающимся телом.
-

2
Угол поворота. Угол поворота тела (обозначается как Θ), вращающегося вокруг неподвижной оси, может быть положительным или отрицательным. Углы, измеренные в направлении против часовой стрелки, считаются положительными; углы, измеренные в направлении по часовой стрелке, считаются отрицательными.
- Угловая скорость по величине равна углу поворота (вокруг точки или оси) в единицу времени.
-

3
Определите угол поворота. Для вычисления угловой скорости тела вы должны знать угол поворота.
- Например, в результате эксперимента вы выяснили, что угол поворота вращающегося тела в определенный момент времени t находится по формуле: Θ = 2t3.
-

4
Вычислите угловую скорость. Мгновенная угловая скорость вращающегося тела равна производной от угла поворота (Θ) по времени (t); в этом случае производная – это быстрота изменения угла поворота за бесконечно малый промежуток времени. Другими словами: ω = dΘ/dt.
- В приведенном выше примере расчеты угловой скорости выглядят следующим образом:
-

5
Вычислите угловое ускорение. Напомним, что угловое ускорение – это быстрота изменения угловой скорости. Таким образом, угловое ускорение равно производной от угловой скорости.
- В приведенном выше примере расчеты углового ускорения выглядят следующим образом:
Реклама
Советы
- Производная от какой-либо величины – это быстрота изменения этой величины за промежуток времени t1 и t2, причем t2 – t1 -> 0, то есть за бесконечно малый промежуток времени.
- Производная от tn по t (где n – любое целое число) вычисляется следующим образом:

- Формула для вычисления угла поворота в определенный момент времени t находится экспериментально (в результате множества измерений).
- Запомните: 1 рад = 57,3 градусов.
Реклама
Об этой статье
Эту страницу просматривали 26 063 раза.
