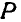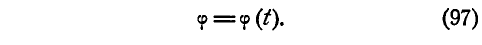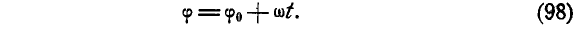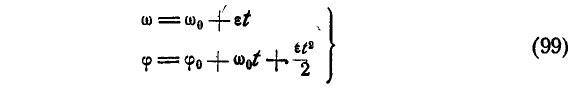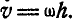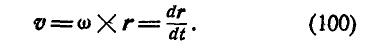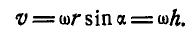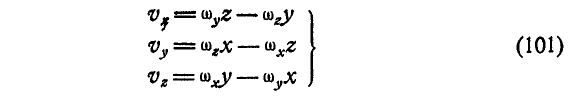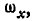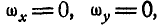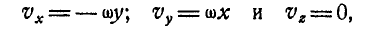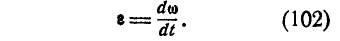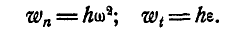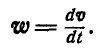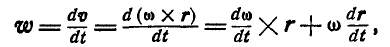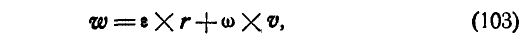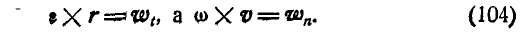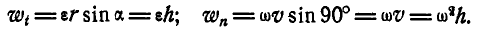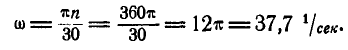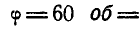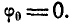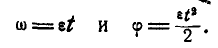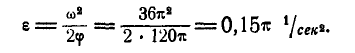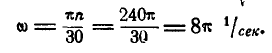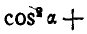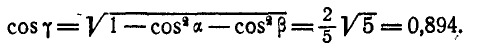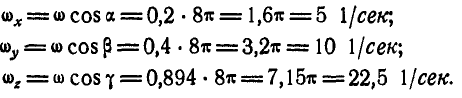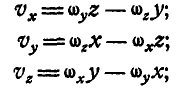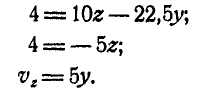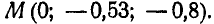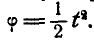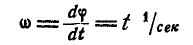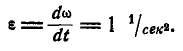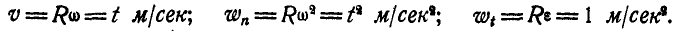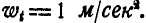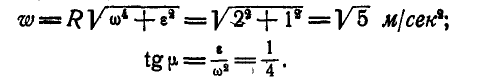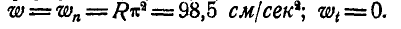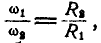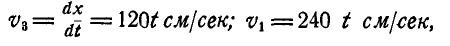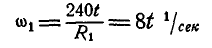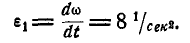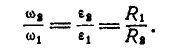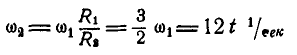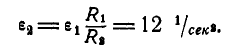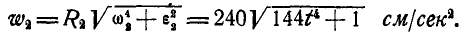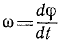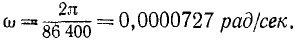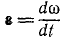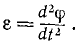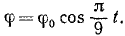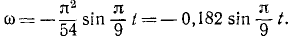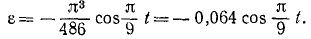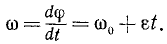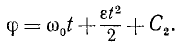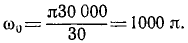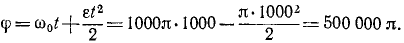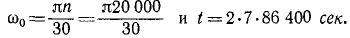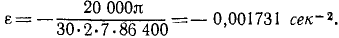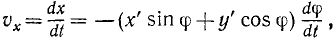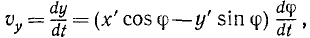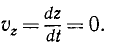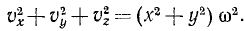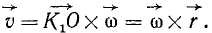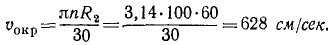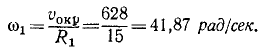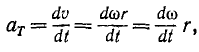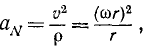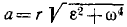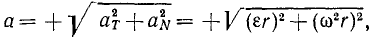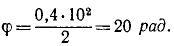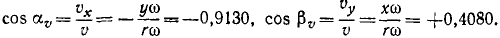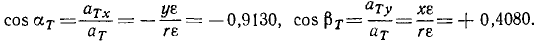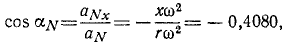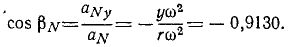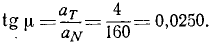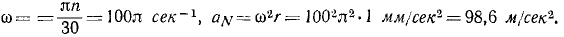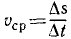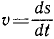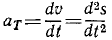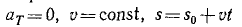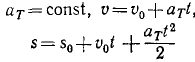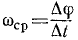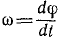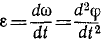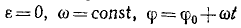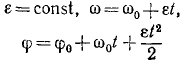Угловое ускорение – что это?
Угловое ускорение (varepsilon) – физическая величина, характеризующая изменение угловой скорости при движении тела.
Единица измерения: (lbrackvarepsilonrbrack=frac1{с^2}) или (с^{-2})
Угловая скорость
Круговым движением точки вокруг оси называют движение, где траектория точки – окружность с центром, который лежит на оси вращения, перпендикулярной плоскости окружности.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Угловая скорость (omega) – векторная физическая величина, характеризующая скорость изменения угла поворота при круговом движении точки или твердого тела.
При движении по окружности (круговом движении) скорость меняет свое направление, значит такое движение не может считаться равномерным, оно ускоренное или равноускоренное (в частных случаях).
Вектор угловой скорости направлен вдоль оси вращения.
Основные формулы для вычисления угловой скорости
Для равномерного вращения (когда за равные отрезки времени тело поворачивается на один и тот же угол):
- (omega=frac nt), где (n) – количество оборотов за единицу времени (t).
- (omega=fracvarphi t), где (varphi) – угол поворота, (t) – время, за которое он совершен.
- (omega=frac{2pi}T), где (Т) – период обращения (время, за которое тело/точка совершает один оборот).
- (omega=2pinu), где (nu) – числом оборотов в единицу времени.
Единица измерения угловой скорости в СИ: (lbrackomegarbrack=frac{рад}с)
Связь между угловой скоростью и нормальным (центростремительным) ускорением
Центростремительное (нормальное) ускорение (a_n) – это составляющая полного ускорения, которая характеризует изменение направления вектора скорости при криволинейном движении. Другим компонентом полного ускорения является тангенциальное ускорение, оно характеризует изменение величины скорости.
Центростремительное ускорение определяется по формуле:
(a_n=frac{V^2}R),
где (V) – скорость движения, (R) – радиус окружности.
Единица измерения в СИ: (lbrack a_nrbrack=frac м{с^2})
Итак, формула связывающая эти две величины:
(a_n=omega^2R)
Основные формулы для расчета углового ускорения
Значение углового ускорения в определенный момент времени вычисляется как первая производная от угловой скорости или вторая производная от угла поворота по времени.
(varepsilon=lim_{triangle trightarrow0}frac{triangleomega}{triangle t}=frac{domega}{dt}=frac{d^2varphi}{dt}=overset.omega=overset{..}varphi)
Угловое ускорение маховика
(varepsilon=fracomega t=frac{2pi n}t), где (n) – количество оборотов за единицу времени (t).
Среднее угловое ускорение
Средним угловым ускорением тела называют отношение изменения угловой скорости к отрезку времени, за который оно совершилось.
(leftlanglevarepsilonrightrangle=frac{triangleomega}{triangle t})
Тангенциальное ускорение
Тангенциальным (касательным) ускорением (a_tau) называют ту составляющую полного ускорения, которая направлена по касательной к траектории движения в данной точке. Тангенциальное ускорение описывает изменение скорости по модулю при криволинейном движении.
(a_tau=varepsilon r), где (varepsilon) – угловое ускорение, (r) – радиус кривизны траектории в заданной точке.
Мгновенное угловое ускорение
Мгновенное угловое ускорение (alpha) есть первая производная угловой скорости по времени или вторая производная углового перемещения по времени.
(alpha=tg(varepsilon)=frac{;domega}{dt}=frac{d^2phi}{dt^2})
Содержание:
Вращение твердого тела вокруг неподвижной оси:
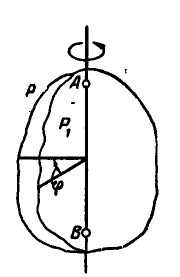
Вращением тела вокруг неподвижной оси называется такое его движение, при котором две точки тела, например А и В, неподвижны (рис. 162). Прямая, проходящая через указанные две неподвижные точки, называется осью вращения. Если мысленно провести через тело две полуплоскости — неподвижную
Рис. 162.
При вращении тела угол поворота его 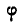
Уравнение (97) называется уравнением вращения; зная его, можно для любого момента t найти угол 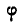
Величины угловой скорости и углового ускорения тела, вращающегося вокруг неподвижной оси, определяются по формулам (87) и (90).
Если 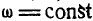
Поэтому такое уравнение по аналогии с равномерным движением точки называется уравнением равномерного вращения.
Точно так же, если 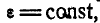
Уравнения равнопеременного вращения тела могут быть выведены аналогично уравнениям (82) и (83) равнопеременного движения точки путем замены линейных характеристик угловыми и записаны в виде:
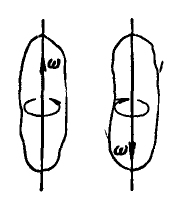
Условимся угловую скорость вращающегося тела изображать вектором, отложенным по оси вращения в такую сторону, чтобы, смотря с конца этого вектора, вращение тела происходило в направлении, противоположном движению часовой стрелки (рис. 163).
Рис. 163.
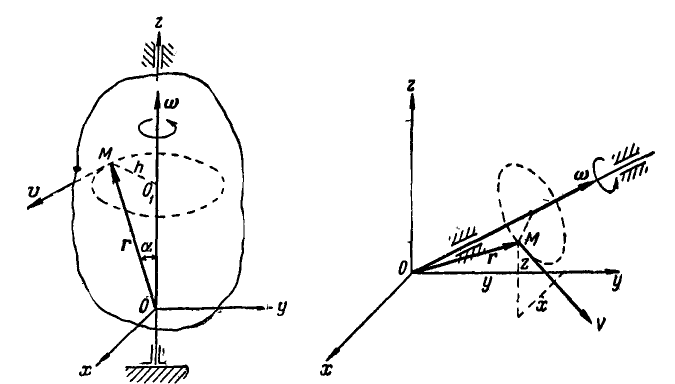
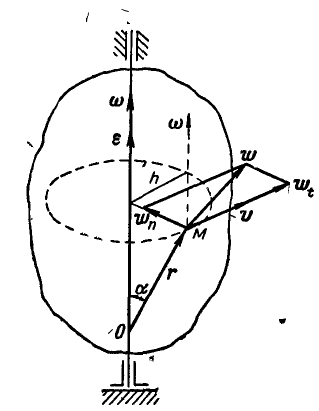
При вращении тела вокруг неподвижной оси (рис. 164) любая точка его М, отстоящая на расстоянии h от оси вращения, описывает окружность радиуса h и имеет линейную скорость, определяемую формулой (89):
Если провести из любой точки О оси радиус-вектор в точку М, то вектор линейной скорости точки М может быть представлен также в виде векторного произведения 
В самом деле, раскрывая векторное произведение, получим величину скорости, определяемую формулой (89):
Вектор же скорости направлен перпендикулярно к плоскости векторов 
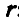
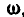
Рис. 164. Рис. 165.
В самом общем случае, когда ось вращения тела составляет любые углы с координатными осями (рис. 165), проекции скорости точки М могут быть найдены по формулам проекций векторного произведения двух векторов (11):
Равенства (101) называются формулами Эйлера. Здесь 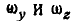
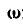
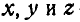
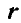
Если ось вращения вертикальна (рис. 164), то 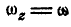
что было получено нами раньше (88). Мы уже знаем, что величина углового ускорения 
Рис. 166.
Введем в рассмотрение вектор углового ускорения е, под которым мы будем понимать векторную величину:
Так как 
При 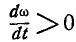
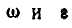
при 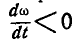
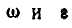
Нормальное и касательное ускорения любой точки М вращающегося тела (рис. 166) Moryт быть найдены по формулам (91):
Дадим векторное обобщение этим величинам. В самом общем случае вектор ускорения может быть найден по формуле (79):
Принимая во внимание формулы (100) и (102), имеем:
или
где
Действительно, в силу определения векторного произведения, находим:
Это приводит нас к формулам (91). Направления же 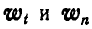
Задача №1
Маховик делает 360 об/мин. Найти его угловую скорость 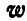
Решение. В нашем случае 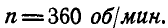
Задача №2
Маховик начинает вращаться равноускоренно из состояния покоя. Сделав с момента начала движения 60 оборотов, маховик имеет угловую скорость, равную 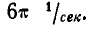
Решение. По условию задачи 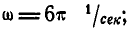
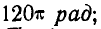
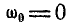
По формулам (99) получаем:
Подставляя значение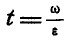
Задача №3
Тело делает 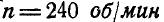
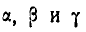
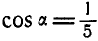
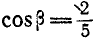
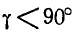
Найти такую точку тела, расположенную в плоскости 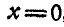
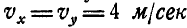
Решение. Угловая скорость:
Для определения 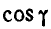
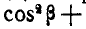
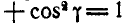
Найдем теперь проекции угловой скорости на координатные оси:
По формулам Эйлера (101) имеем:
или
Из первых двух уравнений находим, что 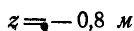
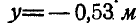
Задача №4
Маховик радиусом R = 1 м вращается вокруг неподвижной оси, проходящей через его центр перпендикулярно к плоскости чертежа, согласно уравнению
Найти скорость и ускорение точки М обода маховика по прошествии 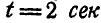
Решение. Найдем сначала по формулам (87) и (90) угловую скорость и угловое ускорение маховика:
и
Далее, линейная скорость, нормальное и касательное ускорения’ точки М в момент t найдутся по формулам (89) и (91):
При 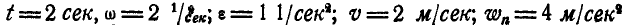
Величина и направление ускорения точки М определятся по формулам (92) и (93):
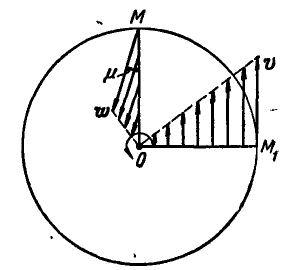
Так как величины линейных скоростей и ускорений точек, расположенных на одном из радиусов’маховика, например ОМ, зависят от величины самого радиуса, входящего в формулы (89) и (92) в первой степени, то отсюда следует, что концы векторов скоростей и ускорений точек одного радиуса будут расположены на прямой (рис. 167). Для удобства выполнения чертежа на радиусе ОМ дано изображение ускорений точек прямой ОМ, а на радиусе 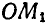
Рис. 167.
Задача №5
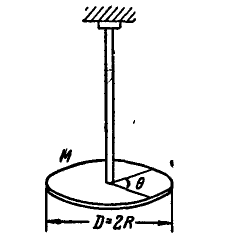
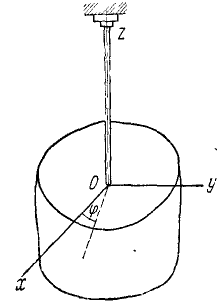
Диск, прикрепленный к вертикальной проволоке, совершает крутильные колебания вокруг оси проволоки так, что угол закручивания его меняется по закону: 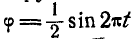
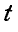
Найти нормальное, касательное и полное ускорения какой-либо точки М на ободе диска в момент 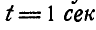
Рис. 168.
Указание: находим сначала угловую скорость и угловое ускорение диска по формулам (87) и (90), а затем ускорение точки М по формулам (91) и (92).
Ответ.
Рис. 169.
Задача №6
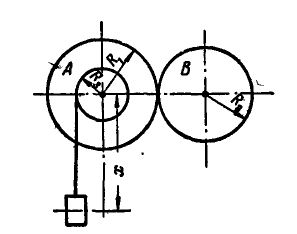
Зубчатое колесо А радиусом 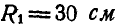
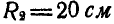
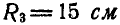
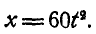
Решение. В общей точке касания колеса А и В имеют одинаковую линейную скорость, равную 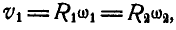
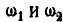
т. е. отношение угловых .скоростей колес обратно пропорционально их радиусам.
Найдем теперь угловую скорость 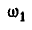
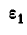
откуда
и
Вращение колес А и В равноускоренное, а поэтому 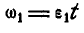
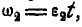
Отсюда угловая скорость 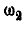
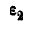
и
Ускорение какой-либо точки обода колеса В находим по формуле (92):
Рис. 170.
Вращение твердого тела вокруг неподвижной оси
Вращением вокруг неподвижной оси называют движение твердого тела, при котором его точки описывают окружности с центрами на одной и той же неподвижной прямой, перпендикулярной к их плоскостям
Вращательное движение
Как было показано, для определения движения твердого тела достаточно определить движение трех его точек, не лежащих на одной прямой. Пусть во- время движения тела две его точки О и O1 остаются неподвижными.
Тогда движение тела можно определить движением третьей точки К, принадлежащей телу и не лежащей на одной прямой с точками О и O1. Выберем эту точку произвольно и, соединив все три точки прямолинейными отрезками, получим треугольник OO1K-Так как точки О и O1 неподвижны, то неподвижна и сторона OO1 треугольника OO1K, и движение точки К, а также и всего тела определится поворотом плоскости треугольника OO1K вокруг прямой OO1. Точку К мы выбрали произвольно, следовательно, поворачивается вокруг прямой OO1 любая плоскость, проведенная в теле через эту прямую. Такое движение тела называют вращательным движением, или, коротко, вращением, а неподвижную прямую OO1, вокруг которой вращается тело, называют осью вращения.
Ось вращения может проходить и за пределами тела. Так, например, Луна, двигаясь вокруг Земли, повернута к ней всегда одной стороной. Движение Луны по отношению к Земле можно назвать вращением. Ось вращения проходит за пределами Луны через центры круговых траекторий ее точек.
Если движение тела определять по движению его точек, то вращение вокруг оси можно определить как движение твердого тела, при котором все точки тела описывают окружности с центрами на одной и той же неподвижной прямой, перпендикулярной к плоскостям этих окружностей, а ось вращения можно определить как неподвижную прямую, на которой расположены центры окружностей, описываемых точками вращающегося тела.
Вращательное движение твердого тела определено, если задан как функция времени угол, на который поворачивается плоскость, проходящая через ось вращения и какую-нибудь точку вращающегося тела: φ=φ(t)
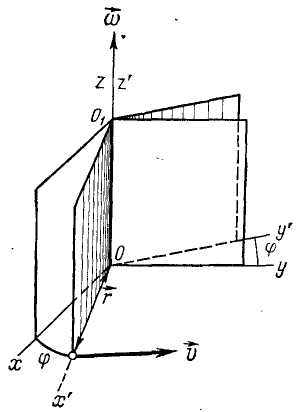
Уравнение вращательного движения. Построим основную систему координат xcyz, направив ось Oz по оси вращения тела (рис. 101). Эта система неподвижная и не связана с вращающимся телом. Построим теперь другую, подвижную, систему координат x’0y’z’, направив ось Oz’ также по оси OO1 вращения тела, а ось Ox’ — на какую-либо точку K1 тела. Эта система координат неизменно связана с телом и поворачивается вместе с ним относительно основной системы xOyz. Угол φ на который поворачивается плоскость, проходящая через ось вращения и какую-нибудь точку вращающегося тела, называют углом поворота и обозначают буквой φ. Так, если в начальное мгновение оси Ox’ и Ox (см. рис. 101) совпадали, то углом поворота мы назовем двугранный угол между неподвижной плоскостью xθz и подвижной плоскостью x’Oz’ или равный ему линейный угол x’Ox’.
Рис. 101
Угол φ можно рассматривать как угловую координату тела, потому что он определяет положение всего вращающегося тела. Измеряется угол φ в радианах.
Будем считать угол φ положительным, если он отсчитан от положительной оси Ox к положительной оси Оу, т. е. против вращения часовой стрелки, если смотреть с положительного направления оси Oz. При отсчете в противоположную сторону будем считать угол отрицательном.
Чтобы определить вращение тела, надо знать угол поворота как некоторую непрерывную однозначную функцию времени:
φ=φ(t) (82)
Уравнение (82) является уравнением вращательного движения твердого тела вокруг неподвижной оси.
Всякая плоскость OO1K, проведенная через ось вращения и какую-либо точку К тела, поворачивается за данное время на такой же угол φ, на который за это же время повернулась плоскость x’Oz’. Это следует из условия неизменяемости твердого тела.
Угловая скорость выражается первой производной от угла поворота по времени:
Угловая скорость. Угол поворота характеризует вращение тела только с геометрической стороны. Чтобы охарактеризовать вращение тела не только в пространстве, но и во времени, возьмем отношение изменения ∆φ угла поворота ко времени Δt, в течение которого это изменение происходило, называемое средней угловой скоростью тела:
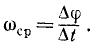
Пределом отношения (83′) при Δt, стремящимся к нулю, является первая производная от угла поворота по времени. Она характеризует изменение угла поворота в данное мгновение, т. е. характеризует вращение тела не только по отношению к окружающему пространству, но и во времени. Эта величина принята за пространственно-временную меру вращения твердого тела вокруг оси и ее называют угловой скоростью тела:
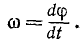
Знак производной (83) указывает, в какую сторону поворачивается тело вокруг оси Oz: если производная (83) положительна, то наблюдатель, смотрящий с положительной стороны оси Oz, видит тело вращающимся против часовой стрелки, т. е. справа налево — от положительного направления оси Ox к положительному направлению оси Оу: при отрицательной производной (83) вращение тела происходит в обратном направлении.
Размерность угловой скорости равна размерности угла поворота, деленной на размерность времени. Но угол поворота является отвлеченной величиной, и размерность его—единица. Следовательно, размерность угловой скорости обратна размерности времени.
[ω]=T-1.
Чаще всего время измеряют в секундах, тогда единица угловой скорости ceκ-1.
Равномерное вращение иногда характеризуют числом п оборотов, совершаемых телом за единицу времени (обычно за минуту).
Найдем соотношение между угловой скоростью ω, выраженной в радианах в секунду, и числом оборотов в минуту. Если тело делает n оборотов в минуту, то оно поворачивается за каждую минуту на 2πn радианов, а за секунду—в 60 раз меньше, следовательно,
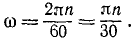
Формулу (84) широко применяют в технической механике. Приближенно можно считать
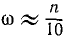
В формулах (84) и (84′) n выражеyо в оборотах за минуту, a ω — в радианах за секунду, как их большей частью и выражают. Однако для очень медленно вращающихся тел число оборотов удобнее считать не за минуту, а за другие единицы времени. Так, Земля вращается вокруг своей оси, делая 1 оборот в сутки. Было бы неудобно считать, что Земля делает 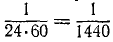
Самые медленные вращения встречаются в звездном мире. Так< например, период обращения Солнца вокруг центра Галактики (Млечного пути) составляет 190 миллионов лет.
Наибольшая угловая скорость, полученная в технике, соответствует миллионам оборотов в минуту. C такой скоростью вращаются гироскопы Гюгенара —маленькие роторы, подвешенные без подшипников в магнитном поле.
За одно и то же время все части твердого тела поворачиваются вокруг оси на один и тот же угол. Следовательно, угловая скорость является общей мерой вращения для всего тела, и в каждое мгновение тело, вращающееся вокруг оси, имеет только одну угловую скорость.
Для тех случаев, когда тело совершает сложное движение, например вращается вокруг оси в то время, как эта ось поворачивается, удобно изображать угловую скорость вектором, направленным вдоль оси вращения. Величина и положение вектора показывают величину угловой скорости и положение оси вращения. Но вектор угловой скорости, как и вектор момента силы относительно точки, отличается от прочих известных нашим читателям векторов (скорость точки, ускорение точки, радиус-вектор, сила и др.) тем, что, изображая его стрелкой соответствующей длины, отложенной вдоль оси вращения, надо (вполне произвольно) условиться относительно направления стрелки. В нашем курсе мы всюду пользуемся правой системой координат, поэтому установим и для вектора угловой скорости правило правого винта, т. е. будем направлять вектор угловой скорости вдоль оси вращения к той ее стороне, с которой вращение тела представляется происходящим против вращения часовой стрелки. Так, например, вектор угловой скорости земного шара, вращающегося с запада на восток, мы направим к северному полюсу: глядя с северного полюса, мы увидели бы Землю вращающейся против часовой стрелки.
Угловое ускорение выражается первой производной от угловой скорости по времени:
Угловое ускорение. Изменение угловой скорости происходит с течением Времени и, вообще говоря, бывает различным в разные моменты времени. Пространственно-временную меру, характеризующую изменение угловой скорости тела в данное мгновение, называют угловым ускорением тела.
Поскольку угловая скорость — векторная величина, вектором Должно быть и угловое ускорение. Но при вращении тела вокруг Неподвижной оси мы обычно рассматриваем угловую скорость как скаляр, и потому здесь нас могут интересовать только величина и знак углового ускорения.
Пусть величина угловой скорости изменилась на ∆ω в течение промежутка времени Δt. Предел отношения 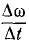
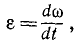
или, принимая во внимание равенство (83),
Следовательно, угловое ускорение выражается первой производной “от угловой скорости по времени, или, что то же, второй производной от угла поворота по времени. Эта величина характеризует быстроту изменения угловой скорости тела, вращающегося вокруг неподвижной оси.
Размерность углового ускорения равна размерности угла поворота, деленной на квадрат размерности времени, т. е. равна единице, деленной на квадрат времени.
[ω]=T-2.
Чаще всего время измеряется в секундах, тогда единица углового ускорения ceκ-2, или по записи, рекомендованной ГОСТом, pa∂/ceκ2.
Если с течением времени абсолютная величина угловой скорости тела увеличивается, то производная 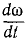
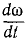
Задача №7
Унифиляр (тело, подвешенное на вертикальном стержне) (рис. 102) закрутили на угол 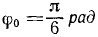
Рис. 102
Определить угловую скорость (в ρa∂/ceκ.) и угловое ускорение (в рад/сек) через каждые 3 сек от начала движения.
Решение. Дифференцируя уравнение движения, получим выражение угловой скорости унифиляра:
Дифференцируя вторично найдем, угловое ускорение унифиляра:
Чтобы определить угол поворота, угловую скорость и угловое ускорение в заданные мгновения, надо в уравнение движения тела и в полученные соотношения подставить t = 3, 6, 9, … и т. д. секунд. Анализируя полученные данные относительно ω и ε, убедимся, что унифиляр совершает крутильные колебания с периодом 18 сек.
- Заказать решение задач по теоретической механике
Равномерное и равнопеременное вращения
Если угловая скорость ω постоянна, то производная 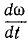
ε = 0, ω = const, φ = φ0+ωt, (86)
где φ0-начальное значение угла.
Формулы (86) справедливы только для равномерного вращения тела и неприменимы при других движениях.
Из различных переменных вращений тела в задачах наиболее часто встречается равнопеременное вращение. Равнопеременным вращением называют такое вращение твердого тела вокруг оси, πph котором угловое ускорение остается постоянным:
ε = const.
Интегрируя это уравнение, находим
ω = εt + C1.
Постоянную интегрирования C1 находим из начальных данных. В начальное мгновение (при t=0) величина угловой скорости была ω0. Подставляя эти частные значения аргумента t и функции ω, находим постоянную C1:
C1 = ω0.
Таким образом,
Интегрируя это равенство, получаем
Постоянную C2 находим из начальных данных. Если при начале вращения тело было повернуто на некоторый угол φ0, то, подставляя φ0 вместо φ и 0 вместо t, найдем C2 = φ0. Для равнопеременного вращения тела имеем:
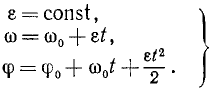
Формулы (87) справедливы только для равнопеременного вращения твердого тела и неприменимы при других движениях.
Задача №8
Барабан суперцентрифуги делает при установившемся движении 30000 об/мин, а после прекращения подачи энергии (на выбеге) вращается равнозамедленно с угловым ускорением ε=π1∕ceκ2. Определить время выбега (время до остановки) и угол поворота барабана за это время.
Решение. В мгновение прекращения подачи энергии угловая скорость барабана была
C этого мгновения барабан вращается равнозамедленно по (87):
ω= 1000π—πt.
В мгновение остановки барабана угловая скорость его равна нулю. Подставляя это значение угловой скорости, находим время выбега.
t = 1000 сек = 16 мин 40 сек.
За это время барабан повернется на угол
Чтобы по углу поворота определить число оборотов, надо поделить этот угол (выраженный в радианах) yа 2π—число радианов в одном обороте.
Ответ. t = 16 мин 40 сек, φ = 250 000 об.
Задача №9
В инерционном аккумуляторе Уфимцева (1918 г.) для ветроэлектрических станций стальной диск вращается в глубоком вакууме, делая 20 000 об/мин. Предоставленный самому себе, он продолжает вращаться в течение двух недель. Определить е диска, считая вращение равнозамедленным.
Решение. Определим начальную угловую скорость диска н время (2 нед.) до остановки в секундах:
Ответ получим, разделив ω0 на t.
Ответ.
Траектории, скорости и ускорения точек вращающегося тела
Точки вращающегося тела, расположенные на одной прямой, параллельной оси вращения, совершают одинаковые движения
Траектории точек вращающегося тела
Вращением тела называют движение, при котором точки тела описывают окружности с центром на оси вращения. Следовательно, по самому определению вращательного движения траектории точек тела—окружности.
Если тело мысленно пересечь какой-либо плоскостью, перпендикулярной оси вращения, то в этой плоскости будут находиться круговые траектории всех расположенных в ней точек тела. Очевидно, что движения точек тела, лежащих на ном в какой-либо из точек к этой плоскости, совершенно одинаковы, а потому и движение точек всего тела может быть полностью охарактеризовано движением точек, лежащих в этой плоскости.
Сохраним и в этом параграфе расположение осей координат (см. рис. 101), при котором оси Oz и Oz’ неподвижной и подвижной систем совпадают с осью вращения тела, а плоскость x’0y’ находится в плоскости хОу.
Возьмем в этом теле какую-либо точку К (рис. 103), координаты которой относительно подвижной системы обозначимx’,y’ и г’. Эти координаты точки К во время вращения тела не меняются, так как оси подвижной системы координат неизменно связаны с телом и вращаются вместе с ним. Координаты той же точки в основной системе обозначим х, у и z.
Координаты х и у точки К связаны с координатами х’ и у’ той же точки формулами, известными из аналитической геометрии и понятными из чертежа (рис. 103):
х = х’ cos φ—y’ sin φ, (88′)
y = x’ sin φ +y’ os φ. (88″)
Если тело вращается, то с течением времени меняется угол φ, являющийся некоторой функцией (71) от времени t, а следовательно, меняются и координаты х и у точки К в основной системе отсчета. Координата же z при направлении оси Oz вдоль оси вращения не изменяется и остается равной z’:
z = z’. (88″‘)
Аналогично можно определить подвижные координаты по неподвижным и углу φ:
х’ = х cos φ у sin φ; y’ = y cos φ—x sinφ; z’ = z.
Скорость точки тела, вращающегося вокруг оси, равна произведению угловой скорости тела на расстояние точки от оси: υ= ωr
Скорости точек вращающегося тела. Для получения проекций скорости на неподвижные оси координат продифференцируем по времени равенства (88), рассматривая φ как функцию времени. Будем иметь
Но согласно (88) выражение, стоящее в скобках в первом из этих равенств, есть у, а во втором х, а потому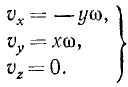
Возводя эти равенства в квадрат и складывая, найдем
Но в левой части мы имеем квадрат полной скорости точки, а в скобках правой части — квадрат расстояния точки от оси. Мы получили одну из главнейших формул кинематики:
υ = ωr (90)
— величина скорости точки вращающегося тела равна произведению угловой скорости тела на расстояние точки от оси вращения.
Таким образом, для определения скорости точки вращающегося тела нет необходимости знать ее координаты, надо знать лишь расстояние точки от оси вращения и угловую скорость тела.
Можно определить угловую скорость тела по скорости какой-либо из его точек и по расстоянию этой точки от оси вращения:
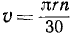
По этим формулам можно определить скорость любой точки вращающегося тела, независимо от того, какую форму имеет тело и находится точка на поверхности или внутри тела. Скорость точки тела, вращающегося вокруг оси, называют вращательной скоростью точки. Она направлена перпендикулярно к плоскости, проходящей через точку и ось вращения, против хода часовой стрелки или по ходу часовой стрелки в зависимости от знака производной (83).
Если же смотреть на тело с той стороны оси вращения, куда мы направили вектор 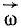
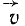
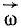
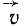
Следовательно, вектор вращательной скорости точки и по величине и по направлению можно рассматривать как момент вектора угловой скорости тела относительно этой точки. Его можно представить в виде векторного произведения аналогично тому, как это сделано в статике с моментом силы относительно точки.
Вращательную скорость точек, лежащих на поверхности цилиндра (шкива, барабана, махового колеса, вала и т. п.), вращающегося вокруг своей оси, называют окружной скоростью тела. Окружная скорость равна произведению ω на радиус R тела:
υoκp = ωR.
Задача №10
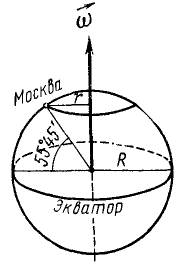
Определить вращательную скорость точек земной поверхности на экваторе и на широте Москвы (55°45′) при вращении Земли вокруг оси (рис. 104). Средний радиус Земли 6371 км и cos 55o45′ = 0,5628.
Рис. 104
Решение. Вращаясь вокруг своей оси, Земля совершает один оборот (2π рад) за сутки (86 400 сек), и угловая скорость Земли ω=727∙10-7 pa∂/ceκ. Умножая угловую скорость на радиус Земли, выраженный в метрах (6371 ∙ 103), найдем вращательную скорость точек Земли на экваторе:
υ= ωR=727 • 6371 • 10-4 = 463 м/сек.
Для определения вращательной скорости точек в Москве надо умножить ω Земли на расстояние г от Москвы до земной оси:
υ = 727 • 10-7 • 0,5628 • 6371 • 103 = 261 м/сек.
Ответ. Вращательная скорость точек на экваторе 463 м/сек, в Москве 261 м/сек.
Она направлена против вращения часовой стрелки, если смотреть с северного полюса.
Задача №11
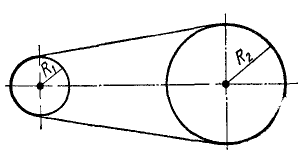
Шкив динамомашины R1= 15 см (рис. 105) вращается посредством бесконечного ремня от паровой машины со шкивом R2 — 60 см, делающим 100 об/мин. Определить угловую скорость ω1 шкива динамомашины.
Рис. 105
Решение. Определим окружную скорость шкива паровой машины:
Такова же величина скорости частиц ремня, а следовательно, и окружная скорость шкива динамомашины. Его угловая скорость
Ответ. ω1=41,87 рад/сек, n = 400 об/мин.
Касательное ускорение точки вращающегося тела равно произведению углового ускорения тела на расстояние точки от оси вращения тела: αr=er
Ускорение точек вращающегося тела
Если в выражении касательного (69) и нормального (74) ускорений вместо скорости v мы подставим выражение (90) вращательной скорости, то получим касательное и нормальное ускорения точки тела, вращающегося вокруг неподвижной оси.
Касательное ускорение
или
aτ = εr. (92)
Касательное ускорение точки вращающегося тела равно произведению углового ускорения тела на расстояние точки от оси вращения.
Центростремительное ускорение точки вращающегося тела равно произведению квадрата угловой скорости тела на расстояние точки от оси вращения тела:
αN=ω2r
Каждая точка вращающегося тела описывает окружность, а потому радиус кривизны р траектории точки равен расстоянию этой точки от оси вращения тела. Имеем
или
αN=ω2r
Нормальное ускорение точки вращающегося тела обычно называют центростремительным ускорением. Оно равно произведению квадрата угловой скорости на расстояние точки от оси вращения тела.
Величина полного ускорения точки тела, вращающегося вокруг оси, выражается формулой
Зная касательное и центростремительное ускорения, определим по формуле (75) величину полного ускорения этой точки:
или
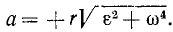
Иногда бывает необходимо определить проекции ускорения точки вращающегося тела на неподвижные оси координат. Для этого продифференцируем равенства (89) по времени, учитывая, что при вращении тела меняется не только его угловая скорость, но и координаты х и у его точек:
ax =—уε—υyω, ay = xε+υλω, αz = 0.
Подставляя вместо υx и υy их значения (89), найдем проекции ускорения точки вращающегося тела на неподвижные оси:
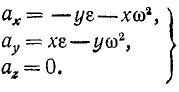
Возводя в квадрат и складывая, найдем
a2 = (x2 + y2) (ε2 + ω4),
или, так как x2+y2 = r2, получаем уже знакомую нам формулу (94). Следовательно,
aTх=—yε; αTy = xε; aNх= — xω2; aNy=-yω2. (95′)
Задача №12
Тело вращается вокруг оси Oz без начальной угловой скорости и с постоянным угловым ускорением ε = 0,4 рад/сек2. Определить для t = 10 сек: 1) координаты точки К тела, если при t = 0 координаты точки К были: х = +10, y=0, z-0∙, 2) ее вращательную скорость; 3) направляющие косинусы вращательной скорости; 4) касательное и центростремительное ускорения той же точки; 5) направляющие косинусы касательного и центростремительного ускорений; 6) угол, составляемый векторами полного и центростремительного ускорений.
Решение. Тело вращается равноускоренно; по (87) найдем угловое ускорение, угловую скорость и угол поборота тела для заданного мгновения: ε = 0,4 ρaд/ceκ2; ω = 0,4 • 10 = 4 ρaд/ceκ;
Тело повернулось за 10 сек на 20 рад. Переведем радианы в градусы:
ar = 1145о54’56”,
за вычетом полных оборотов определим угол αr, составляемый радиусом-вектором с осью Ox (рис. 106):
20 рад = 65о54’56”,
По тригонометрическим таблицам находим: cos ar = 0,4080, sin ar = 0,9130. Приняв во внимание, что расстояние точки К от оси вращения тела равно 10 см, найдем координаты точки К в мгновение t=10 сек:
х=10 cos ar = +4,080 см,
y = 10 sin ar = +9,130 см.
Величину вращательной скорости определим по (90):
υ = ωr = 4 • 10 = 40 см/ceκ.
Чтобы определить направляющие косинусы вращательной скорости, найдем сначала по (89) ее проекции на оси координат:
υx= — yω = — 36,52 см/сек,
υy= +xω = + 16,32 см/сек
по затем по (62) — направляющие косинусы:
Определим по (92) величину касательного ускорения:
aτ=εr = 0,4 ∙10 = 4 см/ceκ2
и по (95′) — проекции касательного ускорения на оси х и у:
aTx = — yε=—3,652 см/сек2, aTy = xε =+1,632 см/сек2.
Разделив проекции на модуль касательного ускорения, найдем направляющие косинусы касательного ускорения:
Мы видим, что направляющие косинусы касательного ускорения тождественны с направляющими косинусами скорости.
Напомним, что знак направляющего косинуса определяется знаком числителя. Если ω и ε имеют одинаковые знаки (как в данной задаче), то тело вращается ускоренно и направление касательных ускорений его точек совпадает с направлением их скоростей, если же знаки ω и ε различны, то вращение замедленное и векторы касательных ускорений и скоростей точек направлены в противоположные стороны.
Величину центростремительного ускорения определим по (93);
aN=ω2r = 42∙10 = 160 см/сек2
и по (95′) —его проекции на оси координат:
aNx=—xω2= —65,280 см/сек2,
aNy = — yω2 = —146,080 см/сек2.
Проекции нормального ускорения точки на оси координат имеют знаки, обратные знаку соответствующей координаты точки. В самом деле, ayx отрицательна, если абсцисса х положительна, и положительна, если х отрицательна (аналогично и ayy). Следовательно, центростремительное ускорение всегда направлено к началу координат, т. е. к центру круговой траектории точки.
Разделив проекции центростремительного ускорения на его модуль, найдем направляющие косинусы центростремительного ускорения:
Так как касательное ускорение перпендикулярно к центростремительному, то (по условию перпендикулярности, известному из аналитической геометрии) сумма произведений соответствующих направляющих косинусов должна равняться нулю. Действительно,
cos aT cos aN + cos βT cos βN = ( — 0,9130) ( —0,4080) + ( + 0,4080) ( — 0,9130) =0.
Определим теперь тангенс угла между направлением полного и нормального ускорений:
Пользуясь таблицами тригонометрических функций, определим, что угол равен lo26’0″.
Ответ. 1) х = + 4,080 см, у = + 9,130 см; 2) υ = 40 см/сек, 3)cos aυ=—0,9130, cos βυ = +0.4080; 4) aT = 4 см/сек1, aN= 160 см/сек2; 5) cos aT=—0,9130, cos βT= +0,4080, cos aN = – 0,4080, cos βN=—0,9130; 6) угол равен lo26’0″.
Задача №13
При сборке ротора молотковой дробилки была допущена неточность, в результате которой центр тяжести ротора отстоит от оси вращения на расстоянии 1 мм. Определить центростремительное ускорение центра тяжести ротора, если n = 3000 об/мин.
Решение. По формулам (84) и (93) имеем
Ответ. aN=98,6 м/сек2 ≈ 10g.
Зависимости между углом поворота, угловой скоростью, угловым ускорением и временем аналогичны зависимостям между расстоянием, скоростью, касательным ускорением и временем
Аналогия формул
Формулы кинематики вращательного движения аналогичны соответствующим формулам кинематики точки и могут быть из них получены, если заменить расстояние s углом поворота φ, скорость υ— угловой скоростью ω и касательное ускорение αT-угловым ускорением ε. Это правило является мнемоническим, оно непригодно для вывода формул, но может облегчить их запоминание. Ниже приведен ряд формул, получающихся одна из другой такой заменой.
| Движение точки | Вращение точки |
|
Уравнение движения по траектории Средняя скорость точки Величина скорости точки Величина касательного ускорения Равномерное движение точки Равнопеременное движение |
Уравнение вращения вокруг оси Средняя угловая скорость тела Величина угловой скорости тела Величина углового ускорения Равномерное вращение тела Равнопеременное вращение |
- Сферическое движение твердого тела
- Плоско-параллельное движение твердого тела
- Движение твердого тела, имеющего неподвижную точку
- Движение твердого тела
- Теория пар, не лежащих в одной плоскости
- Произвольная пространственная система сил
- Центр параллельных сил и центр тяжести
- Поступательное движение твердого тела
Передаточные
механизмы предназначены для передачи
вращения от одною вала. называемого
ведущим, к другому, называемому ведомым.
Если оси ведущего и ведомого валов
параллельны или пересекаются, то
вращение можно передать с помощью
фрикционной или зубчатой передачи (рис.
10.8 – 10.11).
Во
фрикционной
передаче вращение передается вследствие
действия силы сцепления на поверхности
соприкасающихся колес, в зубчатой
передаче – от зацепления зубьев.
Вращательная скорость
в точке соприкасания колес относится
к точкам обоих колес, т. е. ее модуль
определяется как
.
откуда
.
Таким
образом, угловые
скорости колес фрикционной или зубчатой
передачи обратно пропорциональны
радиусам колес.
Отношение
угловой скорости ведущего колеса к
угловой скорости ведомого колеса
называется передаточным числам:
.

Рис.
10.8 Рис. 10.9

Рис.
10.10 Рис. 10.11
Передаточное
число можно вычислить как обратное
отношение радиусов колес:
.
Так
как числа зубьев пропорциональны длинам
окружностей и, следовательно, радиусам,
то передаточное число определяется и
по числу зубьев:
.
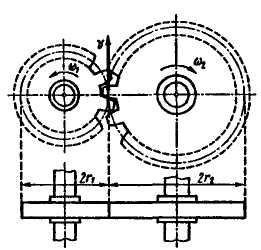
При
внешнем зацеплении (рис. 10.8) направление
вращения ведущего и ведомого колес
противоположное, а при внутреннем (рис.
10.9) – одинаковое.
Кроме
фрикционной и зубчатой передач существует
передача на расстоянии с помощью гибкой
связи (ремня, троса, цепи) (рис. 10.11).
Taк как скорости
всех точек ремня одинаковы и ремень не
скользит по поверхности шкива, то к
ременной передаче относятся те же
соотношения:
.
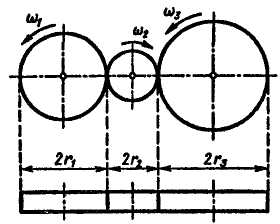
Применяются
также серии колес с неподвижными осями
вращения в виде последовательного ряда
с паразитными
колесами (рис. 10.12) и последовательного
ряда
с
кратным
зацеплением
(рис. 10.13), называемые рядовыми
соединениями колес.

Рис.
10.12 Рис. 10.13
Определим
передаточное число фрикционной передачи
в виде рядового соединения с паразитными
колесами:
для
колес 1-2
;
для
колес 2-3
.
Перемножаем
левые и правые части, получаем
.
Для
зубчатых колес
.
Передаточное
число рядового соединения с паразитными
колесами равно отношению радиусов
(чисел зубьев) ведомого и ведущего колес
и не зависит от радиусов (чисел зубьев)
паразитных колес.
Определим
передаточное число рядового соединения
с кратным зацеплением.
Частное
передаточное число для колес 1-2
.
Частное
передаточное число для колес 3-4
.
Так
как колеса 2—3 соединены жестко, т. е.
то общее передаточное число
равно произведению передаточных чисел:
.
Для
зубчатых колес
.
Таким
образом, общее
передаточное число рядового соединения
колес с кратным зацеплением равно
произведению чисел зубьев ведомых
колес, деленному на произведение чисел
зубьев ведущих колес.
В
рассмотренных выше передачах при
равномерном вращении ведущего вала
ведомый вал вращается тоже равномерно.
Для
получения переменной угловой скорости
ведомого вала применяются передачи,
в которых расстояние от точки соприкасания
колес до оси одного из валов или обоих
валов изменяется.

Рис.
10.14 Рис. 10.15
Во
фрикционной передаче, изображенной на
рис. 10.14, колесо 1 перемещается вдоль
его оси и отношение угловых скоростей
зависит от переменного расстояния х:
.
На
рис.10.15 изображены эллиптические колеса,
оси вращения которых находятся в фокусах
эллипсов. Отношение угловых скоростей
зависит от переменных расстояний
и
,
где
.
Пример
1.
Вал начинает вращаться равноускоренно
из состояния покоя. В
первые 20
с
он совершает
100 оборотов.
Каковы его
угловые
скорость и ускорение по истечении
20 с?
Решение.
Так как вал начинает вращаться из
состояния покое, то ω0=0.
В этом
случае уравнения
при
имеют вид
,
(1)
Из
уравнения
(1) находим
,
где
.
Пример
2. Лебедка
(рис. 2.2.1), поднимающая груз по наклонной
плоскости, состоит из двух валов 1 л 2 с
шестернями (зубчатыми колесами), числа
зубьев которых равны соответственно
z1
= 12 и z2=
48. К валу 2 прикреплен барабан радиусом
r=
0,3 м,
на который наматывается грузовой трос.
Вал 1 вращается равноускоренно с угловым
ускорением ε1
= 8 с–2.
Определить скорость, ускорение и
перемещение груза, а также ускорение
точки В
барабана в момент времени t
= 1 с.
В начальный момент времени система
находилась в покое.

Рис.
2.2.1
Решение.
Найдем угловую скорость ω1
ведущего вала 1 из условия, что оно
вращается с угловым ускорением ε1
= const,
учитывая, что
.
Интегрируя последнее уравнение по
времени, получаем
.
Постоянную
интегрирования получаем из начального
условия: при t=
0 ω1
= 0 (система находилась в покое),
следовательно C1
= 0.
Итак,
угловая скорость вала 1 определяется
уравнением
.
При
t
= 1 с получаем
.
Шестерни
1 и 2 взаимодействуют без проскальзывания.
Поэтому скорости точек их касания (точка
А)
будут одинаковы:
.
Отсюда
находим угловую скорость ω2
вала 2, учитывая, что
:
.
Угловое
ускорение вала 2 равно
.
Поскольку
трос нерастяжим и относительно барабана
не проскальзывает, то скорость груза v
будет равна скорости любой из точек
на ободе барабана, в частности, скорости
точки В:
v
= vB
= ω2r
= 0,6t=|t=1
c
=0,6 м/с.
Ускорение
точки В
равно векторной сумме касательного
(вращательного) и нормального
(центростремительного) ускорений:
.
Направление
вращательного ускорения определяется
направлением углового ускорения ε2,
а его модуль равен
м/с2.
Центростремительное ускорение направлено
к оси вращения вала 2 и равно по модулю
м/с2.
Модуль
ускорения точки В
м/с2.
Ускорение
груза можно найти, взяв производную по
времени от его скорости, так как это
касательное ускорение:
м/с2.
Перемещение
груза определяется интегрированием
модуля скорости по времени:
м.
Ответ:
v
= 0,6 м/с;
а
= 0,6 м/с2;
s
= 0,3 м;
аB
= = 1,34 м/с2.
Пример
3. Маховик
радиусом R
= 0,5 м
вращается так, что его угловая скорость
меняется в соответствии с уравнением
.
Для момента времени t
= 0,5 с
после начала движения определить
скорость и ускорение точки на ободе
маховика. Установить, за какое время
маховик сделает 100 полных оборотов.

Рис.
2.2.2
Решение.
Для момента времени t
= 0,5 с
получаем ω = 0,680 с–1,
и скорость точки на ободе маховика равна
v
= ωR
= 0,340 м/с.
Угловое ускорение
маховика
.
Ускорение
точки на ободе маховика равно сумме
двух составляющих ускорений:
,
где
и
— касательное (вращательное) и
нормальное (центростремительное)
ускорения точки.
Учитывая,
что вращательное ускорение равно по
модулю
,
найдем
=0,680
м/с2;
центростремительное ускорение
.
Модуль полного ускорения точки
м/с.
Направления
скорости и ускорений показаны на
рис. 2.2.2.
Поскольку
значения величин угловой скорости и
углового ускорения имеют одинаковые
знаки, вращение тела ускоренное.
Соответственно, совпадают по направлению
угловая скорость и угловое ускорение
тела, а также скорость точки и вращательное
ускорение.
Поворот
маховика на 100 полных оборотов
соответствует углу его поворота φ
= 200π
рад.
Выражение для угла поворота найдем из
уравнения
.
Имеем
.
Итак,
,
откуда находим t
= 2,19 с.
Пример
4.
Вращение
маховика в
период пуска
машины определяется уравнением
где t
– в
с,
φ
– в рад.
Определить модуль и направление
ускорения точки, отстоящей от оси
вращения на расстоянии
50 см,
в тот момент, когда ее скорость равна
8
м/с.

Рис.
2.2.3
Решение.
По уравнению вращения маховика находим
его угловые скорость и ускорение согласно
формулам:
(1)
(2)
Пользуясь
формулой,
находим момент времени t1,
когда скорость точки М
равна
8 м/с:
По
этому значению
из (1) находим
t1:
По
уравнению
(2) вычисляем
ε,
а затем по формулам
модули
вращательного,
центростремительного
и полного
ускорений точки М
в этот момент времена:

Как
видно, модуль полного ускорения точки
весьма мало отличается от модуля
центростремительного ускорения точки
(рис. 2.2.3).
Направление
ускорения
точки
определяется
углом β,
образованным ускорением
и радиусом
СМ:
Пример
5. Груз А,
подвешенный к нити АВ,
намотанной на барабан, опускается
равноускоренно из состояния покоя,
приводя во вращение барабан. За первые
3 с
барабан совершает 9 оборотов.
Определить в конце 5-й секунды скорость
и ускорение точки обода барабана, а
также груза А,
если диаметр барабана D
= 30 см
(рис. 2.2.4, а).

Рис.
2.2.4
Решение.
Барабан вращается равноускоренно
согласно уравнению:
.
Формула
угловой скорости имеет вид:
.
Для
того чтобы начальное значение угла
поворота
было равно нулю, следует неподвижную
полуплоскость поместить в начальном
положении подвижной полуплоскости,
вращающейся с барабаном. Выполним это
и получим
.
При
вращении из состояния покоя начальная
угловая скорость барабана равна нулю
.
При этих условиях
;
(1)
.
(2)
Так
как при t
= 3 с
рад,
то из уравнения (1) определим угловое
ускорение
:
.
Из
уравнения (2) найдем угловую скорость
барабана в конце 5-й секунды:
.
Определим
в точке В
обода барабана (рис. 2.2.4, б)
модули вращательной скорости, вращательного
и центростремительного ускорений в
этот же момент времени по формулам:
(модуль
вращательного ускорения точки тела при
равнопеременном вращении одинаков для
всех моментов времени);
.
Модуль
полного ускорения точки обода барабана
определяется по формуле:
.
Вследствие
незначительной величины модуля
вращательного ускорения по сравнению
с модулем центростремительного ускорения
полное ускорение приближенно равно
центростремительному.
.
Ускорение
груза (рис. 2.2.4,
б) равно
вращательному ускорению точки обода:
.
Пример
6. Центробежный
регулятор вращается с постоянной угловой
скоростью ω
вокруг вертикальной оси. Угол АСВ
равен 60о,
а ускорение шаров А
и В
равно по величине 100g,
где g=980
см/с2.
Стержни АС,
ВС,
АD
и BD
одинаковой длины l=10
см.
Сколько оборотов в минуту делает
регулятор (рис. 2.2.5)?

Рис.
2.2.5
Решение.
Для того чтобы найти величину угловой
скорости регулятора, напишем зависимость
ускорения шара от параметров регулятора.
Так как регулятор вращается с постоянной
скоростью, то ускорение шара будет
центростремительным ускорением, модуль
которого определяется формулой
,
где
r
– кратчайшее расстояние шара до оси
вращения.
С
другой стороны, согласно условию,
.
Приравнивая эти два выражения нормального
ускорения шара, находим:
.
Угловая
скорость регулятора будет равна
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Тема: Определить угловое ускорение маховика (Прочитано 3981 раз)
0 Пользователей и 1 Гость просматривают эту тему.
6. Маховик начал вращаться равноускоренно и за промежуток времени Δt = 20 с достиг частоты вращения n = 800 мин-1. Определить угловое ускорение ε маховика. Ответ округлить до целого числа рад/с2. Сделать рисунок.
Записан
Решение.
Угловая скорость маховика при равноускоренном движении по окружности определяется по формуле
[ begin{align}
& omega ={{omega }_{0}}+varepsilon cdot t,,(1),{{omega }_{0}}=0,omega =varepsilon cdot t,varepsilon =frac{omega }{t}(2),omega =2cdot pi cdot n(3),varepsilon =frac{2cdot pi cdot n}{t}(4). \
& varepsilon =frac{2cdot 3,14cdot 800}{20cdot 60}=4. \
end{align} ]
ω – угловая скорость, ε – угловое ускорение.
Ответ: 4 рад/с2.
« Последнее редактирование: 21 Октября 2018, 13:46 от alsak »
Записан
Угловое ускорение объекта обусловлено вращательным движением объекта вокруг своей оси из точки центра тяжести, а крутящий момент отвечает за вращательное движение объекта.
Поскольку сила приложена к телу по касательной, эквивалентная сила действует на точку, расположенную напротив нее, и действует в противоположном направлении, что стремится вращать ее с угловым ускорением, и, следовательно, крутящий момент и угловое ускорение входят в картину в картине. случае вращающегося тела.
Связь между крутящим моментом и угловым ускорением
Чистый крутящий момент, действующий на объект, прямо пропорционален угловому ускорению объекта и обратно пропорционален инерции вращения вокруг его оси вращения.
Скорость, приобретаемая объектом, зависит от крутящего момента, приложенного к телу, и угловое ускорение – это изменение угловой скорости со временем вращения объекта вокруг оси.
Формула крутящего момента и углового ускорения
We знать, что крутящий момент является произведением силы, приложенной к объекту, и того, насколько далеко он смещен от приложенной силы.
τ = сила * перемещение
И F=ма
Рассмотрим круглый диск радиуса ‘r’, и к диску приложена сила F, чтобы вращать его вокруг оси, создающей крутящий момент τ, движущийся с угловым ускорением α.
θ является угловое смещение диска при приложении крутящего момента, ω – угловая скорость а – ускорение диска.
Пусть смещение равно ‘r’ от оси вращения, тогда получим
т = ма*р
Если объект вращается с угловой скоростью ω, то угловая скорость связана с угловым ускорением как α=ω/t а ускорение объекта связано с угловым ускорением как
а=ра
Используя это в приведенном выше уравнении, мы имеем
т = г-н2
Термин г-н2 есть не что иное, как момент инерции объекта, распространенный во всех измерениях объекта. Следовательно,
а=Iα
Это уравнение, обозначающее связь между крутящим моментом и угловым ускорением объекта.
График крутящего момента и углового ускорения
Ссылаясь на уравнение, дающее связь крутящего момента и углового ускорения объекта, которое мы нашли выше, мы можем построить график крутящего момента и углового ускорения.
Предположим, что момент инерции равен I=0.67 кг·м.2, затем
Если α=10, то
τ=Iα
=0.67*10=6.7 Нм
Если α=20, то
τ= 0.67* 20=13.4 Нм
Если α =30, то
τ= 0.67* 30=20.1 Нм
Следовательно, мы получаем график зависимости крутящего момента от углового ускорения в секунду, как показано ниже:
Наклон графика зависимости крутящего момента от углового ускорения, очевидно, даст нам момент инерции тела, и видно, что угловое ускорение линейно возрастает с увеличением крутящего момента.
Следовательно, если мы узнали крутящий момент, придаваемый объекту, и угловое ускорение, которое приобретает объект, то можем узнать момент инерции объекта, построив график зависимости крутящего момента от углового ускорения.
Крутящий момент и направление углового ускорения
Если мы внимательно посмотрим на приведенную ниже диаграмму, мы сможем понять, что сила приложена к объекту с касательной к нему и соответствующий ей объект начинает вращаться с угловым ускорением, перпендикулярным приложенной к объекту силе.
Крутящий момент, создаваемый на оси вращения, показан на диаграмме, которая перпендикулярна силе, а также угловому ускорению объекта.
То же самое мы можем изобразить на трех осях, как показано ниже:
На этой диаграмме мы ясно видим, что сила, угловое ускорение и крутящий момент лежат перпендикулярно друг другу.
Если сила приложена к оси x, то направление углового ускорения объекта будет перпендикулярно силе в направлении y, а соответствующий крутящий момент будет приложен по азимутальной оси, которая перпендикулярна оси z к обеим сторонам. .
Эту же мысль можно запомнить, используя правило большого пальца правой руки.
Если вы держите правую руку, как показано на рисунке выше, большой палец обозначает направление крутящего момента, действующего на объект, изогнутые пальцы представляют направление углового ускорения объекта, а сила, перпендикулярная обоим, обозначается ладонь вашей руки.
Как найти крутящий момент с угловым ускорением?
Угловое ускорение объекта является результатом действия крутящего момента на его тело.
Крутящий момент легко найти, зная угловое ускорение объекта и момент инерции по формуле τ=Iα, где τ — крутящий момент, действующий на тело, I — момент инерции, а альфа — угловое ускорение объекта.
Момент инерции представляет собой произведение суммы всех масс частицы, составляющей объект, на квадрат расстояния от точки углового ускорения края объекта до оси вращения и является тенденцией объект для снижения углового ускорения.
Если твердый диск массой 1 кг и радиусом 12 см вращается с угловым ускорением 2π рад/с2 тогда какой крутящий момент приложен к диску?
Данный: м =1кг
г = 12 см = 0.12 м
а =2π рад/с2
Момент инерции диска равен
Теперь мы можем рассчитать крутящий момент, действующий на диск, как
Следовательно, крутящий момент, приложенный к объекту, составляет 0.045 Нм.
Как найти угловое ускорение по крутящему моменту?
Как только к телу будет приложен крутящий момент, оно начнет вращаться с некоторым угловым ускорением, зависящим от момента инерции тела.
Угловое ускорение можно рассчитать исходя из величины крутящего момента, приложенного к объекту, по формуле α= τ/I . Приложенный крутящий момент создаст угловое ускорение, в то время как момент инерции тела попытается одновременно противодействовать этому угловому ускорению.
Каково угловое ускорение шара для боулинга массой 800 г и радиусом 12 см, если крутящий момент 3.5 раз 10-4 Nm применяется к мячу?
Данный: т=3.5 *10-4 Nm
г = 12 см = 0.12 м
м = 800 г = 0.8 кг
Теперь давайте сначала рассчитаем момент инерции шара для боулинга. Так как шар для боулинга имеет сферическую форму
Следовательно, угловое ускорение шара для боулинга равно
Угловое ускорение шара для боулинга равно 0.076 м/с.2.
Возникает ли угловое ускорение за счет крутящего момента?
Угловое ускорение является результатом вращательного движения объекта, которое достигается за счет приложения к телу крутящего момента.
Крутящий момент создается приложением силы, перпендикулярной оси вращения тела, и тело начинает вращаться вокруг своей оси вращения, образуя угол 90 градусов к направлению приложенного крутящего момента.
Крутящий момент и угловое ускорение маховика
Маховик — это механизм, используемый для хранения энергии внутри него и вырабатывающий большое количество электроэнергии, когда ему придается крутящий момент для ускорения.
Рассмотрим маховик, вращающийся по часовой стрелке, когда на него действует сила F, как показано на рисунке ниже. Радиус маховика равен «r», а его ось вращения расположена в центре.
Крутящий момент, действующий на маховик, равен
τ=сила*смещение
Сила тяжести, действующая на маховик, равна F=mg, а радиальное смещение маховика происходит по его радиусу ‘r’.
Отсюда получаем выражение для крутящего момента в виде
τ=мгр
Так как маховик поднят на высоту h, потери потенциальной энергии в машине равны mgh.
Кинетическая энергия вращающегося маховика, вращающегося с угловой скоростью ω, равна
КЭ =1/2Iω2
Где I — момент инерции, а ω — угловая скорость объекта.
Угловое ускорение объекта представляет собой изменение угловой скорости во времени и определяется выражением
α=dω/dt
Крутящий момент на маховике равен
τ=Iα
Замена на альфа
τ =Idω/dt
Это уравнение не зависит от углового ускорения.
We знать, что крутящий момент прямо пропорционально угловому ускорению по уравнению
τ=Iα
Следовательно, угловое ускорение есть отношение крутящего момента к моменту инерции объекта.
α =τ/I
Итак, мы нашли уравнение крутящего момента для маховика, давайте подставим его сюда в это уравнение, чтобы найти угловое ускорение.
α =мгр/I
Умножая r в числителе и знаменателе, получаем
α = г-н2г/л
Так как я=мистер2 используя это в уравнении выше
α =Ig/Ir
α=г/р
Компания угловое ускорение обратно пропорционально к радиусу объекта; это означает, что если диаметр объекта больше, угловое ускорение объекта будет меньше.
Крутящий момент и угловое ускорение для твердого тела
Твердое тело — это твердый объект, который не деформируется ни в какой последовательности, а масса непрерывно распределяется в твердом теле.
Момент инерции твердого тела постоянен и прямо пропорционален угловому моменту вращающегося тела. Он задается соотношением как
I=L/ω
Следовательно, крутящий момент на твердом теле равен
А крутящий момент связан с моментом инерции уравнением
Подставляя сюда уравнение момента импульса в это уравнение, получаем
ω есть не что иное, как угловая скорость и равна угловому ускорению во времени.
Отсюда получаем, что крутящий момент, действующий на твердое тело, также равен моменту количества движения тела в единицу времени.
Следовательно, теперь мы можем найти угловое ускорение объекта как
По этой формуле можно найти угловое ускорение твердого тела.
Каковы угловое ускорение и крутящий момент на цилиндрическом стержне твердой массы?
Рассмотрим цилиндрический стержень длиной «L», вращаемый по часовой стрелке, тогда крутящий момент, действующий на цилиндрический стержень массы м
Сила гравитации равна F=mg, а r составляет половину длины стержня, расстояние от оси вращения до точки, в которой действует сила.
Поскольку угол, образуемый вращающейся осью с угловым ускорением объекта, составляет 90 градусов,
Sin900=1
Крутящий момент к угловому ускорению стержня равен
Теперь приравнивая оба уравнения,
Следовательно, мы получили угловое ускорение жесткого цилиндрического стержня.
Часто задаваемые вопросы
Каковы крутящий момент и угловое ускорение, если ребенок массой 21 кг сидит на карусели массой 60 кг радиусом 1.2 м и для ее вращения приложена сила 230 Н?
Данный: Вес ребенка m=21кг
Вес карусели М=60кг.
Радиус карусели r=1.2м.
F = 230 Н
Момент инерции карусели равен
Момент инерции ребенка, сидящего на карусели, равен
Следовательно, полный момент инерции равен
Крутящий момент, действующий на карусель, равен
Отсюда угловое ускорение карусели от крутящего момента 276 Нм равно
Угловое ускорение карусели равно 4.76 м / с2.
Каковы угловое ускорение и крутящий момент потолочного вентилятора массой 5.4 кг, имеющего 3 лопасти длиной 1 м и центральный диск радиусом 12 см? Масса каждой лопасти составляет 800 граммов, а центр тяжести весит 3 кг.
Данный: Масса лопастей m=800г=0.8кг.
Масса диска М =3кг
Длина 3-х лопастей L = 1м
Радиус диска r = 12 см = 0.12 м
Общая масса вентилятора 5.4 кг.
Крутящий момент лопастей вентилятора
Момент инерции лопасти
Следовательно, момент инерции 3-х лопастей равен
Момент инерции диска равен
Следовательно, полный момент инерции равен
Следовательно, теперь мы можем вычислить угловое ускорение вентилятора
Компания угловое ускорение потолочный вентилятор 64.33 рад/с2.