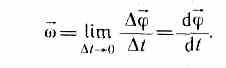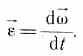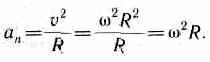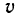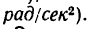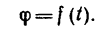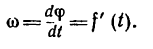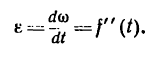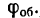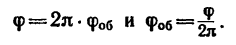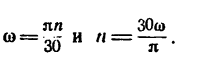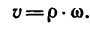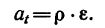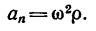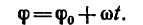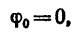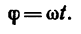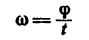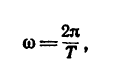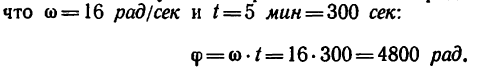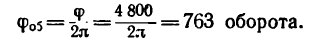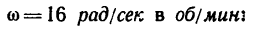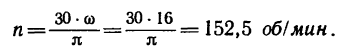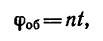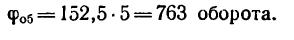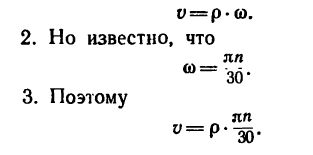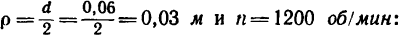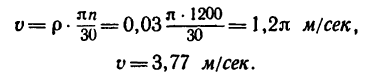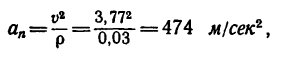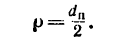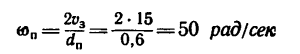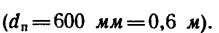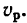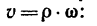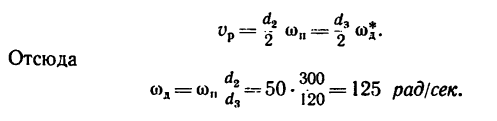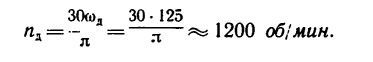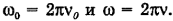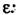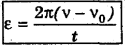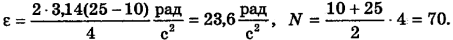Маховое колесо радиуса начинает вращаться равноускоренно из состояния покоя. Через 10 мин после начала движения оно имеет угловую скорость, равную
. Определить угловое ускорение колеса; скорость и ускорение точки на ободе колеса и число оборотов через 10 мин после начала вращения.
Решение:
1. Колесо вращается равноускоренно, т.е. его угловое ускорение ε постоянно. При этом угловая скорость и угол поворота колеса изменяются по законам:
где , т.к. движение начинается из состояния покоя.
Подставляя и
, находим
причем , где N – число оборотов колеса. Тогда
оборотов.
2. Скорость точки на ободе колеса определяется по формуле и равна
м/с. Скорость направлена по касательной к окружности радиуса R, т.е. перпендикулярно радиусу ОМ.
3. Ускорение точки на ободе колеса складывается из касательного и нормального ускорений: . Значения касательного и нормального ускорений соответственно равны:
. Модуль ускорения точки равен
Векторы скорости и ускорения точки показаны на рисунке 2.2.2.
Подставляя числовые значения, находим:
aτ = 0,628 см/с2, an = 47,37 м/с2, a = 47,4 м/с2.


рис. 2.2.2 рис. 2.2.3 рис. 2.2.4
Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.
Угловая скорость
Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.
Обозначение угловой скорости: ω (омега).
Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.
С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.
Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:
Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.
Быстрота изменения угла φ (перемещения плоскости П из положения П1 в положение П2) – это и есть угловая скорость:
Приняв вектор k как единичный орт положительного направления оси, получим:
Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.
Формулы угловой скорости
Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:
- если известно количество оборотов n за единицу времени t:
- если задан угол поворота φ за единицу времени:
- если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:
Размерности угловой скорости:
- Количество оборотов за единицу времени [об/мин], [c-1].
- Угол поворота за единицу времени [рад/с].
Определение угловой скорости
Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.
Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.
Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.
Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.
Другие примеры решения задач >
Угловое ускорение
Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:
Обозначение: ε (Эпсилон)
Единицы измерения углового ускорения: [рад/с2], [с-2]
Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.
Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).
Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:
Расчет углового ускорения
Пример: По заданному значению касательной составляющей полного ускорения aτ точки B, расположенной на расстоянии r от центра вращения колеса.
Требуется определить величину и направление углового ускорения колеса ε, если aτ = 10 м/с2, r = 50 см.
Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.
Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.
В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:
Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость
ω = 1,5 с-1 = 9,42 рад/с.
Смотрите также:
- Примеры расчета угловой скорости и ускорения
- Скорости и ускорения точек вращающегося тела
Рассмотрим
твердое тело, которое вращается
вокруг неподвижной оси. Тогда отдельные
точки этого тела будут описывать
окружности разных радиусов, центры
которых лежат на оси вращения. Пусть
некоторая точка движется по окружности
радиуса R
(рис.6).
Ее положение через промежуток времени
t
зададим
углом .
Элементарные (бесконечно малые) углы
поворота рассматривают как векторы.
Модуль вектора d
равен
углу поворота, а его направление совпадает
с направлением поступательного
движения острия винта, головка которого
вращается в направлении движения
точки по окружности, т. е. подчиняется
правилу
правого, винта (рис.6).
Векторы, направления которых связываются
с направлением вращения, называются
псевдовекторами
или
аксиальными
векторами. Эти
векторы не имеют определенных точек
приложения: они могут откладываться
из любой точки оси вращения.
Угловой
скоростью называется
векторная величина, равная первой
производной угла поворота тела по
времени:
Вектор
«в направлен вдоль оси вращения по
правилу правого винта, т. е. так же, как
и вектор d
(рис. 7). Размерность угловой скорости
dim=T-1,
a .
ее единица — радиан в секунду (рад/с).
Линейная скорость
точки (см. рис. 6)
В векторном виде
формулу для линейной скорости можно
написать как векторное произведение:
При
этом модуль векторного произведения,
по определению, равен
,
а
направление совпадает с
направлением
поступательного движения правого винта
при его вращении от
к R.
Если
=const,
то
вращение равномерное и его можно
характеризовать периодом
вращения Т
—
временем, за которое точка совершает
один полный оборот, т. е. поворачивается
на угол 2.
Так как промежутку времени t=T
соответствует =2,
то =
2/Т,
откуда
Число
полных оборотов, совершаемых телом при
равномерном его движении по окружности,
в единицу времени называется частотой
вращения:
Угловым
ускорением называется
векторная величина, равная первой
производной угловой скорости по
времени:
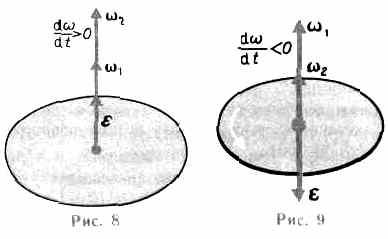
При вращении тела
вокруг неподвижной оси вектор углового
ускорения направлен вдоль оси вращения
в сторону вектора элементарного
приращения угловой скорости. При
ускоренном движении вектор
13
сонаправлен
вектору
(рис.8),
при замедленном.— противонаправлен
ему (рис. 9).
Тангенциальная
составляющая ускорения
Нормальная
составляющая ускорения
Таким
образом, связь между линейными (длина
пути s,
пройденного
точкой по дуге окружности радиуса R,
линейная
скорость v,
тангенциальное
ускорение а,
нормальное ускорение аn)
и угловыми величинами (угол поворота
,
угловая скорость (о, угловое ускорение
)
выражается следующими формулами:
В
случае равнопеременного движения точки
по окружности (=const)
где
0
— начальная угловая скорость.
Контрольные
вопросы
• Что
называется материальной точкой? Почему
в механике вводят такую модель?
• Что
такое система отсчета?
• Что
такое вектор перемещения? Всегда ли
модуль вектора перемещения равен отрезку
пути,
пройденному точкой?
• Какое
движение называется поступательным?
вращательным?
• Дать
определения векторов средней скорости
и среднего ускорения, мгновенной
скорости
и мгновенного
ускорения. Каковы их направления?
• Что
характеризует тангенциальная
составляющая ускорения? нормальная
составляющая
ускорения? Каковы
их модули?
• Возможны
ли движения, при которых отсутствует
нормальное ускорение? тангенциальное
ускорение? Приведите
примеры.
• Что
называется угловой скоростью? угловым
ускорением? Как определяются их
направления?
• Какова
связь между линейными и угловыми
величинами?
Задачи
1.1.
Зависимость
пройденного телом пути от времени
задается уравнением s
= A+Вt+Сt2+Dt3
(С
= 0,1 м/с2,
D
= 0,03 м/с3).
Определить: 1) через какое время после
начала движения ускорение а тела будет
равно 2 м/с2;
2) среднее ускорение <а>
тела за этот промежуток времени. [ 1) 10
с; 2) 1,1 м/с2]
1.2.
Пренебрегая сопротивлением воздуха,
определить угол, под которым тело брошено
к горизонту, если максимальная высота
подъема тела равна 1/4 дальности его
полета. [45°]
1.3.
Колесо
радиуса R
=
0,1 м вращается так, что зависимость
угловой скорости от времени задается
уравнением
= 2At+5Вt4
(A=2
рад/с2
и B=1
рад/с5).
Определить полное ускорение точек обода
колеса через t=1
с после начала вращения и число оборотов,
сделанных колесом за это время. [а =
8,5 м/с2;
N
= 0,48]
14
1.4.
Нормальное ускорение точки, движущейся
по окружности радиуса r=4
м,
задается уравнением аn=А+-Bt+Ct2
(A=1
м/с2,
В=6
м/с3,
С=3
м/с4).
Определить: 1) тангенциальное ускорение
точки; 2) путь, пройденный точкой за время
t1=5
с после начала движения; 3) полное
ускорение для момента времени t2=1
с. [ 1) 6 м/с2;
2) 85 м; 3) 6,32 м/с2]
1.5.
Частота
вращения колеса при равнозамедленном
движении за t=1
мин
уменьшилась от 300 до 180 мин-1.
Определить: 1) угловое ускорение колеса;
2) число полных оборотов, сделанных
колесом за это время. [1)
0,21 рад/с2;
2) 360]
1.6.
Диск
радиусом R=10
см вращается вокруг неподвижной оси
так, что зависимость угла поворота
радиуса диска от времени задается
уравнением =A+Bt+Ct2+Dt3
(B
= l рад/с,
С=1
рад/с2,
D=l
рад/с3).
Определить для точек на ободе колеса к
концу второй секунды после начала
движения: 1) тангенциальное ускорение
а;
2) нормальное ускорение аn;
3) полное ускорение а. [ 1) 0,14 м/с2;
2) 28,9 м/с2;
3) 28,9 м/с2]
Соседние файлы в папке Трофимова
- #
- #
- #
- #
- #
- #
Вращательное движение твердого тела:
При поступательном движении тела все его точки движутся по одинаковым траекториям и в каждый данный момент они имеют равные скорости и равные ускорения.
Поэтому поступательное движение тела задают движением какой-либо одной точки, обычно движением центра тяжести.
Рассматривая в какой-либо задаче движение автомобиля (задача 147-29) или тепловоза , фактически рассматриваем движение их центров тяжести.
Вращательное движение тела нельзя отождествить с движением какой-либо одной его точки. Ось любого вращающегося тела (маховика дизеля, ротора электродвигателя, шпинделя станка, лопастей вентилятора и т. п.) в процессе движения занимает в пространстве относительно окружающих неподвижных тел одно и то же место.
Движение материальной точки или поступательное движение тела характеризуют в зависимости от времени линейные величины s (путь, расстояние),
Вращательное движение тела в зависимости от времени t характеризуют угловые величины: 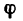
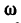
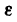
Закон вращательного движения тела выражается уравнением
Угловая скорость — величина, характеризующая быстроту вращения тела, определяется в общем случае как производная угла поворота по времени
Угловое ускорение – величина, характеризующая быстроту изменения угловой скорости, определяется как производная угловой скорости
Приступая к решению задач на вращательное движение тела, необходимо иметь в виду, что в технических расчетах и задачах, как правило, угловое перемещение выражается не в радианах 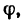
Поэтому необходимо уметь переходить от числа оборотов к ра-дианному измерению углового перемещения и наоборот.
Так как один полный оборот соответствует 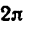
Угловая скорость в технических расчетах очень часто измеряется в оборотах, произведенных в одну минуту (об/мин), поэтому необходимо отчетливо уяснить, что 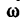
Переход от одних единиц угловой скорости к другим производится по формулам
При вращательном движении тела все его точки движутся по окружностям, центры которых расположены на одной неподвижной прямой (ось вращающегося тела). Очень важно при решении задач, приведенных в этой главе, ясно представлять зависимость между угловыми величинами 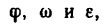
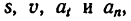
Если р- расстояние от геометрической оси вращающегося тела до какой-либо точки А (на рис. 205 р=ОА), то зависимость между 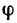
s—p-
Зависимость между угловой скоростью тела и скоростью точки в каждый данный момент выражается равенством
Касательное ускорение точки зависит от углового ускорения и определяется формулой
Нормальное ускорение точки зависит от угловой скорости тела и определяется зависимостью
При решении задачи, приведенной в этой главе, необходимо ясно понимать, что вращением называется движение твердого тела, а не точки. Отдельно взятая материальная точка не вращается, а движется но окружности — совершает криволинейное движение.
Равномерное вращательное движение
Если угловая скорость 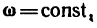
Уравнение равномерного вращения имеет вид
В частном случае, когда начальный угол поворота
Угловую скорость равномерно вращающегося тела
можно выразить и так:
где Т — период вращения тела; 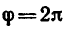
Задача №1
Маховое колесо вращается равномерно с угловой скоростью 16 рад/сек. Определить, сколько оборотов сделает колесо за 5 мин вращения.
Решение 1.
1. Находим угол поворота маховика в радианах, имея в виду,
2. Находим число оборотов маховика:
Таким образом, за 5 мин маховик сделает 763 оборота. Решение 2.
1. Переведем угловую скорость
2. Имея в виду, что уравнение равномерного вращательного движения можно представить так:
где 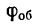
Задача №2
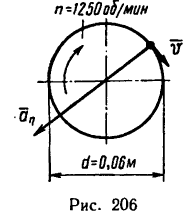
Вал, диаметр которого 0,06 м, вращается равномерно и делает 1200 об/мин. Определить скорость и ускорение точек вала на его поверхности (рис 206). Решение.
1. Скорость точки вращающегося тела можно найти по формуле
4 Подставим сюда
Вал вращается равномерно, значит скорость точек остается
численно неизменной. По этой же касательное ускорение.
5. Нормальное ускорение найдем из формулы
которое также в данном случае остается по модулю неизменным.
Задача №3
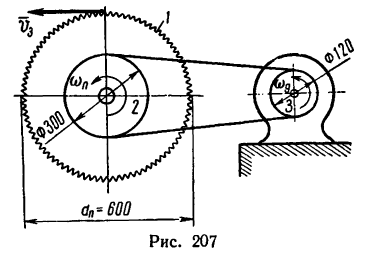
Дисковая пила 1 имеет диаметр 600 мм.
На валу пилы насажен шкив 2 диаметром 300 мм, а шкив
соединен бесконечным ремнем со шкивом двигателя 3 (рис. 207) дна» метром 120 мм. С какой угловой скоростью должен вращаться шкив двигателя, чтобы скорость зубьев пилы не превышала 15 м/сек?
Решение.
1. Так как пила 1 и шкив 2 насажены на одном валу, то они имеют одну и ту же угловую скорость <о„ и скорость зубьев пилы 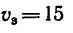
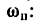
2. Находим угловую скорость шкива 2, который обеспечивает необходимую рабочую скорость зубьев пилы:
3. Теперь найдем угловую скорость юд шкива двигателя. Шкивы 2 и 3 соединены бесконечным ремнем. Полагая, что
ремень не растягивается и не проскальзывает на шкивах, можно считать, что все его точки движутся с одной и той же скоростью Ор. Это означает, что скорости точек, расположенных на поверхностях обоих шкивов, одинаковы и равны
Поэтому применим зависимость
Отсюда
4. Если перевести эту угловую скорость в об[мин, то
Таким образом, для того чтобы зубья пилы имели скорость 15 м/сек, шкив двигателя должен вращаться с угловой скоростью 125 рад/сек или 1200 об/мин.
- Равнопеременное вращательное движение
- Неравномерное вращательное движение
- Плоскопараллельное движение тела
- Определение передаточных отношений различных передач
- Равнопеременное движение точки
- Неравномерное движение точки по любой траектории
- Определение траектории, скорости и ускорения точки
- Кинематический способ определения радиуса кривизны траектории
Пример решения задачи №30.
Маховое колесо, вращаясь равноускоренно, увеличило за t = 4 с частоту вращения с 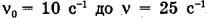
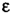
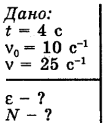
Решение:
Угловое ускорение колеса 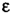
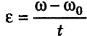
Начальную 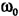
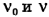
Так мы найдем искомое угловое ускорение
Число оборотов N выразим через среднюю частоту вращения 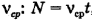
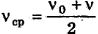
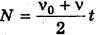
Произведем вычисления:
Ответ: 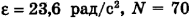
Эта задача взята со страницы подробного решения задач по физике, там теория и задачи по всем темам физики, можете посмотреть:
Физика — задачи с решениями и примерами
Возможно вам будут полезны ещё вот эти задачи: