Как найти угловое ускорение точки колеса

Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.

Обозначение угловой скорости: ω (омега).

Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.

С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.

Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:

Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.

Быстрота изменения угла φ (перемещения плоскости П из положения П₁ в положение П₂) – это и есть угловая скорость:

Приняв вектор k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

1. если известно количество оборотов n за единицу времени t:
   
2. если задан угол поворота φ за единицу времени:
   
3. если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:
   

Размерности угловой скорости:

• Количество оборотов за единицу времени [об/мин], [c^-1].
• Угол поворота за единицу времени [рад/с].

Определение угловой скорости

Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.

Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.

Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.

Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.

Другие примеры решения задач >

Угловое ускорение

Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:

Обозначение: ε (Эпсилон)

Единицы измерения углового ускорения: [рад/с²], [с^-2]

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

Расчет углового ускорения

Пример: По заданному значению касательной составляющей полного ускорения a_τ точки B, расположенной на расстоянии r от центра вращения колеса.

Требуется определить величину и направление углового ускорения колеса ε, если a_τ = 10 м/с², r = 50 см.

Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.

Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

ω = 1,5 с^-1 = 9,42 рад/с.

Смотрите также:

• Примеры расчета угловой скорости и ускорения
• Скорости и ускорения точек вращающегося тела

Зубчатые колеса 1 и 2 радиусов r₁ и r₂, соответственно, находятся во внешнем зацеплении (рис. 2.2.3). Колесо 1 имеет в данный момент угловую скорость ω₁ и угловое ускорение ε₁. Найти угловую скорость и угловое ускорение колеса 2, а также касательные и нормальные ускорения находящихся в соприкосновении точек колес.

Решение:

1. Скорости точек соприкосновения колес, находящихся в зацеплении, равны, т.е.

,

откуда

в любой момент времени.

2. Найдем угловое ускорение колеса 2:

Отсюда следует, что угловые ускорения колес связаны такой же зависимостью, как и угловые скорости, а касательные ускорения точек соприкосновения колес равны между собой:

Нормальные ускорения точек соприкосновения колес определяются формулами .

Направления векторов , , , показаны на рисунке 2.2.4.

рис. 2.2.4

Лень разбираться с решением задач? Добро пожаловать к нам в телеграм, где собрана интересная и полезная информация для учащихся и не только. 

Движение по окружности: определение, примеры

Движение по окружности – самый простой случай криволинейного движения. 

Примеры движения по окружности:

• грузовик движется по мосту с радиусом кривизны R;
• атлет крутит шар в руке, перед тем как бросить его;
• космическая станция летает по кругу над поверхностью Земли;
• катафот вращается на раскрученном колесе велосипеда.

Приведем ниже кинематические соотношения для поступательного и вращательного движений:

Вопросы на движение по окружности

Вопрос 1. Как направлено центростремительное ускорение?

Ответ. Центростремительное ускорение направлено по радиус-вектору к центру окружности.

Вопрос 2. Велосипед катится по прямой. Как можно описать движение точки на ободе его колеса? Является ли это движение движением по окружности?

Ответ. Это одновременно поступательное движение и движение по окружности. Траекторией такого движения будет спираль.

Вопрос 3. Как направлено ускорение, если тело движется по окружности неравномерно?

Ответ. В таком случае к центростремительному (или нормальному) ускорению добавляется тангенциальное ускорение, направленное по касательной к окружности. Полное ускорение тела представляет собой векторную сумму тангенциального и нормального ускорений.

Вопрос 4. Что такое линейная и угловая скорость?

Ответ. Линейная скорость – это скорость точки, движущейся поступательно. Она измеряется в метрах в секунду. Угловая скорость – скорость, с которой меняется угол, на который поворачивается радиус-вектор точки при движении по окружности.

Вопрос 5. При поступательном движении мерой инерции является масса. А что является мерой инерции при вращательном движении?

Ответ. При вращательном движении мерой инерции является момент инерции. Это отдельная обширная тема, задачи на нахождение и использование момента инерции рассмотрены в других статьях по физике.

Задачи на движение по окружности

Как решать задачи на движение по окружности? Так же, как и все остальные! Для начала, вот памятка по решению физических задач и полезный список формул. Кстати! Для всех наших читателей действует скидка 10% на любой вид работы.

Задача №1. Нахождение линейной скорости при движении по окружности

Условие

Тело движется по окружности с ускорением 3 метра на секунду в квадрате по окружности радиусом 40 метров. Какова линейная скорость тела?

Решение

В данном случае ввиду имеется нормальное ускорение. Поэтому, для решения достаточно вспомнить всего одну формулу:

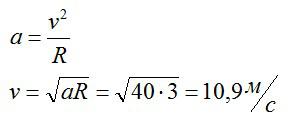
Ответ: 10,9 м/с.

Задача №2. Нахождение углового ускорения

Условие

Колесо, вращаясь с постоянным ускорением, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найти угловое ускорение колеса.

Решение

Запишем закон вращения, учитывая, что по условию начальная угловая скорость равна нулю:

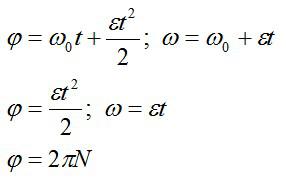
Выразим угловое ускорение из первого уравнения, а время – из второго. Затем подставим выраженное время в выражение для ускорения и сократим:

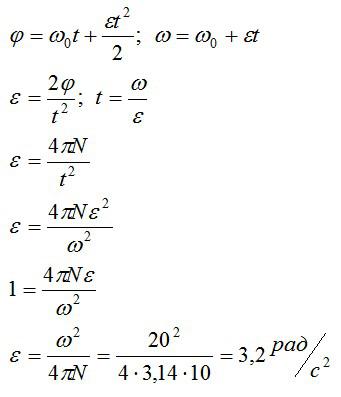
Ответ: 3,2 радиан на секунду в квадрате.

Чтобы перевести угол из радианов в градусы достаточно запомнить соотношение: в одном полном обороте 2пи радиан, или 360 градусов. Следовательно, в одном радиане примерно 57,3 градуса.

Задача №3. Нахождение скорости движения по окружности

Условие

Во сколько раз линейная скорость точки обода колеса радиусом 8 см больше линейной скорости точки, расположенной на 3 см ближе к оси вращения колеса?

Решение

Две точки вращаются на одном колесе, а значит, с одинаковой частотой. Используем соотношения для скорости:

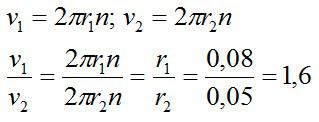
Ответ: скорость точки на ободе больше в 1,6 раза.

Задача №4. Нахождение периода и частоты при движении по окружности

Условие

Маховик равномерно вращается и за время t=1 мин совершает N=2400 оборотов. Какова частота вращения маховика, период обращения и линейная скорость точки, расположенной на расстоянии 10 сантиметров от центра маховика?

Решение

По определению:

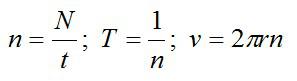
Подставим значения, предварительно переведя все величины в систему СИ, и вычислим:

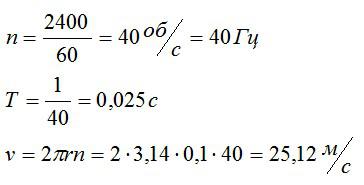
Ответ: 40 Гц; 0,025 с; 25,12 м/с.

Задача №5. Нахождение полного ускорения при движении по окружности

Условие

Тело вращается вокруг стационарной оси по закону фи=10+20t-2t^2. Нужно найти полное ускорение точки, находящейся на расстоянии 10 см от оси вращения в момент времени t=4c.

Решение

Полное ускорение – векторная сумма нормального и тангенциального ускорений.

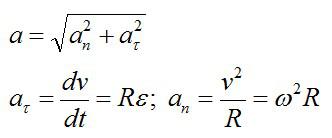
Вспоминаем, что скорость и ускорение можно вычислить через производные, зная закон движения:

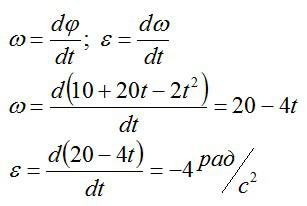
Подставляем значение t из условия и вычисляем:

 
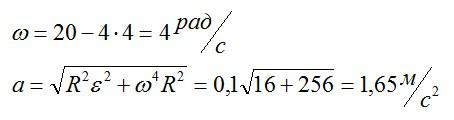
Ответ: 1,65 метра в секунду.

Нужна помощь в выполнении заданий? Обращайтесь в профессиональный студенческий сервис в любое время.

Рассмотрим
твердое тело, которое враща­ется
вокруг неподвижной оси. Тогда от­дельные
точки этого тела будут описывать
окружности разных радиусов, центры
ко­торых лежат на оси вращения. Пусть
не­которая точка движется по окружности
радиуса R
(рис.6).
Ее положение через промежуток времени
t
зададим
углом .
Элементарные (бесконечно малые) углы
поворота рассматривают как векторы.
Мо­дуль вектора d
равен
углу поворота, а его направление совпадает
с направле­нием поступательного
движения острия винта, головка которого
вращается в на­правлении движения
точки по окружности, т. е. подчиняется
правилу
правого, винта (рис.6).
Векторы, направления которых связываются
с направлением вращения, называются
псевдовекторами
или
акси­альными
векторами. Эти
векторы не имеют определенных точек
приложения: они мо­гут откладываться
из любой точки оси вращения.

Угловой
скоростью называется
вектор­ная величина, равная первой
производной угла поворота тела по
времени:

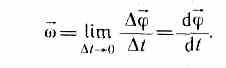
Вектор
«в направлен вдоль оси вращения по
правилу правого винта, т. е. так же, как
и вектор d
(рис. 7). Размерность угловой скорости
dim=T^-1,
a .
ее единица — радиан в секунду (рад/с).

Линейная скорость
точки (см. рис. 6)

В векторном виде
формулу для линейной скорости можно
написать как вектор­ное произведение:

При
этом модуль векторного произведе­ния,
по определению, равен

,
а
направление совпадает с
направлением
поступательного движения правого винта
при его вращении от 
к R.

Если
=const,
то
вращение равномер­ное и его можно
характеризовать перио­дом
вращения Т
—
временем, за которое точка совершает
один полный оборот, т. е. поворачивается
на угол 2.
Так как промежутку времени t=T
соответствует =2,
то =
2/Т,
откуда

Число
полных оборотов, совершаемых телом при
равномерном его движении по окружности,
в единицу времени называет­ся частотой
вращения:

Угловым
ускорением называется
век­торная величина, равная первой
производ­ной угловой скорости по
времени:

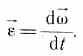
При вращении тела
вокруг неподвижной оси вектор углового
ускорения направлен вдоль оси вращения
в сторону вектора элементарного
приращения угловой ско­рости. При
ускоренном движении вектор

13

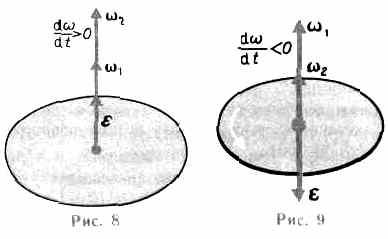
 сонаправлен
вектору 
(рис.8),
при замедленном.— противонаправлен
ему (рис. 9).

Тангенциальная
составляющая ускорения

Нормальная
составляющая ускорения

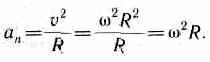
Таким
образом, связь между линейны­ми (длина
пути s,
пройденного
точкой по дуге окружности радиуса R,
линейная
ско­рость v,
тангенциальное
ускорение а_,
нор­мальное ускорение а_n)
и угловыми величи­нами (угол поворота
,
угловая скорость (о, угловое ускорение
)
выражается сле­дующими формулами:

В
случае равнопеременного движения точки
по окружности (=const)

где
₀
— начальная угловая скорость.

Контрольные
вопросы

• Что
называется материальной точкой? Почему
в механике вводят такую модель?

• Что
такое система отсчета?

• Что
такое вектор перемещения? Всегда ли
модуль вектора перемещения равен отрезку
пути,

пройденному точкой?

• Какое
движение называется поступательным?
вращательным?

• Дать
определения векторов средней скорости
и среднего ускорения, мгновенной
скорости

и мгновенного
ускорения. Каковы их направления?

• Что
характеризует тангенциальная
составляющая ускорения? нормальная
составляющая

ускорения? Каковы
их модули?

• Возможны
ли движения, при которых отсутствует
нормальное ускорение? тангенциальное

ускорение? Приведите
примеры.

• Что
называется угловой скоростью? угловым
ускорением? Как определяются их
направления?

• Какова
связь между линейными и угловыми
величинами?

Задачи

1.1.
Зависимость
пройденного телом пути от времени
задается уравнением s
= A+Вt+Сt²+Dt³
(С
= 0,1 м/с²,
D
= 0,03 м/с³).
Определить: 1) через какое время после
начала движения ускорение а тела будет
равно 2 м/с²;
2) среднее ускорение <а>
тела за этот промежуток времени. [ 1) 10
с; 2) 1,1 м/с²]

1.2.
Пренебрегая сопротивлением воздуха,
определить угол, под которым тело брошено
к гори­зонту, если максимальная высота
подъема тела равна 1/4 дальности его
полета. [45°]

1.3.
Колесо
радиуса R
=
0,1 м вращается так, что зависимость
угловой скорости от времени задается
уравнением 
= 2At+5Вt⁴
(A=2
рад/с²
и B=1
рад/с⁵).
Определить полное ускорение точек обода
колеса через t=1
с после начала вращения и число оборотов,
сделан­ных колесом за это время. [а =
8,5 м/с²;
N
= 0,48]

14

1.4.
Нормальное ускорение точки, движущейся
по окружности радиуса r=4
м,
задается уравнением а_n=А+-Bt+Ct²
(A=1
м/с²,
В=6
м/с³,
С=3
м/с⁴).
Определить: 1) тангенциальное ускорение
точки; 2) путь, пройденный точкой за время
t₁=5
с после начала движения; 3) полное
ускорение для момента времени t₂=1
с. [ 1) 6 м/с²;
2) 85 м; 3) 6,32 м/с²]

1.5.
Частота
вращения колеса при равнозамедленном
движении за t=1
мин
уменьшилась от 300 до 180 мин^-1.
Определить: 1) угловое ускорение колеса;
2) число полных оборотов, сделанных
колесом за это время. [1)
0,21 рад/с²;
2) 360]

1.6.
Диск
радиусом R=10
см вращается вокруг неподвижной оси
так, что зависимость угла поворота
радиуса диска от времени задается
уравнением =A+Bt+Ct²+Dt³
(B
= l рад/с,
С=1
рад/с²,
D=l
рад/с³).
Определить для точек на ободе колеса к
концу второй секунды после начала
движения: 1) тангенциальное ускорение
а_;
2) нормальное ускорение а_n;
3) полное ускорение а. [ 1) 0,14 м/с²;
2) 28,9 м/с²;
3) 28,9 м/с²]

Соседние файлы в папке Трофимова

• #
• #
• #
• #
• #
• #