Как найти угловое ускорение зная угол поворота - Сайт, где вы сможете решить свои вопросы

Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.

Обозначение угловой скорости: ω (омега).

Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.

С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.

Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:

Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.

Быстрота изменения угла φ (перемещения плоскости П из положения П₁ в положение П₂) – это и есть угловая скорость:

Приняв вектор k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

если известно количество оборотов n за единицу времени t:
если задан угол поворота φ за единицу времени:
если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:

Размерности угловой скорости:

Количество оборотов за единицу времени [об/мин], [c^-1].
Угол поворота за единицу времени [рад/с].

Определение угловой скорости

Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.

Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.

Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.

Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.

Другие примеры решения задач >

Угловое ускорение

Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:

Обозначение: ε (Эпсилон)

Единицы измерения углового ускорения: [рад/с²], [с^-2]

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

Расчет углового ускорения

Пример: По заданному значению касательной составляющей полного ускорения a_τ точки B, расположенной на расстоянии r от центра вращения колеса.

Требуется определить величину и направление углового ускорения колеса ε, если a_τ = 10 м/с², r = 50 см.

Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.

Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

ω = 1,5 с^-1 = 9,42 рад/с.

Смотрите также:

Примеры расчета угловой скорости и ускорения
Скорости и ускорения точек вращающегося тела

Источник

Угловое ускорение – что это?

Угловое ускорение (varepsilon) – физическая величина, характеризующая изменение угловой скорости при движении тела.

Единица измерения: (lbrackvarepsilonrbrack=frac1{с^2}) или (с^{-2})

Угловая скорость

Круговым движением точки вокруг оси называют движение, где траектория точки – окружность с центром, который лежит на оси вращения, перпендикулярной плоскости окружности.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Угловая скорость (omega) – векторная физическая величина, характеризующая скорость изменения угла поворота при круговом движении точки или твердого тела.

При движении по окружности (круговом движении) скорость меняет свое направление, значит такое движение не может считаться равномерным, оно ускоренное или равноускоренное (в частных случаях).

Вектор угловой скорости направлен вдоль оси вращения.

Основные формулы для вычисления угловой скорости

Для равномерного вращения (когда за равные отрезки времени тело поворачивается на один и тот же угол):

(omega=frac nt), где (n) – количество оборотов за единицу времени (t).
(omega=fracvarphi t), где (varphi) – угол поворота, (t) – время, за которое он совершен.
(omega=frac{2pi}T), где (Т) – период обращения (время, за которое тело/точка совершает один оборот).
(omega=2pinu), где (nu) – числом оборотов в единицу времени.

Единица измерения угловой скорости в СИ: (lbrackomegarbrack=frac{рад}с)

Связь между угловой скоростью и нормальным (центростремительным) ускорением

Центростремительное (нормальное) ускорение (a_n) – это составляющая полного ускорения, которая характеризует изменение направления вектора скорости при криволинейном движении. Другим компонентом полного ускорения является тангенциальное ускорение, оно характеризует изменение величины скорости.

Центростремительное ускорение определяется по формуле:

(a_n=frac{V^2}R),

где (V) – скорость движения, (R) – радиус окружности.

Единица измерения в СИ: (lbrack a_nrbrack=frac м{с^2})

Итак, формула связывающая эти две величины:

(a_n=omega^2R)

Основные формулы для расчета углового ускорения

Значение углового ускорения в определенный момент времени вычисляется как первая производная от угловой скорости или вторая производная от угла поворота по времени.

(varepsilon=lim_{triangle trightarrow0}frac{triangleomega}{triangle t}=frac{domega}{dt}=frac{d^2varphi}{dt}=overset.omega=overset{..}varphi)

Угловое ускорение маховика

(varepsilon=fracomega t=frac{2pi n}t), где (n) – количество оборотов за единицу времени (t).

Среднее угловое ускорение

Средним угловым ускорением тела называют отношение изменения угловой скорости к отрезку времени, за который оно совершилось.

(leftlanglevarepsilonrightrangle=frac{triangleomega}{triangle t})

Тангенциальное ускорение

Тангенциальным (касательным) ускорением (a_tau) называют ту составляющую полного ускорения, которая направлена по касательной к траектории движения в данной точке. Тангенциальное ускорение описывает изменение скорости по модулю при криволинейном движении.

(a_tau=varepsilon r), где (varepsilon) – угловое ускорение, (r) – радиус кривизны траектории в заданной точке.

Мгновенное угловое ускорение

Мгновенное угловое ускорение (alpha) есть первая производная угловой скорости по времени или вторая производная углового перемещения по времени.

(alpha=tg(varepsilon)=frac{;domega}{dt}=frac{d^2phi}{dt^2})

Источник

Загрузить PDF

Угловое ускорение, обозначаемое α, характеризует быстроту изменения угловой скорости тела. Чтобы вычислить угловое ускорение, вы должны знать определения угла поворота и угловой скорости. Угол поворота, обозначаемый Θ, характеризует вращение тела вокруг центра вращения; угловая скорость, обозначаемая ω, характеризует скорость вращения тела вокруг центра вращения.

Шаги

1
Проверьте вращающееся тело. Перед любыми расчетами убедитесь, что рассматриваемое тело движется по идеальной окружности вокруг центра вращения (или оси вращения).
- Для понимания этой концепции представьте камень, привязанный к концу веревки. Теперь возьмите другой конец веревки и покрутите камень. Линия, проходящая через вашу руку, является осью вращения; камень, привязанный к веревке, является вращающимся телом.
2
Угол поворота. Угол поворота тела (обозначается как Θ), вращающегося вокруг неподвижной оси, может быть положительным или отрицательным. Углы, измеренные в направлении против часовой стрелки, считаются положительными; углы, измеренные в направлении по часовой стрелке, считаются отрицательными.
- Угловая скорость по величине равна углу поворота (вокруг точки или оси) в единицу времени.
3
Определите угол поворота. Для вычисления угловой скорости тела вы должны знать угол поворота.
- Например, в результате эксперимента вы выяснили, что угол поворота вращающегося тела в определенный момент времени t находится по формуле: Θ = 2t³.
4
Вычислите угловую скорость. Мгновенная угловая скорость вращающегося тела равна производной от угла поворота (Θ) по времени (t); в этом случае производная – это быстрота изменения угла поворота за бесконечно малый промежуток времени. Другими словами: ω = dΘ/dt.
- В приведенном выше примере расчеты угловой скорости выглядят следующим образом:
5
Вычислите угловое ускорение. Напомним, что угловое ускорение – это быстрота изменения угловой скорости. Таким образом, угловое ускорение равно производной от угловой скорости.
- В приведенном выше примере расчеты углового ускорения выглядят следующим образом:
Реклама

Советы

Производная от какой-либо величины – это быстрота изменения этой величины за промежуток времени t1 и t2, причем t2 – t1 -> 0, то есть за бесконечно малый промежуток времени.
Производная от tⁿ по t (где n – любое целое число) вычисляется следующим образом:
Формула для вычисления угла поворота в определенный момент времени t находится экспериментально (в результате множества измерений).
Запомните: 1 рад = 57,3 градусов.

Об этой статье

Эту страницу просматривали 26 063 раза.

Была ли эта статья полезной?

Источник

Угловое ускорение
${boldsymbol varepsilon }={frac {{mathrm d}{boldsymbol omega }}{{mathrm d}t}}={boldsymbol {dot omega }}$
Единицы измерения
СИ	рад/с²
СГС	рад/с²
Примечания
псевдовектор

Угловое ускорение — псевдовекторная физическая величина, равная первой производной от псевдовектора угловой скорости по времени

${displaystyle {vec {varepsilon }}={frac {d{vec {omega }}}{dt}}.}$

Угловое ускорение характеризует интенсивность изменения модуля и направления угловой скорости при движении твёрдого тела.

Как приходят к понятию углового ускорения: ускорение точки твёрдого тела при свободном движении[править | править код]

К понятию углового ускорения можно прийти, рассматривая вычисление ускорения точки твёрдого тела, совершающего свободное движение. Скорость точки тела при свободном движении, согласно формуле Эйлера, равна

${displaystyle {vec {v}}_{B}={vec {v}}_{A}+{vec {omega }}times {vec {AB}},}$

где ${vec v}_{A}$ — скорость точки тела , принятой в качестве полюса; — псевдовектор угловой скорости тела; — вектор, выпущенный из полюса в точку, скорость которой вычисляется. Дифференцируя по времени данное выражение и используя формулу Ривальса^[1], имеем

${displaystyle {vec {a_{B}}}={vec {a_{A}}}+{vec {varepsilon }}times {vec {AB}}+{vec {omega }}times ({vec {omega }}times {vec {AB}})}$

${displaystyle {vec {a_{B}}}={vec {a_{A}}}+{vec {a_{BA}^{rot}}}+{vec {a_{BA}^{axis}}},}$

где ${vec a}_{A}$ — ускорение полюса ; ${vec varepsilon }={frac {d{vec omega }}{dt}}$ — псевдовектор углового ускорения. Составляющая ускорения точки , вычисляемая через угловое ускорение называется вращательным ускорением точки вокруг полюса

${displaystyle {vec {a}}_{BA}^{,rot}={vec {varepsilon }}times {vec {AB}}.}$

Последнее слагаемое в полученной формуле, зависящее от угловой скорости, называют осестремительным ускорением ускорением точки вокруг полюса

${displaystyle {vec {a}}_{BA}^{,axis}={vec {omega }}times left({vec {omega }}times {vec {AB}}right).}$

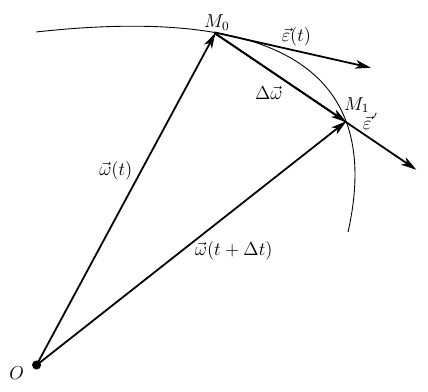
Геометрический смысл псевдовектора углового ускорения[править | править код]

Псевдовектор направлен по касательной к годографу угловой скорости. Действительно, рассмотрим два значения вектора угловой скорости, в момент времени и в момент времени . Оценим изменение угловой скорости за рассматриваемый промежуток времени Delta t

Отнесём это изменение к тому промежутку времени, за которое оно произошло

${displaystyle {frac {Delta {vec {omega }}}{Delta t}}={vec {varepsilon }}^{,,'}.}$

Получившийся вектор называется вектором среднего углового ускорения. Он занимает положение секущей, пересекая годограф вектора угловой скорости в точках $M_{0}$ и $M_{1}$ . Перейдём к пределу при

${displaystyle lim _{Delta tto 0}{frac {Delta {vec {omega }}}{Delta t}}={frac {d{vec {omega }}}{dt}}={vec {varepsilon }}.}$

Вектор среднего углового ускорения перейдёт в вектор мгновенного углового ускорения и займёт положение касательной в точке $M_{0}$ к годографу угловой скорости.

Выражение вектора углового ускорения через параметры конечного поворота[править | править код]

При рассмотрении вращения тела через параметры конечного поворота, вектор углового ускорения можно расписать формулой

${displaystyle {vec {varepsilon }}=left(1-cos varphi right)left({vec {u}}times {frac {d^{2}{vec {u}}}{dt^{2}}}right)+{dot {varphi }}left(1+cos varphi right){frac {d{vec {u}}}{dt}}+{dot {varphi }}sin varphi left({vec {u}}times {frac {d{vec {u}}}{dt}}right)+sin varphi ,{frac {d^{2}{vec {u}}}{dt^{2}}}+{ddot {varphi }},{vec {u}},}$

где vec u — орт, задающий направление оси поворота; varphi — угол, на который совершается поворот вокруг оси vec u .

Угловое ускорение при вращении тела вокруг неподвижной оси[править | править код]

При вращении тела вокруг неподвижной оси, проходящей через неподвижные точки тела $O_{1}$ и $O_{2}$ , производные орта оси вращения равны нулю

${displaystyle {frac {d{vec {u}}}{dt}}={frac {d^{2}{vec {u}}}{dt^{2}}}=0.}$

В этом случае вектор углового ускорения определяется тривиально через вторую производную угла поворота

или

где — алгебраическая величина углового ускорения. В этом случае псевдовектор углового ускорения, как и угловая скорость, направлен вдоль оси вращения тела. Если первая и вторая производные угла поворота имеют одинаковый знак

(),

то вектор углового ускорения и вектор угловой скорости совпадают по направлению (тело вращается ускоренно). В противном случае, при , векторы угловой скорости и углового ускорения направлены в противоположные стороны (тело вращается замедленно).

В курсе теоретической механики традиционным является подход, при котором понятие угловой скорости и углового ускорения вводится при рассмотрении вращения тела вокруг неподвижной оси. При этом в качестве закона движения рассматривается зависимость от времени угла поворота тела

В этом случае закон движения точки тела может быть выражен естественным способом, как длина дуги окружности, пройденная точкой при повороте тела от некоторого начального положения ${displaystyle varphi _{0}=varphi (t_{0}).}$

${displaystyle s(t)=R,left(varphi (t)-varphi _{0}right),}$

где — расстояние от точки до оси вращения (радиус окружности, по которой движется точка). Дифференцируя последнее соотношение по времени получаем алгебраическую скорость точки

${displaystyle {frac {ds}{dt}}=v_{tau }=R,{frac {dvarphi }{dt}}=omega ,R,}$

где ${displaystyle omega ={frac {dvarphi }{dt}}}$ — алгебраическая величина угловой скорости. Ускорение точки тела при вращении может быть представлено как геометрическая сумма тангенциального и нормального ускорения

${displaystyle {vec {a}}_{M}={vec {a}}_{M}^{,tau }+{vec {a}}_{M}^{,n},}$

причём тангенциальное ускорение получается как производная от алгебраической скорости точки

${displaystyle a_{M}^{,tau }={frac {dv_{tau }}{dt}}={frac {d}{dt}}left(omega ,Rright)=R,{frac {domega }{dt}}=varepsilon ,R,}$

где ${displaystyle varepsilon ={frac {domega }{dt}}={frac {d^{2}varphi }{dt^{2}}}}$ — алгебраическая величина углового ускорения. Нормальное ускорение точки тела может быть вычислено по формулам

${displaystyle a_{M}^{,n}={frac {v_{tau }^{2}}{R}}=omega ^{2},R.}$

Выражение псевдовектора углового ускорения через тензор поворота тела[править | править код]

Если поворот твёрдого тела задан тензором ранга (линейным оператором), выраженным, например, через параметры конечного поворота

${displaystyle B_{,m}^{,p}=left(1-cos varphi right),u^{,p},u_{,m}+cos varphi ,delta _{,m}^{,p}+sin varphi ,g^{,pl},epsilon _{,lkm},u^{,k},}$

где ${displaystyle delta _{,m}^{,p}}$ — символ Кронекера; ${displaystyle epsilon _{,lkj}}$ — тензор Леви-Чивиты, то, псевдовектор углового ускорения может быть вычислен по формуле

${displaystyle varepsilon ^{,i}={frac {1}{2}},epsilon ^{ikl},g_{,lp},left(B_{,m}^{',p},{ddot {B}}_{,k}^{,m}+{dot {B}}_{,m}^{',p},{dot {B}}_{,k}^{,m}right),}$

где ${displaystyle B_{,m}^{',p}}$ — тензор обратного преобразования, равный

${displaystyle B_{,m}^{',p}=left(1-cos varphi right),u^{,p},u_{,m}+cos varphi ,delta _{,m}^{,p}-sin varphi ,g^{,pl},epsilon _{,lkm},u^{,k}.}$

Примечания[править | править код]

↑ В.И. Дронг, В.В. Дубинин, М.М. Ильин и др.; под ред. К.С. Колесникова, В.В. Дубинина. Курс теоретической механики: учебник для вузов. — 2017. — С. 101, 111. — 580 с. — ISBN 978-5-7038-4568-4.

Литература[править | править код]

Тарг С. М. Краткий курс теоретической механики — 10-е изд., перераб. и доп. — М.: Высш. шк., 1986 — 416 С.
Погорелов Д. Ю. Введение в моделирование динамики систем тел: Учебное пособие. — Брянск: БГТУ, 1997. — 197 С.

Источник

Download Article

Different ways to calculate rotation speed

Download Article

Most people have a general understanding of the idea of velocity and acceleration. Velocity is the measure of how fast an object is moving, and acceleration is the measure of how quickly the object’s velocity is changing (i.e., speeding up or slowing down). When the object is moving in a circle, such as a spinning tire or a rotating CD, velocity and acceleration are generally measured by the angle of rotation. They are then called angular velocity and angular acceleration. If you know the object’s velocity over some period of time, you can calculate its average angular acceleration. Alternatively, you may have a function to calculate the object’s position. With this information, you can calculate its angular acceleration at any chosen instant.

1

Determine the function for angular position. In some cases, you may be provided with a function or formula that predicts or assigns the position of an object with respect to time. In other cases, you may derive the function from repeated experiments or observations. For this article, we assume that the function has been provided or previously calculated.^[1]
2

Find the function for angular velocity. Velocity is the measure of how fast an object changes its position. In layman’s terms, we think of this as its speed. In mathematical terms, the change of position over time can be found by finding the derivative of the position function. The symbol for angular velocity is . Angular velocity is generally measured in units of radians divided by time (radians per minute, radians per second, etc.).^[2]

Advertisement
3

Find the function for angular acceleration. Acceleration is the measure of how fast an object’s velocity is changing over time. You can mathematically calculate the angular acceleration by finding the derivative of the function for angular velocity. Angular acceleration is generally symbolized with , the Greek letter alpha. Angular acceleration is reported in units of velocity per time, or generally radians divided by time squared (radians per second squared, radians per minute squared, etc.).^[3]
4

Apply the data to find instantaneous acceleration. Once you have derived the function for instantaneous acceleration as the derivative of velocity, which in turn is the derivative of position, you are ready to calculate the instantaneous angular acceleration of the object at any chosen time.^[4]

1
2
Measure final angular velocity. The second piece of information that you need is the angular velocity of the spinning or rotating object at the end of the time period that you want to measure. This is to be called the “final” velocity.^[6]
- A compact disc plays in the machine by rotating at an angular velocity of 160 radians per second.
- The roller coaster, after applying its brakes to the spinning wheels, ultimately reaches an angular velocity of zero when it stops. This will be its final angular velocity.
3
Measure the elapsed time. To calculate the average angular velocity of the spinning or rotating object, you need to know the amount of time that passes during your observation. This can be found by direct observation and measurement, or the information can be provided for a given problem.^[7]
- The owner’s manual for the CD player provides the information that the CD reaches its playing speed in 4.0 seconds.
- From observations of roller coasters being tested, it has been found that they can come to a complete stop within 2.2 seconds from when the brakes are initially applied.
4

Calculate the average angular acceleration. If you know the initial angular velocity, the final angular velocity, and the elapsed time, fill that data into the equation and find the average angular acceleration.^[8]

1

Understand the concept of angular motion. When people think of the speed of an object, they often consider linear motion – that is, objects traveling mostly in a straight line. This would include a car, a plane, a ball that is thrown or any number of other objects. However, angular motion describes objects that spin or rotate. Think of the earth spinning on its axis. The position or speed of the earth can be measured with angular quantities. A spinning compact disc (or record player, if you’re old enough), electrons on their axes, or the wheels of a car on the axle are other examples of rotating objects that can be measured through angular motion.^[9]
2
Visualize angular position. When you measure the position of a moving vehicle, for example, you can measure the distance traveled in a straight line from the starting point. With a rotating object, the measurement is generally done in terms of the angle around a circle. By convention, the starting or “zero” point is generally a horizontal radius from the center to the right side of the circle. The distance traveled is measured by the size of the angle , measured from that horizontal radius.^[10]
- The angle that is being measured is commonly represented by , the Greek letter theta.
- Positive motion is measured in a counterclockwise direction. Negative motion is measured in a clockwise direction.
3

Measure angular motion in radians. Linear travel is generally measured in some unit of distance, such as miles, meters, inches or some other unit of length. Rotational or angular motion is generally measured in units called radian. A radian is a fraction of the circle. For standard reference, mathematicians use the “unit circle,” which has a standard radius of 1 unit.^[11]
4
Understand the concept of angular acceleration. Angular acceleration is the measurement of how fast or slow a rotating object is changing its velocity. In other words, is the spinning speeding up or slowing down? If you know the angular velocity at a starting time and then at a later ending time, you can calculate the average angular acceleration over that time interval. If you know the function for the object’s position, you can use calculus to derive the instantaneous angular acceleration at any chosen time.^[12]
- People often use the word “acceleration” to mean speeding up, and “deceleration” to mean slowing down. In mathematical and physical terms, however, only the word “acceleration” is used. If the object is speeding up, the acceleration is positive. If it is slowing down, the acceleration is negative.

Add New Question

Question

What are the formulas to find the initial acceleration of an object?

Initial acceleration generally has to be given as a condition of the problem or the experiment.
Question

What is the direction of radial and tangential acceleration and how do they affect each other?

Angular (or radial) measurements are generally counterclockwise. Tangential acceleration means the straight line direction of the tangent at some measured point along the circle. The tangent is a line that is perpendicular to the radius at that point.
Question

How can you find angular acceleration in revolutions per second squared?

This article shows how to find acceleration in radians per second squared. To convert the number of radians to the number of revolutions, recall that 1 full circle (or 1 revolution) is equal to 2pi radians. This is roughly equivalent to 6.28 radians per revolution. If you know the acceleration in radians per second squared, divide that answer by 6.28 to get revolutions per second squared.

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

Remember to express final results with the proper units. Angular position is usually expressed in radians. Angular velocity is expressed in radians per time. Angular acceleration is expressed in units of radians per time squared.

Thanks for submitting a tip for review!

References

About This Article

Article SummaryX

To calculate instantaneous angular acceleration, start by determining the function for angular position, or the position of the object with respect to time. Next, find the angular velocity, which is the measure of how fast the object changes its position. Then, find the derivative of the function for angular velocity in order to determine the function for angular acceleration. Finally, plug in the data to find the instantaneous acceleration of the object at any chosen time. To learn more, including how to calculate average angular acceleration, read on.

Did this summary help you?

Thanks to all authors for creating a page that has been read 90,899 times.

Did this article help you?

Источник

Угловая скорость

Формулы угловой скорости

Определение угловой скорости

Угловое ускорение

Расчет углового ускорения

Угловое ускорение – что это?

Угловая скорость

Основные формулы для вычисления угловой скорости

Связь между угловой скоростью и нормальным (центростремительным) ускорением

Основные формулы для расчета углового ускорения

Угловое ускорение маховика

Среднее угловое ускорение

Тангенциальное ускорение

Мгновенное угловое ускорение

Шаги

Советы

Об этой статье

Была ли эта статья полезной?

Как приходят к понятию углового ускорения: ускорение точки твёрдого тела при свободном движении[править | править код]

Геометрический смысл псевдовектора углового ускорения[править | править код]

Выражение вектора углового ускорения через параметры конечного поворота[править | править код]

Угловое ускорение при вращении тела вокруг неподвижной оси[править | править код]

Выражение псевдовектора углового ускорения через тензор поворота тела[править | править код]

Примечания[править | править код]

Литература[править | править код]

Video

References

About This Article

Did this article help you?

Вам также может понравиться

Как найти номер числовой последовательности

Как составить заявление на обжалование решения мсэ

Как составить документ в формате pdf

Добавить комментарий Отменить ответ