Как найти угловой диаметр солнца

From Wikipedia, the free encyclopedia

The angular diameter, angular size, apparent diameter, or apparent size is an angular distance describing how large a sphere or circle appears from a given point of view. In the vision sciences, it is called the visual angle, and in optics, it is the angular aperture (of a lens). The angular diameter can alternatively be thought of as the angular displacement through which an eye or camera must rotate to look from one side of an apparent circle to the opposite side. Humans can resolve with their naked eyes diameters of up to about 1 arcminute (approximately 0.017° or 0.0003 radians).^[1] This corresponds to 0.3 m at a 1 km distance, or to perceiving Venus as a disk under optimal conditions.

Formula[edit]

The angular diameter of a circle whose plane is perpendicular to the displacement vector between the point of view and the center of said circle can be calculated using the formula^[2]

in which is the angular diameter in degrees, and is the actual diameter of the object, and is the distance to the object. When , we have , and the result obtained is in radians.

For a spherical object whose actual diameter equals and where is the distance to the center of the sphere, the angular diameter can be found by the formula

The difference is due to the fact that the apparent edges of a sphere are its tangent points, which are closer to the observer than the center of the sphere. The difference is significant only for spherical objects of large angular diameter, since the following small-angle approximations hold for small values of :^[3]

Estimating angular diameter using the hand[edit]

Estimates of angular diameter may be obtained by holding the hand at right angles to a fully extended arm, as shown in the figure.^[4][5][6]

Use in astronomy[edit]

In astronomy, the sizes of celestial objects are often given in terms of their angular diameter as seen from Earth, rather than their actual sizes. Since these angular diameters are typically small, it is common to present them in arcseconds (″). An arcsecond is 1/3600th of one degree (1°) and a radian is 180/π degrees. So one radian equals 3,600 × 180/ arcseconds, which is about 206,265 arcseconds (1 rad ≈ 206,264.806247″). Therefore, the angular diameter of an object with physical diameter d at a distance D, expressed in arcseconds, is given by:^[7]

.

These objects have an angular diameter of 1″:

• an object of diameter 1 cm at a distance of 2.06 km
• an object of diameter 725.27 km at a distance of 1 astronomical unit (AU)
• an object of diameter 45 866 916 km at 1 light-year
• an object of diameter 1 AU (149 597 871 km) at a distance of 1 parsec (pc)

Thus, the angular diameter of Earth’s orbit around the Sun as viewed from a distance of 1 pc is 2″, as 1 AU is the mean radius of Earth’s orbit.

The angular diameter of the Sun, from a distance of one light-year, is 0.03″, and that of Earth 0.0003″. The angular diameter 0.03″ of the Sun given above is approximately the same as that of a human body at a distance of the diameter of Earth.

This table shows the angular sizes of noteworthy celestial bodies as seen from Earth:

Celestial object	Angular diameter or size	Relative size
Magellanic Stream	over 100°
Gum Nebula	36°
Milky Way	30° (by 360°)
Width of spread out hand with arm streched out	20°	353 meter at 1 km distance
Serpens-Aquila Rift	20° by 10°
Canis Major Overdensity	12° by 12°
Smith’s Cloud	11°
Large Magellanic Cloud	10.75° by 9.17°	Note: brightest galaxy, other than the Milky Way, in the night sky (0.9 apparent magnitude (V))
Barnard’s loop	10°
Zeta Ophiuchi Sh2-27 nebula	10°
Width of fist with arm streched out	10°	175 meter at 1 km distance
Sagittarius Dwarf Spheroidal Galaxy	7.5° by 3.6°
Northern Coalsack Nebula	7° by 5°[8]
Coalsack nebula	7° by 5°
Cygnus OB7	4° by 7°[9]
Rho Ophiuchi cloud complex	4.5° by 6.5°
Hyades	5°30′	Note: brightest star cluster in the night sky, 0.5 apparent magnitude (V)
Small Magellanic Cloud	5°20′ by 3°5′
Andromeda Galaxy	3°10′ by 1°	About six times the size of the Sun or the Moon. Only the much smaller core is visible without long-exposure photography.
Veil Nebula	3°
Heart Nebula	2.5° by 2.5°
Westerhout 5	2.3° by 1.25°
Sh2-54	2.3°
Carina Nebula	2° by 2°	Note: brightest nebula in the night sky, 1.0 apparent magnitude (V)
North America Nebula	2° by 100′
In the Moon’s sky the apparent size of Earth	2° – 1°48′[10]	Appearing about three to four times larger than the Moon in Earth’s sky
Orion Nebula	1°5′ by 1°
Width of little finger with arm streched out	1°	17.5 meter at 1 km distance
Moon	34′6″ – 29′20″	32.5–28 times the maximum value for Venus (orange bar below) / 2046–1760″ the Moon has a diameter of 3,474 km
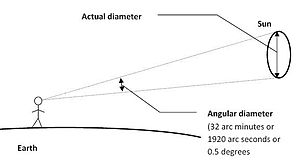
Sun	32′32″ – 31′27″	31–30 times the maximum value for Venus (orange bar below) / 1952–1887″ the Sun has a diameter of 1,391,400 km
Helix Nebula	about 16′ by 28′
Spire in Eagle Nebula	4′40″	length is 280″
Venus	1′6″ – 0′9.7″
International Space Station (ISS)	1′3″	;[11] the ISS has a width of about 108 m
Maximum resolvable diameter by the human eye	1′	;[12] 0.3 meter at 1 km distance[13]
About 100 km on the surface of the Moon	1′	Comparable to the size of features like large lunar craters, such as the Copernicus crater, a prominent bright spot in the eastern part of Oceanus Procellarum on the waning side, or the Tycho crater within a bright area in the south, of the lunar near side.
Jupiter	50.1″ – 29.8″
Maximum resolvable point/gap by the human eye	40″	;[12] at close view the width of a 0.04 mm very thin hair[13]
Mars	25.1″ – 3.5″
Saturn	20.1″ – 14.5″
Mercury	13.0″ – 4.5″
Uranus	4.1″ – 3.3″
Neptune	2.4″ – 2.2″
Ganymede	1.8″ – 1.2″	Ganymede has a diameter of 5,268 km
An astronaut (~1.7 m) at a distance of 350 km, the average altitude of the ISS	1″
Maximum resolvable diameter by Galileo Galilei’s largest 38mm refracting telescopes	~1″	;[14] Note: 30x[15] magnification, comparable to very strong contemporary terrestrial binoculars
Ceres	0.84″ – 0.33″
Vesta	0.64″ – 0.20″
Pluto	0.11″ – 0.06″
Eris	0.089″ – 0.034″
R Doradus	0.062″ – 0.052″	Note: R Doradus is thought to be the extrasolar star with the largest apparent size as viewed from Earth
Betelgeuse	0.060″ – 0.049″
Alphard	0.00909″
Rho Cassiopeiae	0.0072″
Alpha Centauri A	0.007″
Canopus	0.006″
Sirius	0.005936″
Altair	0.003″
Deneb	0.002″
Proxima Centauri	0.001″
Alnitak	0.0005″
Proxima Centauri b	0.00008″
Event horizon of black hole M87* at center of the M87 galaxy, imaged by the Event Horizon Telescope in 2019.	0.000025″ (2.5×10−5)	Comparable to a tennis ball on the Moon
A star like Alnitak at a distance where the Hubble Space Telescope would just be able to see it[16]	6×10−10 arcsec

The table shows that the angular diameter of Sun, when seen from Earth is approximately 32′ (1920″ or 0.53°), as illustrated above.

Thus the angular diameter of the Sun is about 250,000 times that of Sirius. (Sirius has twice the diameter and its distance is 500,000 times as much; the Sun is 10¹⁰ times as bright, corresponding to an angular diameter ratio of 10⁵, so Sirius is roughly 6 times as bright per unit solid angle.)

The angular diameter of the Sun is also about 250,000 times that of Alpha Centauri A (it has about the same diameter and the distance is 250,000 times as much; the Sun is 4×10¹⁰ times as bright, corresponding to an angular diameter ratio of 200,000, so Alpha Centauri A is a little brighter per unit solid angle).

The angular diameter of the Sun is about the same as that of the Moon. (The Sun’s diameter is 400 times as large and its distance also; the Sun is 200,000 to 500,000 times as bright as the full Moon (figures vary), corresponding to an angular diameter ratio of 450 to 700, so a celestial body with a diameter of 2.5–4″ and the same brightness per unit solid angle would have the same brightness as the full Moon.)

Even though Pluto is physically larger than Ceres, when viewed from Earth (e.g., through the Hubble Space Telescope) Ceres has a much larger apparent size.

Angular sizes measured in degrees are useful for larger patches of sky. (For example, the three stars of the Belt cover about 4.5° of angular size.) However, much finer units are needed to measure the angular sizes of galaxies, nebulae, or other objects of the night sky.

Degrees, therefore, are subdivided as follows:

• 360 degrees (°) in a full circle
• 60 arc-minutes (′) in one degree
• 60 arc-seconds (″) in one arc-minute

To put this in perspective, the full Moon as viewed from Earth is about 1⁄2°, or 30′ (or 1800″). The Moon’s motion across the sky can be measured in angular size: approximately 15° every hour, or 15″ per second. A one-mile-long line painted on the face of the Moon would appear from Earth to be about 1″ in length.

In astronomy, it is typically difficult to directly measure the distance to an object, yet the object may have a known physical size (perhaps it is similar to a closer object with known distance) and a measurable angular diameter. In that case, the angular diameter formula can be inverted to yield the angular diameter distance to distant objects as

In non-Euclidean space, such as our expanding universe, the angular diameter distance is only one of several definitions of distance, so that there can be different “distances” to the same object. See Distance measures (cosmology).

Non-circular objects[edit]

Many deep-sky objects such as galaxies and nebulae appear non-circular and are thus typically given two measures of diameter: major axis and minor axis. For example, the Small Magellanic Cloud has a visual apparent diameter of 5° 20′ × 3° 5′.

Defect of illumination[edit]

Defect of illumination is the maximum angular width of the unilluminated part of a celestial body seen by a given observer. For example, if an object is 40″ of arc across and is 75% illuminated, the defect of illumination is 10″.

See also[edit]

• Angular diameter distance
• Angular resolution
• Solid angle
• Visual acuity
• Visual angle
• Perceived visual angle
• List of stars with resolved images
• Apparent magnitude

References[edit]

External links[edit]

• Small-Angle Formula
• Visual Aid to the Apparent Size of the Planets

Угловой диаметр, угловой размер, кажущийся диаметр, или кажущийся размер – угловое измерение, описывающее, насколько большой сфера или круг выглядит с данной точки зрения. В науках о зрении это называется углом обзора, а в оптике это угловая апертура (из объектив ). В качестве альтернативы угловой диаметр можно рассматривать как угол, на который глаз или камера должны повернуться, чтобы смотреть с одной стороны видимого круга на противоположную. Угловой радиус равен половине углового диаметра.

Содержание

• 1 Формула
• 2 Оценка углового диаметра с помощью руки
• 3 Использование в астрономии
  • 3.1 Некруглые объекты
  • 3.2 Дефект освещения
• 4 См. Также
• 5 Ссылки
• 6 Внешние ссылки

Формула

Диаграмма для формулы углового диаметра

Угловой диаметр окружности, плоскость которой перпендикулярна вектору смещения между точкой вид и центр указанного круга можно рассчитать по формуле

δ = 2 arctan ⁡ (d 2 D), { displaystyle delta = 2 arctan left ({ frac {d} {2D}} справа),}

, где δ { displaystyle delta}– угловой диаметр, а d { displaystyle d}– фактический диаметр объекта, а D { displaystyle D}– расстояние до объекта. Когда D ≫ d { displaystyle D gg d}, мы имеем δ ≈ d / D { displaystyle delta приблизительно d / D}, и полученный результат выражен в радианах.

. Для сферического объекта, фактический диаметр которого равен dact, { displaystyle d _ { mathrm {act}},}и где D { displaystyle D}– расстояние до центра сферы, угловой диаметр можно найти по формуле

δ = 2 arcsin ⁡ (dact 2 D) { displaystyle delta = 2 arcsin left ({ frac {d _ { mathrm {act}}} {2D}} right)}

Разница в том, что видимые края сферы являются точками касания, которые находятся ближе к наблюдателю, чем к центру сферы. Для практического использования различие имеет значение только для сферических объектов, которые находятся относительно близко, поскольку приближение малых углов справедливо для x ≪ 1 { displaystyle x ll 1}:

arcsin ⁡ x ≈ arctan ⁡ x ≈ x { displaystyle arcsin x приблизительно arctan x приблизительно x}.

Оценка углового диаметра с помощью руки

Приблизительные углы 10 °, 20 °, 5 ° и 1 ° для длина вытянутой руки.

Оценки углового диаметра могут быть получены, если держать руку под прямым углом к ​​полностью вытянутой руке, как показано на рисунке.

Использование в астрономии

Угловой диаметр: угол, образуемый объектом

В астрономии размеры небесных объектов часто задаются в терминах их углового диаметра, как видно из Земля, а не их реальные размеры. Поскольку эти угловые диаметры обычно малы, их принято представлять в угловых секундах (″). Угловая секунда равна 1/3600 одной градуса (1 °), а радиан – 180 / π { displaystyle pi}градусов. Таким образом, один радиан равен 3600 * 180 / π { displaystyle pi}arcseconds, что составляет около 206 265 угловых секунд (1 рад ≈ 206 264,806247 дюймов). Следовательно, угловой диаметр объекта с физическим диаметром d на расстоянии D, выраженное в секундах дуги, определяется как:

δ = 206, 265 (d / D) arcseconds { displaystyle delta = 206,265 ~ (d / D) ~ mathrm {arcseconds}}.

Эти объекты имеют угловой диаметр 1 ″:

• объект диаметром 1 см на расстоянии 2,06 км
• объект диаметром 725,27 км на расстоянии 1 астрономическая единица (AU)
• объект диаметром 45 866 916 км на расстоянии 1 светового года
• объект диаметром 1 AU (149 597 871 км) на расстоянии 1 парсек (пк)

Таким образом, угловой диаметр орбиты Земли вокруг Солнца, если смотреть с расстояния в 1 пк, равен 2 ″, поскольку 1 а.е. радиус орбиты Земли.

Угловой диаметр Солнца с расстояния в один световой год составляет 0,03 ″, а диаметр Ea rth 0,0003 ″. Угловой диаметр Солнца 0,03 дюйма, указанный выше, примерно такой же, как у человеческого тела на расстоянии диаметра Земли.

В этой таблице показаны угловые размеры примечательных небесных тел как видно с Земли:

Небесное тело	Угловой диаметр или размер	Относительный размер
Галактика Андромеды	3 ° 10 ′ на 1 °	Примерно в шесть раз больше Солнца или Луны. Без фотографии с большой выдержкой.
Солнце	31′27 ″ – 32′32 ″	в 30–31 раз больше максимального значения для Венеры (внизу) / 1887–1952 ″
Луна	29′20 ″ – 34′6 ″	в 28–32,5 раза больше максимального значения для Венеры (оранжевая полоса внизу) / 1760–2046 ″
Туманность Хеликс	примерно 16 ‘на 28’
Шпиль в туманности Орла	4’40 ″	длина 280 ″
Венера	9,7 ″ – 1 ′ 6 ″
Юпитер	29,8 ″ – 50,1 ″
Сатурн	14,5 ″ – 20,1 ″
Марс	3,5 ″ – 25,1 ″
Меркурий	4,5 ″ – 13,0 ″
Уран	3,3–4,1 дюйма
Нептун	2,2–2,4 дюйма
Церера	0,33–0,84 дюйма
Веста	0,20–0,64 дюйма
Плутон	0,06 ″ – 0,11 ″
R Doradus	0,052 ″ – 0,062 ″
Бетельгейзе	0,049 ″ – 0,060 ″
Эрис	0,034 ″ – 0,089 ″
Alphard	0,00909 ″
Альфа Центавра A	0,007 ″
Канопус	0,006 ″
Сириус	0,005936 ″
Альтаир	0,003 ″
Денеб	0,002 ″
Проксима Центавра	0,001 ″
Алнитак	0,000 5 ″
Горизонт событий черной дыры M87 * в центре галактики M87, полученный телескопом Event Horizon Telescope в 2019 году.	0,000025 ″ (2,5 × 10)
Звезда, подобная Альнитак, на таком расстоянии, на котором космический телескоп Хаббл сможет ее увидеть	6 × 10 угловых секунд

Сравнение углового диаметра Солнца, Луны и планет. Чтобы получить точное представление о размерах, просмотрите изображение с расстояния, в 103 раза превышающего ширину “Луны: макс.” круг. Например, если на вашем мониторе ширина этого круга составляет 5 см, просматривайте его с расстояния 5,15 м. На этой фотографии сравниваются видимые размеры Юпитера и его четырех галилеевых спутников ( Каллисто при максимальном удлинении ) с видимым диаметром полной Луны во время их соединения 10 апреля 2017 года.

Таблица показывает, что угловой диаметр Солнца, если смотреть с Земли, составляет приблизительно 32 ‘(1920 ″ или 0,53 °), как показано выше.

Таким образом, угловой диаметр Солнца примерно в 250 000 раз больше, чем у Сириуса. (Сириус имеет вдвое больший диаметр, а расстояние до него в 500000 раз больше; Солнце в 10 раз ярче, что соответствует соотношению угловых диаметров 10, поэтому Сириус примерно в 6 раз ярче на единицу телесного угла.)

Угловой диаметр Солнца также примерно в 250 000 раз больше, чем у Альфа Центавра A (у него примерно такой же диаметр, а расстояние в 250 000 раз больше; Солнце 4 В 10 раз ярче, что соответствует соотношению угловых диаметров 200000, поэтому Альфа Центавра A немного ярче на единицу телесного угла).

Угловой диаметр Солнца примерно такой же, как у Луны. (Диаметр Солнца в 400 раз больше, равно как и расстояние до него; Солнце в 200000-500000 раз ярче полной Луны (цифры меняются), что соответствует отношению углового диаметра от 450 до 700, то есть небесное тело с диаметром 2,5–4 ″ и такой же яркости на единицу телесного угла будет иметь такую ​​же яркость, как полная Луна.)

Даже несмотря на то, что Плутон физически больше Цереры, если смотреть с Земли (например, через Космический телескоп Хаббла ) Церера имеет гораздо больший видимый размер.

Угловые размеры, измеряемые в градусах, полезны для больших участков неба. (Например, три звезды Пояса покрывают угловой размер около 4,5 °.) Однако для измерения угловых размеров галактик, туманностей или других объектов требуются гораздо более точные единицы измерения. ночное небо.

Следовательно, градусы подразделяются следующим образом:

• 360 градусов (°) по полному кругу
• 60 угловые минуты (′) в один градус
• 60 угловых секунд (″) за одну угловую минуту

Чтобы представить это в перспективе, полная Луна, если смотреть с Земли составляет около ⁄ 2 °, или 30 ‘(или 1800 ″). Движение Луны по небу можно измерить по угловому размеру: примерно 15 ° каждый час или 15 дюймов в секунду. Линия длиной в одну милю, нарисованная на лице Луны, будет казаться с Земли примерно 1 дюйм в длину.

Минимальное, среднее и максимальное расстояние от Луны до Земли с учетом ее углового диаметра, если смотреть с поверхности Земли, в масштабе

В астрономии обычно трудно напрямую измерить расстояние до объекта, но объект может иметь известный физический размер (возможно, он похож на более близкий объект с известным расстоянием) и измеримый угловой диаметр. В этом случае формулу углового диаметра можно инвертировать, чтобы получить расстояние по угловому диаметру до удаленных объектов как

d ≡ 2 D tan ⁡ (δ 2) { displaystyle d Equiv 2D tan left ({ frac { delta} {2}} right)}.

В неевклидовом пространстве, таком как наша расширяющаяся Вселенная, расстояние по угловому диаметру является лишь одним из нескольких определений расстояния, так что может быть разные «расстояния» до одного и того же объекта. См. Измерения расстояния (космология).

Некруглые объекты

Многие объекты глубокого космоса, такие как галактики и туманности кажутся некруглыми и, таким образом, обычно имеют две меры диаметра: большую ось и малую ось. Например, Малое Магелланово Облако имеет видимый диаметр 5 ° 20 ′ × 3 ° 5 ′.

Дефект освещения

Дефект освещения – максимальная угловая ширина неосвещенной части небесного тела, видимой данным наблюдателем. Например, если объект имеет диаметр 40 дюймов по дуге и освещен на 75%, дефект освещения составляет 10 дюймов.

См. Также

• Расстояние углового диаметра
• Угловое разрешение
• Телесный угол
• Острота зрения
• Угол зрения
• Иллюзия угла зрения
• Список звезд с разрешенными изображениями

Ссылки

Внешние ссылки

• Формула малого угла
• Наглядное указание на видимый размер планет

Солнце
Снимок солнца в видимом свете с солнечными пятнами и потемнением к краю, сделан в 2013 году
Снимок Солнца в условном цвете, ультрафиолетовый спектр (длина волны 30,4 нм), сделан в 2010 году
Основные характеристики
Среднее расстояние от Земли	1,496⋅1011 м[1] (8,31 световых минут) 1 а. е.
Средний горизонтальный параллакс	8,794″
Видимая звёздная величина (V)	−26,74m[1]
Абсолютная звёздная величина	4,83m[1]
Спектральный класс	G2V
Параметры орбиты
Расстояние от центра Галактики	~2,5⋅1020 м (26 000 св. лет)
Расстояние от плоскости Галактики	~4,6⋅1017 м (48 св. лет)
Галактический период обращения	2,25-2,50⋅108 лет
Скорость	~2,2⋅105 м/с[2] (на орбите вокруг центра Галактики) 19,4 км/с[1] (относительно соседних звёзд)
Физические характеристики
Средний диаметр	1,392⋅109 м (109 диаметров Земли)[1]
Экваториальный радиус	6,9551⋅108 м[3]
Длина окружности экватора	4,37001⋅109 м[3]
Полярное сжатие	9⋅10−6
Площадь поверхности	6,07877⋅1018 м² (11 918 площадей Земли)[3]
Объём	1,40927⋅1027 м³ (1 301 019 объёмов Земли)[3]
Масса	1,9885⋅1030 кг (332 940 масс Земли)[1]
Средняя плотность	1,409 г/см³[3]
Ускорение свободного падения на экваторе	274,0 м/с²[1][3] (27,96 g[3])
Вторая космическая скорость (для поверхности)	617,7 км/с (55,2 земных)[3]
Эффективная температура поверхности	5780 К[4]
Температура короны	~1 500 000 К
Температура ядра	~15 700 000 К
Светимость	3,828⋅1026 Вт[1] (~3,75⋅1028 Лм)
Энергетическая яркость	2,009⋅107 Вт/(м²·ср)
Характеристики вращения
Наклон оси	7,25°[1][3] (относительно плоскости эклиптики) 67,23° (относительно плоскости Галактики)
Прямое восхождение северного полюса	286,13°[5] (19 ч 4 мин 30 с)
Склонение северного полюса	+63,87°[5]
Сидерический период вращения внешних видимых слоёв (на широте 16°)	25,38 дней[1] (25 дней 9 ч 7 мин 13 с)[5]
(на экваторе)	25,05 дней[1]
(у полюсов)	34,3 дней[1]
Скорость вращения внешних видимых слоёв (на экваторе)	7284 км/ч
Состав фотосферы[6][7]
Водород	73,46 %
Гелий	24,85 %
Кислород	0,77 %
Углерод	0,29 %
Железо	0,16 %
Неон	0,12 %
Азот	0,09 %
Кремний	0,07 %
Магний	0,05 %
Сера	0,04 %

Со́лнце (астр. ☉) — одна из звёзд нашей Галактики (Млечный Путь) и единственная звезда Солнечной системы. Вокруг Солнца обращаются другие объекты этой системы: планеты и их спутники, карликовые планеты и их спутники, астероиды, метеороиды, кометы и космическая пыль.

По спектральной классификации Солнце относится к типу G2V (жёлтый карлик). Средняя плотность Солнца составляет 1,4 г/см³ (в 1,4 раза больше, чем у воды). Эффективная температура поверхности Солнца — 5780 кельвин^[4]. Поэтому Солнце светит почти белым светом, но прямой свет Солнца у поверхности нашей планеты приобретает некоторый жёлтый оттенок из-за более сильного рассеяния и поглощения коротковолновой части спектра атмосферой Земли (при ясном небе, вместе с голубым рассеянным светом от неба, солнечный свет вновь даёт белое освещение).

Солнечное излучение поддерживает жизнь на Земле (свет необходим для начальных стадий фотосинтеза), определяет климат. Светимость Солнца (суммарное количество энергии, выделяемое Солнцем за одну секунду) L_⊙ = 3,827⋅10²⁶ Вт.

Солнце состоит из водорода (массовое содержание водорода X ≈ 73 %), гелия (массовое содержание Y ≈ 25 %^[8]) и других элементов с меньшей концентрацией (ниже все элементы тяжелее гелия в этом контексте называются металлами, как принято в астрофизике); их общее массовое содержание Z ≈ 2 %^[8]. Наиболее распространёнными элементами тяжелее водорода и гелия, в порядке убывания содержания, являются кислород, углерод, неон, азот, железо, магний, кремний, сера, аргон, алюминий, никель, натрий и кальций. На 1 млн атомов водорода приходится 98 000 атомов гелия, 851 атом кислорода, 398 атомов углерода, 123 атома неона, 100 атомов азота, 47 атомов железа, 38 атомов магния, 35 атомов кремния, 16 атомов серы, 4 атома аргона, 3 атома алюминия, по 2 атома никеля, натрия и кальция, а также малое количество прочих элементов^[9].

Масса Солнца M_⊙ = (1,98847 ± 0,00007)⋅10³⁰ кг^[10], она составляет 99,866 % от суммарной массы всей Солнечной системы^[4].

Солнечный спектр содержит линии ионизированных и нейтральных металлов, а также водорода и гелия. В нашей Галактике (Млечный Путь) насчитывается от 200 до 400 миллиардов звёзд^[11][12]. При этом 85 % звёзд нашей галактики — это звёзды, менее яркие, чем Солнце (в большинстве своём красные карлики). Как и все звёзды главной последовательности, Солнце вырабатывает энергию путём термоядерного синтеза гелия из водорода. В случае Солнца более 99 % энергии выделяется через протон-протонный цикл, тогда как для более массивных звёзд главной последовательности преимущественным путём синтеза гелия является CNO-цикл.

Солнце — ближайшая к Земле звезда. Средняя удалённость Солнца от Земли — 149,6 млн км^[1] — приблизительно равна астрономической единице, а видимый угловой диаметр при наблюдении с Земли, как и у Луны, — чуть больше полуградуса (31—32 минуты). Солнце находится на расстоянии около 26 000 световых лет от центра Млечного Пути и вращается вокруг него на ящичной орбите, делая один оборот за 225—250 миллионов лет^[13]. Орбитальная скорость Солнца равна 217 км/с — таким образом, световой год оно проходит примерно за 1400 земных лет, а одну астрономическую единицу — за 8 земных суток^[14].

В настоящее время Солнце находится во внутреннем крае рукава Ориона нашей Галактики, между рукавом Персея и рукавом Стрельца, и движется через Местное межзвёздное облако — область повышенной плотности, расположенную в имеющем меньшую плотность Местном пузыре — зоне рассеянного высокотемпературного межзвёздного газа. Из звёзд, принадлежащих 50 самым близким звёздным системам в пределах 17 световых лет, известным в настоящее время, Солнце является четвёртой по яркости звездой (его абсолютная звёздная величина +4,83^m).

Общие сведения

Солнце принадлежит к первому типу звёздного населения. Одна из распространённых теорий возникновения Солнечной системы предполагает, что её формирование было вызвано взрывами одной или нескольких сверхновых звёзд^[15]. Это предположение основано, в частности, на том, что в веществе Солнечной системы содержится аномально большая доля золота и урана, которые могли бы быть результатом эндотермических реакций, вызванных этим взрывом, или ядерного превращения элементов путём поглощения нейтронов веществом массивной звезды второго поколения.

Излучение Солнца — основной источник энергии на Земле. Его мощность характеризуется солнечной постоянной — мощностью излучения, проходящего через площадку единичной площади, перпендикулярную солнечным лучам и расположенную на расстоянии одной астрономической единицы от Солнца (то есть на орбите Земли) вне земной атмосферы. Эта постоянная равна приблизительно 1,37 кВт/м².

Проходя сквозь атмосферу Земли, солнечное излучение теряет в энергии примерно 370 Вт/м², и до земной поверхности доходит только 1000 Вт/м² (при ясной погоде и когда Солнце находится в зените). Эта энергия может использоваться в различных естественных и искусственных процессах. Так, растения, используя её посредством фотосинтеза, синтезируют органические соединения с выделением кислорода. Прямое нагревание солнечными лучами или преобразование энергии с помощью фотоэлементов может быть использовано для производства электроэнергии (солнечными электростанциями) или выполнения другой полезной работы. Путём фотосинтеза была в далёком прошлом получена и энергия, запасённая в нефти и других видах ископаемого топлива.

Ультрафиолетовое излучение Солнца имеет антисептические свойства, позволяющие использовать его для дезинфекции воды и различных предметов. Оно также вызывает загар и имеет другие биологические эффекты, например стимулирует производство в организме витамина D. Воздействие ультрафиолетовой части солнечного спектра сильно ослабляется озоновым слоем в земной атмосфере, поэтому интенсивность ультрафиолетового излучения на поверхности Земли сильно меняется с широтой. Угол, под которым Солнце стоит над горизонтом в полдень, влияет на многие типы биологической адаптации, например от него зависит цвет кожи человека в различных регионах земного шара^[16].

Наблюдаемый с Земли путь Солнца по небесной сфере изменяется в течение года. Путь, описываемый в течение года той точкой, которую занимает Солнце на небе в определённое заданное время, называется аналеммой и имеет форму цифры 8, вытянутой вдоль оси север — юг. Самая заметная вариация в видимом положении Солнца на небе — его колебание вдоль направления север — юг с амплитудой 47° (вызванное наклоном плоскости эклиптики к плоскости небесного экватора, равным 23,5°). Существует также другая компонента этой вариации, направленная вдоль оси восток — запад и вызванная увеличением скорости орбитального движения Земли при её приближении к перигелию и уменьшением — при приближении к афелию. Первое из этих движений (север — юг) является причиной смены времён года.

Земля проходит через точку афелия в начале июля и удаляется от Солнца на расстояние 152 млн км, а через точку перигелия — в начале января и приближается к Солнцу на расстояние 147 млн км^[17]. Видимый диаметр Солнца между этими двумя датами меняется на 3 %^[18]. Поскольку разница в расстоянии составляет примерно 5 млн км, то в афелии Земля получает примерно на 7 % меньше тепла. Таким образом, зимы в северном полушарии немного теплее, чем в южном, а лето немного прохладнее.

Солнце — магнитоактивная звезда. Она обладает сильным магнитным полем, напряжённость которого меняется со временем и которое меняет направление приблизительно каждые 11 лет, во время солнечного максимума. Вариации магнитного поля Солнца вызывают разнообразные эффекты, совокупность которых называется солнечной активностью и включает в себя такие явления, как солнечные пятна, солнечные вспышки, вариации солнечного ветра и т. д., а на Земле вызывает полярные сияния в высоких и средних широтах и геомагнитные бури, которые негативно сказываются на работе средств связи, средств передачи электроэнергии, а также негативно воздействует на живые организмы (вызывают головную боль и плохое самочувствие у людей, чувствительных к магнитным бурям)^[19][20]. Предполагается, что солнечная активность играла большую роль в формировании и развитии Солнечной системы. Она также оказывает влияние на структуру земной атмосферы.

Жизненный цикл

Солнце является молодой звездой третьего поколения (популяции I) с высоким содержанием металлов, то есть оно образовалось из останков звёзд первого и второго поколений (соответственно популяций III и II).

Текущий возраст Солнца (точнее время его существования на главной последовательности), оценённый с помощью компьютерных моделей звёздной эволюции, равен приблизительно 4,5 миллиарда лет^[21].

Считается^[21], что Солнце сформировалось примерно 4,5 миллиарда лет назад, когда быстрое сжатие под действием сил гравитации облака молекулярного водорода (также, возможно, облака из смеси молекулярного водорода и атомов других химических элементов) привело к образованию в нашей области Галактики звезды первого типа звёздного населения типа T Тельца.

Звезда такой массы, как Солнце, должна существовать на главной последовательности в общей сложности примерно 10 млрд лет. Таким образом, сейчас Солнце находится примерно в середине своего жизненного цикла^[22]. На современном этапе в солнечном ядре идут термоядерные реакции превращения водорода в гелий. Каждую секунду в ядре Солнца около 4 миллионов тонн вещества превращается в лучистую энергию, в результате чего генерируется солнечное излучение и поток солнечных нейтрино.

По мере того, как Солнце постепенно расходует запасы своего водородного горючего, оно становится всё горячее, а его светимость медленно, но неуклонно увеличивается. К возрасту 5,6 млрд лет, через 1,1 млрд лет от настоящего времени, наше дневное светило будет ярче на 11 %, чем сейчас^[23].

Уже в этот период, ещё до стадии красного гиганта, возможно исчезновение или кардинальное изменение жизни на Земле из-за повышения температуры поверхности планеты, вызванного увеличением яркости Солнца и парникового эффекта, индуцированного парами воды^{[24][25][26][27]}. К этому моменту Солнце достигнет максимальной поверхностной температуры (5800 К) за всё своё время эволюции в прошлом и будущем вплоть до фазы белого карлика; на следующих стадиях температура фотосферы будет меньше.
Несмотря на прекращение жизни в её современном понимании, жизнь на планете может остаться в глубинах морей и океанов^[28].

К возрасту 8 млрд лет (через 3,5 млрд лет от настоящего времени) яркость Солнца возрастёт на 40 %^[23]. К тому времени условия на Земле, возможно, будут подобны нынешним условиям на Венере: вода с поверхности планеты исчезнет полностью и улетучится в космос. Скорее всего, это приведёт к окончательному уничтожению всех наземных форм жизни^[28]. По мере того как водородное топливо в солнечном ядре будет выгорать, его внешняя оболочка будет расширяться, а ядро — сжиматься и нагреваться.

Когда Солнце достигнет возраста 10,9 млрд лет (6,4 млрд лет от настоящего времени), водород в ядре кончится, а образовавшийся из него гелий, ещё неспособный в этих условиях к термоядерному горению, станет сжиматься и уплотняться ввиду прекращения ранее поддерживавшего его «на весу» потока энергии из центра. Горение водорода будет продолжаться в тонком внешнем слое ядра. На этой стадии радиус Солнца достигнет 1,59 R_⊙, а светимость будет в 2,21 раза больше современной. В течение следующих 0,7 млрд лет Солнце будет относительно быстро расширяться (до 2,3 R_⊙), сохраняя почти постоянную светимость, а его температура упадёт с 5500 K до 4900 K^[28]. В конце этой фазы, достигнув возраста 11,6 млрд лет (через 7 млрд лет от настоящего времени) Солнце станет субгигантом^[28].

Приблизительно через 7,6—7,8^[29][28] миллиарда лет, к возрасту 12,2 млрд лет, ядро Солнца разогреется настолько, что запустит процесс горения водорода в окружающей его оболочке^[29]. Это повлечёт за собой бурное расширение внешних оболочек светила, таким образом Солнце покинет главную последовательность, на которой оно находилось почти с момента своего рождения, и станет красным гигантом, перейдя на вершину ветви красных гигантов диаграммы Герцшпрунга — Рассела^[29]. В этой фазе радиус Солнца увеличится в 256 раз по сравнению с современным^[29]. Расширение звезды приведёт к сильному увеличению её светимости (в 2700 раз) и охлаждению поверхности до 2650 К^[29]. По-видимому, расширяющиеся внешние слои Солнца в это время достигнут современной орбиты Земли. При этом исследования показывают, что ещё до этого момента из-за усиления солнечного ветра вследствие многократного увеличения площади поверхности Солнце потеряет более 28 %^[28] своей массы, и это приведёт к тому, что Земля перейдёт на более далёкую от Солнца орбиту, избежав, таким образом, поглощения внешними слоями солнечной плазмы^[30][26]. Хотя исследования 2008 года показывают, что Земля, скорее всего, будет поглощена Солнцем вследствие замедления вращения Солнца и последующих приливных взаимодействий с его внешней оболочкой^[29], которые приведут к приближению орбиты Земли обратно к Солнцу.
Даже если Земля избежит поглощения Солнцем, вся вода на ней перейдёт в газообразное состояние, а её атмосфера будет сорвана сильнейшим солнечным ветром^[31].

Данная фаза существования Солнца продлится около 10 миллионов лет. Когда температура в ядре достигнет 100 млн К, произойдёт гелиевая вспышка, и начнётся термоядерная реакция синтеза углерода и кислорода из гелия^[28]. Солнце, получившее новый источник энергии, уменьшится в размере до 9,5 R_⊙^[28]. Спустя 100—110 млн лет, когда запасы гелия иссякнут, повторится бурное расширение внешних оболочек звезды, и она снова станет красным гигантом^[28]. Этот период существования Солнца будет сопровождаться мощными вспышками, временами его светимость будет превышать современный уровень в 5200 раз^[28][32]. Это будет происходить от того, что в термоядерную реакцию будут вступать ранее не затронутые остатки гелия^[32]. В таком состоянии Солнце просуществует около 20 млн лет^[28].

Масса Солнца недостаточна для того, чтобы его эволюция завершилась взрывом сверхновой. После того как Солнце пройдёт фазу красного гиганта, термические пульсации приведут к тому, что его внешняя оболочка будет сорвана, и из неё образуется планетарная туманность. В центре этой туманности останется сформированный из ядра Солнца белый карлик, очень горячий и плотный объект, по размерам сопоставимый с планетой Земля^[28]. Изначально этот белый карлик будет иметь температуру поверхности 120 000 К^[28] и светимость 3500^[28] солнечных, но в течение многих миллионов и миллиардов лет будет остывать и угасать. Данный жизненный цикл считается типичным для звёзд малой и средней массы.

Структура

Внутреннее строение Солнца

Солнечное ядро

Центральная часть Солнца с радиусом примерно 150—175 тыс. км (то есть 20—25 % от радиуса Солнца), в которой идут термоядерные реакции, называется солнечным ядром^[33]. Плотность вещества в ядре составляет примерно 150 000 кг/м³^[34] (в 150 раз выше плотности воды и в ~6,6 раз выше плотности самого плотного металла на Земле — осмия), а температура в центре ядра — более 14 млн К. Анализ данных, проведённый миссией SOHO, показал, что в ядре скорость вращения Солнца вокруг своей оси значительно выше, чем на поверхности^[33][35].
В ядре осуществляется протон-протонная термоядерная реакция, в результате которой из четырёх протонов образуется гелий-4^[36]. При этом каждую секунду в излучение превращаются 4,26 млн тонн вещества, однако эта величина ничтожна по сравнению с массой Солнца — 2⋅10²⁷ тонн. Мощность, выделяемая различными зонами ядра, зависит от их расстояния до центра Солнца. В самом центре она достигает, согласно теоретическим оценкам, 276,5 Вт/м³^[37]. Таким образом, на объём человека (0,05 м³) приходится выделение тепла 285 Ккал/день (1192 кДж/день), что на порядок меньше удельного тепловыделения живого бодрствующего человека. Удельное же тепловыделение всего объёма Солнца ещё на два порядка меньше. Благодаря столь скромному удельному энерговыделению запасов «топлива» (водорода) хватает на несколько миллиардов лет поддержания термоядерной реакции.

Ядро — единственное место на Солнце, в котором энергия и тепло получается от термоядерной реакции, остальная часть звезды нагрета этой энергией. Вся энергия ядра последовательно проходит сквозь слои, вплоть до фотосферы, с которой излучается в виде солнечного света и кинетической энергии^[38][39].

Зона лучистого переноса

Над ядром, на расстояниях примерно от 0,2—0,25 до 0,7 радиуса Солнца от его центра, находится зона лучистого переноса. В этой зоне перенос энергии происходит главным образом с помощью излучения и поглощения фотонов. При этом направление каждого конкретного фотона, излучённого слоем плазмы, никак не зависит от того, какие фотоны плазмой поглощались, поэтому он может как проникнуть в следующий слой плазмы в лучистой зоне, так и переместиться назад, в нижние слои. Из-за этого промежуток времени, за который многократно переизлучённый фотон (изначально возникший в ядре) достигает конвективной зоны, согласно современным моделям Солнца, может лежать в пределах от 10 тысяч до 170 тысяч лет (иногда встречающаяся цифра в миллионы лет считается завышенной)^[40].

Перепад температур в данной зоне составляет от 2 млн К на поверхности до 7 млн К в глубине^[41]. При этом в данной зоне отсутствуют макроскопические конвекционные движения, что говорит о
том, что адиабатический градиент температуры в ней больше, чем градиент лучевого равновесия^[42]. Для сравнения, в красных карликах давление не может препятствовать перемешиванию вещества и зона конвекции начинается сразу от ядра. Плотность вещества в данной зоне колеблется от 0,2 (на поверхности) до 20 (в глубине) г/см³^[41].

Конвективная зона Солнца

Ближе к поверхности Солнца температуры и плотности вещества уже недостаточно для полного переноса энергии путём переизлучения. Возникает вихревое перемешивание плазмы, и перенос энергии к поверхности (фотосфере) совершается преимущественно движениями самого вещества. С одной стороны, вещество фотосферы, охлаждаясь на поверхности, погружается вглубь конвективной зоны. С другой стороны, вещество в нижней части получает излучение из зоны лучевого переноса и поднимается наверх, причём оба процесса идут со значительной скоростью. Такой способ передачи энергии называется конвекцией, а подповерхностный слой Солнца толщиной примерно 200 000 км, где она происходит, — конвективной зоной. По мере приближения к поверхности температура падает в среднем до 5800 К, а плотность газа до менее 1/1000 плотности земного воздуха^[41].

По современным данным, роль конвективной зоны в физике солнечных процессов исключительно велика, так как именно в ней зарождаются разнообразные движения солнечного вещества. Термики в конвективной зоне вызывают на поверхности гранулы (которые по сути являются вершинами термиков) и супергрануляцию. Скорость потоков составляет в среднем 1—2 км/с, а максимальные её значения достигают 6 км/с. Время жизни гранулы составляет 10—15 минут, что сопоставимо по времени с периодом, за который газ может однократно обойти вокруг гранулы. Следовательно, термики в конвективной зоне находятся в условиях, резко отличных от условий, способствующих возникновению ячеек Бенара^[43]. Также движения в этой зоне вызывают эффект магнитного динамо и, соответственно, порождают магнитное поле, имеющее сложную структуру^[41].

Атмосфера Солнца

Фотосфера

Фотосфера (слой, излучающий свет) образует видимую поверхность Солнца. Её толщина соответствует оптической толщине приблизительно в 2/3 единиц^[44]. В абсолютных величинах фотосфера достигает толщины, по разным оценкам, от 100^[45] до 400 км^[1]. Из фотосферы исходит основная часть оптического (видимого) излучения Солнца, излучение же из более глубоких слоёв до нас уже не доходит. Температура по мере приближения к внешнему краю фотосферы уменьшается с 6600 К до 4400 К^[1]. Эффективная температура фотосферы в целом составляет 5772 К^[1]. Она может быть рассчитана по закону Стефана — Больцмана, согласно которому мощность излучения абсолютно чёрного тела прямо пропорциональна четвёртой степени температуры тела. Водород при таких условиях сохраняется почти полностью в нейтральном состоянии. Фотосфера образует видимую поверхность Солнца, по которой определяются размеры Солнца, расстояние от Солнца и т. д. Так как газ в фотосфере является относительно разреженным, то скорость его вращения много меньше скорости вращения твёрдых тел^[45]. При этом газ в экваториальной и полярных областях, движется неравномерно — на экваторе он делает оборот за 24 дня, на полюсах — за 30 дней^[45].

Хромосфера

Хромосфера (от др.-греч. χρῶμα — цвет, σφαῖρα — шар, сфера) — внешняя оболочка Солнца толщиной около 2000 км, окружающая фотосферу^[46]. Происхождение названия этой части солнечной атмосферы связано с её красноватым цветом, вызванным тем, что в видимом спектре хромосферы доминирует красная H-альфа линия излучения водорода из серии Бальмера. Верхняя граница хромосферы не имеет выраженной гладкой поверхности, из неё постоянно происходят горячие выбросы, называемые спикулами. Число спикул, наблюдаемых одновременно, составляет в среднем 60—70 тыс.^[47] Из-за этого в конце XIX века итальянский астроном Секки, наблюдая хромосферу в телескоп, сравнил её с горящими прериями. Температура хромосферы увеличивается с высотой от 4000 до 20 000 К (область температур больше 10 000 К относительно невелика)^[46].

Плотность хромосферы невелика, поэтому яркость недостаточна для наблюдения в обычных условиях. Но при полном солнечном затмении, когда Луна закрывает яркую фотосферу, расположенная над ней хромосфера становится видимой и светится красным цветом. Её можно также наблюдать в любое время с помощью специальных узкополосных оптических фильтров. Кроме уже упомянутой линии H-альфа с длиной волны 656,3 нм, фильтр также может быть настроен на линии Ca II K (393,4 нм) и Ca II H (396,8 нм).

Основные хромосферные структуры, которые видны в этих линиях^[48]:

• хромосферная сетка, покрывающая всю поверхность Солнца и состоящая из линий, окружающих ячейки супергрануляции размером до 30 тыс. км в поперечнике;
• флоккулы — светлые облакоподобные образования, чаще всего приуроченные к районам с сильными магнитными полями — активным областям, часто окружают солнечные пятна;
• волокна и волоконца (фибриллы) — тёмные линии различной ширины и протяжённости, как и флоккулы, часто встречаются в активных областях.

Корона

Корона — последняя внешняя оболочка Солнца. Корона в основном состоит из протуберанцев и энергетических извержений, исходящих и извергающихся на несколько сотен тысяч и даже более миллиона километров в пространство, образуя солнечный ветер. Средняя корональная температура составляет от 1 до 2 млн К, а максимальная, в отдельных участках, — от 8 до 20 млн К^[49]. Несмотря на такую высокую температуру, она видна невооружённым глазом только во время полного солнечного затмения, так как плотность вещества в короне мала, а потому невелика и её яркость. Необычайно интенсивный нагрев этого слоя вызван, по-видимому, эффектом магнитного пересоединения^[49][50] и воздействием ударных волн (см. Проблема нагрева короны). Форма короны меняется в зависимости от фазы цикла солнечной активности: в периоды максимальной активности она имеет округлую форму, а в минимуме — вытянута вдоль солнечного экватора. Поскольку температура короны очень велика, она интенсивно излучает в ультрафиолетовом и рентгеновском диапазонах. Эти излучения не проходят сквозь земную атмосферу, но в последнее время появилась возможность изучать их с помощью космических аппаратов. Излучение в разных областях короны происходит неравномерно. Существуют горячие активные и спокойные области, а также корональные дыры с относительно невысокой температурой в 600 000 К, из которых в пространство выходят магнитные силовые линии. Такая («открытая») магнитная конфигурация позволяет частицам беспрепятственно покидать Солнце, поэтому солнечный ветер испускается в основном из корональных дыр.

Видимый спектр солнечной короны состоит из трёх различных составляющих, названных L, K и F компонентами (или, соответственно, L-корона, K-корона и F-корона; ещё одно название L-компоненты — E-корона^[51]. K-компонента — непрерывный спектр короны. На его фоне до высоты 9—10′ от видимого края Солнца видна эмиссионная L-компонента. Начиная с высоты около 3′ (угловой диаметр Солнца — около 30′) и выше виден фраунгоферов спектр, такой же как и спектр фотосферы. Он составляет F-компоненту солнечной короны. На высоте 20′ F-компонента доминирует в спектре короны. Высота 9-10′ принимается за границу, отделяющую внутреннюю корону от внешней. Излучение Солнца с длиной волны менее 20 нм, полностью исходит из короны^[51]. Это означает, что, например, на распространённых снимках Солнца на длинах волн 17,1 нм (171 Å), 19,3 нм (193 Å), 19,5 нм (195 Å), видна исключительно солнечная корона с её элементами, а хромосфера и фотосфера — не видны. Две корональные дыры, почти всегда существующие у северного и южного полюсов Солнца, а также другие, временно появляющиеся на его видимой поверхности, практически совсем не испускают рентгеновское излучение.

Солнечный ветер

Из внешней части солнечной короны истекает солнечный ветер — поток ионизированных частиц (в основном протонов, электронов и α-частиц), распространяющийся с постепенным уменьшением своей плотности, до границ гелиосферы. Солнечный ветер разделяют на два компонента — медленный солнечный ветер и быстрый солнечный ветер. Медленный солнечный ветер имеет скорость около 400 км/с и температуру 1,4—1,6⋅10⁶ К и по составу близко соответствует короне. Быстрый солнечный ветер имеет скорость около 750 км/с, температуру 8⋅10⁵ К, и по составу похож на вещество фотосферы^[52]. Медленный солнечный ветер вдвое более плотный и менее постоянный, чем быстрый. Медленный солнечный ветер имеет более сложную структуру с регионами турбулентности^[53].

В среднем Солнце излучает с ветром около 1,3⋅10³⁶ частиц в секунду^[53][54]. Следовательно, полная потеря массы Солнцем (на данный вид излучения) составляет за год 2—3⋅10⁻¹⁴ солнечных масс^[55]. Потеря за 150 млн лет эквивалентна земной массе^[56]. Многие природные явления на Земле связаны с возмущениями в солнечном ветре, в том числе геомагнитные бури и полярные сияния.

Первые прямые измерения характеристик солнечного ветра были проведены в январе 1959 года советской станцией «Луна-1»^[57]. Наблюдения проводились с помощью сцинтилляционного счётчика и газового ионизационного детектора^[58]. Три года спустя такие же измерения были проведены американскими учёными с помощью станции «Маринер-2»^[59]. В конце 1990-х годов с помощью Ультрафиолетового коронального спектрометра (англ. Ultraviolet Coronal Spectrometer (UVCS)) на борту спутника SOHO были проведены наблюдения областей возникновения быстрого солнечного ветра на солнечных полюсах.

Магнитные поля Солнца

Происхождение и виды солнечных магнитных полей

Так как солнечная плазма имеет достаточно высокую электропроводность, в ней могут возникать электрические токи и, как следствие, магнитные поля. Непосредственно наблюдаемые в солнечной фотосфере магнитные поля принято разделять на два типа, в соответствии с их масштабом.

Крупномасштабное (общее или глобальное) магнитное поле с характерными размерами, сравнимыми с размерами Солнца, имеет среднюю напряжённость на уровне фотосферы порядка нескольких гаусс. В минимуме цикла солнечной активности оно имеет приблизительно дипольную структуру, при этом напряжённость поля на полюсах Солнца максимальна. Затем, по мере приближения к максимуму цикла солнечной активности, напряжённости поля на полюсах постепенно уменьшаются и через один-два года после максимума цикла становятся равными нулю (так называемая «переполюсовка солнечного магнитного поля»). На этой фазе общее магнитное поле Солнца не исчезает полностью, но его структура носит не дипольный, а квадрупольный характер. После этого напряжённость солнечного диполя снова возрастает, но при этом он имеет уже другую полярность. Таким образом, полный цикл изменения общего магнитного поля Солнца, с учётом перемены знака, равен удвоенной продолжительности 11-летнего цикла солнечной активности — примерно 22 года («закон Хейла»).

Средне- и мелкомасштабные (локальные) поля Солнца отличаются значительно бо́льшими напряжённостями полей и меньшей регулярностью. Самые мощные магнитные поля (до нескольких тысяч гаусс) наблюдаются в группах солнечных пятен в максимуме солнечного цикла. При этом типична ситуация, когда магнитное поле пятен в западной («головной») части данной группы, в том числе самого крупного пятна (т. н. «лидера группы») совпадает с полярностью общего магнитного поля на соответствующем полюсе Солнца («p-полярностью»), а в восточной («хвостовой») части — противоположна ему («f-полярность»). Таким образом, магнитные поля пятен имеют, как правило, биполярную или мультиполярную структуру. В фотосфере также наблюдаются униполярные области магнитного поля, которые, в отличие от групп солнечных пятен, располагаются ближе к полюсам и имеют значительно меньшую напряжённость магнитного поля (несколько гаусс), но большую площадь и продолжительность жизни (до нескольких оборотов Солнца).

Согласно современным представлениям, разделяемым большей частью исследователей, магнитное поле Солнца генерируется в нижней части конвективной зоны с помощью механизма гидромагнитного конвективного динамо, а затем всплывает в фотосферу под воздействием магнитной плавучести. Этим же механизмом объясняется 22-летняя цикличность солнечного магнитного поля.

Существуют также некоторые указания^[60] на наличие первичного (то есть возникшего вместе с Солнцем) или, по крайней мере, очень долгоживущего магнитного поля ниже дна конвективной зоны — в лучистой зоне и ядре Солнца.

Солнечная активность и солнечный цикл

Комплекс явлений, вызванных генерацией сильных магнитных полей на Солнце, называют солнечной активностью. Эти поля проявляются в фотосфере как солнечные пятна и вызывают такие явления, как солнечные вспышки, генерацию потоков ускоренных частиц, изменения в уровнях электромагнитного излучения Солнца в различных диапазонах, корональные выбросы массы, возмущения солнечного ветра, вариации потоков галактических космических лучей (Форбуш-эффект) и т. д.

С солнечной активностью связаны также вариации геомагнитной активности (в том числе и магнитные бури), которые являются следствием достигающих Земли возмущений межпланетной среды, вызванных, в свою очередь, активными явлениями на Солнце.

Одним из наиболее распространённых показателей уровня солнечной активности является число Вольфа, связанное с количеством солнечных пятен на видимой полусфере Солнца. Общий уровень солнечной активности меняется с характерным периодом, примерно равным 11 годам (так называемый «цикл солнечной активности» или «одиннадцатилетний цикл»). Этот период выдерживается неточно и в XX веке был ближе к 10 годам, а за последние 300 лет варьировался примерно от 7 до 17 лет. Циклам солнечной активности принято приписывать последовательные номера, начиная от условно выбранного первого цикла, максимум которого был в 1761 году. В 2000 году наблюдался максимум 23-го цикла солнечной активности.

Существуют также вариации солнечной активности большей длительности. Так, во второй половине XVII века солнечная активность и, в частности, её одиннадцатилетний цикл были сильно ослаблены (минимум Маундера). В эту же эпоху в Европе отмечалось снижение среднегодовых температур (т. н. Малый ледниковый период), что, возможно, вызвано воздействием солнечной активности на климат Земли. Существует также точка зрения, что глобальное потепление до некоторой степени вызвано повышением глобального уровня солнечной активности во второй половине XX века. Тем не менее, механизмы такого воздействия пока ещё недостаточно ясны.

Самая большая группа солнечных пятен за всю историю наблюдений возникла в апреле 1947 года в южном полушарии Солнца. Её максимальная длина составляла 300 000 км, максимальная ширина — 145 000 км, а максимальная площадь превышала 6000 миллионных долей площади полусферы (мдп) Солнца^[61], что примерно в 36 раз больше площади поверхности Земли. Группа была легко видна невооружённым глазом в предзакатные часы. Согласно каталогу Пулковской обсерватории, эта группа (№ 87 за 1947 год) проходила по видимой с Земли полусфере Солнца с 31 марта по 14 апреля 1947 года, максимальная её площадь составила 6761 мдп, а максимальная площадь наибольшего пятна в группе — 5055 мдп; количество пятен в группе достигало 172^[62].

Солнце как переменная звезда

Так как магнитная активность Солнца подвержена периодическим изменениям, а вместе с этим изменяется и его светимость (или Солнечная цикличность), его можно рассматривать как переменную звезду. В годы максимума активности Солнце ярче, чем в годы минимума. Амплитуда изменений солнечной постоянной достигает 0,1 % (в абсолютных значениях это 1 Вт/м², тогда как среднее значение солнечной постоянной — 1361,5 Вт/м²)^[63].

Также некоторые исследователи относят Солнце к классу низкоактивных переменных звёзд типа BY Дракона. Поверхность таких звёзд покрыта пятнами (до 30 % от общей площади), и за счёт вращения звёзд наблюдаются изменения их блеска. У Солнца такая переменность очень слабая^[64][65].

Планетная система

Вокруг Солнца обращается большое количество небесных тел меньшего размера, а именно:

• Восемь больших планет (Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун) и их спутники.
• Множество астероидов и планет-карликов, которые группируются в пояс астероидов и пояс Койпера.
• Кометы.

Самые далёкие из этих тел удалены на расстояния порядка 100 а. е. от Солнца.
В состав Солнечной системы включают также гипотетическое облако Оорта, которое должно быть расположено ещё в примерно 1000 раз дальше. Все объекты Солнечной системы образовались в то же время, что и Солнце, из того же газопылевого облака.

Солнце и Земля

Спектральный диапазон электромагнитного излучения Солнца очень широк — от радиоволн^[66] до рентгеновских лучей — однако максимум его интенсивности приходится на видимый свет (жёлто-зелёную часть спектра).

Для людей, животных и растений солнечный свет является очень важным. У значительной их части свет вызывает изменение циркадного ритма. Так, на человека, по некоторым исследованиям, оказывает влияние свет интенсивности более 1000 люкс^[67], причём его цвет имеет значение^[68]. В тех областях Земли, которые в среднем за год получают мало солнечного света, например, тундре, устанавливается низкая температура (до −35 °C зимой), короткий сезон роста растений, малое биоразнообразие и низкорослая растительность^[69].

В зелёных листьях растений содержится зелёный пигмент хлорофилл. Этот пигмент служит улавливателем световой энергии в процессе фотосинтеза — сложного цикла реакций синтеза органических веществ из углекислого газа и воды с использованием энергии света. Одним из продуктов фотосинтеза является кислород^[70]. Таким образом, фотосинтез обеспечивает возможность существования жизни на Земле. Животные существуют за счёт поедания растений, которые накапливают энергию Солнца в виде энергии химических соединений, и дыхания выделяемым ими кислородом^[71].

Земная поверхность и нижние слои воздуха — тропосфера, где образуются облака и возникают другие метеорологические явления, непосредственно получают энергию от Солнца. Основной приток энергии в систему атмосфера — Земля обеспечивается излучением Солнца в спектральном диапазоне от 0,1 до 4 мкм. При этом в диапазоне от 0,3 мкм до 1,5—2 мкм атмосфера Земли прозрачна для солнечного излучения почти полностью. В ультрафиолетовой области спектра (для волн короче 0,3 мкм) излучение поглощается в основном слоем озона, расположенного на высотах 20—60 км. Рентгеновское и гамма-излучение до поверхности Земли практически не доходят^[72]. Плотность мощности излучения Солнца на расстоянии 1 астрономической единицы вне атмосферы Земли равна около 1367 Вт/м² (солнечная постоянная). По данным за 2000—2004 годы^[73], усреднённый по времени и по поверхности Земли, этот поток составляет 341 Вт/м²^[74][75] или 1,74⋅10¹⁷ Вт в расчёте на полную поверхность Земли (полная светимость Солнца примерно в 2,21⋅10⁹ раза больше).

Помимо этого, в атмосферу Земли проникает поток ионизированных частиц (в основном гелиево-водородной плазмы), истекающий из солнечной короны со скоростью 300—1200 км/с в окружающее космическое пространство (солнечный ветер). Во многих районах близ полюсов планеты это приводит к полярным сияниям («северным сияниям»). Также с солнечным ветром связано множество других природных явлений, в частности, магнитные бури^[76]. Магнитные бури, в свою очередь, могут воздействовать на земные организмы. Раздел биофизики, изучающий подобные влияния, называется гелиобиологией.

Также важным для живых организмов является излучение Солнца в ультрафиолетовом диапазоне. Так, под действием ультрафиолета образуется жизненно необходимый витамин D^[77]. При его недостатке возникает серьёзное заболевание — рахит^[78]. Из-за недостатка ультрафиолетовых лучей может нарушиться нормальное поступление кальция, вследствие чего усиливается хрупкость мелких кровеносных сосудов, увеличивается проницаемость тканей. Однако длительное действие ультрафиолета способствует развитию меланомы, различных видов рака кожи, ускоряет старение и появление морщин. От избыточного излучения Землю предохраняет озоновый слой, без которого, как считается, жизнь не смогла бы вообще выбраться из океанов^[79].

Солнечные затмения

Солнечные затмения упоминаются уже в античных источниках^[80]. Однако наибольшее число датированных описаний содержится в западно-европейских средневековых хрониках и анналах. Например, солнечное затмение упоминает Максимин Трирский, который записал, что в «538 г. 16 февраля, с первого до третьего часа было солнечное затмение»^[81].

Возникает данное явление из-за того, что Луна закрывает (затмевает) полностью или частично Солнце от наблюдателя на Земле. Солнечное затмение возможно только в новолуния, когда сторона Луны, обращённая к Земле, не освещена, и сама Луна не видна. Затмения возможны только если новолуние происходит вблизи одного из двух лунных узлов (точки пересечения видимых орбит Луны и Солнца), не далее чем примерно в 12 градусах от одного из них. По астрономической классификации, если затмение хотя бы где-то на поверхности Земли может наблюдаться как полное, оно называется полным^[82]. Если затмение может наблюдаться только как частное (такое бывает, когда конус тени Луны проходит вблизи земной поверхности, но не касается её), затмение классифицируется как частное. Когда наблюдатель находится в тени от Луны, он наблюдает полное солнечное затмение. Когда он находится в области полутени, он может наблюдать частное солнечное затмение. Помимо полных и частных солнечных затмений, бывают кольцеобразные затмения. Визуально при кольцеобразном затмении Луна проходит по диску Солнца, но оказывается меньше Солнца в диаметре, и не может скрыть его полностью. Данное явление вызвано изменением угловых размеров Луны на небе вследствие эллиптичности её орбиты^[83][84].

В год на Земле может происходить от 2 до 5 солнечных затмений, из которых не более двух — полные или кольцеобразные^[85][86].
В среднем за сто лет происходит 237 солнечных затмений, из которых 160 — частные, 63 — полные, 14 — кольцеобразные^[87]. В определённой точке земной поверхности затмения в большой фазе происходят достаточно редко, ещё реже наблюдаются полные солнечные затмения. Так, на территории Москвы с XI по XVIII век можно было наблюдать 159 солнечных затмений с фазой больше 0,5, из которых всего 3 полных (11.08.1124, 20.03.1140 и 7.06.1415)^[88]. Ещё одно полное солнечное затмение произошло 19 августа 1887 года. Кольцеобразное затмение можно было наблюдать в Москве 26 апреля 1827 года. Очень сильное затмение с фазой 0,96 произошло 9 июля 1945 года. Следующее полное солнечное затмение ожидается в Москве 16 октября 2126 года.

Полные солнечные затмения позволяют наблюдать корону и ближайшие окрестности Солнца, что в обычных условиях крайне затруднено (хотя с 1996 года астрономы получили возможность постоянно обозревать окрестности нашей звезды благодаря работе спутника SOHO (англ. Solar and Heliospheric Observatory — солнечная и гелиосферная обсерватория)). Французский учёный Пьер Жансен во время полного солнечного затмения в Индии 18 августа 1868 года впервые исследовал хромосферу Солнца и получил спектр нового химического элемента. Этот элемент назвали в честь Солнца — гелием^[89]. В 1882 году, 17 мая, во время солнечного затмения наблюдателями из Египта была замечена комета, пролетающая вблизи Солнца^[90].

Солнце и другие звёзды

Название	Расстояние, св.лет
Проксима Центавра	4,2421 ± 0,0016
α Центавра A	4,3650 ± 0,0068
α Центавра B	4,3650 ± 0,0068
Звезда Барнарда	5,9630 ± 0,0109
Луман 16	6,588 ± 0,062
WISE 0855–0714	7,27 ± 0.13
Вольф 359	7,7825 ± 0,0390
Лаланд 21185	8,2905 ± 0,0148
Сириус A	8,5828 ± 0,0289
Сириус B	8,5828 ± 0,0289

Ближайшие к Солнцу звёзды

Ближайшие к Солнцу три звезды находятся на расстоянии примерно 4,3 светового года (около 270 тыс. а. е.). Они составляют звёздную систему Альфа Центавра и движутся по сложным траекториям вокруг друг друга. На текущий момент ближе всех находится Проксима Центавра.

Двойники Солнца

В настоящее время известны несколько «двойников» Солнца, которые являются практически полными аналогами нашей звезды по массе, светимости, температуре (±50 К), металличности (±12 %), возрасту (±1 млрд лет) и т. д.^[91], среди которых:

• Бета Гончих Псов;
• 18 Скорпиона;
• 37 Близнецов;
• HD 44594;
• HIP 56948.

Движение Солнца

Солнце вместе с Солнечной системой совершает сложное движение относительно других тел Вселенной.

Относительно ближайших звёзд оно движется со скоростью около 20 км/с в сторону точки, имеющей экваториальные координаты α = 270°, δ = 30° (в созвездии Геркулеса).

Однако эта скорость намного меньше скорости движения Солнца относительно центра Галактики. Вместе с зоной синхронного вращения (коротации) Галактики, Солнце вращается по эллиптической орбите вокруг её центра, совершая оборот за 225—250 млн лет. При этом линейная скорость составляет 220—240 км/с^[92]. Её направление сравнительно медленно, но меняется (на противоположное оно изменится через половину периода — около 125 млн лет). В настоящее время этот вектор направлен в сторону созвездия Лебедя. Помимо движения вокруг центра Галактики, Солнце совершает также колебания относительно плоскости галактики, пересекая её каждые 30—35 миллионов лет (по другим расчётам — каждые 20-25 млн лет) и оказываясь то в северном, то в южном галактическом полушарии. Нахождение в зоне коротации максимизирует интервал между прохождением Солнцем спиральных рукавов^[93].

Также Солнце вместе со всей Галактикой совершает движение относительно центра Местной группы галактик^[94].

В 1969 году была впервые выделена дипольная компонента^[95] в реликтовом излучении: температура его оказалась не одинакова по всему небу. В направлении созвездия Льва она была на 0,1 % выше среднего, и на 0,1 % ниже в противоположном^[96]. Это следствие эффекта Доплера, возникающего при движении Солнца относительно реликтового фона со скоростью примерно 370 км/с в сторону созвездия Льва. Это движение складывается из движения Солнца относительно центра Галактики, движения Галактики относительно центра масс Местной группы, и собственного движения Местной группы. Скорость последнего, по современным данным, составляет 627±22 км/с и направлена в сторону точки с галактическими координатами , ^[97][98] (эта точка располагается в созвездии Гидры^[99]).

На пути вокруг центра Галактики Солнце движется в настоящее время сквозь область разреженного горячего газа, известную как Местный пузырь и через находящееся в этой области Местное межзвёздное облако, которое выдувается из области звездообразования под названием Ассоциация Скорпиона-Центавра. Солнце движется сквозь область Местного пузыря последние 5 или даже 10 млн лет., оно вошла в Местное межзвёздное облако где-то между 44 и 150 тыс. лет назад и, как ожидается, останется в его пределах ещё в течение 10—12 тыс. лет^[100][101].

Исследования Солнца

Ранние наблюдения Солнца

С самых ранних времён человечество отмечало важную роль Солнца — яркого диска на небе, несущего свет и тепло.

Во многих доисторических и античных культурах Солнце почиталось как божество. Культ Солнца занимал важное место в религиях цивилизаций Египта, инков, ацтеков. Многие древние памятники связаны с Солнцем: например, мегалиты точно отмечают положение летнего солнцестояния (одни из крупнейших мегалитов такого рода находятся в Набта-Плайя (Египет) и в Стоунхендже (Великобритания)), пирамиды в Чичен-Ице (Мексика) построены таким образом, чтобы тень от Земли скользила по пирамиде в дни весеннего и осеннего равноденствий, и так далее. Древнегреческие астрономы, наблюдая видимое годовое движение Солнца вдоль эклиптики, считали Солнце одной из семи планет (от др.-греч. ἀστὴρ πλανήτης — блуждающая звезда). В некоторых языках Солнцу, наравне с планетами, посвящён день недели.

Развитие современного научного понимания

Одним из первых попытался взглянуть на Солнце с научной точки зрения греческий философ Анаксагор. Он говорил, что Солнце — это не колесница Гелиоса, как учила греческая мифология, а гигантский, «размерами больше, чем Пелопоннес», раскалённый металлический шар. За это еретическое учение он был брошен в тюрьму, приговорён к смерти и освобождён только благодаря вмешательству Перикла.

Идея о том, что Солнце — это центр, вокруг которого обращаются планеты, высказывалась Аристархом Самосским и древнеиндийскими учёными (см. Гелиоцентрическая система мира). Эта теория была возрождена Коперником в XVI веке.

Первым расстояние от Земли до Солнца пытался вычислить Аристарх Самосский, измеряя угол между Солнцем и Луной в фазу первой или последней четверти и определяя из соответствующего прямоугольного треугольника отношение расстояния от Земли до Луны к расстоянию от Земли до Солнца^[102]. По Аристарху, расстояние до Солнца в 18 раз больше расстояния до Луны. На самом деле расстояние до Солнца в 394 раза больше расстояния до Луны. А вот расстояние до Луны в античности было определено весьма точно Гиппархом, причём он использовал другой метод, предложенный Аристархом Самосским^[102].

Китайские астрономы в течение столетий, со времён династии Хань, наблюдали солнечные пятна. Впервые пятна были зарисованы в 1128 году в хронике Иоанна Вустерского^[103]. С 1610 года начинается эпоха инструментального исследования Солнца. Изобретение телескопа и его специальной разновидности для наблюдения за Солнцем — гелиоскопа — позволило Галилею, Томасу Хэрриоту, Кристофу Шейнеру и другим учёным рассмотреть солнечные пятна. Галилей, по-видимому, первым среди исследователей признал пятна частью солнечной структуры, в отличие от Шейнера, посчитавшего их проходящими перед Солнцем планетами. Это предположение позволило Галилею открыть вращение Солнца и вычислить его период. Приоритету открытия пятен и их природе была посвящена более чем десятилетняя полемика между Галилеем и Шейнером, однако, скорее всего, первое наблюдение и первая публикация не принадлежат ни одному из них^[104].

Первую более или менее приемлемую оценку расстояния от Земли до Солнца способом параллакса получили Джованни Доменико Кассини и Жан Рише. В 1672 году, когда Марс находился в великом противостоянии с Землёй, они измерили положение Марса одновременно в Париже и в Кайенне — административном центре Французской Гвианы. Наблюдавшийся параллакс составил 24″. По результатам этих наблюдений было найдено расстояние от Земли до Марса, которое было затем пересчитано в расстояние от Земли до Солнца — 140 млн км.

В начале XIX века отец Пьетро Анджело Секки (итал. Pietro Angelo Secchi), главный астроном Ватикана, положил начало такому направлению исследования в астрономической науке, как спектроскопия, разложив солнечный свет на составные цвета. Стало понятно, что таким образом можно изучать состав звёзд, и Фраунгофер обнаружил линии поглощения в спектре Солнца. Благодаря спектроскопии был обнаружен новый элемент в составе Солнца, который назвали гелием в честь древнегреческого бога Солнца Гелиоса.

Долгое время непонятными оставались источники солнечной энергии. В 1848 году Роберт Майер выдвинул метеоритную гипотезу, согласно которой Солнце нагревается благодаря бомбардировке метеоритами. Однако при таком количестве метеоритов сильно нагревалась бы и Земля; кроме того, земные геологические напластования состояли бы в основном из метеоритов; наконец, масса Солнца должна была расти, и это сказалось бы на движении планет^[105]. Поэтому во второй половине XIX века многими исследователями наиболее правдоподобной считалась теория, развитая Гельмгольцем (1853) и лордом Кельвином^[106], которые предположили, что Солнце нагревается за счёт медленного гравитационного сжатия («механизм Кельвина — Гельмгольца»). Основанные на этом механизме расчёты оценивали максимальный возраст Солнца в 20 млн лет, а время, через которое Солнце потухнет — не более чем в 15 млн^[105]. Однако эта гипотеза противоречила геологическим данным о возрасте горных пород, которые указывали на намного бо́льшие цифры. Так, например, Чарльз Дарвин отметил, что эрозия вендских отложений продолжалась не менее 300 млн лет^[107]. Тем не менее, энциклопедия Брокгауза и Ефрона считает гравитационную модель единственно допустимой^[105].

Только в XX веке было найдено правильное решение этой проблемы. Первоначально Резерфорд выдвинул гипотезу, что источником внутренней энергии Солнца является радиоактивный распад^[108]. В 1920 году Артур Эддингтон предположил, что давление и температура в недрах Солнца настолько высоки, что там может идти термоядерная реакция, при которой четыре ядра водорода (протоны) сливаются в ядро гелия-4. Так как масса последнего меньше, чем сумма масс четырёх свободных протонов, то часть из-за дефекта массы в этой реакции переходит в энергию фотонов^[109]. То, что водород преобладает в составе Солнца, подтвердила в 1925 году Сесилия Пейн. Теория термоядерного синтеза была развита в 1930-х годах астрофизиками Субраманьяном Чандрасе́каром и Хансом Бете. Бете детально рассчитал две главные термоядерные реакции, которые являются источниками энергии Солнца^[110][111]. Наконец, в 1957 году появилась работа Маргарет Бербидж «Синтез элементов в звёздах»^[112], в которой было показано, что большинство элементов во Вселенной возникло в результате нуклеосинтеза, идущего в звёздах.

В 1905 году Джордж Эллери Хейл (англ. George Ellery Hale) в обсерватории Маунт-Вилсон установил первый солнечный телескоп в построенной небольшой обсерватории, и занялся поиском ответа на происхождение пятен на Солнце, открытых Галилеем. Джордж Хейл открыл, что пятна на Солнце вызваны магнитным полем, поскольку оно приводит к снижению температуры поверхности. Именно магнитное поле на поверхности Солнца вызывает солнечные ветры — извержение плазмы солнечной короны на сотни тысяч километров в пространство.

В январе 2020 года телескоп Национального научного фонда США сделал самые точные в истории снимки Солнца. На них хорошо видны «ячейки», по которым движется плазма^[113].

Космические исследования Солнца

Атмосфера Земли препятствует прохождению многих видов электромагнитного излучения из космоса. Кроме того, даже в видимой части спектра, для которой атмосфера довольно прозрачна, изображения космических объектов могут искажаться её колебаниями, поэтому наблюдения этих объектов лучше производить на больших высотах (в высокогорных обсерваториях, с помощью приборов, поднятых в верхние слои атмосферы, и т. п.) или даже из космоса. Верно это и в отношении наблюдений Солнца. Если нужно получить очень чёткое изображение Солнца, исследовать его ультрафиолетовое или рентгеновское излучение, точно измерить солнечную постоянную, то наблюдения и съёмки проводят с аэростатов, ракет, спутников и космических станций.

Фактически первые внеатмосферные наблюдения Солнца были проведены вторым искусственным спутником Земли «Спутник-2» в 1957 году. Наблюдения проводились в нескольких спектральных диапазонах от 1 до 120 Å, выделяемых при помощи органических и металлических фильтров^[114]. Обнаружение солнечного ветра опытным путём было осуществлено в 1959 году с помощью ионных ловушек космических аппаратов «Луна-1» и «Луна-2», экспериментами на которых руководил Константин Грингауз^{[115][116][117]}.

Другими космическими аппаратами, исследовавшими солнечный ветер, были созданные NASA спутники серии «Пионер» с номерами 5—9, запущенные между 1960 и 1968 годами. Эти спутники обращались вокруг Солнца вблизи орбиты Земли и выполнили детальные измерения параметров солнечного ветра.

В 1970-е годы в рамках совместного проекта США и Германии были запущены спутники «Гелиос-I» и «Гелиос-II» (англ. Helios^[en]). Они находились на гелиоцентрической орбите, перигелий которой лежал внутри орбиты Меркурия, примерно в 40 млн км от Солнца. Эти аппараты помогли получить новые данные о солнечном ветре.

В 1973 году вступила в строй космическая солнечная обсерватория Apollo Telescope Mount^[en] (англ.) на американской космической станции Скайлэб. С помощью этой обсерватории были сделаны первые наблюдения солнечной переходной области и ультрафиолетового излучения солнечной короны в динамическом режиме. С её помощью были также открыты корональные выбросы массы и корональные дыры, которые, как сейчас известно, тесно связаны с солнечным ветром.

В 1980 году НАСА вывело на околоземную орбиту космический зонд Solar Maximum Mission (SolarMax), который был предназначен для наблюдений ультрафиолетового, рентгеновского и гамма-излучения от солнечных вспышек в период высокой солнечной активности. Однако всего через несколько месяцев после запуска из-за неисправности электроники зонд перешёл в пассивный режим.

В 1984 году космическая экспедиция STS-41C на шаттле «Челленджер» устранила неисправность зонда и снова запустила его на орбиту. После этого, до своего входа в атмосферу в июне 1989 года, аппарат получил тысячи снимков солнечной короны^[118]. Его измерения помогли также выяснить, что мощность полного излучения Солнца за полтора года наблюдений изменилась только на 0,01 %.

Японский спутник «Yohkoh» (яп. ようこう ё:ко:, «солнечный свет»), запущенный в 1991 году, проводил наблюдения излучения Солнца в рентгеновском диапазоне. Полученные им данные помогли учёным идентифицировать несколько разных типов солнечных вспышек и показали, что корона даже вдали от областей максимальной активности намного более динамична, чем принято было считать. «Ёко» функционировал в течение полного солнечного цикла и перешёл в пассивный режим во время солнечного затмения 2001 года, когда он потерял свою ориентировку на Солнце. В 2005 году спутник вошёл в атмосферу и был разрушен^[119].

Очень важной для исследований Солнца является программа SOHO (SOlar and Heliospheric Observatory), организованная совместно Европейским космическим агентством и NASA. Запущенный 2 декабря 1995 года космический аппарат SOHO вместо планируемых двух лет работает уже более десяти лет (по данным на 2009 год). Он оказался настолько полезным, что 11 февраля 2010 года был запущен следующий, аналогичный космический аппарат SDO (Solar Dynamics Observatory)^[120]. SOHO находится в точке Лагранжа между Землёй и Солнцем и с момента запуска передаёт на Землю изображения Солнца в различных диапазонах длин волн. Кроме своей основной задачи — исследования Солнца — SOHO исследовал большое количество комет, в основном очень малых, которые испаряются по мере своего приближения к Солнцу^[121].

Все эти спутники наблюдали Солнце из плоскости эклиптики и поэтому могли детально изучить только далёкие от его полюсов области. В 1990 году был запущен космический зонд «Улисс» для изучения полярных областей Солнца. Сначала он совершил гравитационный манёвр возле Юпитера, чтобы выйти из плоскости эклиптики. По счастливому стечению обстоятельств ему также удалось наблюдать столкновение кометы Шумейкеров — Леви 9 с Юпитером в 1994 году. После того как он вышел на запланированную орбиту, он приступил к наблюдению солнечного ветра и напряжённости магнитного поля на высоких гелиоширотах. Выяснилось, что солнечный ветер на этих широтах имеет скорость примерно 750 км/с, что меньше, чем ожидалось, и что на них существуют большие магнитные поля, рассеивающие галактические космические лучи^[122].

Состав солнечной фотосферы хорошо изучен с помощью спектроскопических методов, однако данных о соотношении элементов в глубинных слоях Солнца гораздо меньше. Для того, чтобы получить прямые данные о составе Солнца, был запущен космический зонд Genesis. Он вернулся на Землю в 2004 году, однако был повреждён при приземлении из-за неисправности одного из датчиков ускорения и не раскрывшегося вследствие этого парашюта. Несмотря на сильные повреждения, возвращаемый модуль доставил на Землю несколько пригодных для изучения образцов солнечного ветра.

22 сентября 2006 года на орбиту Земли была выведена солнечная обсерватория Hinode (Solar-B). Обсерватория создана в японском институте ISAS, где разрабатывалась обсерватория Yohkoh (Solar-A) и оснащена тремя инструментами: SOT — солнечный оптический телескоп, XRT — рентгеновский телескоп и EIS — изображающий спектрометр ультрафиолетового диапазона. Основной задачей Hinode является исследование активных процессов в солнечной короне и установление их связи со структурой и динамикой магнитного поля Солнца^[123].

В октябре 2006 года была запущена солнечная обсерватория STEREO. Она состоит из двух идентичных космических аппаратов на таких орбитах, что один из них постоянно отстаёт от Земли, а другой её обгоняет. Это позволяет получать стереоизображения Солнца и таких солнечных явлений, как корональные выбросы массы.

В январе 2009 года состоялся запуск российского спутника «Коронас-Фотон» с комплексом космических телескопов «Тесис»^[124]. В состав обсерватории входит несколько телескопов и спектрогелиографов крайнего ультрафиолетового диапазона, а также коронограф широкого поля зрения, работающий в линии ионизованного гелия HeII 304 A. Целью миссии «Тесис» является исследование наиболее динамичных солнечных процессов (вспышек и корональных выбросов массы), а также круглосуточный мониторинг солнечной активности с целью раннего прогнозирования геомагнитных возмущений.

11 февраля 2010 года США вывели на геостационарную орбиту новую солнечную обсерваторию SDO (Solar Dynamic Observatory)^[125].

Наблюдения за Солнцем и опасность для зрения

Для эффективного наблюдения Солнца существуют специальные, так называемые солнечные телескопы, которые установлены во многих обсерваториях мира. Наблюдения Солнца имеют ту особенность, что яркость Солнца велика, а следовательно, светосила солнечных телескопов может быть небольшой. Гораздо важнее получить как можно больший масштаб изображения, и для достижения этой цели солнечные телескопы имеют очень большие фокусные расстояния (метры и десятки метров). Вращать такую конструкцию нелегко, однако этого и не требуется. Положение Солнца на небе ограничивается сравнительно узким поясом, его максимальная ширина — 46 градусов. Поэтому солнечный свет с помощью зеркал направляют в стационарно установленный телескоп, а затем проецируют на экран или рассматривают с помощью затемнённых фильтров.

Солнце — далеко не самая мощная звезда из всех существующих, но оно находится относительно близко к Земле и поэтому для нас светит очень ярко — в 400 000 раз ярче полной Луны. Из-за этого смотреть на дневное Солнце невооружённым глазом крайне опасно, а смотреть в бинокль или телескоп без специального светофильтра категорически нельзя — это может нанести необратимый вред зрению (ожог сетчатки и роговой оболочки, разрушение палочки, колбочки, и привести к световой слепоте)^[126][127]. Наблюдения Солнца невооружённым глазом без урона зрению возможны лишь на восходе или закате (тогда блеск Солнца ослабевает в несколько тысяч раз), или днём с применением светофильтров. При любительских наблюдениях в бинокль или телескоп также следует использовать затемняющий светофильтр, помещённый перед объективом. Однако лучше пользоваться другим способом — проецировать солнечное изображение через телескоп на белый экран. Даже с маленьким любительским телескопом можно таким образом изучать солнечные пятна, а в хорошую погоду увидеть грануляцию и факелы на поверхности Солнца. Однако в этом случае существует риск повреждения самого телескопа, поэтому перед использованием этого способа следует прочитать инструкцию к телескопу. В частности, при данном методе наблюдения Солнца подвержены риску повреждения телескопы-рефлекторы и катадиоптрические телескопы. Кроме того, для любого телескопа ни в коем случае нельзя смотреть через него напрямую на Солнце без специального светофильтра, а при проецировании изображения на экран не рекомендуется держать его долго, без перерывов, направленным на Солнце^[128].

Теоретические проблемы

Проблема солнечных нейтрино

Ядерные реакции, происходящие в ядре Солнца, приводят к образованию большого количества электронных нейтрино. При этом измерения потока нейтрино на Земле, которые постоянно производятся с конца 1960-х годов, показали, что количество регистрируемых солнечных электронных нейтрино приблизительно в два-три раза меньше, чем предсказывает стандартная солнечная модель, описывающая процессы в Солнце. Это рассогласование между экспериментом и теорией получило название «проблема солнечных нейтрино» и более 30 лет было одной из загадок солнечной физики. Положение осложняется тем, что нейтрино крайне слабо взаимодействует с веществом, и создание нейтринного детектора, который способен достаточно точно измерить поток нейтрино даже такой мощности, как исходящий от Солнца — технически сложная и дорогостоящая задача (см. Нейтринная астрономия).

Предлагалось два главных пути решения проблемы солнечных нейтрино. Во-первых, можно было модифицировать модель Солнца таким образом, чтобы уменьшить предполагаемую термоядерную активность (а, значит, и температуру) в его ядре и, следовательно, поток излучаемых Солнцем нейтрино. Во-вторых, можно было предположить, что часть электронных нейтрино, излучаемых ядром Солнца, при движении к Земле превращается в нерегистрируемые обычными детекторами нейтрино других поколений (мюонные и тау-нейтрино)^[129]. Сегодня понятно, что правильным, скорее всего, является второй путь.

Для того чтобы имел место переход одного сорта нейтрино в другой — то есть происходили так называемые нейтринные осцилляции — нейтрино должно иметь отличную от нуля массу. В настоящее время установлено, что это действительно так^[130]. В 2001 году в нейтринной обсерватории в Садбери были непосредственно зарегистрированы солнечные нейтрино всех трёх сортов, и было показано, что их полный поток согласуется со стандартной солнечной моделью. При этом только около трети долетающих до Земли нейтрино оказывается электронными. Это количество согласуется с теорией, которая предсказывает переход электронных нейтрино в нейтрино другого поколения как в вакууме (собственно «нейтринные осцилляции»), так и в солнечном веществе («эффект Михеева — Смирнова — Вольфенштейна»). Таким образом, в настоящее время проблема солнечных нейтрино, по-видимому, решена.

Проблема нагрева короны

Над видимой поверхностью Солнца (фотосферой), имеющей температуру около 6000 К, находится солнечная корона с температурой более 1 000 000 К. Можно показать, что прямого потока тепла из фотосферы недостаточно для того, чтобы привести к такой высокой температуре короны.

Предполагается, что энергия для нагрева короны поставляется турбулентными движениями подфотосферной конвективной зоны. При этом для переноса энергии в корону предложено два механизма. Во-первых, это волновое нагревание — звук и магнитогидродинамические волны, генерируемые в турбулентной конвективной зоне, распространяются в корону и там рассеиваются, при этом их энергия переходит в тепловую энергию корональной плазмы. Альтернативный механизм — магнитное нагревание, при котором магнитная энергия, непрерывно генерируемая фотосферными движениями, высвобождается путём пересоединения магнитного поля в форме больших солнечных вспышек или же большого количества мелких вспышек^[131].

В настоящий момент неясно, какой тип волн обеспечивает эффективный механизм нагрева короны. Можно показать, что все волны, кроме магнитогидродинамических альвеновских, рассеиваются или отражаются до того, как достигнут короны^[132], диссипация же альвеновских волн в короне затруднена. Поэтому современные исследователи сконцентрировали основное внимание на механизм нагревания с помощью солнечных вспышек. Один из возможных кандидатов в источники нагрева короны — непрерывно происходящие мелкомасштабные вспышки^[133], хотя окончательная ясность в этом вопросе ещё не достигнута.

Солнце в мировой культуре

В религии и мифологии

Как и многие другие природные явления, на протяжении всей истории человеческой цивилизации во многих культурах Солнце было объектом поклонения. Культ Солнца существовал в Древнем Египте, где солнечным божеством являлся Ра^[134]. У греков богом Солнца был Гелиос^[135], который, по преданию, ежедневно проезжал по небу на своей колеснице. В древнерусском языческом пантеоне было два солнечных божества — Хорс (собственно олицетворённое солнце) и Даждьбог. Кроме того, годовой празднично-ритуальный цикл славян, как и других народов, был тесно связан с годовым солнечным циклом, и ключевые его моменты (солнцестояния) олицетворялись такими персонажами, как Коляда (Овсень) и Купала.

У большинства народов солнечное божество было мужского пола (например, в английском языке применительно к Солнцу используется личное местоимение «he» — «он»), но в скандинавской мифологии Солнце (Суль) — женское божество.

В Восточной Азии, в частности, во Вьетнаме Солнце обозначается символом 日 (китайский пиньинь rì), хотя есть также и другой символ — 太阳 (тай ян). В этих коренных вьетнамских словах, слова nhật и thái dương указывают на то, что в Восточной Азии Луна и Солнце считались двумя противоположностями — инь и ян. Как вьетнамцы, так и китайцы в древности считали их двумя первичными природными силами, причём Луна считалась связанной с инь, а Солнце — с ян^[136].

В оккультизме

В каббале Солнце соотносится со сфирой Тиферет (См. также Халдейский ряд)^[137].
В астрологии соотносится с духом, сознанием, а также жизненными силами организма^{[138][неавторитетный источник]}. В астрологии каждому человеку приписывается знак зодиака по условному положению Солнца среди зодиакальных созвездий в день рождения.

В языках мира

Во многих индоевропейских языках Солнце обозначается словом, имеющим корень sol. Так, слово sol означает «Солнце» на латыни и в современных португальском, испанском, исландском, датском, норвежском, шведском, каталанском и галисийском языках. В английском языке слово Sol также иногда (преимущественно в научном контексте) используется для обозначения Солнца, однако главным значением этого слова является имя римского бога^[139][140]. В персидском языке sol означает «солнечный год». От этого же корня происходят древнерусское слово сълньце, современное русское солнце, а также соответствующие слова во многих других славянских языках.

В честь Солнца названа валюта государства Перу (новый соль), ранее называвшаяся инти (так назывался бог солнца у инков, занимавший ключевое место в их астрономии и мифологии), что в переводе с языка кечуа означает солнце.

Городские легенды о Солнце

В 2002 и последующих годах в СМИ появилось сообщение, что через 6 лет Солнце взорвётся (то есть превратится в сверхновую звезду)^[141]. Источником информации назывался «голландский астрофизик доктор Пирс ван дер Меер (Piers van der Meer), эксперт Европейского космического агентства». В действительности в ЕКА нет сотрудника с таким именем^[142]. Более того, астрофизика с таким именем вообще не существует. Водородного топлива Солнцу хватит на несколько миллиардов лет. По истечении этого времени Солнце разогреется до высоких температур (хотя и не сразу — этот процесс займёт десятки или сотни миллионов лет), но не станет сверхновой звездой. Солнце в принципе не может превратиться в сверхновую звезду из-за недостаточной массы.

Исходное сообщение опубликовано в «Weekly World News» — газете, известной своей склонностью к публикации сомнительной информации^[143].

См. также

• Эрикссон-Глоб — «Солнце» в Шведской Солнечной системе
• Солнечная энергия

Примечания

Литература

• Аббот Ч. Солнце / Перевод с английского Н. Я. Бугославской; под редакцией Е. Я. Перепёлкина. — Москва—Ленинград: ОНТИ, 1936. — 462 с.
• Солнечная система. В 2 томах / Под ред. Дж. Койпера; пер. с англ.; редактор тома В. А. Крат. — М.: Издательство иностранной литературы, 1957. — Т. 1 : Солнце. — 609 с.
• Колтун М. М. Солнце и человечество. — М.: Детская литература, 1981. — 127 с. — 100 000 экз.
• Степанян Н. Н. Наблюдаем Солнце. — М.: Наука, 1992. — 128 с. — ISBN 5-02-014358-8.
• Michael Stix. The Sun. An Introduction. — 2nd Edition. — Springer, 2002. — ISBN 3-540-42886-0.
• Cohen, Richard. Chasing the Sun: the Epic Story of the Star that Gives us Life (англ.). — Simon & Schuster, 2010. — ISBN 978-1-4000-6875-3.
• Солнце / Э. Е. Дубов // Большая Советская Энциклопедия / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская Энциклопедия, 1976. — Т. 24, кн. I : Собаки — Струна. — С. 150—154. — 631 000 экз.
• Кочаров Г. Е. Солнце // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 589—598. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
• Шкловский И. С. §9. Проблемы нейтринного излучения Солнца // Звезды: их рождение, жизнь и смерть. — 3-е изд. — М.: Наука, 1984. — С. 110—117. — 100 000 экз.
• Thompson, M. J. Solar interior: Helioseismology and the Sun’s interior (англ.) // Astronomy & Geophysics  (англ.) (рус. : journal. — 2004. — Vol. 45, no. 4. — P. 21—25.

Ссылки

• Солнечная активность (недоступная ссылка — история). USAP. Дата обращения: 24 июня 2011. Архивировано 10 августа 2011 года.
• Энциклопедия Солнца. Тесис. Дата обращения: 9 июля 2015.
• Солнце. Астронет. Астронет. Дата обращения: 9 сентября 2007. Архивировано 10 августа 2011 года.
• Солнце и Земля. Единые колебания
• Солнце. Солнечная система. Общая астрономия
• Путешествие из центра Солнца. Популярная механика. Дата обращения: 26 ноября 2011.
• Солнце сейчас, фотография из обсерватории солнечной динамики NASA. sdo.gsfc.nasa.gov. Дата обращения: 22 марта 2011. Архивировано 10 августа 2011 года.
• Эдвард Кононович. Солнце. Энциклопедия Кругосвет. Дата обращения: 26 октября 2013. Архивировано 8 января 2014 года.
• Astronomy Picture of the Day. The Not So Quiet Sun (англ.) (6 августа 2010). Дата обращения: 16 февраля 2014.

Владимир Юрьевич Протасов
«Квант» №2, 2010

Небо над головой — самый древний учебник геометрии. Первые понятия, такие как точка и круг, — оттуда. Скорее даже не учебник, а задачник. В котором отсутствует страничка с ответами. Два круга одинакового размера — Солнце и Луна — движутся по небу, каждый со своей скоростью. Остальные объекты — светящиеся точки — движутся все вместе, словно они прикреплены к сфере, вращающейся со скоростью 1 оборот в 24 часа. Правда, среди них есть исключения — 5 точек движутся как им вздумается. Для них подобрали особое слово — «планета», по-гречески — «бродяга». Сколько человечество существует, оно пытается разгадать законы этого вечного движения. Первый прорыв произошел в III веке до н.э., когда греческие ученые, взяв на вооружение молодую науку — геометрию, смогли получить первые результаты об устройстве Вселенной. Об этом и пойдет речь.

Чтобы иметь некоторое представление о сложности задачи, рассмотрим такой пример. Представим себе светящийся шар диаметром 10 см, неподвижно висящий в пространстве. Назовем его S. Вокруг него на расстоянии чуть больше 10 метров обращается маленький шарик Z диаметром 1 миллиметр, а вокруг Z на расстоянии 6 см обращается совсем крохотный шарик L, его диаметр — четверть миллиметра. На поверхности среднего шарика Z живут микроскопические существа. Они обладают неким разумом, но покидать пределы своего шарика не могут. Всё, что они могут, — смотреть на два других шара — S и L. Спрашивается, могут ли они узнать диаметры этих шаров и измерить расстояния до них? Сколько ни думай, дело, казалось бы, безнадежное. Мы нарисовали сильно уменьшенную модель Солнечной системы (S — Солнце, Z — Земля, L — Луна).

Вот такая задача стояла перед древними астрономами. И они ее решили! Более 22 веков назад, не пользуясь ничем, кроме самой элементарной геометрии — на уровне 8 класса (свойства прямой и окружности, подобные треугольники и теорема Пифагора). И, конечно, наблюдая за Луной и за Солнцем.

Над решением трудились несколько ученых. Мы выделим двух. Это математик Эратосфен, измеривший радиус земного шара, и астроном Аристарх, вычисливший размеры Луны, Солнца и расстояния до них. Как они это сделали?

Как измерили земной шар

То, что Земля не плоская, люди знали давно. Древние мореплаватели наблюдали, как постепенно меняется картина звездного неба: становятся видны новые созвездия, а другие, напротив, заходят за горизонт. Уплывающие вдаль корабли «уходят под воду», последними скрываются из вида верхушки их мачт. Кто первый высказал идею о шарообразности Земли, неизвестно. Скорее всего — пифагорейцы, считавшие шар совершеннейшей из фигур. Полтора века спустя Аристотель приводит несколько доказательств того, что Земля — шар. Главное из них: во время лунного затмения на поверхности Луны отчетливо видна тень от Земли, и эта тень круглая! С тех пор постоянно предпринимались попытки измерить радиус земного шара. Два простых способа изложены в упражнениях 1 и 2. Измерения, правда, получались неточными. Аристотель, например, ошибся более чем в полтора раза. Считается, что первым, кому удалось сделать это с высокой точностью, был греческий математик Эратосфен Киренский (276–194 до н. э.). Его имя теперь всем известно благодаря решету Эратосфена — способу находить простые числа (рис. 1).

Если вычеркнуть из натурального ряда единицу, затем вычеркивать все четные числа, кроме первого (самого числа 2), затем все числа, кратные трем, кроме первого из них (числа 3), и т. д., то в результате останутся одни простые числа. Среди современников Эратосфен был знаменит как крупнейший ученый-энциклопедист, занимавшийся не только математикой, но и географией, картографией и астрономией. Он долгое время возглавлял Александрийскую библиотеку — центр мировой науки того времени. Работая над составлением первого атласа Земли (речь, конечно, шла об известной к тому времени ее части), он задумал провести точное измерение земного шара. Идея была такова. В Александрии все знали, что на юге, в городе Сиена (современный Асуан), один день в году, в полдень, Солнце достигает зенита. Исчезает тень от вертикального шеста, на несколько минут освещается дно колодца. Происходит это в день летнего солнцестояния, 22 июня — день наивысшего положения Солнца на небе. Эратосфен направляет своих помощников¹ в Сиену, и те устанавливают, что ровно в полдень (по солнечным часам) Солнце находится точно в зените. Одновременно (как написано в первоисточнике: «в тот же час»), т. е. в полдень по солнечным часам, Эратосфен измеряет длину тени от вертикального шеста в Александрии. Получился треугольник ABC (АС — шест, АВ — тень, рис. 2).

Итак, солнечный луч в Сиене (N) перпендикулярен поверхности Земли, а значит, проходит через ее центр — точку Z. Параллельный ему луч в Александрии (А) составляет угол γ = ACB с вертикалью. Пользуясь равенством накрест лежащих углов при параллельных, заключаем, что AZN = γ. Если обозначить через l длину окружности, а через х длину ее дуги AN, то получаем пропорцию . Угол γ в треугольнике АВС Эратосфен измерил, получилось 7,2°. Величина х — не что иное, как длина пути от Александрии до Сиены, примерно 800 км. Ее Эратосфен аккуратно вычисляет, исходя из среднего времени движения верблюжьих караванов, регулярно ходивших между двумя городами, а также используя данные бематистов — людей специальной профессии, измерявших расстояния шагами. Теперь осталось решить пропорцию , получив длину окружности (т. е. длину земного меридиана) l = 40000 км. Тогда радиус Земли R равен l/(2π), это примерно 6400 км. То, что длина земного меридиана выражается столь круглым числом в 40000 км, не удивительно, если вспомнить, что единица длины в 1 метр и была введена (во Франции в конце XVIII века) как одна сорокамиллионная часть окружности Земли (по определению!). Эратосфен, конечно, использовал другую единицу измерения — стадий (около 200 м). Стадиев было несколько: египетский, греческий, вавилонский, и каким из них пользовался Эратосфен — неизвестно. Поэтому трудно судить наверняка о точности его измерения. Кроме того, неизбежная ошибка возникала в силу географического положения двух городов. Эратосфен рассуждал так: если города находятся на одном меридиане (т. е. Александрия расположена в точности к северу от Сиены), то полдень в них наступает одновременно. Поэтому, сделав измерения во время наивысшего положения Солнца в каждом городе, мы должны получить правильный результат. Но на самом деле Александрия и Сиена — далеко не на одном меридиане. Сейчас в этом легко убедиться, взглянув на карту, но у Эратосфена такой возможности не было, он как раз и работал над составлением первых карт. Поэтому его метод (абсолютно верный!) привел к ошибке в определении радиуса Земли. Тем не менее, многие исследователи уверены, что точность измерения Эратосфена была высока и что он ошибся менее чем на 2%. Улучшить этот результат человечество смогло только через 2 тысячи лет, в середине XIX века. Над этим трудилась группа ученых во Франции и экспедиция В. Я. Струве в России. Даже в эпоху великих географических открытий, в XVI веке, люди не смогли достичь результата Эратосфена и пользовались неверным значением длины земной окружности в 37000 км. Ни Колумб, ни Магеллан не знали, каковы истинные размеры Земли и какие расстояния им придется преодолевать. Они-то считали, что длина экватора на 3 тысячи км меньше, чем на самом деле. Знали бы — может, и не поплыли бы.

В чем причина столь высокой точности метода Эратосфена (конечно, если он пользовался нужным стадием)? До него измерения были локальными, на расстояниях, обозримых человеческим глазом, т. е. не более 100 км. Таковы, например, способы в упражнениях 1 и 2. При этом неизбежны ошибки из-за рельефа местности, атмосферных явлений и т. д. Чтобы добиться большей точности, нужно проводить измерения глобально, на расстояниях, сравнимых с радиусом Земли. Расстояние в 800 км между Александрией и Сиеной оказалось вполне достаточным.

Упражнения
1. Как вычислить радиус Земли по следующим данным: с горы высотой 500 м просматриваются окрестности на расстоянии 80 км?
2. Как вычислить радиус Земли по следующим данным: корабль высотой 20 м, отплыв от берега на 16 км, полностью исчезает из вида?
3. Два друга — один в Москве, другой — в Туле, берут по метровому шесту и ставят их вертикально. В момент, в течение дня, когда тень от шеста достигает наименьшей длины, каждый из них измеряет длину тени. В Москве получилось а см, а в Туле — b см. Выразите радиус Земли через а и b. Города расположены на одном меридиане на расстоянии 185 км.

Как видно из упражнения 3, опыт Эратосфена можно проделать и в наших широтах, где Солнце никогда не бывает в зените. Правда, для этого нужны две точки обязательно на одном меридиане. Если же повторить опыт Эратосфена для Александрии и Сиены, и при этом сделать измерения в этих городах одновременно (сейчас для этого есть технические возможности), то мы получим верный ответ, при этом будет не важно, на каком меридиане находится Сиена (почему?).

Как измерили Луну и Солнце. Три шага Аристарха

Греческий остров Самос в Эгейском море — теперь глухая провинция. Сорок километров в длину, восемь — в ширину. На этом крохотном острове в разное время родились три величайших гения — математик Пифагор, философ Эпикур и астроном Аристарх. Про жизнь Аристарха Самосского известно мало. Даты жизни приблизительны: родился около 310 до н.э., умер около 230 до н.э. Как он выглядел, мы не знаем, ни одного изображения не сохранилось (современный памятник Аристарху в греческом городе Салоники — лишь фантазия скульптора) . Много лет провел в Александрии, где работал в библиотеке и в обсерватории. Главное его достижение — книга «О величинах и расстояниях Солнца и Луны», — по единодушному мнению историков, является настоящим научным подвигом. В ней он вычисляет радиус Солнца, радиус Луны и расстояния от Земли до Луны и до Солнца. Сделал он это в одиночку, пользуясь очень простой геометрией и всем известными результатами наблюдений за Солнцем и Луной. На этом Аристарх не останавливается, он делает несколько важнейших выводов о строении Вселенной, которые намного опередили свое время. Не случайно его назвали впоследствии «Коперником античности».

Вычисление Аристарха можно условно разбить на три шага. Каждый шаг сводится к простой геометрической задаче. Первые два шага совсем элементарны, третий — чуть посложнее. В геометрических построениях мы будем обозначать через Z, S и L центры Земли, Солнца и Луны соответственно, а через R, R_s и R_l — их радиусы. Все небесные тела будем считать шарами, а их орбиты — окружностями, как и считал сам Аристарх (хотя, как мы теперь знаем, это не совсем так). Мы начинаем с первого шага, и для этого немного понаблюдаем за Луной.

Шаг 1. Во сколько раз Солнце дальше, чем Луна?

Как известно, Луна светит отраженным солнечным светом. Если взять шар и посветить на него со стороны большим прожектором, то в любом положении освещенной окажется ровно половина поверхности шара. Граница освещенной полусферы — окружность, лежащая в плоскости, перпендикулярной лучам света. Таким образом, Солнце всегда освещает ровно половину поверхности Луны. Видимая нам форма Луны зависит от того, как расположена эта освещенная половина. При новолунии, когда Луна вовсе не видна на небе, Солнце освещает ее обратную сторону. Затем освещенная полусфера постепенно поворачивается в сторону Земли. Мы начинаем видеть тонкий серп, затем — месяц («растущая Луна»), далее — полукруг (эта фаза Луны называется «квадратурой»). Затем день ото дня (вернее, ночь от ночи) полукруг дорастает до полной Луны. Потом начинается обратный процесс: освещенная полусфера от нас отворачивается. Луна «стареет», постепенно превращаясь в месяц, повернутый к нам левой стороной, подобно букве «С», и, наконец, в ночь новолуния исчезает. Период от одного новолуния до другого длится примерно четыре недели. За это время Луна совершает полный оборот вокруг Земли. От новолуния до половины Луны проходит четверть периода, отсюда и название «квадратура».

Замечательная догадка Аристарха состояла в том, что при квадратуре солнечные лучи, освещающие половину Луны, перпендикулярны прямой, соединяющей Луну с Землей. Таким образом, в треугольнике ZLS угол при вершине L — прямой (рис. 3). Если теперь измерить угол LZS, обозначим его через α, то получим, что  = cos α. Для простоты мы считаем, что наблюдатель находится в центре Земли. Это несильно повлияет на результат, поскольку расстояния от Земли до Луны и до Солнца значительно превосходят радиус Земли. Итак, измерив угол α между лучами ZL и ZS во время квадратуры, Аристарх вычисляет отношение расстояний до Луны и до Солнца. Как одновременно застать Солнце и Луну на небосводе? Это можно сделать ранним утром. Сложность возникает по другому, неожиданному, поводу. Во времена Аристарха не было косинусов. Первые понятия тригонометрии появятся позже, в работах Аполлония и Архимеда. Но Аристарх знал, что такое подобные треугольники, и этого было достаточно. Начертив маленький прямоугольный треугольник Z’L’S’ с тем же острым углом α = L’Z’S’ и измерив его стороны, находим, что , и это отношение примерно равно 1/400.

Получается, что Солнце в 400 раз дальше от Земли, чем Луна. Эту константу — отношение расстояний от Земли до Солнца и от Земли до Луны — мы будем обозначать буквой κ. Итак, мы нашли, что κ = 400.

Шаг 2. Во сколько раз Солнце больше Луны?

Для того чтобы найти отношение радиусов Солнца и Луны, Аристарх привлекает солнечные затмения (рис. 4). Они происходят, когда Луна загораживает Солнце. При частичном, или, как говорят астрономы, частном, затмении Луна лишь проходит по диску Солнца, не закрывая его полностью. Порой такое затмение даже нельзя разглядеть невооруженным глазом, Солнце светит как в обычный день. Лишь сквозь сильное затемнение, например, закопченное стекло, видно, как часть солнечного диска закрыта черным кругом. Гораздо реже происходит полное затмение, когда Луна на несколько минут полностью закрывает солнечный диск.

В это время становится темно, на небе появляются звезды. Затмения наводили ужас на древних людей, считались предвестниками трагедий. Солнечное затмение наблюдается по-разному в разных частях Земли. Во время полного затмения на поверхности Земли возникает тень от Луны — круг, диаметр которого не превосходит 270 км. Лишь в тех районах земного шара, по которым проходит эта тень, можно наблюдать полное затмение. Поэтому в одном и том же месте полное затмение происходит крайне редко — в среднем раз в 200–300 лет. Аристарху повезло — он смог наблюдать полное солнечное затмение собственными глазами. На безоблачном небе Солнце постепенно начало тускнеть и уменьшаться в размерах, установились сумерки. На несколько мгновений Солнце исчезло. Потом проглянул первый луч света, солнечный диск стал расти, и вскоре Солнце засветило в полную силу. Почему затмение длится столь короткое время? Аристарх отвечает: причина в том, что Луна имеет те же видимые размеры на небе, что и Солнце. Что это значит? Проведем плоскость через центры Земли, Солнца и Луны. Получившееся сечение изображено на рисунке 5a. Угол между касательными, проведенными из точки Z к окружности Луны, называется угловым размером Луны, или ее угловым диаметром. Так же определяется угловой размер Солнца. Если угловые диаметры Солнца и Луны совпадают, то они имеют одинаковые видимые размеры на небе, а при затмении Луна действительно полностью загораживает Солнце (рис. 5б), но лишь на мгновение, когда совпадут лучи ZL и ZS. На фотографии полного солнечного затмения (см. рис. 4) ясно видно равенство размеров.

Вывод Аристарха оказался поразительно точен! В реальности средние угловые диаметры Солнца и Луны отличаются всего на 1,5%. Мы вынуждены говорить о средних диаметрах, поскольку они меняются в течение года, так как планеты движутся не по окружностям, а по эллипсам.

Соединив центр Земли Z с центрами Солнца S и Луны L, а также с точками касания Р и Q, получим два прямоугольных треугольника ZSP и ZLQ (см. рис. 5a). Они подобны, поскольку у них есть пара равных острых углов β/2. Следовательно, . Таким образом, отношение радиусов Солнца и Луны равно отношению расстояний от их центров до центра Земли. Итак, R_s/R_l = κ = 400. Несмотря на то, что их видимые размеры равны, Солнце оказалось больше Луны в 400 раз!

Равенство угловых размеров Луны и Солнца — счастливое совпадение. Оно не вытекает из законов механики. У многих планет Солнечной системы есть спутники: у Марса их два, у Юпитера — четыре (и еще несколько десятков мелких), и все они имеют разные угловые размеры, не совпадающие с солнечным.

Теперь мы приступаем к решающему и самому сложному шагу.

Шаг 3. Вычисление размеров Солнца и Луны и расстояний до них

Итак, нам известно отношение размеров Солнца и Луны и отношение их расстояний до Земли. Эта информация относительна: она восстанавливает картину окружающего мира лишь с точностью до подобия. Можно удалить Луну и Солнце от Земли в 10 раз, увеличив во столько же раз их размеры, и видимая с Земли картина останется такой же. Чтобы найти реальные размеры небесных тел, надо соотнести их с каким-то известным размером. Но из всех астрономических величин Аристарху пока известен только радиус² земного шара R = 6400 км. Поможет ли это? Хоть в каком-то из видимых явлений, происходящих на небе, появляется радиус Земли? Не случайно говорят «небо и земля», имея в виду две несовместные вещи. И всё же такое явление есть. Это — лунное затмение. С его помощью, применив довольно хитроумное геометрическое построение, Аристарх вычисляет отношение радиуса Солнца к радиусу Земли, и цепь замыкается: теперь мы одновременно находим радиус Луны, радиус Солнца, а заодно и расстояния от Луны и от Солнца до Земли.

При лунном затмении Луна уходит в тень Земли. Спрятавшись за Землю, Луна лишается солнечного света, и, таким образом, перестает светить. Она не исчезает из вида полностью, поскольку небольшая часть солнечного света рассеивается земной атмосферой и доходит до Луны в обход Земли. Луна темнеет, приобретая красноватый оттенок (через атмосферу лучше всего проходят красные и оранжевые лучи). На лунном диске при этом отчетливо видна тень от Земли (рис. 6). Круглая форма тени еще раз подтверждает шарообразность Земли. Аристарха же интересовал размер этой тени. Для того, чтобы определить радиус круга земной тени (мы сделаем это по фотографии на рисунке 6), достаточно решить простое упражнение.

Упражнение 4. На плоскости дана дуга окружности. С помощью циркуля и линейки постройте отрезок, равный ее радиусу.

Выполнив построение, находим, что радиус земной тени примерно в раза больше радиуса Луны. Обратимся теперь к рисунку 7. Серым цветом закрашена область земной тени, в которую попадает Луна при затмении. Предположим, что центры окружностей S, Z и L лежат на одной прямой. Проведем диаметр Луны M₁M₂, перпендикулярный прямой LS. Продолжение этого диаметра пересекает общие касательные окружностей Солнца и Земли в точках D₁ и D₂. Тогда отрезок D₁D₂ приближенно равен диаметру тени Земли. Мы пришли к следующей задаче.

Задача 1. Даны три окружности с центрами S, Z и L, лежащими на одной прямой. Отрезок D₁D₂, проходящий через L, перпендикулярен прямой SL, а его концы лежат на общих внешних касательных к первой и второй окружностям. Известно, что отношение отрезка D₁D₂ к диаметру третьей окружности равно t, а отношение диаметров первой и третьей окружности равно ZS/ZL = κ. Найдите отношение диаметров первой и второй окружностей.

Если решить эту задачу, то будет найдено отношение радиусов Солнца и Земли. Значит, будет найден радиус Солнца, а с ним и Луны. Но решить ее не удастся. Можете попробовать — в задаче не достает одного данного. Например, угла между общими внешними касательными к первым двум окружностям. Но даже если этот угол был бы известен, решение будет использовать тригонометрию, которую Аристарх не знал (мы формулируем соответствующую задачу в упражнении 6). Он находит более простой выход. Проведем диаметр A₁A₂ первой окружности и диаметр B₁B₂ второй, оба — параллельные отрезку D₁D₂. Пусть C₁ и С₂ — точки пересечения отрезка D₁D₂ с прямыми A₁B₁ и А₂В₂ соответственно (рис. 8). Тогда в качестве диаметра земной тени возьмем отрезок C₁C₂ вместо отрезка D₁D₂. Стоп, стоп! Что значит, «возьмем один отрезок вместо другого»? Они же не равны! Отрезок C₁C₂ лежит внутри отрезка D₁D₂, значит C₁C₂ < D₁D_2. Да, отрезки разные, но они почти равны. Дело в том, что расстояние от Земли до Солнца во много раз больше диаметра Солнца (примерно в 215 раз). Поэтому расстояние ZS между центрами первой и второй окружности значительно превосходит их диаметры. Значит, угол между общими внешними касательными к этим окружностям близок к нулю (в реальности он примерно 0,5°), т. е. касательные «почти параллельны». Если бы они были в точности параллельны, то точки A₁ и B₁ совпадали бы с точками касания, следовательно, точка C₁ совпала бы с D₁, а C₂ с D₂, и значит, C₁C₂ = D₁D₂. Таким образом, отрезки C₁C₂ и D₁D₂ почти равны. Интуиция и здесь не подвела Аристарха: на самом деле отличие между длинами отрезков составляет менее сотой доли процента! Это — ничто по сравнению с возможными погрешностями измерений. Убрав теперь лишние линии, включая окружности и их общие касательные, приходим к такой задаче.

Задача 1′. На боковых сторонах трапеции А₁А₂С₂С₁ взяты точки B₁ и В₂ так, что отрезок В₁В₂ параллелен основаниям. Пусть S, Z u L — середины отрезков А₁А₂, B₁B₂ и C₁C₂ соответственно. На основании C₁C₂ лежит отрезок М₁М₂ с серединой L. Известно, что и . Найдите А₁А₂/B₁B₂.

Решение. Так как , то , а значит, треугольники A₂SZ и M₁LZ подобны с коэффициентом SZ/LZ = κ. Следовательно, A₂SZ = M₁LZ, и поэтому точка Z лежит на отрезке M₁A₂. Аналогично, Z лежит на отрезке М₂А₁ (рис. 9). Так как C₁C₂ = t·М₁М₂ и , то .

Далее, треугольники A₂C₂M₁ и A₂B₂Z подобны. Их коэффициент подобия равен

Следовательно,

С другой стороны,

Значит, . Из этого равенства сразу получаем, что .

Итак, отношение диаметров Солнца и Земли равно , а Луны и Земли равно .

Подставляя известные нам величины κ = 400 и t = 8/3, получаем, что Луна примерно в 3,66 раза меньше Земли, а Солнце в 109 раз больше Земли. Так как радиус Земли R нам известен, находим радиус Луны R_l = R/3,66 и радиус Солнца R_s = 109R.

Теперь расстояния от Земли до Луны и до Солнца вычисляются в один шаг, это может быть сделано с помощью углового диаметра. Угловой диаметр β Солнца и Луны составляет примерно полградуса (если быть совсем точным, 0,53°). Как древние астрономы его измеряли, об этом речь впереди. Опустив касательную ZQ на окружность Луны, получаем прямоугольный треугольник ZLQ с острым углом β/2 (рис. 10).

Из него находим , что примерно равно 215R_l, или 62R. Аналогично, расстояние до Солнца равно 215R_s  = 23 455R.

Всё. Размеры Солнца и Луны и расстояния до них найдены.

Упражнения
5. Докажите, что прямые A₁B₁, A₂B₂ и две общие внешние касательные к первой и второй окружностям (см. рис. 8) пересекаются в одной точке.
6. Решите задачу 1, если дополнительно известен угол между касательными между первой и второй окружностью.
7. Солнечное затмение может наблюдаться в одних частях земного шара и не наблюдаться других. А лунное затмение?
8. Докажите, что солнечное затмение может наблюдаться только во время новолуния, а лунное затмение — только во время полнолуния.
9. Что происходит на Луне, когда на Земле происходит лунное затмение?

О пользе ошибок

На самом деле всё было несколько сложнее. Геометрия только формировалась, и многие привычные для нас еще с восьмого класса школы вещи были в то время совсем не очевидны. Аристарху потребовалось написать целую книгу, чтобы изложить то, что мы изложили на трех страницах. И с экспериментальными измерениями тоже всё было непросто. Во-первых, Аристарх ошибся с измерением диаметра земной тени во время лунного затмения, получив отношение t = 2 вместо . Кроме того, он, вроде бы, исходил из неверного значения угла β — углового диаметра Солнца, считая его равным 2°. Но эта версия спорная: Архимед в своем трактате «Псаммит» пишет, что, напротив, Аристарх пользовался почти правильным значением в 0,5°. Однако самая ужасная ошибка произошла на первом шаге, при вычислении параметра κ — отношения расстояний от Земли до Солнца и до Луны. Вместо κ = 400 у Аристарха получилось κ = 19. Как можно было ошибиться более чем в 20 раз? Обратимся еще раз к шагу 1, рисунок 3. Для того чтобы найти отношение κ = ZS/ZL, Аристарх измерил угол α = SZL, и тогда κ = 1/cos α. Например, если угол α был бы равен 60°, то мы получили бы κ = 2, и Солнце было бы вдвое дальше от Земли, чем Луна. Но результат измерения оказался неожиданным: угол α получался почти прямым. Это означало, что катет ZS во много раз превосходит ZL. У Аристарха получилось α = 87°, и тогда cos α =1/19  (напомним, что все вычисления у нас — приближенные). Истинное значение угла , и cos α =1/400. Так погрешность измерения менее чем в 3° привела к ошибке в 20 раз! Завершив вычисления, Аристарх приходит к выводу, что радиус Солнца равен 6,5 радиусов Земли (вместо 109).

Ошибки были неизбежны, учитывая несовершенные измерительные приборы того времени. Важнее то, что метод оказался правильным. Вскоре (по историческим меркам, т. е. примерно через 100 лет) выдающийся астроном античности Гиппарх (190 – ок. 120 до н.э.) устранит все неточности и, следуя методу Аристарха, вычислит правильные размеры Солнца и Луны. Возможно, ошибка Аристарха оказалась в конце концов даже полезной. До него господствовало мнение, что Солнце и Луна либо вовсе имеют одинаковые размеры (как и кажется земному наблюдателю), либо отличаются несильно. Даже отличие в 19 раз удивило современников. Поэтому не исключено, что, найди Аристарх правильное отношение κ = 400, в это никто бы не поверил, а может быть, и сам ученый отказался бы от своего метода, сочтя результат несуразным. Известный принцип гласит, что геометрия — это искусство хорошо рассуждать на плохо выполненных чертежах. Перефразируя, можно сказать, что наука в целом — это искусство делать верные выводы из неточных, или даже ошибочных, наблюдений. И Аристарх такой вывод сделал. За 17 веков до Коперника он понял, что в центре мира находится не Земля, а Солнце. Так впервые появилась гелиоцентрическая модель и понятие Солнечной системы.

Что в центре?

Господствовавшее в Древнем Мире представление об устройстве Вселенной, знакомое нам по урокам истории, заключалось в том, что в центре мира — неподвижная Земля, вокруг нее по круговым орбитам вращаются 7 планет, включая Луну и Солнце (которое тоже считалось планетой). Завершается всё небесной сферой с прикрепленными к ней звездами. Сфера вращается вокруг Земли, делая полный оборот за 24 часа. Со временем в эту модель многократно вносились исправления. Так, стали считать, что небесная сфера неподвижна, а Земля вращается вокруг своей оси. Затем стали исправлять траектории движения планет: круги заменили циклоидами, т. е. линиями, которые описывают точки окружности при ее движении по другой окружности (об этих замечательных линиях можно прочитать в книгах Г. Н. Бермана «Циклоида», А. И. Маркушевича «Замечательные кривые», а также в «Кванте»: статья С. Верова «Тайны циклоиды» №8, 1975, и статья С. Г. Гиндикина «Звездный век циклоиды», №6, 1985). Циклоиды лучше согласовывались с результатами наблюдений, в частности, объясняли «попятные» движения планет. Это — геоцентрическая система мира, в центре которой — Земля («гея»). Во II веке она приняла окончательный вид в книге «Альмагест» Клавдия Птолемея (87–165), выдающегося греческого астронома, однофамильца египетских царей. Со временем некоторые циклоиды усложнялись, добавлялись всё новые промежуточные окружности. Но в целом система Птолемея господствовала около полутора тысячелетий, до XVI века, до открытий Коперника и Кеплера. Поначалу геоцентрической модели придерживался и Аристарх. Однако, вычислив, что радиус Солнца в 6,5 раз больше радиуса Земли, он задал простой вопрос: почему такое большое Солнце должно вращаться вокруг такой маленькой Земли? Ведь если радиус Солнца больше в 6,5 раз, то его объем больше почти в 275 раз! Значит, в центре мира должно находиться Солнце. Вокруг него вращаются 6 планет, включая Землю.³ А седьмая планета, Луна, вращается вокруг Земли. Так появилась гелиоцентрическая система мира («гелиос» — Солнце). Уже сам Аристарх отмечал, что такая модель лучше объясняет видимое движение планет по круговым орбитам, лучше согласуется с результатами наблюдений. Но ее не приняли ни ученые, ни официальные власти. Аристарх был обвинен в безбожии и подвергся преследованиям. Из всех астрономов античности только Селевк стал сторонником новой модели. Больше ее не принял никто, по крайней мере, у историков нет твердых сведений на этот счет. Даже Архимед и Гиппарх, почитавшие Аристарха и развившие многие его идеи, не решились поставить Солнце в центр мира. Почему?

Почему мир не принял гелиоцентрической системы?

Как же получилось, что в течение 17 веков ученые не принимали простой и логичной системы мира, предложенной Аристархом? И это несмотря на то, что официально признанная геоцентрическая система Птолемея часто давала сбои, не согласуясь с результатами наблюдений за планетами и за звездами. Приходилось добавлять всё новые окружности (так называемые вложенные циклы) для «правильного» описания движения планет. Самого Птолемея трудности не пугали, он писал: «К чему удивляться сложному движению небесных тел, если их сущность нам неизвестна?» Однако уже к XIII веку этих окружностей накопилось 75! Модель стала столь громоздкой, что начали раздаваться осторожные возражения: неужели мир в самом деле устроен так сложно? Широко известен случай с Альфонсом X (1226–1284), королем Кастилии и Леона, государства, занимавшего часть современной Испании. Он, покровитель наук и искусств, собравший при своем дворе пятьдесят лучших астрономов мира, на одной из научных бесед обмолвился, что «если бы при сотворении мира Господь оказал мне честь и спросил моего совета, многое было бы устроено проще». Подобная дерзость не прощалась даже королям: Альфонс был низложен и отправлен в монастырь.⁴ Но сомнения остались. Часть из них можно было бы разрешить, поставив Солнце в центр Вселенной и приняв систему Аристарха. Его труды были хорошо известны. Однако еще много веков никто из ученых не решался на такой шаг. Причины были не только в страхе перед властями и официальной церковью, которая считала теорию Птолемея единственно верной. И не только в инертности человеческого мышления: не так-то просто признать, что наша Земля — не центр мира, а лишь рядовая планета. Все-таки для настоящего ученого ни страх, ни стереотипы — не препятствия на пути к истине. Гелиоцентрическая система отвергалась по вполне научным, можно даже сказать, геометрическим причинам. Если допустить, что Земля вращается вокруг Солнца, то ее траектория — окружность с радиусом, равным расстоянию от Земли до Солнца. Как мы знаем, это расстояние равно 23 455 радиусов Земли, т. е. более 150 миллионов километров. Значит, Земля в течение полугода перемещается на 300 миллионов километров. Гигантская величина! Но картина звездного неба для земного наблюдателя при этом остается такой же. Земля то приближается, то удаляется от звезд на 300 миллионов километров, но ни видимые расстояния между звездами (например, форма созвездий), ни их яркость не меняются. Это означает, что расстояния до звезд должны быть еще в несколько тысяч раз больше, т. е. небесная сфера должна иметь совершенно невообразимые размеры! Это, между прочим, осознавал и сам Аристарх, который писал в своей книге: «Объем сферы неподвижных звезд во столько раз больше объема сферы с радиусом Земля-Солнце, во сколько раз объем последней больше объема земного шара», т. е. по Аристарху выходило, что расстояние до звезд равно (23 455)²R, это более 3,5 триллионов километров. В реальности расстояние от Солнца до ближайшей звезды еще примерно в 11 раз больше. (В модели, которую мы представили в самом начале, когда расстояние от Земли до Солнца равно 10 м, расстояние до ближайшей звезды равно … 2700 километров!) Вместо компактного и уютного мира, в центре которого находится Земля и который помещается внутри относительно небольшой небесной сферы, Аристарх нарисовал бездну. И эта бездна испугала всех.

Венера, Меркурий и невозможность геоцентрической системы

Между тем невозможность геоцентрической системы мира, с круговыми движениями всех планет вокруг Земли, может быть установлена с помощью простой геометрической задачи.

Задача 2. На плоскости даны две окружности с общим центром О, по ним равномерно движутся две точки: точка М по одной окружности и точка V по другой. Докажите, что либо они двигаются в одном направлении с одинаковой угловой скоростью, либо в некоторый момент времени угол MOV тупой.

Решение. Если точки движутся в одном направлении с разными скоростями, то через некоторое время лучи ОМ и OV окажутся сонаправленными. Далее угол MOV начинает монотонно возрастать до следующего совпадения, т. е. до 360°. Следовательно, в некоторый момент он равен 180°. Случай, когда точки движутся в разных направлениях, рассматривается так же.

Теорема. Ситуация, при которой все планеты Солнечной системы равномерно вращаются вокруг Земли по круговым орбитам, невозможна.

Доказательство. Пусть О — центр Земли, М — центр Меркурия, а V — центр Венеры. Согласно многолетним наблюдениям, у Меркурия и Венеры разные периоды обращения, а угол MOV никогда не превосходит 76°. В силу результата задачи 2 теорема доказана.

Конечно, древние греки неоднократно встречались с подобными парадоксами. Именно поэтому, чтобы спасти геоцентрическую модель мира, они заставили планеты двигаться не по окружностям, а по циклоидам.

Доказательство теоремы не совсем честно, поскольку Меркурий и Венера вращаются не в одной плоскости, как в задаче 2, а в разных. Хотя плоскости их орбит почти совпадают: угол между ними — всего несколько градусов. В упражнении 10 мы предлагаем вам устранить этот недостаток и решить аналог задачи 2 для точек, вращающихся в разных плоскостях. Другое возражение: может быть, угол MOV бывает тупым, но мы этого не видим, поскольку на Земле в это время день? Принимаем и это. В упражнении 11 нужно доказать, что для трех вращающихся радиусов всегда настанет момент времени, когда они будут образовывать друг с другом тупые углы. Если на концах радиусов — Меркурий, Венера и Солнце, то в этот момент времени Меркурий и Венера будут видны на небе, а Солнце — нет, т. е. на земле будет ночь. Но должны предупредить: упражнения 10 и 11 значительно сложнее задачи 2. Наконец, в упражнении 12 мы предлагаем вам, ни много ни мало, вычислить расстояние от Венеры до Солнца и от Меркурия до Солнца (они, конечно, вращаются вокруг Солнца, а не вокруг Земли). Убедитесь сами, насколько это просто, после того, как мы узнали метод Аристарха.

Упражнения
10. В пространстве даны две окружности с общим центром О, по ним равномерно с разными угловыми скоростями движутся две точки: точка М по одной окружности и точка V по другой. Докажите, что в некоторый момент угол MOV тупой.
11. На плоскости даны три окружности с общим центром О, по ним равномерно с разными угловыми скоростями движутся три точки. Докажите, что в некоторый момент все три угла между лучами с вершиной О, направленными в данные точки, тупые.
12. Известно, что максимальное угловое расстояние между Венерой и Солнцем, т. е. максимальный угол между лучами, направленными с Земли к центрам Венеры и Солнца, равно 48°. Найдите радиус орбиты Венеры. То же — для Меркурия, если известно, что максимальное угловое расстояние между Меркурием и Солнцем равно 28°.

Последний штрих: измерение угловых размеров Солнца и Луны

Следуя шаг за шагом рассуждениям Аристарха, мы упустили лишь один аспект: как измерялся угловой диаметр Солнца? Сам Аристарх этого не делал, пользуясь измерениями других астрономов (по-видимому, не совсем верными). Напомним, что радиусы Солнца и Луны он смог вычислить, не привлекая их угловые диаметры. Посмотрите еще раз на шаги 1, 2 и 3: нигде значение углового диаметра не используется! Он нужен только для вычисления расстояний до Солнца и до Луны. Попытка определить угловой размер «на глазок» успеха не приносит. Если попросить несколько человек оценить угловой диаметр Луны, большинство назовут угол от 3 до 5 градусов, что в разы больше истинного значения. Сказывается обман зрения: ярко-белая Луна на фоне темного неба кажется массивной. Первым, кто провел математически строгое измерение углового диаметра Солнца и Луны, был Архимед (287— 212до н.э.) Он изложил свой метод в книге «Псаммит» («Исчисление песчинок»). Сложность задачи он осознавал: «Получить точное значение этого угла — дело нелегкое, потому что ни глаз, ни руки, ни приборы, при помощи которых производится отсчет, не обеспечивают достаточной точности». Поэтому Архимед не берется вычислить точное значение углового диаметра Солнца, он лишь оценивает его сверху и снизу. Он помещает круглый цилиндр на конце длинной линейки, напротив глаза наблюдателя. Линейка направляется на Солнце, и цилиндр придвигается к глазу до тех пор, пока он не заслонит собой Солнце полностью. Затем наблюдатель уходит, а на конце линейки отмечается отрезок MN, равный размеру человеческого зрачка (рис. 11).

Тогда угол α₁ между прямыми МР и NQ меньше углового диаметра Солнца, а угол α₂ = POQ — больше. Мы обозначили через PQ диаметр основания цилиндра, а через О — середину отрезка MN. Итак, α₁ < β < α₂ (докажите это в упражнении 13). Так Архимед находит, что угловой диаметр Солнца заключен в пределах от 0,45° до 0,55°.

Неясным остается, почему Архимед измеряет Солнце, а не Луну. Он был хорошо знаком с книгой Аристарха и знал, что угловые диаметры Солнца и Луны одинаковы. Луну же измерять гораздо удобнее: она не слепит глаза и границы ее видны отчетливее.

Некоторые древние астрономы измеряли угловой диаметр Солнца, исходя из продолжительности солнечного или лунного затмения. (Попробуйте восстановить этот способ в упражнении 14.) А можно сделать то же, не дожидаясь затмений, а просто наблюдая закат Солнца. Выберем для этого день весеннего равноденствия 22 марта, когда Солнце восходит точно на востоке, а заходит точно на западе. Это означает, что точки восхода Е и заката W диаметрально противоположны. Для земного наблюдателя Солнце движется по окружности с диаметром EW. Плоскость этой окружности составляет с плоскостью горизонта угол 90° – γ, где γ — географическая широта точки М, в которой находится наблюдатель (например, для Москвы γ = 55,5°, для Александрии γ = 31°). Доказательство приведено на рисунке 12. Прямая ZP — ось вращения Земли, перпендикулярная плоскости экватора. Широта точки М — угол между отрезком ZP и плоскостью экватора. Проведем через центр Солнца S плоскость α, перпендикулярную оси ZP.

Плоскость горизонта касается земного шара в точке М. Для наблюдателя, находящегося в точке М, Солнце в течение дня движется по окружности в плоскости α с центром Р и радиусом PS. Угол между плоскостью α и плоскостью горизонта равен углу MZP, который равен 90° – γ, поскольку плоскость α перпендикулярна ZP, а плоскость горизонта перпендикулярна ZM. Итак, в день равноденствия Солнце заходит за горизонт под углом 90° – γ. Следовательно, во время заката оно проходит дугу окружности, равную β/cos γ, где β — угловой диаметр Солнца (рис. 13). С другой стороны, за 24 часа оно проходит по этой окружности полный оборот, т. е. 360°.

Получаем пропорцию где Т — продолжительность заката (единица измерения — час). Зная γ и измерив время Т, находим β = 0,53°.

Упражнения
13. Докажите, что угол α₁ между прямыми МР и NQ (см. рис. 11) меньше углового диаметра Солнца, а угол α₂ = POQ — больше.
14. Предложите способ измерения угловых размеров Луны во время лунного затмения.

С автором статьи можно связаться по адресу: v-protassov@yandex.ru.

---

¹ В некоторых источниках сообщается легенда о том, что одним из них был друг Эратосфена — великий Архимед.
² Неизвестно, знал ли Аристарх об измерении Эратосфена или пользовался другим значением радиуса Земли. Это не так важно, поскольку он брал радиус Земли в качестве единицы длины.
³ Именно шесть, а не девять, поскольку Уран, Нептун и Плутон были открыты гораздо позже. Совсем недавно, 13 сентября 2006 года, по решению Международного астрономического союза (IAU) Плутон лишился статуса планеты. Так что планет в Солнечной системе теперь восемь.
⁴ Истинной причиной опалы короля Альфонса была, видимо, обычная борьба за власть, но его ироничное замечание об устройстве мира послужило веским поводом для его недругов.

Угловой диаметр Земли и Солнца

Вырежем
из бумаги кружочек диаметром 0.5 см. Если
этот кружочек держать перед глазами в
вытянутой руке, то придвигая, то отодвигая
его, можно добиться, что он закроет
полностью Луну. Измерив, расстояние
кружочка до глаза и определив отношение
этого расстояния к диаметру кружочка,
можно определить отношение расстояния
до Луны к ее диаметру. Это отношение
равно примерно 110. Интересно, что отношение
расстояния до Солнца к его диаметру
примерно такое же. Только измерения с
Солнцем проводить без специальных очков
нельзя. Но, то, что эти отношения одинаковы,
доказывается тем, что в моменты солнечных
затмений лунный диск полностью закрывает
Солнце.

Угол,
под которым мы наблюдаем космическое
тело, называется его угловым диаметром.
Угловой диаметр Луны и Солнца можно
выразить в радианах или в градусах

Размер Луны и ее расстояние от Земли

Древние
греки знали отношение диаметра Луны к
ее расстоянию до Земли. Если каким-то
образом теперь определить диаметр луны,
то можно определить и расстояние ее до
Земли. Размер Луны измерил Аристарх
Самосский (310 – 230 г. до н. э.)

Для
измерения диаметра Луны Аристарх
использовал Лунное затмение. Представим,
что прямо за Луной имеется очень большой
экран, на котором можно наблюдать тень
от Земли.

Тогда
можно было бы легко найти отношение
диаметра тени Земли к диаметру лунного
диска. К сожалению такого экрана, нет,
и мы не можем видеть всей тени Земли.
Мы можем видеть начало Лунного затмения,
когда тень Земли настигает Луну. Если
в этот момент начать отсчет времени, то
время до того момента, когда Луна
достигнет противоположного края земной
тени, будет пропорционально ее размеру.
Время же от начала затмения до того
момента, когда  Луна полностью скроется
в Земной тени, будет пропорционально
размерам лунного диска. Измерив эти два
отрезка времени, можно найти отношение
диаметра тени Земли к диаметру лунного
диска. Проведя соответствующие измерения,
Аристарх получил, что диаметры относятся
друг к другу как 2.5 к 1. Так как Солнце не
является точечным источником света, то
диаметр тени Земли не равен ее диаметру,
а меньше. Аристарх знал, что тени от Луны
на Земле не видно. Это означает, что
лучи, идущие от противоположных сторон
Луны сходятся у земной поверхности.

Эти
знания позволили Аристарху вычислить
размеры Луны и ее расстояние до Земли
в земных радиусах. Как он это сделал, и
сколько у него получилось? Оценить
погрешность в сравнении с современными
данными. В дальнейшем Аристарх и его
последователи уточнили результат. У
них получилось, что расстояние от Земли
до Луны равно 60 земным радиусам. Оцените
точность этого результата.

Размеры Солнца и его расстояние до Земли

Измерить
расстояние от Земли до Солнца трудно
даже сейчас. Как хотя бы примерно оценить
это расстояние придумал тоже Аристарх.
Он наблюдал за Луной в той стадии, когда
видна точно ее половина.

Солнечный
свет в это момент должен падать точно
перпендикулярно прямой ВС. Следовательно
треугольник АВС получается прямоугольный.
Аристарх измерил угол между направлениями
на Луну и на Солнце (φ). Угол ВАС него
получился равен 3°. Какое расстояние до
Солнца получилось у Аристарха? Как это
значение согласуется с современными
данными? За счет чего могла возникнуть
ошибка в измерениях Аристарха? Итак,
астрономам из Александрии были известны
весьма точно размеры Земли, Луны и
расстояния до Луны. Имелась очень грубая
оценка расстояния до Солнца. Совсем не
были известны расстояния до планет и
до звезд. Они знали только, что планеты
находятся дальше, чем Луна, а звезды
дальше Солнца и планет.

Измерение
расстояний в астрономии одна из самых
важных и трудных задач, так как мы лишены
прямого контакта с исследуемыми телами.
Однако методы бесконтактных определений
расстояний были известны уже давно –
это методы параллактических углов. Для
измерения расстояния до тел Солнечной
системы применяется метод параллакса.
Сейчас для определения расстояния до
некоторых тел (Луна, Венера) используют
методы радиолокации: посылают радиосигнал
на планету, сигнал отражается и фиксируется
приёмной антенной. Галактика располагается
гораздо ближе к Туманности Андромеды,
а от нас удалена на 2,2- 2,7 млн. световых
лет (по разным оценкам).  Все остальные
галактики ближайшего окружения –
карликовые эллиптические и неправильные,
которые, как мы помним, тоже редко бывают
большими. Но две ближайших к нам
неправильных галактики можно назвать
крупными представителями рода неправильных
галактик. Магеллановы Облака являются
спутниками
нашей Галактики Млечный Путь – это еще
два внегалактических объекта, видимые
невооруженным глазом, правда, в южном
полушарии.