

Калькулятор онлайн.
Уравнение прямой касательной к графику функции в заданной точке
Эта математическая программа находит уравнение касательной к графику функции ( f(x) ) в заданной пользователем
точке ( x_0 ).
Программа не только выводит уравнение касательной, но и отображает процесс решения задачи.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Статью из энциклопедии о касательной прямой вы можете посмотреть
здесь (статья из Википедии).
Если вам нужно найти производную функции, то для этого у нас есть задача Найти производную.
Примеры подробного решения >>
Введите выражение функции ( f(x)) и число (x_0) – абсциссу точки в которой нужно построить касательную
Наши игры, головоломки, эмуляторы:
Немного теории.
Угловой коэффициент прямой
Напомним, что графиком линейной функции ( y=kx+b) является прямая. Число (k=tg alpha ) называют угловым коэффициентом
прямой, а угол ( alpha ) – углом между этой прямой и осью Ox
Если ( k>0), то (0< alpha < frac{pi}{2} ), в этом случае функция ( y=kx+b) возрастает.
Если ( k<0), то (-frac{pi}{2}< alpha < 0 ), в этом случае функция ( y=kx+b) убывает.
Уравнение касательной к графику функции
Если точка М(а; f(a)) принадлежит графику функции у = f(x) и если в этой точке к графику функции можно
провести касательную, не перпендикулярную оси абсцисс, то из геометрического смысла производной следует, что угловой
коэффициент касательной равен f'(a). Далее мы выработаем алгоритм составления уравнения касательной к графику любой функции.
Пусть даны функция у = f(x) и точка М(а; f(a)) на графике этой функции; пусть известно, что существует f'(a). Составим уравнение
касательной к графику заданной функции в заданной точке. Это уравнение, как уравнение любой прямой, не параллельной оси ординат,
имеет вид y = kx + b, поэтому задача состоит в нахождении значений коэффициентов k и b.
С угловым коэффициентом k все понятно: известно, что k = f'(a). Для вычисления значения b воспользуемся тем, что искомая прямая
проходит через точку М(а; f(a)). Это значит, что если подставить координаты точки М в уравнение прямой, получим верное
равенство: (f(a)=ka+b ), т.е. ( b = f(a) – ka ).
Осталось подставить найденные значения коэффициентов k и b в уравнение прямой:
$$ y=kx+b $$
$$ y=kx+ f(a) – ka $$
$$ y=f(a)+ k(x-a) $$
$$ y=f(a)+ f'(a)(x-a) $$
Нами получено уравнение касательной к графику функции ( y = f(x) ) в точке ( x=a ).
Алгоритм нахождения уравнения касательной к графику функции ( y=f(x) )
1. Обозначить абсциссу точки касания буквой ( a )
2. Вычислить ( f(a) )
3. Найти (f'(x) ) и вычислить (f'(a) )
4. Подставить найденные числа ( a, f(a), f'(a) ) в формулу ( y=f(a)+ f'(a)(x-a) )
Уравнение касательной онлайн
Уравнение касательной
к графику функции
в точке
имеет вид:
Уравнение касательной онлайн
Переменная функции:
Точка в которой необходимо найти касательную:
Написать уравнение касательной к функцииfxx24x7в точкеx00
Установить калькулятор на свой сайт
Другие полезные разделы:
Нахождение производной функции онлайн
Уравнение нормали к графику функции онлайн
Таблица производных
Оставить свой комментарий:
Онлайн калькулятор для вычисления уравнения касательной к графику функции.
Ряд Маклорена (=Макларена) это ряд Тейлора в окрестности точки а=0.
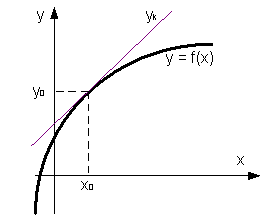
Вычисление значения функции y0 в точке x0:y0 = f(x0). Если исходное значение y0
задано, то переходим к п.2.
Нахождение производной y'(x).
Вычисление значения производной при x0.
Запись уравнения касательной к кривой линии в форме: yk = y0 + y'(y0)(x – x0)
Калькулятор поможет составить и решить уравнение касательной к графику функции онлайн.
Для получения полного хода решения нажимаем в ответе Step-by-step.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Примеры решений
Ранг матрицы
Умножение матриц
Метод Гаусса
Найти производную
Найти интеграл
Решение СЛАУ методом Крамера
Диф уравнения онлайн
Определитель матрицы
Точки разрыва функции
-
- Математика онлайн
- Линейная алгебра
- Вычислительная математика
- Теория вероятностей
- Математическая статистика
- Статистика онлайн
-
- Математический анализ
- Свойства функций y=f(x)
- Предел функции
- Точки разрыва функции
- Первый замечательный предел
- Второй замечательный предел
- Производная функции
- Уравнение касательной к кривой
- Дифференциал функции
- Правило Лопиталя
- Экстремумы функций одной переменной
- Асимптоты графика функции
- ✍ Помощь в решении контрольных
Уравнение касательной к кривой линии
Уравнение касательной в общем виде записывается как: yk=y0+y'(x0)(x-x0)
Назначение. Онлайн-калькулятор предназначен для нахождения уравнения касательной к графику функции. Решение оформляется в формате Word (см. пример).
- Шаг №1
- Шаг №2
- Видеоинструкция
Примеры:
Функция задана в явном виде, например y = 1/2*x3+5*x
Функция задана в неявном виде, например y2 – 1/2*x3 – 8
Функция задана в параметрическом виде, например x = 5*cos(t);y = 3*sin(t)
Функция задана в явном виде,
Функция задана в неявном виде
Функция задана в параметрическом виде
Алгоритм составления уравнения касательной к графику функции
- Вычисление значения функции y0 в точке x0:y0 = f(x0). Если исходное значение y0 задано, то переходим к п.2.
- Нахождение производной y'(x).
- Вычисление значения производной при x0.
- Запись уравнения касательной к кривой линии в форме: yk = y0 + y'(y0)(x – x0)
Касательные к кривым второго порядка
| Уравнение линии | Уравнение касательной | |
| Эллипс | 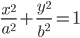 |
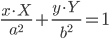 |
| Гипербола | 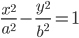 |
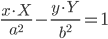 |
| Парабола | y2 = 2px | yY = p(X + x) |
см. также Касательная плоскость к поверхности.
| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|

Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки

Примеры
-
касательная:f(x)=frac{1}{x^2},:(-1,:1)
-
касательная:f(x)=x^3+2x,::x=0
-
касательная:f(x)=4x^2-4x+1,::x=1
-
касательная:y=e^{-x}cdot ln(x),:(1,0)
-
касательная:f(x)=sin (3x),:(frac{pi }{6},:1)
-
касательная:y=sqrt{x^2+1},:(0,:1)
- Показать больше
Описание
Поэтапное вычисление уравнений касательной
tangent-line-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
Slope, Distance and More
Ski Vacation? Nope, this is serious stuff; it’s about finding the slope of a line, finding the equation of a line…
Read More
Введите Задачу
Сохранить в блокнот!
Войти

