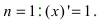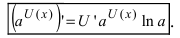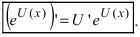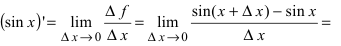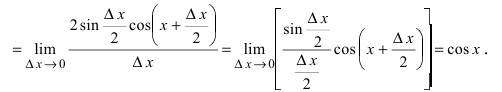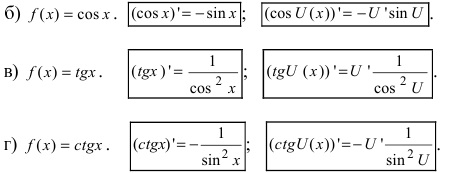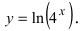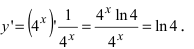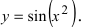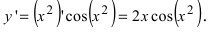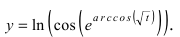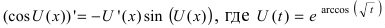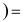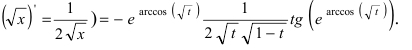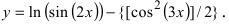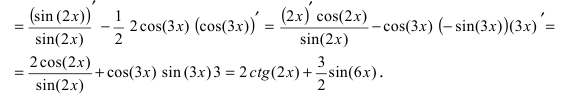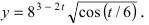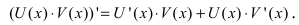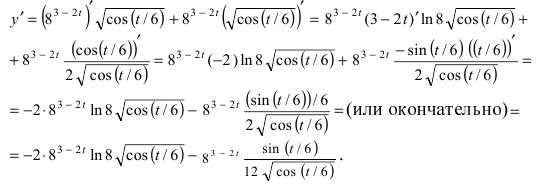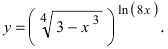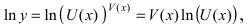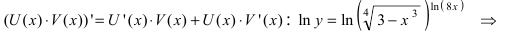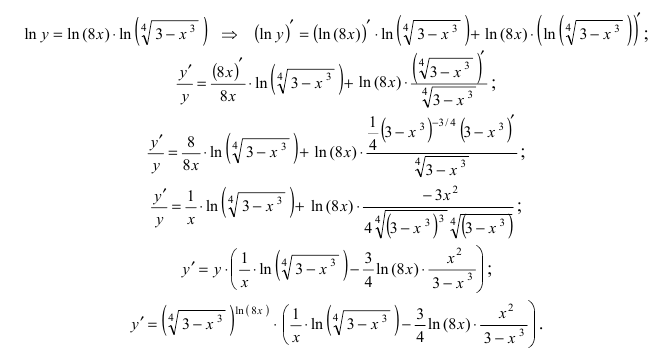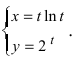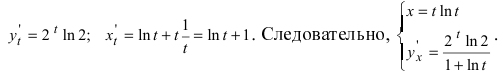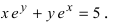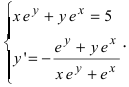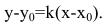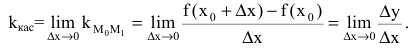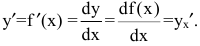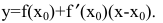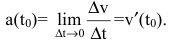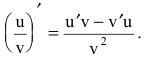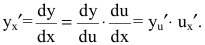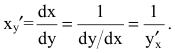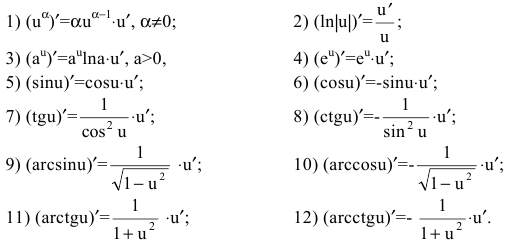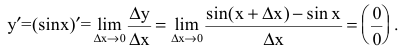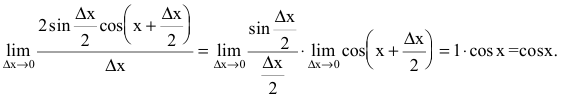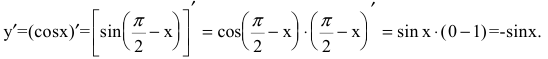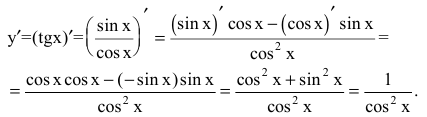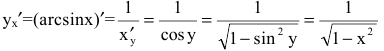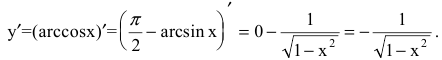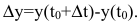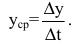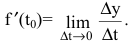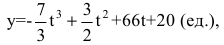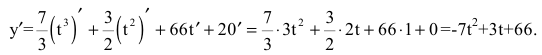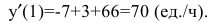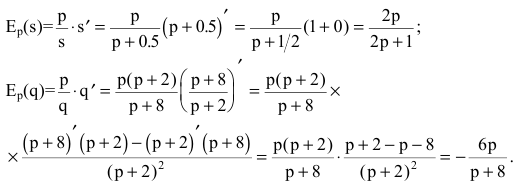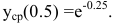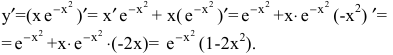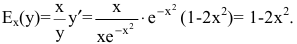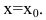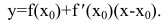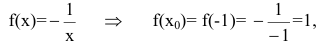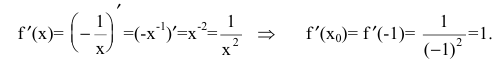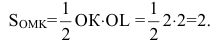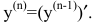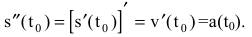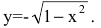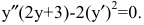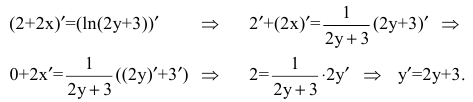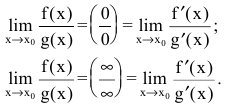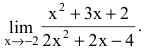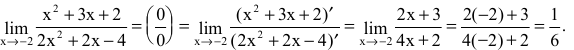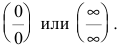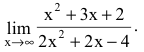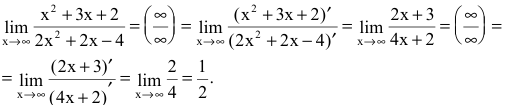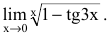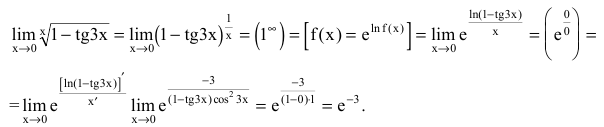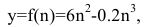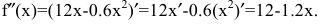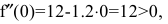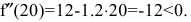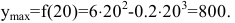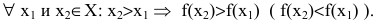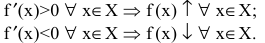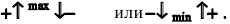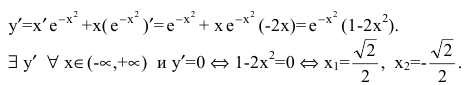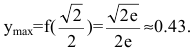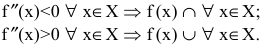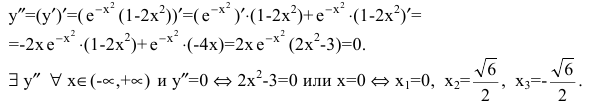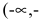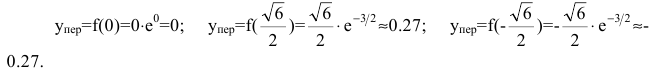Рассмотрим
кривую, уравнение которой имеет вид
Уравнение
касательной к данной кривой в точке
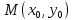

Нормалью
к кривой в данной точке называется
прямая, проходящая через данную точку,
перпендикулярную к касательной в этой
точке.
Уравнение
нормали к данной кривой в точке


Длина
отрезка касательной, заключенного между
точкой касания и осью абсцисс называется
длиной
касательной,
проекция этого отрезка на ось абсцисс
называется подкасательной.
Длина
отрезка нормали, заключенного между
точкой касания и осью абсцисс называется
длиной
нормали,проекция
этого отрезка на ось абсцисс называется
поднормалью.
Пример
17
Написать
уравнения касательной и нормали к кривой


Решение:
Найдем
значение функции в точке

Найдем
производную заданной функции в точке
Уравнение
касательной найдем по формуле (34):
Уравнение
нормали найдем по формуле (35):
Ответ:
Уравнение
касательной :
Уравнение
нормали :
Пример
18
Написать
уравнения касательной и нормали, длины
касательной и подкасательной, длины
нормали и поднормали для эллипса
в
точке

для которой
Решение:
Найдем

параметрически по формуле (10):
Найдем
координаты точки касания

и значение производной в точке касания

Уравнение
касательной найдем по формуле (34):
Найдем
координаты


касательной с осью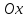
Длина
касательной равна длине отрезка

Согласно
определению, подкасательная

Где
угол
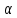
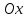

равный
Таким
образом, подкасательная

Уравнение
нормали найдем по формуле (35):
Найдем
координаты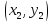

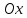
Длина
нормали равна длине отрезка

Согласно
определению, поднормаль
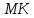
Где
угол

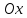

Поэтому,
поднормаль
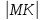
Ответ:
Уравнение
касательной :
Уравнение
нормали :
Длина
касательной

подкасательная
Длина
нормали

Задания
7. Написать
уравнения касательной и нормали:
1. К параболе в точке, абсцисса которой

2.
К окружности

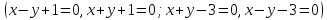
3.
К циклоиде


4.
В каких точках кривой

а)
оси Оx; б) прямой

10.
Промежутки монотонности функции.
Экстремумы функции.
Условие
монотонности функции:
Для
того, чтобы дифференцируемая на


чтобы во всех точках, принадлежащих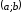

Для
того, чтобы дифференцируемая на

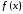
чтобы во всех точках, принадлежащих
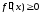
Промежутки,
на которых производная функции сохраняет
определенный знак, называются промежутками
монотонности
функции
Пример
19
Найти
промежутки монотонности функции

Решение:
Найдем
производную функции
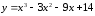
Найдем
промежутки знакопостоянства полученной
производной. Для этого
разложим полученный
квадратный трехчлен на множители:

Исследуем
знак полученного выражения, используя
метод интервалов.
Таким
образом, получаем согласно (36), (37),что
заданная функция возрастает на

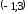
Ответ:
Заданная
функция

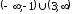

Определение
Функция


максимум (минимум),
если существует такая окрестность
точки

что для всех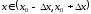
(
Локальный
минимум или максимум функции

экстремумом.
Необходимое
условие существования экстремума.
Пусть
функция
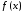
точки
Если функция
в точке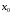
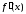

Точка

точкой
функции

если производная

Достаточные
условия наличия экстремума в критической
точке
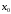
Пусть
точка

Первое
достаточное условие экстремума:
Пусть
функция




Точка

при переходе через
производная
функции меняет знак с плюса на минус.
Точка

переходе через
производная
функции меняет знак с минуса на плюс.
Пример
20
Найти
экстремумы функции

Решение:
Найдем
производную заданной функции
Приравнивая
в полученной производной к нулю числитель
и знаменатель, найдем критические точки:
Исследуем
знак производной, используя метод
интервалов.

Из
рисунка видно, что при переходе через
точку

минус. Следовательно, в точке
локальный максимум.
При
переходе через точку

плюс.
Следовательно,
в точке

локальный минимум.
При
переходе через точку

критическая точка
функции.
Ответ:

локальный максимум,
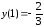
локальный минимум.
Второе
достаточное условие экстремума:
Если
первые
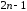

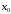
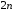
производная функции



причем,
если
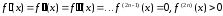
(38)
то
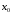
минимум
если

(39)
то
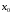
максимум.
Пример
21
Найти
экстремумы функции, пользуясь второй
производной

Решение:
ОДЗ:

Найдем
первую производную заданной функции
Найдем
критические точки функции:
Точку

определена только в левой окрестности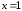
Найдем
вторую производную
Находим
Таким
образом, на основании (39) делаем вывод
о том, что при

Ответ:

локальный максимум.
Задания
8.
Исследовать
на возростание и убывание функции:
|
1. |
2. |
3. |
|
4. |
5. |
6. |
Исследовать
на экстремумы функции:
|
7. |
|
|
|
8. |
|
|
|
9. |
|
|
|
10. |
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вывод уравнения нормали к графику функции
Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Замечание 1
Нормаль — это прямая, которая образует с касательной к графику функции угол в $90°$.
Рисунок 1. Нормальный перпендикуляр к графику касательной. Автор24 — интернет-биржа студенческих работ
В связи с тем, что нормаль перпендикулярна к касательной, её угловой коэффициент будет величиной, обратной к угловому коэффициенту касательной:
$k_{норм}=- frac{1}{k_{к}}= -1 frac{1}{f’(x_0)}$.
Пользуясь полученным выводом, запишем уравнение нормали к графику функции:
$y – y_0 = – frac{1}{f’(x_0)} cdot (x – x_0) left(1right) $, здесь $x_0$ и $y_0$ — координаты точки для которой строится искомая линия, при этом производная в этой точке $f’(x_0) ≠ 0$.
Порядок действий при поиске уравнения нормальной прямой если задана координата $x_0$:
- Вычисляется, чему равен нулевой игрек $y(x_0)$ для функции.
- Затем нужно определить производную.
- Нужно высчитать затем, чему равен $f’(x)$ в точке $x_0$, найденное значение — коэффициент касательной.
- Все найденные значения подставляются в формулу $(1)$.
Напомним также как выглядит само уравнение касательной:
$y – y_0 = f’(x_0) cdot (x – x_0)$.
Пример 1
Найдите уравнение нормали для функции $y=x^2$ в точке $x_0=2$.
Решение:
Производная данной функции составит $y’(x) = 2x$, затем найдём, чему равен наш подопытный кролик-функция в заданной точке $y_0= x^2 = 2^2 = 4$.
Теперь нужно высчитать производную функции в точке $x_0$: $y’(2) = 2 x = 2 cdot 2= 4$.
Все полученные значения расставляем по своим местам в формулу $(1)$:
$y-4=-frac{1}{4} cdot (x – 2)$
Уравнение нормали найдено.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 07.05.2023
Рассмотрим график функции в декартовой системе координат
(рис. 10.2). Возьмем на графике точку
и точку
. Проведем через эти точки прямую
. Эта прямая называется Секущей. Ее уравнением будет
, а угловой коэффициент этой прямой равен тангенсу угла наклона секущей:
Если то секущая MN поворачивается вокруг точки
и переходит в касательную с угловым коэффициентом
Если , то секущая MN поворачивается вокруг точки М и в пределе переходит в касательную с угловым коэффициентом

Угловой коэффициент касательной к графику функции в данной точке равен значению производной функции в этой
точке: .
Геометрический смысл производной состоит в том, что производная равна угловому коэффициенту касательной к графику функции в данной точке.
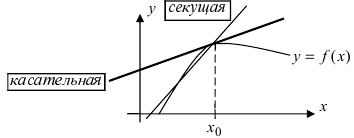
Значение производной в точке
равно тангенсу угла наклона касательной (рис. 10.3).
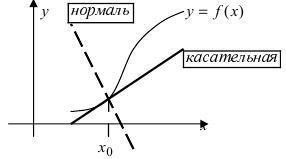
Нормаль – это прямая, перпендикулярная к касательной в точке касания (рис. 10.3).
Уравнение касательной к кривой в точке
запишем как уравнение прямой, которая проходит через заданную точку:
.
Уравнение нормали к кривой в точке
запишем так:

Пример 1. Напишите уравнение касательной к графику функции в точке с абсциссой
.
Решение. 1) Найдем значение функции, если :
.
2) Найдем первую производную функции: .
3) Найдем значение производной, если :
.
4) Запишем уравнение касательной, которая проходит через данную точку :
или
.
Ответ. Уравнение касательной: .
Пример 2. Напишите уравнение нормали к графику функции в точке с абсциссой
.
Решение. 1) Найдем значение функции, если :
.
2) Найдем первую производную функции: .
3) Найдем значение производной, если :
.
4) Запишем уравнение нормали, которая проходит через данную точку :

.
Ответ. Уравнение нормали: .
Рассмотрим задачу о свободном падении тела и найдем мгновенную скорость его движения.
Из физики мы знаем, что 
За время тело проходит расстояние

– расстояние

, откуда
.
Приращение функции будет равно:
Найдем предел отношения приращения функции к приращению ее аргумента T , если ΔT Стремится к нулю:

В левой части равенства мы получили значение производной функции , а в правой части значение мгновенной скорости тела в момент времени T0.
Физический смысл производной. Производная функции в точке
есть мгновенная скорость изменения функции в точке
, т. е. скорость протекания процесса, который описывается зависимостью
.
Например, если дана функция , то ее производная будет
, тогда значение производной в точке
будет
, а значение производной в точке
будет
. Это значит, что в точке
функция изменяется в 4 раза быстрее аргумента
, а в точке
изменяется в 6 раз быстрее (т. е. различная скорость изменения функции или протекания процесса). В этом и состоит физический смысл производной.
Операция нахождения (взятия) производной функции называется Дифференцированием функции.
Ответьте на вопросы
1. Что показывает угловой коэффициент K в уравнении прямой ?
2. Чему равен угловой коэффициент касательной к кривой в точке ?
3. Как найти угловой коэффициент нормали к кривой в точке ?
4. В чем состоит геометрический смысл производной?
5. В чем состоит физический смысл производной?
| < Предыдущая | Следующая > |
|---|
Загрузить PDF
Загрузить PDF
Угловой коэффициент характеризует угол наклона прямой к оси абсцисс (угловой коэффициент численно равен тангенсу этого угла). Угловой коэффициент присутствует в уравнении прямой и используется в математическом анализе кривых, где всегда равен производной функции. Для облегчения понимания углового коэффициента представьте, что он влияет на скорость изменения функции, то есть чем больше значение углового коэффициента, тем больше значение функции (при одном и том же значении независимой переменной).
-
1
Используйте угловой коэффициент для нахождения угла наклона прямой к оси абсцисс и направления этой прямой. Вычислить угловой коэффициент довольно легко, если вам дано уравнение прямой. Запомните, что в любом уравнении прямой:
-
2
Для нахождения углового коэффициента необходимо найти значение k (коэффициент при «х»). Если данное вам уравнение имеет вид
, то для нахождения углового коэффициента вам нужно просто посмотреть на число, стоящее перед «х». Обратите внимание, что k (угловой коэффициент) всегда находится при независимой переменной (в данном случае «х»). Если вы запутались, просмотрите следующие примеры:
-
3
Если данное вам уравнение имеет вид, отличный от
, обособьте зависимую переменную. В большинстве случаев зависимая переменная обозначается как «у», а для ее обособления можно выполнять операции сложения, вычитания, умножения и другие. Помните, что любая математическая операция должна быть выполнена на обеих сторонах уравнения (чтобы не менять его исходного значения). Вам необходимо привести любое данное вам уравнение к виду
. Рассмотрим пример:
Реклама
-
1
Для вычисления углового коэффициента воспользуйтесь графиком и двумя точками. Если вам дан просто график функции (без уравнения), вы все еще можете найти угловой коэффициент. Для этого вам понадобятся координаты любых двух точек, лежащих на этом графике; координаты подставляются в формулу:
. Чтобы избежать ошибок при вычислении углового коэффициента, запомните следующее:
- Если график возрастает, то угловой коэффициент имеет положительное значение.
- Если график убывает, то угловой коэффициент имеет отрицательное значение.
- Чем больше значение углового коэффициента, тем круче график (и наоборот).
- Угловой коэффициент прямой, параллельной оси абсцисс, равен 0.
- Угловой коэффициент прямой, параллельной оси ординат, не существует (он бесконечен).[4]
-
2
Найдите координаты двух точек. На графике отметьте любые две точки и найдите их координаты (х,у). Например, на графике лежат точки А(2,4) и В(6,6).[5]
- В паре координат первое число соответствует «х», а второе – «у».
- Каждому значению «х» соответствует определенное значение «у».
-
3
Приравняйте x1, y1, x2, y2 к соответствующим значениям. В нашем примере с точками А(2,4) и В(6,6):
- x1: 2
- y1: 4
- x2: 6
-
y2: 6[6]
-
4
Подставьте найденные значения в формулу для вычисления углового коэффициента. Чтобы найти угловой коэффициент, используются координаты двух точек и следующая формула:
. Подставьте в нее координаты двух точек.
-
5
Объяснение сути формулы. Угловой коэффициент равен отношению изменения координаты «у» (двух точек) к изменению координаты «х» (двух точек). Изменение координаты – это разность между значениями соответствующей координаты первой и второй точек.
-
6
Другой вид формулы для вычисления углового коэффициента. Стандартная формула для вычисления углового коэффициента: k =
. Но она может иметь следующий вид: k = Δy/Δx, где Δ – это греческая буква «дельта», обозначающая в математике разность. То есть, Δx = x_2 – x_1, а Δy = y_2 – y_1.[8]
Реклама
-
1
Научитесь брать производные от функций. Производная характеризует скорость изменения функции в определенной точке, лежащей на графике этой функции. В данном случае графиком может быть как прямая, так и кривая линия. То есть производная характеризует скорость изменения функции в конкретный момент времени. Вспомните общие правила, по которым берутся производные, и только потом переходите к следующему шагу.
- Прочитайте статью Как брать производную.
- Как брать простейшие производные, например, производную показательного уравнения, описано этой статье. Вычисления, представленные в следующих шагах, будут основаны на описанных в ней методах.
-
2
Научитесь различать задачи, в которых угловой коэффициент требуется вычислить через производную функции. В задачах не всегда предлагается найти угловой коэффициент или производную функции. Например, вас могут попросить найти скорость изменения функции в точке А(х,у). Также вас могут попросить найти угловой коэффициент касательной в точке А(х,у). В обоих случаях необходимо брать производную функции.
-
3
Возьмите производную данной вам функции. Здесь строить график не нужно – вам понадобится только уравнение функции. В нашем примере возьмите производную функции
. Берите производную согласно методам, изложенным в упомянутой выше статье:
- Производная:
- Производная:
-
4
В найденную производную подставьте координаты данной вам точки, чтобы вычислить угловой коэффициент. Производная функции равна угловому коэффициенту в определенной точке. Другими словами, f'(х) – это угловой коэффициент функции в любой точке (x,f(x)). В нашем примере:
-
5
Если возможно, проверьте полученный ответ на графике. Помните, что угловой коэффициент можно вычислить не в каждой точке. Дифференциальное исчисление рассматривает сложные функции и сложные графики, где угловой коэффициент можно вычислить не в каждой точке, а в некоторых случаях точки вообще не лежат на графиках. Если возможно, используйте графический калькулятор, чтобы проверить правильность вычисления углового коэффициента данной вам функции. В противном случае проведите касательную к графику в данной вам точке и подумайте, соответствует ли найденное вами значение углового коэффициента тому, что вы видите на графике.
- Касательная будет иметь тот же угловой коэффициент, что и график функции в определенной точке. Для того, чтобы провести касательную в данной точке, двигайтесь вправо/влево по оси Х (в нашем примере на 22 значения вправо), а затем вверх на единицу по оси Y. Отметьте точку, а затем соедините ее с данной вам точкой. В нашем примере соедините точки с координатами (4,2) и (26,3).
Реклама
Об этой статье
Эту страницу просматривали 143 928 раз.
Была ли эта статья полезной?
Содержание:
Дифференциальное исчисление
Понятие производной
Приращение аргумента и функции
Пусть дан график непрерывной функции.
Определение: Разность между конечным и начальным значениями аргумента называется его приращением, т.е.
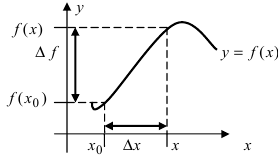
Рис. 69. Приращения аргумента и функции
Теорема: Если 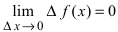
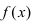
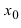
Доказательство: Приращение функции 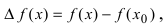
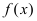
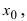
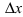
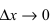
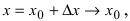
Отсюда следует, что 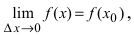
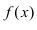
Задачи, приводящие к понятию производной
1. Физика. Пусть материальная точка движется прямолинейно согласно закону 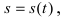
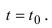
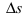
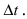
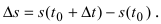
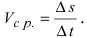
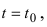
2. Геометрия. Пусть дан график функции 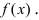
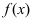
Определение: Касательной называется предельное положение секущей прямой 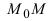
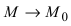
Рис. 70. Касательная к графику функции
Вычислим тангенс угла наклона секущей 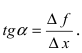
Производная функции. Ее механический и геометрический смысл
Определение: Производной функции 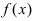
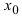
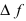
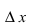
Из рассмотренных выше задач следует, что с точки зрения механики производная определяет мгновенную скорость движения, а с геометрической точки зрения производная функции равна тангенсу угла наклона касательной к положительному направлению оси абсцисс в заданной точке, в которой вычисляется значение производной.
Уравнение касательной и нормали в заданной точке графика функции f(x)
Пусть дан график функции 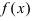
Рис. 71. Касательная и нормаль.
Требуется составить уравнения касательной и нормали в точке 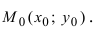
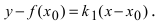
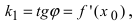
Так как нормаль перпендикулярна к касательной, то ее угловой коэффициент 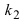
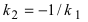
Следовательно, уравнение нормали имеет следующий вид:
Пример:
Найти угловой коэффициент касательной в точке 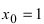
Решение:
Так как 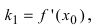
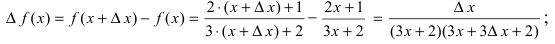
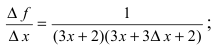
Вычислим значение производной в точке 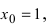
Дифференцируемость непрерывных функций
Определение: Нахождение конечной производной от непрерывной функции называется дифференцированием.
Теорема: Если функция 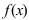
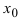
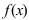
Доказательство: Если функция 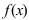
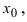
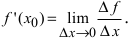
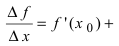
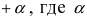
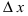
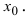
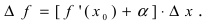
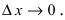
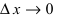
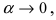
По теореме получаем, что функция 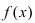
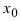
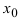
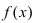
Замечание: Утверждение, обратное к рассмотренному в теореме что всякая непрерывная в точке 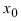
Пример:
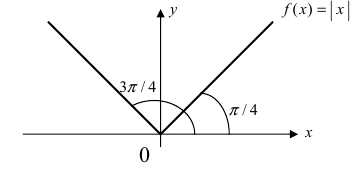
Дифференцируема ли функция 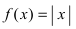
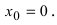
Рис. 72. График функции
Решение:
В точке 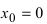
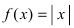
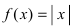
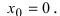
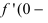
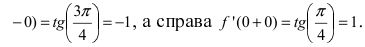
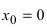
Пример:
Дифференцируема ли функция
Решение:
В точке 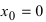
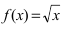
Следовательно, в точке 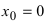
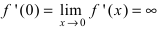
Правила дифференцирования
Вычисление производной согласно определению является трудоемкой задачей. В связи с этим были получены следующие правила дифференцирования:
1. Производная от суммы (разности) двух функций равна сумме (разности) производных от этих функций, т.е.
Доказательство: Пусть 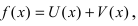
Приращение функции будет равно: 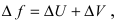
Замечание: Производная от суммы (разности) любого числа функций равна сумме (разности) производных от этих функций.
2. Производная от произведения двух функций вычисляется по формуле:
Доказательство: Пусть 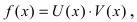
Приращение функции будет равно: 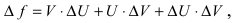
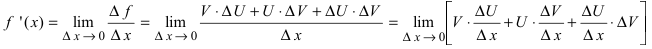
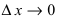
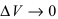
3. Производная от частного двух функций вычисляется согласно формуле:
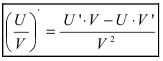
4. Производная от обратной функции вычисляется по формуле:
Доказательство: Так как 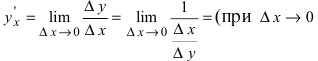
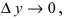
5. Производная от сложной функции 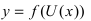
Доказательство: Так как 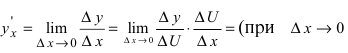
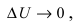
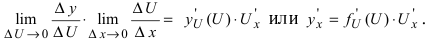
Производная от основных элементарных функций
1. Постоянная функция 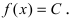
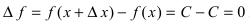
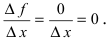
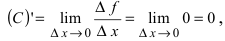
Следствие: При вычислении производной от произведения константы С на функцию 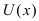
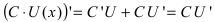
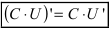
Следствие: Аналогично поступают при вычислении производной от частного 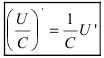
2. Логарифмическая функция 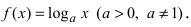
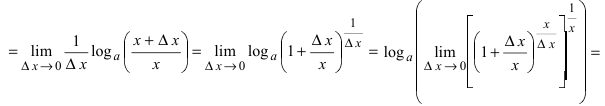
Следствие: Производная от сложной логарифмической функции равна
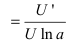
Следствие: Если основание логарифма 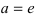
3. Степенная функция 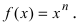
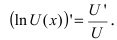
Отсюда находим 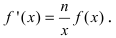
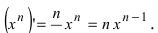
Следствие: Наиболее распространенными являются случаи:
- а)
- б)
;
- в)
4. Показательная функция 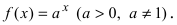
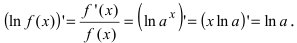
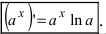
Следствие: Если основание показательной функции а=е, то 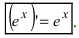
5. Тригонометрические функции: a) 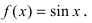
Следовательно, 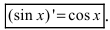
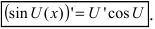
6. Обратные тригонометрические функции:
a) 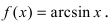
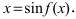
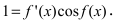
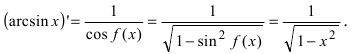
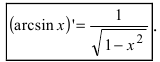
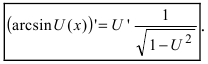
Пример:
Найти производную функции
Решение:
По правилу дифференцирования сложной функции и с учетом выражения для логарифмической и показательной функций имеем
Пример:
Найти производную функции
Решение:
В данном случае производная
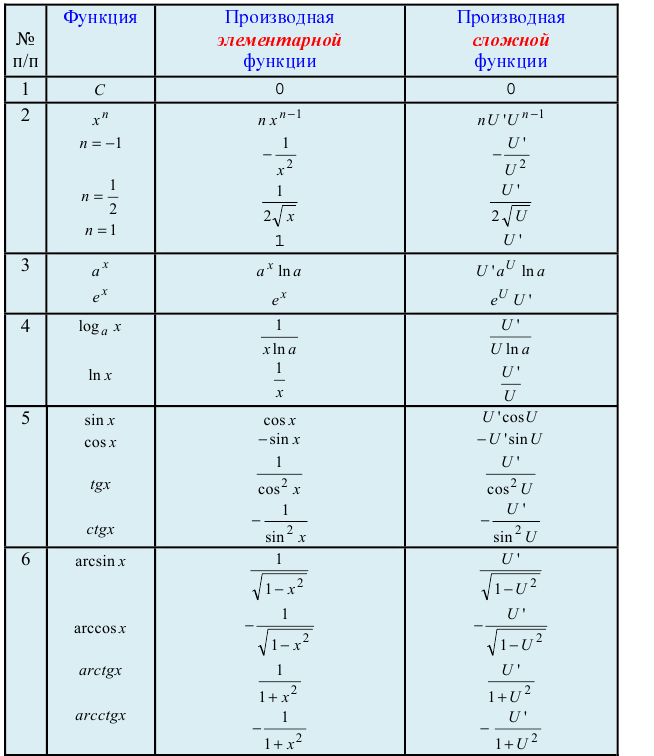
Полученные производные от элементарных функций сведем в таблицу:
Пример:
Найти производную функции
Решение:
По правилу дифференцирования сложной функции 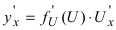
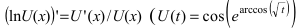
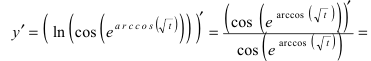
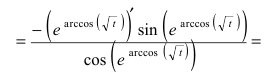
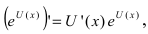
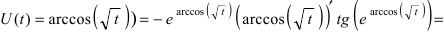
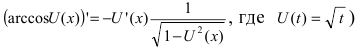
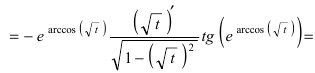
Пример:
Найти производную функции
Решение:
По правилу дифференцирования разности функций 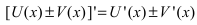
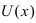
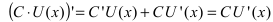
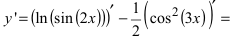
Пример:
Найти производную функции
Решение:
По правилу дифференцирования произведения функций
В результате действий, получаем:
Пример:
Найти производную функции
Решение:
По условию задачи дана показательно-степенная функция 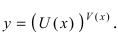
и правила дифференцирования произведения функций
Производная от параметрически и неявно заданных функций
Определение: Если функция 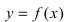
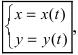
Чтобы продифференцировать параметрически заданную функцию, надо из первого уравнения системы найти обратную функцию t(x) и подставить ее во второе уравнение системы. В результаты этих действий получается сложная функция, производная от которой равна 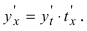
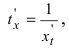
Пример:
Найти производную функции
Решение:
Вычислим производные от заданных функций по параметру t:
Определение: Если функция y = f(x) задается в виде соотношения F(x, у) = 0, из которого нельзя явно выразить переменную у через х или наоборот, то говорят, что функция задана в неявном виде.
Дифференцирование таких функций осуществляется с учетом того, что переменная у является сложной функцией, т.е. зависит от переменной х.
Пример:
Найти производную функции
Решение:
Продифференцируем данное соотношение с учетом вышеизложенного материала получим 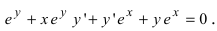
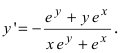
—–вышмат
Дифференциальное исчисление
Производная функции, ее геометрический и физический смыслы
При изучении различных экономических процессов, описываемых функциями, существенную роль играют скорость роста процесса, ускорение роста, оптимальный режим и другие характеристики, которые исследуются с помощью производной.
Рассмотрим геометрическую задачу о проведении касательной к плоской кривой Пусть на плоскости Оху дана непрерывная кривая y=f(x). Необходимо найти уравнение касательной к этой кривой в точке 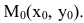
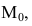
Касательной называется прямая, к которой стремится секущая при стремлении второй точки секущей к первой. Дадим аргументу 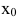
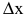
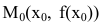
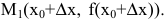
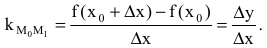
Это и есть производная функции y=f(x) в точке 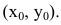
Производная функции имеет несколько обозначений:
Следовательно, уравнение касательной к кривой y=f(x) в точке 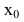
Нахождение мгновенной скорости прямолинейно движущейся точки
Пусть точка М движется прямолинейно и s=f(t) – путь, проходимый ею за время t. Средней скоростью прямолинейного движения за время 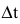
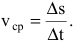
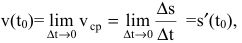
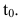
Если v=f(t) – функция, описывающая процесс изменения скорости неравномерного движения в зависимости от времени t, то (мгновенное) ускорение материальной точки в фиксированный момент времени 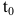
Вывод. Производная есть предел отношения приращения функции к бес- конечно малому приращению аргумента.
Важно отметить, что запись 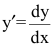
Дифференциалом функции одной переменной называется произведение ее производной на приращение аргумента: 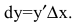
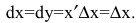
Нахождение для заданной функции ее производной называется дифференцированием данной функции. А учение о производной и ее приложениях является предметом дифференциального исчисления. Фундамент дифференциального исчисления составляют основные правила и формулы дифференцирования функций. Используя их, можно найти производную и дифференциал любой элементарной функции.
Основные правила дифференцирования
Внимание! Для существования производной в некоторой точке необходимо, чтобы функция была непрерывна в этой точке. Однако не всякая непрерывная в точке функция имеет в ней производную.
Теорема 1. Производная постоянной равна нулю: с’=0.
Теорема 2. Пусть u=u(x), v=v(x) – дифференцируемые функции. Тогда:
- производная суммы конечного числа дифференцируемых функций равна сумме производных этих функций: (u+v)’=u’+v’;
- производная произведения конечного числа дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные: (uv)’=u’v+v’u; в частности, постоянный множитель можно выносить за знак производной: (cu)’=cu’;
- производная частного двух дифференцируемых функций может быть найдена по формуле:
Теорема 3. Производная сложной функции равна ее производной по промежуточному аргументу, умноженной на производную промежуточного аргумента.
Действительно, пусть задана сложная функция y=f[u(x)]. Тогда
Теорема 4. Производная обратной функции есть величина, обратная производной прямой функции.
Так, если 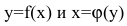
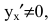
Таблица производных
Приведем основные формулы дифференцирования функций. Пусть u=u(x) – дифференцируемая функция.
Тогда
Выведем производные некоторых функций.
1. Если y=sinx, то
Используя формулу разности синусов
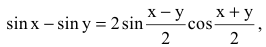
Так как любую тригонометрическую функцию можно вывести через синус, то нетрудно найти производные остальных тригонометрических функций.
2. Пусть y=cosx. Тогда по теореме о производной сложной функции
3. Для функции y=tgx воспользуемся правилом дифференцирования частного:
4. Представим y=ctgx как степенную функцию от тангенса. Тогда
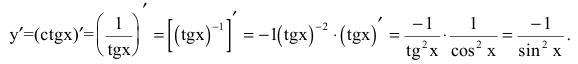
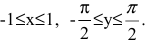
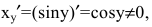
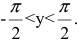
и при х=±1 производная не существует.
6. Производную y=arccosx получим из соотношения 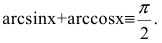
Предельный анализ в экономике
Задача о производительности труда
Пусть функция y=f(t) выражает количество произведенной продукции у за время t и необходимо найти производительность труда в момент времени 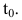
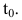
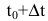
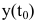
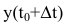
Средней производительностью труда называется отношение количества произведенной продукции к затраченному времени, т.е.
Производительность труда в момент времени 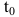
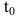
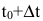
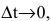
Пример №34
Объем продукции хлебобулочных изделий, произведенных бригадой пекарей в течение смены, может быть описан функцией
где t – время в часах. Вычислить производительность труда через час после начала работы.
Решение:
Производительность труда выражается производной
В заданный момент времени соответственно имеем:
Задача о предельных издержках производства
Издержки производства у будем рассматривать как функцию количества выпускаемой продукции х. Тогда 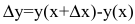
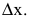
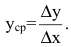
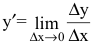
Аналогичным образом могут быть определены предельная выручка, предельный доход, предельная полезность и другие предельные величины. Таким образом, производная выступает как скорость изменения некоторого экономического процесса во времени или относительно исследуемого фактора.
Для исследования экономических процессов часто используется понятие эластичности функции. Эластичностью функции 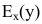
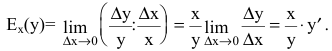
Пример №35
Опытным путем установлены функции спроса 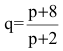
- 1) равновесную цену, при которой спрос и предложение совпадают;
- 2) эластичность спроса и предложения для этой цены;
- 3) изменение дохода при увеличении цены на 5% от равновесной.
Решение:
1) равновесная цена определяется из условия q=s: 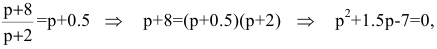
2) найдем эластичности спроса и предложения:
Для равновесной цены p=2 имеем:
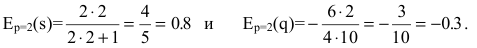
3) при увеличении цены на 5% относительно равновесной спрос уменьшится на 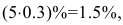
Пример №36
Зависимость между издержками производства у и объемом выпускаемой продукции х выражается функцией 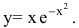
Решение:
1) функция средних издержек (на единицу продукции) выражается отношением 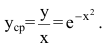
Функция предельных издержек выражается производной
При х=0.5 предельные издержки составят
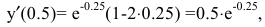
2) эластичность издержек у относительно объема выпускаемой продукции х рассчитывается по формуле:
При 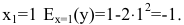
При 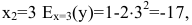
- Заказать решение задач по высшей математике
Уравнение нормали к плоской кривой
Нормалью называется прямая, проходящая через точку касания перпендикулярно касательной. Если касательная в точке 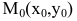
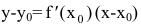
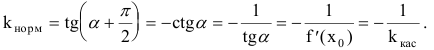
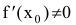
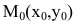
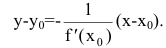
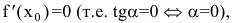
Пример №37
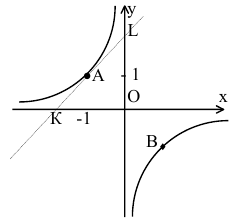
Показать, что для гиперболы ху=-1 площадь треугольника, образованного координатными осями и касательной в точке А(-1,1), равна квадрату полуоси гиперболы.
Решение:
В общем курсе аналитической геометрии давалось каноническое уравнение гиперболы. «Школьная» гипербола ху=а получается из уравнения 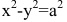
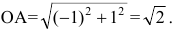
Составим уравнение касательной к гиперболе ху=-1 в вершине А(-1,1). Общее уравнение касательной к кривой y=f(x) в точке 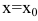
В нашем случае
Искомое уравнение касательной имеет вид:
Найдем точки пересечения касательной с осями координат:
Тогда треугольник, образованный координатными осями и касательной, будет иметь вершины О(0,0), К(-2,0) и L(0,2). Т.к. треугольник прямоугольный, то его площадь равна
2=2. Задача решена.
Производные высших порядков
До сих пор мы рассматривали производную y’=f'(x) от функции y=f(x), называемую производной первого порядка. По производная y’=f'(x) сама является функцией, которая также может иметь производную. Производной второго порядка называется производная от производной первого порядка (у’)’ и обозначается 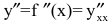
Ранее было установлено, что если точка движется прямолинейно по закону s=s(t) (где s – путь, t – время), то 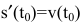
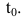
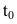
В этом состоит механический смысл второй производной.
Пример №38
Известно, что траекторией брошенного камня является парабола. Найти его скорость и ускорение.
Решение:
Запишем уравнение траектории брошенного камня 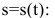
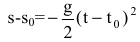
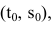
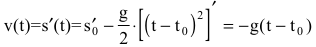
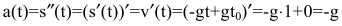
Производная неявной функции
Выше было рассмотрено дифференцирование явных функций, заданных формулой y=f(x), правая часть которых не содержала зависимой переменной. Если же функция y=f(x) задана уравнением F(x,y)=0, не разрешенным относительно зависимой переменной, то говорят, что функция у задана неявно.
Внимание! Не всякое уравнение F(x,y)=0 определяет неявную функцию. Например, уравнение 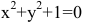
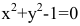
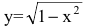
Часто разрешить уравнение F(x,y)=0 относительно переменной затруднительно. В таком случае функцию приходится изучать, пользуясь непосредственно уравнением, определяющим ее. Рассмотрим дифференцирование неявной функции, заданной уравнением F(x,y)=0.
Для нахождения производной функции у, заданной неявно, нужно продифференцировать обе части уравнения, рассматривая у как функцию от х. Затем из полученного уравнения найти производную у’.
Пример №39
Покажите, что функция y=f(x), заданная неявно выражением 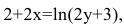
Решение:
Найдем первую производную данной функции. Для этого продифференцируем обе части уравнения 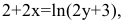
Найдем вторую производную:
Подставим найденные выражения в дифференциальное уравнение:
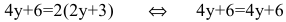
Правило Лопиталя
С помощью производной можно находить многие пределы. Следующее утверждение позволит свести предел отношения двух функций с случае неопределенностей вида 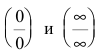
Правило Лопиталя. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если этот предел существует:
Внимание! В правой части формул берется отношение производных, а не производная отношения.
Пример №40
Вычислить предел
Решение:
Имеем неопределенность вида 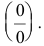
Замечание. Правило Лопиталя можно применять повторно, если вновь приходим к соотношению неопределенностей вида
Пример №41
Вычислить предел
Решение:
Числитель и знаменатель дроби непрерывны, дифференцируемы и стремятся к бесконечности. Следовательно, можно применить правило Лопиталя (в данном примере мы воспользовались им дважды):
Замечание. Другие неопределенности раскрываются по правилу Лопиталя, если их предварительно свести к основному виду 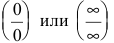
Пример №42
Найти
Решение:
Преобразуя выражение и используя непрерывность показательной функции, получим:
Оптимизация (процесс нахождения экстремума максимума или минимума экономических функций)
В этом параграфе оптимизацию будем понимать как процесс нахождения экстремума (максимума или минимума) экономических функций, т.е. выбор наилучшего варианта из множества возможных. Говорят, что в точке 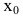
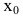
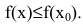
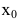
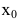
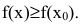
Внимание! Не следует путать понятие локального экстремума функции с ее наибольшим или наименьшим значением (так называемым глобальным максимумом или минимумом). Па одном промежутке функция может иметь несколько экстремумов, причем минимум может оказаться больше максимума подобно тому, как впадина в горах может иметь большую отметку над уровнем моря, чем невысокая вершина. А наибольшее и наименьшее значение непрерывной на отрезке функции может достигаться как в точках экстремума, так и на концах отрезка.
Геометрически в точке экстремума касательная к графику функции либо горизонтальна, либо не существует. Следовательно, непрерывная функция может иметь экстремум лишь в тех точках, где производная функции равна нулю или не существует (необходимое условие экстремума). Точки, в которых выполнено необходимое условие экстремума, называются критическими. (Иногда точки, в которых производная обращается в нуль, называют стационарными.)
Замечание Критическая точка не обязательно является точкой экстремума. Это лишь точка возможного экстремума функции.
Достаточное условие экстремума. Если в критической точке вторая производная положительна, то это точка минимума, а если отрицательна – точка максимума.
Для запоминания этой теоремы предлагаем мнемоническое правило: если плюс – котелок наполняется, если минус – опустошается.
Пример №43
Пусть в краткосрочном плане производственная функция зависит только от численности персонала и имеет вид
где у – выпуск продукции, а n- число работающих. Определить численность персонала, при которой выпуск у достигает максимального значения.
Решение:
Выпуск продукции y=f(n) – функция натурального аргумента. Для решения задачи рассмотрим обобщенную функцию действительного аргумента 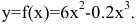
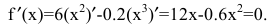
Решая квадратное уравнение, легко находим 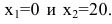
При 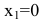
следовательно, в данной точке имеется минимум. Это естественно, т.к. нет выпуска продукции, если нет рабочих. Для второй точки
Поэтому в точке 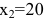
Исследование функции на монотонность
С помощью производной можно найти промежутки возрастания и убывания функции. Функция y=f(x) называется возрастающей (убывающей) на промежутке X, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции:
Возрастающие и убывающие функции называются монотонными.
Достаточное условие монотонности. Если производная дифференцируемой функции положительна (отрицательна) внутри некоторого промежутка X, то она возрастает (убывает) на этом промежутке:
Таким образом, если при переходе через критическую точку производная дифференцируемой функции меняет знак с плюса на минус, то это точка (локального) максимума, а если с минуса на плюс – точка (локального) минимума (достаточное условие экстремума):
Если изменение знака производной не происходит, то экстремума нет.
Пример. Исследовать функцию 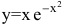
Решение. Область определения функции 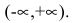
Эти точки разбивают область определения функции на интервалы монотонности. Результаты исследования удобно представить в таблице.
Итак, функция убывает на интервалах 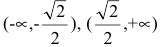
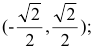
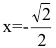
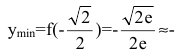
а 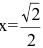
Выпуклость и вогнутость графика функции
Точки перегиба
График дифференцируемой функции y=f(x) называется выпуклым (выпуклым вверх) в точке 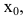
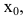
Достаточное условие направления выпуклости. Если вторая производная дважды дифференцируемой функции отрицательна (положительна‘) внутри некоторого промежутка, то функция выпукла (вогнута) на этом промежутке:
Следовательно, если вторая производная дважды дифференцируемой функции при переходе через некоторую точку меняет знак, то это точка перегиба (достаточное условие перегиба):
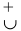
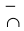
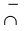
Отсюда вытекает необходимое условие перегиба: вторая производная дважды дифференцируемой функции в точке перегиба равна нулю или не существует.
Замечание. Если критическая точка дифференцируемой функции не является точкой экстремума, то это точка перегиба.
Пример №44
Исследовать функцию 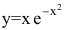
Решение:
Область определения функции 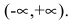
Эти точки разбивают область определения функции на интервалы, в которых сохраняется направление выпуклости или вогнутости. Результаты удобно представить в таблице.
Кривая, изображающая график функции, выпукла на интервалах 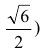
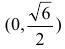
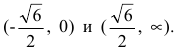
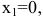
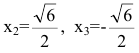
- Исследование функций с помощью производных
- Формула Тейлора и ее применение
- Интегрирование рациональных дробей
- Интегрирование тригонометрических функций
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы
- Непрерывность функций и точки разрыва
- Точки разрыва и их классификация



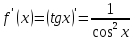


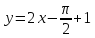












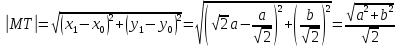



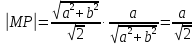


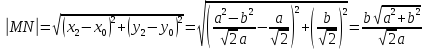


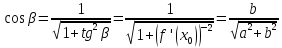

















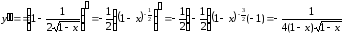

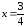

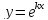

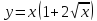



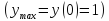


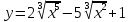
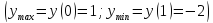
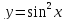


























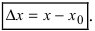
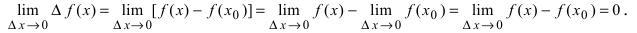
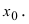
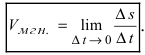
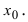
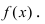
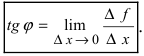
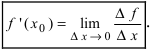
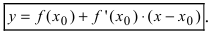
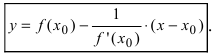
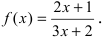
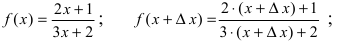
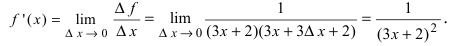
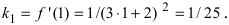
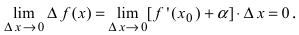
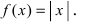
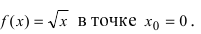
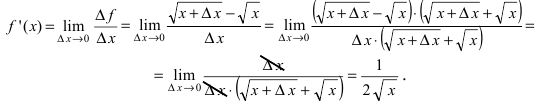
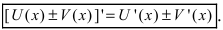
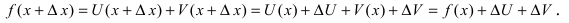
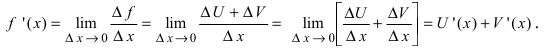
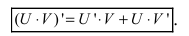
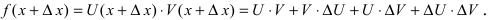
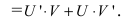
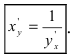
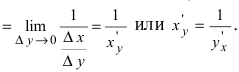
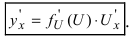
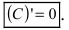
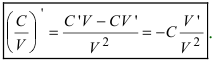
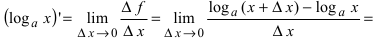
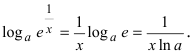
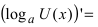
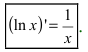
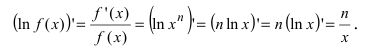
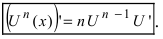
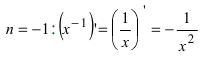
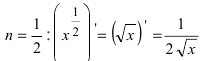 ;
;