Как найти угловой коэффициент прямой калькулятор

Как найти угловой коэффициент прямой калькулятор

bold{mathrm{Basic}} bold{alphabetagamma} bold{mathrm{ABGamma}} bold{sincos} bold{gedivrightarrow} bold{overline{x}spacemathbb{C}forall} bold{sumspaceintspaceproduct} bold{begin{pmatrix}square&square\square&squareend{pmatrix}} bold{H_{2}O}
square^{2} x^{square} sqrt{square} nthroot[msquare]{square} frac{msquare}{msquare} log_{msquare} pi theta infty int frac{d}{dx}
ge le cdot div x^{circ} (square) |square| (f:circ:g) f(x) ln e^{square}
left(squareright)^{‘} frac{partial}{partial x} int_{msquare}^{msquare} lim sum sin cos tan cot csc sec
alpha beta gamma delta zeta eta theta iota kappa lambda mu
nu xi pi rho sigma tau upsilon phi chi psi omega
A B Gamma Delta E Z H Theta K Lambda M
N Xi Pi P Sigma T Upsilon Phi X Psi Omega
sin cos tan cot sec csc sinh cosh tanh coth sech
arcsin arccos arctan arccot arcsec arccsc arcsinh arccosh arctanh arccoth arcsech
begin{cases}square\squareend{cases} begin{cases}square\square\squareend{cases} = ne div cdot times < > le ge
(square) [square] ▭:longdivision{▭} times twostack{▭}{▭} + twostack{▭}{▭} – twostack{▭}{▭} square! x^{circ} rightarrow lfloorsquarerfloor lceilsquarerceil
overline{square} vec{square} in forall notin exist mathbb{R} mathbb{C} mathbb{N} mathbb{Z} emptyset
vee wedge neg oplus cap cup square^{c} subset subsete superset supersete
int intint intintint int_{square}^{square} int_{square}^{square}int_{square}^{square} int_{square}^{square}int_{square}^{square}int_{square}^{square} sum prod
lim lim _{xto infty } lim _{xto 0+} lim _{xto 0-} frac{d}{dx} frac{d^2}{dx^2} left(squareright)^{‘} left(squareright)^{”} frac{partial}{partial x}
(2times2) (2times3) (3times3) (3times2) (4times2) (4times3) (4times4) (3times4) (2times4) (5times5)
(1times2) (1times3) (1times4) (1times5) (1times6) (2times1) (3times1) (4times1) (5times1) (6times1) (7times1)
mathrm{Радианы} mathrm{Степени} square! ( ) % mathrm{очистить}
arcsin sin sqrt{square} 7 8 9 div
arccos cos ln 4 5 6 times
arctan tan log 1 2 3 –
pi e x^{square} 0 . bold{=} +

Подпишитесь, чтобы подтвердить свой ответ

Подписаться

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

  • наклон:3x+3y-6=0

  • наклон:f(x)=2x-1

  • наклон:(-1,:1),:(-2,:-3)

  • наклон:(-1,:-2),:(1,:2)

  • наклон:(0,:-4),:(-1,:-7)

  • наклон:(-4,:2),:(0,:3)

  • Показать больше

Описание

Поэтапное вычисление углового коэффициента прямой

slope-calculator

functions-line-calculator

ru

Блог-сообщения, имеющие отношение к Symbolab

  • Slope, Distance and More

    Ski Vacation? Nope, this is serious stuff; it’s about finding the slope of a line, finding the equation of a line…

    Read More

    • Введите Задачу

    Сохранить в блокнот!

    Войти

    Источник

    Угловой коэффициент прямой —  коэффициент, характеризующий степень наклона прямой. Коэффициент k в уравнении y=kx+b прямой на координатной плоскости, численно равен тангенсу угла (составляющего наименьший поворот от оси Ox к оси Оу) между положительным направлением оси абсцисс и данной прямой линией

    Калькулятор нахождения углового коэффициента

    Онлайн калькулятор нахождения углового коэффициента прямой. Простое нахождение значения углового коэффициента онлайн

    slope_k

    • Прямая линия возрастающая, если она идет вверх с лева на право. Угловой коэффициент положителен, k>0.
    • Прямая линия убывает, если она идет вниз слева направо. Угловой коэффициент отрицательный, k<0.
    • Если прямая линия горизонтальна, то угловой коэффициент равен 0
    • Угловой коэффициент не существует (иногда формально говорят «обращается в бесконечность») для прямых, параллельных оси Oy.

    Формула углового коэффициента прямой

    k = (Y2 — Y1) / (X2 — X1)
    (или)
    k = (Y1 — Y2) / (X1 — X2)

    где,

    • k = Угловой коэффициент прямой,
    • X1, X2 = X координаты,
    • Y1, Y2 = Y координаты.

    Пример нахождения углового коэффициента:

    Предположим, прямая проходит через две точки: P = (1, 2) и Q = (13, 8). Разделив разницу y-координат на разницу x-координат, можно получить угловой коэффициент прямой:

    • k = (Y2 — Y1) / (X2 — X1)
    • = (8-2)/(13-1)
    • = 6/12
    • = 1/2

    Поскольку угловой коэффициент положительный, направление линии возрастающее. Поскольку |k|<1, наклон прямой не очень крутой (наклон <45°).

    В качестве другого примера рассмотрим линию, которая проходит через точки (4, 15) и (3, 21). Угловой коэффициент равен

    • k = (Y2 — Y1) / (X2 — X1)
    • = (21-15)/(3-4)
    • = 6/-1
    • = —6

    Поскольку угловой коэффициент является отрицательным, то прямая уменьшается. Поскольку |k|>1, наклон прямой достаточно крутой (уклон >45°).

    Синонимы: наклон, тангенс, slope of the line, slope



    людей нашли эту статью полезной. А Вы?

    Источник

    На этой странице вы найдете два калькулятора, которые строят уравнение прямой по координатам двух точек, принадлежащих этой прямой.

    Первый калькулятор находит уравнение прямой с угловым коэффициентом, то есть уравнение в форме y=ax+b. Также он строит график и отдельно выводит угловой коэффициент и значение y в месте пересечения прямой с осью ординат.

    Второй калькулятор находит параметрические уравнения прямой, то есть систему уравнений вида x=at+x_0\y=bt+y_0. Он также строит график и отдельно выводит направляющий вектор.

    Формулы расчета можно найти под калькуляторами.

    PLANETCALC, Уравнение прямой с угловым коэффициентом по двум точкам

    Уравнение прямой с угловым коэффициентом по двум точкам

    Первая точка

    Вторая точка

    Значение y в точке пересечения с осью ординат

    Точность вычисления

    Знаков после запятой: 2

    PLANETCALC, Параметрическое уравнение прямой

    Параметрическое уравнение прямой

    Первая точка

    Вторая точка

    Параметрическое уравнение для x

    Параметрическое уравнение для y

    Точность вычисления

    Знаков после запятой: 2

    Уравнение прямой с угловым коэффициентом

    Найдем уравнение прямой с угловым коэффициентом по двум известным точкам (x_0, y_0) и (x_1, y_1).

    Нам надо найти угловой коэффициент a и y координату точки пересечения прямой с осью ординат b.

    Мы можем составить следующие уравнения для двух точек относительно a и b
    y_0=ax_0+b\y_1=ax_1+b

    Вычитаем первое из второго
    y_1 - y_0=ax_1 - ax_0+b - b\y_1 - y_0=ax_1 - ax_0\y_1 - y_0=a(x_1 -x_0)

    Откуда
    a=frac{y_1 - y_0}{x_1 -x_0}

    b можно найти как
    b=y-ax
    Таким образом, как только мы нашли а, для расчета b достаточно только подставить значения x_0, y_0, a или x_1, y_1, a в выражение выше.

    Параметрическое уравнение прямой

    Найдем параметрическое уравнение прямой по двум известным точкам (x_0, y_0) и (x_1, y_1).

    Нам надо найти компоненты направляющего вектора.
    D=begin{vmatrix}d_1\d_2end{vmatrix}=begin{vmatrix}x_1-x_0\y_1-y_0end{vmatrix}
    Этот вектор описывает величину и направление воображаемого движения по прямой от первой до второй точки.

    Имея направляющий вектор, легко записать параметрические уравнения прямой
    x=d_1t+x_0\y=d_2t+y_0
    Обратите внимание, что если t = 0, то x = x_0, y = y_0 и если t = 1, то x = x_1, y = y_1

    Источник

    Угловой коэффициент прямой

    Что такое угловой коэффициент прямой? Если представить прямую, проходящую через две точки в прямоугольной системе координат (ОX, OY), то тангенс угла, образованного осью ОX и прямой – угловой коэффициент заданной прямой.

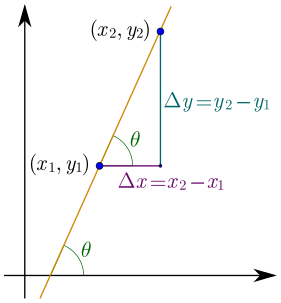
    Например, угловой коэффициент прямой (а), проходящей через точки А (X1, Y1) и В (X2, Y2) будет равняться тангенсу (tg) треугольника, гипотенузой которого будет прямая (а) или отрезок АВ.

    Таким образом можно узнать угол наклона прямой (а) к оси абсцисс ОХ. Угол определяется между осью ОХ и прямой (а) в направлении против часовой стрелки. То есть, если коэффициент наклона больше нуля (k›0), то угол наклона тупой. Если коэффициент наклона меньше нуля (k‹0), то угол наклона острый. Если коэффициент (k) равен нулю, то прямая (а) расположена параллельно оси ОХ. Если коэффициент (k) не существует – определяется в бесконечность – значит, прямая (а) расположена в системе координат параллельно оси OY.

    Рассчитать угловой коэффициент можно с помощью онлайн калькулятора. Стоит всего лишь подставить данные точек в системе координат, через которые проходит заданная прямая, и калькулятор рассчитает угловой коэффициент. Подставив значения в уравнение прямой с угловым коэффициентом, можно определить – принадлежит ли некая произвольно заданная точка в системе координат данной прямой.

    ×

    Пожалуйста напишите с чем связна такая низкая оценка:

    ×

    Для установки калькулятора на iPhone – просто добавьте страницу
    «На главный экран»

    Для установки калькулятора на Android – просто добавьте страницу
    «На главный экран»

    Источник

    Угловой коэффициент прямой

    Точка, прямая, плоскость

    Угловой коэффициент (обозн. k) относится к величинам, характеризующим положение прямой на плоскости.

    Угловой коэффициент определяет угол наклона прямой к оси Ох. Это — угол, на который следует повернуть ось абсцисс, чтобы она совпала либо оказалась параллельна прямой. Угол наклона находится в пределах от 0 до 180, отсчитывается от оси Ох к прямой против часовой стрелки.

    Тангенс угла наклона (a) прямой к оси Ох будет угловым коэффициентом, т.е. k = tg a.

    Угловой коэффициент характеризует направление прямой:

    • если k = 0, прямая параллельна оси Ох;
    • если k › 0, угол наклона прямой к оси Ох острый, вычисляем по формуле a = arctg k;
    • если k ‹ 0, угол наклона тупой, вычисляем: a = π — arctg |k|;
    • углового коэффициента нет у прямой, расположенной перпендикулярно к оси Ох.

    Если рассматривать прямую на координатной плоскости, то ее уравнение будет иметь вид: y = kx + b, где k — угловой коэффициент прямой, b — действительное число. В уравнении прямой такого вида число, стоящее перед х и будет угловым коэффициентом.

    Если даны координаты 2-х точек, через которые проходит прямая, можно вычислить угловой коэффициент прямой, воспользовавшись следующим уравнением: (х — х1) / (х2 — х1) = (у — у1) / (у2 — у1), где (х1;у1), (х2;у2) — координаты точек.
    Решаем уравнение, после чего приводим его к виду y = kx + b и находим угловой коэффициент k.

    Калькулятор поможет вам быстро вычислить угловой коэффициент. Для этого:

    • в окна калькулятора вводим данные точек (X1,Y1) (X2,Y2), через которые лежит прямая;
    • жмем кнопку Рассчитать. Получаем величину углового коэффициента.

    Источник

    Добавить комментарий