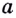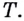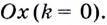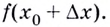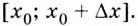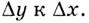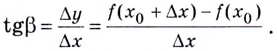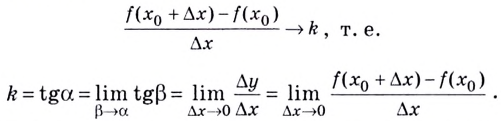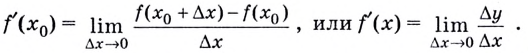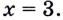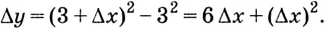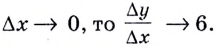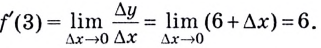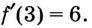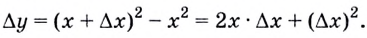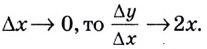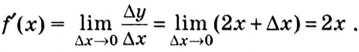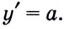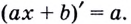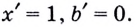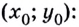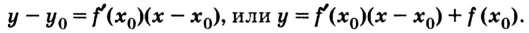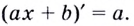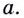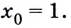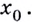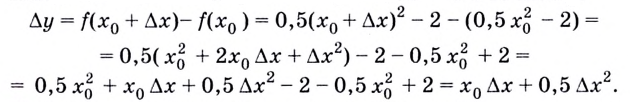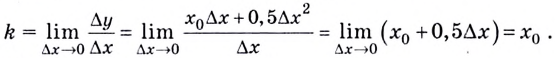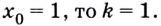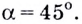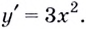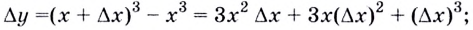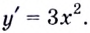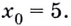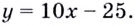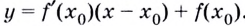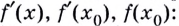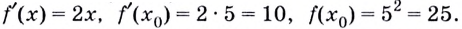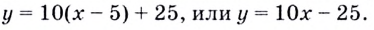Как найти угловой коэффициент секущей графика

Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной

Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.

Определения и понятия

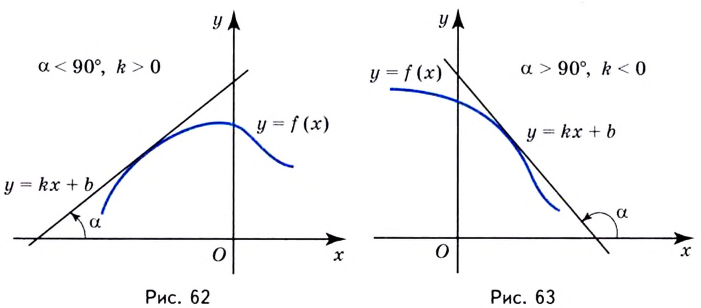
Угол наклона прямой y = k x + b называется угол α , который отсчитывается от положительного направления оси о х к прямой y = k x + b в положительном направлении.

На рисунке направление о х обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.

Угловой коэффициент прямой y = k x + b называют числовым коэффициентом k .

Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k = t g α .

• Угол наклона прямой равняется 0 только при параллельности о х и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0 . Значит, вид уравнения будет y = b .
• Если угол наклона прямой y = k x + b острый, тогда выполняются условия 0 α π 2 или 0 ° α 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α > 0 , причем имеется возрастание графика.
• Если α = π 2 , тогда расположение прямой перпендикулярно о х . Равенство задается при помощи равенства x = c со значением с , являющимся действительным числом.
• Если угол наклона прямой y = k x + b тупой, то соответствует условиям π 2 α π или 90 ° α 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

Определение 3

Секущей называют прямую, которая проходит через 2 точки функции f ( x ) . Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.

По рисунку видно, что А В является секущей, а f ( x ) – черная кривая, α – красная дуга, означающая угол наклона секущей.

Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника А В С можно найти по отношению противолежащего катета к прилежащему.

Получаем формулу для нахождения секущей вида:

k = t g α = B C A C = f ( x B ) – f x A x B – x A , где абсциссами точек А и В являются значения x A , x B , а f ( x A ) , f ( x B ) – это значения функции в этих точках.

Очевидно, что угловой коэффициент секущей определен при помощи равенства k = f ( x B ) – f ( x A ) x B – x A или k = f ( x A ) – f ( x B ) x A – x B , причем уравнение необходимо записать как y = f ( x B ) – f ( x A ) x B – x A · x – x A + f ( x A ) или
y = f ( x A ) – f ( x B ) x A – x B · x – x B + f ( x B ) .

Секущая делит график визуально на 3 части: слева от точки А , от А до В , справа от В . На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.

По определению видно, что прямая и ее секущая в данном случае совпадают.

Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у = 0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.

Касательная к графику функции f ( x ) в точке x 0 ; f ( x 0 ) называется прямая, проходящая через заданную точку x 0 ; f ( x 0 ) , с наличием отрезка, который имеет множество значений х , близких к x 0 .

Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y = x + 1 , считается касательной к y = 2 x в точке с координатами ( 1 ; 2 ) . Для наглядности, необходимо рассмотреть графики с приближенными к ( 1 ; 2 ) значениями. Функция y = 2 x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.

Очевидно, что y = 2 x сливается с прямой у = х + 1 .

Для определения касательной следует рассмотреть поведение касательной А В при бесконечном приближении точки В к точке А . Для наглядности приведем рисунок.

Секущая А В , обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной α x .

Касательной к графику функции y = f ( x ) в точке А считается предельное положение секущей А В при В стремящейся к А , то есть B → A .

Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.

Геометрический смысл производной функции в точке

Перейдем к рассмотрению секущей А В для функции f ( x ) , где А и В с координатами x 0 , f ( x 0 ) и x 0 + ∆ x , f ( x 0 + ∆ x ) , а ∆ x обозначаем как приращение аргумента. Теперь функция примет вид ∆ y = ∆ f ( x ) = f ( x 0 + ∆ x ) – f ( ∆ x ) . Для наглядности приведем в пример рисунок.

Рассмотрим полученный прямоугольный треугольник А В С . Используем определение тангенса для решения, то есть получим отношение ∆ y ∆ x = t g α . Из определения касательной следует, что lim ∆ x → 0 ∆ y ∆ x = t g α x . По правилу производной в точке имеем, что производную f ( x ) в точке x 0 называют пределом отношений приращения функции к приращению аргумента, где ∆ x → 0 , тогда обозначим как f ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x .

Отсюда следует, что f ‘ ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x , где k x обозначают в качестве углового коэффициента касательной.

То есть получаем, что f ’ ( x ) может существовать в точке x 0 причем как и касательная к заданному графику функции в точке касания равной x 0 , f 0 ( x 0 ) , где значение углового коэффициента касательной в точке равняется производной в точке x 0 . Тогда получаем, что k x = f ‘ ( x 0 ) .

Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.

Уравнение касательной прямой

Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x 0 при пересечении.

Уравнение касательной к графику функции y = f ( x ) в точке x 0 , f 0 ( x 0 ) принимает вид y = f ‘ ( x 0 ) · x – x 0 + f ( x 0 ) .

Имеется в виду, что конечным значением производной f ‘ ( x 0 ) можно определить положение касательной, то есть вертикально при условии lim x → x 0 + 0 f ‘ ( x ) = ∞ и lim x → x 0 – 0 f ‘ ( x ) = ∞ или отсутствие вовсе при условии lim x → x 0 + 0 f ‘ ( x ) ≠ lim x → x 0 – 0 f ‘ ( x ) .

Расположение касательной зависит от значения ее углового коэффициента k x = f ‘ ( x 0 ) . При параллельности к оси о х получаем, что k k = 0 , при параллельности к о у – k x = ∞ , причем вид уравнения касательной x = x 0 возрастает при k x > 0 , убывает при k x 0 .

Произвести составление уравнения касательной к графику функции y = e x + 1 + x 3 3 – 6 – 3 3 x – 17 – 3 3 в точке с координатами ( 1 ; 3 ) с определением угла наклона.

Решение

По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, ( 1 ; 3 ) является точкой касания, тогда x 0 = – 1 , f ( x 0 ) = – 3 .

Необходимо найти производную в точке со значением – 1 . Получаем, что

y ‘ = e x + 1 + x 3 3 – 6 – 3 3 x – 17 – 3 3 ‘ = = e x + 1 ‘ + x 3 3 ‘ – 6 – 3 3 x ‘ – 17 – 3 3 ‘ = e x + 1 + x 2 – 6 – 3 3 y ‘ ( x 0 ) = y ‘ ( – 1 ) = e – 1 + 1 + – 1 2 – 6 – 3 3 = 3 3

Значение f ’ ( x ) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.

Тогда k x = t g α x = y ‘ ( x 0 ) = 3 3

Отсюда следует, что α x = a r c t g 3 3 = π 6

Ответ: уравнение касательной приобретает вид

y = f ‘ ( x 0 ) · x – x 0 + f ( x 0 ) y = 3 3 ( x + 1 ) – 3 y = 3 3 x – 9 – 3 3

Для наглядности приведем пример в графической иллюстрации.

Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.

Выяснить наличие существования касательной к графику заданной функции
y = 3 · x – 1 5 + 1 в точке с координатами ( 1 ; 1 ) . Составить уравнение и определить угол наклона.

Решение

По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.

Перейдем к нахождению производной

y ‘ = 3 · x – 1 5 + 1 ‘ = 3 · 1 5 · ( x – 1 ) 1 5 – 1 = 3 5 · 1 ( x – 1 ) 4 5

Если x 0 = 1 , тогда f ’ ( x ) не определена, но пределы записываются как lim x → 1 + 0 3 5 · 1 ( x – 1 ) 4 5 = 3 5 · 1 ( + 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ и lim x → 1 – 0 3 5 · 1 ( x – 1 ) 4 5 = 3 5 · 1 ( – 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ , что означает существование вертикальной касательной в точке ( 1 ; 1 ) .

Ответ: уравнение примет вид х = 1 , где угол наклона будет равен π 2 .

Для наглядности изобразим графически.

Найти точки графика функции y = 1 15 x + 2 3 – 4 5 x 2 – 16 5 x – 26 5 + 3 x + 2 , где

1. Касательная не существует;
2. Касательная располагается параллельно о х ;
3. Касательная параллельна прямой y = 8 5 x + 4 .

Решение

Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x ∈ – ∞ ; 2 и [ – 2 ; + ∞ ) . Получаем, что

y = – 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ – ∞ ; – 2 1 15 x 3 – 6 x 2 + 9 x + 12 , x ∈ [ – 2 ; + ∞ )

Необходимо продифференцировать функцию. Имеем, что

y ‘ = – 1 15 x 3 + 18 x 2 + 105 x + 176 ‘ , x ∈ – ∞ ; – 2 1 15 x 3 – 6 x 2 + 9 x + 12 ‘ , x ∈ [ – 2 ; + ∞ ) ⇔ y ‘ = – 1 5 ( x 2 + 12 x + 35 ) , x ∈ – ∞ ; – 2 1 5 x 2 – 4 x + 3 , x ∈ [ – 2 ; + ∞ )

Когда х = – 2 , тогда производная не существует, потому что односторонние пределы не равны в этой точке:

lim x → – 2 – 0 y ‘ ( x ) = lim x → – 2 – 0 – 1 5 ( x 2 + 12 x + 35 = – 1 5 ( – 2 ) 2 + 12 ( – 2 ) + 35 = – 3 lim x → – 2 + 0 y ‘ ( x ) = lim x → – 2 + 0 1 5 ( x 2 – 4 x + 3 ) = 1 5 – 2 2 – 4 – 2 + 3 = 3

Вычисляем значение функции в точке х = – 2 , где получаем, что

1. y ( – 2 ) = 1 15 – 2 + 2 3 – 4 5 ( – 2 ) 2 – 16 5 ( – 2 ) – 26 5 + 3 – 2 + 2 = – 2 , то есть касательная в точке ( – 2 ; – 2 ) не будет существовать.
2. Касательная параллельна о х , когда угловой коэффициент равняется нулю. Тогда k x = t g α x = f ‘ ( x 0 ) . То есть необходимо найти значения таких х , когда производная функции обращает ее в ноль. То есть значения f ’ ( x ) и будут являться точками касания, где касательная является параллельной о х .

Когда x ∈ – ∞ ; – 2 , тогда – 1 5 ( x 2 + 12 x + 35 ) = 0 , а при x ∈ ( – 2 ; + ∞ ) получаем 1 5 ( x 2 – 4 x + 3 ) = 0 .

– 1 5 ( x 2 + 12 x + 35 ) = 0 D = 12 2 – 4 · 35 = 144 – 140 = 4 x 1 = – 12 + 4 2 = – 5 ∈ – ∞ ; – 2 x 2 = – 12 – 4 2 = – 7 ∈ – ∞ ; – 2 1 5 ( x 2 – 4 x + 3 ) = 0 D = 4 2 – 4 · 3 = 4 x 3 = 4 – 4 2 = 1 ∈ – 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ – 2 ; + ∞

Вычисляем соответствующие значения функции

y 1 = y – 5 = 1 15 – 5 + 2 3 – 4 5 – 5 2 – 16 5 – 5 – 26 5 + 3 – 5 + 2 = 8 5 y 2 = y ( – 7 ) = 1 15 – 7 + 2 3 – 4 5 ( – 7 ) 2 – 16 5 – 7 – 26 5 + 3 – 7 + 2 = 4 3 y 3 = y ( 1 ) = 1 15 1 + 2 3 – 4 5 · 1 2 – 16 5 · 1 – 26 5 + 3 1 + 2 = 8 5 y 4 = y ( 3 ) = 1 15 3 + 2 3 – 4 5 · 3 2 – 16 5 · 3 – 26 5 + 3 3 + 2 = 4 3

Отсюда – 5 ; 8 5 , – 4 ; 4 3 , 1 ; 8 5 , 3 ; 4 3 считаются искомыми точками графика функции.

Рассмотрим графическое изображение решения.

Черная линия – график функции, красные точки – точки касания.

1. Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 8 5 . Для этого нужно решить уравнение вида y ‘ ( x ) = 8 5 . Тогда, если x ∈ – ∞ ; – 2 , получаем, что – 1 5 ( x 2 + 12 x + 35 ) = 8 5 , а если x ∈ ( – 2 ; + ∞ ) , тогда 1 5 ( x 2 – 4 x + 3 ) = 8 5 .

Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что

– 1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 – 4 · 43 = – 28 0

Другое уравнение имеет два действительных корня, тогда

1 5 ( x 2 – 4 x + 3 ) = 8 5 x 2 – 4 x – 5 = 0 D = 4 2 – 4 · ( – 5 ) = 36 x 1 = 4 – 36 2 = – 1 ∈ – 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ – 2 ; + ∞

Перейдем к нахождению значений функции. Получаем, что

y 1 = y ( – 1 ) = 1 15 – 1 + 2 3 – 4 5 ( – 1 ) 2 – 16 5 ( – 1 ) – 26 5 + 3 – 1 + 2 = 4 15 y 2 = y ( 5 ) = 1 15 5 + 2 3 – 4 5 · 5 2 – 16 5 · 5 – 26 5 + 3 5 + 2 = 8 3

Точки со значениями – 1 ; 4 15 , 5 ; 8 3 являются точками, в которых касательные параллельны прямой y = 8 5 x + 4 .

Ответ: черная линия – график функции, красная линия – график y = 8 5 x + 4 , синяя линия – касательные в точках – 1 ; 4 15 , 5 ; 8 3 .

Возможно существование бесконечного количества касательных для заданных функций.

Написать уравнения всех имеющихся касательных функции y = 3 cos 3 2 x – π 4 – 1 3 , которые располагаются перпендикулярно прямой y = – 2 x + 1 2 .

Решение

Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется – 1 , то есть записывается как k x · k ⊥ = – 1 . Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k ⊥ = – 2 , тогда k x = – 1 k ⊥ = – 1 – 2 = 1 2 .

Теперь необходимо найти координаты точек касания. Нужно найти х , после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x 0 получаем, что k x = y ‘ ( x 0 ) . Из данного равенства найдем значения х для точек касания.

y ‘ ( x 0 ) = 3 cos 3 2 x 0 – π 4 – 1 3 ‘ = 3 · – sin 3 2 x 0 – π 4 · 3 2 x 0 – π 4 ‘ = = – 3 · sin 3 2 x 0 – π 4 · 3 2 = – 9 2 · sin 3 2 x 0 – π 4 ⇒ k x = y ‘ ( x 0 ) ⇔ – 9 2 · sin 3 2 x 0 – π 4 = 1 2 ⇒ sin 3 2 x 0 – π 4 = – 1 9

Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.

3 2 x 0 – π 4 = a r c sin – 1 9 + 2 πk или 3 2 x 0 – π 4 = π – a r c sin – 1 9 + 2 πk

3 2 x 0 – π 4 = – a r c sin 1 9 + 2 πk или 3 2 x 0 – π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 – a r c sin 1 9 + 2 πk или x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z – множество целых чисел.

Найдены х точек касания. Теперь необходимо перейти к поиску значений у :

y 0 = 3 cos 3 2 x 0 – π 4 – 1 3

y 0 = 3 · 1 – sin 2 3 2 x 0 – π 4 – 1 3 или y 0 = 3 · – 1 – sin 2 3 2 x 0 – π 4 – 1 3

y 0 = 3 · 1 – – 1 9 2 – 1 3 или y 0 = 3 · – 1 – – 1 9 2 – 1 3

y 0 = 4 5 – 1 3 или y 0 = – 4 5 + 1 3

Отсюда получаем, что 2 3 π 4 – a r c sin 1 9 + 2 πk ; 4 5 – 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; – 4 5 + 1 3 являются точками касания.

Ответ: необходимы уравнения запишутся как

y = 1 2 x – 2 3 π 4 – a r c sin 1 9 + 2 πk + 4 5 – 1 3 , y = 1 2 x – 2 3 5 π 4 + a r c sin 1 9 + 2 πk – 4 5 + 1 3 , k ∈ Z

Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.

Рисунок показывает, что расположение функции идет на промежутке [ – 10 ; 10 ] , где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y = – 2 x + 1 2 . Красные точки – это точки касания.

Касательная к окружности, эллипсу, гиперболе, параболе

Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.

Касательная к окружности

Для задания окружности с центром в точке x c e n t e r ; y c e n t e r и радиусом R применяется формула x – x c e n t e r 2 + y – y c e n t e r 2 = R 2 .

Данное равенство может быть записано как объединение двух функций:

y = R 2 – x – x c e n t e r 2 + y c e n t e r y = – R 2 – x – x c e n t e r 2 + y c e n t e r

Первая функция располагается вверху, а вторая внизу, как показано на рисунке.

Для составления уравнения окружности в точке x 0 ; y 0 , которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y = R 2 – x – x c e n t e r 2 + y c e n t e r или y = – R 2 – x – x c e n t e r 2 + y c e n t e r в указанной точке.

Когда в точках x c e n t e r ; y c e n t e r + R и x c e n t e r ; y c e n t e r – R касательные могут быть заданы уравнениями y = y c e n t e r + R и y = y c e n t e r – R , а в точках x c e n t e r + R ; y c e n t e r и
x c e n t e r – R ; y c e n t e r будут являться параллельными о у , тогда получим уравнения вида x = x c e n t e r + R и x = x c e n t e r – R .

Касательная к эллипсу

Когда эллипс имеет центр в точке x c e n t e r ; y c e n t e r с полуосями a и b , тогда он может быть задан при помощи уравнения x – x c e n t e r 2 a 2 + y – y c e n t e r 2 b 2 = 1 .

Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что

y = b a · a 2 – ( x – x c e n t e r ) 2 + y c e n t e r y = – b a · a 2 – ( x – x c e n t e r ) 2 + y c e n t e r

Если касательные располагаются на вершинах эллипса, тогда они параллельны о х или о у . Ниже для наглядности рассмотрим рисунок.

Написать уравнение касательной к эллипсу x – 3 2 4 + y – 5 2 25 = 1 в точках со значениями x равного х = 2 .

Решение

Необходимо найти точки касания, которые соответствуют значению х = 2 . Производим подстановку в имеющееся уравнение эллипса и получаем, что

x – 3 2 4 x = 2 + y – 5 2 25 = 1 1 4 + y – 5 2 25 = 1 ⇒ y – 5 2 = 3 4 · 25 ⇒ y = ± 5 3 2 + 5

Тогда 2 ; 5 3 2 + 5 и 2 ; – 5 3 2 + 5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.

Перейдем к нахождению и разрешению уравнения эллипса относительно y . Получим, что

x – 3 2 4 + y – 5 2 25 = 1 y – 5 2 25 = 1 – x – 3 2 4 ( y – 5 ) 2 = 25 · 1 – x – 3 2 4 y – 5 = ± 5 · 1 – x – 3 2 4 y = 5 ± 5 2 4 – x – 3 2

Очевидно, что верхний полуэллипс задается с помощью функции вида y = 5 + 5 2 4 – x – 3 2 , а нижний y = 5 – 5 2 4 – x – 3 2 .

Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2 ; 5 3 2 + 5 будет иметь вид

y ‘ = 5 + 5 2 4 – x – 3 2 ‘ = 5 2 · 1 2 4 – ( x – 3 ) 2 · 4 – ( x – 3 ) 2 ‘ = = – 5 2 · x – 3 4 – ( x – 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = – 5 2 · 2 – 3 4 – ( 2 – 3 ) 2 = 5 2 3 ⇒ y = y ‘ ( x 0 ) · x – x 0 + y 0 ⇔ y = 5 2 3 ( x – 2 ) + 5 3 2 + 5

Получаем, что уравнение второй касательной со значением в точке
2 ; – 5 3 2 + 5 принимает вид

y ‘ = 5 – 5 2 4 – ( x – 3 ) 2 ‘ = – 5 2 · 1 2 4 – ( x – 3 ) 2 · 4 – ( x – 3 ) 2 ‘ = = 5 2 · x – 3 4 – ( x – 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = 5 2 · 2 – 3 4 – ( 2 – 3 ) 2 = – 5 2 3 ⇒ y = y ‘ ( x 0 ) · x – x 0 + y 0 ⇔ y = – 5 2 3 ( x – 2 ) – 5 3 2 + 5

Графически касательные обозначаются так:

Касательная к гиперболе

Когда гипербола имеет центр в точке x c e n t e r ; y c e n t e r и вершины x c e n t e r + α ; y c e n t e r и x c e n t e r – α ; y c e n t e r , имеет место задание неравенства x – x c e n t e r 2 α 2 – y – y c e n t e r 2 b 2 = 1 , если с вершинами x c e n t e r ; y c e n t e r + b и x c e n t e r ; y c e n t e r – b , тогда задается при помощи неравенства x – x c e n t e r 2 α 2 – y – y c e n t e r 2 b 2 = – 1 .

Гипербола может быть представлена в виде двух объединенных функций вида

y = b a · ( x – x c e n t e r ) 2 – a 2 + y c e n t e r y = – b a · ( x – x c e n t e r ) 2 – a 2 + y c e n t e r или y = b a · ( x – x c e n t e r ) 2 + a 2 + y c e n t e r y = – b a · ( x – x c e n t e r ) 2 + a 2 + y c e n t e r

В первом случае имеем, что касательные параллельны о у , а во втором параллельны о х .

Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.

Составить уравнение касательной к гиперболе x – 3 2 4 – y + 3 2 9 = 1 в точке 7 ; – 3 3 – 3 .

Решение

Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что

x – 3 2 4 – y + 3 2 9 = 1 ⇒ y + 3 2 9 = x – 3 2 4 – 1 ⇒ y + 3 2 = 9 · x – 3 2 4 – 1 ⇒ y + 3 = 3 2 · x – 3 2 – 4 и л и y + 3 = – 3 2 · x – 3 2 – 4 ⇒ y = 3 2 · x – 3 2 – 4 – 3 y = – 3 2 · x – 3 2 – 4 – 3

Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7 ; – 3 3 – 3 .

Очевидно, что для проверки первой функции необходимо y ( 7 ) = 3 2 · ( 7 – 3 ) 2 – 4 – 3 = 3 3 – 3 ≠ – 3 3 – 3 , тогда точка графику не принадлежит, так как равенство не выполняется.

Для второй функции имеем, что y ( 7 ) = – 3 2 · ( 7 – 3 ) 2 – 4 – 3 = – 3 3 – 3 ≠ – 3 3 – 3 , значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.

y ‘ = – 3 2 · ( x – 3 ) 2 – 4 – 3 ‘ = – 3 2 · x – 3 ( x – 3 ) 2 – 4 ⇒ k x = y ‘ ( x 0 ) = – 3 2 · x 0 – 3 x 0 – 3 2 – 4 x 0 = 7 = – 3 2 · 7 – 3 7 – 3 2 – 4 = – 3

Ответ: уравнение касательной можно представить как

y = – 3 · x – 7 – 3 3 – 3 = – 3 · x + 4 3 – 3

Наглядно изображается так:

Касательная к параболе

Чтобы составить уравнение касательной к параболе y = a x 2 + b x + c в точке x 0 , y ( x 0 ) , необходимо использовать стандартный алгоритм, тогда уравнение примет вид y = y ‘ ( x 0 ) · x – x 0 + y ( x 0 ) . Такая касательная в вершине параллельна о х .

Следует задать параболу x = a y 2 + b y + c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у . Получаем, что

x = a y 2 + b y + c ⇔ a y 2 + b y + c – x = 0 D = b 2 – 4 a ( c – x ) y = – b + b 2 – 4 a ( c – x ) 2 a y = – b – b 2 – 4 a ( c – x ) 2 a

Графически изобразим как:

Для выяснения принадлежности точки x 0 , y ( x 0 ) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна о у относительно параболы.

Написать уравнение касательной к графику x – 2 y 2 – 5 y + 3 , когда имеем угол наклона касательной 150 ° .

Решение

Начинаем решение с представления параболы в качестве двух функций. Получим, что

– 2 y 2 – 5 y + 3 – x = 0 D = ( – 5 ) 2 – 4 · ( – 2 ) · ( 3 – x ) = 49 – 8 x y = 5 + 49 – 8 x – 4 y = 5 – 49 – 8 x – 4

Значение углового коэффициента равняется значению производной в точке x 0 этой функции и равняется тангенсу угла наклона.

k x = y ‘ ( x 0 ) = t g α x = t g 150 ° = – 1 3

Отсюда определим значение х для точек касания.

Первая функция запишется как

y ‘ = 5 + 49 – 8 x – 4 ‘ = 1 49 – 8 x ⇒ y ‘ ( x 0 ) = 1 49 – 8 x 0 = – 1 3 ⇔ 49 – 8 x 0 = – 3

Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150 ° для такой функции не существует.

Вторая функция запишется как

y ‘ = 5 – 49 – 8 x – 4 ‘ = – 1 49 – 8 x ⇒ y ‘ ( x 0 ) = – 1 49 – 8 x 0 = – 1 3 ⇔ 49 – 8 x 0 = – 3 x 0 = 23 4 ⇒ y ( x 0 ) = 5 – 49 – 8 · 23 4 – 4 = – 5 + 3 4

Имеем, что точки касания – 23 4 ; – 5 + 3 4 .

Ответ: уравнение касательной принимает вид

Угловой коэффициент.

Угловой коэффициент— коэффициент k в уравнении прямой на плоскости y = kx + b. Он численно равняется тангенсу угла между выбранной прямой и осью 0х. Этот угол отсчитывается от положительного направления оси 0х до прямой против хода часовой стрелки и располагается и пределах от 0 до 180 градусов.

Для обозначения углового коэффициента употребляют латинский символ k. И, основываясь на определении получаем:

Когда прямая параллельна оси 0х или совпадает с ней, то угол ее наклона расценивают, как равный нулю.

Когда прямая параллельна оси 0у, то угловой коэффициент отсутствует и принято указывать, что угловой коэффициент обращается в бесконечность.

Положительный угловой коэффициент прямой свидетельствует о росте графика функции, отрицательный угловой коэффициент – об убывании.

При этом большим значениям углового коэффициента k будет соответствовать более крутая прямая, а меньшим – более пологая.

Угловой коэффициент прямой так же есть возможность вычислить, когда установлены координаты двух произвольных точек прямой:

Тогда, в образовавшемся прямоугольном треугольнике M₁РM₂ вычисляем тангенс:

Касательная к графику функции, как составить уравнение, свойства, угловой коэффициент касательной проведенной к графику функции, формула, примеры решения

На экзаменах по дисциплинам с физико-математическим уклоном или при расчетах встречается тип задач о касательной к графику функции.

Однако следует разобраться в основных терминах и соотношениях.

Специалисты рекомендуют пользоваться специальным алгоритмом, позволяющим правильно находить точку касания прямой с какой-либо фигурой.

Общие сведения

Касательной называется прямая, имеющая с фигурой или графиком заданной функции одну общую точку. Однако иногда она проходит через 2 точки. В этом случае ее называют секущей. Прямая задается следующим уравнением: y = kx + b. Значение «k» — это угловой коэффициент.

Для решения задач следует разобрать основные понятия, определения, формулы и свойства касательной.

Кроме того, очень важно понять ее геометрический смысл, поскольку без него будет сложно разобраться в более сложных дисциплинах с физико-математическим уклоном.

Определения и понятия

У касательной есть определенный параметр — угол наклона (а).

Его необходимо отсчитывать от оси абсцисс (только положительное направление) к прямой, заданной графиком y = kx + b.

От него зависит ее расположение.

Коэффициент «к» равен значению тангенса угла наклона, т. е. tg(a).

Математики сделали некоторые выводы, которые основываются на значении углового коэффициента:

В первом, втором и третьем случаях коэффициент является положительным, а в последнем — отрицательным. Эти факты следует учитывать при решении задач. Касательная прямая может являться и секущей, т. е. соприкасаться с графиком функции сразу в двух и более точках. Следует отметить, что при параллельности прямой оси ОХ (y = b), она может пересекать функцию бесконечное число раз.

Существует еще одно определение: касательной к функции вида y = f(x) в точке (х0, f(x0)) является прямая, которая проходит через эту точку с тем условием, что отрезок имеет множество значений, близких к ней (х -> x0).

Геометрический смысл

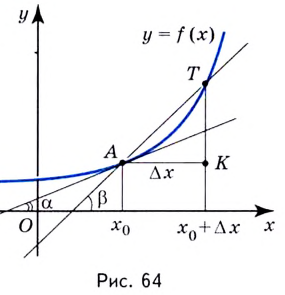
Пусть дана некоторая функция y = f(x) и секущая АВ (рис. 1). Координаты последней в точках А и В следующие: А(х0;f(x0)) и В(х0+zx;f(x0+zx)). Величина «zx» — приращение аргумента по х, которое показано стрелками. Если подставить координаты в функцию, то она имеет такой вид: zy = zf(x) = f(x0+zx) — f(zx).

Рисунок 1. Геометрический смысл.

Соотношение, которое было получено выше, называется производной. Если к графику в точке проведена секущая или касательная, то тангенс угла будет равен самой производной заданной функции в точке с координатой х0.

Из этого определения можно сделать вывод о существовании производной. Если значение последней равно 0, то, следовательно, не существует общих точек с заданной фигурой.

Касательные к фигурам и графикам

При решении задач следует обратить внимание на частные случаи. Нужно произвести расчеты уравнения прямой или найти точки соприкосновения с окружностью, эллипсом, гиперболой или параболой. Очень распространенная задача встречается также в механике о ременной передаче.

Частные случаи позволят найти оптимальное решение и метод расчета, поскольку экономия времени является важным элементом при научных исследованиях, написании контрольных работ и сдаче экзаменов. Важный этап — идентификация типа задачи. Касательная к вышеперечисленным фигурам — основной тип заданий, но существуют и более сложные функции.

Например, сложно составить уравнение прямой, которая имеет точки касания с какой-либо сложной функцией.

В некоторых случаях необходимо перед выполнением расчетов ее упростить, т. е. привести подобные слагаемые, раскрыть скобки или воспользоваться другими приемами для упрощения выражения.

Одна и несколько окружностей

Радиус, который проводится через точку касания, составляет с касательной прямой угол (перпендикулярен). Перпендикуляр к касательной, проходящий через точку касания, является радиусом или диаметром заданного круга. Из этого следует, что радиус является нормалью по отношению к прямой. Секущая — прямая, которая проходит через график или фигуру, но имеет от двух и более точек пересечения.

Формула окружности с центром в точке О (xc;yc) и радиусом R имеет следующий вид: sqr(х-хc) + sqr(y-yc) = R^2.

Для решения следует выразить значение у, но при этом нужно рассматривать 2 случая:

y = sqrt[R^2 — (х-хc)^2] + yц.

y = -sqrt[R^2 — (х-хc)^2] + yц.

Две функции являются полукругами и вместе образуют окружность. Чтобы составить график круга в точке (х0;у0), нужно уравнение в этой точке. В точках с координатами (хц;yц+R) и (хц;yц-R) уравнения касательных к окружности задаются следующими уравнениями: y = yц + R и y = yц — R. Если взять точки (хц+R;yц) и (хц-R;yц), они будут иметь такую форму: x = xц + R и x = xц — R.

В случае для двух окружностей всего можно провести до 4 касательных (2 внешних и 2 внутренних). Это зависит от случая расположения фигур. Точкой пересечения внешних считается внешняя гомотетия (подобие), а внутренних — в центре внутреннего подобия. Внешними называются прямые, которые касаются внешних точек круга. Если касательные являются внутренними, то они пересекают линию, соединяющую центры окружностей.

Следует отметить, что внешний и внутренний центры гомотетии лежат на некоторой прямой. Она проходит через центры заданных окружностей. Это был рассмотрен случай, когда одна окружность меньше другой.

Однако при равенстве их диаметров появляются некоторые свойства: внешние касательные параллельны и внешнего центра гомотетии не существует.

Основные соотношения можно вывести, используя уравнение прямой (касательной) и расстояние от точки до прямой. Пусть окружности с радиусами R1 и R2 имеют следующие координаты центров: с1(х1;у1) и с2(х2;у2). Уравнение прямой записывается таким образом: ах + by + c = 0. Расстояния до прямой от точек с1 и с2 вычисляются таким образом: ах1 + by1 + c = R1 и ах2 + by2 + c = R2. Формула находится с помощью вычитания первого уравнения из второго: а(х2 — х1) + b(y2 — у1) = R2 — R1. Следовательно, расстояние вычисляется по следующей формуле: d = sqrt[(х2 — х1)^2 + (y2 — у1)^2].

Эллипс, гипербола и парабола

Пусть задан эллипс с полуосями a и b.

Его центром является точка с координатами (xц;уц). Уравнение, описывающее фигуру имеет такой вид: [(х — хц)^2 / a^2] + [(y — yц)^2 / b^2] = 1. Необходимо выразить переменную y. Функция будет состоять из двух полуэллипсов: y = (b/a) * sqrt[a^2 — (x-xц)^2] + yц и y = -(b/a) * sqrt[a^2 — (x-xц)^2] + yц. Касательные к геометрической фигуре могут быть параллельными оси ОХ или ОУ.

В некоторых случаях график задан уравнениями кривых, к которым относятся гипербола и парабола. Пусть первая имеет координаты центра (xц;уц) с вершинами (xц+а;уц) и (xц-a;уц). Ее уравнение принимает такой вид: [(х — хц)^2 / a^2] — [(y — yц)^2 / b^2] = 1. Если же ее вершины имеют такие координаты (xц;уц+b) и (xц;уц-b), то она описывается следующим равенством [(х — хц)^2 / a^2] — [(y — yц)^2 / b^2] = -1. В последнем равенстве меняется знак. При решении нужно разбить на две объединенные функции:

y = (b/a) * sqrt[(x-xц)^2 — a^2] + yц и y = -(b/a) * sqrt[(x-xц)^2 — a^2] + yц.

y = (b/a) * sqrt[(x-xц)^2 + a^2] + yц и y = -(b/a) * sqrt[(x-xц)^2 + a^2] + yц.

В первом случае прямые параллельны оси ординат, а во втором — абсцисс. Чтобы написать уравнение прямой, нужно определить, к какой из функций принадлежит точка, выполнив подстановку в текущие равенства. После этого их следует проверить на тождественность.

Чтобы записать уравнение прямой-касательной к параболе y = ax^2 + bx + c в точке с координатами (x0;y(x0)), нужно привести равенство к следующему виду: y = y'(x0) * (x-x0) + y(x0). Из формулы можно сделать вывод о том, что прямая параллельна оси абсцисс. Параболу нужно рассматривать, как объединение двух функций (x = ay^2 + by + c). Рекомендуется решить его относительно y. Дискриминант вычисляется таким образом: D = b^2 — 4a(c — x).

В зависимости от его значения находятся корни:

D>0: y = [-b + sqrt(D)] / 2a и y = [-b — sqrt(D)] / 2a.

D=0: y = -b / 2a.

D Примеры решения

Существует несколько типов задач на нахождение уравнения прямой, которая соприкасается с заданным графиком функции. Самой простой является задача со следующей формулировкой: прямая является касательной к графику функции. Найдите все точки касания. В этом случае задается уравнение графика функции и прямой. Некоторые задания считаются более сложными. В них необходимо написать уравнение касательной или касательных.

Рекомендации специалистов

Для решения задачи нужно внимательно прочитать условие и выяснить величины, которые следует найти. Все построено на нахождении производной функции. После этого нужно подставить значение координат точки в выражение первообразной. В некоторых случаях функция задается параметрически. Для удобства ее рекомендуется перевести в каноническую форму.

Рекомендуется разбивать задачу на несколько подзадач, поскольку будет очень просто выполнить проверку и исправить найденные ошибки. Существует несколько способов нахождения уравнения касательной: автоматизированный и ручной. В первом случае нужно использовать программное обеспечение. Оптимальным решением проблемы является онлайн-калькулятор.

При ручном режиме нужно решать, а иногда выполнить построение графика. Для оптимизации вычислений можно использовать Excel. График должен быть качественно построен и предельно понятен. В некоторых случая нужно будет вычислять предельные значения используя границы (lim).

Упражнения и ход вычислений

Нужно написать уравнение прямой-касательной к y(x) = x^3 — 2x^2 + 3 в т. xо = 2. Следует воспользоваться следующим алгоритмом:

Значение в х0 = 1: y(2) = 2 * 2^2 — 3 * 2 + 1 = 3.

Производная в заданной точке: y'(2) = 4x — 3 = 5.

Подстановка: y = y(2) + y'(2) * (x — x0) = 3 + 5(x — 2) = 3 + 5x — 10 = 5x — 7.

Одним из типов задач является нахождение точек, лежащих на ОХ, в которых прямые (касательные) || OX. Задана функция f(x) = x^3 — x^2 — 3x + 7. Угол наклона равен 0 градусов, т. к. касательная || OX (производная в точках касания равна 0).

Алгоритм решения следующий:

Найти производную исходной функции: f'(x) = 3x^2 — 2x — 3.

Если приравнять выражение к 0, то получится обычное квадратное уравнение: 3x^2 — 2x — 3 = 0.

Дискриминант: D = b^2 — 4ac = 4 — 4 * 3 * (-3) = 40.

Уравнение имеет 2 корня: х1 = (2 — sqr(40)) / 6 = (1 — sqr(10)) / 3 и x2 = (1 + sqr(10)) / 3.

Рекомендуется оставить в таком виде, поскольку при вычислении кубического корня появятся некоторые погрешности. В этих примерах необязательно составление графика.

Таким образом, геометрический смысл уравнения касательной к функции — производная. Следует изучить основные понятия, формулы и разобрать решение типовых задач. Также нужно повторить таблицу производных функций.

[spoiler title=”источники:”]

http://www.calc.ru/Uglovoy-Koeffitsiyent.html

http://sprint-olympic.ru/uroki/algebra/77841-kasatelnaia-k-grafiky-fynkcii-kak-sostavit-yravnenie-svoistva-yglovoi-koefficient-kasatelnoi-provedennoi-k-grafiky-fynkcii-formyla-primery-resheniia.html

[/spoiler]

Алгебра и начала анализа, 11 класса.

Урок №14. Геометрический смысл производной.

Перечень вопросов, рассматриваемых в теме

1) Геометрический смысл производной;

2) Алгоритм нахождения касательной к графику функции в точке;

3) Сравнение производных заданной функции по ее графику в различных точках.

Глоссарий по теме

Число k= tgα называется угловым коэффициентом прямой, а угол α – углом между этой прямой и осью Ох.

Геометрический смысл производной. Производная в точке x₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.

Дополнительная литература:

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Напомним, что графиком линейной функции у=кх + b является прямая.

Число k= tgα называется угловым коэффициентом прямой, а угол α – углом между этой прямой и осью Ох.

Если k>0, то 0<α< π/2, в этом случае функция возрастает

Если k<0, то – π/2<α<0, в этом случае функция убывает

Геометрический смысл производной. Производная в точке x₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

Рассмотрим график функции y = f ( x ):

Из рисунка видно, что для любых двух точек A и B графика функции: f(x0+Δx)/f(x0)Δx=tgα, где  – угол наклона секущей AB. 

Таким образом, разностное отношение равно угловому коэффициенту секущей. 

Если зафиксировать точку A и двигать по направлению к ней точку B, то Δx неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. 

Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A.

Отсюда следует:

производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.

В этом и состоит геометрический смысл производной.

Уравнение касательной к графику функции y=f(x) в точке x₀:

Примеры и разбор решения заданий тренировочного модуля

№1. Составить уравнение касательной к графику функции y=x+e^-2x, параллельной прямой y=-x

Решение:

Угловой коэффициент касательной равен значению производной в точке касания x₀. Т.к. касательная параллельна прямой y=-x, значит ее угловой коэффициент равен –1. Таким образом, f'(x₀) = -1.

Уравнение касательной:

Уравнение касательной: y=1-1(x-0) = 1-x

Ответ: y=1-x.

№2. На параболе у=х²-2х-8 найти точку М, в которой касательная к ней параллельна прямой 4х+у+4=0.

Решение:

Определим угловой коэффициент касательной к параболе у=х²-2х-8:

k =у’=(х²-2х-8)’=2х-2.

Найдем угловой коэффициент прямой 4х+у+4=0:

у=-4х-4, k =-4.

Касательная к параболе и данная прямая по условию параллельны. Следовательно, их угловые коэффициенты равны, т.е.

2х-2=-4;

х=-1 – абсцисса точки касания.

Ординату точки касания М вычислим из уравнения данной параболы у=х²-2х-8, т.е.

у(-1)=(-1)²-2(-1)-8=-5, М(-1;-5).

Ответ: М(-1;-5).

Вы уже знаете, какую прямую называют касательной к окружности. А что понимают, например, под касательной к синусоиде? Прямая

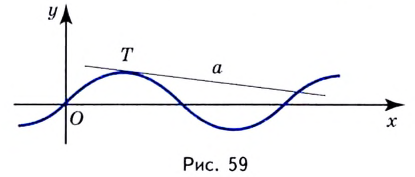
Пусть даны график функции  и на ней точка  которая не является концом графика (рис. 60). Обозначим на данном графике по разные стороны от  произвольные точки  Прямые  — секущие. Если же точки  двигаясь по графику, приближать достаточно близко к  как угодно близко будут приближаться к некоторой прямой  Такую прямую  (если она существует) называют касательной к графику функции  в точке 

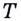
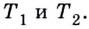
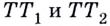
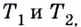
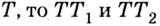
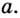
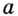
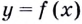
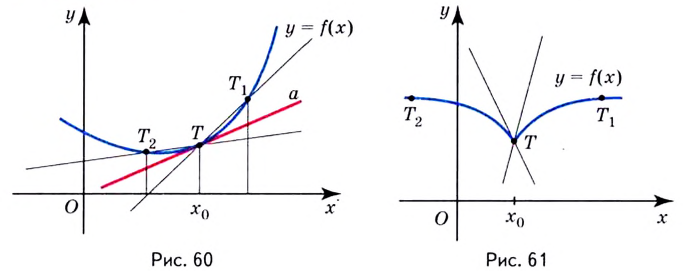
Если график функции такой, как показано на рисунке 61, то при неограниченном приближении точек  к точке  предельные положения секущих — прямые  — не совпадут. Говорят, что в точке  касательной к графику функции  не существует.

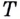
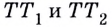
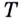
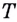
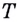
И если  — крайняя точка графика, то касательной к нему в точке  не существует.

Понятие касательной к графику часто используют для исследования функций. Рассмотрим этот вопрос сначала в общем виде.

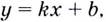
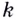
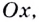
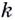
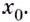
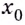
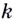
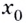
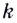
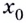
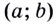
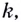
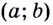
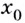
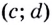
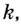
Касательная — это прямая. Её уравнение имеет вид  где  — угловой коэффициент — тангенс угла между лучом касательной, расположенным выше оси  и положительным направлением этой оси. Обратите внимание на угловой коэффициент  касательной, проведённой к графику какой-либо функции в его точке с абсциссой  Если число  принадлежит промежутку возрастания функции, то соответствующее значение  положительное (рис. 62). Если  принадлежит промежутку убывания функции, то  — отрицательное (рис. 63). И наоборот: если каждому значению  из некоторого промежутка  соответствует положительное значение  то на  данная функция возрастает; если каждому значению  из некоторого промежутка  соответствует отрицательное значение  то на  функция убывает. Заслуживают внимания и те точки графика функции, в которых касательная не существует, и в которых она параллельна оси 

Итак, зная угловые коэффициенты касательных к графику функции в тех или иных точках, можно сделать вывод, возрастает данная функция в этих точках, или убывает.

Поскольку для исследования функций важно уметь определять угловой коэффициент касательной к её графику, то рассмотрим подробнее связь этого коэффициента с исследуемой функцией.

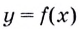
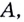
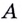
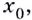
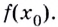
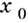
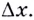
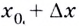
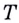
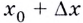
Пусть даны график функции  и на ней точку  в которой существует касательная к графику (рис. 64). Если абсцисса точки  равна  то её ордината —  Дадим значению аргумента  приращение  Тогда значению аргумента  на графике функции соответствует точка  с абсциссой  и ординатой 

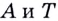
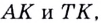
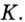
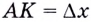
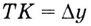
Через точки  проведём прямые  параллельные осям абсцисс и ординат. Они пересекутся в некоторой точке  Тогда  — приращение аргумента, а  — приращение функции на 

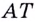
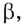
Угловой коэффициент секущей  равен тангенсу угла  т. е. отношению 

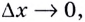
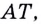
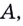
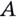
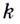
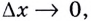
Если  то секущая  поворачиваясь вокруг точки  приближается к касательной, проведённой в точке  к графику данной функции. Итак, если  — угловой коэффициент этой касательной и  то

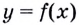
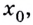
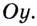
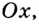
Так определяется угловой коэффициент касательной к графику функции  в некоторой точке  если касательная в ней не параллельна оси  Если касательная к графику функции в некоторой точке параллельна оси  то угловой коэффициент этой касательной равен нулю.

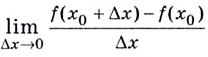
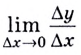
К вычислению значения выражения   или  приводит решение многих задач по механике, электричеству, биологии, экономике, статистике и т. д. Именно поэтому это выражение получило специальное название — производная.

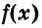
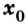
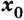
Производной функции  в точке  называют предел отношения приращения функции в точке  к приращению аргумента, если приращение аргумента стремится к нулю, а предел существует.

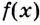
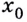
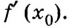
Производную функции  в точке  обозначают  Её определение записывают также в виде равенства:

Пример:

Найдите производную функции 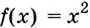 в точке 

Решение:

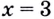
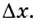
Дадим аргументу  приращение  Соответствующее приращение функции 

Тогда 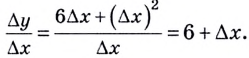 Если 

Следовательно, 

Ответ. 

Так решают задачу, пользуясь определением производной функции в точке.

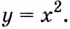
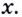
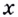
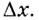
До сих пор речь шла о производной функции в точке. А можно рассматривать производную функции и как функцию. Пусть, например, дана функция Найдём её производную в произвольной точке  Для этого дадим значению приращение  Соответствующее ему приращение функции

Поэтому 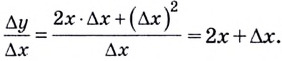 Если 

Имеем 

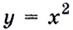
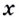
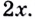
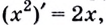
Следовательно, производная функции  в каждой её точке  равна  Пишут:  или, если 

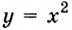
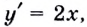
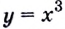
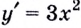
Обратите внимание! Производная функции в точке — это число. Когда же говорят о производной, не указывая «в точке», подразумевают производную как функцию: производной функции  есть функция  производной функции  есть функция  и т. д.

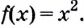
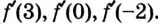
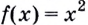
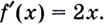
Зная это, производную функции в точке можно вычислять проще, чем по определению производной функции в точке. Пример 2. Дана функция Найдите  Решение. Производной функции  является функция  Поэтому 

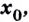
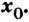
 Нахождение производной называется дифференцированием.  Функция, которая имеет производную в точке  называется дифференцируемой в точке  Функция, дифференцируемая в каждой точке некоторого промежутка, называется дифференцируемой на этом промежутке.

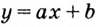
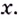
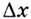
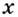
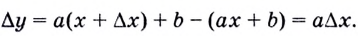
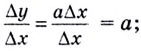
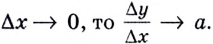
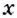
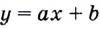
Докажем, например, что линейная функция  дифференцируема в каждой точке  Действительно, приращению  её аргумента  соответствует приращение функции  Поэтому  и если  А это и значит, что в каждой точке  функция  имеет производную

 Пишут

 В частности:

 Производная постоянной равна нулю.

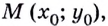
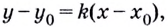
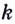
Из курса планиметрии известно, что уравнение прямой, проходящей через заданную точку  имеет вид  где  — угловой коэффициент прямой.

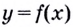
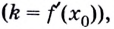
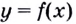
Поскольку для касательной к графику функции  угловой коэффициент равен значению производной в точке касания  то можем записать общий вид уравнения касательной, проведённой к графику функции  в точке касания 

До сих пор речь шла о касательных к криволинейным графикам. Но графиком функции может быть и прямая или часть прямой. Поэтому для обобщения договариваются касательной к прямой в любой её точке считать эту самую прямую. Касательной к отрезку или лучу в любой его внутренней точке считают прямую, которой принадлежит этот отрезок или луч.

Выше было установлено, что производная линейной функции равна коэффициенту при переменной, т.е 

Полученный результат имеет очевидный геометрический смысл: касательная к прямой — графику функции 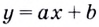 — есть эта самая прямая, её угловой коэффициент равен 

• Заказать решение задач по высшей математике

Пример:

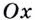
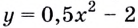
Найдите угол, который образуете положительным направлением оси касательная к графику функции  в точке 

Решение:

Определим сначала угловой коэффициент этой касательной по формуле 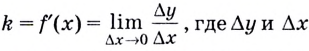 — приращения функции и приращения аргумента соответственно.

Найдем приращение функции 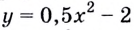 в точке 

Найдём угловой коэффициент касательной:

Поскольку 

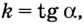
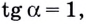
Известно также, что  поэтому  отсюда 

Пример:

Докажите, что для функции 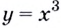 производной есть функция 

Решение:

  Если  А это и означает, что производной функции  является функция 

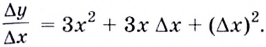
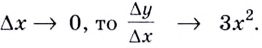
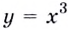
Пример:

Напишите уравнение касательной к графику функции 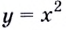 в его точке с абсциссой 

Решение:

Способ 1. Уравнение касательной имеет вид  Угловой коэффициент  равен значению производной функции  в точке  Значит, уравнение касательной Координаты точки касания  Точка с такими координатами принадлежит касательной, поэтому  отсюда Следовательно, уравнение касательной имеет вид: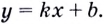 

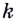
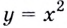
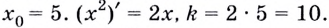
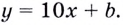
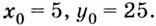
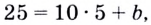
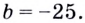
Способ 2. Запишем общий вид уравнения касательной:

Найдём 

Подставим найденные значения в уравнение касательной:

Была ли эта статья полезной?