Уравнения сторон треугольника
Как составить уравнение сторон треугольника по координатам его вершин?
Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.
Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)
Составить уравнения сторон треугольника.
1) Составим уравнение прямой AB, проходящей через 2 точки A и B.
Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:
Таким образом, уравнение стороны AB
2) Прямая BC проходит через точки B(7;-4) и C(3;7):
Отсюда уравнение стороны BC —
3) Прямая AC проходит через точки A(-5;1) и C(3;7):
Уравнение прямой с угловым коэффициентом: теория, примеры, решение задач
Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.
Угол наклона прямой и угловой коэффициент прямой
Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси О х с их угловым коэффициентом. Допустим, что задана декартова система координат О х на плоскости.
Угол наклона прямой к оси О х , расположенный в декартовой системе координат О х у на плоскости, это угол, который отсчитывается от положительного направления О х к прямой против часовой стрелки.
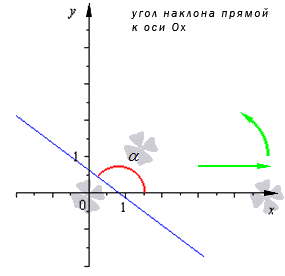
Когда прямая параллельна О х или происходит совпадение в ней, угол наклона равен 0 . Тогда угол наклона заданной прямой α определен на промежутке [ 0 , π ) .
Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.
Стандартное обозначение буквой k . Из определения получим, что k = t g α . Когда прямая параллельна Ох, говорят, что угловой коэффициент не существует, так как он обращается в бесконечность.
Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.

Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.
Посчитать угловой коэффициент прямой при угле наклона равном 120 ° .
Из условия имеем, что α = 120 ° . По определению необходимо вычислить угловой коэффициент. Найдем его из формулы k = t g α = 120 = – 3 .
Если известен угловой коэффициент, а необходимо найти угол наклона к оси абсцисс, тогда следует учитывать значение углового коэффициента. Если k > 0 , тогда угол прямой острый и находится по формуле α = a r c t g k . Если k 0 , тогда угол тупой, что дает право определить его по формуле α = π – a r c t g k .
Определить угол наклона заданной прямой к О х при угловом коэффициенте равном 3 .
Из условия имеем, что угловой коэффициент положительный, а это значит, что угол наклона к О х меньше 90 градусов. Вычисления производятся по формуле α = a r c t g k = a r c t g 3 .
Ответ: α = a r c t g 3 .
Найти угол наклона прямой к оси О х , если угловой коэффициент = – 1 3 .
Если принять за обозначение углового коэффициента букву k , тогда α является углом наклона к заданной прямой по положительному направлению О х . Отсюда k = – 1 3 0 , тогда необходимо применить формулу α = π – a r c t g k При подстановке получим выражение:
α = π – a r c t g – 1 3 = π – a r c t g 1 3 = π – π 6 = 5 π 6 .
Ответ: 5 π 6 .
Уравнение с угловым коэффициентом
Уравнение вида y = k · x + b , где k является угловым коэффициентом, а b некоторым действительным числом, называют уравнением прямой с угловым коэффициентом. Уравнение характерно для любой прямой, непараллельной оси О у .
Если подробно рассмотреть прямую на плоскости в фиксированной системе координат, которая задана уравнением с угловым коэффициентом, который имеет вид y = k · x + b . В данном случае значит, что уравнению соответствуют координаты любой точки прямой. Если подставить координаты точки М , M 1 ( x 1 , y 1 ) , в уравнение y = k · x + b , тогда в этом случае прямая будет проходить через эту точку, иначе точка не принадлежит прямой.
Задана прямая с угловым коэффициентом y = 1 3 x – 1 . Вычислить, принадлежат ли точки M 1 ( 3 , 0 ) и M 2 ( 2 , – 2 ) заданной прямой.
Необходимо подставить координаты точки M 1 ( 3 , 0 ) в заданное уравнение, тогда получим 0 = 1 3 · 3 – 1 ⇔ 0 = 0 . Равенство верно, значит точка принадлежит прямой.
Если подставим координаты точки M 2 ( 2 , – 2 ) , тогда получим неверное равенство вида – 2 = 1 3 · 2 – 1 ⇔ – 2 = – 1 3 . Можно сделать вывод, что точка М 2 не принадлежит прямой.
Ответ: М 1 принадлежит прямой, а М 2 нет.
Известно, что прямая определена уравнением y = k · x + b , проходящим через M 1 ( 0 , b ) , при подстановке получили равенство вида b = k · 0 + b ⇔ b = b . Отсюда можно сделать вывод, что уравнение прямой с угловым коэффициентом y = k · x + b на плоскости определяет прямую, которая проходит через точку 0 , b . Она образует угол α с положительным направлением оси О х , где k = t g α .
Рассмотрим на примере прямую, определенную при помощи углового коэффициента, заданного по виду y = 3 · x – 1 . Получим, что прямая пройдет через точку с координатой 0 , – 1 с наклоном в α = a r c t g 3 = π 3 радиан по положительному направлению оси О х . Отсюда видно, что коэффициент равен 3 .
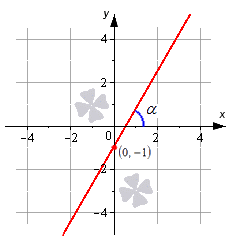
Уравнение прямой с угловым коэффициентом, проходящей через заданную точку
Необходимо решить задачу, где необходимо получить уравнение прямой с заданным угловым коэффициентом, проходящим через точку M 1 ( x 1 , y 1 ) .
Равенство y 1 = k · x + b можно считать справедливым, так как прямая проходит через точку M 1 ( x 1 , y 1 ) . Чтобы убрать число b, необходимо из левой и правой частей вычесть уравнение с угловым коэффициентом. Из этого следует, что y – y 1 = k · ( x – x 1 ) . Данное равенство называют уравнением прямой с заданным угловым коэффициентом k, проходящая через координаты точки M 1 ( x 1 , y 1 ) .
Составьте уравнение прямой, проходящей через точку М 1 с координатами ( 4 , – 1 ) , с угловым коэффициентом равным – 2 .
Решение
По условию имеем, что x 1 = 4 , y 1 = – 1 , k = – 2 . Отсюда уравнение прямой запишется таким образом y – y 1 = k · ( x – x 1 ) ⇔ y – ( – 1 ) = – 2 · ( x – 4 ) ⇔ y = – 2 x + 7 .
Ответ: y = – 2 x + 7 .
Написать уравнение прямой с угловым коэффициентом, которое проходит через точку М 1 с координатами ( 3 , 5 ) , параллельную прямой y = 2 x – 2 .
По условию имеем, что параллельные прямые имеют совпадающие углы наклона, отсюда значит, что угловые коэффициенты являются равными. Чтобы найти угловой коэффициент из данного уравнения, необходимо вспомнить его основную формулу y = 2 x – 2 , отсюда следует, что k = 2 . Составляем уравнение с угловым коэффициентом и получаем:
y – y 1 = k · ( x – x 1 ) ⇔ y – 5 = 2 · ( x – 3 ) ⇔ y = 2 x – 1
Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно
Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись. Для этого необходимо представлять в другом виде. Например, уравнение вида y = k · x + b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.
Можем получить каноническое уравнение прямой на плоскости, используя уравнение прямой с угловым коэффициентом. Получаем x – x 1 a x = y – y 1 a y . Необходимо слагаемое b перенести в левую часть и поделить на выражение полученного неравенства. Тогда получим уравнение вида y = k · x + b ⇔ y – b = k · x ⇔ k · x k = y – b k ⇔ x 1 = y – b k .
Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.
Привести уравнение прямой с угловым коэффициентом y = – 3 x + 12 к каноническому виду.
Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:
y = – 3 x + 12 ⇔ – 3 x = y – 12 ⇔ – 3 x – 3 = y – 12 – 3 ⇔ x 1 = y – 12 – 3
Ответ: x 1 = y – 12 – 3 .
Общее уравнение прямой проще всего получить из y = k · x + b , но для этого необходимо произвести преобразования: y = k · x + b ⇔ k · x – y + b = 0 . Производится переход из общего уравнения прямой к уравнениям другого вида.
Дано уравнение прямой вида y = 1 7 x – 2 . Выяснить, является ли вектор с координатами a → = ( – 1 , 7 ) нормальным вектором прямой?
Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:
y = 1 7 x – 2 ⇔ 1 7 x – y – 2 = 0
Коэффициенты перед переменными являются координатами нормального вектора прямой. Запишем это так n → = 1 7 , – 1 , отсюда 1 7 x – y – 2 = 0 . Понятно, что вектор a → = ( – 1 , 7 ) коллинеарен вектору n → = 1 7 , – 1 , так как имеем справедливое соотношение a → = – 7 · n → . Отсюда следует, что исходный вектор a → = – 1 , 7 – нормальный вектор прямой 1 7 x – y – 2 = 0 , значит, считается нормальным вектором для прямой y = 1 7 x – 2 .
Решим задачу обратную данной.
Необходимо перейти от общего вида уравнения A x + B y + C = 0 , где B ≠ 0 , к уравнению с угловым коэффициентом. для этого решаем уравнение относительно у. Получим A x + B y + C = 0 ⇔ – A B · x – C B .
Результат и является уравннием с угловым коэффициентом, который равняется – A B .
Задано уравнение прямой вида 2 3 x – 4 y + 1 = 0 . Получить уравнение данной прямой с угловым коэффициентом.
Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:
2 3 x – 4 y + 1 = 0 ⇔ 4 y = 2 3 x + 1 ⇔ y = 1 4 · 2 3 x + 1 ⇔ y = 1 6 x + 1 4 .
Ответ: y = 1 6 x + 1 4 .
Аналогичным образом решается уравнение вида x a + y b = 1 , которое называют уравнение прямой в отрезках, или каноническое вида x – x 1 a x = y – y 1 a y . Нужно решить его относительно у, только тогда получим уравнение с угловым коэффициентом:
x a + y b = 1 ⇔ y b = 1 – x a ⇔ y = – b a · x + b .
Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:
x – x 1 a x = y – y 1 a y ⇔ a y · ( x – x 1 ) = a x · ( y – y 1 ) ⇔ ⇔ a x · y = a y · x – a y · x 1 + a x · y 1 ⇔ y = a y a x · x – a y a x · x 1 + y 1
Имеется прямая, заданная уравнением x 2 + y – 3 = 1 . Привести к виду уравнения с угловым коэффициентом.
Исходя из условия, необходимо преобразовать, тогда получим уравнение вида _formula_. Обе части уравнения следует умножить на – 3 для того, чтобы получить необходимо уравнение с угловым коэффициентом. Преобразуя, получим:
y – 3 = 1 – x 2 ⇔ – 3 · y – 3 = – 3 · 1 – x 2 ⇔ y = 3 2 x – 3 .
Ответ: y = 3 2 x – 3 .
Уравнение прямой вида x – 2 2 = y + 1 5 привести к виду с угловым коэффициентом.
Необходимо выражение x – 2 2 = y + 1 5 вычислить как пропорцию. Получим, что 5 · ( x – 2 ) = 2 · ( y + 1 ) . Теперь необходимо полностью его разрешить, для этого:
5 · ( x – 2 ) = 2 · ( y + 1 ) ⇔ 5 x – 10 = 2 y + 2 ⇔ 2 y = 5 x – 12 ⇔ y = 5 2 x
Ответ: y = 5 2 x – 6 .
Для решения таких заданий следует приводит параметрические уравнения прямой вида x = x 1 + a x · λ y = y 1 + a y · λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.
Найти угловой коэффициент прямой, если она задана параметрическими уравнениями x = λ y = – 1 + 2 · λ .
Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:
x = λ y = – 1 + 2 · λ ⇔ λ = x λ = y + 1 2 ⇔ x 1 = y + 1 2 .
Теперь необходимо разрешить данное равенство относительно y , чтобы получить уравнение прямой с угловым коэффициентом. для этого запишем таким образом:
x 1 = y + 1 2 ⇔ 2 · x = 1 · ( y + 1 ) ⇔ y = 2 x – 1
Отсюда следует, что угловой коэффициент прямой равен 2 . Это записывается как k = 2 .
Решить треугольник Онлайн по координатам
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
Тема: Как вычеслить угловой коэффициент стороны треугольника ? Уравнение стороны нашел (Прочитано 9462 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Уравнение стороны треугольника : 3x-4y+8=0.
помогите пожалуйста с угловым коэффициентом , какего вычеслить ( то что он вычесляется по формуле: у= кх+в я знаю но не получается у меня со знаками путаюсь )

выразите из вашего уравнения y

Решение задач – практическое искусство; научиться ему можно, только подражая хорошим образцам и постоянно практикуясь….
Уравнение стороны треугольника : 3x-4y+8=0.
помогите пожалуйста с угловым коэффициентом , какего вычеслить ( то что он вычесляется по формуле: у= кх+в я знаю но не получается у меня со знаками путаюсь )
Есл имеется общее уравнение прямой ( Ax+By+C=0 ) (как у вас), то угловой коэффициент равен ( k=-frac{A}{B} ) либо
выразите из вашего уравнения y
т.е. сведите его к виду
то что он вычесляется по формуле: у= кх+в я знаю

А коэффициент “С” куда пропадет ?
ребят помогите решением пожалуйста . для наглядности

выразите из вашего уравнения y

Решение задач – практическое искусство; научиться ему можно, только подражая хорошим образцам и постоянно практикуясь….
А коэффициент “С” куда пропадет ?
никуда не пропадет, просто он никак не влияет на угловой коэффициент прямой
x+y+3=0 => y=-x-3 => k=-1

1. Уравнение сторон АВ и ВС и их угловые коэффициенты.
В задании даны координаты точек, через которые проходят эти прямые, поэтому воспользуемся уравнением прямой, проходящей через две заданные точки $$frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1}$$ подставляем и получаем уравнения
уравнение прямой AB $$frac{x+6}{6+6}=frac{y-8}{-1-8} => y = -frac{3}{4}x + frac{7}{2}$$ угловой коэффициент прямой AB равен (k_{AB} = -frac{3}{4})
уравнение прямой BC $$frac{x-4}{6-4}=frac{y-13}{-1-13} => y = -7x + 41$$ угловой коэффициент прямой BC равен (k_{BC} = -7)
2. Угол В в радианах с точностью до двух знаков
Угол B – угол между прямыми AB и BC, который рассчитывается по формуле $$tgphi=|frac{k_2-k_1}{1+k_2*k_1}|$$подставляем значения угловых коэффициентов этих прямых и получаем $$tgphi=|frac{-7+frac{3}{4}}{1+7*frac{3}{4}}| = 1 => phi = frac{pi}{4} approx 0.79$$
3.Длину стороны АВ
Длина стороны AB рассчитывается как расстояние между точками и равна (d = sqrt{(x_2-x_1)^2+(y_2-y_1)^2}) => $$d_{AB} = sqrt{(6+6)^2+(-1-8)^2} = 15$$
4.Уравнение высоты CD и ее длину.
Уравнение высоты будем находить по формуле прямой проходящей через заданную точку С(4;13) в заданном направлении – перпендикулярно прямой AB по формуле (y-y_0=k(x-x_0)). Найдем угловой коэффициент высоты (k_{CD}) воспользовавшись свойством перпендикулярных прямых (k_1=-frac{1}{k_2}) получим $$k_{CD}= -frac{1}{k_{AB}} = -frac{1}{-frac{3}{4}} = frac{4}{3}$$ Подставляем в уравнение прямой, получаем $$y – 13 = frac{4}{3}(x-4) => y = frac{4}{3}x+frac{23}{3}$$ Длину высоты будем искать как расстояние от точки С(4;13) до прямой AB по формуле $$d = frac{Ax_0+By_0+C}{sqrt{A^2+B^2}}$$ в числителе уравнение прямой AB, приведем его к этому виду (y = -frac{3}{4}x + frac{7}{2} => 4y+3x-14 = 0) , подставляем полученное уравнение и координаты точки в формулу $$d = frac{4*13+3*4-14 }{sqrt{4^2+3^2}} = frac{50}{5} =10$$
5. Уравнение медианы АЕ и координаты точки К пересечение этой медианы с высотой CD.
Уравнение медианы будем искать как уравнение прямой, проходящей через две заданные точки А(-6;8) и E , где точка E – середина между точками B и C и ее координаты находятся по формуле (E(frac{x_2+x_1}{2};frac{y_2+y_1}{2})) подставляем координаты точек (E(frac{6+4}{2};frac{-1+13}{2})) => (E(5; 6)), тогда уравнение медианы AE буде следующее $$frac{x+6}{5+6}=frac{y-8}{6-8} => y = -frac{2}{11}x + frac{76}{11}$$Найдем координаты точки пересечения высот и медианы, т.е. найдем их общую точку Для этого составим систему уравнение $$begin{cases}y = -frac{2}{11}x + frac{76}{11}\y = frac{4}{3}x+frac{23}{3}end{cases}=>begin{cases}11y = -2x +76\3y = 4x+23end{cases}=>$$$$begin{cases}22y = -4x +152\3y = 4x+23end{cases}=> begin{cases}25y =175\3y = 4x+23end{cases}=> $$$$begin{cases}y =7\ x=-frac{1}{2}end{cases}$$ Координаты точки пересечения (K(-frac{1}{2};7))
6.Уравнение прямой что проходит через точку К параллельно к стороне АВ.
Если прямая параллельны, то их угловые коэффициенты равны, т.е. (k_{AB}=k_{K} = -frac{3}{4}) , также известны координаты точки (K(-frac{1}{2};7)), т.е. для нахождения уравнения прямой применим формулу уравнения прямой, проходящей через заданную точку в заданном направлении (y – y_0=k(x-x_0)), подставляем данные и получаем $$y – 7= -frac{3}{4}(x-frac{1}{2}) => y = -frac{3}{4}x + frac{53}{8}$$
8. Координаты точки М которая симметрична точке А относительно прямой CD.
Точка M лежит на прямой AB, т.к. CD – высота к этой стороне. Найдем точку пересечения CD и AB для этого решим систему уравнений $$begin{cases}y = frac{4}{3}x+frac{23}{3}\y = -frac{3}{4}x + frac{7}{2}end{cases} =>begin{cases}3y = 4x+23\4y =-3x + 14end{cases} => $$$$begin{cases}12y = 16x+92\12y =-9x + 42end{cases} =>
begin{cases}0= 25x+50\12y =-9x + 42end{cases} => $$$$begin{cases}x=-2\y=5 end{cases}$$ Координаты точки D(-2;5). По условию AD=DK, это расстояние между точками находится по формуле Пифагора (d = sqrt{(x_2-x_1)^2+(y_2-y_1)^2}), где AD и DK – гипотенузы равных прямоугольных треугольников, а (Δx =x_2-x_1) и (Δy=y_2-y_1) – катеты этих треугольников, т.е. найдем катеты найдем и координаты точки M. (Δx=x_D-x_A = -2+6=4), а (Δy=y_D-y_A = 5-8=-3), тогда координаты точки M будут равны (x_M-x_D = Δx => x_D +Δx =-2+4=2 ), а (y_M-y_D = Δy => y_D +Δy =5-3=2 ), получили, что координаты точки (M(2;2))
9. Нанесем точки и прямые на декартовую систему координат
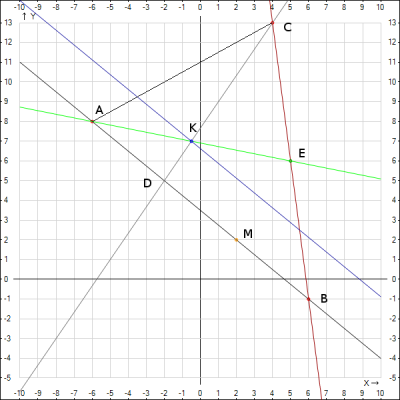
Загрузить PDF
Загрузить PDF
Угловой коэффициент характеризует угол наклона прямой к оси абсцисс (угловой коэффициент численно равен тангенсу этого угла). Угловой коэффициент присутствует в уравнении прямой и используется в математическом анализе кривых, где всегда равен производной функции. Для облегчения понимания углового коэффициента представьте, что он влияет на скорость изменения функции, то есть чем больше значение углового коэффициента, тем больше значение функции (при одном и том же значении независимой переменной).
-

1
Используйте угловой коэффициент для нахождения угла наклона прямой к оси абсцисс и направления этой прямой. Вычислить угловой коэффициент довольно легко, если вам дано уравнение прямой. Запомните, что в любом уравнении прямой:
-

2
Для нахождения углового коэффициента необходимо найти значение k (коэффициент при «х»). Если данное вам уравнение имеет вид
, то для нахождения углового коэффициента вам нужно просто посмотреть на число, стоящее перед «х». Обратите внимание, что k (угловой коэффициент) всегда находится при независимой переменной (в данном случае «х»). Если вы запутались, просмотрите следующие примеры:
-

3
Если данное вам уравнение имеет вид, отличный от
, обособьте зависимую переменную. В большинстве случаев зависимая переменная обозначается как «у», а для ее обособления можно выполнять операции сложения, вычитания, умножения и другие. Помните, что любая математическая операция должна быть выполнена на обеих сторонах уравнения (чтобы не менять его исходного значения). Вам необходимо привести любое данное вам уравнение к виду
. Рассмотрим пример:
Реклама
-

1
Для вычисления углового коэффициента воспользуйтесь графиком и двумя точками. Если вам дан просто график функции (без уравнения), вы все еще можете найти угловой коэффициент. Для этого вам понадобятся координаты любых двух точек, лежащих на этом графике; координаты подставляются в формулу:
. Чтобы избежать ошибок при вычислении углового коэффициента, запомните следующее:
- Если график возрастает, то угловой коэффициент имеет положительное значение.
- Если график убывает, то угловой коэффициент имеет отрицательное значение.
- Чем больше значение углового коэффициента, тем круче график (и наоборот).
- Угловой коэффициент прямой, параллельной оси абсцисс, равен 0.
- Угловой коэффициент прямой, параллельной оси ординат, не существует (он бесконечен).[4]
-

2
Найдите координаты двух точек. На графике отметьте любые две точки и найдите их координаты (х,у). Например, на графике лежат точки А(2,4) и В(6,6).[5]
- В паре координат первое число соответствует «х», а второе – «у».
- Каждому значению «х» соответствует определенное значение «у».
-

3
Приравняйте x1, y1, x2, y2 к соответствующим значениям. В нашем примере с точками А(2,4) и В(6,6):
- x1: 2
- y1: 4
- x2: 6
-
y2: 6[6]
-

4
Подставьте найденные значения в формулу для вычисления углового коэффициента. Чтобы найти угловой коэффициент, используются координаты двух точек и следующая формула:
. Подставьте в нее координаты двух точек.
-

5
Объяснение сути формулы. Угловой коэффициент равен отношению изменения координаты «у» (двух точек) к изменению координаты «х» (двух точек). Изменение координаты – это разность между значениями соответствующей координаты первой и второй точек.
-

6
Другой вид формулы для вычисления углового коэффициента. Стандартная формула для вычисления углового коэффициента: k =
. Но она может иметь следующий вид: k = Δy/Δx, где Δ – это греческая буква «дельта», обозначающая в математике разность. То есть, Δx = x_2 – x_1, а Δy = y_2 – y_1.[8]
Реклама
-

1
Научитесь брать производные от функций. Производная характеризует скорость изменения функции в определенной точке, лежащей на графике этой функции. В данном случае графиком может быть как прямая, так и кривая линия. То есть производная характеризует скорость изменения функции в конкретный момент времени. Вспомните общие правила, по которым берутся производные, и только потом переходите к следующему шагу.
- Прочитайте статью Как брать производную.
- Как брать простейшие производные, например, производную показательного уравнения, описано этой статье. Вычисления, представленные в следующих шагах, будут основаны на описанных в ней методах.
-

2
Научитесь различать задачи, в которых угловой коэффициент требуется вычислить через производную функции. В задачах не всегда предлагается найти угловой коэффициент или производную функции. Например, вас могут попросить найти скорость изменения функции в точке А(х,у). Также вас могут попросить найти угловой коэффициент касательной в точке А(х,у). В обоих случаях необходимо брать производную функции.
-

3
Возьмите производную данной вам функции. Здесь строить график не нужно – вам понадобится только уравнение функции. В нашем примере возьмите производную функции
. Берите производную согласно методам, изложенным в упомянутой выше статье:
- Производная:
- Производная:
-

4
В найденную производную подставьте координаты данной вам точки, чтобы вычислить угловой коэффициент. Производная функции равна угловому коэффициенту в определенной точке. Другими словами, f'(х) – это угловой коэффициент функции в любой точке (x,f(x)). В нашем примере:
-

5
Если возможно, проверьте полученный ответ на графике. Помните, что угловой коэффициент можно вычислить не в каждой точке. Дифференциальное исчисление рассматривает сложные функции и сложные графики, где угловой коэффициент можно вычислить не в каждой точке, а в некоторых случаях точки вообще не лежат на графиках. Если возможно, используйте графический калькулятор, чтобы проверить правильность вычисления углового коэффициента данной вам функции. В противном случае проведите касательную к графику в данной вам точке и подумайте, соответствует ли найденное вами значение углового коэффициента тому, что вы видите на графике.
- Касательная будет иметь тот же угловой коэффициент, что и график функции в определенной точке. Для того, чтобы провести касательную в данной точке, двигайтесь вправо/влево по оси Х (в нашем примере на 22 значения вправо), а затем вверх на единицу по оси Y. Отметьте точку, а затем соедините ее с данной вам точкой. В нашем примере соедините точки с координатами (4,2) и (26,3).
Реклама
Об этой статье
Эту страницу просматривали 143 640 раз.
Была ли эта статья полезной?
Тема
2.2. Прямая на плоскости
Д
ве
взаимно перпендикулярные прямые, на
каждой из которых указано
положительное направление и масштаб,
образуют прямоугольную декартову
систему координат (рис: 2.6). :
Рис. 2.6
Точка
![]()
называется началом координат, ось
![]() –
–
осью абсцисс, ось
![]()
-осью ординат. Положение на плоскости
любой точки
![]()
определяется двумя числами (координатами):
![]()
(рис.2.6).
Теорема 2.9 Расстояние
![]()
между точками
![]()
и
![]()
(рис.2.7) измеряется по
формуле
![]()

Рис. 2.7
Теорема 2.10 Если
точка
![]()
делит отрезок
![]()
в отношении
![]()
(![]()
называется коэффициентом
пропорциональности), то ее координаты
находят так;
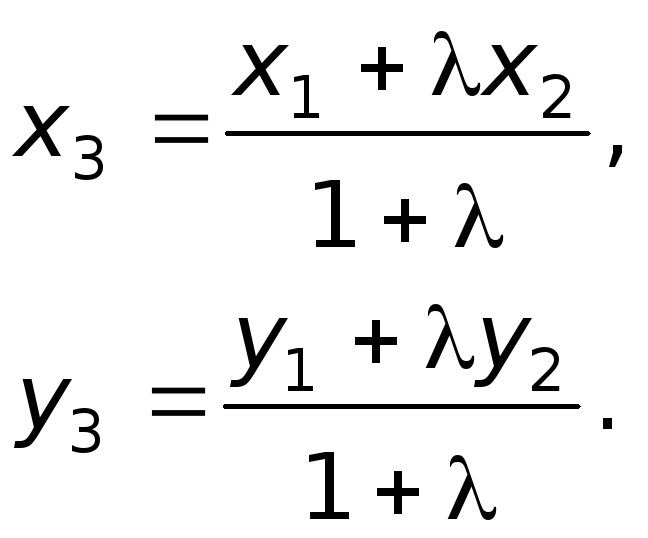
Следствие В частном случае, когда
отрезок делится пополам,
![]() ,
,
получим так называемые формулы половинного
деления;
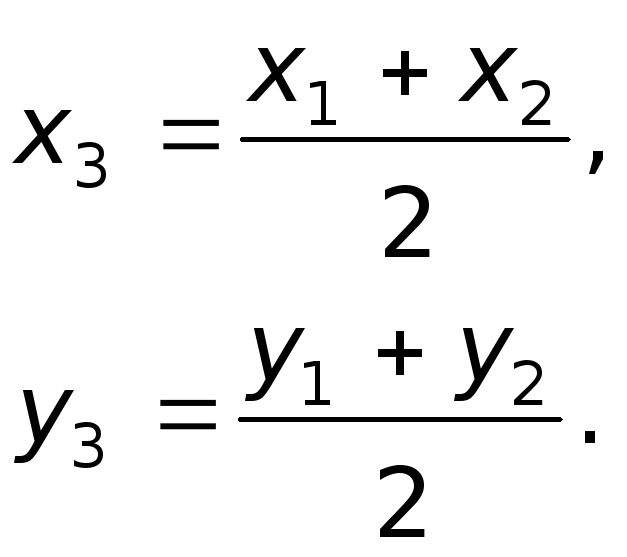
Теорема 2.11 Площадь
треугольника
![]()
с известными вершинами
![]()
равна;

В декартовом базисе прямая изображается
уравнением первой степени с двумя
неизвестными
![]()
и
![]()
Рассмотрим различные формы задания
уравнения прямой на плоскости.
Теорема 2.12 В прямоугольной системе
координат
![]()
любая прямая задается уравнением первой
степени, называемым общим уравнением
прямой
![]() ,
,
где
![]()
– постоянные коэффициенты, причем
![]() .
.
Уравнение прямой с угловым коэффициентом:
![]()
З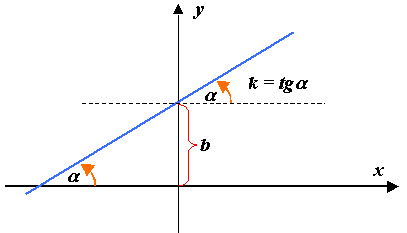
десь
параметры
![]()
и
![]()
имеют определенный геометрический
смысл (рис2.8).
Рис. 2.8
![]()
и называется угловым коэффициентом.
![]()
– угол, образованный прямой
с положительным направлением
![]() .
.
В качестве положительного направления
измерения угла а принято направление
против хода часовой стрелки (рис.
2.8).
![]()
– отрезок, отсекаемый прямой на оси
ординат.
Выполнив несложные алгебраические
преобразования, можно от общего уравнения
прямой перейти к уравнению прямой с
угловым коэффициентом. При этом
![]() ,
,
![]()
Уравнение прямой в отрезках
выглядит так:
![]() .
.
З![]()
![]() десь
десь
![]()
и
![]() –
–
отрезки, отсекаемые прямой на осях
абсцисс и ординат соответственно. Их
связь с коэффициентами общего уравнения
,
.
В этой форме можно представить уравнение
прямой, не проходящей через начало
координат, т.е. если
![]() .
.
Нормальное уравнение прямой:
![]()
Геометрический смысл коэффициентов
этого уравнения:
![]()
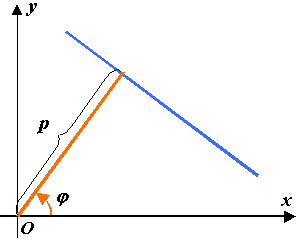
– длина перпендикуляра,
опущенного из начала координат на
прямую;
![]()
– угол, образованный этим перпендикуляром,
с положительным направлением оси
![]() (рис.2.9).
(рис.2.9).
Рис. 2.9
Чтобы перейти к этому виду уравнения
прямой, надо умножить все члены общего
уравнения на нормирующий множитель
![]() .
.
Знак
![]()
выбирается таким образом, чтобы
![]()
Уравнение пучка прямых описывает
множество прямых, проходящих через
точку
![]()
с известными координатами:
![]() .
.
Уравнение прямой, проходящей через
две точки
![]()
и
![]() :
:
![]()
Угол между прямыми
![]()
в зависимости от формы задания уравнений
прямых может быть найден по формуле:
![]()
![]() или
или
.
З
десь
угол
![]()
измеряется от прямой с угловым
коэффициентом
![]()
или
![]()
до прямой с параметрами
![]()
или
![]()
(рис.2.10):
Рис. 2.10
Из этих формул легко выводятся условия
параллельности:
![]()
или
![]()
и перпендикулярности прямых:
![]()
или
![]() .
.
Координаты точки пересечения
двух прямых определяются как
решение системы, составленной из
уравнений прямых.
Теорема 2.13
Расстояние
![]()
от точки
![]()
до прямой
![]()
(или
![]() )
)
определяется по формулам:
![]()
или
![]()
Задача 2.5 Дано общее уравнение прямой
![]() .
.
Написать: а) уравнение с угловым
коэффициентом; б) уравнение в отрезках;
в) нормальное уравнение. Построить
прямую.
Решение
а) Оставим член с
![]()
слева, а остальные перенесем в правую
часть уравнения. Затем разделим обе
части на коэффициент при
![]() ,
,
т.е. на -3. В результате
получим уравнение с угловым коэффициентом
Задача 2.6 Написать
уравнение прямой, проходящей через
точку
![]()
и отсекающей от координатного угла
треугольник, площадью равной
3.
Решение
О
чевидно,
что таких прямых будет 2,
а треугольники образованы во
втором и четвертом квадрантах (рис.2.11):
Рис. 2.11
Запишем уравнение пучка прямых, проходящих
через точку
![]() :
:
![]()
Преобразуем его к уравнению в отрезках:
 .
.
Таким образом,
![]()
Так как
![]()
и
![]()
имеют разные знаки, то площадь указанных
в условии задачи треугольников может
быть найдена по формуле
![]()
Отсюда
![]()
или

Решив квадратное уравнение, найдем
![]()
Тогда уравнения прямых будут иметь вид:
![]()
Задача 2.7 Дан
треугольник с вершинами
![]()
и
![]() .
.
Написать уравнения сторон треугольника,
медианы
![]() ,
,
высоты
![]() ,
,
найти длины медианы
![]()
и высоты
![]() ,
,
угол при вершине
![]() ,
,
площадь треугольника
![]() .
.
Решение
П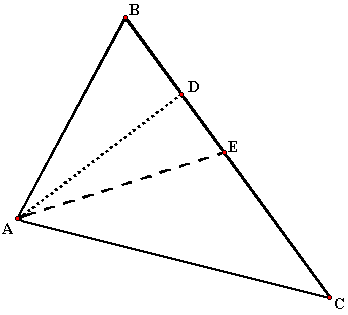
остроим
треугольник с указанными вершинами и
отметим все перечисленные элементы
(рис. 2.12).
Рис. 2.12
Уравнения, сторон треугольника получим,
используя уравнения прямой, проходящей
через две точки.



Уравнение
![]()
можно было записать и без таких выкладок,
учитывая, что обе точки лежат на оси
![]() .
.
Для нахождения уравнения медианы
![]()
предварительно определим координаты
точки
![]()
как середины отрезка
![]() :
:

Тогда уравнение медианы
![]()
будет иметь вид
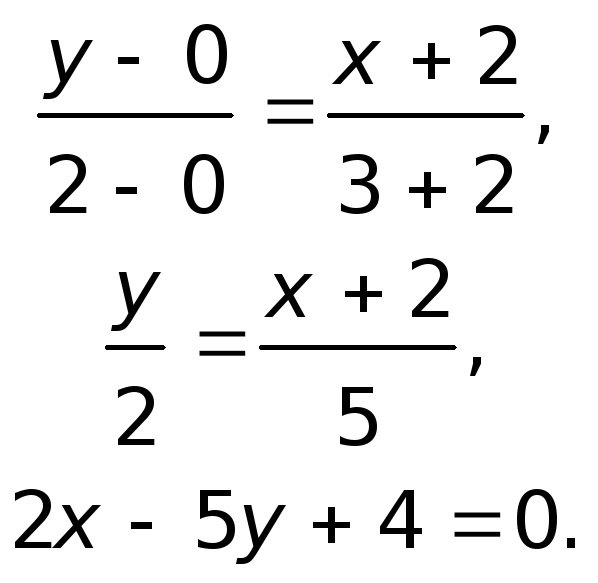
Длину
![]()
определим как расстояние между точками
![]()
и
![]() :
:
![]() .
.
Запишем уравнение пучка прямых, проходящих
через вершину
![]() :
:
![]()
Так как высота
![]()
перпендикулярна стороне треугольника
![]() ,
,
то их угловые коэффициенты связаны так:
![]()
Из уравнения
![]()
легко найти
![]()
Тогда
![]() ,
,
и уравнение высоты
![]()
будет
![]()
или
![]() .
.
Длину высоты
![]()
определим как расстояние от точки
![]()
до прямой
![]() :
:
![]()
Так как мы установили общие уравнения
прямых
![]()
и
![]() ,
,
то воспользуемся соответствующей
формулой для определения угла при
вершине
![]()
треугольника
![]() .
.
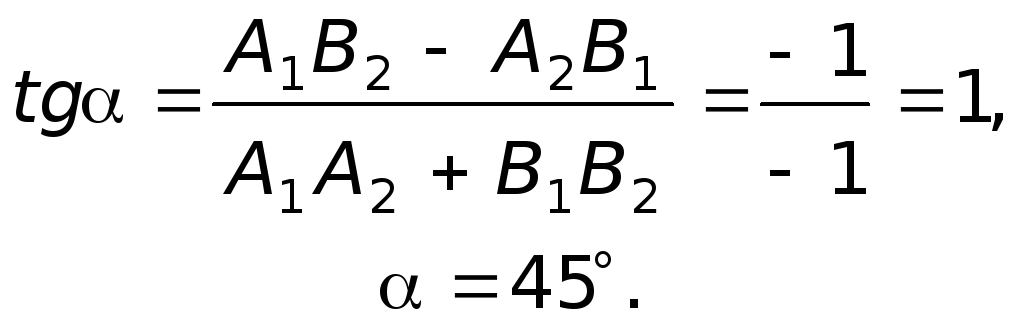
Площадь треугольника
![]()
равна
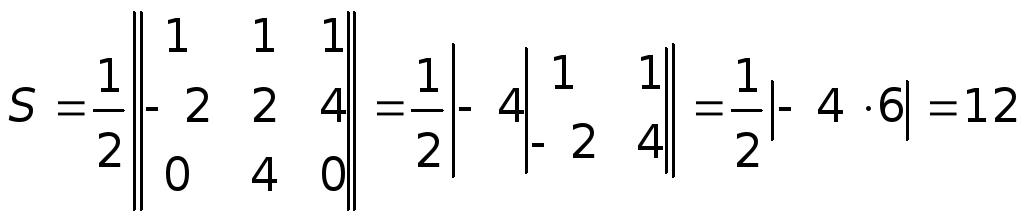 .
.
Задача 2.8 Найти
точку пересечения медиан и точку
пересечения высот треугольника, вершины
которого
![]()
и
![]() .
.
Решение
С
троим
треугольник, показываем точки пересечения
его медиан и высот (рис.2.13).
Рис.2.13
Определим координаты точки
![]()
как середины отрезка
![]() ,
,
воспользовавшись формулами половинного
деления
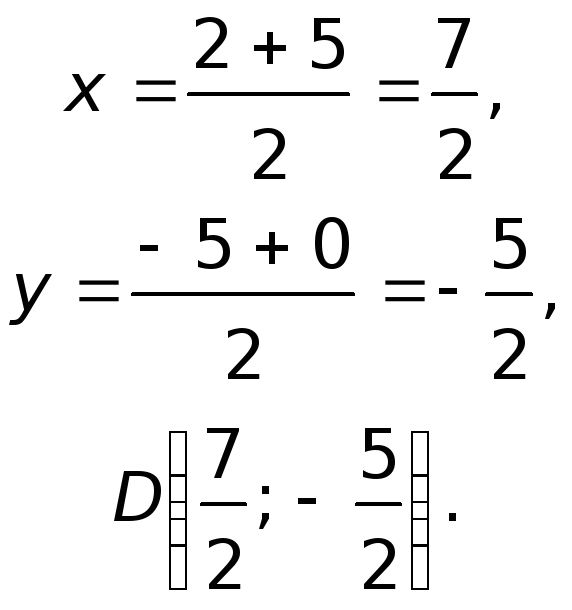
Для определения координат точки
пересечения медиан
![]()
воспользуемся свойством этой точки,
согласно которому она делит медиану
![]()
в отношении
![]() ,
,
считая от вершины, т.е.
![]() .
.
Тогда для точки
![]()
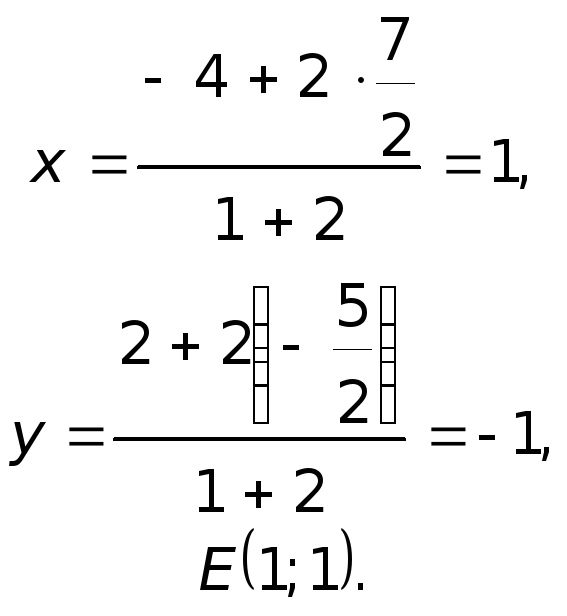
Треугольник
![]()
является равнобедренным, так как длины
сторон
![]()
и
![]()
равны:
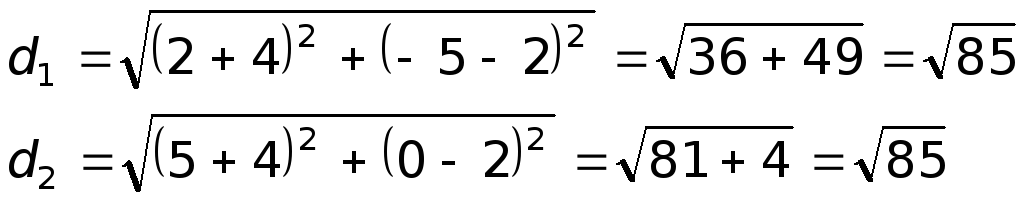
Следовательно, медиана
![]()
будет и высотой. Отсюда уравнение высоты
![]()
определим как уравнение прямой, проходящей
через точки
![]() :
:
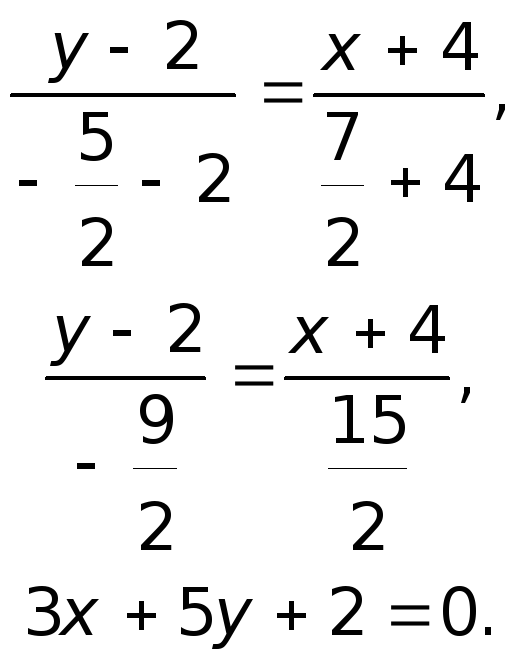
Уравнение пучка прямых, проходящих
через точку
![]()
может быть записано как
![]() .
.
Уравнение
![]()
находим через известные координаты
концов отрезка:

Так как высота
![]()
перпендикулярна
![]() ,
,
то ее угловой коэффициент
![]()
и уравнение
![]()
будет
![]()
или
![]()
Координаты точки
![]()
пересечения высот
![]()
и
![]()
определим из решения системы, составленной
из уравнений высот:
![]()

![]()
47
Соседние файлы в папке высшая математика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #


