Как найти угловой радиус планеты

Угол, под которым
с Земли виден диск светила, называется
его угловым
диаметром.
Угловые диаметры некоторых небесных
тел (Солнца, Луны, планет) можно определить
непосредственно из наблюдений.

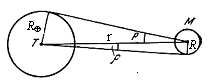
Рис. 2.4. Определение
линейных размеров светил.

Если известен
угловой диаметр (или радиус) светила и
его расстояние от Земли, то легко
вычислить его истинный диаметр (или
радиус) в линейных мерах. Действительно,
если (рис. 2.4) —
угловой радиус светила М, r
— расстояние между центрами светила и
Земли, р — горизонтальный экваториальный
параллакс светила, а R_
и R — линейные
радиусы Земли Т и светила М, то

,

(2.12)

а, учитывая, что
угол 
мал и

:

,

(2.13)

где

— угловой
радиус, выраженный в угловых секундах.

С учетом формулы (2.9) соотношение (2.13)
может быть приведено к следующему виду:

,

(2.14)

т.е.
чтобы вычислить
линейный радиус небесного тела, необходимо
измерить его угловой радиус и горизонтальный
параллакс.

Форму небесных тел можно определить,
измеряя различные диаметры их дисков.
Если тело сплющенное, то один из его
диаметров окажется больше, а один —
меньше всех других диаметров. Измерения
диаметров планет показали, что помимо
Земли сплющенную форму имеют Марс,
Юпитер, Сатурн, Уран и Нептун.

Линейные размеры
и форма небесных тел, угловые размеры
которых непосредственно измерить нельзя
(например, малые планеты и звезды),
определяются специальными методами.

§ 2.5. Измерение расстояний до звезд

Т.к. звезды удалены
от нас на огромные расстояния, то их
суточное параллактическое смещение
исключительно мало, поэтому оно не может
быть измерено.

Расстояния до
звезд определяются по их годичному
параллактическому смещению,
которое обусловлено перемещением
наблюдателя (вместе с Землей) по земной
орбите (рис. 2.5).

Рис. 2.5. Годичный
параллакс звезд.

Угол, под которым
со звезды был бы виден средний радиус
земной орбиты при условии, что направление
на звезду перпендикулярно к радиусу,
называется годичным
параллаксом звезды
.
Если СТ = а_
есть средний радиус земной орбиты, МС
= r
— расстояние звезды М
от Солнца С
(гелиоцентрическое
расстояние),
а угол 
— годичный параллакс звезды, то из
прямоугольного треугольника СТМ
имеем

.

(2.15)

Годичные параллаксы
звезд меньше 1“, и поэтому, учитывая,
что

,
получим:

,

(2.16)

где

— годичный
параллакс, выраженный в угловых секундах.

Расстояние r
по этим формулам получается в тех же
единицах, в которых выражено среднее
расстояние а_
Земли от Солнца.

Т.к. звезды находятся
на очень больших расстояниях от Земли,
то их гелиоцентрические расстояния и
расстояния от Земли будем считать
одинаковыми.

Расстояние,
соответствующее годичному параллаксу
в 1“,
называется парсеком.

Если расстояния
до звезд измерять в парсеках (пс),
то

.

(2.17)

Кроме этого,
расстояния до звезд измеряют также в
световых
годах.

Световой год
— расстояние,
которое свет проходит за один год,
распространяясь со скоростью около 300
000 км/с.

Запишем соотношения
между единицами расстояния в астрономии:

1 пс
= 3,1¹³
км
= 206 265 а.е.
= 3,26 светового
года;

1 световой
год = 9,46¹²
км =
63 240 а.е.;

1 а.е.=
149,6 
10⁶
км.

Расстояния до
небесных тел, находящихся за пределами
Солнечной системы, обычно выражаются
в парсеках, килопарсеках (1 000 пс)
и мегапарсеках (1 000 000 пс),
а также в световых годах.

Установлено, что
ближайшей к Солнцу звездой является
звезда Проксима
Центавра, которая имеет годичный
параллакс 
= 0“,772.
Следовательно, она находится от нас на
расстоянии 1,3 пс
или 4,2 светового
года.

Современные
астрономические приборы позволяют в
настоящее время измерить годичные
параллаксы, не меньшие 0“,005.
Это дает возможность определить
расстояния методом годичного параллакса,
не превышающие 200 пс.
Расстояния до более далеких объектов
определяются другими способами.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Вы уже знаете, что ещё в Древней Греции учёными и мыслителями
было установлено, что наша планета не является плоской, а имеет шарообразную
форму. Представление о Земле как о шаре, который свободно, без всякой опоры
находится в космическом пространстве, является одним из величайших достижений
древнего мира.

Первый известный науке метод определения размеров Земли
применил греческий учёный Эратосфен, живший в Египте. Его идея была достаточно
проста. Итак, Эратосфен выбрал два города — Александрию и Сиену (ныне Асуан) —
расположенных на одном земном меридиане.

Далее он обозначил длину дуги меридиана между двумя городами
через l, а её
угловое значение в градусах как п.

Тогда длина дуги в 1^о выбранного меридиана равна

А длина всей окружности меридиана: L = 360^o ∙ l₀.

С другой стороны, он знал, что длина окружности равна: L =
2πR.

Приравняв правые части последних двух уравнений, легко
получить искомый радиус земного шара:

Теперь было необходимо определить длину дуги меридиана в градусной
мере. Очевидно, что она равна разности географических широт Александрии и
Сиены. Так вот, чтобы определить эту разность Эратосфен придумал хитрый способ.
Он знал, что в полдень дня летнего Солнцестояния в Сиене Солнце находится в
зените и освещает дно самых глубоких колодцев. А в Александрии Солнце до зенита
не доходит. Поэтому шест, вбитый вертикально в землю должен отбрасывать тень.
Измерив длину этой тени можно легко определить искомую длину дуги меридиана,
которая у Эратосфена оказалась равной 7,2^о.

Ну а расстояние между Александрией и Сиеной ему было хорошо
известно: оно составляло пять тысяч греческих стадий.

Подставив все данные в формулу для длины окружности
меридиана, Эратосфен получил значение в 250 000 стадий.

Стадий — это весьма неоднозначная единица измерения
расстояния. Но, как правило, за стадий принимали расстояние, которое проходит
легковооружённый воин за промежуток времени от появления первого луча солнца
при его восходе до того момента, когда весь солнечный диск окажется над горизонтом.

Однако если учесть, что расстояние между Александрией и
Асуаном по прямой примерно равно 844 километрам, то можно полагать, что одна
стадия примерно равна 169 метрам.

Тогда искомая длина всей окружности меридиана равна
42 250 километрам, что совсем не плохо для того времени.

Современная наука располагает более точными способами
измерения расстояний на земной поверхности. Одним из них является метод
триангуляций, основанный на явлении параллактического смещения.

Параллактическое смещение — это изменение направления
на предмет при перемещении наблюдателя. С его помощью можно измерить расстояние
на основе измерения длины одной из сторон (базиса) и двух прилегающих к
ней углов в треугольнике.

Суть метода триангуляций состоит в следующем. По обе стороны
дуги, длину которой нужно измерить, выбирается несколько точек на расстоянии не
более 50 километров друг от друга, на которых устанавливаются геодезические
вышки. При этом из каждой точки должны быть видны по крайней мере две другие
точки. Далее тщательным образом измеряется длина базиса (с точностью до одного
миллиметра). После этого с вершины вышки при помощи теодолита измеряются углы
между направлениями на два-три соседних пункта. Измерив углы в треугольнике,
одной из сторон которого является базис, геодезисты получают возможность
вычислить длину двух других его сторон по известным тригонометрическим
формулам. Проводя затем измерение углов из пунктов, расстояние между которыми
уже вычислено, можно узнать длину очередных двух сторон и так далее. Затем, по
вычисленным сторонам, определяется искомая длина дуги.

В XVIII веке использование триангуляционных измерений в
экваториальных широтах и вблизи северного полярного круга, показало, что длина
дуги в 1^о меридиана не одинакова и увеличивается к полюсам. Из этого
следовало, что наша планета не является идеальным шаром и её полярный радиус
почти на 21 километр короче экваториального. Поэтому в геодезии и форму Земли
считают геоидом, то есть телом с поверхностью, близкой к поверхности спокойного
океана и продолженной под материками.

В настоящее время форму Земли принято характеризовать
следующими физическими характеристиками:

·                   полярное сжатие — 0,0033528;

·                   экваториальный радиус — 6378,1 км;

·                   полярный радиус — 6356,8 км;

·                   средний радиус — 6371,0 км;

·                  
и длина окружности экватора — 40 075,017 км.

Долгое время загадкой для многих астрономов являлось истинное
расстояние от Земли до Солнца. Измерить его смогли лишь во второй половине XVIII века,
когда был впервые определён горизонтальный параллакс Солнца. По сути дела, при
этом измеряется параллактическое смещение объекта, находящегося за пределами
Земли, а базисом является её радиус.

Горизонтальным параллаксом называется угол, под
которым со светила виден радиус Земли, перпендикулярный лучу зрения.

Зная горизонтальный параллакс светила, можно, по известным
тригонометрическим соотношениям, определить его расстояние от центра Земли:

Очевидно, что чем дальше расположено светило, те меньше его
горизонтальный параллакс. Например, наибольший параллакс, в среднем 57ʹ,
имеет спутник Земли — Луна. У Солнца он значительно меньше и примерно
составляет 8,794ʹʹ. Такому параллаксу соответствует среднее
расстояние от Земли до Солнца, примерно равное 149,6 миллиона километров.

На одном из прошлых уроков мы говорили о том, что это
расстояние в астрономии принимается за одну астрономическую единицу. С её
помощью удобно измерять расстояния между телами в Солнечной системе.

Но вернёмся к нашей формуле. Итак, из геометрии вам должно
быть известно, что при малых значениях угла его синус примерно равен самому углу,
выраженному в радианах. Если учесть, что в одном радиане содержится 206
265ʹʹ, то легко можно получить формулу, удобную для вычислений:

Для примера, давайте с вами определим расстояние от Земли до
Юпитера в момент противостояния, если его горизонтальный параллакс был равен
2,2ʹʹ. Радиус Земли примем равным 6371 километру.

Эту же задачу можно было решить несколько иначе.

В настоящее время для более точного определения расстояний до
тел в Солнечной системе применяется более точный метод измерений — радиолокационный.
Измерив время, необходимое для того, чтобы радиолокационный импульс достиг
небесного тела, отразился и вернулся на Землю, вычисляют расстояние до этого
тела по формуле:

где с — это скорость света в вакууме.

С разработкой методов определения расстояний до тел в
Солнечной системе учёным не составило большого труда придумать и способ
определения их размеров. В частности, при наблюдениях небесного тела Солнечной
системы с Земли можно измерить угол, под которым оно видно наблюдателю, то есть
его угловой размер (или угловой диаметр), а, следовательно, и угловой радиус.

А зная угловой радиус и расстояние до светила, можно
вычислить его линейный радиус:

.

Только в этой формуле угловой радиус должен быть выражен в
радианах.

Если в записанное уравнение подставить формулу для
определения расстояний методом горизонтального параллакса и упростить её,
используя тот факт, что значения углов ρ и р малы, то получим
формулу, по которой можно определять линейные размеры небесных тел:

Но помните, пользоваться ей можно тогда, когда видны диски
светил.

Для примера давайте решим с вами такую задачу. При наблюдении
прохождения Меркурия по диску Солнца определили, что его угловой радиус равен
5,5’’, а горизонтальный параллакс — 14,4’’. Чему равен линейный радиус
Меркурия?

И покидает поле брани,
И отступает “Аполлон”.
Стартуют рыцари иные
К сетям сатурновых колец,
Туда, где жжёт дыханье Ио
И ощущается конец
Той Удивительной Системы
Владений Царственной Звезды,
Которой уроженцы все мы.
И. Галкин

Урок 5/11

 презентация

Тема: Определение расстояний до тел СС и размеров этих небесных тел.

Цель: Рассмотреть различные способы определения расстояния до тел СС. Дать понятие горизонтального параллакса и закрепить способ нахождения расстояния и размеров тел через горизонтальный параллакс.

Задачи:
1. Обучающая:   Ввести понятия геометрического (параллактического), «радиолокационного» и «лазерного» методов определения расстояний до тел Солнечной системы. Вывести формулу для определения радиуса небесных тел Солнечной системы (понятия: линейный радиус, угловой радиус). Использовать решение задач для продолжения формирования расчетных навыков.
2. Воспитывающая: раскрыв тему урока что современная наука располагает различными методами определения расстояний до небесных тел и их размеров для получения достоверные сведения о масштабах Солнечной системы и размерах входящих в нее небесных тел, содействовать формированию мировоззренческой идеи о познаваемости мира.
3. Развивающая: показать, что на первый взгляд неразрешимая проблема определения расстояний до небесных тел и радиусов небесных тел в настоящее время решается различными методами.

Знать:
I-й уровень (стандарт) – способы определения расстояний до тел СС, понятие базиса и параллакса, способ определения размера Земли и любого небесного тела.
II-й уровень – способы определения расстояний до тел СС, понятие базиса и параллакса, способ определения размера Земли и любого небесного тела. Что диаметр Луны во столько раз меньше диаметра Солнца, во сколько раз расстояние от Луны до Земли меньше расстояния от Земли до Солнца.

Уметь:
I-й уровень (стандарт) -определять расстояния до тел СС используя параллакс и данные радиолокации, определять размеры небесных тел.
II-й уровень -определять расстояния до тел СС используя параллакс и данные радиолокации, определять размеры небесных тел.

Оборудование: Таблицы: «Солнечная система», теодолит, к/ф «Радиолокация», диапозитивы, диафильм «Определение расстояний до небесных тел». CD- “Red Shift 5.1”. ШАК.

Межпредметная связь: Градусная и радианная меры угла, смежные и вертикальные углы. Шар и сфера (математика, 5, 7, 10, 11 кл.). Расстояние от Земли до Луны и Солнца. Сравнительные размеры Солнца и Земли, Земли и Луны (природоведение, 5 кл). Скорость распространения электромагнитных волн. Метод радиолокации (физика, 11 кл).

Ход урока:

I. Опрос учащихся (5-7 минут). Диктант.
 

1. Ученый, создатель гелиоцентрической системы мира. (Н. Коперник)
2. Ближайшая точка орбиты ИСЗ. (Перигей)
3. Значение астрономической единицы. (1 а. е.=149600000км )
4. Основные законы небесной механики. (4 закона-3Вт и 3-й закон Коперника)
5. Планета, открытая на «кончике пера». (Нептун)
6. Значение круговой (I космической) скорости для Земли. (7,9 км/с)
7. Отношение квадратов периодов обращения двух планет равно 8. Чему равно отношение больших полуосей этих планет? (2)
8. В какой точке эллиптической орбиты ИСЗ имеет минимальную скорость? (В апогее)
9. Немецкий астроном, открывший законы движения планет (И. Кеплер)
10. Формула третьего закона Кеплера, после уточнения И. Ньютона.
11. Вид орбиты межпланетной станции, посланной для облета Луны. (Эллипс)
12. Чем отличается первая космическая скорость от второй. (в раз >)
13. В какой конфигурации находится Венера, если она наблюдается на фоне диска Солнца? (Соединение нижнее)
14. В какой конфигурации Марс ближе всего к Земле. (В противостоянии)
15. Виды периодов движения Луны = (временных)? (Сидерический, синодический).

II Новый материал

1) Определение расстояний до небесных тел.
     В астрономии нет единого универсального способа определения расстояний. По мере перехода от близких небесных тел к более далеким одни методы определения расстояний сменяют другие, служащие, как правило, основой для последующих. Точность оценки расстояний ограничивается либо точностью самого грубого из методов, либо точностью измерения астрономической единицы длины (а. е.).
1-й способ: (известен) По третьему закону Кеплера можно определить расстояние до тел СС, зная периоды обращений и одно из расстояний. 

    Приближённый метод.

2-й способ: Определение расстояний до Меркурия и Венеры в моменты элонгации (из прямоугольного треугольника по углу элонгации).
3-й способ: Геометрический (параллактический).
  Пример: Найти неизвестное расстояние АС.
  [АВ] – Базис – основное известное расстояние, т. к. углы САВ и СВА – известны, то по формулам тригонометрии (теорема синусов) можно в ? найти неизвестную сторону, т. е. [CА]. Параллактическим  смещением называется изменение направления на предмет при перемещении наблюдателя.
  Параллакс- угол (АСВ), под которым из недоступного места виден базис (АВ – известный отрезок). В пределах СС за базис берут экваториальный радиус Земли R=6378км.

     Пусть К – местонахождение наблюдателя, из которого светило видно на горизонте. Из рисунка видно, что из прямоугольного треугольника гипотенуза, расстояние D равно: , так как при малом значении угла если выражать величину угла в радианах и учитывать, что угол выражен в секундах дуги, а 1рад =57,3⁰=3438’=206265“, то и получается вторая формула.

Угол (ρ) под которым со светила, находящегося на горизонте (? R – перпендикулярно лучу зрения) был бы виден экваториальный радиус Земли называется горизонтальным экваториальным параллаксом светила.
Т.к. со светила никто наблюдать не будет в силу объективных причин, то горизонтальный параллакс определяют так:

1. измеряем высоту светила в момент верхней кульминации из двух точек земной поверхности, находящихся на одном географическом меридиане и имеющем известные географические широты.
2. из полученного четырехугольника вычисляют все углы (в т. ч. параллакс).

АОВ=n=φА-φВ(разность географических широт) е=АВ – длина дуги вдоль меридиана т.к. е10=е/n=2πR/3600 ,то  [форм 21].  Аналогичным способом в 240г до НЭ (рисунок выше) определяет радиус Земли географ Эратосфен.   L/800=3600/7,20

б) Определение размера небесных тел.

Р- параллакс. ρ – угловой радиус светила Из прямоугольных треугольников дважды используя формулу R=r. sin ρ (чертёж) получим  [форм. 22]

III. Закрепление материала

1. Пример 7 (стр. 51).
2. CD- “Red Shift 5.1” – Определить на данный момент удаленность нижних (планет земной группы, верхних планет, планет гигантов) от Земли и Солнца в а.е.
3. Угловой радиус Марса 9,6″, а горизонтальный параллакс 18″. Чему равен линейный радиус Марса? [Из формулы 22 получим 3401,6 км. (фактически 3396 км)].
4. Каково расстояние между лазерным отражателем на Луне и телескопом на Земле, если импульс возвратился через 2,43545с? [ из формулы R=(c^.t)/2 R=3^.10^8.2,43545/2≈365317500,92м≈365317,5км]
5. Расстояние от Земли до Луны в перигее 363000км, а в апогее 405000км. Определите горизонтальный параллакс Луны в этих положениях. [ из формулы D=(206265″/p)*R_⊕ отсюда р=(206265″/D)*R_⊕; р_А=(206265″/405000)*6378≈3248,3″≈54,1′, р_П= (206265″/363000)*6378≈3624,1″≈60,4′].
6. Тест с картинками по главе 2.
7. Дополнительно, для тех кто сделал – кроссворд.

Планета СС  [Меркурий] Ближайшая к Земле точка орбиты ИСЗ  [перигей] Ученый, создатель гелиоцентрической системы мира  [Коперник] Угол под которым со светила виден R Земли  [параллакс] Ученый, направивший первым в 1609г телескоп на небо [Галилей] Сторона горизонта  [север]

Итог:
1) Что такое параллакс?
2) Какими способами можно определить расстояние до тел СС?
3) Что такое базис? Что принимается за базис для определения расстояния до тел СС?
4) Как зависит параллакс от удаленности небесного тела?
5) Как зависит размер тела от угла?
6)  Оценки

Домашнее задание: §11; вопросы и задания стр. 52, стр. 52-53 знать и уметь. Повторить полностью вторую главу. СР№6, ПР№4.
Можно задать по данному разделу подготовить кроссворд, опросчик, реферат об одном из ученых-астрономов или истории астрономии (один из вопросов или направлений).
   Можно предложить практическую работу “Определение размера Луны”.
   В период полнолуния, используя две соединенные под прямым углом линейки, определяются видимые размеры лунного диска: поскольку треугольники KCD и КАВ подобны, из теоремы о подобии треугольников следует, что: АВ/СD=KB/KD. Диаметр Луны АВ = (CD^.KB)/KD. Расстояние от Земли до Луны берёте из справочных таблиц (но лучше, если сумеете вычислить его сами).

   Если планируется еще один урок по обобщению материала 2-й главы, то можно предложить:
1. Вопросы экспресс опроса
1. Можно ли наблюдать Меркурий по вечерам на востоке?
2. Что такое соединение?
3. Можно ли наблюдать Венеру утром на востоке, а вечером на западе?
4.Угловое расстояние планеты от Солнца равно 55°.Какая это планета, верхняя или нижняя?
5. Что такое конфигурация?
6. Какие планеты могут пройти на фоне диска Солнца?
7. Во время каких конфигураций хорошо видны нижние планеты?
8. Во время каких конфигураций хорошо видны верхние планеты?
9. Что такое сидерический период планеты?
10. Что такое синодический период?
11. Что такое горизонтальный параллакс?
12. Что называется параллактическим смещением?
13. Когда верхняя планета находится в квадратуре?
14. Что такое элонгация?
15. При каком соединении можно наблюдать внутреннюю планету?
2. Также можно дать . КР№2, Тест №2
 

Урок оформила члены кружка “Интернет-технологии” – Леоненко Катя (11кл)

Изменен 10.11.2009 года

«Планетарий»  410,05 мб	Ресурс позволяет установить на компьютер учителя или учащегося полную версию инновационного учебно-методического комплекса “Планетарий”. “Планетарий” –  подборка тематических статей – предназначены для использования учителями и учащимися на уроках физики, астрономии или естествознания в 10-11 классах.  При установке комплекса рекомендуется использовать только английские буквы в именах папок.
Демонстрационные материалы 13,08 мб	Ресурс представляет собой демонстрационные материалы инновационного учебно-методического комплекса “Планетарий”.
Планетарий 2,67 мб	Данный ресурс представляет собой интерактивную модель “Планетарий”, которая позволяет изучать звездное небо посредством работы с данной моделью. Для полноценного использования ресурса необходимо установить Java Plug-in
Урок	Тема урока	Разработки уроков в коллекции ЦОР	Статистическая графика из ЦОР
Урок 11	Определение расстояния до тел Солнечной системы и размеров этих тел		Параллакс светила 130,1 кб Определение расстояния по параллаксу 128,5 кб

Решебник по астрономии 11 класс на урок №10 (рабочая тетрадь) – Определение расстояний до небесных тел в Солнечной системе и их размеров

1. Закончите предложения.

Для измерения расстояний в пределах Солнечной системы используют астрономическую единицу (а. е.), которая равна среднему расстоянию от Земли до Солнца.

1 а.е. = 149 600 000 км

Расстояние до объекта по времени прохождения радиолокационного сигнала можно определить по формуле , где S = 1/2·ct, где S — расстояние до объекта, c — скорость света, t — время прохождения светила.

2. Дайте определения понятиям «параллакс» и «базис»; на рисунке 10.1 покажите эти величины.

Параллакс — угол p, под которым из недоступного места (точка C) будет виден отрезок AB, называемый базисом.

Базис — тщательно измеренное расстояние от точки A (наблюдатель) до какой-либо достигнутой для наблюдения точки B.

3. Как с помощью понятий параллакса и базиса определить расстояние до удаленного недоступного объекта С (рис. 10.1)?

По величине базиса и прилегающим к нему углам треугольника ABC найти расстояние AC. При измерениях на Земле этот метод называют триангуляцией.

4. Угол, под которым со светила S виден радиус Земли, перпендикулярный лучу зрения, называется горизонтальным параллаксом p (рис, 10.2). Определите расстояния: а) до Луны, если ее горизонтальный параллакс p = 57′; б) до Солнца, горизонтальный параллакс которого p = 8,8″.

Решение.

5. Дополните рисунок 10.3 необходимыми построениями и выведите формулу, позволяющую определить радиус небесного светила (в радиусах Земли), если известны угловой радиус светила p и его горизонтальный параллакс p.

r = D · sin(ρ); R = D · sin(ρ)/sin(p) · R; r = ρ»/p» · R.

6. Решите следующие задачи (при расчетах считайте, что c = 3 · 10⁵ км/с, R₃ = 6370 км).

Вариант 1.

1. Радиолокатор зафиксировал отраженный сигнал от пролетающего вблизи Земли астероида через t — 0,667 с. На каком расстоянии от Земли находился в это время астероид?

2. Определите расстояние от Земли до Марса во время великого противостояния, когда его горизонтальный параллакс p = 23,2″.

3. При наблюдении прохождения Меркурия по диску Солнца определили, что его угловой радиус p = 5,5″, а горизонтальный параллакс p = 14,4″. Определите линейный радиус Меркурия.

Вариант 2.

1. Сигнал, посланный радиолокатором к Венере, возвратился назад через t — 4 мин 36 с. На каком расстоянии в это время находилась Венера в своем нижнем соединении?

Ответ: 41 млн км.

2. На какое расстояние к Земле подлетал астероид Икар, если его горизонтальный параллакс в это время был p = 18,0″?

Ответ: 1,22 млн км.

3. С помощью наблюдений определили, что угловой радиус Марса p = 9,0″, а горизонтальный параллакс p = 16,9″. Определите линейный радиус Марса.

Ответ: 3390 км.