Содержание
- Как найти угловые размеры солнца
- Введение в угловые размеры
- Как найти угловые размеры солнца
- Заключение
- Как найти угловые размеры солнца: подробное руководство
- 1. Использование простейшего инструмента
- 2. Использование отражающего телескопа
- 3. Использование специального электронного оборудования
- 4. Измерение угловых размеров солнца с помощью триангуляции
- Итог
- Как найти угловые размеры солнца
- Способ 1: Использование солнечного затмения
- Способ 2: Использование солнечного диска
- Способ 3: Использование затмений спутников
- Итог
Как найти угловые размеры солнца
Солнце – одно из самых ярких небесных тел нашей планетной системы. Его изучение представляет большой интерес для науки, но также и для любителей астрономии. Чтобы эффективно исследовать эту звезду, необходимо знать ее угловые размеры. Но как их найти?
Введение в угловые размеры
Угловой размер – это угол, занимаемый обьектом на небосводе. Он измеряется в градусах, минутах и секундах и определяет насколько большой объект выглядит на небе. Угловой размер можно рассчитать, используя оптическое оборудование и точные математические формулы.
Как найти угловые размеры солнца
Солнце – это ярчайшее небесное тело в нашей солнечной системе. Его угловой размер может быть вычислен по формуле:
Угловой размер = диаметр солнца / расстояние от Земли до Солнца
Для измерения диаметра солнца следует использовать специальные солнечные фильтры. Они необходимы для безопасного измерения размера солнца. Без использования фильтра можно получить травмы глаз.
Расстояние от Земли до Солнца называется астрономическим единицей (А.Е.). Оно равно приблизительно 149,6 миллионов километров. Для более точных измерений расстояния можно использовать радары и другое оборудование, которое позволяет измерить время, требующееся для прохождения радиоволн от Земли до Солнца и обратно.
После того, как диаметр солнца и расстояние от Земли до Солнца были измерены, можно использовать формулу, описанную выше, для вычисления углового размера солнца.
Заключение
Найти угловые размеры солнца довольно интересно и важно для любителей астрономии и профессиональных ученых. Для этого необходимо использовать определенное оборудование и правильные математические формулы. Мы рекомендуем изучить эту тему более детально, чтобы лучше понимать небесные явления и улучшить навыки астрономии.
Как найти угловые размеры солнца: подробное руководство
Наблюдение солнца может быть захватывающей и поучительной деятельностью, особенно если вы понимаете, какие параметры вы можете измерить. Одним из наиболее важных параметров являются угловые размеры солнца. Эти измерения могут быть использованы для определения расстояния до солнца, его размера и других свойств. В данной статье мы рассмотрим различные методы для измерения угловых размеров солнца.
1. Использование простейшего инструмента
Чтобы определить угловые размеры солнца, можно использовать самый простой инструмент — ваш палец. Выставьте руку так, чтобы ваш палец был вытянут вверху. Закройте один глаз и найдите солнце в поле зрения. Далее сравните размеры солнца и вашего пальца. Это может помочь вам оценить угловые размеры солнца.
2. Использование отражающего телескопа
Отражательный телескоп может быть использован для измерения угловых размеров солнца. Для начала необходимо настроить телескоп на солнечное излучение. Затем измерьте диаметр изображения солнца на экране телескопа. Это даст вам угловой размер.
3. Использование специального электронного оборудования
Существует также специальное электронное оборудование, которое может быть использовано для измерения угловых размеров солнца. Это может быть полезным инструментом для людей, которые занимаются научной работой, но не обязательно для обычных наблюдателей.
4. Измерение угловых размеров солнца с помощью триангуляции
Метод триангуляции может быть использован для измерения угловых размеров солнца. Для выполнения этого метода необходимо иметь два точных наблюдения в разных местах на Земле одновременно. Это даст вам возможность измерить углы на земной поверхности, которые можно использовать для расчета угловых размеров солнца.
Итог
Наблюдение за солнцем может быть увлекательным и интересным занятием. Измерение угловых размеров солнца может помочь вам получить более полное представление о солнечной системе и ее свойствах. В этой статье мы рассмотрели различные методы измерения угловых размеров солнца, от использования простых инструментов, таких как палец, до специального электронного оборудования. Используйте эти методы, чтобы узнать больше о солнце и его свойствах!
Как найти угловые размеры солнца
Солнце — наша ближайшая звезда и один из наиболее важных объектов в нашей солнечной системе. Найдя угловые размеры солнца, мы можем определить его удаленность и диаметр, а также использовать эту информацию для многих других научных расчетов. Но как это сделать? Ниже мы рассмотрим несколько способов.
Способ 1: Использование солнечного затмения
Солнечное затмение происходит, когда Луна перекрывает Солнце, что образует затмение. Это даёт ученым отличную возможность измерить размеры и удаленность Солнца с высокой точностью. Угловое расстояние между Солнцем и Луной можно измерять, используя специальные инструменты, такие как астрономический телескоп или спутниковые наблюдения. Поскольку затмение Солнца происходит не так часто, это не самый практичный способ для определения размеров Солнца, но он даёт наиболее точные результаты.
Способ 2: Использование солнечного диска
Другой способ определения размера Солнца — это измерения диаметра солнечного диска, когда он проходит через некоторые фиксированные точки на земле. Точная триангуляция позволяет вычислить размеры Солнца. Это можно сделать, используя солнечные фильтры на телескопе или с помощью специальных приборов, таких как гелиоскопы. Несмотря на то, что этот способ не настолько точен, как использование солнечного затмения, он является более доступным и практичным.
Способ 3: Использование затмений спутников
Солнечные затмения не единственные затмения, которые можно использовать для определения размеров Солнца. Затмения спутников других планет в нашей солнечной системе, таких как Юпитер или Сатурн, также могут помочь в измерении Солнца. Затмения этих спутников происходят намного чаще, чем затмения солнца, и хотя они происходят под другими углами, это все равно дает ученым возможность получить достаточно точные измерения размеров Солнца.
Итог
Существует несколько способов, с помощью которых можно определить угловые размеры солнца. Самый точный способ — это использование солнечного затмения, но это происходит не так часто, как хотелось бы. Измерение диаметра солнечного диска является более доступным способом, а также можно использовать затмения спутников других планет. Независимо от выбранного метода, эти измерения позволяют нам лучше понимать нашу ближайшую звезду и мир вокруг нас.
From Wikipedia, the free encyclopedia
The angular diameter, angular size, apparent diameter, or apparent size is an angular distance describing how large a sphere or circle appears from a given point of view. In the vision sciences, it is called the visual angle, and in optics, it is the angular aperture (of a lens). The angular diameter can alternatively be thought of as the angular displacement through which an eye or camera must rotate to look from one side of an apparent circle to the opposite side. Humans can resolve with their naked eyes diameters of up to about 1 arcminute (approximately 0.017° or 0.0003 radians).[1] This corresponds to 0.3 m at a 1 km distance, or to perceiving Venus as a disk under optimal conditions.
Formula[edit]
Diagram for the formula of the angular diameter
The angular diameter of a circle whose plane is perpendicular to the displacement vector between the point of view and the center of said circle can be calculated using the formula[2]
in which 




For a spherical object whose actual diameter equals 

The difference is due to the fact that the apparent edges of a sphere are its tangent points, which are closer to the observer than the center of the sphere. The difference is significant only for spherical objects of large angular diameter, since the following small-angle approximations hold for small values of 
Estimating angular diameter using the hand[edit]
Approximate angles of 10°, 20°, 5°, and 1° for the hand outstretched arm’s length
Estimates of angular diameter may be obtained by holding the hand at right angles to a fully extended arm, as shown in the figure.[4][5][6]
Use in astronomy[edit]
Angular diameter: the angle subtended by an object
In astronomy, the sizes of celestial objects are often given in terms of their angular diameter as seen from Earth, rather than their actual sizes. Since these angular diameters are typically small, it is common to present them in arcseconds (″). An arcsecond is 1/3600th of one degree (1°) and a radian is 180/π degrees. So one radian equals 3,600 × 180/
.
These objects have an angular diameter of 1″:
- an object of diameter 1 cm at a distance of 2.06 km
- an object of diameter 725.27 km at a distance of 1 astronomical unit (AU)
- an object of diameter 45 866 916 km at 1 light-year
- an object of diameter 1 AU (149 597 871 km) at a distance of 1 parsec (pc)
Thus, the angular diameter of Earth’s orbit around the Sun as viewed from a distance of 1 pc is 2″, as 1 AU is the mean radius of Earth’s orbit.
The angular diameter of the Sun, from a distance of one light-year, is 0.03″, and that of Earth 0.0003″. The angular diameter 0.03″ of the Sun given above is approximately the same as that of a human body at a distance of the diameter of Earth.
This table shows the angular sizes of noteworthy celestial bodies as seen from Earth:
| Celestial object | Angular diameter or size | Relative size |
|---|---|---|
| Magellanic Stream | over 100° | |
| Gum Nebula | 36° | |
| Milky Way | 30° (by 360°) | |
| Width of spread out hand with arm streched out | 20° | 353 meter at 1 km distance |
| Serpens-Aquila Rift | 20° by 10° | |
| Canis Major Overdensity | 12° by 12° | |
| Smith’s Cloud | 11° | |
| Large Magellanic Cloud | 10.75° by 9.17° | Note: brightest galaxy, than the Milky Way, in the night sky (0.9 apparent magnitude (V)) |
| Barnard’s loop | 10° | |
| Zeta Ophiuchi Sh2-27 nebula | 10° | |
| Width of fist with arm streched out | 10° | 175 meter at 1 km distance |
| Sagittarius Dwarf Spheroidal Galaxy | 7.5° by 3.6° | |
| Northern Coalsack Nebula | 7° by 5°[8] | |
| Coalsack nebula | 7° by 5° | |
| Cygnus OB7 | 4° by 7°[9] | |
| Rho Ophiuchi cloud complex | 4.5° by 6.5° | |
| Hyades | 5°30′ | Note: brightest star cluster in the night sky, 0.5 apparent magnitude (V) |
| Small Magellanic Cloud | 5°20′ by 3°5′ | |
| Andromeda Galaxy | 3°10′ by 1° | About six times the size of the Sun or the Moon. Only the much smaller core is visible without long-exposure photography. |
| Veil Nebula | 3° | |
| Heart Nebula | 2.5° by 2.5° | |
| Westerhout 5 | 2.3° by 1.25° | |
| Sh2-54 | 2.3° | |
| Carina Nebula | 2° by 2° | Note: brightest nebula in the night sky, 1.0 apparent magnitude (V) |
| North America Nebula | 2° by 100′ | |
| In the Moon’s sky the apparent size of Earth | 2° – 1°48′[10] | Appearing about three to four times larger than the Moon in Earth’s sky |
| Orion Nebula | 1°5′ by 1° | |
| Width of little finger with arm streched out | 1° | 17.5 meter at 1 km distance |
| Moon | 34′6″ – 29′20″ | 32.5–28 times the maximum value for Venus (orange bar below) / 2046–1760″ the Moon has a diameter of 3,474 km |
| Sun | 32′32″ – 31′27″ | 31–30 times the maximum value for Venus (orange bar below) / 1952–1887″ the Sun has a diameter of 1,391,400 km |
| Helix Nebula | about 16′ by 28′ | |
| Spire in Eagle Nebula | 4′40″ | length is 280″ |
| Venus | 1′6″ – 0′9.7″ |
|
| International Space Station (ISS) | 1′3″ | ;[11] the ISS has a width of about 108 m |
| Maximum resolvable diameter by the human eye | 1′ | ;[12] 0.3 meter at 1 km distance[13] |
| About 100 km on the surface of the Moon | 1′ | Comparable to the size of features like large lunar craters, such as the Copernicus crater, a prominent bright spot in the eastern part of Oceanus Procellarum on the waning side, or the Tycho crater within a bright area in the south, of the lunar near side. |
| Jupiter | 50.1″ – 29.8″ |
|
| Maximum resolvable point/gap by the human eye | 40″ | ;[12] at close view the width of a 0.04 mm very thin hair[13] |
| Mars | 25.1″ – 3.5″ |
|
| Saturn | 20.1″ – 14.5″ |
|
| Mercury | 13.0″ – 4.5″ |
|
| Uranus | 4.1″ – 3.3″ |
|
| Neptune | 2.4″ – 2.2″ |
|
| Ganymede | 1.8″ – 1.2″ |
Ganymede has a diameter of 5,268 km |
| An astronaut (~1.7 m) at a distance of 350 km, the average altitude of the ISS | 1″ | |
| Maximum resolvable diameter by Galileo Galilei’s largest 38mm refracting telescopes | ~1″ | ;[14] Note: 30x[15] magnification, comparable to very strong contemporary terrestrial binoculars |
| Ceres | 0.84″ – 0.33″ |
|
| Vesta | 0.64″ – 0.20″ |
|
| Pluto | 0.11″ – 0.06″ |
|
| Eris | 0.089″ – 0.034″ |
|
| R Doradus | 0.062″ – 0.052″ |
Note: R Doradus is thought to be the extrasolar star with the largest apparent size as viewed from Earth |
| Betelgeuse | 0.060″ – 0.049″ |
|
| Alphard | 0.00909″ |
|
| Rho Cassiopeiae | 0.0072″ |
|
| Alpha Centauri A | 0.007″ |
|
| Canopus | 0.006″ |
|
| Sirius | 0.005936″ |
|
| Altair | 0.003″ |
|
| Deneb | 0.002″ |
|
| Proxima Centauri | 0.001″ |
|
| Alnitak | 0.0005″ | |
| Proxima Centauri b | 0.00008″ | |
| Event horizon of black hole M87* at center of the M87 galaxy, imaged by the Event Horizon Telescope in 2019. | 0.000025″
(2.5×10−5) |
Comparable to a tennis ball on the Moon |
| A star like Alnitak at a distance where the Hubble Space Telescope would just be able to see it[16] | 6×10−10 arcsec |
Log-log plot of aperture diameter vs angular resolution at the diffraction limit for various light wavelengths compared with various astronomical instruments. For example, the blue star shows that the Hubble Space Telescope is almost diffraction-limited in the visible spectrum at 0.1 arcsecs, whereas the red circle shows that the human eye should have a resolving power of 20 arcsecs in theory, though normally only 60 arcsecs.
Comparison of angular diameter of the Sun, Moon and planets. To get a true representation of the sizes, view the image at a distance of 103 times the width of the “Moon: max.” circle. For example, if this circle is 5 cm wide on your monitor, view it from 5.15 m away.
The table shows that the angular diameter of Sun, when seen from Earth is approximately 32′ (1920″ or 0.53°), as illustrated above.
Thus the angular diameter of the Sun is about 250,000 times that of Sirius. (Sirius has twice the diameter and its distance is 500,000 times as much; the Sun is 1010 times as bright, corresponding to an angular diameter ratio of 105, so Sirius is roughly 6 times as bright per unit solid angle.)
The angular diameter of the Sun is also about 250,000 times that of Alpha Centauri A (it has about the same diameter and the distance is 250,000 times as much; the Sun is 4×1010 times as bright, corresponding to an angular diameter ratio of 200,000, so Alpha Centauri A is a little brighter per unit solid angle).
The angular diameter of the Sun is about the same as that of the Moon. (The Sun’s diameter is 400 times as large and its distance also; the Sun is 200,000 to 500,000 times as bright as the full Moon (figures vary), corresponding to an angular diameter ratio of 450 to 700, so a celestial body with a diameter of 2.5–4″ and the same brightness per unit solid angle would have the same brightness as the full Moon.)
Even though Pluto is physically larger than Ceres, when viewed from Earth (e.g., through the Hubble Space Telescope) Ceres has a much larger apparent size.
Angular sizes measured in degrees are useful for larger patches of sky. (For example, the three stars of the Belt cover about 4.5° of angular size.) However, much finer units are needed to measure the angular sizes of galaxies, nebulae, or other objects of the night sky.
Degrees, therefore, are subdivided as follows:
- 360 degrees (°) in a full circle
- 60 arc-minutes (′) in one degree
- 60 arc-seconds (″) in one arc-minute
To put this in perspective, the full Moon as viewed from Earth is about 1⁄2°, or 30′ (or 1800″). The Moon’s motion across the sky can be measured in angular size: approximately 15° every hour, or 15″ per second. A one-mile-long line painted on the face of the Moon would appear from Earth to be about 1″ in length.
Minimum, mean and maximum distances of the Moon from Earth with its angular diameter as seen from Earth’s surface, to scale
In astronomy, it is typically difficult to directly measure the distance to an object, yet the object may have a known physical size (perhaps it is similar to a closer object with known distance) and a measurable angular diameter. In that case, the angular diameter formula can be inverted to yield the angular diameter distance to distant objects as
In non-Euclidean space, such as our expanding universe, the angular diameter distance is only one of several definitions of distance, so that there can be different “distances” to the same object. See Distance measures (cosmology).
Non-circular objects[edit]
Many deep-sky objects such as galaxies and nebulae appear non-circular and are thus typically given two measures of diameter: major axis and minor axis. For example, the Small Magellanic Cloud has a visual apparent diameter of 5° 20′ × 3° 5′.
Defect of illumination[edit]
Defect of illumination is the maximum angular width of the unilluminated part of a celestial body seen by a given observer. For example, if an object is 40″ of arc across and is 75% illuminated, the defect of illumination is 10″.
See also[edit]
- Angular diameter distance
- Angular resolution
- Solid angle
- Visual acuity
- Visual angle
- Perceived visual angle
- List of stars with resolved images
- Apparent magnitude
References[edit]
- ^ Yanoff, Myron; Duker, Jay S. (2009). Ophthalmology 3rd Edition. MOSBY Elsevier. p. 54. ISBN 978-0444511416.
- ^ This can be derived using the formula for the length of a cord found at “Circular Segment”. Archived from the original on 2014-12-21. Retrieved 2015-01-23.
- ^ “A Taylor series for the functionarctan” (PDF). Archived from the original (PDF) on 2015-02-18. Retrieved 2015-01-23.
- ^ “Coordinate Systems”. Archived from the original on 2015-01-21. Retrieved 2015-01-21.
- ^ “Photographing Satellites”. 8 June 2013. Archived from the original on 21 January 2015.
- ^ Wikiversity: Physics and Astronomy Labs/Angular size
- ^ Michael A. Seeds; Dana E. Backman (2010). Stars and Galaxies (7 ed.). Brooks Cole. p. 39. ISBN 978-0-538-73317-5.
- ^ O’Meara, Stephen James (2019-08-06). “The coalsacks of Cygnus”. Astronomy.com. Retrieved 2023-02-10.
- ^ Dobashi, Kazuhito; Matsumoto, Tomoaki; Shimoikura, Tomomi; Saito, Hiro; Akisato, Ko; Ohashi, Kenjiro; Nakagomi, Keisuke (2014-11-24). “Colliding Filaments and a Massive Dense Core in the Cygnus Ob 7 Molecular Cloud”. The Astrophysical Journal. American Astronomical Society. 797 (1): 58. doi:10.1088/0004-637x/797/1/58. ISSN 1538-4357. S2CID 118369651.
- ^ Gorkavyi, Nick; Krotkov, Nickolay; Marshak, Alexander (2023-03-24). “Earth observations from the Moon’s surface: dependence on lunar libration”. Atmospheric Measurement Techniques. Copernicus GmbH. 16 (6): 1527–1537. doi:10.5194/amt-16-1527-2023. ISSN 1867-8548.
- ^ “Problem 346: The International Space Station and a Sunspot: Exploring angular scales” (PDF). Space Math @ NASA !. 2018-08-19. Retrieved 2022-05-20.
- ^ a b Wong, Yan (2016-01-24). “How small can the naked eye see?”. BBC Science Focus Magazine. Retrieved 2022-05-23.
- ^ a b “Sharp eyes: how well can we really see?”. Science in School – scienceinschool.org. 2016-09-07. Retrieved 2022-05-23.
- ^ Graney, Christopher M. (Dec 10, 2006). “The Accuracy of Galileo’s Observations and the Early Search for Stellar Parallax”. arXiv:physics/0612086. doi:10.1007/3-540-50906-2_2.
- ^ “Galileo’s telescope – How it works”. Esposizioni on-line – Istituto e Museo di Storia della Scienza (in Italian). Retrieved May 21, 2022.
- ^ 800 000 times smaller angular diameter than that of Alnitak as seen from Earth. Alnitak is a blue star so it gives off a lot of light for its size. If it were 800 000 times further away then it would be magnitude 31.5, at the limit of what Hubble can see.
External links[edit]
- Small-Angle Formula
- Visual Aid to the Apparent Size of the Planets
Угловой диаметр, угловой размер, кажущийся диаметр, или кажущийся размер – угловое измерение, описывающее, насколько большой сфера или круг выглядит с данной точки зрения. В науках о зрении это называется углом обзора, а в оптике это угловая апертура (из объектив ). В качестве альтернативы угловой диаметр можно рассматривать как угол, на который глаз или камера должны повернуться, чтобы смотреть с одной стороны видимого круга на противоположную. Угловой радиус равен половине углового диаметра.
Содержание
- 1 Формула
- 2 Оценка углового диаметра с помощью руки
- 3 Использование в астрономии
- 3.1 Некруглые объекты
- 3.2 Дефект освещения
- 4 См. Также
- 5 Ссылки
- 6 Внешние ссылки
Формула

Угловой диаметр окружности, плоскость которой перпендикулярна вектору смещения между точкой вид и центр указанного круга можно рассчитать по формуле
- δ = 2 arctan (d 2 D), { displaystyle delta = 2 arctan left ({ frac {d} {2D}} справа),}
, где δ { displaystyle delta}




. Для сферического объекта, фактический диаметр которого равен dact, { displaystyle d _ { mathrm {act}},}

- δ = 2 arcsin (dact 2 D) { displaystyle delta = 2 arcsin left ({ frac {d _ { mathrm {act}}} {2D}} right)}
Разница в том, что видимые края сферы являются точками касания, которые находятся ближе к наблюдателю, чем к центру сферы. Для практического использования различие имеет значение только для сферических объектов, которые находятся относительно близко, поскольку приближение малых углов справедливо для x ≪ 1 { displaystyle x ll 1}
- arcsin x ≈ arctan x ≈ x { displaystyle arcsin x приблизительно arctan x приблизительно x}
.
Оценка углового диаметра с помощью руки

Оценки углового диаметра могут быть получены, если держать руку под прямым углом к полностью вытянутой руке, как показано на рисунке.
Использование в астрономии
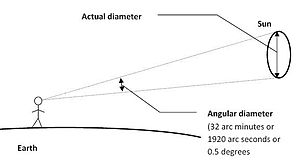
В астрономии размеры небесных объектов часто задаются в терминах их углового диаметра, как видно из Земля, а не их реальные размеры. Поскольку эти угловые диаметры обычно малы, их принято представлять в угловых секундах (″). Угловая секунда равна 1/3600 одной градуса (1 °), а радиан – 180 / π { displaystyle pi}

- δ = 206, 265 (d / D) arcseconds { displaystyle delta = 206,265 ~ (d / D) ~ mathrm {arcseconds}}
.
Эти объекты имеют угловой диаметр 1 ″:
- объект диаметром 1 см на расстоянии 2,06 км
- объект диаметром 725,27 км на расстоянии 1 астрономическая единица (AU)
- объект диаметром 45 866 916 км на расстоянии 1 светового года
- объект диаметром 1 AU (149 597 871 км) на расстоянии 1 парсек (пк)
Таким образом, угловой диаметр орбиты Земли вокруг Солнца, если смотреть с расстояния в 1 пк, равен 2 ″, поскольку 1 а.е. радиус орбиты Земли.
Угловой диаметр Солнца с расстояния в один световой год составляет 0,03 ″, а диаметр Ea rth 0,0003 ″. Угловой диаметр Солнца 0,03 дюйма, указанный выше, примерно такой же, как у человеческого тела на расстоянии диаметра Земли.
В этой таблице показаны угловые размеры примечательных небесных тел как видно с Земли:
| Небесное тело | Угловой диаметр или размер | Относительный размер |
|---|---|---|
| Галактика Андромеды | 3 ° 10 ′ на 1 ° | Примерно в шесть раз больше Солнца или Луны. Без фотографии с большой выдержкой. |
| Солнце | 31′27 ″ – 32′32 ″ | в 30–31 раз больше максимального значения для Венеры (внизу) / 1887–1952 ″ |
| Луна | 29′20 ″ – 34′6 ″ | в 28–32,5 раза больше максимального значения для Венеры (оранжевая полоса внизу) / 1760–2046 ″ |
| Туманность Хеликс | примерно 16 ‘на 28’ | |
| Шпиль в туманности Орла | 4’40 ″ | длина 280 ″ |
| Венера | 9,7 ″ – 1 ′ 6 ″ |
|
| Юпитер | 29,8 ″ – 50,1 ″ |
|
| Сатурн | 14,5 ″ – 20,1 ″ |
|
| Марс | 3,5 ″ – 25,1 ″ |
|
| Меркурий | 4,5 ″ – 13,0 ″ |
|
| Уран | 3,3–4,1 дюйма |
|
| Нептун | 2,2–2,4 дюйма |
|
| Церера | 0,33–0,84 дюйма |
|
| Веста | 0,20–0,64 дюйма |
|
| Плутон | 0,06 ″ – 0,11 ″ |
|
| R Doradus | 0,052 ″ – 0,062 ″ |
|
| Бетельгейзе | 0,049 ″ – 0,060 ″ |
|
| Эрис | 0,034 ″ – 0,089 ″ |
|
| Alphard | 0,00909 ″ |
|
| Альфа Центавра A | 0,007 ″ |
|
| Канопус | 0,006 ″ |
|
| Сириус | 0,005936 ″ |
|
| Альтаир | 0,003 ″ |
|
| Денеб | 0,002 ″ |
|
| Проксима Центавра | 0,001 ″ |
|
| Алнитак | 0,000 5 ″ | |
| Горизонт событий черной дыры M87 * в центре галактики M87, полученный телескопом Event Horizon Telescope в 2019 году. | 0,000025 ″
(2,5 × 10) |
|
| Звезда, подобная Альнитак, на таком расстоянии, на котором космический телескоп Хаббл сможет ее увидеть | 6 × 10 угловых секунд |


Таблица показывает, что угловой диаметр Солнца, если смотреть с Земли, составляет приблизительно 32 ‘(1920 ″ или 0,53 °), как показано выше.
Таким образом, угловой диаметр Солнца примерно в 250 000 раз больше, чем у Сириуса. (Сириус имеет вдвое больший диаметр, а расстояние до него в 500000 раз больше; Солнце в 10 раз ярче, что соответствует соотношению угловых диаметров 10, поэтому Сириус примерно в 6 раз ярче на единицу телесного угла.)
Угловой диаметр Солнца также примерно в 250 000 раз больше, чем у Альфа Центавра A (у него примерно такой же диаметр, а расстояние в 250 000 раз больше; Солнце 4 В 10 раз ярче, что соответствует соотношению угловых диаметров 200000, поэтому Альфа Центавра A немного ярче на единицу телесного угла).
Угловой диаметр Солнца примерно такой же, как у Луны. (Диаметр Солнца в 400 раз больше, равно как и расстояние до него; Солнце в 200000-500000 раз ярче полной Луны (цифры меняются), что соответствует отношению углового диаметра от 450 до 700, то есть небесное тело с диаметром 2,5–4 ″ и такой же яркости на единицу телесного угла будет иметь такую же яркость, как полная Луна.)
Даже несмотря на то, что Плутон физически больше Цереры, если смотреть с Земли (например, через Космический телескоп Хаббла ) Церера имеет гораздо больший видимый размер.
Угловые размеры, измеряемые в градусах, полезны для больших участков неба. (Например, три звезды Пояса покрывают угловой размер около 4,5 °.) Однако для измерения угловых размеров галактик, туманностей или других объектов требуются гораздо более точные единицы измерения. ночное небо.
Следовательно, градусы подразделяются следующим образом:
- 360 градусов (°) по полному кругу
- 60 угловые минуты (′) в один градус
- 60 угловых секунд (″) за одну угловую минуту
Чтобы представить это в перспективе, полная Луна, если смотреть с Земли составляет около ⁄ 2 °, или 30 ‘(или 1800 ″). Движение Луны по небу можно измерить по угловому размеру: примерно 15 ° каждый час или 15 дюймов в секунду. Линия длиной в одну милю, нарисованная на лице Луны, будет казаться с Земли примерно 1 дюйм в длину.

В астрономии обычно трудно напрямую измерить расстояние до объекта, но объект может иметь известный физический размер (возможно, он похож на более близкий объект с известным расстоянием) и измеримый угловой диаметр. В этом случае формулу углового диаметра можно инвертировать, чтобы получить расстояние по угловому диаметру до удаленных объектов как
- d ≡ 2 D tan (δ 2) { displaystyle d Equiv 2D tan left ({ frac { delta} {2}} right)}
.
В неевклидовом пространстве, таком как наша расширяющаяся Вселенная, расстояние по угловому диаметру является лишь одним из нескольких определений расстояния, так что может быть разные «расстояния» до одного и того же объекта. См. Измерения расстояния (космология).
Некруглые объекты
Многие объекты глубокого космоса, такие как галактики и туманности кажутся некруглыми и, таким образом, обычно имеют две меры диаметра: большую ось и малую ось. Например, Малое Магелланово Облако имеет видимый диаметр 5 ° 20 ′ × 3 ° 5 ′.
Дефект освещения
Дефект освещения – максимальная угловая ширина неосвещенной части небесного тела, видимой данным наблюдателем. Например, если объект имеет диаметр 40 дюймов по дуге и освещен на 75%, дефект освещения составляет 10 дюймов.
См. Также
- Расстояние углового диаметра
- Угловое разрешение
- Телесный угол
- Острота зрения
- Угол зрения
- Иллюзия угла зрения
- Список звезд с разрешенными изображениями
Ссылки
Внешние ссылки
- Формула малого угла
- Наглядное указание на видимый размер планет
В журнале “Наука и жизнь” № 12 за 2006 год на просьбу читателя В. Билетова объяснить, почему сильно меняется диаметр Солнца в течение суток, дан ответ, что диаметр Солнца всегда постоянен – это действительно так, и он равен 1/108 радиана. Но размер Солнца все-таки кажется нам гораздо больше при восходе и закате. Угловые размеры Солнца и Луны около горизонта воспринимаются нами в 2,5-3,5 раза большими, чем когда они высоко в небе.
В книге М. Миннарта “Свет и цвет в природе” объясняется этот психологический эффект: кажущаяся сплюснутость небесного свода. Мы воспринимаем Солнце и Луну на таком же расстоянии, как и окружающее их небо, поэтому низкое Солнце представляется нам во много раз дальше, чем высокое. Так как его угловой размер остается одинаковым, мы бессознательно приписываем Солнцу в несколько раз большую величину. Кажущаяся форма неба – определяющий фактор в видимом размере Солнца.
Определить угловой размер Солнца безопасным методом можно, измерив параметры его проекции от небольшого отверстия, например от листвы деревьев. В этом случае его угловой размер
С = D / L (в радианах),
где D – диаметр проекции Солнца на экран; L – расстояние от отверстия до экрана.
Любопытно, что угловые размеры Солнца и Луны приблизительно совпадают, что позволяет наблюдать корону Солнца во время его полного затмения.
Угловой размер (иногда также угол зрения) — это угол между прямыми линиями, соединяющими диаметрально противоположные крайние точки измеряемого (наблюдаемого) объекта и глаз наблюдателя.
Под угловым размером может также пониматься не плоский угол, под которым виден объект, а телесный угол.
В геометрии[править | править код]
Если отрезок длиной D перпендикулярен линии наблюдения (более того, она является серединным его перпендикуляром) и находится на расстоянии L от наблюдателя, то точная формула для углового размера этого отрезка: 

Понятие углового размера очень важно в геометрической оптике, и в особенности применительно к органу зрения — глазу. Глаз способен регистрировать именно угловой размер объекта. Его реальный, линейный размер определяется мозгом по оценке расстояния до объекта и из сравнения с другими, уже известными телами.
Согласно геометрии предмет, удалённый от глаза на расстояние, в 57 раз большее его поперечника, должен представляться наблюдателю под углом почти в 1°.
В астрономии[править | править код]
Сравнение угловых размеров Солнца, Луны и планет. Размеры приведены в угловых минутах (‘) и секундах (“) Иллюстрация приведена не в масштабе: для того, чтобы получить точное представление о размерах, нужно рассматривать это изображение с расстояния, в 102.6 раз превышающего ширину кружка «Moon: max.». Например, если диаметр этого кружка на вашем мониторе составляет 10 см, то смотреть следует с расстояния 10,26 м.
Угловой размер астрономического объекта, видимый с Земли, обычно называется угловым диаметром или видимым диаметром. Вследствие удалённости всех объектов, угловые диаметры планет и звёзд очень малы и измеряются в угловых минутах (′) и секундах(″). Например, средний видимый диаметр Луны равен 31′05″ (вследствие эллиптичности лунной орбиты угловой размер изменяется от 29′20″ до 33′32″), или 
См. также[править | править код]
- Угловое разрешение
- Арктангенс
- Глаз
Примечания[править | править код]
- ↑ Климишин И. А. Астрономия наших дней. — Рипол Классик, 1980. — С. 99. — 561 с.
Ссылки[править | править код]
- Малоугловые формулы (англ.)
- Видимый размер планет (англ.)












 .
. .
.
