Как найти угловую скорость блока - Сайт, где вы сможете решить свои вопросы

2017-10-27

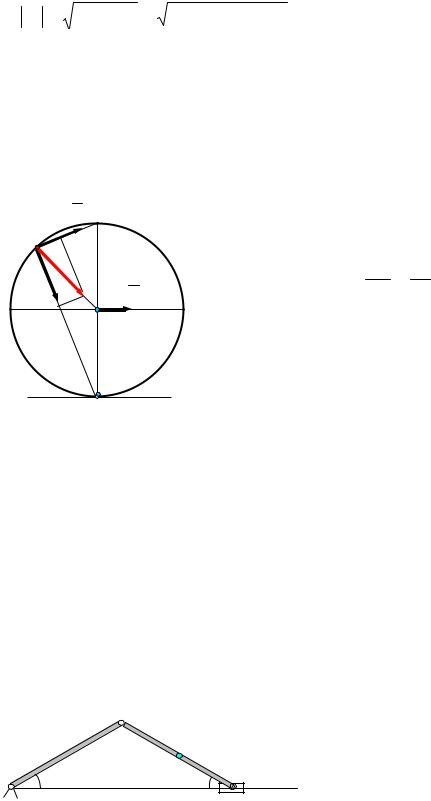
Найти угловую скорость блока (диаметр 10 см) машины Атвуда через 10 сек после начала движения грузов, если более тяжелый груз опустился за это время на 0,5 м (рис.).

Решение:

Линейная скорость $v$ какой-либо точки вращающегося тела, кратчайшее расстояние этой точки от оси вращения $r$ и его угловая скорость $omega$ связаны формулой

$omega = frac{v}{r}$,

где $r$ — кратчайшее расстояние от оси вращения до точки вращающегося тела.

Для определения со необходимо найти только линейную скорость какой-либо точки обода блока.

Очевидно, линейная скорость точки обода блока в любой момент времени будет равна скорости движения грузов при отсутствии скольжения нити.

Так как грузы движутся под действием постоянной силы, равной разности весов грузов, то движение их будет равноускоренным. Поэтому скорость их, а следовательно, и скорость точек обода блока через $t$ секунд после начала движения составит

$v = at$,

где $a$ — ускорение, с которым движутся грузы. Из выражения

$s = frac{at^{2}}{2}$

найдем ускорение $a$:

$a = frac{2s}{t^{2}}$.

Подставив в уравнение $v = at$ вместо $a$ его значение, получим

$v = frac{2s}{t}$.

Подставив это выражение в первое уравнение, найдем

$omega = frac{2s}{rt}$.

Произведем вычисления

$omega = frac{2 cdot 0,5 сек}{0,05 м cdot 10 сек } = 2 сек^{-1}$.

Источник

Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.

Обозначение угловой скорости: ω (омега).

Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.

С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.

Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:

Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.

Быстрота изменения угла φ (перемещения плоскости П из положения П₁ в положение П₂) – это и есть угловая скорость:

Приняв вектор k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

если известно количество оборотов n за единицу времени t:
если задан угол поворота φ за единицу времени:
если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:

Размерности угловой скорости:

Количество оборотов за единицу времени [об/мин], [c^-1].
Угол поворота за единицу времени [рад/с].

Определение угловой скорости

Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.

Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.

Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.

Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.

Другие примеры решения задач >

Угловое ускорение

Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:

Обозначение: ε (Эпсилон)

Единицы измерения углового ускорения: [рад/с²], [с^-2]

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

Расчет углового ускорения

Пример: По заданному значению касательной составляющей полного ускорения a_τ точки B, расположенной на расстоянии r от центра вращения колеса.

Требуется определить величину и направление углового ускорения колеса ε, если a_τ = 10 м/с², r = 50 см.

Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.

Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

ω = 1,5 с^-1 = 9,42 рад/с.

Смотрите также:

Примеры расчета угловой скорости и ускорения
Скорости и ускорения точек вращающегося тела

Источник

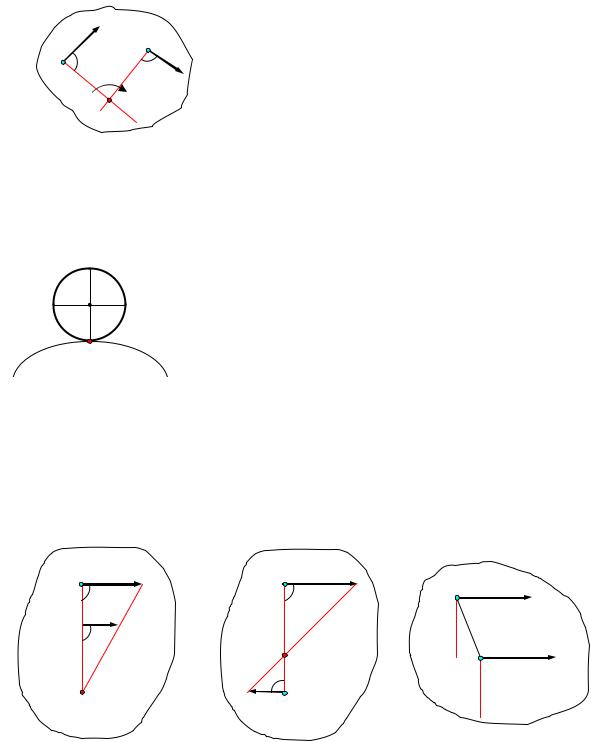
Рис.12

Способы нахождения мгновенного центра скоростей

Для определения положения мгновенного центра скоростей плоской фигуры необходимо знать только направления скоростей двух ее точек.

Указанные свойства позволяют определить положение мгновенного центра скоростей плоской фигуры в различных случаях.

	VA		1. Если скорости двух точек не параллельны,
А	В	VB	то мгновенный центр скоростей лежит в точке
900	пересечения перпендикуляров к ним, что следует из
	900
			теоремы о существовании мгновенного центра ско-

Рростей (рис.12).

2. Если плоское движение осуществляется

качением без скольжения одного твердого тела по неподвижной поверхности другого, то точка их контакта Р имеет в данный момент скорость, равную нулю, и, следовательно, будет мгновен-

ным центром скоростей (рис.13).

3. Если скорости двух точек А и В плоской фигуры параллельны и с прямой, соединяющей эти точки, составляют прямые углы, то мгновенный центр скоростей Р находится как точка пересечения об-

Рщего перпендикуляра, восстановленного к скоро-

Рис.13	стям в данных точках, и прямой, проходящей через
концы векторов скоростей (рис.14 и рис.15).

4. Если скорости двух точек параллельны и с прямой, соединяющей точки образуют острые углы, то мгновенный центр скоростей не суще-

ствует (находится в бесконечности). В этом случае скорости всех точек плоской фигуры равны, а угловая скорость равна нулю (рис. 16).

А	VA	А		VA	А	VA
90	0	90	0

В 90V0B

Р VB

Р	900
В
	VB
Рис. 14	Рис. 15	Рис. 16

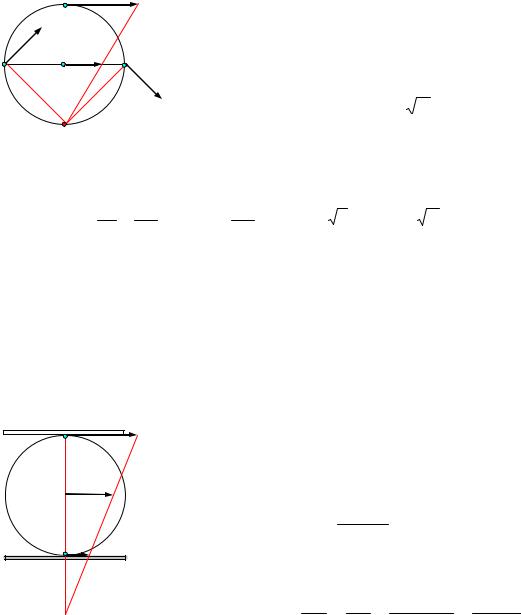
Решение задач с помощью мгновенного центра скоростей.

Задача 1. Найти скорости точек А, В и D обода колеса, катящегося по прямолинейному рельсу без скольжения, если скорость центра колеса С равна VC.

Определить скорости точек А, В, D и угловую скорость колеса.

Решение. Мгновенный центр скоростей

Р колеса находится (рис.177) в

точке контакта колеса с неподвижной плоскостью. Скорости точек А, В, D

перпендикулярны к отрезкам, соединяющим эти

точки с точкой Р, модули скоростей пропорцио-

нальны их длинам:

Расстояния точек А и В до мгновенного цен-

тра скоростей одинаковы,

следовательно, скоро-

сти этих точек равны

VA =VB =VC

Скорость точки D равна 2VC , так как рас-

стояние точки D

до мгновенного центра скоро-

Рис.17

VA =

стей в два раза больше расстояния СР .

; V

=V AP ;

AP = R 2, V

=V 2.

C CP

Угловая скорость колеса равна

ω =

Задача.2. Диск зажат между двумя рейками, (рис.18) которые движутся со скоростями V1 и V2 (V1 > V2).

Определить угловую скорость диска и скорость его центра, если его радиус равен R.

АVAa

С VC с

ВVB

Рис.18

Решение. Скорость точки А диска равна скорости верхней рейки, а скорость точки В – скорости нижней рейки. Мгновенный центр скоростей находится в точке Р (рис.16). Скорость точки С является средней линией трапеции ВАав:

VC = V1 +2V2 .

Угловая скорость

ω = VAPA = VBPB = APVA −−VBPB = V12−RV2 .

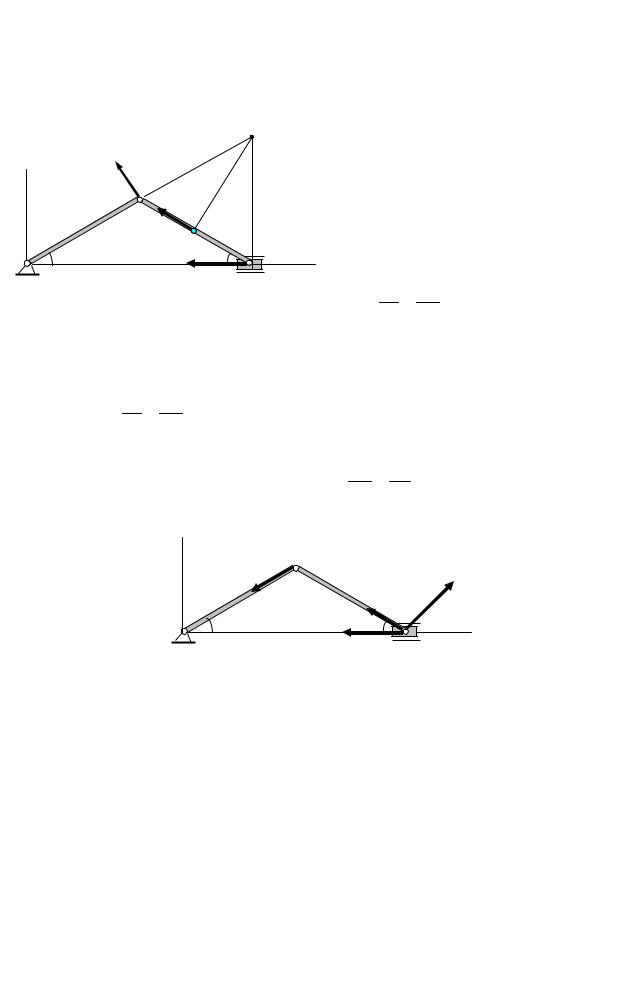
Задача 3. Кривошипно-шатунный механизм

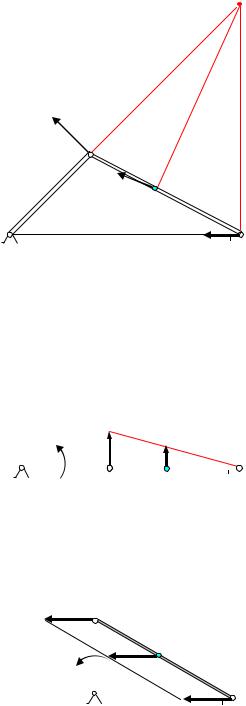
Угловая скорость кривошипа равна ωОА. Определить угловую скорость шатуна и скорости точек А,В, и С для трех положений механизма.

Кривошип ОА вращается вокруг точки О, шатун АВ совершает плоское движение в плоскости чертежа. Во всех случаях скорость точки А перпендикулярна кривошипу и равна VA =ωOA OA. , а скорость точки В направлена по

горизонтальной прямой.

1. Кривошип ОА образует острый угол с горизонтальной прямой

(рис.19). В этом случае мгновенный

центр скоростей шатуна находится в

точке Р, где пересекаются восстановлен-

ные в точках А и В перпендикуляры к

скоростям в этих точках.

= BP

VB =VA AP .

Скорость точки С направлена перпенди-

кулярно отрезку РС и находится из про-

порции:

CP .

Угловая скорость шатуна равна

Pис.19

ωAB =

2. Кривошип и шатун расположены на одной прямой (рис.20).

В этом положении мгновенный центр скоростей находится в точке В,

поэтому скорость VB

равна нулю. Ско-

рость точки С находится из пропорции:

V =V

Угловая скорость шатуна равна

Рис.20

ωAB =

VA A

Кривошип

занимает

вертикальное положение (рис.21). В

этом случае мгновенный центр скоростей

шатуна находится в бесконечности, скоро-

VВ

сти всех его точек равны, угловая скорость

шатуна равна нулю.

Рис. 21

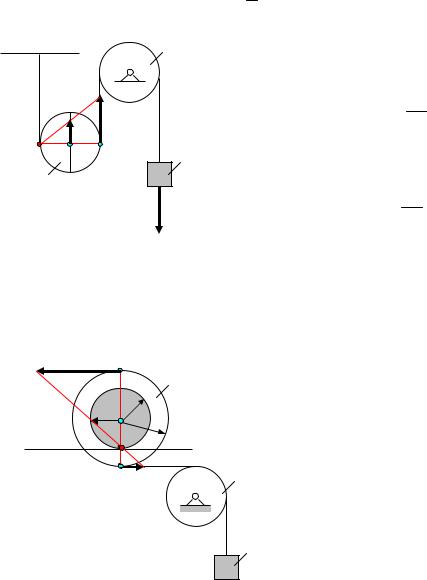
Задача 4. Определить скорости точек А, В, Р подвижного блока 3 (рис.22) и его угловую скорость, если скорость тела 1 равна V1

Решение. Подвижный блок совершает плоское движение. Скорость точки контакта Р подвижного блока с неподвижной нитью равна нулю: VР = 0, т.е. точка Р – мгновенный центр скоростей подвижного блока.

Скорость точки С перпендикулярна отрезку, соединяющему ее с мгновенный центром скоростей: VC CP .

			2
		О
	VС	VА

Р С	А	1

3	B

	Рис.22	V1

Скорости точек при плоском движении пропорциональны расстояниям до мгновенного центра скоростей

VC = CP .

VA AP

VA = V1, так как точка А и тело 1 связаны нерастяжимой нитью, тогда

VC = 0,5R .

V1 R

Следовательно, VC = 0,5 VA = 0,5 V1.

Задача 5. Определить угловую скорость и скорости точек А, В, С и Р катушки 3 (рис.23), если скорость груза 1 равна V1.

VA	A	3

VC	С	R
r
	P	B VB	2

		O

Рис.23

Решение. Скорость точки В катушки равна скорость груза 1, так как они связаны нерастяжимой нитью: VВ = V1.

При качении без скольжения в точке контакта катушки с рельсом находится мгновенный центр скоростей Р. Скорости точек А и С перпендикулярны отрезкам, соединяющим эти точки с мгновенным центром скоростей и пропорциональны их расстояниям до мгновенного центра скоростей, поэтому

	VC	=	CP	;	VC	=	r	.
V	BP	V	R −r

	B				B

Отсюда			VC	= VB	r	= V1	r
		R − r	R

Аналогично определим скорость точки А.
VA =	AP	;	VA =	r +R	.
BP
V		V		R −r
B			B

Следовательно,

V		=V	r +R	=V	r +R	.
	B R −r
	A		B R −r

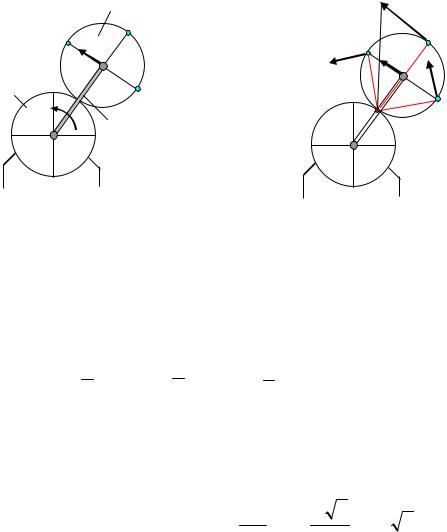
Задача 6. Определить угловую скорость и скорости точек А, В, D, E шестерни 3 (рис.24), которую приводит в движение кривошип ОА, вращающийся вокруг оси О неподвижной шестерни 1 с угловой скоростью ωОА.

	3			VD
	D
В VA		В		D
А	VВ	VA
		VE
1	Е
		А	Е
ωАВ			P
2

Решение. Скорость точки А, принадлежащей кривошипу ОА, перпендикулярна кривошипу и равна VA = ωAB AB.

Шестерня 3 совершает плоское движение, ее мгновенный центр скоростей находится в точке зацепления Р с неподвижной шестерней 1 (рис. 24а). Скорости точек В, Е и D перпендикулярны отрезкам, соединяющим их с мгновенным центром скоростей.

VB BP , VD DP , VE EP .

Скорости точек пропорциональны отрезкам, соединяющим эти точки с мгновенным центром скоростей Р.

VB =VE , так как расстояния этих точек до мгновенного центра скоростей равны: ВР = ЕР.

		VA	= AP ; откуда VB =VA BP	=VA	R	2	=VA 2.
	V		R
	BP	AP
			B
Аналогично определяем скорость точки D.
	VA	=	AP ;	откуда VD =VA DP =VA 2R	= 2VA.

V	DP	AP	R
	D

Задача 7. Определить скорости точек А, В, С, D и угловые скорости звеньев механизма, изображенного на рис. 25, если угловая скорость криво-

шипа ОА равна ωОА.

Решение. Во всех вариантах скорость точки А, являющейся концом кривошипа ОА, равна VA = ωОА OA и перпендикулярна кривошипу.

Звенья ОА и ОВ механизма (рис.25) совершают вращательное движение. Скорость точки А, являющейся концом кривошипа ОА, равна VA = ωОА OA и перпендикулярна кривошипу.

Скорость VB OB .Звенья АС и ВD совершают плоское движение. Звено

Р2

СD движется

поступательно, по-

этому скорости точек C и D равны:

VC = VD .

Мгновенный

центр

скоростей

звена АС лежит в точке Р1 пересе-

ωOA O

чения перпендикуляров к скоростям

в точках А и С.

VC С

1 .

A AP

Угловая скорость звена АС равна

ωAC =

Рис.25

Р1

AP1

Проведем

перпендикуляры к

скоростям VВ

и VD , точка их пересечения Р2

– мгновенный центр скоростей

VB	BP2			BP
звена ВD. V	= DP , откуда	2
VB =VD DP .
D	2			2
Угловая скорость звена ВD равна
	ωBD =	VB	.

		BP2

Задача 8. Определить скорости точек А, D и угловые скорости звеньев механизма, изображенного на рис. 26, если угловая скорость кривошипа ОА

равна ωОА.

Скорость точки А равна VA = ωОА OA и перпендикулярна кривошипу ОА. Звено АВ совершается плоское движение, скорость точки В направлена вертикально вниз. Мгновенный центр в данный момент находится в бесконечности, поэтому скорости всех его точек равны, а угловая скорость ωAB = 0 .

Скорость точки D перпендикулярна кривошипу О2D, следовательно, мгновенный центр скоростей звена ВD совпадает с точкой О2.

					Тогда	VD =	DO2 ;	откуда
О1	А			D			VB	BO2
				DO2 .
	ωОА	VD	90	0	V	=V
		D	B	BO2
	VA	В		О2					BD
		Угловая скорость	звена

					равна ωBD =	VB	= VD .
		VB					BO2	DO2

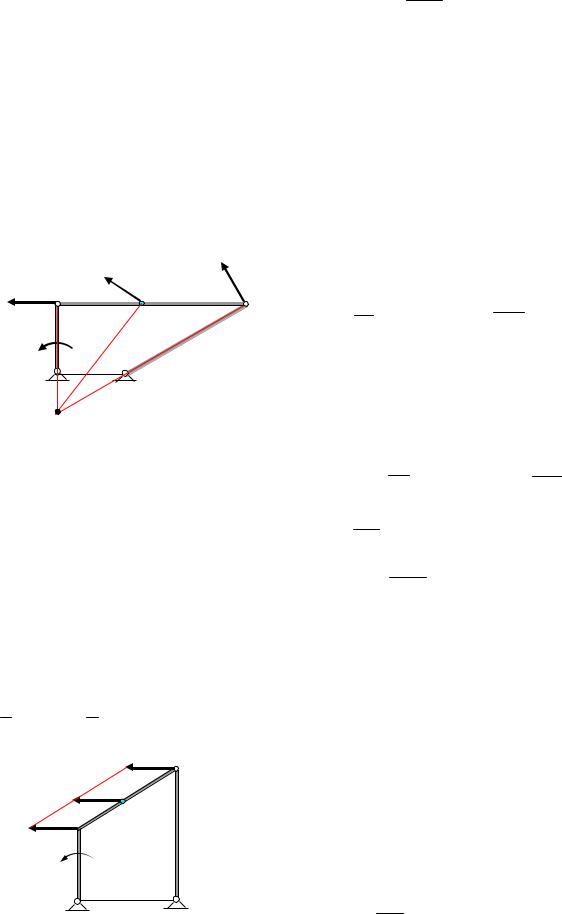
	Угловая скорость кривошипа O2D равна ωBD	= VD .
								DO2
	Задача 9. Определить скорости точек А, С, D и угловые скорости звень-
ев механизма, изображенного на рис. 25,	если угловая скорость кривошипа
ОА равна ωОА (рис.27).
	Решение. Звенья О1А и О2В совершают вращательные движения, поэто-
му скорость точки А направлена перпендикулярно кривошипу О1А и равна
	VA = ωОА· OA.
	Скорость точки D перпендикулярна звену О2D.
	Звено АD совершает плоское движение, мгновенный центр скоростей
этого звена лежит в точке Р пересечения перпендикуляров, проведенных в
			VD	точках А и D к скоростям VA и VD.
		VC	Скорость точки D находим из про-
VA	А	D
С	порции	VD		DP	. VD	=VA DP .
				=
ωОА					VA		AP		AP
		Соединим	точек	С с мгновенным
	О1
	О2		центром скоростей Р, скорость точки С

				будет направлена перпендикулярно от-
	Р			резку СР.
	Рис.27			Модуль этой скорости найдем из
			пропорции		VC	= CP	, VC =VA CP .

								VA	AP	AP
	Угловая скорость звена АD равна ωAD =	VA .
						AP	VD .
	Угловая скорость кривошипа равна	ω		=
	O2D		O2 D

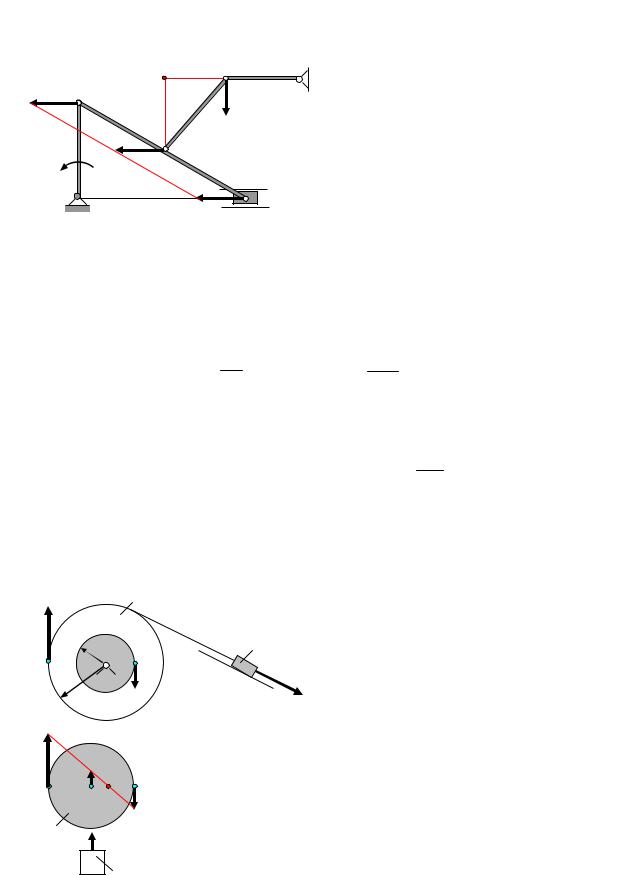
Задача 10. Определить скорости точек А, В, С, и угловые скорости звеньев механизма, изображенного на рис. 28, если угловая скорость криво-

шипа ОА равна ωОА.

Решение. Звенья ОА и DB совершают вращательные движения, поэтому

VA OA , VB

ωОА А

BD . Скорость точки А равна VA = ωОА· OA. Звено совершает

VВ	плоское движение, так как скорости точек А и В
		В	параллельны, то мгновенный центр скоростей

С	этого звена находится в бесконечности, поэтому
скорости всех его точек геометрически равны

	VA = VB = VC.
	Угловая скорость звена AВ равна нулю. Уг-
D	ловая скорость кривошипа ВD равна
	ωBD = VB .
	BD

Рис.28

	Задача 11. Определить скорости точек А, В, С, D и угловые скорости
звеньев механизма, изображенного на рис. 29,	если угловая скорость криво-
	Р	D		шипа ОА равна ωОА.
	О2	Решение.	Скорость точки А
VA	А
VD		перпендикулярна	кривошипу	и
			равна VA = ωОА· OA. Звено АВ со-

	VC	С		вершает	плоское	движение,	ско-
ωОА		рость VВ точки В направлена гори-

	О1	VВ	В	зонтально влево. В данном положе-
			нии	мгновенный	центр скоростей
		Рис.29		звена АВ находится в бесконечно-
			сти, поэтому скоростей всех	его
точек геометрически равны: VA = VB = VC.
	Звено CD совершает плоское движение, мгновенный центр скоростей
этого звена лежит в точке Р пересечения перпендикуляров, проведенных к
	скоростям в точках С и D. Скорость точки D найдем из пропорции
		VC =	CP	, VD =VC	DP .
		V	DP		CP
		D
Угловая скорость звена СD равна ωCD = VC .
				CP	= VD .
Угловая скорость кривошипа О D равна	ω
			2		O2D	DP

Задача 12. Определить скорость точки С и угловую скорость подвижного блока 3 (рис.30), если скорость тела 1 равна V1, r = 0,5R.

Решение. Блок 2 вращается вокруг точки О, скорость его точки В по ве-

личине равна скорости тела 1, так

как они связаны нерастяжимой ни-

r O

тью: VB = V1.Скорость

точек

при

вращательном

движении пропор-

циональны

их

радиусам

вращения,

поэтому

0,5R

= 0,5 .

Сле-

довательно, VA = 0,5 VB.

Подвижный

блок 3 совершает

плоское движение,

при этом

VD =

VB, VК = VA, так как соответствую-

щие точки связаны нерастяжимыми

нитями.

Рассмотрим движение блока 3.

	Рис.30	Мгновенный центр скоростей нахо-
	дится в точке пересечения Р общего

		17

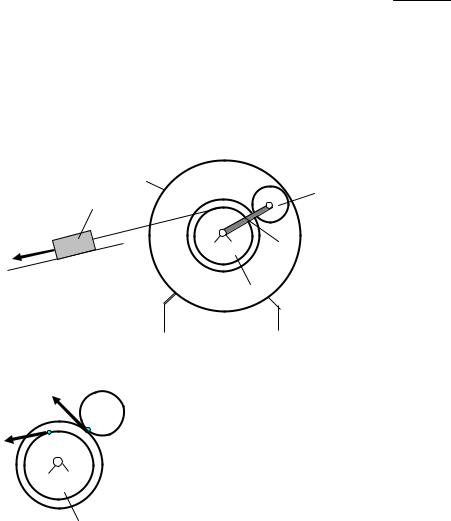
перпендикуляра, проведенного к скоростям VD и VК , и прямой, проходящей через концы этих векторов. Конец вектора скорости VС точки С лежит на прямой, соединяющей концы векторов скоростей VD и VК .

VК = VA = 0,5VB, VD = VB , тогда VК = 0,5VD.

Составим пропорцию:

VK = KP

VD DP .

Обозначив СР = х, тогда KP = R – x, DP = R + x. Подставив эти значения в пропорцию, получим

0,5 V	R − x		R
V	D =	,	откуда x =	.
R + x
3
D

Тогда расстояние точки К до мгновенного центра скоростей Р равно KP = R – x = 2/3 R, т.е. расстояние точки С до мгновенного центра скоростей в два раза меньше, чем то же расстояние до точки К, поэтому скорость точки будет в два раза меньше скорости точки К. VC = 0,5· VK = 0,5 VA = 0,25 V1.

Угловая скорость блока 3 равна ω3 = CPVC = 0,25RV1 3 = 0,75VR1 .

Скорость груза 4, подвешенного на нити в точке С, равна скорости точки С.

V4 = VC = 0,25 V1.

Задача 13. Определить скорость точки С и угловую скорость кривошипа ОС указанного на рис.31 механизма, если скорость тела 1 равна V1 (радиусы тел 3 и 5 заданы).

Решение. Данный механизм со-

стоит из пяти, соединенных между

собой тел.

1. Тело 1, двигаясь вниз по на-

клонной плоскости, сообщает телу 3

вращательное движение вокруг точ-

ки О.

Рис.31

В свою очередь тело 3, находясь

в зацеплении с телом 5, сообщает

ему плоское движение.

Точка С тела 5 приводит в движение кривошип ОС, кото-

рый вращается вокруг точки О.

2. Рассмотрим движение тела 3 (рис.31а). Скорость

точки А равна скорости груза 1, так как они связаны не-

растяжимой нитью. Определим скорость точки К.

Скорости точек вращающегося тела относятся как

их радиусы вращения:

Рис. 31 а

Отсюда скорость

VC	P	VK =VA	R	=V1	R	.
r
	5			r
K	C	3. Рассмотрим движение тела 5 (рис.31
б).	Точка Р является мгновенным центром

скоростей, так как в этой точке тело 5 находится в зацеплении с неподвижной шестер-

3ней 2. Скорость точки находим из пропорции

Рис. 31 б

=VK

=V1 R .

VC =VK

C 5

2r3

2 r

4. Кривошип вращается (рис.31в) вокруг точки О

определим по форму-

с угловой скоростью, которую

ле

ωOC =

Рис. 31 в

Задача 14. Кривошип ОС соединяющий центры трех шестерен одинакового радиуса R (рис.32), вращается вокруг точки О с угловой скоростью ω.

			VС	Шестерня	1 закреплена	неподвижно,
			шестерни 2 и 3 приводятся в движение
			D
			кривошипом. Определить скорости точек
		VA	С	контакта	между шестернями, скорость
		точки D и угловые скорости подвижных
ω
	А	3	шестерен.
О			2	Решение.
		1. Рассмотрим движение кривошипа.
	1
		Скорости точек А и С (рис.32) на-

				правлены	перпендикулярно	кривошипу

	Рис.32		ОС и равны

VA = ω·OA = 2 ω R, VC = ω·OC = 4 ω R.

2. Рассмотрим движение шестерни 2.

Шестерня 2 совершает плоское движение, (рис.32 а) скорость точки А известна. В точке контакта с неподвижной шестерней 1 находится мгновенный центр скоростей Р.

Скорость VK направлена перпендику-

лярно отрезку КР,

модуль ее определяет-

VК

VС

ся из пропорции

= 2 ,

откуда VK = 2 VA = 4ω R.

О Р

Угловая скорость шестерни 2 равна

ω2

2ω R

= 2ω .

Рис.32 а

3. Определим характер движения шес-

терни 3.

Скорости точек С и D шестерни 3 равны по модулю и параллельны, следовательно, шестерня 3 совершает поступательное движение, угловая скорость такого движения равна нулю.

Упражнения.

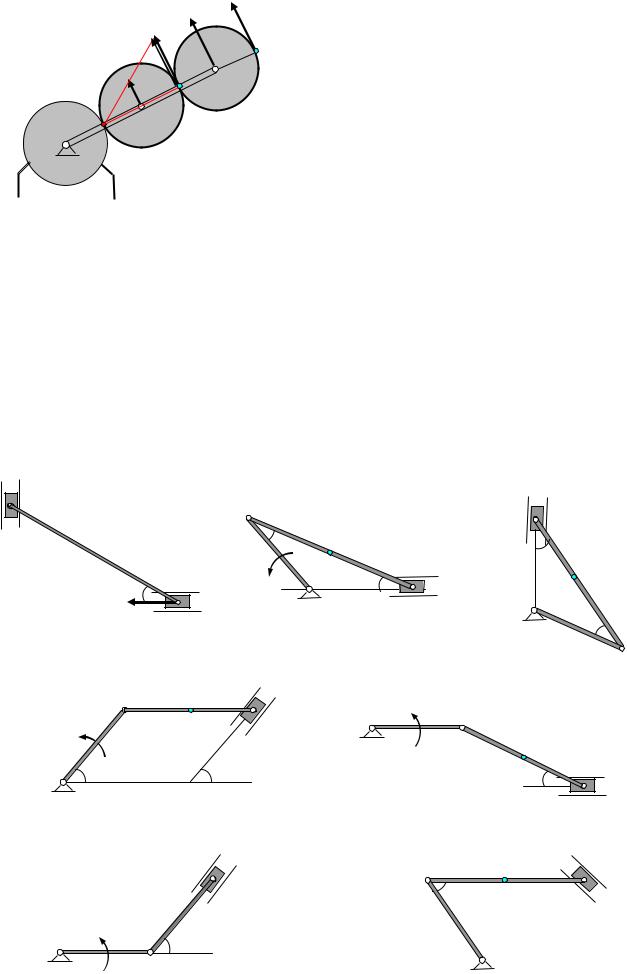
Определить с помощью мгновенного центра скоростей скорости точек А, В и С в механизмах, представленных на чертежах

А									В
				А

				300	C					300

	30	0	В	ωОА	О	300	В			C
					О
	VВ
Рис.1			Рис.2				300

											А
				В						Рис. 3
	A		C			ωОА
				O	A
ωОА
									C
O	450			450					30	0	В
							Рис.5

	Рис.4

				B			А	C		В

								600
O	ωОА		450					О
		A								20

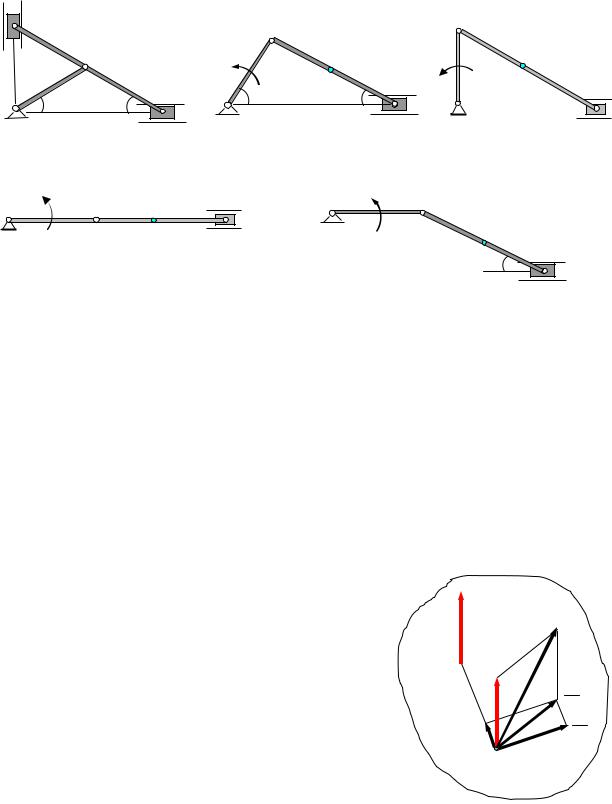
Ускорения точек плоской фигуры.

Движение плоской фигуры в своей плоскости можно разложить на поступательное движение вместе с произвольно выбранной точкой, принимаемой за полюс, и вращательное движение вокруг этого полюса.

Следовательно, ускорение любой точки при плоском движении равно

геометрической сумме двух ускорений: ускорения выбранного полюса, и ускорения, полученного данной точкой при ее вращательном движении вокруг полюса.

Пусть известно ускорение точки А плоской фигуры, тогда ускорение другой точки этой фигуры будет равно (рис.33).

aB = aA + aBA ,

где ускорение вращательного движения точки А вокруг точки В раскладывается на нормальное и касательное ускорения:

aBA = aBAτ + aBAn .

a BA a n a BAτ

BA B

Рис.33

Касательное ускорение вращательного движения точки вокруг полюса направлено перпендикулярно отрезку АВ, соединяющему точку В с полюсом А, и равно

aτBA = ε BA.

Нормальное ускорение направлено по отрезку ВА к полюсу А и равно

aBAn =ω2 BA.

Окончательно, полное ускорение точки В равно геометрической сумме трех ускорений: ускорения выбранного полюса А, нормального и касательного ускорений вращательного движения точки В вокруг этого полюса:

aB = aA +aBAn +aBAτ .

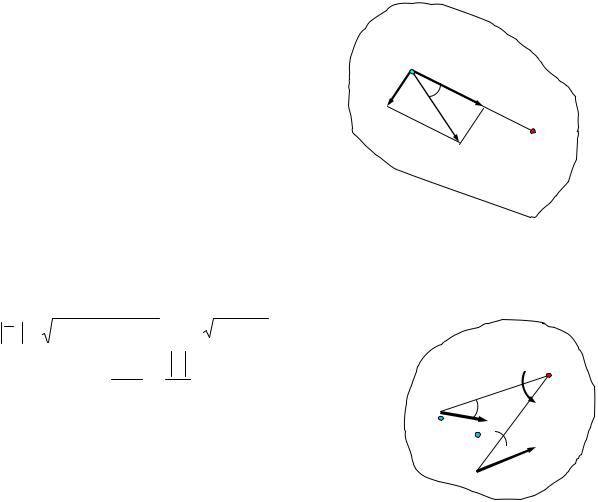
Мгновенным центром ускорений называется точка, принадлежащая связанной с плоской фигурой плоскости, ускорение которой в данный момент равно нулю.

Если за полюс выбрать мгновенный центр ускорений, то ускорение произвольной точки плоской фигуры определяется как ускорение вращательного движения вокруг мгновенного центра ускорений (рис.34).

	aA = aAL = aALn + aALτ ,
где L –мгновенный	центр ускорений, aALn	–
нормальное		τ	касательное ус-	А
ускорение, aAL –	aALτ	ε aALn
корение точки А вращательного движения пло-
ской фигуры вокруг мгновенного центра уско-		L
рений.	aALn =ω2 AL,	aτAL =ε AL.		aA

Ускорение aALn	– направлено по AL , уско-
рение aALτ	– перпендикулярно AL. Ускорение		Рис.34
aA точки А образует угол α с отрезком AL со-

единяющим точку А с мгновенным центром ускорений и равно (рис.35)

aA = (aALn )2 +(aτAL )2 = AL ω4 +ε2 ,
tgα = aτAL	=	ε	.	L
aALn		ω2	А	ε

Таким образом, если известно ускорение точки А плоской фигуры, то, чтобы найти положение мгновенного центра ускорений, следует это ускорение повернуть вокруг точки А на угол α в сторону вращения фигуры и на полученной прямой отложить расстояние

Если известны направления ускорений двух точек плоской фигуры, то мгновенный центр ускорений определяется как точка пересечения получен-

ных поворотом этих ускорений на один и тот же угол α = arctq ωε2 в сторону вращения.

Задача1. Центр колеса, катящегося без скольжения по горизонтальной плоскости, в данный момент имеет скорость VC = 2 м/c и ускорение аC = 1,6 м/c. Радиус колеса R = 0,4 м. Определить точек В и Р (рис. 36).

Решение. Так как скорость и ускорение точки С известны, то принимаем точку С за полюс.

	С	aC	В	aC	Тогда aB = aC +aBCn +aBCτ
	aP = aC +aPCn +aPCτ ,
			VC
aPCn			a n	где
					BC
τ						aBCn = ω2 BC = ω2 R,	aPCn = ω2 PC = ω2 R,

aPC	Р	aC		τ	= ε BC = ε R,	τ
Рис. 36				aBC	aPC = ε BC = ε R.

Мгновенный центр скоростей колеса находится в точке Р – точке каса-

ния колеса с неподвижной плоскостью, поэтому

VC = ωCP =ω R, откуда ω =

, при t = 1c, ω =ω =

=5 (1/ c).

0,4

Угловое ускорение колеса

ε =

dω

dVC

, при t =1 c, ε =

1,6

= 4 (1/ c2 )

0,4

Тогда

aτBC = ε R =

R = aC ,

aτPC = ε R =

R = aC .

Ускорение точки Р будет направлено к центру колеса точке С и равно

aP = aBCn =ω2 R = 52 0,4 =10 (м/ c2 ) .

Для определения ускорения в точке В спроектируем векторное равенство aB = aC +aBCn +aBCτ на горизонтальную ось x и вертикальную ось у:

aBx	= aC − aBCn = aC −ω2 R =1,6 −52 0,4 = −8,4 ( м/ с2 )
aBy	= −aτDC = −aC = −1,6 ( м/ c2 )
aB =	aBx2 + aBy2 = (−8,4)2 +(−1,6)2 ≈ 8,55 ( м/ c).

Задача 2. Колесо радиуса R = 0,4 м катится без скольжения так, что центр колеса имеет постоянную скорость VC =2 м/c. Определить ускорения точек Р и М обода колеса(рис.37)

Решение. Так как скорость центра колеса является постоянной, то его

ускорение рений.

aMτ

aMn

aC = 0 , следовательно, точка С будет мгновенным центром уско-

aMC VC

Мгновенный центр скоростей находится в точке Р – точке контакта с неподвижной плоскостью. Значит

ω = CPVC = VRC = const.

Отсюда следует,

&	tgα =	ε	= 0, α = 0.

чтоε =ω = 0,	ω	2

Следовательно, ускорения всех точек колеса будут направлены к центру колеса и равны

	aM =ω2	2
Рис.37	CM = ω2 R = VC .

			R

Ускорение точки М, находящейся на ободе колеса, являясь полным ускорением криволинейного движения, раскладывается на касательное, направленное по скорости в этой точке, и нормальное ускорение, направленное по перпендикуляру к скорости, т.е. по прямой, соединяющей точку М с мгновенным центром скоростей. (рис.37.).

aM = aMn + aMτ ; aMn = aM cosα, aτM = aM sin α.

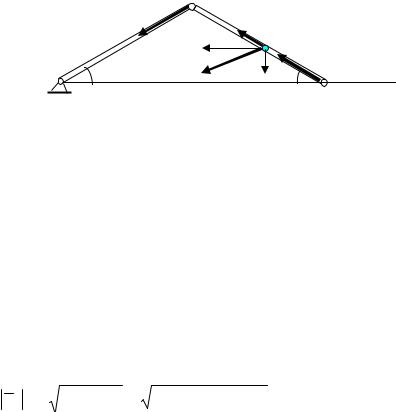
Задача 3. Определить скорости точек А, В, С и ускорения точек А и В кри- вошипно-шатунного механизма (рис.38), если кривошип вращается с посто-

y							янной угловой скоростью ωОА = 2
	А					1/с, ОА = АВ = 0,6 м, МВ = 0,3 м, ϕ

				C				=300.

О		ϕ	ϕ			В x	Решение. Скорость точки А
					(рис. 39) перпендикулярна криво-


			Рис.38					шипу ОА и равна
								VA =ωOA OA =1,2 м/c.

	Звено АВ совершает плоское движение/ Скорость точки В направлена
горизонтально, что обусловлено направляющими, вдоль которых движется
ползун В.
	Для определения скоростей точек А и В, принадлежащих шатуну АВ, оп-
ределим положение мгновенного центра скоростей этого звена. Проведем
			P		перпендикуляры	к	скоростям	в
				точках А и В, мгновенный центр

y	VA				скоростей Р находится в точке их
	A			пересечения.

		VC				Скорости точек при плоском
			C		движении пропорциональны рас-
О	300	300	x	стояниями до мгновенного центра
			В		скоростей.
		VB			VB =	AP
	Рис.39				. В треугольнике АВР:
АР = ВР, следовательно, VB=VA=1,2 м/с.	VA	BP

	Скорость VC	точки С направлена перпендикулярно отрезку СР, соеди-
няющему точку С с мгновенным скоростей. Значение скорости VC находим
из пропорции: VC	= CP . Из треугольника АСР:	СР =AP sin 60.
	VA	AP
	Следовательно, VC= VA sin 600 = 1,03 м/с.
	Угловая скорость шатуна равна	ωAB = VA	= 1,2	= 2	м/c.
					AP	0,6
		y		А
			aAn
				аВАn		aBAτ
		О	300
			aB		В	x


			Рис.40
	Ускорение точки А представляет собой нормальное ускорение аАn , на-
правленное по кривошипу (рис. 40)
	aAn =ωOA2	OA =2,4 м/c.
Ускорение точки В направлено по оси х и определяется векторным равенст-
вом:		aB = aAn +aBA = aAn +aBAn +aBAτ ,
					(а)
где векторы aBAn	и aBAτ	представляют собой составляющие ускорения вра-
щательного движения звена АВ вокруг точки А. Вектор	aBAn	направлен по
радиусу вращения ВА , ускорение aBAτ	– перпендикулярно АВ.
									25

Нормальное ускорение

aBAn =ωAB2 AB =2,4 м/с.

Таким образом, в уравнении (а) неизвестными являются ускорения aB и aBAτ . Для их определения спроектируем равенство (а) на оси х и у.

На ось х:

−aB

= −aAn cos 300

−aBAn cos 300

+ aτBA sin 300 .

(б)

На ось у:

0 = −aAn sin 300

+aBAn

sin 300 +aτBA cos300 .

(в)

Из уравнения (в) находим aτBA = aAn tg300 −aBAn

tg300 =0.

Угловое ускорение шатуна равно нулю.

Из уравнения (б) получаем aB =2,06 м/с.

Определим ускорение точки С (рис.41 ).

aC = aAn +aCA = aAn +aCAn +aCAτ

(г)

аАn

аCx

аCА

аn

300

аC

аCy

ВА В

Рис.41

Касательное ускорение

aCAτ = 0

Нормальное ускорение

aCAn =ω2 AC = 22 0,6 =1,2 (м/ c2 ).

Находим проекции уравнения (г)на оси Ох и Оу:

aCx = −aAn cos300 −aCAn cos300	= −1,82 (м/ c2 ).
aC y = −aAn sin 302 +aCAn sin 300 = −2,4 0,5 +1,2 0,5 = −0,6( м/ c2 ).
Ускорение точки С равно
aC = aCx2 +aCy2 = (1,82)2 +(−0,6)2	=1,91 ( м/ c2 )

Контрольрые вопросы

1.Определение плоскопараллельного движения.

2.Уравнения движения плоской фигуры.

3.Определение скоростей точек плоской фигуры.

4.Теорема Жуковского.

5.Мгновенный центр скоростей. Свойства м.ц.с.

6.Способы нахождения мгновенного центра скоростей.

7.Решение задач с помощью мгновенного центра скоростей.

8.Ускорения точек плоской фигуры.

Библиографический список

1.Бутенин Н.В и др. Курс теоретической механики.

Лань, 2002.- 736 стр.

2.Тарг С.М. Краткий курс теоретической механики. Высшая школа, 2004. – 416 стр.

3.Яблонский А.А., Никифорова В.М. Курс теоретической механики. Интеграл-Пресс, 2004. – 608 стр.

4.Яблонский А.А. Сборник заданий для курсовых работ по теоретической механике. Интеграл-Пресс, 2004. – 384 стр.

Соседние файлы в папке Термех

Источник

Володька – 7 ноября, 2009 – 17:32

На наклонной плоскости с углом наклона 10° лежат два бруска массой 1 и 2 кг, связанные между собою нитью. Ко второму бруску прикреплена нить, перекинутая через неподвижный блок, укрепленный на вершине наклонной плоскости. Блок имеет форму диска массой 0,8 кг и радиусом 10 см. Найти угловую скорость блока спустя одну секунду от начала вращения, если за свободный конец нити потянуть вниз с силой 2 Н. Коэффициенты трения брусков о плоскость соответственно равные и одинаковы и равны 0,2.

ВУЗ ОМГУПС, задания из методички дал преподаватель, 1 курс, ЭМФ.

версия для печати

Источник

Макеты страниц

Для определения искомых кинематических характеристик (угловой скорости тела или скоростей его точек) надо знать модуль и направление скорости какой-нибудь одной точки и направление скорости другой точки сечения этого тела (кроме случаев а) и в), рассмотренных в конце § 56). С определения этих характеристик по данным задачи и следует начинать решение.

Механизм, движение которого исследуется, надо изображать на чертеже в том положении, для которого требуется определить соответствующие характеристики. При расчете следует помнить, что понятие о мгновенном центре скоростей имеет место для данного твердого тела. В механизме, состоящем из нескольких тел, каждое непоступательно движущееся тело имеет в данный момент времени свой мгновенный центр скоростей и свою угловую скорость.

Задача 61. Определить скорость точки М обода катящегося колеса (см. задачу 59) с помощью мгновенного центра скоростей.

Рис. 156

Рис. 157

Решение. Точка касания колеса Р (рис. ) является мгновенным центром скоростей, поскольку Следовательно, Так как прямой угол PMD опирается на диаметр, то направление вектора скорости любой точки обода проходит через точку D.

Составляя пропорцию и замечая, что , находим .

Чем точка М дальше от Р, тем ее скорость больше; наибольшую скорость имеет верхний конец D вертикального диаметра. Угловая скорость колеса согласно формуле (57) имеет значение

Аналогичная картина распределения скоростей имеет место при качении колеса или шестерни по любой цилиндрической поверхности (см. рис. 152).

Задача 62. Определить скорость центра С подвижного блока радиуса и его угловую скорость (рис. 157), если груз А поднимается со скоростью а груз В опускается со скоростью Нить при своем движении по подвижному блоку не проскальзывает, а ее ветви вертикальны.

Решение. Так как нить по подвижному блоку не проскальзывает, то скорости точек а и блока равны по модулю скоростям грузов, т. е. Зная скорости точек а и и полагая для определенности, что находим положение мгновенного центра скоростей Р подвижного блока таким же приемом, как и в случае, показанном на рис. 153, б. Скорость центра С блока изображается вектором Для определения модуля и угловой скорости <й подвижного блока составляем, пользуясь формулой (58), равенства:

Отсюда, так как находим:

При центр С блока поднимается; если он будет опускаться. При получим

Для случая, когда оба груза А и В опускаются, значения найдем, заменив в полученных формулах на

Задача 63. В кривошипно-ползунном механизме (рис. 158) кривошип ОА длиной вращается с угловой скоростью Длина шатуна При данном угле определить: 1) скорость ползуна В;

2) положение точки М шатуна АВ, имеющей наименьшую скорость; 3) угловую скорость шатуна. Рассмотреть дополнительно положения механизма при

Рис. 158

Решение. Из данных задач следует, что точка А имеет скорость, численно равную и направленную перпендикулярно ОА, а скорость точки В направлена вдоль ВО. Этих данных достаточно для определения всех кинематических характеристик шатуна АВ.

1. По теореме о проекциях скоростей Но поскольку угол OAD, как внешний угол треугольника ОАВ, равен то следовательно.

Исключим из этого равенства угол . Из треугольника ОАВ кроме того,

В результате находим

2. Восставляя из точек А и В перпендикуляры к скоростям этих точек, определяем мгновенный центр скоростей Р для шатуна АВ (линия АР является продолжением ОА). Наименьшую скорость имеет точка ближе всего расположенная к центру Р, т. е. лежащая на перпендикуляре РМ к АВ. Скорость этой точки

3. Угловая скорость шатуна АВ согласно формуле (57)

Длина РВ (или РА) вычисляется по данным задачи.

4. При угле (рис. 159, а) перпендикуляр АВ к скорости и перпендикуляр к направлению пересекаются в точке В. Следовательно, точка В является в этом положении мгновенным центром скоростей и («мертвое» положение механизма). Для этого положения

Распределение скоростей точек шатуна А В показано на чертеже.

5. При угле (рис. 159, б) скорости направлены параллельно и перпендикуляры к ним пересекаются в бесконечности. Следовательно, в этот момент времени все точки шатуна имеют одинаковые скорости, равные

Рис. 159

Рис. 160

Задача 64. Кривошип ОА (рис, 160), вращающийся вокруг оси О с угловой скоростью несет на себе ось подвижной шестерни 1, катящейся по неподвижной шестерне 2. Радиусы шестерен одинаковы и равны . К шестерне 1 шарнирно прикреплен шатун BD длиной l, соединенный с коромыслом DC. Определить угловую скорость сйщэ шатуна в момент, когда он перпендикулярен кривошипу ОА, если в этот момент

Решение. Для определения надо знать скорость какой-нибудь точки шатуна BD и положение его мгновенного центра скоростей. Найдем скорость точки В, пользуясь тем, что она одновременно принадлежит шестерне 1. Для шестерни 1 известны скорость мгновенный центр скоростей Следовательно, и по теореме о проекциях скоростей откуда

Теперь для шатуна BD известны скорость и направление скорости Восставляя перпендикуляры к найдем мгновенный центр скоростей шатуна. При этом, как легко видеть, отрезок Тогда

Заметим, что нельзя пытаться искать какой-нибудь мгновенный центр скоростей, восставляя перпендикуляр к оси Точки А и D принадлежит разным телам, и пересечение указанных перпендикуляров никакого центра скоростей не дает (срави. с задачей 65).

Задача 65. На ось О (рис. 161) независимо друг от друга насажены шестерня и кривошип ОА, вращающийся с угловой скоростью Кривошип несет ось А шестерни 2, наглухо скрепленной с шатуном АВ, проходящим через качающуюся муфту С. Радиусы шестерен 1 к 2 одинаковы Определить угловую скорость о», шестерни 1 в тот момент времени, когда если при этом

Решение. Для определения угловой скорости шестерни 1 надо найти скорость ее точки Е. Эту скорость найдем, пользуясь тем, что такую же скорость имеет точка Е шестерни 2. Для шестерни 2 известны направление и модуль скорости точки А:

Кроме того, мы знаем направление скорости но в данном случае этого недостаточно, так как По теореме проекций значение также не найдется, так как перпендикулярны АЕ. Поэтому для дальнейшего решения воспользуемся тем, что шестерня 2 и шатун АВ образуют одно тело склепаны). Для этого тела знаем направление скорости точки С: вектор направлен вдоль СА, так как в точке С шатун может только проскальзывать вдоль муфты. Восставляя перпендикуляры к находим мгновенный центр скоростей Ртела ВАЕ.

По данным задачи 30°, откуда и Поэтому

Тогда из пропорции находим, что Отсюда

Рис. 161

Рис. 162

Задача 66. В механизме, изображенном на рис. 162, кривошипы 1 и 2 длиной и соответственно могут вращаться независимо друг от друга вокруг их осей . При данных углах найти: 1) чему должны равняться угловые скорости кривошипов, чтобы шарнир С механизма имел в данный момент времени заданную скорость направленную под углом у к звену АС; 2) чему будет равна скорость если кривошипы имеют заданные угловые скорости

Оглавление

ПРЕДИСЛОВИЕ К ДЕСЯТОМУ ИЗДАНИЮ
ВВЕДЕНИЕ
Раздел первый. СТАТИКА ТВЕРДОГО ТЕЛА
§ 1. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО; СИЛА. ЗАДАЧИ СТАТИКИ
§ 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ СТАТИКИ
§ 3. СВЯЗИ И ИХ РЕАКЦИИ
Глава II. СЛОЖЕНИЕ СИЛ. СИСТЕМА СХОДЯЩИХСЯ СИЛ
§ 4. ГЕОМЕТРИЧЕСКИЙ СПОСОБ СЛОЖЕНИЯ СИЛ. РАВНОДЕЙСТВУЮЩАЯ СХОДЯЩИХСЯ СИЛ; РАЗЛОЖЕНИЕ СИЛ
§ 5. ПРОЕКЦИЯ СИЛЫ НА ОСЬ И НА ПЛОСКОСТЬ. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ И СЛОЖЕНИЯ СИЛ
§ 6. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
§ 7. РЕШЕНИЕ ЗАДАЧ СТАТИКИ
Глава III. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА. ПАРА СИЛ
§ 8. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА (ИЛИ ТОЧКИ)
§ 9. ПАРА СИЛ. МОМЕНТ ПАРЫ
§ 10. ТЕОРЕМЫ ОБ ЭКВИВАЛЕНТНОСТИ И О СЛОЖЕНИИ ПАР
Глава IV. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЦЕНТРУ. УСЛОВИЯ РАВНОВЕСИЯ
§ 11. ТЕОРЕМА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ
§ 12. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
§ 13. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ. ТЕОРЕМА О МОМЕНТЕ РАВНОДЕЙСТВУЮЩЕЙ
Глава V. ПЛОСКАЯ СИСТЕМА СИЛ
§ 14. АЛГЕБРАИЧЕСКИЕ МОМЕНТЫ СИЛЫ И ПАРЫ
§ 15. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
§ 16. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ
§ 17. РЕШЕНИЕ ЗАДАЧ
§ 19. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ ТЕЛ (КОНСТРУКЦИИ)
§ 20. ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ УСИЛИЙ
§ 21. РАСПРЕДЕЛЕННЫЕ СИЛЫ
§ 22. РАСЧЕТ ПЛОСКИХ ФЕРМ
Глава VI. ТРЕНИЕ
§ 23. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ
§ 24. РЕАКЦИИ ШЕРОХОВАТЫХ СВЯЗЕЙ. УГОЛ ТРЕНИЯ
§ 25. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
§ 26. ТРЕНИЕ НИТИ О ЦИЛИНДРИЧЕСКУЮ ПОВЕРХНОСТЬ
§ 27. ТРЕНИЕ КАЧЕНИЯ
Глава VII. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
§ 28. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ. ВЫЧИСЛЕНИЕ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИСТЕМЫ СИЛ
§ 29. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
§ 30. РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ
Глава VIII. ЦЕНТР ТЯЖЕСТИ
§ 31. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ
§ 32. СИЛОВОЕ ПОЛЕ. ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА
§ 33. КООРДИНАТЫ ЦЕНТРОВ ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ
§ 34. СПОСОБЫ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ ТЕЛ
§ 35. ЦЕНТРЫ ТЯЖЕСТИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ
Раздел второй. КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА
§ 36. ВВЕДЕНИЕ В КИНЕМАТИКУ
§ 37. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
§ 38. ВЕКТОР СКОРОСТИ ТОЧКИ
§ 39. ВЕКТОР УСКОРЕНИЯ ТОЧКИ
§ 40. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ
§ 41. РЕШЕНИЕ ЗАДАЧ КИНЕМАТИКИ ТОЧКИ
§ 42. ОСИ ЕСТЕСТВЕННОГО ТРЕХГРАННИКА. ЧИСЛОВОЕ ЗНАЧЕНИЕ СКОРОСТИ
§ 43. КАСАТЕЛЬНОЕ и НОРМАЛЬНОЕ УСКОРЕНИЯ ТОЧКИ
§ 44. НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ ДВИЖЕНИЯ ТОЧКИ
§ 45. ГРАФИКИ ДВИЖЕНИЯ, СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ
§ 46. РЕШЕНИЕ ЗАДАЧ
§ 47. СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ В ПОЛЯРНЫХ КООРДИНАТАХ
Глава X. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
§ 48. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ
§ 49. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ ОСИ, УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ
§ 50. РАВНОМЕРНОЕ И РАВНОПЕРЕМЕННОЕ ВРАЩЕНИЯ
§ 51. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ВРАЩАЮЩЕГОСЯ ТЕЛА
Глава XI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
§ 52. УРАВНЕНИЯ ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ (ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ). РАЗЛОЖЕНИЕ ДВИЖЕНИЯ НА ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ
§ 53. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
§ 54. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
§ 55. ТЕОРЕМА О ПРОЕКЦИЯХ СКОРОСТЕЙ ДВУХ ТОЧЕК ТЕЛА
§ 56. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С ПОМОЩЬЮ МГНОВЕННОГО ЦЕНТРА СКОРОСТЕЙ. ПОНЯТИЕ О ЦЕНТРОИДАХ
§ 57. РЕШЕНИЕ ЗАДАЧ
§ 58. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
§ 59. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ
ГЛАВА XII. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
§ 60. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ
§ 61. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА
§ 62. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ТЕЛА
§ 63. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА
Глава XIII. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
§ 64. ОТНОСИТЕЛЬНОЕ, ПЕРЕНОСНОЕ И АБСОЛЮТНОЕ ДВИЖЕНИЯ
§ 65. ТЕОРЕМА О СЛОЖЕНИИ СКОРОСТЕЙ
§ 66. ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЙ (ТЕОРЕМА КОРИОЛИСА)
§ 67. РЕШЕНИЕ ЗАДАЧ
Глава XIV. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
§ 68. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНЫХ ДВИЖЕНИЙ
§ 69. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ДВУХ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
§ 70. ЦИЛИНДРИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ
§ 71. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
§ 72. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЙ. ВИНТОВОЕ ДВИЖЕНИЕ
Раздел третий. ДИНАМИКА ТОЧКИ
Глава XV. ВВЕДЕНИЕ В ДИНАМИКУ. ЗАКОНЫ ДИНАМИКИ
§ 74. ЗАКОНЫ ДИНАМИКИ. ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ
§ 75. СИСТЕМЫ ЕДИНИЦ
§ 76. ОСНОВНЫЕ ВИДЫ СИЛ
Глава XVI. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ, РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ ТОЧКИ
§ 77. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
§ 78. РЕШЕНИЕ ПЕРВОЙ ЗАДАЧИ ДИНАМИКИ (ОПРЕДЕЛЕНИЕ СИЛ ПО ЗАДАННОМУ ДВИЖЕНИЮ)
§ 79. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ
§ 80. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
§ 81. ПАДЕНИЕ ТЕЛА В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ (В ВОЗДУХЕ)
§ 82. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ
Глава XVII. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
§ 83. КОЛИЧЕСТВО ДВИЖЕНИЯ ТОЧКИ. ИМПУЛЬС СИЛЫ
§ 84. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ
§ 85. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ (ТЕОРЕМА МОМЕНТОВ)
§ 86. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ. ЗАКОН ПЛОЩАДЕЙ
§ 87. РАБОТА СИЛЫ. МОЩНОСТЬ
§ 88. ПРИМЕРЫ ВЫЧИСЛЕНИЯ РАБОТЫ
§ 89. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТОЧКИ
Глава XVIII. НЕСВОБОДНОЕ И ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЯ ТОЧКИ
§ 90. НЕСВОБОДНОЕ ДВИЖЕНИЕ ТОЧКИ
§ 91. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
§ 92. ВЛИЯНИЕ ВРАЩЕНИЯ ЗЕМЛИ НА РАВНОВЕСИЕ И ДВИЖЕНИЕ ТЕЛ
§ 93. ОТКЛОНЕНИЕ ПАДАЮЩЕЙ ТОЧКИ ОТ ВЕРТИКАЛИ ВСЛЕДСТВИЕ ВРАЩЕНИЯ ЗЕМЛИ
Глава XIX. ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ ТОЧКИ
§ 94. СВОБОДНЫЕ КОЛЕБАНИЯ БЕЗ УЧЕТА СИЛ СОПРОТИВЛЕНИЯ
§ 95. СВОБОДНЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ (ЗАТУХАЮЩИЕ КОЛЕБАНИЯ)
§ 96. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНС
Глава XX. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ
§ 97. ДВИЖЕНИЕ БРОШЕННОГО ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ
§ 98. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ЭЛЛИПТИЧЕСКИЕ ТРАЕКТОРИИ
§ 99. ПОНЯТИЕ О НЕВЕСОМОСТИ. МЕСТНЫЕ СИСТЕМЫ ОТСЧЕТА
Раздел четвертый. ДИНАМИКА СИСТЕМЫ И ТВЕРДОГО ТЕЛА
§ 100. МЕХАНИЧЕСКАЯ СИСТЕМА. СИЛЫ ВНЕШНИЕ И ВНУТРЕННИЕ
§ 101. МАССА СИСТЕМЫ. ЦЕНТР МАСС
§ 102. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ. РАДИУС ИНЕРЦИИ
§ 103. МОМЕНТЫ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ. ТЕОРЕМА ГЮЙГЕНСА
§ 104. ЦЕНТРОБЕЖНЫЕ МОМЕНТЫ ИНЕРЦИИ. ПОНЯТИЯ О ГЛАВНЫХ ОСЯХ ИНЕРЦИИ ТЕЛА
§ 105. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ
Глава XXII. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС СИСТЕМЫ
§ 106. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ
§ 107. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС
§ 108. ЗАКОН СОХРАНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА МАСС
§ 109. РЕШЕНИЕ ЗАДАЧ
Глава XXIII. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ
§ 110. КОЛИЧЕСТВО ДВИЖЕНИЯ СИСТЕМЫ
§ 111. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
§ 112. ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ
§ 113. ПРИЛОЖЕНИЕ ТЕОРЕМЫ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА)
§ 114. ТЕЛО ПЕРЕМЕННОЙ МАССЫ. ДВИЖЕНИЕ РАКЕТЫ
Глава XXIV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ
§ 115. ГЛАВНЫЙ МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ
§ 116. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ (ТЕОРЕМА МОМЕНТОВ)
§ 117. ЗАКОН СОХРАНЕНИЯ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ
§ 118. РЕШЕНИЕ ЗАДАЧ
§ 119. ПРИЛОЖЕНИЕ ТЕОРЕМЫ МОМЕНТОВ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА)
§ 120. УСЛОВИЯ РАВНОВЕСИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
Глава XXV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
§ 121. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ СИСТЕМЫ
§ 122. НЕКОТОРЫЕ СЛУЧАИ ВЫЧИСЛЕНИЯ РАБОТЫ
§ 123. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
§ 124. РЕШЕНИЕ ЗАДАЧ
§ 125. СМЕШАННЫЕ ЗАДАЧИ
§ 126. ПОТЕНЦИАЛЬНОЕ СИЛОВОЕ ПОЛЕ И СИЛОВАЯ ФУНКЦИЯ
§ 127. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
Глава XXVI. ПРИЛОЖЕНИЕ ОБЩИХ ТЕОРЕМ К ДИНАМИКЕ ТВЕРДОГО ТЕЛА
§ 128. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
§ 129. ФИЗИЧЕСКИЙ МАЯТНИК. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ
§ 130. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
§ 131. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ГИРОСКОПА
§ 132. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
Глава XXVII. ПРИНЦИП ДАЛАМБЕРА
§ 133. ПРИНЦИП ДАЛАМБЕРА ДЛЯ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ
§ 134. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИЛ ИНЕРЦИИ
§ 135. РЕШЕНИЕ ЗАДАЧ
§ 136. ДИНАМИЧЕСКИЕ РЕАКЦИИ, ДЕЙСТВУЮЩИЕ НА ОСЬ ВРАЩАЮЩЕГОСЯ ТЕЛА. УРАВНОВЕШИВАНИЕ ВРАЩАЮЩИХСЯ ТЕЛ
Глава XXVIII. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ И ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
§ 137. КЛАССИФИКАЦИЯ СВЯЗЕЙ
§ 138. ВОЗМОЖНЫЕ ПЕРЕМЕЩЕНИЯ СИСТЕМЫ. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ
§ 139. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
§ 140. РЕШЕНИЕ ЗАДАЧ
§ 141. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
Глава XXIX. УСЛОВИЯ РАВНОВЕСИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ
§ 142. ОБОБЩЕННЫЕ КООРДИНАТЫ И ОБОБЩЕННЫЕ СКОРОСТИ
§ 143. ОБОБЩЕННЫЕ СИЛЫ
§ 144. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ
§ 145. УРАВНЕНИЯ ЛАГРАНЖА
§ 146. РЕШЕНИЕ ЗАДАЧ
Глава XXX. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ ОКОЛО ПОЛОЖЕНИЯ УСТОЙЧИВОГО РАВНОВЕСИЯ
§ 147. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ
§ 148. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
§ 149. МАЛЫЕ ЗАТУХАЮЩИЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
§ 150. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ
Глава XXXI. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ УДАРА
§ 151. ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ УДАРА
§ 152. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УДАРА
§ 153. КОЭФФИЦИЕНТ ВОССТАНОВЛЕНИЯ ПРИ УДАРЕ
§ 154. УДАР ТЕЛА О НЕПОДВИЖНУЮ ПРЕГРАДУ
§ 155. ПРЯМОЙ ЦЕНТРАЛЬНЫЙ УДАР ДВУХ ТЕЛ (УДАР ШАРОВ)
§ 156. ПОТЕРЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ПРИ НЕУПРУГОМ УДАРЕ ДВУХ ТЕЛ. ТЕОРЕМА КАРНО
§ 157. УДАР ПО ВРАЩАЮЩЕМУСЯ ТЕЛУ. ЦЕНТР УДАРА

Источник

Угловая скорость

Формулы угловой скорости

Определение угловой скорости

Угловое ускорение

Расчет углового ускорения

Способы нахождения мгновенного центра скоростей

Вам также может понравиться

Как найти билеты для фрэнка

Как найти много ресурсов в майнкрафте

Правильный десятиугольник как найти углы

Добавить комментарий Отменить ответ