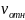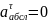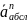Как найти угловую скорость колеса автомобиля

Иногда применительно к автомобилям всплывают вопросы из математики и физики. В частности, одним из таких вопросов является угловая скорость. Она имеет отношение как к работе механизмов, так и к прохождению поворотов. Разберёмся же, как определить эту величину, в чём она измеряется и какими формулами тут нужно пользоваться.

Как определить угловую скорость: что это за величина?

С физико-математической точки зрения эту величину можно определить следующим образом: это данные, которые показывают, как быстро некая точка осуществляет оборот вокруг центра окружности, по которой она движется.

ПОСМОТРЕТЬ ВИДЕО

Эта, казалось бы, чисто теоретическая величина, имеет немалое практическое значение при эксплуатации автомобиля. Вот лишь несколько примеров:

• Необходимо правильно соотносить движения, с которыми вращаются колёса при повороте. Угловая скорость колеса автомобиля, движущегося по внутренней части траектории, должна быть меньше, чем у внешнего.
• Требуется рассчитывать, насколько быстро в автомобиле вращается коленвал.
• Наконец, сама машина, проходя поворот, тоже имеет определённую величину параметров движения – и от них на практике зависит устойчивость автомобиля на трассе и вероятность опрокидывания.

Формула времени, за которое вращается точка по окружности заданного радиуса

Для того, чтобы рассчитывать угловую скорость, используется следующая формула:

ω = ∆φ /∆t

Где:

• ω (читается «омега») – собственно вычисляемая величина.
• ∆φ (читается «дельта фи») – угол поворота, разница между угловым положением точки в первый и последний момент времени измерения.
• ∆t
  (читается «дельта тэ») – время, за которое произошло это самое смещение. Точнее, поскольку «дельта», это означает разницу между значениями времени в момент, когда было начато измерение и когда закончено.

Приведённая выше формула угловой скорости применяется лишь в общих случаях. Там же, где речь идёт о равномерно вращающихся объектах или о связи между движением точки на поверхности детали, радиусом и временем поворота, требуется использовать другие соотношения и методы. В частности, тут уже будет необходима формула частоты вращения.

Угловая скорость измеряется в самых разных единицах. В теории часто используется рад/с (радиан в секунду) или градус в секунду. Однако эта величина мало что означает на практике и использоваться может разве что в конструкторской работе. На практике же её больше измеряют в оборотах за секунду (или минуту, если речь идёт о медленных процессах). В этом плане она близка к частоте вращения.

Угол поворота и период обращения

Гораздо более часто, чем угол поворота, используется частота вращения, которая показывает, сколько оборотов делает объект за заданный период времени. Дело в том, что радиан, используемый для расчётов – это угол в окружности, когда длина дуги равна радиусу. Соответственно в целой окружности находится 2 π радианов. Число же π – иррациональное, и его нельзя свести ни к десятичной, ни к простой дроби. Поэтому в том случае, если происходит равномерное вращение, проще считать его в частоте. Она измеряется в об/мин – оборотах в минуту.

Если же дело касается не длительного промежутка времени, а лишь того, за который происходит один оборот, то здесь используется понятие периода обращения. Она показывает, как быстро совершается одно круговое движение. Единицей измерения здесь будет выступать секунда.

Связь угловой скорости и частоты вращения либо периода обращения показывает следующая формулы:

ω = 2 π / T = 2 π *f,

где:

• ω – угловая скорость в рад/с;
• T – период обращения;
• f – частота вращения.

Получить любую из этих трёх величин из другой можно с помощью правила пропорций, не забыв при этом перевести размерности в один формат (в минуты либо секунды)

Чему равна угловая скорость в конкретных случаях?

Приведём пример расчёта на основе приведённых выше формул. Допустим, имеется автомобиль. При движении на 100 км/ч его колесо, как показывает практика, делает в среднем 600 оборотов за минуту (f = 600 об/мин). Рассчитаем угловую скорость.

Для начала переведем об/мин в об/с. Для этого разделим 600 на 60 (число секунд в минуте) и получим 10 об/с . Попутно мы получили и период обращения: эта величина является обратной по отношению к частоте и при измерении в секундах 0,1 с.

Далее используем формулу:

ω = 2 π *f

Поскольку точно выразить π десятичными дробями невозможно, результат примерно равен будет 62,83 рад/с.

Связь угловой и линейной скоростей

На практике часто приходится проверять не только ту скорость, с какой изменяется угловое положение у вращающейся точки, но и скорость её самой применительно к линейному движению. В приведённом выше примере были сделаны расчёты для колеса – но колесо движется по дороге и либо вращается под действием скорости автомобиля, либо само ему эту скорость обеспечивает. Значит, каждая точка на поверхности колеса помимо угловой будет иметь и линейную скорость.

Рассчитать её проще всего через радиус. Поскольку скорость зависит от времени (которым будет период обращения) и пройденного расстояния (которым является длина окружности), то, учитывая приведённые выше формулы, угловая и линейная скорость будут соотноситься так:

V = ωR

Где:

• V – линейная скорость;
• R – радиус.

Из формулы очевидно, что чем больше радиус, тем выше и значение такой скорости. Применительно к колесу с самой большой скоростью будет двигаться точка на внешней поверхности протектора (R максимален), но вот точно в центре ступицы линейная скорость будет равна нулю.

Ускорение, момент и связь их с массой

Помимо приведённых выше величин, с вращением связано ещё несколько моментов. Учитывая же, сколько в автомобиле крутящихся деталей разного веса, их практическое значение нельзя не учесть.

Равномерное вращение – это важная вещь. Вот только нет ни одной детали, которая бы всё время крутилась равномерно. Число оборотов любого крутящегося узла, от коленвала до колеса, всегда в конечном итоге растёт, а затем падает. И та величина, которая показывает, насколько выросли обороты, называется угловым ускорением. Поскольку она производная от угловой скорости, измеряется она в радианах на секунду в квадрате (как линейное ускорение – в метрах на секунду в квадрате).

С движением и её изменением во времени связан и другой аспект – момент импульса. Если до этого момента мы могли рассматривать только чисто математические особенности движения, то здесь уже нужно учитывать то, что каждая деталь имеет массу, которая распределена вокруг оси. Он определяется соотношением начального положения точки с учётом направления движения – и импульса, то есть произведения массы на скорость. Зная момент импульса, возникающий при вращении, можно определить, какая нагрузка будет приходиться на каждую деталь при её взаимодействии с другой

Шарнир как пример передачи импульса

Характерным примером того, как применяются все перечисленные выше данные, является шарнир равных угловых скоростей (ШРУС) . Эта деталь используется прежде всего на переднеприводных автомобилях, где важно не только обеспечить разный темп вращения колёс при повороте – но и при этом их управляемость и передачу на них импульса от работы двигателя.

ПОСМОТРЕТЬ ВИДЕО

Конструкция этого узла как раз и предназначена для того, чтобы:

• уравнивать между собой, как быстро вращаются колёса;
• обеспечивать вращение в момент поворота;
• гарантировать независимость задней подвеске.

В результате все формулы, приведённые выше, учитываются в работе ШРУС.

Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.

Обозначение угловой скорости: ω (омега).

Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.

С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.

Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:

Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.

Быстрота изменения угла φ (перемещения плоскости П из положения П₁ в положение П₂) – это и есть угловая скорость:

Приняв вектор k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

1. если известно количество оборотов n за единицу времени t:
   
2. если задан угол поворота φ за единицу времени:
   
3. если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:
   

Размерности угловой скорости:

• Количество оборотов за единицу времени [об/мин], [c^-1].
• Угол поворота за единицу времени [рад/с].

Определение угловой скорости

Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.

Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.

Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.

Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.

Другие примеры решения задач >

Угловое ускорение

Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:

Обозначение: ε (Эпсилон)

Единицы измерения углового ускорения: [рад/с²], [с^-2]

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

Расчет углового ускорения

Пример: По заданному значению касательной составляющей полного ускорения a_τ точки B, расположенной на расстоянии r от центра вращения колеса.

Требуется определить величину и направление углового ускорения колеса ε, если a_τ = 10 м/с², r = 50 см.

Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.

Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

ω = 1,5 с^-1 = 9,42 рад/с.

Смотрите также:

• Примеры расчета угловой скорости и ускорения
• Скорости и ускорения точек вращающегося тела

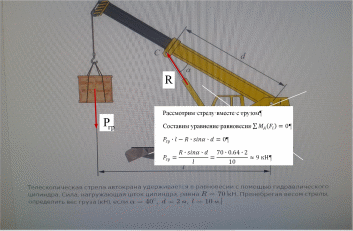
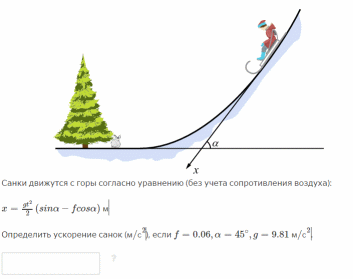
Определить
угловую скорость (рад/с) колеса автомобиля,
движущегося со скоростью 35
км/ч, если радиус колеса 0,49
м.

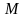
Решение

Переведем
скорость автомобиля в систему СИ:

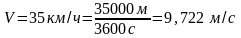
Автомобиль
совершает поступательное движение,
поэтому скорость центра колеса параллельна
поверхности и равна скорости автомобиля.
Так как колесо движется без проскальзывания,
то скорость точки М равна нулю и она
является мгновенным центром скоростей
колеса. Тогда

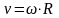
Откуда
получаем

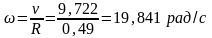
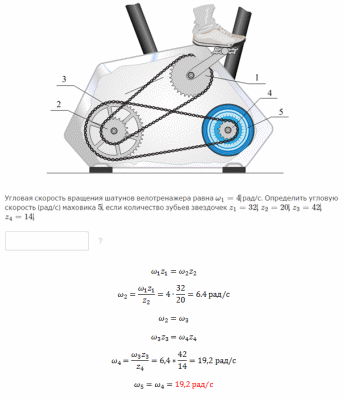
Две
параллельные рейки 1 и 2 суммирующего
механизма движутся в одну сторону с
постоянными скоростями V₁
и V_2.

Определить
скорость центральной рейки 3 (см/с), ecли
V₁=
0,7 см/с, V₂
= 4,2 см/с.

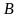
Решение

Так
как зацепление реек с зубьями шестерни
жесткое, то скорости точек А и В центральной
шестерни равны скоростям соответствующих
реек.

Найдем
мгновенный центр скоростей центральной
шестерни, построив перпендикуляр к
векторам скоростей точек А и В и проведя
прямую, проходящую через концы этих
векторов. Тогда точка Р будет мгновенным
центром скоростей шестерни. Обозначим
радиус шестерни R, тогда

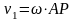
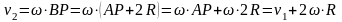
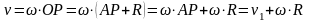
Из
второго уравнения получаем:

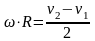
Тогда
третье уравнение можно записать в виде:

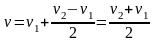
Откуда
получаем:

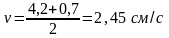
Скорость
поршня ДВС в данном положении равна v
=
1,8 м/c.

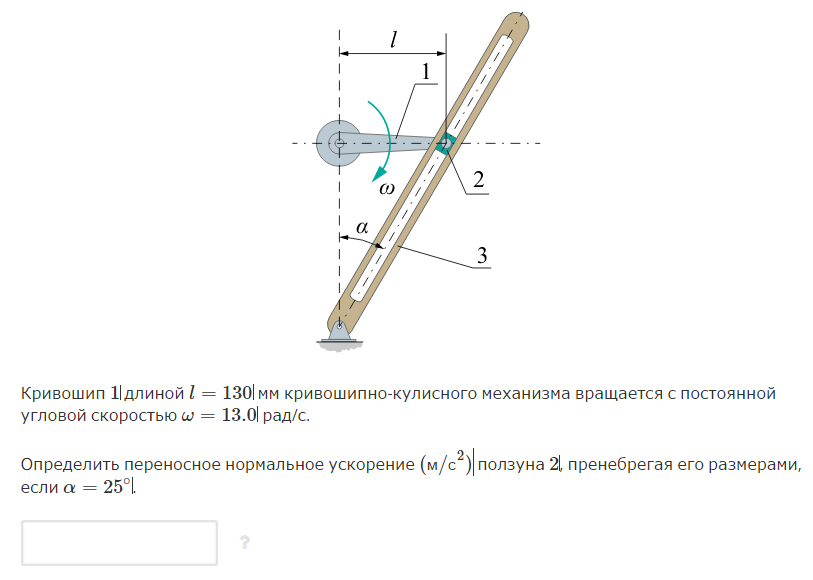
Определить
частоту вращения кривошипа (об/мин),
если его длина 39
мм, α = 14° , β = 28° . Ответ округлить до
ближайшего целого числа

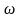
Решение

Так
как кривошип совершает вращательное
движение, то скорость точки А будет
перпендикулярно кривошипу и по теореме
о проекциях скоростей твердого тела:

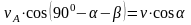
Откуда
получаем:

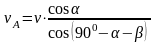
Тогда
угловая скорость кривошипа:

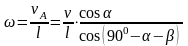
Но
так как

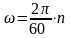
То

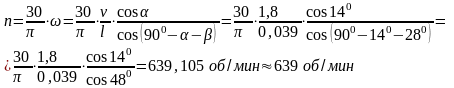
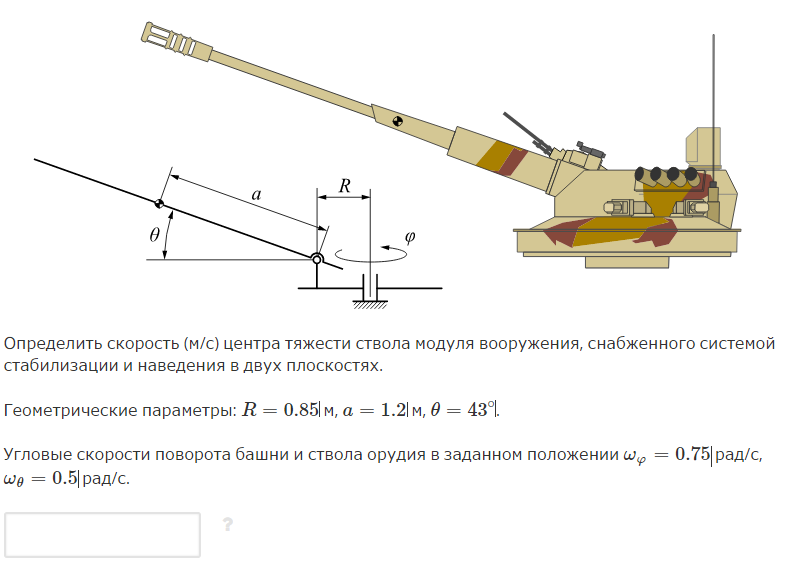
Относительное движение:
поворот в вертикальной плоскости

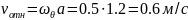
Переносное движение:
поворот в горизонтальной плоскости

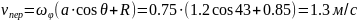
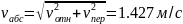
Выдвижение стрелы –
относительное движение

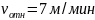
Вращение стрелы в
вертикальной плоскости – переносное
движение

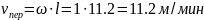
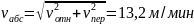
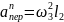
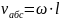
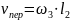
Где

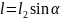
Т.к.

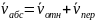
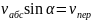
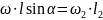
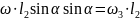
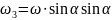
L=130мм=0,13м

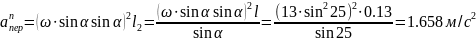
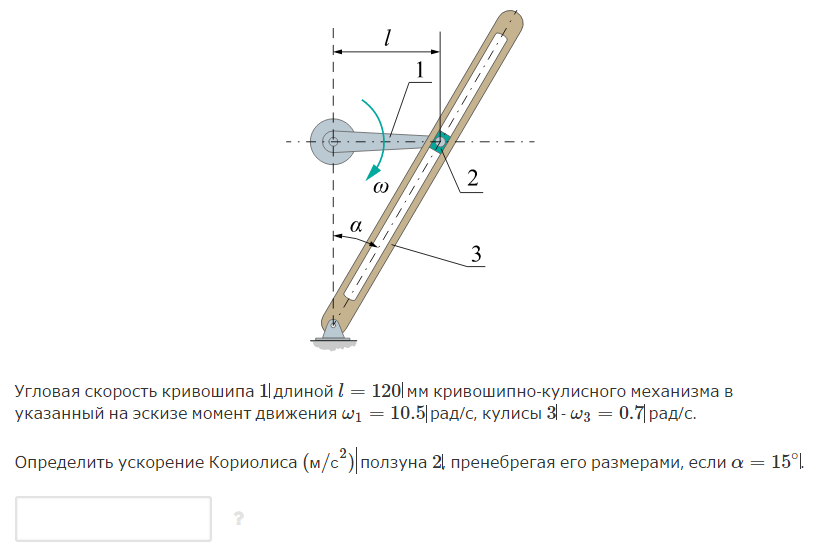
Ускорение Кориолиса
равно

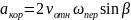
Где

– угол между относительной скорость и
осью переносного вращения

В данном случает

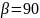
Переносное движение
– это вращение кулисы, следовательно:

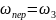
Для определения

,
спроецируем

на ось х (см.рисунок, который
не соответствует вашим данным)

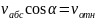
L=120мм=0,12м

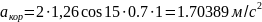
Следовательно:

,
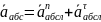
т.к. у кривошипа постоянная скорость
вращения

направлено от ползуна к центру вращения
кривошипа.

,
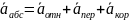
т.к. переносное движение поступательное

Спроецируем данное
выражение на ось х

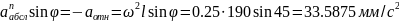
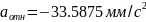
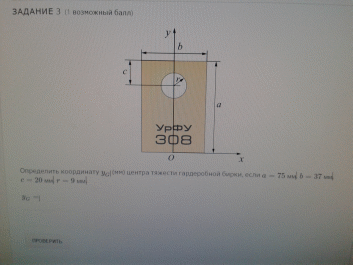
координата
прямоугольника: y₁=а/2=37,5
мм; площадь прямоугольника: S₁=ab=2775
мм²

координата
окружности: y₂=a-c=75-20=55мм;
площадь окружности: S₂=-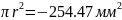

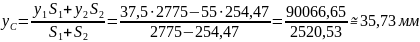
координата
y₁=a=10см

координата
y₂=2a+b=22,07см

координата
y_C
найдем по формуле

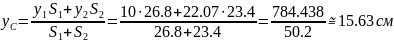
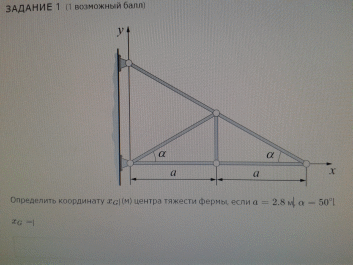
Ферма
состоит из 6 стержней.

х₁=а/2=1,4м;
х₂=а/2=1,4м;
х₃=а/2=1,4м;
х₄=а=2,8м;
х₅=а+а/2=4,2м;
х₆=а+а/2=4,2м

l₁=
а/cosα=2.8/0.64=4.36м;
l₂=
а/cosα=2.8/0.64=4.36м;
l₃=a=2.8м;
l₄=atgα=2.8tg50=3,34м;
l₅=а/cosα=2.8/0.64=4.36м;
l₆=а=2,8
м

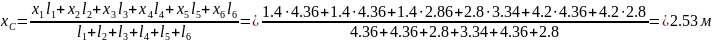
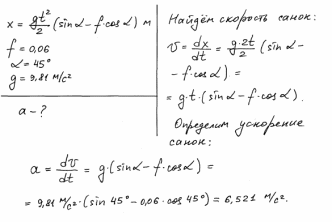
Соседние файлы в предмете Теоретическая механика

• #
• #
• #
• #
• #
• #

В полях “Шина №1” следует указать стандартный типоразмер для вашей машины. Он обычно указан на табличке, наклеенной в проёме водительской двери.

В поля “Шина №2” введите параметры шины, которую хотите сравнить с эталоном (с шиной №1).

Диаметр нового колеса (шины) не должен отличаться более чем на 3% от диаметра колеса, установленного заводом изготовителем автомобиля.

Маркировка шин и расшифровка

Ширина шины по маркировке

Ширина шины (W_шины) указана первым числом в маркировке в миллиметрах: 225/50 R16

Как посчитать высоту профиля шины

Высота профиля указана в маркировке шины вторым числом в процентах от первого числа (ширины шины): 225/50 R16

Таким образом, чтобы определить её в миллиметрах нужен расчет по следующей формуле:

Формула

H_{профиля в мм} = (W_шины ⋅ H_{профиля в %}) / 100

Пример

Для примера посчитаем чему равна высота профиля шины со следующей маркировкой: 205 / 55 R16

H_{профиля} = (205 ⋅ 55) / 100 = 113 мм = 11.3 см

Диаметр диска по маркировке шины

Обычно диаметр диска (посадочный диаметр) указан после буквы R (иногда В, D или буква не указана): 225/50 R16.

Этот параметр указан в дюймах, поэтому если требуется перевести его в сантиметры, его следует умножить на 2.54.

Диаметр шины по маркировке

Расчет диаметра колеса легко произвести, зная диаметр диска и высоту профиля шины.

Формула

Пример

Для примера определим диаметр шины в сантиметрах со следующей маркировкой: 205 / 55 R16

1. Определим высоту профиля: H_{профиля} = (205 ⋅ 55) / 100 = 113 мм = 11.3 см
2. Переведём посадочный диаметр из дюймов в сантиметры: D_диска = 16 ⋅ 2.54 = 40.64 см
3. Определим диаметр шины: D_шины = 40.64 + 2 ⋅ 11.3 = 63.2 см

Длина окружности шины

Для того, чтобы рассчитать длину окружности шины С_шины нужно знать её диаметр D_шины. Расчет осуществляется по следующей формуле:

Формула

С_шины = π ⋅ D_шины , где π ≈ 3.14

Пример

Возьмём диаметр шины из предыдущего примера D_шины = 63.2 см и определим длину окружности шины с маркировкой: 205 / 55 R16

С_шины = 63.2 ⋅ 3.14 = 198.44 см

Число оборотов колеса за 1 км

Для того, чтобы определить число оборотов колеса, при котором оно преодолеет расстояние в один километр, нужно знать длину внешней окружности шины.

Формула

Пример

Для колеса с длиной окружности шины 198.44 см посчитаем число оборотов за 1 км:

Число оборотов = 100000 / 198.44 = 503.9 ≈ 504 об./км

Как влияет размер шин на показание спидометра

Если диаметр колеса больше или меньше стандартного, то показания спидометра не будут отражать реальную скорость автомобиля. Так, например, если диаметр шины меньше стандартного, то спидометр будет показывать скорость больше, чем она есть на самом деле. И на оборот.

Влияние размера шин на клиренс

Чем больше диаметр шины, тем больше клиренс. При этом если, например, вы поменяли колесо с диаметром 60 см, на колесо с диаметром 64 см, то клиренс вырос на 2 см.

Угловая и линейная скорость

Переход от угловой к линейной скорости.

Сегодня смотрел на детей, катающихся на карусели, и подумал — а интересно, с какой скоростью они крутятся.
Подумав еще, понял, что ответить на этот вопрос очень просто, достаточно подсчитать, сколько оборотов в минуту они совершают.

Зная число оборотов в минуту, можно найти угловую скорость в радианах в секунду — за один оборот угол меняется на радиан, за минуту – радиан, и соответственно за секунду — радиан.

Это угловая скорость — радиан/сек. Переход к линейной тривиален — углу в 1 радиан соответствует дуга окружности равная радиусу, соответственно,

Вот и все, а ниже калькулятор. Скорость в м/с приводит к км/час, чтобы было понятнее.

[spoiler title=”источники:”]

http://poschitat.online/shinnyi-kalkulyator

http://planetcalc.ru/556/

[/spoiler]