
Пример решения задачи №68.
Обруч массой m = 1 кг и радиусом R = 0,2 м вращается равномерно с частотой 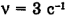 относительно оси
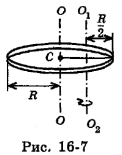
относительно оси 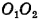 , проходящей через середину его радиуса перпендикулярно плоскости обруча (рис. 16-7). Определить момент импульса обруча L.
, проходящей через середину его радиуса перпендикулярно плоскости обруча (рис. 16-7). Определить момент импульса обруча L.
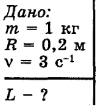
Решение:
Момент импульса твердого тела равен произведению момента инерции этого тела J и его угловой скорости 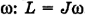
Момент инерции обруча J относительно оси 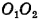 по теореме Штейнера равен сумме момента инерции этого обруча
по теореме Штейнера равен сумме момента инерции этого обруча 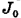 относительно оси 00, проходящей через его центр С, и произведения массы обруча m на квадрат расстояния d между осями
относительно оси 00, проходящей через его центр С, и произведения массы обруча m на квадрат расстояния d между осями 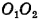 и ОО, которое, как следует из рис. 16-7, равно
и ОО, которое, как следует из рис. 16-7, равно
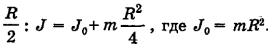
Угловая скорость 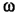 обруча связана с его частотой вращения v соотношением
обруча связана с его частотой вращения v соотношением
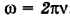
Подставив выражение для момента инерции J и угловой скорости со в формулу момента импульса, получим 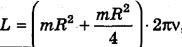
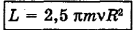
Подставим числа и произведем вычисления:
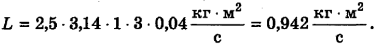
Ответ: 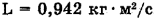 .
.
Эта задача взята со страницы подробного решения задач по физике, там теория и задачи по всем темам физики, можете посмотреть:
Физика — задачи с решениями и примерами
Возможно вам будут полезны ещё вот эти задачи:

Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.
Угловая скорость
Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.
Обозначение угловой скорости: ω (омега).
Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.
С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.

Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:

Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.
Быстрота изменения угла φ (перемещения плоскости П из положения П1 в положение П2) – это и есть угловая скорость:

Приняв вектор k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.
Формулы угловой скорости
Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:
- если известно количество оборотов n за единицу времени t:

- если задан угол поворота φ за единицу времени:

- если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:

Размерности угловой скорости:
- Количество оборотов за единицу времени [об/мин], [c-1].
- Угол поворота за единицу времени [рад/с].
Определение угловой скорости
Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.

Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.

Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.
Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.
Другие примеры решения задач >
Угловое ускорение
Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:

Обозначение: ε (Эпсилон)
Единицы измерения углового ускорения: [рад/с2], [с-2]
Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.
Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).
Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:
Расчет углового ускорения
Пример: По заданному значению касательной составляющей полного ускорения aτ точки B, расположенной на расстоянии r от центра вращения колеса.

Требуется определить величину и направление углового ускорения колеса ε, если aτ = 10 м/с2, r = 50 см.

Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.
Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.
В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость
ω = 1,5 с-1 = 9,42 рад/с.
Смотрите также:
- Примеры расчета угловой скорости и ускорения
- Скорости и ускорения точек вращающегося тела
Помогаю со студенческими работами здесь
Охарактеризовать движение гантелей после соударения, найти угловую скорость вращения гантелей
Четыре одинаковых шара массы m каждый объединены попарно с помощью невесомых стержней длины l в две…
 Определите угловую скорость w вращения колеса
Определите угловую скорость w вращения колеса
Раздел скорее всего не тот, но помоги решить) уже голова не варит просто!
1)Определите угловую…
 Определить угловую скорость вращения звезд
Определить угловую скорость вращения звезд
Помогите(
При вращении двух звезд («белых карликов») массами m1 = 7·10^30кг и m2 = 3·10^30 кг…
Определить угловую скорость вращения диска с пулей и работу, совершенную силами сопротивления
Во вращающийся с угловой скоростью ю1 = 5 с-1 диск массой
М = 10 кг и радиусом R = 10 см попадает…
Искать еще темы с ответами
Или воспользуйтесь поиском по форуму:
Знаток
(289),
закрыт
8 месяцев назад
Хулиганов Иосиф
Искусственный Интеллект
(268409)
9 лет назад
Угловая скорость обруча в системе отсчета, связанной с центром обруча, равна ω=V0/R Угловая скорость направлена перпендикулярно плоскости обруча “от нас”. Скорость т. А в системе, связанной с центром обруча равна V0 и направлена вертикально вверх. В системе же отсчета, связанной с горизонтальной поверхностью, скорость т. А равна V0*корень (2) и направлена под углом 45° вверх по отношению к вектору V0 скорости центра обруча.
|
Если у обруча поступательная скорость отсутствует( в условии об этом умалчивается), то обруч обладает кинетической энергией только вращательного движения: |
