Как найти угловую скорость равномерного вращения

Содержание:

Определение и формула угловой скорости
Равномерное вращение
Формула, связывающая линейную и угловую скорости
Единицы измерения угловой скорости
Примеры решения задач

Определение и формула угловой скорости

Определение

Круговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность
с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.

Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.

Перемещение при вращении характеризуют при помощи угла поворота
$(varphi)$ . Часто используют вектор элементарного поворота
$bar{dvarphi}$ , который равен по величине элементарному углу поворота тела
$(d varphi)$ за маленький отрезок времени dt и направлен по мгновенной оси вращения в сторону,
откуда этот поворот виден реализующимся против часовой стрелки. Надо отметить, что только элементарные угловые перемещения являются векторами.
Углы вращения на конечные величины векторами не являются.

Определение

Угловой скоростью называют скорость изменения угла поворота и обозначают ее обычно буквой
$omega$ . Математически определение угловой скорости записывают так:

$$bar{omega}=frac{d bar{varphi}}{d t}=dot{bar{varphi}}(1)$$

Угловая скорость – векторная величина (это аксиальный вектор). Она имеет направление вдоль мгновенной оси вращения совпадающее
с направлением поступательного правого винта, если его вращать в сторону вращения тела (рис.1).

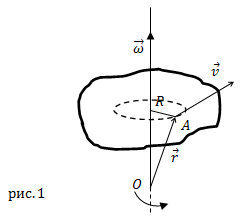
Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости),
так и за счет поворота оси вращения в пространстве ($bar{omega}$ при этом изменяет направление).

Равномерное вращение

Если тело за равные промежутки времени поворачивается на один и тот же угол,
то такое вращение называют равномерным. При этом модуль угловой скорости находят как:

$$omega=frac{varphi}{t}(2)$$

где $(varphi)$ – угол поворота, t – время, за которое этот поворот совершён.

Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот
($Delta varphi=2 pi$). Угловая скорость связана с периодом обращения как:

$$omega=frac{2 pi}{T}(3)$$

С числом оборотов в единицу времени ($nu) угловая скорость связана формулой:

$$omega=2 pi nu(4)$$

Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения,
но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно
с данной мгновенной величиной скорости.

Формула, связывающая линейную и угловую скорости

Линейная скорость $bar{v}$ точки А (рис.1), которая расположена
на расстоянии R от оси вращения связана с вектором угловой скорости следующим векторным произведением:

$$bar{v}=[bar{omega} bar{R}](5)$$

где $bar{R}$ – перпендикулярная к оси вращения компонента радиус-вектора точки
$A (bar{r})$ (рис.1). Вектор
$bar{r}$ проводят от точки, находящейся на оси вращения к рассматриваемой точке.

Единицы измерения угловой скорости

Основной единицей измерения угловой скорости в системе СИ является: [$omega$]=рад/с

В СГС: [$omega$]=рад/с

Примеры решения задач

Пример

Задание. Движение тела с неподвижной осью задано уравнением
$varphi=2 t-4 t^{3}$,
$(varphi)$ в рад, t в сек.
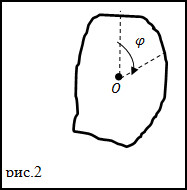
Начало вращения при t=0 c. Положительным считают углы указанные направлением стрелки (рис.2). В каком направлении (
относительно часовой стрелки поворачивается тело) в момент времени t=0,5 c.

Решение. Для нахождения модуля угловой скорости применим формулу:

$$omega=frac{d varphi}{d t}(1.1)$$

Используем заданную в условии задачи функцию
$varphi(t)$, возьмем производную от нее по времени, получим функцию
$omega(t)$:

$$omega(t)=2-8 t^{2}(1.2)$$

Вычислим, чему будет равна угловая скорость в заданный момент времени (при t=0,5 c):

$$omega(t)=2-8(0,5)^{2}=0left(frac{r a d}{c}right)$$

Ответ. В заданный момент времени тело имеет угловую скорость равную нулю, следовательно, она останавливается.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Скорости вращения тела заданы системой уравнений:

$$left{begin{array}{c}bar{omega}_{1}=t^{2 bar{i}} \ bar{omega}_{2}=2 t^{2} bar{j}end{array}right.$$

где $bar{i}$ и
$bar{j}$ – единичные ортогональные векторы. На какой угол $(varphi)$ поворачивается тело за время равное 3 с?

Решение. Определим, какова функция, которая связывает модуль скорости вращения тела и время (t)
($omega(t)$). Так как вектора
$bar{i}$ и
$bar{j}$ перпендикулярны друг другу, значит:

$$omega=sqrt{omega_{1}^{2}+omega_{2}^{2}}=sqrt{left(t^{2}right)^{2}+left(2 t^{2}right)^{2}}=t^{2} sqrt{5}(2.2)$$

Модуль угловой скорости связан с углом поворота как:

$$omega=frac{d varphi}{d t}(2.3)$$

Следовательно, угол поворота найдем как:

$$varphi=int_{t_{1}}^{t_{2}} omega d t=int_{0}^{3} t^{2} sqrt{5} d t=left.sqrt{5} frac{t^{3}}{3}right|_{0} ^{3} approx 20(mathrm{rad})$$

Ответ. $varphi = 20$ рад.

Читать дальше: Формула удельного веса.

Источник

Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.

Обозначение угловой скорости: ω (омега).

Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.

С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.

Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:

Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.

Быстрота изменения угла φ (перемещения плоскости П из положения П₁ в положение П₂) – это и есть угловая скорость:

Приняв вектор k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

если известно количество оборотов n за единицу времени t:
если задан угол поворота φ за единицу времени:
если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:

Размерности угловой скорости:

Количество оборотов за единицу времени [об/мин], [c^-1].
Угол поворота за единицу времени [рад/с].

Определение угловой скорости

Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.

Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.

Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.

Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.

Другие примеры решения задач >

Угловое ускорение

Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:

Обозначение: ε (Эпсилон)

Единицы измерения углового ускорения: [рад/с²], [с^-2]

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

Расчет углового ускорения

Пример: По заданному значению касательной составляющей полного ускорения a_τ точки B, расположенной на расстоянии r от центра вращения колеса.

Требуется определить величину и направление углового ускорения колеса ε, если a_τ = 10 м/с², r = 50 см.

Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.

Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

ω = 1,5 с^-1 = 9,42 рад/с.

Смотрите также:

Примеры расчета угловой скорости и ускорения
Скорости и ускорения точек вращающегося тела

Источник

Угловая скорость

Размерность	T ⁻¹
Единицы измерения
СИ	рад/с
СГС	рад/с
Другие единицы	градус/с об/с об/мин

Углова́я ско́рость — векторная величина, характеризующая быстроту и направление вращения материальной точки или абсолютно твёрдого тела относительно оси вращения. Модуль угловой скорости для вращательного движения совпадает с мгновенной угловой частотой вращения, а направление перпендикулярно плоскости вращения и связано с направлением вращения правилом правого винта. Строго говоря, угловая скорость представляется псевдовектором (аксиальным вектором), и может быть также представлена в виде кососимметрического тензора^[1].

Угловая скорость в двухмерном пространстве[править | править код]

Этот раздел статьи ещё не написан.

Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (31 августа 2016)

Векторное представление в трёхмерном пространстве[править | править код]

В трёхмерном пространстве вектор угловой скорости по величине равен углу поворота точки вокруг центра вращения за единицу времени:

${displaystyle omega ={frac {dvarphi }{dt}},}$

а направлен по оси вращения согласно правилу буравчика, то есть в ту сторону, в которую ввинчивался бы буравчик или винт с правой резьбой, если бы вращался в эту сторону. Другой мнемонический подход для запоминания взаимной связи между направлением вращения и направлением вектора угловой скорости состоит в том, что для условного наблюдателя, находящегося на конце вектора угловой скорости, выходящего из центра вращения, само вращение выглядит происходящим против часовой стрелки.

Угловая скорость является аксиальным вектором (псевдовектором). При отражении осей системы координат компоненты обычного вектора (например, радиус-вектора точки) меняют знак. В то же время компоненты псевдовектора (в частности, угловой скорости) при таком преобразовании координат остаются прежними.

Тензорное представление[править | править код]

Этот раздел статьи ещё не написан.

Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (31 августа 2016)

Единицы измерения[править | править код]

Единица измерения угловой скорости, принятая в Международной системе единиц (СИ) и в системах СГС и МКГСС, — радиан в секунду (русское обозначение: рад/с, международное: rad/s)^[2]^{[Комм 1]}. В технике также используются обороты в секунду, намного реже — градусы, минуты, секунды дуги в секунду, грады в секунду. Часто в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли просто на глаз, подсчитывая число оборотов за единицу времени.

Свойства[править | править код]

Угловая скорость (синяя стрелка) в полторы единицы по часовой стрелке

Угловая скорость (синяя стрелка) в одну единицу против часовой стрелки (вектор угловой скорости направлен навстречу направлению взгляда наблюдателя)

Вектор мгновенной скорости любой точки абсолютно твёрдого тела, вращающегося с угловой скоростью , определяется формулой:

где — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определённом расстоянии (радиусе) от оси вращения можно считать так: Если вместо радианов применять другие единицы измерения углов, то в двух последних формулах появится множитель, не равный единице.

В случае плоского вращения, то есть когда все векторы скоростей точек тела всегда лежат в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось вращения, то есть на прямую, ортогональную плоскости вращения. В этом случае кинематика вращения сильно упрощается. Однако в общем случае угловая скорость может менять со временем направление в трёхмерном пространстве, и такая упрощенная картина не работает.
Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю). Равномерное вращение является частным случаем плоского вращения.
Производная угловой скорости по времени есть угловое ускорение.
Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчёта, отличающихся положением начала отсчёта и скоростью его движения, но двигающихся равномерно прямолинейно и поступательно друг относительно друга. Однако в этих инерциальных системах отсчёта может различаться положение оси или центра вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).
В случае движения точки в трёхмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:

${vec omega }={frac {{vec r}times {vec v}}{({vec r},{vec r})}},$

где

— радиус-вектор точки (из начала координат),

— скорость этой точки,

— векторное произведение,

— скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы

подходящие по определению, по-другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как даёт разные

для каждой точки, а при вращении абсолютно твёрдого тела вектора угловой скорости вращения всех его точек совпадают). Однако в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.

В случае равномерного вращательного движения (то есть движения с постоянным вектором угловой скорости) абсолютно твёрдого тела декартовы координаты точек вращающегося так тела совершают гармонические колебания с угловой (циклической) частотой, равной модулю вектора угловой скорости.

Связь с конечным поворотом в пространстве[править | править код]

{vec {omega }}={vec {n}}{dot {theta }}+{dot {{vec {n}}}}sin theta +{vec {n}}times {dot {{vec n}}}(1-cos theta ).

$omega _{i}={frac {1}{2}}varepsilon _{{ijk}}T_{{jn}}{dot {T}}_{{kn}}.$

$omega _{i}={frac {4T_{{ij}}^{{1/2}}W_{{j}}}{1+V^{2}}}.$

Примечания[править | править код]

Комментарии[править | править код]

↑ Плоский угол, определяемый как отношение длины дуги окружности, заключённой между двумя радиусами, к длине радиуса, безразмерен, поэтому единицей измерения плоских углов является число «один», а единицей измерения угловой скорости в системе СИ — с⁻¹. Однако, в случае плоских углов единице «один» присвоено специальное наименование «радиан» для того, чтобы в каждом конкретном случае облегчить понимание того, какая именно физическая величина имеется в виду^[3].

Источники[править | править код]

↑ Ишлинский А. Ю. Классическая механика и силы инерции / Отв. ред. Б. В. Раушенбах. — М.: «Наука», 1987. — С. 239.
↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 98. — 240 с. — ISBN 5-7050-0118-5.
↑ Units for dimensionless quantities, also called quantities of dimension one (англ.). SI Brochure: The International System of Units (SI). Международное бюро мер и весов (2006; обновлено в 2014). Дата обращения: 2016-1-29.

См. также[править | править код]

Угловая частота
Угловое ускорение
Момент импульса

Литература[править | править код]

Лурье А. И. Аналитическая механика. — М.: ГИФМЛ, 1961. — С. 100-136. — 824 с.

Источник

Равномерное движение по окружности.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: движение по окружности с постоянной по модулю скоростью, центростремительное ускорение.

Равномерное движение по окружности – это достаточно простой пример движения с вектором ускорения, зависящим от времени.

Пусть точка вращается по окружности радиуса . Скорость точки постоянна по модулю и равна . Скорость называется линейной скоростью точки.

Период обращения – это время одного полного оборота. Для периода имеем очевидную формулу:

$T=frac{displaystyle 2pi r}{displaystyle v}$ . (1)

Частота обращения – это величина, обратная периоду:

$nu =frac{displaystyle 1}{displaystyle T}$ .

Частота показывает, сколько полных оборотов точка совершает за секунду. Измеряется частота в об/с (обороты в секунду).

Пусть, например, T=0,1 c . Это означает, что за время 0,1 c точка совершает один полный
оборот. Частота при этом получается равна: об/с; за секунду точка совершает 10 полных оборотов.

Угловая скорость.

Рассмотрим равномерное вращение точки в декартовой системе координат. Поместим начало координат в центре окружности (рис. 1).

Рис. 1. Равномерное движение по окружности

Пусть $M_{0}$ – начальное положение точки; иными словами, при t = 0 точка имела координаты (r, 0) . Пусть за время точка повернулась на угол varphi и заняла положение .

Отношение угла поворота ко времени называется угловой скоростью вращения точки:

$omega =frac{displaystyle varphi }{displaystyle t}$ . (2)

Угол varphi , как правило, измеряется в радианах, поэтому угловая скорость измеряется в рад/с. За время, равное периоду вращения, точка поворачивается на угол 2pi . Поэтому

$omega =frac{displaystyle 2pi }{displaystyle t}$ . (3)

Сопоставляя формулы (1) и (3), получаем связь линейной и угловой скоростей:

. (4)

Закон движения.

Найдём теперь зависимость координат вращающейся точки от времени. Видим из рис. 1, что

Но из формулы (2) имеем: . Следовательно,

. (5)

Формулы (5) являются решением основной задачи механики для равномерного движения точки по окружности.

Центростремительное ускорение.

Теперь нас интересует ускорение вращающейся точки. Его можно найти, дважды продифференцировав соотношения (5):

$v_{displaystyle x}=dot{x}=-omega r sin omega t, v_{displaystyle y}=dot{y}=omega r cosomega t,$

$a_{x}=dot{v_{x}}=-omega ^{2}rcosomega t, a_{y}=dot{v}y=-omega ^{2}rsinomega t.$

С учётом формул (5) имеем:

$a_{x}=-omega^{2}x, a_{y}=-omega^{2}y.$ (6)

Полученные формулы (6) можно записать в виде одного векторного равенства:

$vec{a}=-omega^{2}vec{r},$ (7)

где vec{r} – радиус-вектор вращающейся точки.

Мы видим, что вектор ускорения направлен противоположно радиус-вектору, т. е. к центру окружности (см. рис. 1). Поэтому ускорение точки, равномерно движущейся по окружности, называется центростремительным.

Кроме того, из формулы (7) мы получаем выражение для модуля центростремительного ускорения:

$a=omega^{2}r.$ (8)

Выразим угловую скорость из (4)

$omega =frac{displaystyle v}{displaystyle r}$

и подставим в (8). Получим ещё одну формулу для центростремительного ускорения:

$a=frac{displaystyle v^{2}}{displaystyle r}$ .

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Равномерное движение по окружности.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Содержание материала

Угловая скорость
Формулы угловой скорости
Видео
Угол поворота и период обращения
Равномерное вращение
Как найти угловую скорость без учета времени
Как найти угловую скорость в радианах в секунду
Период и частота
Примеры решения задач