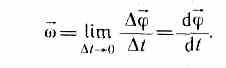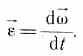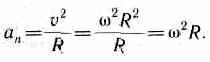Как найти угловую скорость твердого тела

Как найти угловую скорость твердого тела

Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.

Обозначение угловой скорости: ω (омега).

Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.

С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.
Угловая скорость вращающегося тела
Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:

Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.

Быстрота изменения угла φ (перемещения плоскости П из положения П1 в положение П2) – это и есть угловая скорость:

Приняв вектор k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

  1. если известно количество оборотов n за единицу времени t:
    Формула угловой скорости по заданным оборотам
  2. если задан угол поворота φ за единицу времени:
    Формула угловой скорости от угла поворота
  3. если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:

Размерности угловой скорости:

  • Количество оборотов за единицу времени [об/мин], [c-1].
  • Угол поворота за единицу времени [рад/с].

Определение угловой скорости

Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.
Угловая скорость вращения диска
Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.

Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.

Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.

Другие примеры решения задач >

Угловое ускорение

Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:


Обозначение: ε (Эпсилон)

Единицы измерения углового ускорения: [рад/с2], [с-2]

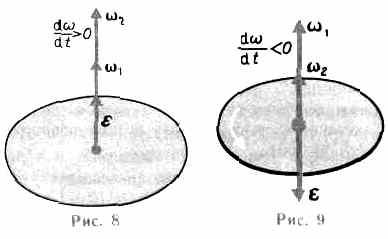
Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

Расчет углового ускорения

Пример: По заданному значению касательной составляющей полного ускорения aτ точки B, расположенной на расстоянии r от центра вращения колеса.
Пример расчета углового ускорения колеса
Требуется определить величину и направление углового ускорения колеса ε, если aτ = 10 м/с2, r = 50 см.

Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.

Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

ω = 1,5 с-1 = 9,42 рад/с.

Смотрите также:

  • Примеры расчета угловой скорости и ускорения
  • Скорости и ускорения точек вращающегося тела
Источник
Угловая скорость
omega
Размерность T −1
Единицы измерения
СИ рад/с
СГС рад/с
Другие единицы градус/с
об/с
об/мин

Углова́я ско́рость — векторная величина, характеризующая быстроту и направление вращения материальной точки или абсолютно твёрдого тела относительно оси вращения. Модуль угловой скорости для вращательного движения совпадает с мгновенной угловой частотой вращения, а направление перпендикулярно плоскости вращения и связано с направлением вращения правилом правого винта. Строго говоря, угловая скорость представляется псевдовектором (аксиальным вектором), и может быть также представлена в виде кососимметрического тензора[1].

Угловая скорость в двухмерном пространстве[править | править код]

Пазлинка и перо

Этот раздел статьи ещё не написан.

Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (31 августа 2016)

Векторное представление в трёхмерном пространстве[править | править код]

В трёхмерном пространстве вектор угловой скорости по величине равен углу поворота точки вокруг центра вращения за единицу времени:

{displaystyle omega ={frac {dvarphi }{dt}},}

а направлен по оси вращения согласно правилу буравчика, то есть в ту сторону, в которую ввинчивался бы буравчик или винт с правой резьбой, если бы вращался в эту сторону. Другой мнемонический подход для запоминания взаимной связи между направлением вращения и направлением вектора угловой скорости состоит в том, что для условного наблюдателя, находящегося на конце вектора угловой скорости, выходящего из центра вращения, само вращение выглядит происходящим против часовой стрелки.

Угловая скорость является аксиальным вектором (псевдовектором). При отражении осей системы координат компоненты обычного вектора (например, радиус-вектора точки) меняют знак. В то же время компоненты псевдовектора (в частности, угловой скорости) при таком преобразовании координат остаются прежними.

Тензорное представление[править | править код]

Пазлинка и перо

Этот раздел статьи ещё не написан.

Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (31 августа 2016)

Единицы измерения[править | править код]

Единица измерения угловой скорости, принятая в Международной системе единиц (СИ) и в системах СГС и МКГСС, — радиан в секунду (русское обозначение: рад/с, международное: rad/s)[2][Комм 1]. В технике также используются обороты в секунду, намного реже — градусы, минуты, секунды дуги в секунду, грады в секунду. Часто в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли просто на глаз, подсчитывая число оборотов за единицу времени.

Свойства[править | править код]

Угловая скорость (синяя стрелка) в полторы единицы по часовой стрелке

Угловая скорость (синяя стрелка) в одну единицу против часовой стрелки (вектор угловой скорости направлен навстречу направлению взгляда наблюдателя)

Вектор мгновенной скорости любой точки абсолютно твёрдого тела, вращающегося с угловой скоростью {vec {omega }}, определяется формулой:

{vec v}=[ {vec omega },{vec r} ],

где {vec {r}} — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определённом расстоянии (радиусе) r от оси вращения можно считать так: {displaystyle v=omega r.} Если вместо радианов применять другие единицы измерения углов, то в двух последних формулах появится множитель, не равный единице.

  • В случае плоского вращения, то есть когда все векторы скоростей точек тела всегда лежат в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось вращения, то есть на прямую, ортогональную плоскости вращения. В этом случае кинематика вращения сильно упрощается. Однако в общем случае угловая скорость может менять со временем направление в трёхмерном пространстве, и такая упрощенная картина не работает.
  • Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю). Равномерное вращение является частным случаем плоского вращения.
  • Производная угловой скорости по времени есть угловое ускорение.
  • Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчёта, отличающихся положением начала отсчёта и скоростью его движения, но двигающихся равномерно прямолинейно и поступательно друг относительно друга. Однако в этих инерциальных системах отсчёта может различаться положение оси или центра вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).
  • В случае движения точки в трёхмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:
{vec omega }={frac {{vec r}times {vec v}}{({vec r},{vec r})}}, где {vec {r}} — радиус-вектор точки (из начала координат), {vec {v}} — скорость этой точки, {vec r}times {vec v} — векторное произведение, ({vec r},{vec r}) — скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы {vec omega }, подходящие по определению, по-другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как даёт разные {vec {omega }} для каждой точки, а при вращении абсолютно твёрдого тела вектора угловой скорости вращения всех его точек совпадают). Однако в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.
  • В случае равномерного вращательного движения (то есть движения с постоянным вектором угловой скорости) абсолютно твёрдого тела декартовы координаты точек вращающегося так тела совершают гармонические колебания с угловой (циклической) частотой, равной модулю вектора угловой скорости.

Связь с конечным поворотом в пространстве[править | править код]

{vec {omega }}={vec {n}}{dot {theta }}+{dot {{vec {n}}}}sin theta +{vec {n}}times {dot {{vec n}}}(1-cos theta ).
omega _{i}={frac {1}{2}}varepsilon _{{ijk}}T_{{jn}}{dot {T}}_{{kn}}.
omega _{i}={frac {4T_{{ij}}^{{1/2}}W_{{j}}}{1+V^{2}}}.

Примечания[править | править код]

Комментарии[править | править код]

  1. ↑ Плоский угол, определяемый как отношение длины дуги окружности, заключённой между двумя радиусами, к длине радиуса, безразмерен, поэтому единицей измерения плоских углов является число «один», а единицей измерения угловой скорости в системе СИ — с−1. Однако, в случае плоских углов единице «один» присвоено специальное наименование «радиан» для того, чтобы в каждом конкретном случае облегчить понимание того, какая именно физическая величина имеется в виду[3].

Источники[править | править код]

  1. ↑ Ишлинский А. Ю. Классическая механика и силы инерции / Отв. ред. Б. В. Раушенбах. — М.: «Наука», 1987. — С. 239.
  2. ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 98. — 240 с. — ISBN 5-7050-0118-5.
  3. ↑ Units for dimensionless quantities, also called quantities of dimension one (англ.). SI Brochure: The International System of Units (SI). Международное бюро мер и весов (2006; обновлено в 2014). Дата обращения: 2016-1-29.

См. также[править | править код]

  • Угловая частота
  • Угловое ускорение
  • Момент импульса

Литература[править | править код]

  • Лурье А. И. Аналитическая механика. — М.: ГИФМЛ, 1961. — С. 100-136. — 824 с.
Источник

Время на прочтение
8 мин

Количество просмотров 26K

Содержание

  1. Что такое тензор и для чего он нужен?
  2. Векторные и тензорные операции. Ранги тензоров
  3. Криволинейные координаты
  4. Динамика точки в тензорном изложении
  5. Действия над тензорами и некоторые другие теоретические вопросы
  6. Кинематика свободного твердого тела. Природа угловой скорости
  7. Конечный поворот твердого тела. Свойства тензора поворота и способ его вычисления
  8. О свертках тензора Леви-Чивиты
  9. Вывод тензора угловой скорости через параметры конечного поворота. Применяем голову и Maxima
  10. Получаем вектор угловой скорости. Работаем над недочетами
  11. Ускорение точки тела при свободном движении. Угловое ускорение твердого тела
  12. Параметры Родрига-Гамильтона в кинематике твердого тела
  13. СКА Maxima в задачах преобразования тензорных выражений. Угловые скорость и ускорения в параметрах Родрига-Гамильтона
  14. Нестандартное введение в динамику твердого тела
  15. Движение несвободного твердого тела
  16. Свойства тензора инерции твердого тела
  17. Зарисовка о гайке Джанибекова
  18. Математическое моделирование эффекта Джанибекова

Введение

Что такое угловая скорость? Скалярная или векторная величина? На самом деле это не праздный вопрос.

Читая лекции по теоретической механике в университете, я, следуя традиционной методике изложения курса кинематики, вводил понятие угловой скорости в теме «Скорость точки тела при вращательном движении». И там угловая скорость впервые появляется как скалярная величина, со следующим определением.

Угловая скорость твердого тела — это первая производная от угла поворота тела по времени
omega = frac{d varphi}{dt}

А вот потом, при рассмотрении каноничной формулы Эйлера для скорости точки тела при вращении

vec{v}_M = vec{omega} times vec{r}

обычно дается следующее определение

Угловая скорость тела — это псевдовектор, направленный вдоль оси вращения тела в ту сторону, откуда вращение выглядит происходящим против часовой стрелки

Ещё одно частное определение, которое, во-первых, утверждает неподвижность оси вращения, во-вторых навязывает рассмотрение лишь правой системы координат. И наконец термин «псевдовектор» обычно объясняется студентам так: «Посмотрите, ведь мы показали, что омега — скалярная величина. А вектор мы вводим для того, чтобы выписать формулу Эйлера».

При рассмотрении сферического движения оказывается потом, что ось вращения меняет направление, угловое ускорение направлено по касательной к годографу угловой скорости и так далее. Неясности и вводные допущения множатся.

Учитывая уровень подготовки школьников, а так же вопиющую глупость, допускаемую в программах подготовки бакалавров, когда теормех начинается с первого (вдумайтесь!) семестра, такие постепенные вводные, на палках, веревках и желудях наверное оправданы.

Но мы с вами заглянем, что называется, «под капот» проблемы и, вооружившись аппаратом тензорного исчисления, выясним, что угловая скорость — это псевдовектор, порождаемый антисимметричным тензором второго ранга.

Думаю для затравки вполне достаточно, а поэтому — начнем!

1. Свободное движение твердого тела. Тензор поворота

Итак, как известно из традиционного вузовского курса теормеха

Если движение, совершаемо телом не ограничено связями, то такое его движение называют свободным

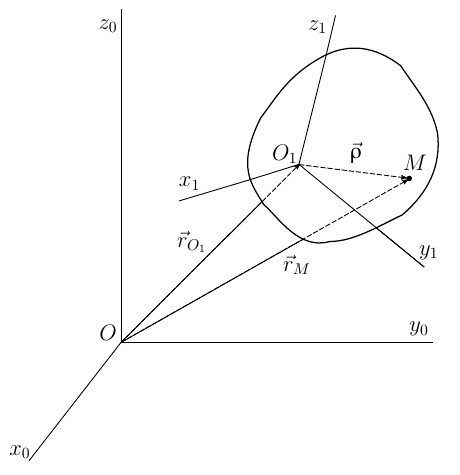
Это — самый общий случай движения тела. Следующий рисунок иллюстрирует тот факт, что свободное движение тела можно представить как сумму двух движений: поступательного вместе с полюсом O_1 и сферического вокруг полюса.

Рис. 1. Обычная иллюстрация из курса теоретической механики: определение положения свободного твердого тела в пространстве.

Напомню, что речь идет об абсолютно твердом теле, то есть теле, расстояния между точками которого не изменяется с течением времени. Ещё можно сказать, что твердое тело представляет собой неизменяемую механическую систему.

Как видно из рисунка 1, обычной практикой является рассмотрение двух систем координат — одна O , x_0 , y_0 , z_0 считается неподвижной и называется базовой, другая O , x_1 , y_1 , z_1 жестко связанна с телом и поворачивается относительно базовой вместе с ним. Такую систему координат называют связанной.

Сначала я тоже хотел ограничиться декартовыми координатами. Но тогда бы мои читатели задали бы мне логичный вопрос — «а зачем тогда тут тензоры?». Поэтому, потратив четыре для в мучительных раздумьях и «нагуляв» окончательное решение пару часов назад, я решил замахнуться на «Вильяма, нашего, Шекспира» и изложить дальнейшие рассуждения в криволинейных координатах.

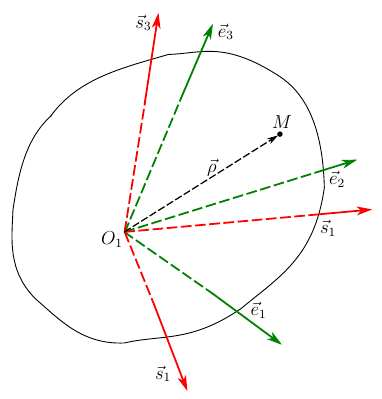
Рис. 2. Ориентация твердого тела в локальном базисе.

Пусть положение полюса Q_1 задается вектором

q^{,i} = q^{,i}(t)

Причем под этим вектором не следует понимать радиус-вектор, так как в криволинейных координатах такое понятие бессмысленно.

В точке O1 задан локальный репер базовой системы координат, образованный тройкой векторов (vec{s}_1, , vec{s}_2, , vec{s}_3). С движущимся телом связан подвижный репер (vec{e}_1, , vec{e}_2, , vec{e}_3). Поворот связанного репера относительно базового можно задать линейным оператором. Получим этот оператор и исследуем его свойства

Рассмотрим некоторую точку M, принадлежащую телу. К ней из полюса можно провести вектор vec{rho} неподвижный относительно связанного репера. Его можно разложить по векторам этого репера

vec{rho} = rho^{,i} vec{e}_i quad (2)

и по векторам базового репера

vec{rho}^{,'} = rho^{,'i} vec{e}_i quad (3)

Каждый вектор связанного репера можно разложить через векторы базового репера

vec{e}_i = beta_{i}^{,,j} vec{s}_j

Подставляем (4) в (2) и сравниваем с (3)

rho^{,'i} vec{s}_i = rho^{i} beta_{i}^{,,j} vec{s}_j quad (5)

Из (5) понятно, что компоненты вектора vec{rho} в базовой системе координат, пересчитываются через его компоненты в связанной системе путем применения линейного оператора

rho^{,'i} = rho^{i} beta_{i}^{,,j} quad (6)

или в безиндексной форме

rho^{,'} = mathbf{B}(t) cdot rho^{i} quad (6)

где столбцы матрицы

mathbf{B} = begin{bmatrix} beta_1^{,,1} && beta_2^{,,1} && beta_3^{,,1} \ beta_1^{,,2} && beta_2^{,,2} && beta_3^{,,2} \ beta_1^{,,3} && beta_2^{,,3} && beta_3^{,,3} end{bmatrix}

– контравариантные компоненты векторов связанного репера по отношению к базовому. Точка, как мы уже отмечали в прошлой статье, обозначает умножение тензоров с последующей сверткой по соседней паре индексов. Линейный оператор

mathbf{B} = mathbf{B}(t) quad (7)

действует на векторы таким образом, что поворачивает их относительно некоторой оси, не меняя длины и угла между векторами. Такое преобразование пространства называется ортогональным. Для того, чтобы таковое преобразование было возможным, оператор (7) должен обладать вполне определенными свойствами. Если длина векторов базиса и углы между ними не меняются, то это означает равенство всех попарных скалярных произведений векторов репера как в базовой, так и в связанной системах координат

vec{e}_{i} cdot vec{e}_j = vec{s}_i cdot vec{s}_j quad (8)

Правая часть (8) — это локальный метрический тензор

vec{e}_{i} cdot vec{e}_j = g_{ij}

g_{kl} , beta_i^{,,l} , beta_j^{,,k} = g_{ij} quad (9)

или

mathbf{B}^T cdot mathbf{g} cdot mathbf{B} = mathbf{g} quad(10)

Оператор mathbf{B} является по сути обыкновенной матрицей поворота координатной системы. И (10) утверждает, что если транспонированную матрицу поворота умножить на метрический тензор, а результат умножить на матрицу поворота мы получим снова метрический тензор. Можно сделать вывод, что

Преобразование координат при повороте является тождественным для метрического тензора, то есть переводит метрический тензор сам в себя.

В выражении (10) нетрудно увидеть преобразование метрического тензора про смене системы координат, о котором мы подробно говорили в самой первой статье цикла

Стоп! Но мы же знаем, что матрицы поворота обычно ортогональны, то есть произведение матрицы поворота на её транспонированную дает единичную матрицу, иными словами, чтобы обратить матрицу поворота её достаточно транспонировать.

Но ортогональность свойственна матрицам поворота, преобразующим ортонормированный декартов базис. Здесь мы имеем дело с локальным базисом, при повороте которого должны сохранятся длины векторов и углы между ними. Если мы примем базис декартовым, то из (10) мы получим привычные свойства матрицы поворота, к примеру её ортогональность.

Для дальнейших вычислений нам потребуется знать, как будет выглядеть матрица обратного преобразования, то есть mathbf{B}^{-1}. Что же, посмотрим. Для этого умножим (10) слева на mathbf{g}^{-1} и справа на mathbf{B}^{-1}

mathbf{g}^{-1} cdot mathbf{B}^T cdot mathbf{g} cdot mathbf{B} cdot mathbf{B}^{-1} = mathbf{g}^{-1} cdot mathbf{g} cdot mathbf{B}^{-1}

откуда незамедлительно получаем

mathbf{B}^{-1} = mathbf{g}^{-1} cdot mathbf{B}^T cdot mathbf{g}

Выходит, что матрица обратного преобразования действительно получается из транспонированной матрицы преобразования, но с участием метрического тензора. Выражения (10) и (11) очень пригодятся нам, а пока сделаем некоторые выводы.

Закон свободного движения твердого тела можно выписать в криволинейных координатах в виде системы уравнений

mathbf{q} = mathbf{q}(t) quad (12)

mathbf{B} = mathbf{B}(t) quad (13)

При этом (12) — закон движения полюса, а (13) — закон сферического движения тела вокруг полюса. При этом (13) — тензор ранга (1,1), называемый тензором поворота.

2. Скорость точки тела при свободном движении. Угловая скорость выходит на сцену

Вычислим скорость точки M, положение которой в связанной системе координат задается постоянными, в силу твердости тела, криволинейными координатами

rho^{,i} = mathop{rm const}

Из курса теоретической механики известна формула, определяющая скорость точки тела в данном движении

vec{v}_M = vec{v}_{O_1} + vecomega times vecrho

где vec{v}_{O_1} — скорость полюса; vecomega times vecrho = vec{u} — скорость точки вокруг полюса.

Так как все координаты, кроме (13) определены относительно базового репера, мы можем записать

q_M^{,(0))i} = q^{(0),i} + beta_{j}^{,,i} , rho^{,(1)j} quad (15)

Индекс в круглых скобках означает систему координат, в которой берутся компоненты (0 — базовая, 1 — связанная). Дифференцируем (15) по времени с учетом (13)

dot q_M^{,(0)i} = dot q^{(0),i} + dotbeta_{j}^{,,i} , rho^{,(1)j}

Перейдем в (16) к связанной системе координат, домножив (15) слева на mathbf{B}^{-1}

dot q_M^{,(1)i} = dot q^{(1),i} + beta_{k}^{,',i} , dotbeta_{j}^{,,k} , rho^{,(1)j} quad (17)

где beta_{k}^{,',i} — компонента оператора обратного преобразования mathbf{B}^{-1}.

Теперь сравним (17) и (14). В последнем слагаемом должно вылезти векторное произведение. Вспоминая определение векторного произведения через тензор Леви-Чивиты, данное во второй статье цикла, замечаем, что на выходе оно дает ковектор, поэтому в (17) перейдем к ковариантым компонентам, домножив это выражение на метрический тензор слева

dot q_{Mi}^{,(1)} = dot q_{,i}^{(1)} + g_{il} , beta_{k}^{,',l} , dotbeta_{j}^{,,k} , rho^{,(1)j} quad (18)

Теперь представим себе, как выглядел бы ковектор скорости точки относительно плюса, записанный через вектор угловой скорости

u_{,i} = varepsilon_{ijk} , omega^{,(1)j} , rho^{,(1)k}

при этом замечая, что

Omega_{,ik}^{,(1)} = varepsilon_{ijk} , omega^{,(1)j}

антисимметричный тензор второго ранга, о котором мы говорили в прошлой статье<. Таким образом, нам бы доказать, что

Omega_{,ij} = g_{,il} , beta_{k}^{,',l} , dotbeta_{j}^{,,k} quad (19)

является антисимметричным тензором второго ранга. Для этого придется доказать, что (19) меняет знак при перестановка индексов (транспонировании). При этом будем учитывать, что метрический тензор — абсолютно симметричный тензор второго ранга и при транспонировании он не меняется. Поэтому исследуем взаимосвязи между матрицами поворота, для чего нам потребуются выражения (10) и (11). Но прежде чем приступить, докажем ещё одно вспомогательное утверждение

3. Лемма о ковариантной производной метрического тензора

Ковариантная производная метрического тензора равна нулю

Обратимся к понятию ковариантной производной вектора, о которой упоминалось в третьей статье. Тогда мы вывели выражения для контравариантных компонент ковариантной производной от вектора

nabla_j , a^m = left(frac{partial a^m}{partial q^j} + a^i , Gamma_{ij}^m right)

Как как и любой вектор, компоненты данного вектора можно трансформировать в ковариантные умножением и сверткой с метрическим тензором

nabla_j a_i = g_{,im} , nabla_j , a^m quad (20)

А можно продифференцировать ковариантные компоненты непосредственно

nabla_j a_i = nabla_j left( g_{,im} , a^m right) = nabla_j , g_{,im} , a^m + g_{,im} , nabla_j , a^m quad (21)

Сравнивая (21) и (20) мы приходим к выводу, что равенство возможно лишь в случае если верно утверждение леммы

nabla_j , g_{,im} = 0 quad (22)

4. Угловая скорость как антисимметричный тензор второго ранга

Теперь, перепишем (19) в безиндексном виде, учтя уравнение (11)

Omega = mathbf{g} cdot mathbf{B}^{-1} cdot mathbf{dot{B}} = mathbf{B}^{,T} cdot mathbf{g} cdot mathbf{dot{B}} quad (23)

Далее, нам нужна связь между оператором поворота и его производной — дифференцируем (10) по времени

mathbf{dot{B}}^T cdot mathbf{g} cdot mathbf{B} + mathbf{B}^T cdot mathbf{g} cdot mathbf{dot{B}} + mathbf{B}^T cdot frac{partial mathbf{g}}{partial mathbf{q}} , mathbf{dot{q}} cdot mathbf{B} = frac{partial mathbf{g}}{partial mathbf{q}} , mathbf{dot{q}}

или, собирая производные от метрического тензора в правой части

mathbf{dot{B}}^T cdot mathbf{g} cdot mathbf{B} + mathbf{B}^T cdot mathbf{g} cdot mathbf{dot{B}} = frac{partial mathbf{g}}{partial mathbf{q}} , mathbf{dot{q}} - mathbf{B}^T cdot frac{partial mathbf{g}}{partial mathbf{q}} , mathbf{dot{q}} cdot mathbf{B} quad (24)

Но, производные от метрического тензора в (24) будут равны нулю, в силу равенства нулю ковариантной производной метрического тензора. Значит правая часть (24) равна нулю

mathbf{dot{B}}^T cdot mathbf{g} cdot mathbf{B} + mathbf{B}^T cdot mathbf{g} cdot mathbf{dot{B}} = 0 quad (25)

Пользуясь свойствами операции транспонирования, преобразуем (25)

left( left( mathbf{dot{B}}^T cdot mathbf{g} cdot mathbf{B} right)^T right)^T + mathbf{B}^T cdot mathbf{g} cdot mathbf{dot{B}} = 0

left( mathbf{B}^T cdot left( mathbf{dot{B}}^T cdot mathbf{g} right)^T right)^T + mathbf{B}^T cdot mathbf{g} cdot mathbf{dot{B}} = 0

left( mathbf{B}^T cdot mathbf{g}^T cdot mathbf{dot{B}} right)^T + mathbf{B}^T cdot mathbf{g} cdot mathbf{dot{B}} = 0&quot;

Так как mathbf{g}^T = mathbf{g} и с учетом (23), получаем

left( mathbf{B}^T cdot mathbf{g} cdot mathbf{dot{B}} right)^T + mathbf{B}^T cdot mathbf{g} cdot mathbf{dot{B}} = 0

Omega^T + Omega = 0 quad (26)

Из (26) непосредственно следует антисимметричность тензора (19)

Omega^T = -Omega quad (26)

Ну а коль скоро (19) антисимметричный тензор, то мы смело переписываем (18)

dot q_{Mi}^{,(1)} = dot q_{,i}^{(1)} + Omega_{,ij}^{(1)} , rho^{,(1)j} quad (28)

Таким образом мы приходим к выводу, что (19) и (23) есть ни что иное как антисимметричный тензор угловой скорости

5. Псевдовектор угловой скорости

Любому антисимметричному тензору можно поставить в соответствие псевдовектор, который мы уже получали в предыдущей статье. Повторим этот результат для тензора угловой скорости

omega^{,j} = frac{1}{2} , varepsilon^{,ijk} , Omega_{,ik} = frac{1}{2} ,varepsilon^{,ijk} , beta_i^{,,p} , g_{,pl} , dotbeta_k^{,,l} quad (29)

Возможно читателю знаком распространенный подход замены векторного произведения на умножение кососимметричной матрицы, построенной из первого вектора по определенному правилу, на второй вектор. Так вот это правило получается естественным путем, если в качестве инструмента использовать тензорное исчисление. Действительно, вот эта кососимметричная матрица, которой в матричном изложении механики заменяют угловую скорость

Omega = sqrt g , begin{bmatrix} 0 &amp;&amp; -omega^{,3} &amp;&amp; omega^{,2} \ omega^{,3} &amp;&amp; 0 &amp;&amp; -omega^{,1} \ -omega^{,2} &amp;&amp; omega^{,1} &amp;&amp; 0 end{bmatrix}

Возможно, внимательный читатель увидит, что в полученной матрице знаки противоположны тем, что мы получали в статье, посвященной антисимметричным тензорам. Да, все верно, ведь в той статье мы сворачивали вектор с тензором Леви-Чивиты по его третьему индексу k, тут мы выполняем свертку по среднему индексу j что дает прямо противоположные знаки.

Матрица (30) частенько встречается в литературе, в частности в трудах Д. Ю. Погорелова, но там она вводится как мнемоническое правило. Формула (29) дает четкую связь между вектором угловой скорости и кососимметричной матрицей. Она же дает возможность перейти от (28) к формуле

dot q_{Mi}^{,(1)} = dot q_{,i}^{(1)} + varepsilon_{,ijk} , omega^{,(1)j} rho^{,(1)k} quad (31)
Что, внезапно, эквивалентно векторному соотношению

vec{v}_M = vec{v}_{O_1} + vec{omega} times vec{rho}

Заключение

В этой статье было много математики. И я вынужден пока ограничится этим материалом — статья вышла длинной и насыщенной формулами. Данная тема будет продолжена и углублена в следующих статьях цикла.

Какой же вывод мы можем сделать сейчас? А вот какой

Угловая скорость твердого тела есть антисимметричный тензор, или, соответствующий ему псевдовектор, порождаемый тензором поворота тела относительно базовой системы координат

Для того чтобы написать эту работу потребовалось перелопатить гору литературы. Основные выкладки выполнены автором самостоятельно. Камнем преткновения были матрицы поворота для случая косоугольных координат. Я не сразу разглядел в соотношении (10) преобразование, оставляющее метрику инвариантной, хотя с учетом ранее написанных статей — следовало бы. Понять эту связь мне помог ужасный по оформлению, но очень толковый сайт «На что похожа математика». Кстати видно, что все соотношения переходят в известные для ортогональных матриц, если метрический тензор сделать единичным.

Разговор о механике твердого тела будет продолжен, а пока — всё. Спасибо за внимание!

Продолжение следует…

Источник

Содержание:

  • Определение и формула угловой скорости
  • Равномерное вращение
  • Формула, связывающая линейную и угловую скорости
  • Единицы измерения угловой скорости
  • Примеры решения задач

Определение и формула угловой скорости

Определение

Круговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность
с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.

Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.

Перемещение при вращении характеризуют при помощи угла поворота
$(varphi)$ . Часто используют вектор элементарного поворота
$bar{dvarphi}$ , который равен по величине элементарному углу поворота тела
$(d varphi)$ за маленький отрезок времени dt и направлен по мгновенной оси вращения в сторону,
откуда этот поворот виден реализующимся против часовой стрелки. Надо отметить, что только элементарные угловые перемещения являются векторами.
Углы вращения на конечные величины векторами не являются.

Определение

Угловой скоростью называют скорость изменения угла поворота и обозначают ее обычно буквой
$omega$ . Математически определение угловой скорости записывают так:

$$bar{omega}=frac{d bar{varphi}}{d t}=dot{bar{varphi}}(1)$$

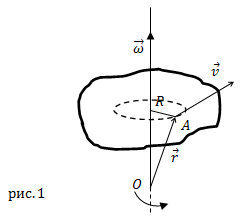
Угловая скорость – векторная величина (это аксиальный вектор). Она имеет направление вдоль мгновенной оси вращения совпадающее
с направлением поступательного правого винта, если его вращать в сторону вращения тела (рис.1).

Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости),
так и за счет поворота оси вращения в пространстве ($bar{omega}$ при этом изменяет направление).

Равномерное вращение

Если тело за равные промежутки времени поворачивается на один и тот же угол,
то такое вращение называют равномерным. При этом модуль угловой скорости находят как:

$$omega=frac{varphi}{t}(2)$$

где $(varphi)$ – угол поворота, t – время, за которое этот поворот совершён.

Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот
($Delta varphi=2 pi$). Угловая скорость связана с периодом обращения как:

$$omega=frac{2 pi}{T}(3)$$

С числом оборотов в единицу времени ($nu) угловая скорость связана формулой:

$$omega=2 pi nu(4)$$

Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения,
но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно
с данной мгновенной величиной скорости.

Формула, связывающая линейную и угловую скорости

Линейная скорость $bar{v}$ точки А (рис.1), которая расположена
на расстоянии R от оси вращения связана с вектором угловой скорости следующим векторным произведением:

$$bar{v}=[bar{omega} bar{R}](5)$$

где $bar{R}$ – перпендикулярная к оси вращения компонента радиус-вектора точки
$A (bar{r})$ (рис.1). Вектор
$bar{r}$ проводят от точки, находящейся на оси вращения к рассматриваемой точке.

Единицы измерения угловой скорости

Основной единицей измерения угловой скорости в системе СИ является: [$omega$]=рад/с

В СГС: [$omega$]=рад/с

Примеры решения задач

Пример

Задание. Движение тела с неподвижной осью задано уравнением
$varphi=2 t-4 t^{3}$,
$(varphi)$ в рад, t в сек.
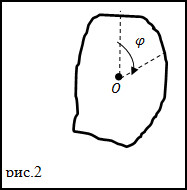
Начало вращения при t=0 c. Положительным считают углы указанные направлением стрелки (рис.2). В каком направлении (
относительно часовой стрелки поворачивается тело) в момент времени t=0,5 c.

Решение. Для нахождения модуля угловой скорости применим формулу:

$$omega=frac{d varphi}{d t}(1.1)$$

Используем заданную в условии задачи функцию
$varphi(t)$, возьмем производную от нее по времени, получим функцию
$omega(t)$:

$$omega(t)=2-8 t^{2}(1.2)$$

Вычислим, чему будет равна угловая скорость в заданный момент времени (при t=0,5 c):

$$omega(t)=2-8(0,5)^{2}=0left(frac{r a d}{c}right)$$

Ответ. В заданный момент времени тело имеет угловую скорость равную нулю, следовательно, она останавливается.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Скорости вращения тела заданы системой уравнений:

$$left{begin{array}{c}bar{omega}_{1}=t^{2 bar{i}} \ bar{omega}_{2}=2 t^{2} bar{j}end{array}right.$$

где $bar{i}$ и
$bar{j}$ – единичные ортогональные векторы. На какой угол $(varphi)$ поворачивается тело за время равное 3 с?

Решение. Определим, какова функция, которая связывает модуль скорости вращения тела и время (t)
($omega(t)$). Так как вектора
$bar{i}$ и
$bar{j}$ перпендикулярны друг другу, значит:

$$omega=sqrt{omega_{1}^{2}+omega_{2}^{2}}=sqrt{left(t^{2}right)^{2}+left(2 t^{2}right)^{2}}=t^{2} sqrt{5}(2.2)$$

Модуль угловой скорости связан с углом поворота как:

$$omega=frac{d varphi}{d t}(2.3)$$

Следовательно, угол поворота найдем как:

$$varphi=int_{t_{1}}^{t_{2}} omega d t=int_{0}^{3} t^{2} sqrt{5} d t=left.sqrt{5} frac{t^{3}}{3}right|_{0} ^{3} approx 20(mathrm{rad})$$

Ответ. $varphi = 20$ рад.

Читать дальше: Формула удельного веса.

Источник

Рассмотрим
твердое тело, которое враща­ется
вокруг неподвижной оси. Тогда от­дельные
точки этого тела будут описывать
окружности разных радиусов, центры
ко­торых лежат на оси вращения. Пусть
не­которая точка движется по окружности
радиуса R
(рис.6).
Ее положение через промежуток времени
t
зададим
углом .
Элементарные (бесконечно малые) углы
поворота рассматривают как векторы.
Мо­дуль вектора d
равен
углу поворота, а его направление совпадает
с направле­нием поступательного
движения острия винта, головка которого
вращается в на­правлении движения
точки по окружности, т. е. подчиняется
правилу
правого, винта (рис.6).
Векторы, направления которых связываются
с направлением вращения, называются
псевдовекторами
или
акси­альными
векторами. Эти
векторы не имеют определенных точек
приложения: они мо­гут откладываться
из любой точки оси вращения.

Угловой
скоростью называется
вектор­ная величина, равная первой
производной угла поворота тела по
времени:

Вектор
«в направлен вдоль оси вращения по
правилу правого винта, т. е. так же, как
и вектор d
(рис. 7). Размерность угловой скорости
dim=T-1,
a .
ее единица — радиан в секунду (рад/с).

Линейная скорость
точки (см. рис. 6)

В векторном виде
формулу для линейной скорости можно
написать как вектор­ное произведение:

При
этом модуль векторного произведе­ния,
по определению, равен

,
а
направление совпадает с
направлением
поступательного движения правого винта
при его вращении от 
к R.

Если
=const,
то
вращение равномер­ное и его можно
характеризовать перио­дом
вращения Т
—
временем, за которое точка совершает
один полный оборот, т. е. поворачивается
на угол 2.
Так как промежутку времени t=T
соответствует =2,
то =
2/Т,
откуда

Число
полных оборотов, совершаемых телом при
равномерном его движении по окружности,
в единицу времени называет­ся частотой
вращения:

Угловым
ускорением называется
век­торная величина, равная первой
производ­ной угловой скорости по
времени:

При вращении тела
вокруг неподвижной оси вектор углового
ускорения направлен вдоль оси вращения
в сторону вектора элементарного
приращения угловой ско­рости. При
ускоренном движении вектор

13

 сонаправлен
вектору 
(рис.8),
при замедленном.— противонаправлен
ему (рис. 9).

Тангенциальная
составляющая ускорения

Нормальная
составляющая ускорения

Таким
образом, связь между линейны­ми (длина
пути s,
пройденного
точкой по дуге окружности радиуса R,
линейная
ско­рость v,
тангенциальное
ускорение а,
нор­мальное ускорение аn)
и угловыми величи­нами (угол поворота
,
угловая скорость (о, угловое ускорение
)
выражается сле­дующими формулами:

В
случае равнопеременного движения точки
по окружности (=const)

где
0
— начальная угловая скорость.

Контрольные
вопросы

• Что
называется материальной точкой? Почему
в механике вводят такую модель?

• Что
такое система отсчета?

• Что
такое вектор перемещения? Всегда ли
модуль вектора перемещения равен отрезку
пути,

пройденному точкой?

• Какое
движение называется поступательным?
вращательным?

• Дать
определения векторов средней скорости
и среднего ускорения, мгновенной
скорости

и мгновенного
ускорения. Каковы их направления?

• Что
характеризует тангенциальная
составляющая ускорения? нормальная
составляющая

ускорения? Каковы
их модули?

• Возможны
ли движения, при которых отсутствует
нормальное ускорение? тангенциальное

ускорение? Приведите
примеры.

• Что
называется угловой скоростью? угловым
ускорением? Как определяются их
направления?

• Какова
связь между линейными и угловыми
величинами?

Задачи

1.1.
Зависимость
пройденного телом пути от времени
задается уравнением s
= A+Вt+Сt2+Dt3
(С
= 0,1 м/с2,
D
= 0,03 м/с3).
Определить: 1) через какое время после
начала движения ускорение а тела будет
равно 2 м/с2;
2) среднее ускорение <а>
тела за этот промежуток времени. [ 1) 10
с; 2) 1,1 м/с2]

1.2.
Пренебрегая сопротивлением воздуха,
определить угол, под которым тело брошено
к гори­зонту, если максимальная высота
подъема тела равна 1/4 дальности его
полета. [45°]

1.3.
Колесо
радиуса R
=
0,1 м вращается так, что зависимость
угловой скорости от времени задается
уравнением 
= 2At+5Вt4
(A=2
рад/с2
и B=1
рад/с5).
Определить полное ускорение точек обода
колеса через t=1
с после начала вращения и число оборотов,
сделан­ных колесом за это время. [а =
8,5 м/с2;
N
= 0,48]

14

1.4.
Нормальное ускорение точки, движущейся
по окружности радиуса r=4
м,
задается уравнением аn=А+-Bt+Ct2
(A=1
м/с2,
В=6
м/с3,
С=3
м/с4).
Определить: 1) тангенциальное ускорение
точки; 2) путь, пройденный точкой за время
t1=5
с после начала движения; 3) полное
ускорение для момента времени t2=1
с. [ 1) 6 м/с2;
2) 85 м; 3) 6,32 м/с2]

1.5.
Частота
вращения колеса при равнозамедленном
движении за t=1
мин
уменьшилась от 300 до 180 мин-1.
Определить: 1) угловое ускорение колеса;
2) число полных оборотов, сделанных
колесом за это время. [1)
0,21 рад/с2;
2) 360]

1.6.
Диск
радиусом R=10
см вращается вокруг неподвижной оси
так, что зависимость угла поворота
радиуса диска от времени задается
уравнением =A+Bt+Ct2+Dt3
(B
= l рад/с,
С=1
рад/с2,
D=l
рад/с3).
Определить для точек на ободе колеса к
концу второй секунды после начала
движения: 1) тангенциальное ускорение
а;
2) нормальное ускорение аn;
3) полное ускорение а. [ 1) 0,14 м/с2;
2) 28,9 м/с2;
3) 28,9 м/с2]

Соседние файлы в папке Трофимова

  • #
  • #
  • #
  • #
  • #
  • #
Источник

Добавить комментарий