Как найти угловую скорость вала двигателя

а) угловая
скорость вращения вала электродвигателя:

_ДВ =n_ДВ/30=

рад/с

б)
частота вращения ведущего вала редуктора:

n₁=
n_дв/ i_р.п.=
1465/3,18 =460,6 мин^-1

угловая
скорость вращения ведущего вала
редуктора:

₁ =n₁/30=

рад/с

в)
частота вращения ведомого вала редуктора:

n₂=n₁/i_зп=
460,6/4=115,1 мин^-1

угловая
скорость вращения ведомого вала
редуктора:

₂=₁/i_зп=
48,18/4=12,04 рад/с

2.4.
Определение вращающих моментов на
валах привода.

а)
Вращающий момент на валу электродвигателя:

Т_ДВ=Р_{ТР ДВ}/_ДВ=

Нм

б)
Вращающий момент на ведущем валу
редуктора из условия постоянства
мощности с учетом потерь:

T₁=T_ДВ
^. i_Р. ^.
_рем
=114,5^.3,18^.0,95^.0,99=324,4 Нм

в)
Вращающий момент на ведомом валу
редуктора :

Т₂= Т_1.i_зп._зп
=324,4^.4^.0,98^.0,99= 1328,8 H_.м

2.5 Мощность на валах привода:

Мощность на валу электродвигателя:

Р_{ТР ДВ} =17,54кВт

Мощность на ведущем валу редуктора:

Р₁= Р_{ТР ДВ}^. _рем
η_подш.=17,5^.0,95^.0,99=16,45кВт.

Мощность на ведомом валу редуктора:

Р₂= P₁^. _зп
η_подш.=16,45^.0,98^.0,99=15,96Вт.

Проверка:

Р_вых=Т₂.
1328,8^.12,04=16кВт.

Величина ошибки: ΔР=(16 -15,96)/16^.100%=0,25
% .

В качестве аналога может быть
использован редуктор цилиндрический
одноступенчатый типа 1ЦУ-200 -4 с крутящим
моментом на выходном валу

Т_вых= 2000Нм и передаточным числом
i_зп =4,0(рис.3) [5, Т.3,
с.485].

Рис.3. Редуктор цилиндрический
одноступенчатый типа 1ЦУ-200

Таблица 2 Основные размеры
редуктора, мм

Типоразмер редуктора	Аw	В	В1	L	L1	L2	L3	L4	L5	L6	H	H0
1ЦУ-200	200	200	136	580	165	437	140	110	230	265	425	212

3.Расчет клиноременной передачи

При передаваемой мощности Р = 16 кВт и
частоте вращения ведущего шкива n₁=
1465 мин^-1 принимаем ремень типа В
ГОСТ 1284.1-80 с параметрами:

ширина ремня W =22 мм, высота
Т₀=13,5 мм, площадь поперечного
сечения А=230 мм² ,наименьший
диаметр ведущего шкива d₁=
200 мм. [1, табл.7.7].

3.1 Вращающий момент на ведущем
шкиве: Т_ДВ= 114,5 Нм

3.2Определение диаметра меньшего шкива:

По ГОСТ 17383-74 [1, табл.7.7] принимаем d₁=
200 мм.

3.3
Определение диаметра большего шкива:

где i_р
– передаточное отношение ременной
передачи;

ε – величина скольжения; ε =0,01

Округляем полученное значение по ГОСТ
17383-84 ; d₂=630мм.

3.4Уточняем передаточное отношение
ременной передачи:

3.5 Межосевое
расстояние:

.Принимаем
а=850мм

3.6Опеределение
длины ремня.

Принимаем L_p=
3150 мм по ГОСТ 1284.1-80 [1, табл.7.7].

3.7Уточняем
межосевое расстояние:

где W
= 0,5π(d₁+d₂)=
0,5^.3,14(610+200)=1303 мм;

y=(d₂
– d₁)² =
(630-200)² =184900 мм².

Рис.4
Схема ременной передачи

3.8.
Определение угла обхвата меньшего
шкива:

3.9.
Определение числа ремней

где С_р
– коэффициент режима работы: С_р
=1,2 [1, табл.7.10];

С_L
– коэффициент, учитывающий влияние
длины ремня С_L =0,95
[1, табл.7.9];

С_α
– коэффициент угла обхвата С_α
=0,96 [1, стр.135];

С_z
– коэффициент, учитывающий число ремней
в передаче :С_z =0,96
[1, с.135].

Р₀-мощность,
передаваемая одним ремнем; Р₀=8,5
кВт[1, табл.7.8].

Принимаем,
исходя из условия кратности числа ремней
целому числу, z=3

3.12
Определение натяжения ветви ремня:

где
скорость ремня:

Θ –
коэффициент, учитывающий центробежную
силу, (Н·с²)/м² Θ =0,1 [1, с.136]

3.13
Определение силы, действующей на вал:

где α₁
– угол обхвата меньшего шкива.

3.14.
Определение рабочего ресурса передачи:

где N_оц–
базовое число циклов [1, с.136]; N_оц=
4,7^.10⁶ циклов ;

L-
длина ремня, мм; L= 3150 мм
;

σ_-1
– предел выносливости материала ремня
МПа; σ_-1 =7 МПа [1, стр.139],;

σ_max
– максимальное напряжение в сечении
ремня, МПа:

σ_max
= σ₁ + σ_u + σ_υ
, МПа;

где σ₁
– напряжение от растяжения ремня, МПа;

,

Где F₁–
натяжение ведущей ветви ремня;

F₁=
F₀+ 0,5F_t;

F_t–
сила тяги ремня; F_t=

F₁=353,2+0,5^.346=526,2Н

σ_u
– напряжение от изгиба ремня, МПа:

,

где Е_u=50
МПа [1, с. 123];

σ_υ
– напряжение от центробежной силы,
МПа:

,

σ_max
=1,77+1,68+0,26 =3,71МПа

где ρ
– плотность ремня, т/м³ ρ
=1100 т/м³ [1, с. 123];

С_i
– коэффициент, учитывающий влияние
передаточного отношения:

;

С_н
– коэффициент, учитывающий режим
нагружения; С_н =1.

Полученная
расчетная долговечность ремня больше
требуемой [Но]=2 000 часов.

Рис.5 Эскиз шкива клиноременной передачи

Таблица 3 Основные размеры
шкивов

	d, мм	dВ, мм	lcт, мм	d ст, мм	tp, мм	c, мм	f, мм	e, мм	в, мм
Ведущий	200	40	48	48	19	25	17	25,5	84
Ведомый	630	42	50	63	19	25	17	25,5	84

Диаметр ступицы d_ст=1,5d_в=1,5^.
40=60мм

Длина ступицы l_ст=1,2
d_в=1,2^. 40=48мм

Длину ступиц принимаем по длине консольных
участков валов 2,
табл.7.1.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Решил подкреплять статьи наглядными примерами для расчетов:

Пример 1:
Двигатель вращается с частотой 3000 об/минуту. Рассчитать угловую скорость вращения коленчатого вала двигателя.

Решение:
За одну секунду коленчатый вал совершает 3000/60 оборотов/с = 50 об/с.
1 оборот = 2п рад.
w = 2п рад/об * 50 об/с = 100п рад/с = 314 рад/с

Ответ: 314 рад/с

Пример 2:
Два автомобиля подняли обороты на старте до значения 3000 об/минуту. Вычислить скорость движения поршней двигателей 2JZ-GTE и М30В34 в положении, когда угол поворота коленчатого вала составляет 45 градусов от ВМТ. Известно, что ход поршня у обоих двигателей составляет 86 мм, а длины шатунов 142 мм и 135 соответственно.

Решение:
w = 314 рад/с
r = 86 мм / 2 = 43 мм = 0,043 м
v (2JZ-GTE, 45 градусов, 3000 об/минуту) = 314 * 0,043 *{ sin (п/4) + sin (п/2) * 0,043 / (2*0,142)} = 13,502 * {0,707 + 1 * 0,1514) = 13,502 * 0,85 = 11,49 м/с
v (М30В34, 45 градусов, 3000 об/минуту) = 314 * 0,043 *{ sin (п/4) + sin (п/2) * 0,043 / (2*0,135)} = 13,502 * {0,707 + 1 * 0,159) = 13,502 * 0,866 = 11,69 м/с

Ответ: v (2JZ-GTE) = 11,49 м/с, v (M30B34) = 11,69 м/с

Пример 3:
Двигатель М30В28 имеет максимальное значение крутящего момента при 4200 об/мин. Вычислить максимальное значение скорости поршня на этих оборотах, если ход поршня составляет 80 мм, а длина шатуна 135 мм:

Пиковое значение скорости достигается в экстремумах ускорения, т.е. когда а = 0.

Т.к. w = const, то е = 0, а следовательно и вся вторая часть уравнения для ускорения равна 0,

тогда пиковое значение скорости достигается, когда

w^2 * r * { cosф + cos2ф * r / l } = 0

w = 2п * 4200 / 60 = 440 рад/с
r = 0,08м / 2 = 0,04 м
l = 0,135 м

Решим уравнение и найдем ф:
440^2 * 0,04 * { cosф + cos2ф * 0,04 / 0,135 } = 0
7744 * (cosф + cos2ф * 0,29) = 0
cosф = — 0,29 cos2ф
cosф = — 0,29 *{2(cosф)^2 -1}
0,58*(cosф)^2 + cosф — 0,29 = 0

Обозначим cosф как х, тогда

0,58 х^2 + x — 0,29 = 0
D = 1 + 4*0,58*0,29 = 1,6728
х1 = (- 1 + 1,6728) / (2 * 0,58) = 0,6728 / 1,16 = 0,58
х2 = (- 1 — 1,6728) / (2 * 0,58) = 2,304

Т.к. х2 > 1, cosф = 0,58 или ф = 0,952 рад

v (М30В28, 0,952 рад, 4200 об/минуту) = 440 * 0,04 *{ sin (0,952) + sin (1,904) * 0,04 / (2*0,135)} = 17,6 * {0,814 + 0,945 * 0,148) = 17,6 * 0,954 = 16,79 м/с

Ответ: 16,79 м/с

Аналогично можете подставить данные своего мотора и решать подобного рода типовые задачи;)

На сим все!

Продолжение следует;)

Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.

Обозначение угловой скорости: ω (омега).

Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.

С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.

Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:

Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.

Быстрота изменения угла φ (перемещения плоскости П из положения П₁ в положение П₂) – это и есть угловая скорость:

Приняв вектор k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

1. если известно количество оборотов n за единицу времени t:
   
2. если задан угол поворота φ за единицу времени:
   
3. если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:
   

Размерности угловой скорости:

• Количество оборотов за единицу времени [об/мин], [c^-1].
• Угол поворота за единицу времени [рад/с].

Определение угловой скорости

Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.

Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.

Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.

Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.

Другие примеры решения задач >

Угловое ускорение

Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:

Обозначение: ε (Эпсилон)

Единицы измерения углового ускорения: [рад/с²], [с^-2]

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

Расчет углового ускорения

Пример: По заданному значению касательной составляющей полного ускорения a_τ точки B, расположенной на расстоянии r от центра вращения колеса.

Требуется определить величину и направление углового ускорения колеса ε, если a_τ = 10 м/с², r = 50 см.

Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.

Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

ω = 1,5 с^-1 = 9,42 рад/с.

Смотрите также:

• Примеры расчета угловой скорости и ускорения
• Скорости и ускорения точек вращающегося тела

Механические и электрические характеристики асинхронных электродвигателей

В данной статье осветим тему механических и электрических характеристик электродвигателей. На примере асинхронного двигателя рассмотрим такие параметры как мощность, работа, КПД, косинус фи, вращающий момент, угловая скорость, линейная скорость и частота. Все эти характеристики оказываются важными при проектировании оборудования, в котором электродвигатели служат в качестве приводных.

Механические характеристики электродвигателя представляют собой зависимость угловой скорости ω от развиваемого им момента на валу, т.е. ω = f (M). Различают естественные и искусственные механические характеристики электродвигателя.

Естественная механическая характеристика соответствует работе электродвигателя с номинальными параметрами при нормальной схеме включения. Искусственная механическая характеристика соответствует работе электродвигателя с параметрами, отличающимися от номинальных, например, при введении сопротивления, изменении питающего напряжения, частоты и др.

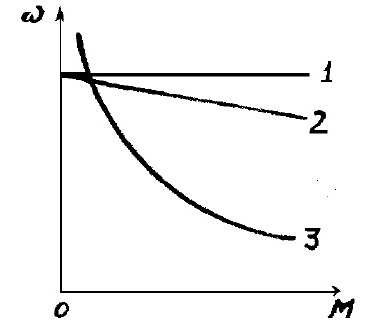
Механические характеристики электродвигателей: 1 — абсолютно жесткая характеристика, 2 — жесткая характеристика, 3 — мягкая механическая характеристика

Сегодня особенно широко распространены в промышленности именно асинхронные электродвигатели, поэтому на их характеристиках и остановимся.

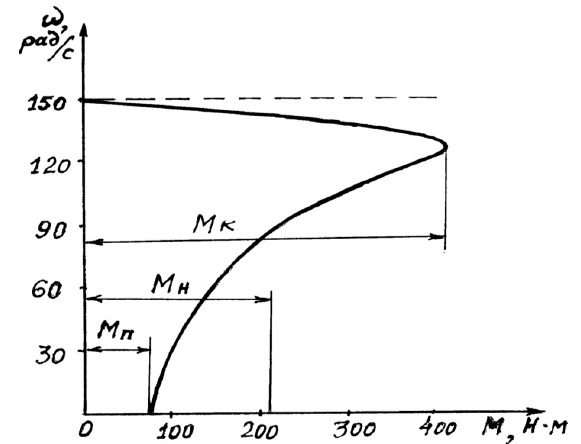
Естественная механическая характеристика асинхронного двигателя

Для примера рассмотрим АИР80В2У3.

Номинальная механическая мощность асинхронного электродвигателя

На шильдике (на паспортной табличке) электродвигателя указывается всегда номинальная механическая мощность на валу данного двигателя. Это не та электрическая мощность, которую данный электродвигатель потребляет из сети.

Так, например, для двигателя АИР80В2У3, номинал в 2200 ватт соответствует именно механической мощности на валу. То есть в оптимальном рабочем режиме данный двигатель способен выполнять механическую работу 2200 джоулей каждую секунду. Обозначим эту мощность как P1 = 2200 Вт.

Номинальная активная электрическая мощность асинхронного электродвигателя

Чтобы определить номинальную активную электрическую мощность асинхронного электродвигателя, опираясь на данные с шильдика, необходимо принять в расчет КПД. Так, для данного электродвигателя КПД составляет 83%.

Что это значит? Это значит, что только часть активной мощности, подаваемой из сети на обмотки статора двигателя, и безвозвратно потребляемой двигателем, преобразуется в механическую мощность на валу. Активная мощность равна P = P1/КПД. Для нашего примера, по представленному шильдику видим, что P1 = 2200, КПД = 83%. Значит P = 2200/0,83 = 2650 Вт.

Номинальная полная электрическая мощность асинхронного электродвигателя

Полная электрическая мощность, подаваемая на статор электродвигателя от сети всегда больше механической мощности на валу и больше активной мощности, безвозвратно потребляемой электродвигателем.

Для нахождения полной мощности достаточно активную мощность разделить на косинус фи. Таким образом, полная мощность S = P/Cosφ. Для нашего примера P = 2650 Вт, Cosφ = 0,87. Следовательно полная мощность S = 2650/0,87 = 3046 ВА.

Номинальная реактивная электрическая мощность асинхронного электродвигателя

Часть полной мощности, подаваемой на обмотки статора асинхронного электродвигателя, возвращается в сеть. Это реактивная мощность Q.

Реактивная мощность связана с полной мощностью через sinφ, и связана с активной и с полной мощностью через квадратный корень. Для нашего примера:

Q = √( 3046 2 — 2650 2 ) = 1502 ВАР

Реактивная мощность Q измеряется в ВАР — в вольт-амперах реактивных.

Теперь давайте рассмотрим механические характеристики нашего асинхронного двигателя: номинальный рабочий момент на валу, угловую скорость, линейную скорость, частоту вращения ротора и ее связь с частотой питания электродвигателя.

Частота вращения ротора асинхронного электродвигателя

Скорость вращательного движения на практике часто оценивается частотой вращения, то есть числом оборотов вала двигателя в минуту. Угловая скорость выражается в радианах в секунду (рад/с). Угловой скоростью удобнее пользоваться при выводе формул и проведении расчетов, частотой вращения — при практической оценке скоростных свойств двигателей.

На шильдике мы видим, что при питании переменным током частотой в 50 Гц, ротор двигателя совершает при номинальной нагрузке 2870 оборотов в минуту, обозначим эту частоту как n1.

Что это значит? Поскольку магнитное поле в обмотках статора создается переменным током частотой 50 Гц, то для двигателя с одной парой полюсов (коим является АИР80В2У3) частота «вращения» магнитного поля, синхронная частота n, оказывается равной 3000 оборотов в минуту, что тождественно 50 оборотам в секунду.

Но поскольку двигатель асинхронный, то п оявление в обмотке ротора ЭДС и вращающего момента возможно только при наличии разности между скоростями магнитного поля и ротора. Это различие называют скольжением (s). Ротор вращается с отставанием на величину скольжения .

Значение s можно определить, разделив разность синхронной и асинхронной частот на синхронную частоту, и выразив это значение в процентах:

s = ( ( n – n1 )/ n) *100%

Для нашего примера s = ( (3000 – 2870)/3000 ) *100% = 4,3%.

Угловая скорость асинхронного двигателя

Угловая скорость ω выражается в радианах в секунду. Для определения угловой скорости достаточно частоту вращения ротора n1 перевести в обороты в секунду (f), и умножить на 2 Пи, поскольку один полный оборот составляет 2 Пи или 2*3,14159 радиан. Для двигателя АИР80В2У3 асинхронная частота n1 составляет 2870 оборотов в минуту, что соответствует 2870/60 = 47,833 оборотам в секунду.

Умножая на 2 Пи, имеем: 47,833*2*3,14159 = 300,543 рад/с. Можно перевести в градусы, для этого вместо 2 Пи подставить 360 градусов, тогда для нашего примера получится 360*47,833 = 17220 градусов в секунду. Однако подобные расчеты обычно ведут именно в радианах в секунду. Поэтому угловая скорость ω = 2*Пи*f, где f = n1/60.

Линейная скорость асинхронного электродвигателя

Линейная скорость v относится к оборудованию, на котором асинхронный двигатель установлен в качестве привода. Так, если на вал двигателя установлен шкив или, скажем, наждачный диск, известного радиуса R, то линейная скорость точки на краю шкива или диска может быть найдена по формуле:

Номинальный вращающий момент асинхронного двигателя

Каждый асинхронный электродвигатель характеризуется номинальным вращающим моментом Мн. Вращающий момент М связан с механической мощностью P1 через угловую скорость следующим образом:

Вращающий момент или момент силы, действующей на определенном расстоянии от центра вращения, для двигателя сохраняется, причем с ростом радиуса уменьшается сила, а чем радиус меньше, тем больше сила, поскольку:

Так, чем больше радиус шкива, тем меньшая сила действует на его краю, а наибольшая сила действует непосредственно на валу электродвигателя.

Для приведенного в качестве примера двигателя АИР80В2У3 мощность P1 равна 2200 Вт, а частота n1 равна 2870 оборотов в минуту или f = 47,833 оборота в секунду. Следовательно угловая скорость составляет 2*Пи*f, то есть 300,543 рад/с, и номинальный вращающий момент Мн равен P1/(2*Пи*f). Мн = 2200/(2*3,14159*47,833) = 7,32 Н*м.

Таким образом, исходя из данных, указанных на шильдике асинхронного электродвигателя, можно найти все основные электрические и механические его параметры.

Надеемся, что данная статья помогла вам разобраться в том, как связаны между собой угловая скорость, частота, вращающий момент, активная, полезная и полная мощность, а также КПД электродвигателя.

Источник

Частота вращения: формула

Количество повторений каких-либо событий или их возникновения за одну единицу таймера называется частотой. Это физическая величина измеряется в герцах – Гц (Hz). Она обозначается буквами ν, f, F, и есть отношение количества повторяющихся событий к промежутку времени, в течение которого они произошли.

При обращении предмета вокруг своего центра можно говорить о такой физической величине, как частота вращения, формула:

где:

• N – количество оборотов вокруг оси или по окружности,
• t – время, за которое они были совершены.

В системе СИ обозначается как – с-1 (s-1) и именуется как обороты в секунду (об/с). Применяют и другие единицы вращения. При описании вращения планет вокруг Солнца говорят об оборотах в часах. Юпитер делает одно вращение в 9,92 часа, тогда как Земля и Луна оборачиваются за 24 часа.

Номинальная скорость вращения

Прежде, чем дать определение этому понятию, необходимо определиться, что такое номинальный режим работы какого-либо устройства. Это такой порядок работы устройства, при котором достигаются наибольшая эффективность и надёжность процесса на продолжении длительного времени. Исходя из этого, номинальная скорость вращения – количество оборотов в минуту при работе в номинальном режиме. Время, необходимое для одного оборота, составляет 1/v секунд. Оно называется периодом вращения T. Значит, связь между периодом обращения и частотой имеет вид:

К сведению. Частота вращения вала асинхронного двигателя – 3000 об./мин., это номинальная скорость вращения выходного хвостовика вала при номинальном режиме работы электродвигателя.

Как найти или узнать частоты вращений различных механизмов? Для этого применяется прибор, который называется тахометр.

Угловая скорость

Когда тело движется по окружности, то не все его точки движутся с одинаковой скоростью относительно оси вращения. Если взять лопасти обычного бытового вентилятора, которые вращаются вокруг вала, то точка расположенная ближе к валу имеет скорость вращения больше, чем отмеченная точка на краю лопасти. Это значит, у них разная линейная скорость вращения. В то же время угловая скорость у всех точек одинаковая.

Угловая скорость представляет собой изменение угла в единицу времени, а не расстояния. Обозначается буквой греческого алфавита – ω и имеет единицу измерения радиан в секунду (рад/с). Иными словами, угловая скорость – это вектор, привязанный к оси обращения предмета.

Формула для вычисления отношения между углом поворота и временным интервалом выглядит так:

где:

• ω – угловая скорость (рад./с);
• ∆ϕ – изменение угла отклонения при повороте (рад.);
• ∆t – время, затраченное на отклонение (с).

Обозначение угловой скорости употребляется при изучении законов вращения. Оно употребляется при описании движения всех вращающихся тел.

Угловая скорость в конкретных случаях

На практике редко работают с величинами угловой скорости. Она нужна при конструкторских разработках вращающихся механизмов: редукторов, коробок передач и прочего.

Вычислить её, применяя формулу, можно. Для этого используют связь угловой скорости и частоты вращения.

где:

• π – число, равное 3,14;
• ν – частота вращения, (об./мин.).

В качестве примера могут быть рассмотрены угловая скорость и частота вращения колёсного диска при движении мотоблока. Часто необходимо уменьшить или увеличить скорость механизма. Для этого применяют устройство в виде редуктора, при помощи которого понижают скорость вращения колёс. При максимальной скорости движения 10 км/ч колесо делает около 60 об./мин. После перевода минут в секунды это значение равно 1 об./с. После подстановки данных в формулу получится результат:

ω = 2*π*ν = 2*3,14*1 = 6,28 рад./с.

К сведению. Снижение угловой скорости часто требуется для того, чтобы увеличить крутящий момент или тяговое усилие механизмов.

Как определить угловую скорость

Принцип определения угловой скорости зависит от того, как происходит движение по окружности. Если равномерно, то употребляется формула:

Если нет, то придётся высчитывать значения мгновенной или средней угловой скорости.

Величина, о которой идёт разговор, векторная, и при определении её направления используют правило Максвелла. В просторечии – правило буравчика. Вектор скорости имеет одинаковое направление с поступательным перемещением винта, имеющего правую резьбу.

Рассмотрим на примере, как определить угловую скорость, зная, что угол поворота диска радиусом 0,5 м меняется по закону ϕ = 6*t:

ω = ϕ / t = 6 * t / t = 6 с-1

Вектор ω меняется из-за поворота в пространстве оси вращения и при изменении значения модуля угловой скорости.

Угол поворота и период обращения

Рассмотрим точку А на предмете, вращающимся вокруг своей оси. При обращении за какой-то период времени она изменит своё положение на линии окружности на определённый угол. Это угол поворота. Он измеряется в радианах, потому что за единицу берётся отрезок окружности, равный радиусу. Ещё одна величина измерения угла поворота – градус.

Когда в результате поворота точка А вернётся на своё прежнее место, значит, она совершила полный оборот. Если её движение повторится n-раз, то говорят о некотором количестве оборотов. Исходя из этого, можно рассматривать 1/2, 1/4 оборота и так далее. Яркий практический пример этому – путь, который проделывает фреза при фрезеровании детали, закреплённой в центре шпинделя станка.

Внимание! Угол поворота имеет направление. Оно отрицательное, когда вращение происходит по часовой стрелке и положительное при вращении против движения стрелки.

Если тело равномерно продвигается по окружности, можно говорить о постоянной угловой скорости при перемещении, ω = const.

В этом случае находят применения такие характеристики, как:

• период обращения – T, это время, необходимое для полного оборота точки при круговом движении;
• частота обращения – ν, это полное количество оборотов, которое совершает точка по круговой траектории за единичный временной интервал.

Интересно. По известным данным, Юпитер обращается вокруг Солнца за 12 лет. Когда Земля за это время делает вокруг Солнца почти 12 оборотов. Точное значение периода обращения круглого гиганта – 11,86 земных лет.

Циклическая частота вращения (обращения)

Скалярная величина, измеряющая частоту вращательного движения, называется циклической частотой вращения. Это угловая частота, равная не самому вектору угловой скорости, а его модулю. Ещё её именуют радиальной или круговой частотой.

Циклическая частота вращения – это количество оборотов тела за 2*π секунды.

У электрических двигателей переменного тока это частота асинхронная. У них частота вращения ротора отстаёт от частоты вращения магнитного поля статора. Величина, определяющая это отставание, носит название скольжения – S. В процессе скольжения вал вращается, потому что в роторе возникает электроток. Скольжение допустимо до определённой величины, превышение которой приводит к перегреву асинхронной машины, и её обмотки могут сгореть.

Устройство этого типа двигателей отличается от устройства машин постоянного тока, где токопроводящая рамка вращается в поле постоянных магнитов. Большое количество рамок вместил в себя якорь, множество электромагнитов составили основу статора. В трёхфазных машинах переменного тока всё наоборот.

При работе асинхронного двигателя статор имеет вращающееся магнитное поле. Оно всегда зависит от параметров:

• частоты питающей сети;
• количества пар полюсов.

Скорость вращения ротора состоит в прямом соотношении со скоростью магнитного поля статора. Поле создаётся тремя обмотками, которые расположены под углом 120 градусов относительно друг друга.

Переход от угловой к линейной скорости

Существует различие между линейной скоростью точки и угловой скоростью. При сравнении величин в выражениях, описывающих правила вращения, можно увидеть общее между этими двумя понятиями. Любая точка В, принадлежащая окружности с радиусом R, совершает путь, равный 2*π*R. При этом она делает один оборот. Учитывая, что время, необходимое для этого, есть период Т, модульное значение линейной скорости точки В находится следующим действием:

ν = 2*π*R / Т = 2*π*R* ν.

Так как ω = 2*π*ν, то получается:

Следовательно, линейная скорость точки В тем больше, чем дальше от центра вращения находится точка.

К сведению. Если рассматривать в качестве такой точки города на широте Санкт-Петербурга, их линейная скорость относительно земной оси равна 233 м/с. Для объектов на экваторе – 465 м/с.

Числовое значение вектора ускорения точки В, движущейся равномерно, выражается через R и угловую скорость, таким образом:

а = ν2/ R, подставляя сюда ν = ω* R, получим: а = ν2/ R = ω2* R.

Это значит, чем больше радиус окружности, по которой движется точка В, тем больше значение её ускорения по модулю. Чем дальше расположена точка твердого тела от оси вращения, тем большее ускорение она имеет.

Поэтому можно вычислять ускорения, модули скоростей необходимых точек тел и их положений в любой момент времени.

Понимание и умение пользоваться расчётами и не путаться в определениях помогут на практике вычислениям линейной и угловой скоростей, а также свободно переходить при расчётах от одной величины к другой.

Видео

Источник