Содержание:
- Определение и формула угловой скорости
- Равномерное вращение
- Формула, связывающая линейную и угловую скорости
- Единицы измерения угловой скорости
- Примеры решения задач
Определение и формула угловой скорости
Определение
Круговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность
с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.
Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.
Перемещение при вращении характеризуют при помощи угла поворота
$(varphi)$ . Часто используют вектор элементарного поворота
$bar{dvarphi}$ , который равен по величине элементарному углу поворота тела
$(d varphi)$ за маленький отрезок времени dt и направлен по мгновенной оси вращения в сторону,
откуда этот поворот виден реализующимся против часовой стрелки. Надо отметить, что только элементарные угловые перемещения являются векторами.
Углы вращения на конечные величины векторами не являются.
Определение
Угловой скоростью называют скорость изменения угла поворота и обозначают ее обычно буквой
$omega$ . Математически определение угловой скорости записывают так:
$$bar{omega}=frac{d bar{varphi}}{d t}=dot{bar{varphi}}(1)$$
Угловая скорость – векторная величина (это аксиальный вектор). Она имеет направление вдоль мгновенной оси вращения совпадающее
с направлением поступательного правого винта, если его вращать в сторону вращения тела (рис.1).
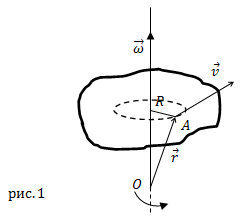
Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости),
так и за счет поворота оси вращения в пространстве ($bar{omega}$ при этом изменяет направление).
Равномерное вращение
Если тело за равные промежутки времени поворачивается на один и тот же угол,
то такое вращение называют равномерным. При этом модуль угловой скорости находят как:
$$omega=frac{varphi}{t}(2)$$
где $(varphi)$ – угол поворота, t – время, за которое этот поворот совершён.
Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот
($Delta varphi=2 pi$). Угловая скорость связана с периодом обращения как:
$$omega=frac{2 pi}{T}(3)$$
С числом оборотов в единицу времени ($nu) угловая скорость связана формулой:
$$omega=2 pi nu(4)$$
Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения,
но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно
с данной мгновенной величиной скорости.
Формула, связывающая линейную и угловую скорости
Линейная скорость $bar{v}$ точки А (рис.1), которая расположена
на расстоянии R от оси вращения связана с вектором угловой скорости следующим векторным произведением:
$$bar{v}=[bar{omega} bar{R}](5)$$
где $bar{R}$ – перпендикулярная к оси вращения компонента радиус-вектора точки
$A (bar{r})$ (рис.1). Вектор
$bar{r}$ проводят от точки, находящейся на оси вращения к рассматриваемой точке.
Единицы измерения угловой скорости
Основной единицей измерения угловой скорости в системе СИ является: [$omega$]=рад/с
В СГС: [$omega$]=рад/с
Примеры решения задач
Пример
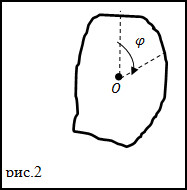
Задание. Движение тела с неподвижной осью задано уравнением
$varphi=2 t-4 t^{3}$,
$(varphi)$ в рад, t в сек.
Начало вращения при t=0 c. Положительным считают углы указанные направлением стрелки (рис.2). В каком направлении (
относительно часовой стрелки поворачивается тело) в момент времени t=0,5 c.
Решение. Для нахождения модуля угловой скорости применим формулу:
$$omega=frac{d varphi}{d t}(1.1)$$
Используем заданную в условии задачи функцию
$varphi(t)$, возьмем производную от нее по времени, получим функцию
$omega(t)$:
$$omega(t)=2-8 t^{2}(1.2)$$
Вычислим, чему будет равна угловая скорость в заданный момент времени (при t=0,5 c):
$$omega(t)=2-8(0,5)^{2}=0left(frac{r a d}{c}right)$$
Ответ. В заданный момент времени тело имеет угловую скорость равную нулю, следовательно, она останавливается.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Скорости вращения тела заданы системой уравнений:
$$left{begin{array}{c}bar{omega}_{1}=t^{2 bar{i}} \ bar{omega}_{2}=2 t^{2} bar{j}end{array}right.$$
где $bar{i}$ и
$bar{j}$ – единичные ортогональные векторы. На какой угол $(varphi)$ поворачивается тело за время равное 3 с?
Решение. Определим, какова функция, которая связывает модуль скорости вращения тела и время (t)
($omega(t)$). Так как вектора
$bar{i}$ и
$bar{j}$ перпендикулярны друг другу, значит:
$$omega=sqrt{omega_{1}^{2}+omega_{2}^{2}}=sqrt{left(t^{2}right)^{2}+left(2 t^{2}right)^{2}}=t^{2} sqrt{5}(2.2)$$
Модуль угловой скорости связан с углом поворота как:
$$omega=frac{d varphi}{d t}(2.3)$$
Следовательно, угол поворота найдем как:
$$varphi=int_{t_{1}}^{t_{2}} omega d t=int_{0}^{3} t^{2} sqrt{5} d t=left.sqrt{5} frac{t^{3}}{3}right|_{0} ^{3} approx 20(mathrm{rad})$$
Ответ. $varphi = 20$ рад.
Читать дальше: Формула удельного веса.
Величина
окружной скорости
(![]()
‒
угловая скорость) несущего винта (НВ)
существенно влияет на ЛТХ вертолета.
Как и для
самолета,
![]()
вертолета в горизонтальном полете
ограничена
располагаемой мощностью
силовой установки. Однако для вертолета
максимальная скорость полета
ограничивается также
влиянием
сжимаемости воздуха на наступающей и
срывом потока
на отступающей лопастях.
Окружную
скорость концов НВ у современных
вертолетов
выбирают из условия, чтобы
несущий винт на режиме висения имел
достаточно высокий КПД 0
(0 = 0,72…0,77),
а на максимальной скорости полета не
было бы срыва потока на отступающей
(идущей
с набегающим потоком) лопасти и явлений
сжимаемости на наступающей, идущей
против потока, лопасти.
Окружная
скорость концов НВ у современных легких
вертолетов принимается равной
= 180…205 м/с [28, 36, 93]. Представляют
практический интерес НВ легких вертолетов
с
= 210…215 м/с.
Следует
учитывать [28], что:
– двигатели
силовых установок вертолетов не
обеспечивают необходимой мощности при
изменении оборотов в широких пределах;
– современные
трансмиссии не дают переменной редукции;
– силу
тяги НВ целесообразно повышать посредством
увеличения шага 0
НВ при уменьшении числа его оборотов
до их минимально допустимой величины.
Минимально
допустимая частота вращения НВ в полете
на всех режимах ограничивается
обеспечением:
– запаса
по срыву потока с лопасти при полете на
скорости
;
– запаса
путевого управления на взлетно-посадочных
режимах
и продольно-поперечного
управления при полете по маршруту;
– прочности
главного редуктора по крутящему моменту
НВ;
– запаса
кинетической энергии вращения НВ для
возможного перехода на режим самовращения;
– функционирования
генераторов переменного тока и всей
системы электроснабжения вертолета.
Максимально
допустимая частота вращения НВ в полете
на всех режимах ограничивается условиями:
– обеспечения
прочности главного редуктора, втулки
НВ, автомата перекоса и лопастей по
центробежным силам;
– предотвращения
волнового кризиса на конце наступающих
лопастей НВ при полете вертолета на
больших высотах и скоростях;
– обеспечения
достаточного запаса по флаттеру лопастей
НВ;
– предотвращения
резкого возрастания уровня вибраций и
переменных напряжений в лопастях НВ в
связи с нестационарностью
характера
развития волнового кризиса;
– предотвращения
возникновения (усиления) тряски вертолета;
– исключения
срабатывания защиты свободной турбины
от
раскрутки, т.е. самопроизвольного
выключения двигателей в полете;
– начала
резкого увеличения мощности, потребной
для вращения несущего винта.
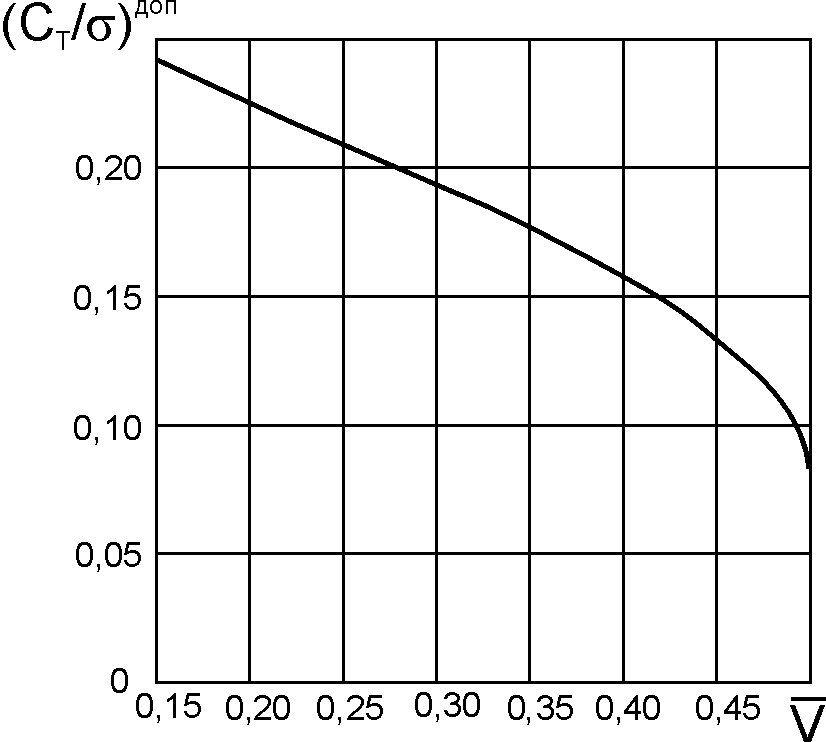
Мерой
оценки влияния срыва потока на НВ
является величина СТ /
‑ отношение коэффициента силы
тяги НВ к коэффициенту заполнения,
которое определяет средний по диску
винта коэффициент
подъемной силы
лопасти
![]()
.
Для прямоугольной в плане лопасти
![]()
.
(3.11)
Предельная
величина СТ /
на азимуте
![]()
= 270º,
определяемая по срыву потока при полете
вертолета вперед, зависит от характеристики
режима работы несущего винта μ
(рис. 3.4) [ 28 ]:
![]()
, (3.12)
где
![]()
‒ угол атаки плоскости диска НВ (
– положительный при наклоне диска НВ
вперед). В горизонтальном полете, когда
мал:
![]()
. (3.12а)
Увеличение
![]()
,
усиливая неравномерность углов атаки
по диску НВ, приводит к срыву потока на
отступающей лопасти и уменьшению
величины СТ /.
Срыв потока сопровождается нарастанием
вибраций и нагрузок на винт и систему
управления в результате больших
переменных
составляющих шарнирных моментов
лопастей, периодически попадающих в
срыв. Поэтому срыв потока на отступающей
лопасти часто является главным фактором,
ограничивающим
.
|
|
|
Рис. 3.4. Зависимость от (или |
Мерой
оценки влияния сжимаемости потока на
характеристики НВ служит число
![]()
для профиля на конце наступающей лопасти
при азимуте = 90º:
![]()
, (3.13)
где
![]()
— скорость звука в воздухе.
Влияние
сжимаемости на характеристики вертолета
количественно можно определить по
данным работ [28, 34, 36, 60, 93].
Для
скоростного профиля при
![]()
увеличение потребной мощности составляет
15…18%; при
![]()
‑ 30%.
![]()
‑
критическое значение, при достижении
которого местная скорость обтекания
хотя бы в одной точке на поверхности
профиля становится равной скорости
звука,
=
0,78…0,82 ‒ для типовых профилей
лопасти НВ. На современных скоростных
вертолетах величина
<
0,92…0,95 (исключение составляет
вертолет Westland G-Lynx, у которого
= 0,97). При
![]()
влияние сжимаемости потока воздуха
незначительно.
Для
уменьшения вредного влияния сжимаемости
при полете на
![]()
в концевых сечениях лопастей применяют
симметричные профили малой относительной
толщины (![]()
= 6…8%),
а также специальные законцовки лопастей
НВ (см. рис. 3.3).
Следует
помнить, что большее значение числа
оборотов НВ
ограничено сжимаемостью
воздуха на азимуте
= 90º,
а малое – срывом потока на азимуте
= 270º.
Решая
уравнения
(3.12) и (3.13) относительно
и
,
получим
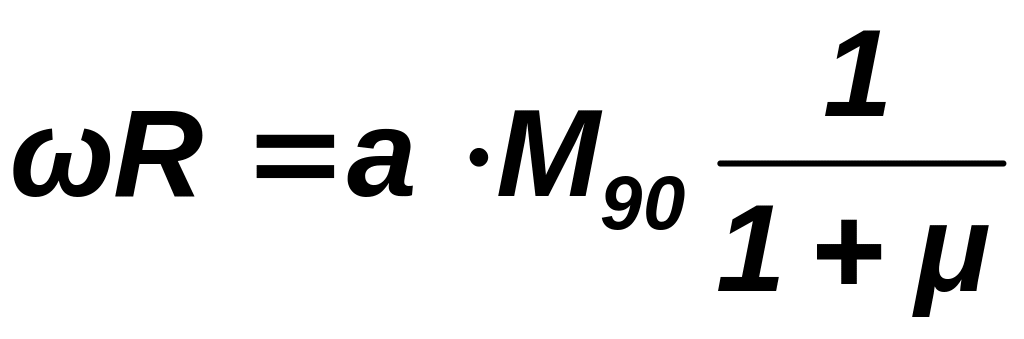
; (3.14)
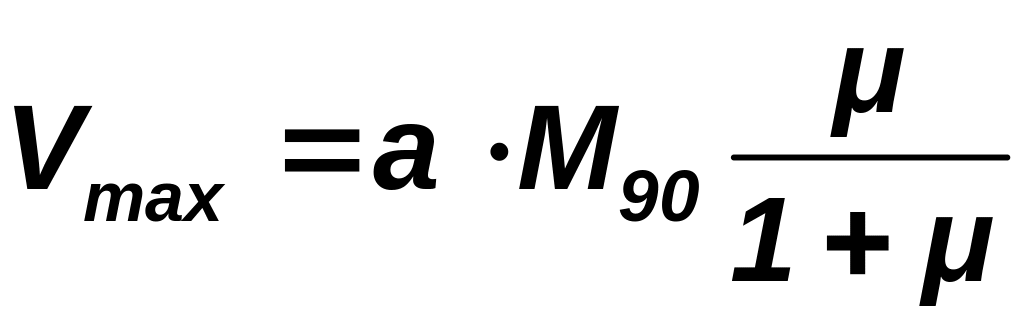
. (3.15)
Используя
выражения (3.14) и (3.15), при заданном
![]()
и выбираемом профиле можно найти
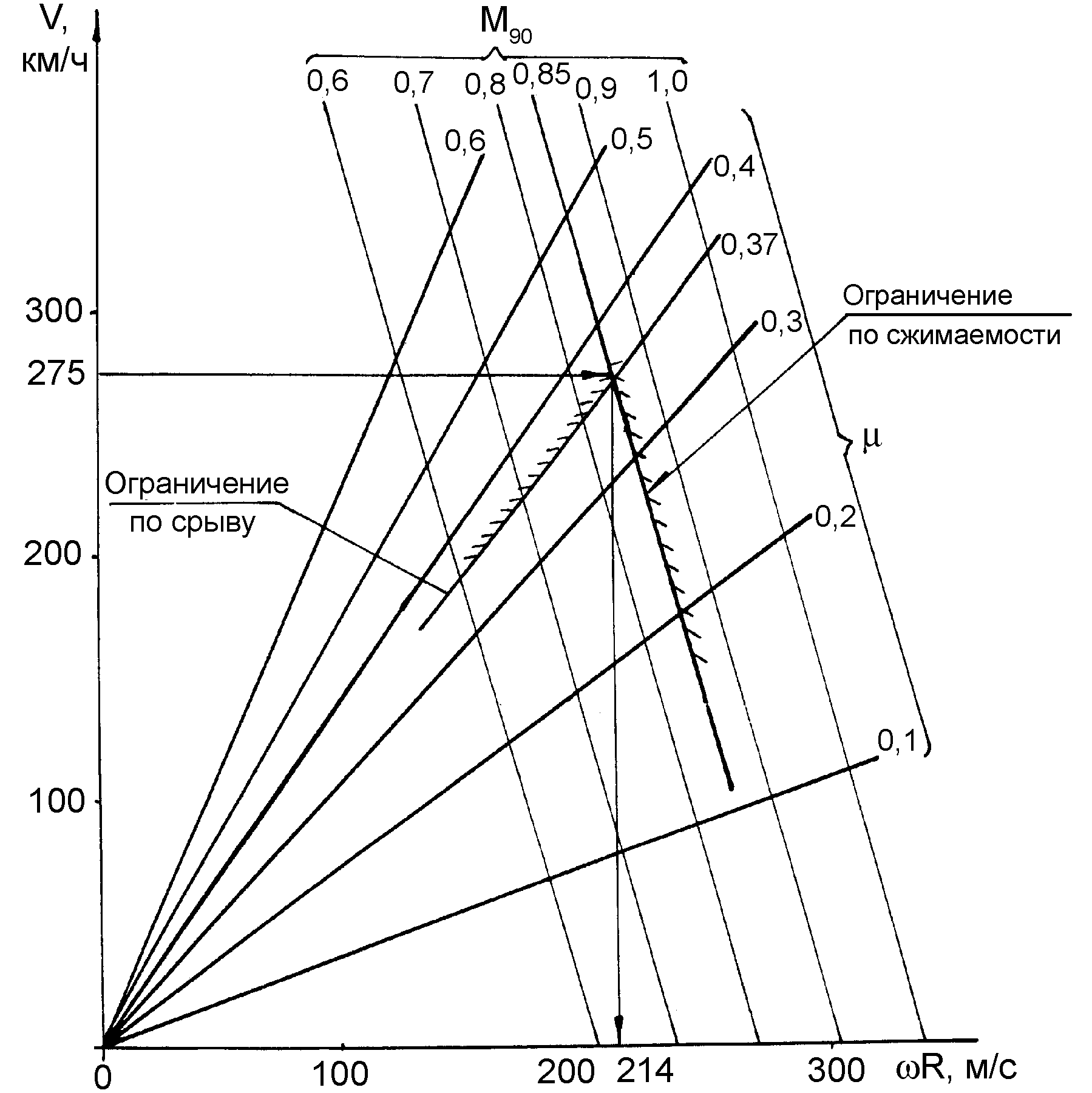
и μ, а также построить диаграмму
![]()
,
а по ней определить
и μ (рис. 3.5).
Ограничение
по
сжимаемости
Ограничение
по
срыву
Рис. 3.5. Диаграмма
зависимости
![]()
от V при
![]()
и
![]()
(= const)
Приведенные рекомендации
и статистические данные позволяют
обоснованно определить окружную скорость
НВ. Например, для
![]()
= 0,85
и
![]()
= 250 км/ч
получим
= 214 м/с
и μ = 0,32.
Для каждого значения
окружной скорости конца лопасти
существует
наивыгоднейшее заполнение НВ, при
котором значение относительного
(вентиляторного) коэффициента полезного
действия винта на режиме висения
вертолета (в отсутствие ограничивающих
поверхностей) максимально [63].
По
выбранной величине ωR определяют частоту
вращения НВ:
![]()
.
(3.16)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
22.11.2019745.47 Кб73.doc
- #
- #
- #
- #
- #
- #
- #
Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.
Угловая скорость
Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.
Обозначение угловой скорости: ω (омега).
Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.
С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.

Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:

Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.
Быстрота изменения угла φ (перемещения плоскости П из положения П1 в положение П2) – это и есть угловая скорость:

Приняв вектор k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.
Формулы угловой скорости
Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:
- если известно количество оборотов n за единицу времени t:

- если задан угол поворота φ за единицу времени:

- если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:

Размерности угловой скорости:
- Количество оборотов за единицу времени [об/мин], [c-1].
- Угол поворота за единицу времени [рад/с].
Определение угловой скорости
Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.

Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.

Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.
Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.
Другие примеры решения задач >
Угловое ускорение
Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:

Обозначение: ε (Эпсилон)
Единицы измерения углового ускорения: [рад/с2], [с-2]
Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.
Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).
Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:
Расчет углового ускорения
Пример: По заданному значению касательной составляющей полного ускорения aτ точки B, расположенной на расстоянии r от центра вращения колеса.

Требуется определить величину и направление углового ускорения колеса ε, если aτ = 10 м/с2, r = 50 см.

Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.
Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.
В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость
ω = 1,5 с-1 = 9,42 рад/с.
Смотрите также:
- Примеры расчета угловой скорости и ускорения
- Скорости и ускорения точек вращающегося тела
Что такое угловая скорость
Угловая скорость (обозначается как (omega)) — векторная величина, характеризующая скорость и направление изменения угла поворота со временем.
Модуль угловой скорости для вращательного движения совпадает с мгновенной угловой частотой вращения, а направление перпендикулярно плоскости вращения и связано с направлением вращения правилом правого винта.
Единица измерения
В Международной системе единиц (СИ) принятой единицей измерения угловой скорости является радиан в секунду (рад/с)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Формула угловой скорости
Вектор угловой скорости определяется отношением угла поворота ((varphi)) к интервалу времени ((mathcal t)), за которое произошел поворот:
(omega=frac{trianglevarphi}{trianglemathcal t})
Зависимость угловой скорости от времени
Зависимость (varphi ) от (mathcal t) наглядно показана на графике:
Угол, на который повернулось тело, характеризуется площадью под кривой.
Угловая скорость вращения, формула
Через частоту
(omega=2pimathcal n)
(mathcal n) — частота вращения ((1/с))
(pi) — число Пи ((approx 3,14))
(mathcal n=frac1T)
(T )— период вращения (время, за которое тело совершает один оборот)
Через радиус
(omega=frac vR)
(v) — линейная скорость(м/с)
(R) — радиус окружности (м)
Как определить направление угловой скорости
Направление скорости в физике можно определять двумя способами:
- Правило буравчика. Буравчик имеет правую резьбу (вращательное движение вправо при закручивании). Если вращать буравчик в направлении вращения тела, он будет завинчиваться (или вывинчиваться) в ту сторону, куда направлена угловая скорость.
- Правило правой руки. Представим, что взяли тело в правую руку. Следует направлять и вращать его туда, куда указывают четыре пальца. Отведенный в сторону большой палец покажет направление угловой скорости при этом вращении.
Связь линейной и угловой скорости
Линейная скорость ((v)) тела, расположенного на расстоянии (R) от оси вращения, прямо пропорциональна угловой скорости.
(v=Romega)
(R) — радиус окружности (м)
Чему равна мгновенная угловая скорость
Мгновенную угловую скорость нужно находить как предел, к которому стремится средняя угловая скорость при (trianglemathcal trightarrow0) :
(omega=lim_{trianglerightarrow0}frac{trianglevarphi}{trianglemathcal t})
Измеряется в рад/с
Угловая скорость – винт
Cтраница 1
Угловая скорость винта пропорциональна смещению ролика от центра диска. При совпадении угловых скоростей винта и гайки положение винта по вертикали остается неизменным.
[2]
Угловую скорость винта или шестерни регулируют механическим способом с помощью коробки подач или электрическим с помощью двигателя.
[3]
Если угловые скорости винта и гайки не равны, то винт будет перемещаться в гайке до тех пор, пока ролик 4 не установится на таком расстоянии от центра диска, при котором будет обеспечено равенство их угловых скоростей.
[4]
ЗО – угловая скорость винта, с J; пг – частота вращения винта, об / мин.
[5]
Связь между угловой скоростью винта и поступательной скоростью гайки определяется следующим образом.
[6]
Jtnj / 30 – угловая скорость винта 3, с 1; nt – частота вращения винта 3, об / мин.
[7]
Для определения относительной скорости точки находим угловую скорость винта по формуле (79.5), соответствующей также вращению тела в одном и том же направлении.
[8]
При выборе параметров РВ необходимо учитывать, что угловая скорость винта, соответствующая гравитационному резонансу, может быть близка к угловой скорости малого газа двигателей, при которой возможна длительная работа.
[9]
МГР – момент трения в паре винт – гайка; со – угловая скорость винта; А – механический эквивалент теплоты.
[10]
По мере вращения заготовки лента передачи 6 все больше перематывается с вала винта 2 и угловая скорость винта увеличивается, соответственно увеличивается скорость перемещения инструмента, а следовательно, и шаг нарезаемой резьбы.
[11]
Упругость в ВШ также помогает решить проблему устранения ударов лопастей по упорам ВШ при изменении угловой скорости винта, связанную с вертикальным расположением его плоскости вращения.
[12]
Винт судна с моментом инерции / приводится во вращение из состояния покоя постоянным вращающим моментом М, встречая при этом сопротивление воды, пропорциональное угловой скорости винта.
[13]
Винт судна имеет момент инерции J и приводится во врашение из состояния покоя постоянным вращающим моментом М, встречая при этом сопротивление воды, пропорциональное угловой скорости винта.
[14]
Из трех кинематических параметров движения судна до удара ( уСх, vCy, cojz) наиболее осуществимо управление величинами vCx, оз ] г. Действительно, vCx управляется снижением или увеличением угловой скорости винта, a ulz – углом отклонения руля.
[15]
Страницы:
1
2