Как найти угловую скорость вращения двигателя

Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.

Обозначение угловой скорости: ω (омега).

Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.

С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.

Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:

Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.

Быстрота изменения угла φ (перемещения плоскости П из положения П₁ в положение П₂) – это и есть угловая скорость:

Приняв вектор k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

1. если известно количество оборотов n за единицу времени t:
   
2. если задан угол поворота φ за единицу времени:
   
3. если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:
   

Размерности угловой скорости:

• Количество оборотов за единицу времени [об/мин], [c^-1].
• Угол поворота за единицу времени [рад/с].

Определение угловой скорости

Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.

Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.

Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.

Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.

Другие примеры решения задач >

Угловое ускорение

Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:

Обозначение: ε (Эпсилон)

Единицы измерения углового ускорения: [рад/с²], [с^-2]

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

Расчет углового ускорения

Пример: По заданному значению касательной составляющей полного ускорения a_τ точки B, расположенной на расстоянии r от центра вращения колеса.

Требуется определить величину и направление углового ускорения колеса ε, если a_τ = 10 м/с², r = 50 см.

Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.

Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

ω = 1,5 с^-1 = 9,42 рад/с.

Смотрите также:

• Примеры расчета угловой скорости и ускорения
• Скорости и ускорения точек вращающегося тела

Линейная скорость вращения, частота и частота угловая

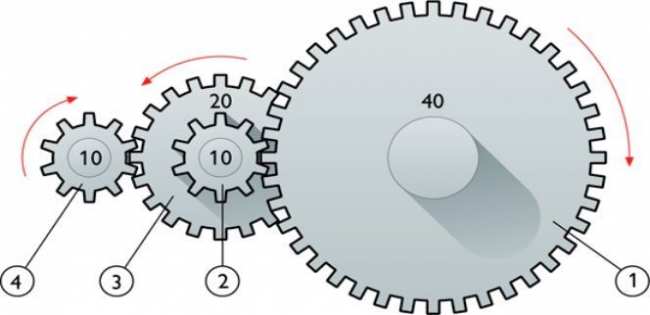
В технике для некоторых вращающих конструкций, например, шестерен и валов, известны их рабочие частоты μ и линейные скорости v. Тем не менее каждую из этих характеристик можно использовать для определения угловой или циклической частоты.

Выше отмечалось, что частота μ измеряется в герцах. Она показывает количество оборотов вращающегося тела за одну секунду. Формула для нее принимает вид:

Если сравнить это выражение с соответствующим равенством для f, то формула, как найти частоту вращения f через μ описывающая, будет иметь вид:

Эта формула интуитивно понятна, поскольку μ показывает количество оборотов за единицу времени, а f отражает ту же самую величину, только представленную в радианах.

Линейная скорость v связана со скоростью угловой ω следующим равенством:

Поскольку модули величин f и ω равны, то из последнего выражения легко получить соответствующую формулу частоты вращения циклической. Запишем ее:

Где r — радиус вращения. Заметим, что скорость v линейно растет при увеличении радиуса r, при этом отношение этих величин является константой. Последнее умозаключение означает, что если измерять циклическую частоту вращения в любой точке сечения вращающегося массивного объекта, то она будет везде одинаковой.

Число оборотов

Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.

Единица СИ частоты (или числа оборотов)

В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.

Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.

Если n — число оборотов, f — частота, T — продолжительность одного оборота, период, ? — угловое перемещение, N — полное число оборотов, t — время, продолжительность вращения, ? — угловая частота, 
то

Угловое перемещение равно произведению полного числа оборотов на 2?:

Угловая скорость

Из формулы для одного оборота следует:

Обратите внимание:• формулы справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.• вопреки своему названию число оборотов n — это не число, а физическая величина.• следует различать число оборотов n и полное число оборотов N

Описывающие вращение физические величины

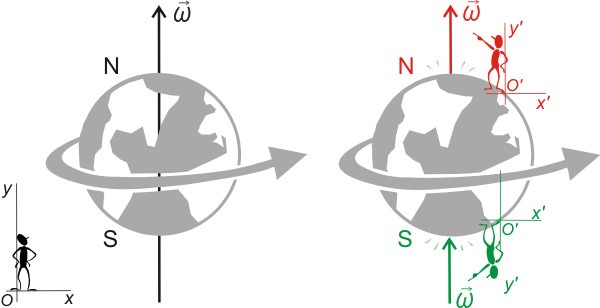
Для численного описания вращения в физике был введен ряд характеристик. Перечислим их и охарактеризуем.

В первую очередь это угол поворота, обозначается θ. Поскольку полная окружность характеризуется центральным углом в 2*pi радиан, то, зная величину θ, на которую повернулось вращающееся тело за определенный промежуток времени, можно определить число оборотов за это время. Кроме того, угол θ позволяет рассчитать линейный путь, пройденный телом вдоль кривой окружности. Соответствующие формулы для числа оборотов n и пройденного пути L имеют вид:

n = θ/(2*pi);

L = θ*r.

Где r — радиус окружности или радиус вращения.

Следующей характеристикой рассматриваемого типа движения является угловая скорость. Ее обычно обозначают буквой ω. Она измеряется в радианах в секунду, то есть показывает величину угла в радианах, на которые поворачивается вращающееся тело за одну секунду. Для угловой скорости в случае равномерного вращения справедлива формула:

ω = θ/t

Мощность вращающихся объектов

Для расчета подобной системы применяют формулу:

N = M * w = (2π * M* n)/60,

где:

• M – момент силы;
• w – угловая скорость, характеризующая вращение;
• n – количество оборотов, которое совершает двигатель или другое устройство за 60 секунд.

Приведенные сведения используют с учетом целевого назначения и реальных условий. Так, в термодинамике необходимо помнить о зависимости эффективности системы от температуры окружающей среды. Тепловые потери нагревателя оценивают по соответствующей мощности на единицу площади поверхности. Аналогичным образом поступают при решении механических задач для расчета тяги, КПД, иных рабочих параметров. Как правило, приходится специальным коэффициентом компенсировать трение.

В электрических цепях ток ограничивает сопротивление проводника. Для небольших расстояний при малой мощности тщательные расчеты не нужны. Однако проект магистральной трассы обязательно содержит соответствующие вычисления. На основе полученных результатов делают выводы о среднегодовых экономических показателях. Следует помнить о необходимости учета искажений, которые добавляют при работе с переменным напряжением реактивные нагрузки.

Задача на определение циклической частоты вращения вала

Угловые частоты вращения содержат полезную информацию, поскольку позволяют рассчитать такие важные физические характеристики, как момент импульса или угловую скорость. Решим такую задачу: известно, что рабочая частота вращения вала составляет 1500 оборотов в минуту. Чему равна циклическая частота для этого вала?

Из единиц измерения, приведенный в условии, понятно, что дана обычная частота μ. Поэтому формула частоты вращения вала циклической имеет вид:

f = 2*pi*μ

Прежде чем ею пользоваться, следует перевести указанную в условии цифру к стандартным единицам измерения, то есть к обратным секундам. Поскольку вал за минуту делает 1500 оборотов, то за секунду он сделает в 60 раз меньше оборотов, то есть 25. То есть частота его вращения равна 25 Гц. Подставляя это число в записанную выше формулу, получаем значение циклической частоты: f = 157 рад/с.

Линейная скорость вращения, частота и частота угловая

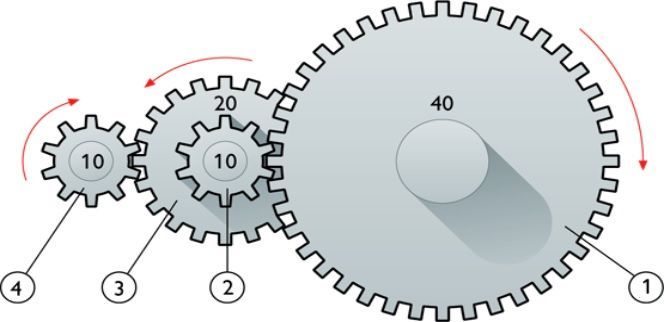
В технике для некоторых вращающих конструкций, например, шестерен и валов, известны их рабочие частоты μ и линейные скорости v. Тем не менее каждую из этих характеристик можно использовать для определения угловой или циклической частоты.

Выше отмечалось, что частота μ измеряется в герцах. Она показывает количество оборотов вращающегося тела за одну секунду. Формула для нее принимает вид:

μ = 1/T

Если сравнить это выражение с соответствующим равенством для f, то формула, как найти частоту вращения f через μ описывающая, будет иметь вид:

f = 2*pi*μ

Эта формула интуитивно понятна, поскольку μ показывает количество оборотов за единицу времени, а f отражает ту же самую величину, только представленную в радианах.

Линейная скорость v связана со скоростью угловой ω следующим равенством:

v = ω*r

Поскольку модули величин f и ω равны, то из последнего выражения легко получить соответствующую формулу частоты вращения циклической. Запишем ее:

f = v/r

Где r — радиус вращения. Заметим, что скорость v линейно растет при увеличении радиуса r, при этом отношение этих величин является константой. Последнее умозаключение означает, что если измерять циклическую частоту вращения в любой точке сечения вращающегося массивного объекта, то она будет везде одинаковой.

Коэффициент полезного действия электромотора

КПД — это характеристика, которая отражает эффективность работы системы при преобразовании энергии в механическую. Выражается отношением полезной энергии к потраченной. По единой системе единиц измерений он обозначается как «eta» и является безразмерным значением, исчисляемым в процентах. Формула КПД электродвигателя через мощность:

eta = P₂ ÷ P₁, где:

P₁ — электрическая (подаваемая) мощность, Вт;

P₂ — полезная (механическая) мощность, Вт;

Также он может быть выражен как:

eta = A ÷ Q × 100 %, где:

A — полезная работа, Дж;

Q — затраченная энергия, Дж.

Чаще коэффициент вычисляют по формуле потребляемой мощности электродвигателя, так как эти показатели всегда легче измерить.

Снижение эффективности работы электродвигателя происходит по причине:

Электрических потерь. Это происходит в результате нагрева проводников от прохождения по ним тока. Магнитных потерь

Вследствие излишнего намагничивания сердечника появляется гистерезис и вихревые токи, что важно учитывать в формуле мощности электродвигателя. Механических потерь

Они связаны с трением и вентиляцией. Дополнительных потерь. Они появляются из-за гармоник магнитного поля, так как статор и ротор имеют зубчатую форму. Также в обмотке присутствуют высшие гармоники магнитодвижущей силы.

Следует отметить, что КПД является одним из самых важных компонентов формулы расчета мощности электродвигателя, так как позволяет получить цифры, наиболее приближенные к действительности. В среднем этот показатель варьирует от 10% до 99%. Она зависит от конструктивного устройства механизма.

Угловая частота, период и угловая скорость

Выше уже отмечалось, что важным свойством любого вращательного движения является время, за которое совершается один оборот. Это время называется периодом вращения. Его обозначают буквой T и измеряют в секундах. Формулу для периода T можно записать через угловую скорость ω. Соответствующее выражение имеет вид:

T = 2*pi/ω

Величина, обратная периоду, называется частотой. Ее измеряют в герцах (Гц). Для кругового движения удобно использовать не саму частоту, а ее угловой аналог. Обозначим ее f. Формула частоты вращения угловой f имеет вид:

f = 2*pi/T

Чтобы рассчитать угловую частоту, необходимо знать период вращательного движения.

Сравнивая две последние формулы, приходим к следующему равенству:

f = ω

Это равенство означает следующее:

• формулы угловой частоты и угловой скорости совпадают, поэтому эти величины равны численно между собой;
• так же как и скорость, частота показывает, на какой угол в радианах поворачивается тело за одну секунду.

Различие между этими величинами единственное: угловая частота является величиной скалярной, скорость же — это вектор.

Переменный синусоидальный ток

Это тот ток, который периодически меняется во времени, и его изменения подчиняются закону синусоиды. Это элементарное движение электрических зарядов, потому дальнейшему разложению на простые токи оно не подлежит.

Вид формулы такого переменного тока:

i = Im*sinωt,

где:

• Im – амплитуда;
• sinωt – фаза синусоидального тока, рад.

Здесь ω = const, называется угловой частотой переменного электричества, причём угол ωt находится в прямой временной зависимости.

Зная частоту f исходного тока, можно вычислить его угловую частоту, применив выражение:

ω = 2πf = 2π/Т.

Тут 2π – это выраженное в радианах значение центрального угла окружности:

• Т = 2 π радиан = 3600;
• Т/2 = π = 1800;
• Т/4 = π/2 = 900.

Если выразить 1 рад в градусах, то он будет равен 57°17′.

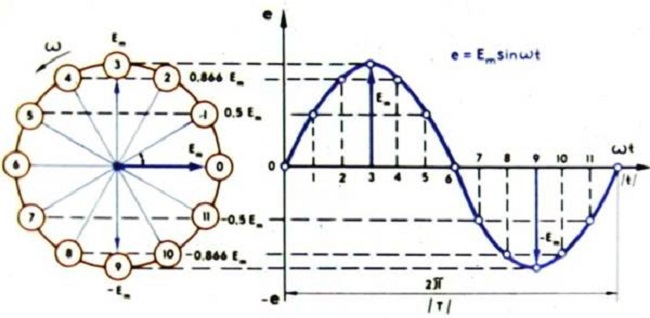Синусоидальное переменное движение электронов

Угловая частота, период и угловая скорость

Выше уже отмечалось, что важным свойством любого вращательного движения является время, за которое совершается один оборот. Это время называется периодом вращения. Его обозначают буквой T и измеряют в секундах. Формулу для периода T можно записать через угловую скорость ω. Соответствующее выражение имеет вид:

Величина, обратная периоду, называется частотой. Ее измеряют в герцах (Гц). Для кругового движения удобно использовать не саму частоту, а ее угловой аналог. Обозначим ее f. Формула частоты вращения угловой f имеет вид:

Чтобы рассчитать угловую частоту, необходимо знать период вращательного движения.

Сравнивая две последние формулы, приходим к следующему равенству:

Это равенство означает следующее:

• формулы угловой частоты и угловой скорости совпадают, поэтому эти величины равны численно между собой;
• так же как и скорость, частота показывает, на какой угол в радианах поворачивается тело за одну секунду.

Различие между этими величинами единственное: угловая частота является величиной скалярной, скорость же — это вектор.

Вращательное движение тела, формулы

Кроме того, эти величины связаны определенным образом с угловым перемещением ?, угловой скоростью ? и угловым ускорением ?.

Sл	перемещение тела по траектории,	метр
Uл	скорость тела при движении по траектории,	метр / секунда
aл	ускорение данного тела при движении по траектории,	метр / секунда2
r	радиус траектории,	метр
d	диаметр траектории,	метр
?	угловое перемещение тела,	радиан
?	угловая скорость тела,	радиан / секунда
?	угловое ускорение тела,	радиан / секунда2
f	частота,	Герц

Примечание:Формулы справедливы для постоянных, мгновенных и средних величин, во всех случаях движения тела по окружности.

Экономическое обоснование эффекта от инвертора

Время окупаемости инвертора рассчитывается отношением затрат на покупку к экономии энергии. Экономия обычно равна от 20 до 40% от номинальной мощности мотора.

Затраты снижают факторы, повышающие производительность частотных преобразователей:

1. Уменьшение затрат на обслуживание.
2. Повышение ресурса двигателя.

Экономия рассчитывается:

где Э – экономия денег в рублях;

Р_пч – мощность инвертора;

Ч – часов эксплуатации в день;

Д – число дней;

К – коэффициент ожидаемого процента экономии;

Т – тариф энергии в рублях.

Время окупаемости равно отношению затрат на покупку инвертора к экономии денег. Расчеты показывают, что период окупаемости получается от 3 месяцев до 3 лет. Это зависит от мощности мотора.

Модуль №4. Частотное регулирование скорости асинхронного двигателя

Watch this video on YouTube

Основные формулы расчета мощности двигателей

Для вычисления реальных характеристик механизмов всегда нужно учитывать много параметров. в первую очередь нужно знать, какой ток подается на обмотки электродвигателя: постоянный или переменный. Принцип их работы отличается, следовательно, отличаются метод вычислений. Если упрощенный вид расчета мощности привода выглядит как:

P_эл = U × I, где

I — сила тока, А;

U — напряжение, В;

P_эл — подведенная электрическая мощность. Вт.

В формуле мощности электродвигателя переменного тока необходимо также учитывать сдвиг фаз (alpha). Соответственно, расчеты для асинхронного привода выглядят как:

P_эл = U × I × cos(alpha).

Кроме активной (подведенной) мощности существует также:

• S — реактивная, ВА. S = P ÷ cos(alpha).
• Q — полная, ВА. Q = I × U × sin(alpha).

В расчетах также необходимо учитывать тепловые и индукционные потери, а также трение. Поэтому упрощенная модель формулы для электродвигателя постоянного тока выглядит как:

P_эл = Pмех + Ртеп +Ринд + Ртр_, где

Рмех — полезная вырабатываемая мощность, Вт;

Ртеп — потери на образование тепла, ВТ;

Ринд — затраты на заряд в индукционной катушке, Вт;

Рт — потери в результате трения, Вт.

Угловая скорость в спорте

Угловая скорость часто используется в спорте. Например, спортсмены уменьшают или увеличивают угловую скорость движения клюшки для гольфа, биты или ракетки, чтобы улучшить результаты. Угловая скорость связана с линейной скоростью так, что из всех точек на отрезке, вращающемся вокруг точки на этом отрезке, то есть вокруг центра вращения, самая отдаленная точка от этого центра движется с самой высокой линейной скоростью. Так, например, если клюшка для гольфа вращается, то конец этой клюшки, больше всего удаленный от центра вращения двигается с самой высокой линейной скоростью. В то же время все точки на этом отрезке движутся с одинаковой угловой скоростью. Поэтому удлиняя клюшку, биту, или ракетку, спортсмен также увеличивает линейную скорость, а соответственно скорость удара, передающуюся мячу, так что он может пролететь на большее расстояние. Укорачивая ракетку или клюшку, даже перехватив ее ниже, чем обычно, наоборот замедляют скорость удара.

При первобытнообщинном строе главными охотниками были мужчины

Спортсменам с более длинными руками и ногами удается добиться бо́льшей угловой скорости

У высоких людей с длинными конечностями есть преимущество в отношении линейной скорости. То есть, передвигая ноги с одинаковой угловой скоростью, они двигают ступни с более высокой линейной скоростью. То же происходит и с их руками. Такое преимущество может быть одной из причин того, что в первобытных обществах мужчины занимались охотой чаще, чем женщины. Вероятно, что из-за этого также в процессе эволюции выиграли более высокие люди. Длинные конечности помогали не только в беге, но и во время охоты — длинные руки бросали копья и камни с большей линейной скоростью. С другой стороны, длинные руки и ноги могут быть неудобством. Длинные конечности имеют больший вес и для их перемещения нужна дополнительная энергия. Кроме этого, когда человек быстро бежит, длинные ноги быстрее двигаются, а значит, при столкновении с препятствием удар будет сильнее, чем у людей с короткими ногами, которые двигаются с той же линейной скоростью.

В гимнастике, фигурном катании и нырянии также используют угловую скорость. Если спортсмен знает угловую скорость, то легко вычислить количество переворотов и других акробатических трюков во время прыжка. Во время кувырков спортсмены обычно прижимают ноги и руки как можно ближе к корпусу, чтобы уменьшить инерцию и увеличить ускорение, а значит и угловую скорость. С другой стороны, во время ныряния или приземления, судьи смотрят, как ровно спортсмен приземлился. На высокой скорости трудно регулировать направление полета, поэтому спортсмены специально замедляют угловую скорость, немного вытягивая от корпуса руки и ноги.

Спортсмены, которые занимаются метанием диска или молота, тоже контролируют линейную скорость с помощью угловой. Если просто бросить молот, не вращая его по кругу на длинной стальной проволоке, увеличивающей линейную скорость, то бросок будет не таким сильным, поэтому молот сначала раскручивают. Олимпийские спортсмены поворачиваются вокруг своей оси от трех до четырех раз, чтобы увеличить угловую скорость до максимально возможной.

Описывающие вращение физические величины

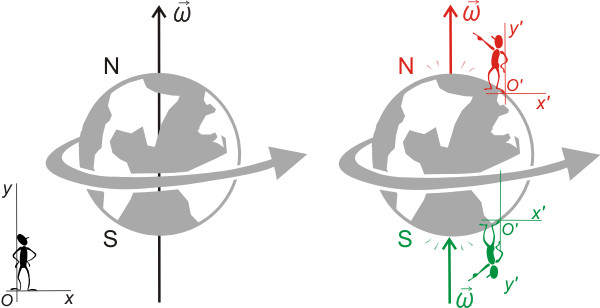
Для численного описания вращения в физике был введен ряд характеристик. Перечислим их и охарактеризуем.

В первую очередь это угол поворота, обозначается θ. Поскольку полная окружность характеризуется центральным углом в 2*pi радиан, то, зная величину θ, на которую повернулось вращающееся тело за определенный промежуток времени, можно определить число оборотов за это время. Кроме того, угол θ позволяет рассчитать линейный путь, пройденный телом вдоль кривой окружности. Соответствующие формулы для числа оборотов n и пройденного пути L имеют вид:

Где r — радиус окружности или радиус вращения.

Следующей характеристикой рассматриваемого типа движения является угловая скорость. Ее обычно обозначают буквой ω. Она измеряется в радианах в секунду, то есть показывает величину угла в радианах, на которые поворачивается вращающееся тело за одну секунду. Для угловой скорости в случае равномерного вращения справедлива формула:

Описывающие вращение физические величины

Для численного описания вращения в физике был введен ряд характеристик. Перечислим их и охарактеризуем.

В первую очередь это угол поворота, обозначается θ. Поскольку полная окружность характеризуется центральным углом в 2*pi радиан, то, зная величину θ, на которую повернулось вращающееся тело за определенный промежуток времени, можно определить число оборотов за это время. Кроме того, угол θ позволяет рассчитать линейный путь, пройденный телом вдоль кривой окружности. Соответствующие формулы для числа оборотов n и пройденного пути L имеют вид:

n = θ/(2*pi);

L = θ*r.

Где r — радиус окружности или радиус вращения.

Следующей характеристикой рассматриваемого типа движения является угловая скорость. Ее обычно обозначают буквой ω. Она измеряется в радианах в секунду, то есть показывает величину угла в радианах, на которые поворачивается вращающееся тело за одну секунду. Для угловой скорости в случае равномерного вращения справедлива формула:

ω = θ/t

Как подключить частотный преобразователь

Если кабель для подключения на 220 В с 1-й фазой, применяется схема «треугольника». Нельзя подключать частотник, если выходной ток выше 50% от номинального значения.

Если кабель питания на три фазы 380 В, то делается схема «звезды». Чтобы проще было подключать питание, предусмотрены контакты и клеммы с буквенными обозначениями.

• Контакты R, S, T предназначены для подключения сети питания по фазам.
• Клеммы U , V , W служат соединением электродвигателя. Для реверса достаточно изменить подключение двух проводов между собой.

В приборе должна быть колодка с клеммой подключения к земле. Подробней, как подключить, здесь.

Циклическая частота вращения (обращения)

Скалярная величина, измеряющая частоту вращательного движения, называется циклической частотой вращения. Это угловая частота, равная не самому вектору угловой скорости, а его модулю. Ещё её именуют радиальной или круговой частотой.

Циклическая частота вращения – это количество оборотов тела за 2*π секунды.

У электрических двигателей переменного тока это частота асинхронная. У них частота вращения ротора отстаёт от частоты вращения магнитного поля статора. Величина, определяющая это отставание, носит название скольжения – S. В процессе скольжения вал вращается, потому что в роторе возникает электроток. Скольжение допустимо до определённой величины, превышение которой приводит к перегреву асинхронной машины, и её обмотки могут сгореть.

Устройство этого типа двигателей отличается от устройства машин постоянного тока, где токопроводящая рамка вращается в поле постоянных магнитов. Большое количество рамок вместил в себя якорь, множество электромагнитов составили основу статора. В трёхфазных машинах переменного тока всё наоборот.

При работе асинхронного двигателя статор имеет вращающееся магнитное поле. Оно всегда зависит от параметров:

• частоты питающей сети;
• количества пар полюсов.

Скорость вращения ротора состоит в прямом соотношении со скоростью магнитного поля статора. Поле создаётся тремя обмотками, которые расположены под углом 120 градусов относительно друг друга.

Задача на определение циклической частоты вращения вала

Угловые частоты вращения содержат полезную информацию, поскольку позволяют рассчитать такие важные физические характеристики, как момент импульса или угловую скорость. Решим такую задачу: известно, что рабочая частота вращения вала составляет 1500 оборотов в минуту. Чему равна циклическая частота для этого вала?

Из единиц измерения, приведенный в условии, понятно, что дана обычная частота μ. Поэтому формула частоты вращения вала циклической имеет вид:

Прежде чем ею пользоваться, следует перевести указанную в условии цифру к стандартным единицам измерения, то есть к обратным секундам. Поскольку вал за минуту делает 1500 оборотов, то за секунду он сделает в 60 раз меньше оборотов, то есть 25. То есть частота его вращения равна 25 Гц. Подставляя это число в записанную выше формулу, получаем значение циклической частоты: f = 157 рад/с.

Период пульсаций и частота

Частота переменного тока может иметь другое название – пульсация. Периодом пульсации называют время единичной пульсации.

Интенсивность циклов

Для электросети с частотой 50 Гц период пульсации составит:

Т = 1/50 = 0,02 с.

При необходимости, зная эту зависимость, можно по времени цикла вычислить частоту.

Опасность разночастотных зарядов

Как постоянный, так и переменный ток при определённых значениях представляет опасность для человека. До 500 В разница в безопасности находится в соотношении 1:3 (42 В постоянного к 120 В переменного).

При значениях выше 500 В это соотношение выравнивается, причём константное электричество вызывает ожоги и электролизацию кожных покровов, изменяющееся – судороги, фибрилляцию и смерть. Тут уже частота пульсации имеет большое значение. Самый опасный интервал частот – от 40 до 60 Гц. Далее с повышением частоты риск поражения уменьшается.

Влияние частоты на пороговый ток

Частота переменного электричества – важный параметр. Она влияет не только на работу электроустановок потребителей, но и на человеческий организм. Изменяя частоту электрических колебаний, можно менять технологические процессы на производстве и качество вырабатываемой энергии.

Генерирование переменного тока

Кроме стандартных генераторов, для производства переменного тока применяются инверторы и фазорасщепители.

Инвертор

Это устройство, с помощью которого из постоянного тока получают его переменный вид. В процессе этого величина выходного напряжения тоже меняется. Схема устройства представляет собой электронный генератор синусоидального импульсного напряжения периодического характера. Есть варианты инверторов, работающих с дискретным сигналом. Инверторы применяют для автономного питания оборудования от аккумуляторов постоянного напряжения.

Инвертор 12/220 В, мощностью 1500 Вт

Фазорасщепитель

Ещё один способ получить несколько фаз из какого-либо сигнала – это выполнить его расщепление на несколько фаз. Это делается с помощью фазорасщепителя. Принудительная обработка сигналов цифрового или аналогового формата используется, как в радиоэлектронике, так и в силовой электротехнике.

Для электроснабжения трёхфазных асинхронных двигателей применяют выполненный на их же базе фазорасщепитель. Для этого обмотки трёхфазного двигателя соединяют не «звездой», а иначе. Две катушки присоединяют между собой последовательно, третью – подключают к средней точке второй обмотки. Двигатель запускают, как однофазный, после разгона в его третьей обмотке наводится ЭДС.

Интересно. В случае расщепления фаз подобным методом сдвиг фаз между 2 и 3 обмоткой составляет не 1200, как должно быть в идеале, а 900.

Главное меню:

• Основы
• Электромашины
• Оборудование
• Нормы
• Подстанция
  • Комплектные трансформаторные подстанции
  • Оборудование подстанций
  • Вакуумные выключатели
    • ВВ/TEL
    • ВР
    • ВРО
    • ВР1
    • ВР1 для КСО
    • ВРС
    • 3АН5
    • ВГГ-10
  • Камеры КСО
  • Ограничители перенапряжений 6(10) кВ
  • Масляный выключатель
    • ВПМ-10
    • Техническое описание ВПМ
    • ВМП-10
    • ВМГ-133
  • Выключатель нагрузки автогазовый ВНА
    • Описание выключателя
    • Изображение выключателя
  • Ремонт электрооборудования
  • Повышение надежности МВ, приводов МВ
  • Установки компенсации реактивной мощности
    • Общие сведения об УКРМ
    • УКРМ 0,4 кВ
    • УКРМ 6(10) кВ
  • Выбор места расположения питающих подстанций
• Электроснабжение
• Освещение
• Воздушная линия

Основы > Задачи и ответы > Сборник задач — электрические машины

Асинхронные электродвигатели (страница 2)

1.

Определить угловую скорость вращении ротора асинхронного электродвигателя, если обмотка статора четырехполюсная, частота напряжения сети, к которой присоединен электродвигатель, 50 Гц и скольжение ротора равно 3,5%.Решение: Частота токов, проходящих в обмотках статора, равна частоте напряжения сети: Кроме того, известно, что обмотка статора четырехполюсная, т. е. число пар полюсов р = 2.

Скорость вращения магнитного потока, вызываемого трехфазной системой токов, проходящих в обмотках статора, зависит от частоты этих токов

и числа пар полюсов обмотки р, так как , откуда число оборотов в минуту вращающегося синхронно магнитного потока Угловая скорость вращения Вращение ротора асинхронного электродвигателя возможно лишь при наличии отставания ротора от вращающегося магнитного потока. Величина, характеризующая это отставание, называется скольжением: — скорость вращения магнитного потока; — скорость вращения ротора.Подставив числовые значения, получим Угловая скорость вращения ротора2. На щитке асинхронного электродвигателя значится: 730 об/мин, 50 Гц.Определить скольжение ротора, вращающегося с указанной скоростью, и число пар полюсов обмотки статора. Каким было скольжение ротора в первые мгновения пуска?Решение: В табл. 13 синхронных скоростей вращения при частоте 50 Гц ближайшей скоростью вращения (по отношению к скорости ) является скорость .Следовательно, скольжение ротора Число пар полюсов обмотки статора

В момент пуска ротор неподвижен

. Поэтому скольжение при пуске Такое значение имеет скольжение ротора в момент пуска любого асинхронного электродвигателя.

Таблица 13

р пар полюсов	1	2	3	4	5
n, об/мин	3000	1500	1000	750	600

3.

В разрыв провода линии, соединяющей контактные кольца ротора асинхронного электродвигателя с трехфазным реостатом, введен магнитоэлектрический амперметр, шкала которого имеет нулевое значение посередине (рис. 80). Разомкнув рубильник, шунтировавший амперметр во время разбега ротора, не поднимая щеток, наблюдали за отклонениями амперметра: оказалось, что за полминуты указательная стрелка прибора совершила 60 полных колебаний.Определить скорость вращения ротора в течение указанного промежутка времени, если обмотка статора шестиполюсная и частота напряжения сети 50 Гц.

Решение:

Полное колебание указательной стрелки соответствует полному периоду тока в обмотке ротора. Если 60 полных колебаний (периодов) произошло за полминуты, то число полных колебаний (периодов) в секунду равно двум. Следовательно, Магнитный поток в асинхронном электродвигателе вращается относительно ротора со скоростью, равной разности скоростей: причем частота тока в роторе Подставив числовые значения, получим

При шестиполюсной обмотке статора и частоте токов в цепи статора

скорость вращения магнитного потока

Подставим в выражение для

откуда скорость вращения ротора4. Когда трехфазный асинхронный двигатель с фазным ротором присоединили к сети с линейным напряжением 220 В, напряжение между контактными кольцами при разомкнутой обмотке ротора составило 90 В.Определить коэффициент трансформации, рассматривая этот электродвигатель как трансформатор в режиме холостого хода, если обмотки статора и ротора соединены звездой.Решение: Фазное напряжение на обмотке статора при схеме соединения звездой в раз меньше линейного напряжения. Следовательно, Фазное напряжение на обмотке ротора Коэффициент трансформации фазных напряжений5. Асинхронный электродвигатель с короткозамкнутым ротором характеризуется отношением вращающих моментов соответственно при пуске и при номинальном режиме .Можно ли осуществить пуск двигателя в случае полной его нагрузки на валу и понижения напряжения в сети на 5 и 10%? К сети присоединен статор.Решение: Вращающий момент асинхронного двигателя прямо пропорционален квадрату напряжения в сети:

Следовательно, если напряжение в сети понизится на 5% и составит

Так как пусковой момент при номинальном напряжении , то при понижении напряжения в сети на 5% пусковой момент Таким образом, пуск при этих условиях позволит электродвигателю развить вращающий момент больше номинального.

Если напряжение в сети понизится на 10% и составит

Пусковой момент при указанном понижении напряжения долю, которую составляет пусковой вращающий момент от вращающего момента при номинальном напряжении. Тогда для возможности пуска электродвигателя при номинальной нагрузке должно быть выполнено равенство Поэтому при пуске электродвигателя напряжение сети может составлять от номинального напряжения долю

Таким образом, при заданной кратности пускового момента от номинального

понижение напряжения в сети может происходить на и пуск может быть осуществлен при номинальной нагрузке на валу электродвигателя.

6. Асинхронный электродвигатель с короткозамкнутым ротором типа А51-4 имеет следующие номинальные данные: ; кратность вращающих моментов .

Определить вращающие моменты: номинальный , максимальный и пусковой Решение:

Номинальный вращающий момент можно определить из основного соотношения измерен в и мощность Р — в Вт. При этом Если подставить сюда в качестве Р мощность, измеренную в киловаттах, то число будет в 1000 раз меньше.Таким образом, при тех же единицах измерения вращающего момента получим Подставим величины номинального режима: Используя известные кратности моментов, максимальный вращающий момент пусковой вращающий момент7. Асинхронный электродвигатель развивает номинальную мощность при номинальной скорости вращения ротора , имея перегрузочную способность 2,1.Выразить зависимость между вращающим, моментом и скольжением ротора S электродвигателя.Решение: Номинальный вращающий момент

Перегрузочная способность

l = 2,1 представляет собой отношение максимального вращающего момента к номинальному вращающему моменту Номинальному вращающему моменту соответствует и номинальное скольжение подставлена ближайшая большая (по отношению к ) синхронная скорость вращения магнитного потока статора.Зависимость между вращающим моментом и скольжением ротора s в асинхронном двигателе выражается формулой означает критическое скольжение, а и s соответствуют одному и тому же режиму работы. Если в левую часть подставить , то в качестве s следует подставить . Тогда можно определить критическое скольжение , при котором имеет место момент . В этом случае получается квадратное уравнение, из которого берут большее значение корня.Так как Разделив на 0,238 левую и правую части равенства и сосредоточив все члены в одной стороне, получим Корни полученного квадратного уравнения Далее берется только больший из корней (при положительном знаке перед корнем):

Подставив в формулу, выражающую зависимость между вращающим моментом

и скольжением ротора s, численные значения , получим требуемую зависимость

Смотри полное содержание по представленным решенным задачам на websor.

Как определить число пар полюсов асинхронного двигателя?

Под скоростью вращения асинхронного электродвигателя обычно понимают угловую частоту вращения его ротора, которая приведена на шильдике (на паспортной табличке двигателя) в виде количества оборотов в минуту.

Трехфазный двигатель можно питать и от однофазной сети, для этого достаточно добавить конденсатор параллельно одной или двум его обмоткам, в зависимости от напряжения сети, но конструкция двигателя от этого не изменится.

Так, если ротор под нагрузкой совершает 2760 оборотов в минуту, то угловая частота данного двигателя будет равна 2760*2пи/60 радиан в секунду, то есть 289 рад/с, что не удобно для восприятия, поэтому на табличке пишут просто «2760 об/мин». Применительно к асинхронному электродвигателю, это обороты с учетом скольжения s.

Синхронная же скорость данного двигателя (без учета скольжения) будет равна 3000 оборотов в минуту, поскольку при питании обмоток статора сетевым током с частотой 50 Гц, каждую секунду магнитный поток будет совершать по 50 полных циклических изменений, а 50*60 = 3000, вот и получается 3000 оборотов в минуту — синхронная скорость асинхронного электродвигателя.

В рамках данной статьи мы поговорим о том, как определить синхронную скорость вращения неизвестного асинхронного трехфазного двигателя, просто взглянув на его статор.

По внешнему виду статора, по расположению обмоток, по количеству пазов, — можно легко определить синхронные обороты электродвигателя если у вас нет под рукой тахометра.

Итак, начнем по порядку и разберем данный вопрос с примерами.

3000 оборотов в минуту

Про асинхронные электродвигатели (смотрите — Виды электродвигателей) принято говорить, что тот или иной двигатель имеет одну, две, три или четыре пары полюсов. Минимум — одна пара полюсов, то есть минимум — два полюса.

Взгляните на рисунок. Здесь вы видите, что в статор уложено по две последовательно соединенные катушки на каждую фазу — в каждой паре катушек одна расположена напротив другой.

Эти катушки и образуют по паре полюсов на статоре.

Одна из фаз показана для ясности красным цветом, вторая — зеленым, третья — черным. Обмотки всех трех фаз устроены одинаково.

Поскольку три эти обмотки питаются по очереди (ток трехфазный), то за 1 колебание из 50 в каждой из фаз — магнитный поток статора один раз обернется на полные 360 градусов, то есть совершит один оборот за 1/50 секунды, значит 50 оборотов получится за секунду. Так и выходит 3000 оборотов в минуту.

Таким образом становится ясно, что для определения синхронных оборотов асинхронного электродвигателя достаточно определить количество пар его полюсов, что легко сделать, сняв крышку и взглянув на статор.

Общее число пазов статора разделите на число пазов, приходящихся на одну секцию обмотки одной из фаз. Если получится 2, то перед вами двигатель с двумя полюсами — с одной парой полюсов.

Следовательно синхронная частота составляет 3000 оборотов в минуту или примерно 2910 с учетом скольжения.

В простейшем случае 12 пазов, по 6 пазов на катушку, и таких катушек 6 — по две на каждую из трех фаз.

Обратите внимание, количество катушек в одной группе для одной пары полюсов может быть не обязательно 1, но и 2 и 3, однако для примера мы рассмотрели вариант с одиночными группами на пару катушек (не будем в рамках данной статьи заострять внимание на способах намотки).

1500 оборотов в минуту

Для получения синхронной скорости в 1500 оборотов в минуту, количество полюсов статора увеличивают вдвое, чтобы за 1 колебание из 50 магнитный поток совершил бы только пол оборота — 180 градусов.

Для этого на каждую фазу делают по 4 секции обмотки. Таким образом, если одна катушка занимает четверть всех пазов, то перед вами двигатель с двумя парами полюсов, образованными четырьмя катушками на фазу.

Например, 6 пазов из 24 занимает одна катушка или 12 из 48, значит перед вами двигатель с синхронной частотой 1500 оборотов в минуту, или с учетом скольжения примерно 1350 оборотов в минуту. На приведенном фото каждая секция обмотки выполнена в виде двойной катушечной группы.

1000 оборотов в минуту

Как вы уже поняли, для получения синхронной частоты в 1000 оборотов в минуту, каждая фаза образует уже три пары полюсов, чтобы за одно колебание из 50 (герц) магнитный поток обернулся бы всего на 120 градусов, и соответствующим образом повернул бы за собой ротор.

Таким образом, минимум 18 катушек установлены на статор, причем каждая катушка занимает шестую часть всех пазов (по шесть катушек на фазу — по три пары). Например, если пазов 24, то одна катушка займет 4 из них. Получится частота с учетом скольжения около 935 оборотов в минуту.

750 оборотов в минуту

Для получения синхронной скорости в 750 оборотов в минуту, необходимо, чтобы три фазы формировали на статоре четыре пары движущихся полюсов, это по 8 катушек на фазу — одна напротив другой — 8 полюсов. Если например на 48 пазов приходится по катушке на каждые 6 пазов — перед вами асинхронный двигатель с синхронными оборотами 750 (или около 730 с учетом скольжения).

500 оборотов в минуту

Наконец, для получения асинхронного двигателя с синхронной скоростью в 500 оборотов в минуту необходимо 6 пар полюсов — по 12 катушек (полюсов) на фазу, чтобы на каждое колебание сети магнитный поток поворачивался бы на 60 градусов. То есть, если например статор имеет 36 пазов, при этом на катушку приходится по 4 паза — перед вами трехфазный двигатель на 500 оборотов в минуту (480 с учетом скольжения).

FAQ по электродвигателям

Какие электродвигатели применяются чаще всего? Какие способы управления электродвигателями используются? Как прозвонить электродвигатель и определить его сопротивление? Как определить мощность электродвигателя? Как увеличить или уменьшить обороты электродвигателя? Как рассчитать ток и мощность электродвигателя? Как увеличить мощность электродвигателя? Каковы потери мощности при подключении трехфазного двигателя к однофазной сети? Какие исполнения двигателей бывают? Зачем электродвигателю тормоз? Как двигатель обозначается на электрических схемах? Почему греется электродвигатель? Типичные неисправности электродвигателей

1. Какие электродвигатели применяются чаще всего?

Наиболее распространены асинхронные электродвигатели с короткозамкнутым ротором. Они имеют сравнительно простую конструкцию и относительно недороги.

Для работы асинхронного двигателя требуется трехфазное напряжение, создающее на обмотках статора вращающееся магнитное поле.

Это поле приводит в движение ротор двигателя, который передает крутящий момент на нагрузку, например, на пропеллер вентилятора или редуктор конвейера.

Изменяя конфигурацию обмоток статора, можно менять основные характеристики привода – частоту оборотов и мощность на валу. В случае работы асинхронного электродвигателя в однофазной сети применяют фазосдвигающие и пусковые конденсаторы.

Также в настоящее время находят применение двигатели постоянного тока. Данные приводы имеют щетки, подверженные износу и искрению.

Кроме того, необходима обмотка подмагничивания (возбуждения), на которую подается постоянное напряжение.

Несмотря на эти недостатки, электродвигатели постоянного тока используются там, где необходимо быстрое изменение скорости вращения и контроль момента, а также при мощностях более 100 кВт.

В быту также применяют коллекторные (щеточные) электродвигатели переменного тока, которые имеют низкую надежность по сравнению с асинхронными.

2. Какие способы управления электродвигателями используются на практике?

Управление электродвигателем подразумевает возможность изменения его скорости и мощности.

Так, если на асинхронный двигатель подать напряжение заданной величины и частоты, он будет вращаться с номинальной скоростью и сможет обеспечить мощность на валу не более номинала.

Если же нужно понизить или повысить скорость электродвигателя, используют преобразователи частоты. ПЧ может обеспечить нужный режим разгона и торможения, а также позволит оперативно управлять частотой работы.

Для обеспечения требуемого разгона и торможения без изменения рабочей частоты применяют устройство плавного пуска (УПП). Если нужно управлять только разгоном двигателя, используют схему включения «звезда-треугольник».

Для запуска двигателей без ПЧ и УПП широко применяются контакторы, которые позволяют дистанционно управлять пуском, остановом и реверсом.

3. Как прозвонить электродвигатель и определить его сопротивление?

Асинхронный электродвигатель, как правило, имеет три обмотки. У каждой обмотки есть по два вывода, которые должны быть обозначены в клеммной коробке двигателя. Если выводы обмоток известны, то можно легко прозвонить каждую из них и сравнить величину сопротивления с остальными обмотками. Если величины сопротивлений отличаются не более, чем на 1%, то скорее всего, обмотки исправны.

Сопротивление обмоток электродвигателя измеряется с помощью омметра, как и сопротивление обмоток трансформатора. Чем больше мощность двигателя, тем меньше сопротивление его обмоток, и наоборот.

4. Как определить мощность электродвигателя?

Проще всего определить номинальную мощность электродвигателя по шильдику. На нем указана механическая мощность (мощность на валу), значение которой всегда меньше потребляемой мощности за счет потерь на трение и нагрев.

Однако, если шильдик на корпусе двигателя отсутствует, можно очень приблизительно оценить характеристики привода по его габаритам.

При одинаковой мощности двигатель с бо́льшим диаметром вала будет иметь более высокую мощность на валу и меньшую частоту оборотов.

Также мощность можно определить по нагрузке и по настройкам защитных устройств, через которые питается двигатель (мотор-автомат, тепловое реле).

Еще один способ – включаем двигатель на номинальную мощность, обеспечив нужную нагрузку на валу. После этого измеряем токоизмерительными клещами ток, который должен быть одинаков по всем обмоткам. Для приблизительной оценки мощности асинхронного двигателя, подключенного по схеме «звезда», нужно разделить номинальный измеренный ток на 2.

5. Как увеличить или уменьшить обороты электродвигателя?

Управление скоростью вращения двигателя необходимо в трех режимах работы – при разгоне, торможении, и в рабочем режиме.

Наиболее универсальный способ управления оборотами — использование частотного преобразователя. Настройками ПЧ можно добиться любой частоты вращения в пределах технической возможности. При этом можно управлять и другими параметрами электродвигателя, а также следить за его состоянием во время работы. Частоту можно менять и плавно, и ступенчато.

Управление оборотами двигателя в режиме разгона и торможения возможно при использовании УПП. Это устройство позволяет значительно снизить пусковой ток за счет плавного разгона с медленным увеличением оборотов.

6. Как рассчитать ток и мощность электродвигателя?

Бывает так, что известен ток асинхронного двигателя (по измерениям в номинальном режиме или по шильдику), но неизвестна его мощность. Как в таком случае рассчитать мощность? Обычно используют следующую формулу:

• Р = I (1,73·U·cosφ·η)
• где: Р – номинальная полезная мощность на валу двигателя в Вт (указывается на шильдике), I – ток двигателя, А, U – напряжение питания обмоток (380 В при подключении в «звезду», 220 В при подключении в «треугольник»),
• cosφ, η – коэффициенты мощности и полезного действия для учета потерь (обычно 0,7…0,8).
• Для расчета тока по известной мощности пользуются обратной формулой:
• I = P/(1,73·U·cosφ·η)
• Для двигателей мощностью 1,5 кВт и более, обмотки которых подключены в «звезду» (это подключение используется чаще всего), существует простое эмпирическое правило – чтобы приблизительно оценить ток двигателя, нужно умножить его мощность на 2.

7. Как увеличить мощность электродвигателя?

Номинальная мощность на валу, которая указывается на шильдике двигателя, обычно ограничивается допустимым током, а значит – нагревом корпуса привода. Поэтому при увеличении мощности необходимо предпринять дополнительные меры по охлаждению электродвигателя, установив отдельный вентилятор.

При использовании преобразователя частоты для повышения мощности можно изменить несущую частоту ШИМ, однако следует избегать перегрева ПЧ. Мощность также можно увеличить с помощью редуктора или ременной передачи, пожертвовав количеством оборотов, если это допустимо.

Если приведенные советы неприменимы – придётся менять двигатель на более мощный.

8. Каковы потери мощности при подключении трехфазного двигателя к однофазной сети (380 на 220)?

При таком подключении используются пусковой и рабочий фазосдвигающие конденсаторы. Номинальную мощность на валу в данном случае получить не удастся, и потери мощности составят 20-30% от номинала. Это происходит из-за невозможности обеспечить отсутствие перекоса по фазам при изменении нагрузки.

9. Какие исполнения двигателей бывают?

В зависимости от исполнения электродвигатели классифицируются по способу монтажа, классу защиты, климатическому исполнению. Существует два основных способа монтажа асинхронных электродвигателей – на лапах и через фланец. Оба варианта исполнения в различных комбинациях показаны в таблице ниже.

Виды климатического исполнения предполагают использование двигателя в определенных климатических зонах: умеренный климат (У), холодный климат (ХЛ), умеренно-холодный климат (УХЛ), тропический климат (Т), общеклиматическое исполнение (О), общеклиматическое морское исполнение (ОМ), всеклиматическое исполнение (В). Также различают категории размещения (на открытом воздухе, под навесом или в помещении и т.д.).

Класс защиты обозначает характер защиты двигателя от попадания пыли и влаги. Наиболее часто встречаются приводы с классами IP55 и IP55.

10. Зачем электродвигателю тормоз?

В некоторых устройствах (лифтах, электроталях, лебедках) при остановке двигателя необходимо зафиксировать его вал в неподвижном состоянии. Для этого применяют электромагнитный механический тормоз, который входит в конструкцию двигателя и располагается в его задней части. Управление тормозом осуществляется с помощью частотного преобразователя или схемы на контакторах.

11. Как двигатель обозначается на электрических схемах?

Электродвигатель обозначается на схемах с помощью буквы «М», вписанной в круг. Также на схемах могут быть указаны порядковый номер двигателя, количество фаз (1 или 3), род тока (переменный или постоянный), способ включения обмоток ( «звезда» или «треугольник»), мощность. Примеры обозначений показаны ниже.

12. Почему греется электродвигатель?

Двигатель может нагреваться по одной из следующих причин:

• износ подшипников и повышенное механическое трение
• увеличение нагрузки на валу
• перекос напряжения питания
• пропадание фазы
• замыкание в обмотке
• проблема с обдувом (охлаждением)

Нагрев двигателя резко снижает его ресурс и КПД, а также может приводить к поломке привода.

1. 13. Типичные неисправности электродвигателей
2. Выделяют два вида неисправностей электродвигателей: электрические и механические.
3. К электрическим относятся неисправности, связанные с обмоткой:

• межвитковое замыкание
• замыкание обмотки на корпус
• обрыв обмотки

Для устранения этих неисправностей требуется перемотка двигателя.

Механические неисправности:

• износ и трение в подшипниках
• проворачивание ротора на валу
• повреждение корпуса двигателя
• проворачивание или повреждение крыльчатки обдува

Замена подшипников должна производиться регулярно с учетом их износа и срока службы. Крыльчатка также меняется в случае повреждения. Остальные неисправности устранению практически не подлежат, и единственный выход — замена двигателя.

Если у вас есть вопросы, ответы на которые вы не нашли в данной статье, напишите нам. Будем рады помочь!

Другие полезные материалы: Выбор электродвигателя Использование тормозных резисторов с преобразователями частоты

Что следует учитывать при выборе асинхронного электродвигателя

При выборе асинхронных электродвигателей переменного тока часто не учитываются требования к конструкции, которые связаны с их применением в составе того или иного оборудования.

Также обычно имеет место подход, основанный на универсальности электродвигателя, и тогда выбор зависит только от его напряжения, мощности и скорости вращения ротора.

Тем не менее есть еще целый ряд дополнительных аспектов для рассмотрения, таких как диапазон напряжения питания, сохранение номинальной мощности при изменении скорости вращения и область применения. Все это в итоге сводится к решению следующих вопросов: какова цель применения электродвигателя, как сделать все быстрее и эффективнее?

Базовые принципы выбора электродвигателя

Отправными точками для выбора асинхронного двигателя являются напряжение питания обмоток статора, создающего магнитное поле, а также номинальная мощность и скорость вращения ротора, которые соответствуют требованиям конкретного применения.

Еще один, не менее важный момент — это необходимый вариант установки двигателя в приводе.

Должен ли двигатель иметь крепление на основании, или он будет помещен на фланец на конце привода, или же должен предоставлять обе возможности? Кроме того, необходимо учитывать характеристики окружающей среды, в которой будет эксплуатироваться двигатель.

При этом для выбора двигателя необходимо знать, потребуется ли ему работать под дождем и имеется ли вообще риск попадания на него воды, а также оценить уровень загрязнения и наличия пыли. Для эксплуатации в жестких условиях хорошо подходят электродвигатели закрытого типа с вентиляторным охлаждением (англ.

totally enclosed fan cooled, TEFC) или электродвигатели закрытого типа без охлаждения (англ. totally enclosed non-vented, TENV). Если среда, в которой будет использоваться двигатель, не загрязнена и он будет эксплуатироваться без риска попадания на него воды, то в этом случае может быть достаточно применения каплезащищенного электродвигателя открытого исполнения (англ. open drip proof, ODP).

Выбор инвертора

Благодаря усилиям лоббистов местных энергетических компаний в сочетании с преимуществами, получаемыми при возможности регулирования скорости вращения ротора двигателей, все более распространенными становятся частотно-регулируемые приводы (ЧРП, англ. variable frequency drive, VFD).

При их использовании особое внимание следует уделять генерации электромагнитных помех, которая характерна для таких приводов исходя из самой их природы.

Для того чтобы электродвигатель мог использоваться с ЧРП, необходимо учитывать несколько технических особенностей, которым должен удовлетворять подходящий по остальным характеристикам электродвигатель. Среди них можно выделить две главные:

Максимально допустимое напряжение изоляции обмоточных проводов статора электродвигателя.

Электрическая прочность изоляции провода, из которого выполнена обмотка статора асинхронного электродвигателя, находится в пределах 1000–1600 В, но, как правило, в документации указывается значение прочности изоляции, равное 1200 В.

Однако чем больше воздушный зазор между приводом и двигателем, тем, естественно, бо́льшим скачкам переходного напряжения, воздействующим на двигатель, он может противостоять.

Электродвигатель, в котором для обмотки статора используется провод с электрической прочностью изоляции провода, равной 1600 В, может иметь ссылку на стандарт Национальной ассоциации производителей электрооборудования (NEMA, США) NEMA MG-1 2003, раздел 4, параграф 31, в котором говорится, что двигатель должен выдерживать без повреждений начальное напряжение коронного разряда (англ. corona inception voltage, CIV) уровнем до 1600 В.

Коэффициент сохранения постоянного крутящего момента (CT) двигателя, часто упоминается как «xx: 1 CT».

Этот показатель дает представление о диапазоне регулирования скорости.

По нему можно узнать, насколько может быть снижена скорость вращения ротора двигателя, при которой он будет работать с сохранением того же крутящего момента (англ.

CT — constant torque, постоянный крутящий момент), что и при номинальной скорости. Ниже этого значения крутящего момента производительность асинхронного электродвигателя снижается.

При этом необходимо учитывать еще один нюанс, который связан с охлаждением электродвигателя. Нужно обязательно уточнить у поставщика, будет ли электродвигатель перегреваться при длительной работе на малых оборотах.

Дело в том, что если двигатель охлаждается за счет крыльчатки, закрепленной на его валу, то на малых скоростях вы столкнетесь с низкой скоростью охлаждающего двигатель потока воздуха.

Если асинхронный электродвигатель работает на низкой скорости и в течение длительного времени используется с большим крутящим моментом, то он будет выделять много тепла — при таких условиях, возможно, придется остановить свой выбор на двигателе с иным методом охлаждения.

Например, для организации принудительного охлаждения можно применить воздуходувное устройство, имеющее собственный, отдельно управляемый двигатель.

Производительность такого устройства не связана с системой управления электропривода.

В этом случае воздушный поток, который обдувает мощный электродвигатель, будет постоянным и достаточным для его охлаждения при низкой или даже при нулевой скорости.

Связь мощности и крутящего момента

При выборе асинхронного электродвигателя еще одним важным аспектом является номинальная, или основная, скорость двигателя. Обычно используются двухполюсные (3600 об/мин) и четырехполюсные (1800 об/мин) электродвигатели.

Однако имеются и коммерчески доступные 6-, 8- и 12-полюсные асинхронные электродвигатели со скоростью вращения ротора 1200, 900
и 600 об/мин соответственно.

Номинальная скорость асинхронного электродвигателя напрямую связана с числом полюсов, которые такой двигатель конструктивно содержит (табл.), и определяется по следующей формуле:

Об/мин = (120 × частота) / N (число полюсов)

В качестве примечания необходимо отметить, что, хотя прямой связи здесь нет, но, как правило, с увеличением количества полюсов возрастают и размеры, а также стоимость электропривода.

Кроме того, пользователям электроприводов, в зависимости от области применения данных устройств, может понадобиться обеспечить необходимый крутящий момент путем изменения скорости. В целом по мере увеличения скорости двигателя крутящий момент уменьшается, что также относится к редукторам и цепным приводам. Это соотношение объясняется следующим уравнением:

мощность (л. с.) = (крутящий момент × × номинальная скорость) / 5252

Крутящий момент, в соответствии с заданной целью, может быть достигнут путем выбора электродвигателя с необходимой мощностью и номинальной скоростью и реализован через любую цепную, ременную передачу или редуктор. Такой подход снижает стоимость привода, его габаритные размеры и время, уходящее на замену его подвижных заменяемых частей в ходе выполнения ремонта или технического обслуживания.

Таблица. Связь между числом полюсов, скоростью (об/мин) и крутящим моментом асинхронного электродвигателя

Число полюсов, N	Скорость, об/мин	Крутящий момент, л. с. / фут-фунт
2	3600	1,46
4	1800	2,92
6	1200	4,38
8	900	5,84
10	720	7,29
12	600	8,75

Примечание. Как правило, увеличение числа полюсов приводит к увеличению габаритов, а следовательно, и к повышению стоимости привода на основе асинхронного электродвигателя

Как определить мощность и обороты электродвигателя без бирки?

При замене сломанного советского электродвигателя на новый, часто оказывается, что на нем нет шильдика. Нам часто задают вопросы: как узнать мощность электродвигателя? Как определить обороты двигателя? В этой статье мы рассмотрим, как определить параметры электродвигателя без бирки — по диаметру вала, размерам, току.

Как определить мощность?

Существует несколько способов определения мощности электродвигателя: диаметру вала, по габариту и длине, по току и сопротивлению, замеру счетчиком электроэнергии.

По габаритным размерам

Все электродвигатели отличаются по габаритным размерам. Определить мощность двигателя можно сравнив габаритные размеры с таблицей определения мощности электродвигателя, перейдя по ссылке габаритно-присоединительные размеры электродвигателей АИР.

• Длина, ширина, высота корпуса
• Расстояние от центра вала до пола
• Длина и диаметр вала
• Крепежные размеры по лапам (фланцу)

По диаметру вала

Определение мощности электродвигателя по диаметру вала — частый запрос для поисковых систем. Но для точного определения этого параметра недостаточно – два двигателя в одном габарите, с одинаковыми валами и частотой вращения могут иметь различную мощность.

Таблица с привязкой диаметров валов к мощности и оборотам для двигателей АИР и 4АМ.

Мощность электродвигателя Р, кВт	Диаметр вала, мм	Переход к модели
3000 об/мин	1500 об/мин	1000 об/мин	750 об/мин
0,18	11	11	14	—	АИР56А2, АИР56В4, АИР63А6
0,25	14	19	АИР56В2, АИР63А4, АИР63В6, АИР71В8
0,37	14	19	22	АИР63А2, АИР63В4, АИР71А6, АИР80А8
0,55	19	АИР63В2, АИР71А4, АИР71В6, АИР80В8
0,75	19	22	24	АИР71А2, АИР71В4, АИР80А6, АИР90LA8
1,1	22	АИР71В2, АИР80А4, АИР80В6, АИР90LB8
1,5	22	24	28	АИР80А2, АИР80В4, АИР90L6, АИР100L8
2,2	24	28	32	АИР80В2, АИР90L4, АИР100L6, АИР112МА8
3	24	32	АИР90L2, АИР100S4, АИР112МА6, АИР112МВ8
4	28	28	38	АИР100S2, АИР100L4, АИР112МВ6, АИР132S8
5,5	32	38	АИР100L2, АИР112М4, АИР132S6, АИР132М8
7,5	32	38	48	АИР112M2, АИР132S4, АИР132М6, АИР160S8
11	38	48	АИР132M2, АИР132М4, АИР160S6, АИР160М8
15	42	48	55	АИР160S2, АИР160S4, АИР160М6, АИР180М8
18,5	55	60	АИР160M2, АИР160M4, АИР180М6, АИР200М8
22	48	55	60	АИР180S2, АИР180S4, АИР200М6, АИР200L8
30	65	АИР180M2, АИР180M4, АИР200L6, АИР225М8
37	55	60	65	75	АИР200M2, АИР200M4, АИР225М6, АИР250S8
45	75	75	АИР200L2, АИР200L4, АИР250S6, АИР250M8
55	65	80	АИР225M2, АИР225M4, АИР250M6, АИР280S8
75	65	75	80	АИР250S2, АИР250S4, АИР280S6, АИР280M8
90	90	АИР250М2, АИР250M4, АИР280M6, АИР315S8
110	70	80	90	АИР280S2, АИР280S4, АИР315S6, АИР315M8
132	100	АИР280M2, АИР280M4, АИР315M6, АИР355S8
160	75	90	100	АИР315S2, АИР315S4, АИР355S6
200	АИР315M2, АИР315M4, АИР355M6
250	85	100	АИР355S2, АИР355S4
315	—	АИР355M2, АИР355M4

По показанию счетчика

Как правило измерение счетчика отображаются в киловаттах (далее кВт). Для точности измерения стоит отключить все электроприборы или воспользоваться портативным счетчиком. Мощность электродвигателя 2,2 кВт, подразумевает что он потребляет 2,2 кВт электроэнергии в час.

Для измерения мощности по показанию счетчика нужно:

1. Подключить мотор и дать ему поработать в течении 6 минут.
2. Замеры счетчика умножить на 10 – получаем точную мощность электромотора.

Расчет мощности по току

• P – мощность электродвигателя;
• U – напряжение;
• Ia – ток 1 фазы;
• Ib – 2 фазы;
• Ic – 3 фазы.

Определение оборотов вала

Асинхронные трехфазные двигатели по частоте вращения ротора делятся 4 типа: 3000, 1500, 1000 и 750 об. мин. Приводим пример маркировки на основании АИР 180:

Самый простой способ определить количество оборотов трехфазного асинхронного электродвигателя – снять задний кожух и посмотреть обмотку статора.

У двигателя на 3000 об/мин катушка обмотки статора занимает половину окружности — 180 °, то есть начало и конец секции параллельны друг другу и перпендикулярны центру. У электромоторов 1500 оборотов угол равен 120 °, у 1000 – 90 °. Схематический вид катушек изображен на чертеже. Все обмоточные данные двигателей смотрите в таблице.

Узнать частоту вращения с помощью амперметра

Узнать обороты вала двигателя, можно посчитав количество полюсов. Для этого нам понадобится миллиамперметр — подключаем измерительный прибор к обмотке статора. При вращении вала двигателя стрелка амперметра будет отклонятся. Число отклонений стрелки за один оборот – равно количеству полюсов.

Если не получилось узнать мощность и обороты

Если не получилось узнать мощность и обороты электродвигатели или вы не уверены в измерениях – обращайтесь к специалистам «Систем Качества». Наши специалисты помогут подобрать нужный мотор или провести ремонт сломанного электродвигателя АИР.

Что такое угловая скорость

​Угловая скорость (обозначается как (omega)) — векторная величина, характеризующая скорость и направление изменения угла поворота со временем.

Модуль угловой скорости для вращательного движения совпадает с мгновенной угловой частотой вращения, а направление перпендикулярно плоскости вращения и связано с направлением вращения правилом правого винта.

Единица измерения

В Международной системе единиц (СИ) принятой единицей измерения угловой скорости является радиан в секунду (рад/с)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Формула угловой скорости

Вектор угловой скорости определяется отношением угла поворота ((varphi)) к интервалу времени ((mathcal t)), за которое произошел поворот:

(omega=frac{trianglevarphi}{trianglemathcal t})

Зависимость угловой скорости от времени

Зависимость (varphi ) от (mathcal t) наглядно показана на графике:

Угол, на который повернулось тело, характеризуется площадью под кривой.

Угловая скорость вращения, формула

Через частоту

(omega=2pimathcal n)

(mathcal n) — частота вращения ((1/с))

(pi) — число Пи ((approx 3,14))

(mathcal n=frac1T)

(T )— период вращения (время, за которое тело совершает один оборот)

Через радиус

(omega=frac vR)

(v) — линейная скорость(м/с)

(R) — радиус окружности (м)

Как определить направление угловой скорости

Направление скорости в физике можно определять двумя способами:

1. Правило буравчика. Буравчик имеет правую резьбу (вращательное движение вправо при закручивании). Если вращать буравчик в направлении вращения тела, он будет завинчиваться (или вывинчиваться) в ту сторону, куда направлена угловая скорость. 
2. Правило правой руки. Представим, что взяли тело в правую руку. Следует направлять и вращать его туда, куда указывают четыре пальца. Отведенный в сторону большой палец покажет направление угловой скорости при этом вращении.

Связь линейной и угловой скорости

Линейная скорость ((v)) тела, расположенного на расстоянии (R) от оси вращения, прямо пропорциональна угловой скорости.

(v=Romega)

(R) — радиус окружности (м)

Чему равна мгновенная угловая скорость

Мгновенную угловую скорость нужно находить как предел, к которому стремится средняя угловая скорость при (trianglemathcal trightarrow0) :

(omega=lim_{trianglerightarrow0}frac{trianglevarphi}{trianglemathcal t})

Измеряется в рад/с

Решил подкреплять статьи наглядными примерами для расчетов:

Пример 1:
Двигатель вращается с частотой 3000 об/минуту. Рассчитать угловую скорость вращения коленчатого вала двигателя.

Решение:
За одну секунду коленчатый вал совершает 3000/60 оборотов/с = 50 об/с.
1 оборот = 2п рад.
w = 2п рад/об * 50 об/с = 100п рад/с = 314 рад/с

Ответ: 314 рад/с

Пример 2:
Два автомобиля подняли обороты на старте до значения 3000 об/минуту. Вычислить скорость движения поршней двигателей 2JZ-GTE и М30В34 в положении, когда угол поворота коленчатого вала составляет 45 градусов от ВМТ. Известно, что ход поршня у обоих двигателей составляет 86 мм, а длины шатунов 142 мм и 135 соответственно.

Решение:
w = 314 рад/с
r = 86 мм / 2 = 43 мм = 0,043 м
v (2JZ-GTE, 45 градусов, 3000 об/минуту) = 314 * 0,043 *{ sin (п/4) + sin (п/2) * 0,043 / (2*0,142)} = 13,502 * {0,707 + 1 * 0,1514) = 13,502 * 0,85 = 11,49 м/с
v (М30В34, 45 градусов, 3000 об/минуту) = 314 * 0,043 *{ sin (п/4) + sin (п/2) * 0,043 / (2*0,135)} = 13,502 * {0,707 + 1 * 0,159) = 13,502 * 0,866 = 11,69 м/с

Ответ: v (2JZ-GTE) = 11,49 м/с, v (M30B34) = 11,69 м/с

Пример 3:
Двигатель М30В28 имеет максимальное значение крутящего момента при 4200 об/мин. Вычислить максимальное значение скорости поршня на этих оборотах, если ход поршня составляет 80 мм, а длина шатуна 135 мм:

Пиковое значение скорости достигается в экстремумах ускорения, т.е. когда а = 0.

Т.к. w = const, то е = 0, а следовательно и вся вторая часть уравнения для ускорения равна 0,

тогда пиковое значение скорости достигается, когда

w^2 * r * { cosф + cos2ф * r / l } = 0

w = 2п * 4200 / 60 = 440 рад/с
r = 0,08м / 2 = 0,04 м
l = 0,135 м

Решим уравнение и найдем ф:
440^2 * 0,04 * { cosф + cos2ф * 0,04 / 0,135 } = 0
7744 * (cosф + cos2ф * 0,29) = 0
cosф = — 0,29 cos2ф
cosф = — 0,29 *{2(cosф)^2 -1}
0,58*(cosф)^2 + cosф — 0,29 = 0

Обозначим cosф как х, тогда

0,58 х^2 + x — 0,29 = 0
D = 1 + 4*0,58*0,29 = 1,6728
х1 = (- 1 + 1,6728) / (2 * 0,58) = 0,6728 / 1,16 = 0,58
х2 = (- 1 — 1,6728) / (2 * 0,58) = 2,304

Т.к. х2 > 1, cosф = 0,58 или ф = 0,952 рад

v (М30В28, 0,952 рад, 4200 об/минуту) = 440 * 0,04 *{ sin (0,952) + sin (1,904) * 0,04 / (2*0,135)} = 17,6 * {0,814 + 0,945 * 0,148) = 17,6 * 0,954 = 16,79 м/с

Ответ: 16,79 м/с

Аналогично можете подставить данные своего мотора и решать подобного рода типовые задачи;)

На сим все!

Продолжение следует;)