Как найти линейную и угловую скорости движения точек экватора Земли по ее радиусу? Объясните как можно подробнее.
Для решения этой типовой задачи нам понадобятся две вещи: радиус окружности и период обращения точки по ней. В самой задаче этих данных, конечно же, нет, но подразумевается, что они нам известны. Ну или будут известны, когда мы найдем учебник или, еще лучше, спросим у гугла.
Итак, экваториальный радиус Земли – 6370 км, а период вращения вокруг своей оси – 24 часа.
Формулу линейной скорости выведем так: Если радиус равен RR, то точка за один оборот пройдет путь, равный длине окружности, т.е. равный 2πR2πR. Почему так? Ответ в геометрии за седьмой класс.
Далее. Путь этот она пройдет за время, равное периоду TT, а значит v=2πR/Tv = 2πR/T.
Ну а что такое угловая скорость? Это отношение угла поворота ко времени, за которое поворот совершен.
Полный оборот по окружности составляет 2π2π радиан по определению. Угловая скорость зависит от периода вращения, следовательно ω=2π/Tω = 2π/T. К сожалению, эта формула только для равномерного движения. К счастью, это наш случай.
Подставим известные величины в формулы и получим:
v=2πR/T=2⋅3.1415⋅6370⋅103м/24⋅602с=40022710м/86400с=463.22v = 2πR/T = 2 cdot 3.1415 cdot6370cdot10^3 м/ 24 cdot60^2 с = 40 022 710м/86 400с = 463.22м/с
ω=2⋅3.1415/24⋅602с=6.283рад/86400с=7,27⋅10−5ω = 2 cdot 3.1415/24cdot 60^2 с = 6.283рад/86 400с = 7,27cdot10^{-5} рад/с
Ответ: ν=463.22ν = 463.22 м/с, w=7,27⋅10−5w = 7,27cdot10^{-5} рад/с.
Теги: физика, механика, кинематика, вращение, задача
Тест по теме “Скорость движения точек экватора Земли”
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки
Быстрое выполнение от 2 часов
Проверка работы на плагиат
С какой скоростью вращается Земля вокруг своей оси? Не для кого не секрет, что смена дня и ночи технически вызвана вращением Земли. Но вам когда-нибудь приходило в голову с какой скоростью она вращается? И как посчитать эту скорость?
Если говорить о равномерном движении по окружности, можно выделить две скорости: угловую (ω) и линейную (v). Давайте найдем и ту, и другую для нашей прекрасной голубой планеты.
Угловая скорость вращения Земли
Угловая скорость определяет то, как быстро изменяется угол с течением в времени. Так как один полный оборот соответствует углу в 360о или 2π, а время, за которое он совершается есть период Т, то угловую скорость можно выразить как:
На всякий случай. Чтобы не было вопросов откуда берется 2π.
Один радиан соответствует углу с дугою равной радиусу. Соответственно чтобы посчитать количество радиан в окружности нам необходимо ее длину то есть 2πR, поделить на радиус R. R и R сокращаем и получаем 2π. Или приближенно 6.28.
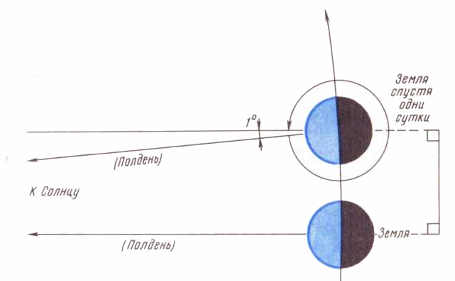
Мы знаем, что в сутках 24 часа, а, следовательно, можно предположить, что период обращения Земли вокруг своей оси Т составит так же 24 часа. Но не торопитесь переводить это время в секунды и подставлять в уравнение, записанное выше. Так как Земля вращается еще вокруг солнца, то период обращения её вокруг собственной оси будет немного короче привычных нам солнечных суток и составит 23 часа 56 минут и 4 секунды. Это так называемые звездные сутки. В пересчете на секунды мы получаем: Т=86164 с.
Теперь можно найти угловую скорость:
Линейная скорость вращения Земли
Если говорить об угловой скорости, то она одинакова для любой точки нашей планеты. И не важно: пингвин в Антарктике, слон в Африке или Вы у себя дома, все будут иметь одинаковую угловую скорость. Но когда речь заходит о скорости линейной, то тут все наоборот. Она будет максимальна на экваторе и убывать к полюсам, так как напрямую зависит от радиуса окружности вращения. А это значит, что если вы залезете на табуретку вкрутить лампочку, то ваша линейная скорость увеличится. Строго говоря, линейная скорость описывает скорее не вращение Земли вокруг своей оси, она описывает вращение каких то отдельных её точек.
Рассчитать линейную скорость очень просто. По определению, скорость — это отношение пройденного пути ко времени, за которое этот путь был совершен. Если за один оборот мы проходим путь, равный длине окружности, а время движения будет ни что иное как период обращения Т, то, выразив длину окружности из известной школьной формулы: L= 2πR, мы получим уравнение для расчета линейной скорости:
Так как угловая скорость , то мы можем смело записать:
Радиус земли на экваторе R = 6378245 м, а значит линейная скорость там будет равна: м/с.
Для сравнения скорость звука в воздухе составляет 365 м/с. А это значит, что, сидя спокойно на стульчике где-нибудь в Африке или Индонезии мы будем двигаться со скоростями, превышающими звук. Если перевести эту величину в километры в час, то получится 1674 км/ч!!! В общем скорости сопоставимые со скоростями сверхзвуковой авиации.
Линейная скорость в зависимости от широты
Но это на экваторе. Ближе к полюсам, как я уже говорил, значение будет ниже. Так как радиус вращения будет снижаться.
Для того чтоб найти радиус вращения на той или иной широте. Необходимо косинус этой широты умножить на земной радиус.
К примеру, для Санкт-Петербурга соответствует шестидесятая северная широта. Косинус шестидесяти градусов как известно одна вторая. То есть радиус вращения будет вдвое меньше земного, а значит и линейная скорость будет так же в два раза меньше экваториальной, всего 837 км/ч.
А с какой линейной скоростью вращаетесь Вы??? Ответы можете писать в комментариях, а я с Вами прощаюсь. Всего хорошего, до скорых встреч.
Содержание:
- Определение и формула угловой скорости
- Равномерное вращение
- Формула, связывающая линейную и угловую скорости
- Единицы измерения угловой скорости
- Примеры решения задач
Определение и формула угловой скорости
Определение
Круговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность
с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.
Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.
Перемещение при вращении характеризуют при помощи угла поворота
$(varphi)$ . Часто используют вектор элементарного поворота
$bar{dvarphi}$ , который равен по величине элементарному углу поворота тела
$(d varphi)$ за маленький отрезок времени dt и направлен по мгновенной оси вращения в сторону,
откуда этот поворот виден реализующимся против часовой стрелки. Надо отметить, что только элементарные угловые перемещения являются векторами.
Углы вращения на конечные величины векторами не являются.
Определение
Угловой скоростью называют скорость изменения угла поворота и обозначают ее обычно буквой
$omega$ . Математически определение угловой скорости записывают так:
$$bar{omega}=frac{d bar{varphi}}{d t}=dot{bar{varphi}}(1)$$
Угловая скорость – векторная величина (это аксиальный вектор). Она имеет направление вдоль мгновенной оси вращения совпадающее
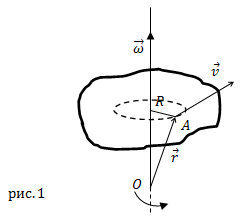
с направлением поступательного правого винта, если его вращать в сторону вращения тела (рис.1).
Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости),
так и за счет поворота оси вращения в пространстве ($bar{omega}$ при этом изменяет направление).
Равномерное вращение
Если тело за равные промежутки времени поворачивается на один и тот же угол,
то такое вращение называют равномерным. При этом модуль угловой скорости находят как:
$$omega=frac{varphi}{t}(2)$$
где $(varphi)$ – угол поворота, t – время, за которое этот поворот совершён.
Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот
($Delta varphi=2 pi$). Угловая скорость связана с периодом обращения как:
$$omega=frac{2 pi}{T}(3)$$
С числом оборотов в единицу времени ($nu) угловая скорость связана формулой:
$$omega=2 pi nu(4)$$
Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения,
но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно
с данной мгновенной величиной скорости.
Формула, связывающая линейную и угловую скорости
Линейная скорость $bar{v}$ точки А (рис.1), которая расположена
на расстоянии R от оси вращения связана с вектором угловой скорости следующим векторным произведением:
$$bar{v}=[bar{omega} bar{R}](5)$$
где $bar{R}$ – перпендикулярная к оси вращения компонента радиус-вектора точки
$A (bar{r})$ (рис.1). Вектор
$bar{r}$ проводят от точки, находящейся на оси вращения к рассматриваемой точке.
Единицы измерения угловой скорости
Основной единицей измерения угловой скорости в системе СИ является: [$omega$]=рад/с
В СГС: [$omega$]=рад/с
Примеры решения задач
Пример
Задание. Движение тела с неподвижной осью задано уравнением
$varphi=2 t-4 t^{3}$,
$(varphi)$ в рад, t в сек.
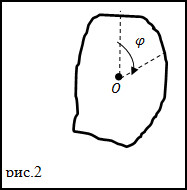
Начало вращения при t=0 c. Положительным считают углы указанные направлением стрелки (рис.2). В каком направлении (
относительно часовой стрелки поворачивается тело) в момент времени t=0,5 c.
Решение. Для нахождения модуля угловой скорости применим формулу:
$$omega=frac{d varphi}{d t}(1.1)$$
Используем заданную в условии задачи функцию
$varphi(t)$, возьмем производную от нее по времени, получим функцию
$omega(t)$:
$$omega(t)=2-8 t^{2}(1.2)$$
Вычислим, чему будет равна угловая скорость в заданный момент времени (при t=0,5 c):
$$omega(t)=2-8(0,5)^{2}=0left(frac{r a d}{c}right)$$
Ответ. В заданный момент времени тело имеет угловую скорость равную нулю, следовательно, она останавливается.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Скорости вращения тела заданы системой уравнений:
$$left{begin{array}{c}bar{omega}_{1}=t^{2 bar{i}} \ bar{omega}_{2}=2 t^{2} bar{j}end{array}right.$$
где $bar{i}$ и
$bar{j}$ – единичные ортогональные векторы. На какой угол $(varphi)$ поворачивается тело за время равное 3 с?
Решение. Определим, какова функция, которая связывает модуль скорости вращения тела и время (t)
($omega(t)$). Так как вектора
$bar{i}$ и
$bar{j}$ перпендикулярны друг другу, значит:
$$omega=sqrt{omega_{1}^{2}+omega_{2}^{2}}=sqrt{left(t^{2}right)^{2}+left(2 t^{2}right)^{2}}=t^{2} sqrt{5}(2.2)$$
Модуль угловой скорости связан с углом поворота как:
$$omega=frac{d varphi}{d t}(2.3)$$
Следовательно, угол поворота найдем как:
$$varphi=int_{t_{1}}^{t_{2}} omega d t=int_{0}^{3} t^{2} sqrt{5} d t=left.sqrt{5} frac{t^{3}}{3}right|_{0} ^{3} approx 20(mathrm{rad})$$
Ответ. $varphi = 20$ рад.
Читать дальше: Формула удельного веса.
как вычислить линейную и угловую скорость вращение точки, находящая на экваторе?
Ученик
(161),
закрыт
4 года назад
Дарья Чарикова
Просветленный
(34703)
12 лет назад
начнем с угловой.. . земля делает полный оборот (2*пи радиан) вокруг своей оси за 24 часа = 24*60минут=24*3600 секунд. Следовательно угловая скорость любой точки Земли (и точки на экваторе в том числе) 2*пи/24/3600 радиан/сек.
Линейная скорость точки на экваторе = угловая скорость * радиус Земли.
радиус Земли примерно равен 6400км=6400 000м
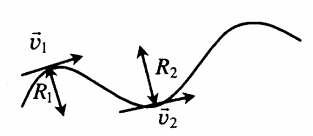
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Линейная и угловая скорости
Линейная скорость
Определение и формулы
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
Определение и формулы
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Полезные факты
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
Полезные факты
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Определение и формула
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с2). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙103 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙106. Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Задание EF18273
Верхнюю точку моста радиусом 100 м автомобиль проходит со скоростью 20 м/с. Центростремительное ускорение автомобиля равно…
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
Ответ: 4
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17763
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза
б) уменьшить в 2 раза
в) увеличить в 4 раза
г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
- Радиус окружности R1 = R.
- Радиус окружности R2 = 4R.
- Центростремительное ускорение: aц.с. = a1 = a2.
Найти нужно ν2.
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Или:
Отсюда:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 21.6k