С какой скоростью вращается Земля вокруг своей оси? Не для кого не секрет, что смена дня и ночи технически вызвана вращением Земли. Но вам когда-нибудь приходило в голову с какой скоростью она вращается? И как посчитать эту скорость?
Если говорить о равномерном движении по окружности, можно выделить две скорости: угловую (ω) и линейную (v). Давайте найдем и ту, и другую для нашей прекрасной голубой планеты.
Угловая скорость вращения Земли
Угловая скорость определяет то, как быстро изменяется угол с течением в времени. Так как один полный оборот соответствует углу в 360о или 2π, а время, за которое он совершается есть период Т, то угловую скорость можно выразить как:
![]()
На всякий случай. Чтобы не было вопросов откуда берется 2π.
Один радиан соответствует углу с дугою равной радиусу. Соответственно чтобы посчитать количество радиан в окружности нам необходимо ее длину то есть 2πR, поделить на радиус R. R и R сокращаем и получаем 2π. Или приближенно 6.28.
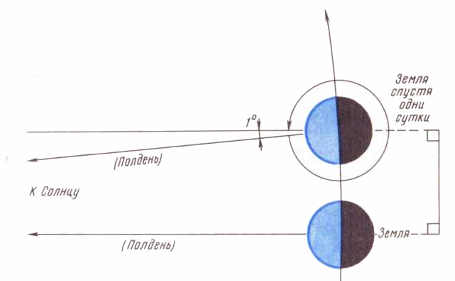
Мы знаем, что в сутках 24 часа, а, следовательно, можно предположить, что период обращения Земли вокруг своей оси Т составит так же 24 часа. Но не торопитесь переводить это время в секунды и подставлять в уравнение, записанное выше. Так как Земля вращается еще вокруг солнца, то период обращения её вокруг собственной оси будет немного короче привычных нам солнечных суток и составит 23 часа 56 минут и 4 секунды. Это так называемые звездные сутки. В пересчете на секунды мы получаем: Т=86164 с.
Теперь можно найти угловую скорость:
![]()
Линейная скорость вращения Земли
Если говорить об угловой скорости, то она одинакова для любой точки нашей планеты. И не важно: пингвин в Антарктике, слон в Африке или Вы у себя дома, все будут иметь одинаковую угловую скорость. Но когда речь заходит о скорости линейной, то тут все наоборот. Она будет максимальна на экваторе и убывать к полюсам, так как напрямую зависит от радиуса окружности вращения. А это значит, что если вы залезете на табуретку вкрутить лампочку, то ваша линейная скорость увеличится. Строго говоря, линейная скорость описывает скорее не вращение Земли вокруг своей оси, она описывает вращение каких то отдельных её точек.
Рассчитать линейную скорость очень просто. По определению, скорость — это отношение пройденного пути ко времени, за которое этот путь был совершен. Если за один оборот мы проходим путь, равный длине окружности, а время движения будет ни что иное как период обращения Т, то, выразив длину окружности из известной школьной формулы: L= 2πR, мы получим уравнение для расчета линейной скорости:
![]()
Так как угловая скорость ![]() , то мы можем смело записать:
, то мы можем смело записать:
![]()
Радиус земли на экваторе R = 6378245 м, а значит линейная скорость там будет равна:![]() м/с.
м/с.
Для сравнения скорость звука в воздухе составляет 365 м/с. А это значит, что, сидя спокойно на стульчике где-нибудь в Африке или Индонезии мы будем двигаться со скоростями, превышающими звук. Если перевести эту величину в километры в час, то получится 1674 км/ч!!! В общем скорости сопоставимые со скоростями сверхзвуковой авиации.

Линейная скорость в зависимости от широты
Но это на экваторе. Ближе к полюсам, как я уже говорил, значение будет ниже. Так как радиус вращения будет снижаться.
Для того чтоб найти радиус вращения на той или иной широте. Необходимо косинус этой широты умножить на земной радиус.
К примеру, для Санкт-Петербурга соответствует шестидесятая северная широта. Косинус шестидесяти градусов как известно одна вторая. То есть радиус вращения будет вдвое меньше земного, а значит и линейная скорость будет так же в два раза меньше экваториальной, всего 837 км/ч.
А с какой линейной скоростью вращаетесь Вы??? Ответы можете писать в комментариях, а я с Вами прощаюсь. Всего хорошего, до скорых встреч.
Содержание
- Как рассчитать угловую скорость планеты?
- Что такое угловая скорость?
- Как рассчитать угловую скорость планеты?
- Общий итог
- Как рассчитать угловую скорость планеты
- Что такое угловая скорость?
- Как рассчитать угловую скорость планеты?
- Пример расчета угловой скорости
- Выводы
- Как рассчитать угловую скорость планеты
- Что такое угловая скорость
- Рассчет угловой скорости планеты
- Заключение
Как рассчитать угловую скорость планеты?
Угловая скорость — это скорость, с которой тело вращается вокруг собственной оси. На земле угловая скорость варьируется в зависимости от широты и составляет около 360 градусов в 24 часа. Но как посчитать угловую скорость другой планеты? Обсудим это подробнее.
Что такое угловая скорость?
Угловая скорость — это физическая величина, которая характеризует скорость вращения тела вокруг своей оси. Она измеряется в радианах в секунду и равна отношению угла поворота к времени, за которое это произошло. Также угловая скорость может быть выражена через линейную скорость и радиус вращения по формуле:
ω = v/r

где:
- ω — угловая скорость,
- v — линейная скорость,
- r — радиус вращения.
Как рассчитать угловую скорость планеты?
Рассчитать угловую скорость планеты можно, зная ее период вращения вокруг своей оси и диаметр. Формула для расчета угловой скорости выглядит так:
ω = 2π/T = V/R
где:
- ω — угловая скорость,
- π — число «пи», равное 3,14,
- T — период вращения планеты в секундах,
- V — объем планеты,
- R — радиус планеты.
Для расчета угловой скорости планеты можно использовать данные из астрономических таблиц. Например, период вращения Земли вокруг своей оси составляет 23 часа 56 минут 4,09053 секунды. Для расчета нужно привести это значение к секундам:
TЗемли = 23 x 3600 + 56 x 60 + 4,09053 = 86164,09053 сек.
Диаметр Земли равен 12756 километров, что составляет 12756000 метров. Радиус Земли будет равен:
R = d/2 = 12756000/2 = 6378000 метров
Подставляя значения в формулу, получим:
ωЗемли = 2 x π / 86164,09053 = 7,29211 x 10ˉ⁵ рад/с
Таким же образом можно рассчитать угловую скорость любой другой планеты. Ниже приведены некоторые данные по периодам вращения и диаметрам планет нашей Солнечной системы:
- Меркурий: период вращения 58,6462 дней, диаметр 4879,4 км.
- Венера: период вращения 243,0185 земных суток, диаметр 12104 км.
- Марс: период вращения 24,62296 земных часов, диаметр 6792 км.
- Юпитер: период вращения 9 часов 56 минут 35,244 секунды, диаметр 143 000 км.
- Сатурн: период вращения 10 часов 39 минут 22,4 секунды, диаметр 120 000 км.
- Уран: период вращения 17 часов 14 минут 24 секунды, диаметр 51 118 км.
- Нептун: период вращения 16 часов 6 минут 36 секунд, диаметр 49 528 км.

Для расчета угловой скорости планеты необходимо привести период вращения к секундам и выразить угловую скорость через радиус. Например, для расчета угловой скорости Юпитера используем формулу:
ωЮпитер = 2 × π ÷ (9 × 60 × 60 + 56 × 60 + 35,244) × (143000 ÷ 2) ≈ 0,000077 раз/с
Общий итог
Рассчитать угловую скорость планеты исходя из данных о ее диаметре и периоде вращения вокруг своей оси не сложно. Для этого необходимо использовать соответствующую формулу. Однако, даже зная угловую скорость планеты, сложно представить, насколько быстрым должно быть вращение земли вокруг своей оси, чтобы совершать полный оборот за 24 часа.
Как рассчитать угловую скорость планеты
Планеты являются частью нашей солнечной системы и движутся вокруг Солнца в определенных орбитах. В то время как путь, который они преодолевают, может быть расчетливо измерен в километрах и милях, угловая скорость, с которой они движутся, является не менее важной характеристикой, которая позволяет ученым лучше понимать их движение и влияние на окружающий мир. В этой статье мы рассмотрим, что такое угловая скорость планеты и как ее рассчитать.
Что такое угловая скорость?
Угловая скорость — это скорость, с которой угол поворота изменяется со временем. Другими словами, это скорость, с которой объект вращается вокруг центра. Угол поворота измеряется в радианах, а время — в секундах, поэтому угловая скорость измеряется в радианах в секунду (рад/с).
Используя терминологию физики, угловая скорость — это вектор, который указывает направление и скорость вращения движущегося объекта вокруг некоторой оси. Угловая скорость также может быть отрицательной, что означает, что объект вращается в противоположном направлении. Например, при обходе планеты она движется по орбите вокруг солнца в одном направлении, а при вращении вокруг своей оси — в другом.
Как рассчитать угловую скорость планеты?
Угловая скорость планеты может быть рассчитана несколькими способами, в зависимости от доступных данных и уровня точности, который вы хотите достичь. Одним из наиболее распространенных методов является использование периода обращения планеты вокруг Солнца и ее орбитального радиуса.
Обратите внимание, что расчет угловой скорости основывается на приближениях и усреднениях, что может влиять на точность результатов. Используйте полученные данные только для общего понимания и не как источник окончательной информации.
Период обращения планеты (T) является временным интервалом, необходимым для того, чтобы планета вернулась в то же самое место в своей орбите вокруг Солнца. Орбитальный радиус (r) показывает расстояние от Солнца до центра планеты. Они могут быть измерены в различных единицах, таких как годы и астрономические единицы для периода, и километры и астрономические единицы для радиуса.
Угловая скорость может быть рассчитана с использованием формулы:
Угловая скорость = 2π / T
где 2π — это полный угол поворота (360 градусов или 2 радиана), а T — это период обращения в секундах.

Теперь можно воспользоваться этой формулой, чтобы рассчитать угловую скорость любой планеты, используя известные данные о ее периоде обращения и орбитальном радиусе.
Пример расчета угловой скорости
Для того чтобы проиллюстрировать этот метод, рассмотрим расчет угловой скорости Земли.
Земля имеет период обращения вокруг Солнца, равный 365,24 суткам (или 31 557 600 секунд), и орбитальный радиус, равный приблизительно 149,6 миллионов километров (или 1 астрономической единице). Используя эти данные, мы можем рассчитать угловую скорость Земли с помощью нашей формулы:

Угловая скорость Земли = 2π / 31 557 600 секунд
Результат этого уравнения даст нам угловую скорость Земли в радианах в секунду.
Угловая скорость Земли составляет приблизительно 0,00000417 рад/с
Выводы
Угловая скорость является важной характеристикой для изучения движения планет в нашей солнечной системе. Она позволяет ученым более полно понимать, как планеты двигаются вокруг Солнца и влияют на нашу планету и окружающую среду. В этой статье мы рассмотрели общую формулу для расчета угловой скорости планеты и рассчитали угловую скорость Земли, используя данную формулу. Хотя есть другие методы расчета угловой скорости, этот простой способ поможет лучше понять эту физическую характеристику планет в нашей солнечной системе.
Как рассчитать угловую скорость планеты
Рассмотрим одну из фундаментальных задач механики — определение угловой скорости планеты. Угловая скорость является векторной величиной, которая определяет угловое перемещение при изменении ориентации тела. Она играет важную роль в изучении кинематики объектов в космическом пространстве. Одним из примеров таких объектов являются планеты.
Что такое угловая скорость
Перед тем, как переходить к рассчету угловой скорости планеты, давайте разберемся с тем, что это такое. Угловая скорость в математике обозначается символом ω и выражается в радианах в секунду (рад/с).
Для того, чтобы проиллюстрировать понятие угловой скорости, рассмотрим следующую ситуацию. Допустим, у нас есть круговое тело, которое находится в состоянии равновесия. Если мы начнем вращать его вокруг определенной оси, то наша задача будет заключаться в том, чтобы определить насколько быстро оно вращается.

Чтобы найти решение этой задачи, мы будем использовать формулу:
ω = dθ/dt
Где θ — это угол поворота, а t — время.
Иными словами, угловая скорость равняется изменению угла за единицу времени. Если мы продолжим вращать тело со скоростью ω, то угол поворота будет увеличиваться на величину, равную ω*t.
Рассчет угловой скорости планеты
Теперь перейдем к рассчету угловой скорости планеты. Для этого нам понадобится знать несколько параметров:
- радиус орбиты планеты;
- период обращения (время, за которое планета совершает полный оборот вокруг своей оси);
- угол поворота.

Первые два параметра относительно легко найти в литературе или в Интернете. Очень часто эти значения представлены в таблицах и имеют достаточно высокую точность. Однако, последний параметр — угол поворота — может быть достаточно сложным, так как он зависит от того, как мы определяем начало отсчета.
Один из способов рассчета угловой скорости планеты заключается в определении угла, который она повернула за определенный промежуток времени. Для этого, необходимо измерить расстояние, на которое переместилась планета в этот промежуток времени, а затем разделить это значение на радиус орбиты.
Один из примеров рассчета угловой скорости планеты можно найти в следующей формуле:
ω = 2π/T
Где T — период обращения планеты вокруг своей оси.
Таким образом, зная радиус орбиты планеты и ее период обращения, мы можем легко определить угловую скорость.
Заключение
Угловая скорость — это необходимая величина для изучения кинематики объектов в космическом пространстве, в том числе и планет. Она определяется изменением угла за единицу времени и выражается в радианах в секунду. Для рассчета угловой скорости планеты необходимы знания о радиусе орбиты и периоде обращения планеты вокруг своей оси. Существует несколько способов рассчета угловой скорости, однако результат во всех случаях будет одинаковым.
Понятие об угловой скорости: вращение Земли вокруг своей оси и вокруг Солнца
Движение нашей планеты в космическом пространстве можно охарактеризовать двумя типами вращения: вокруг собственной оси и вокруг Солнца. В данной статье рассматривается понятие угловой скорости, приводятся необходимые формулы для вычисления этой величины, а также дается расчет скорости угловой вращения Земли вокруг своей оси и вокруг нашей звезды.
Что такое угловая скорость вращения?
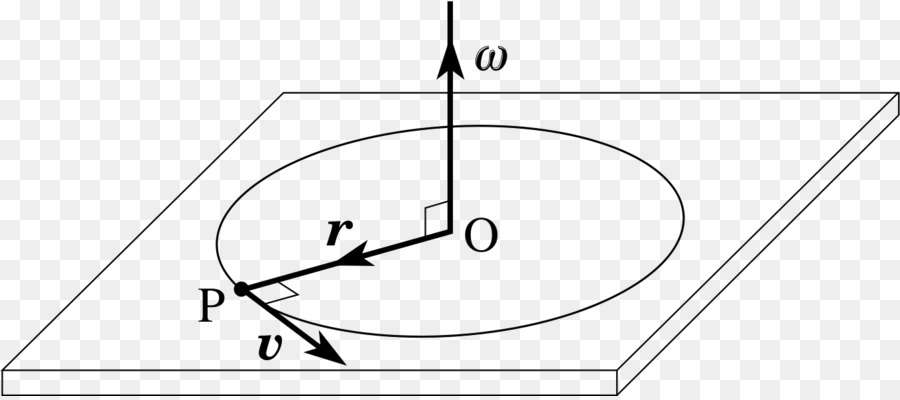
Когда рассматривают перемещение тела в пространстве на большие расстояния, то, как правило, пренебрегают его размерами. В этом случае вводят понятия пути и скорости его движения. Если же решают задачу движения тела вокруг некоторой точки или оси вращения, то пройденный путь всегда равен длине соответствующей окружности, а линейная скорость перемещения заменяется использованием скорости угловой.
 Вам будет интересно: Ортоборная кислота: применение, свойства, польза
Вам будет интересно: Ортоборная кислота: применение, свойства, польза
Угловая скорость вращения представляет собой угол, на который тело поворачивается вокруг соответствующей оси за единицу времени. Исходя из этого определения, единицей измерения рассматриваемой величины будут радианы в секунду (рад/с). Также можно использовать градусы в секунду (˚/c). Обозначается угловая скорость греческой буквой омега ω.
Основные формулы
Прежде чем переходить к вопросу, чему равна скорость вращения Земли угловая, следует познакомиться с основными формулами, описывающими эту величину.
Как известно, угловая мера всей окружности составляет 360 ˚ или 2×π радиан, где π = 3,1416. Если тело совершает вокруг оси полный оборот за время T, тогда можно записать следующее выражение:
Время T называют периодом обращения, а величина f = 1/T показывает, сколько оборотов тело сделает за единицу времени, то есть характеризует частоту его вращения.
Еще одной важной формулой для угловой скорости является выражение, объединяющее линейную скорость и радиус вращения:
Если проверить единицу измерения ω в этом выражении, то получаем те же радианы в секунду (с-1). Формула показывает, что чем меньше расстояние от оси вращения до тела (r), и чем больше его скорость линейная (v), тем больше будет ω.
Из этой формулы можно легко выразить величину v: v = ω×r. Поскольку угловая скорость является величиной постоянной для некоторого рассматриваемого тела, то быстрее будут двигаться те точки, которые находятся дальше от оси вращения.
Рассмотренные формулы и понятия используем для определения скорости угловой вращения Земли вокруг оси и вокруг Солнца.
Вращение нашей планеты вокруг оси
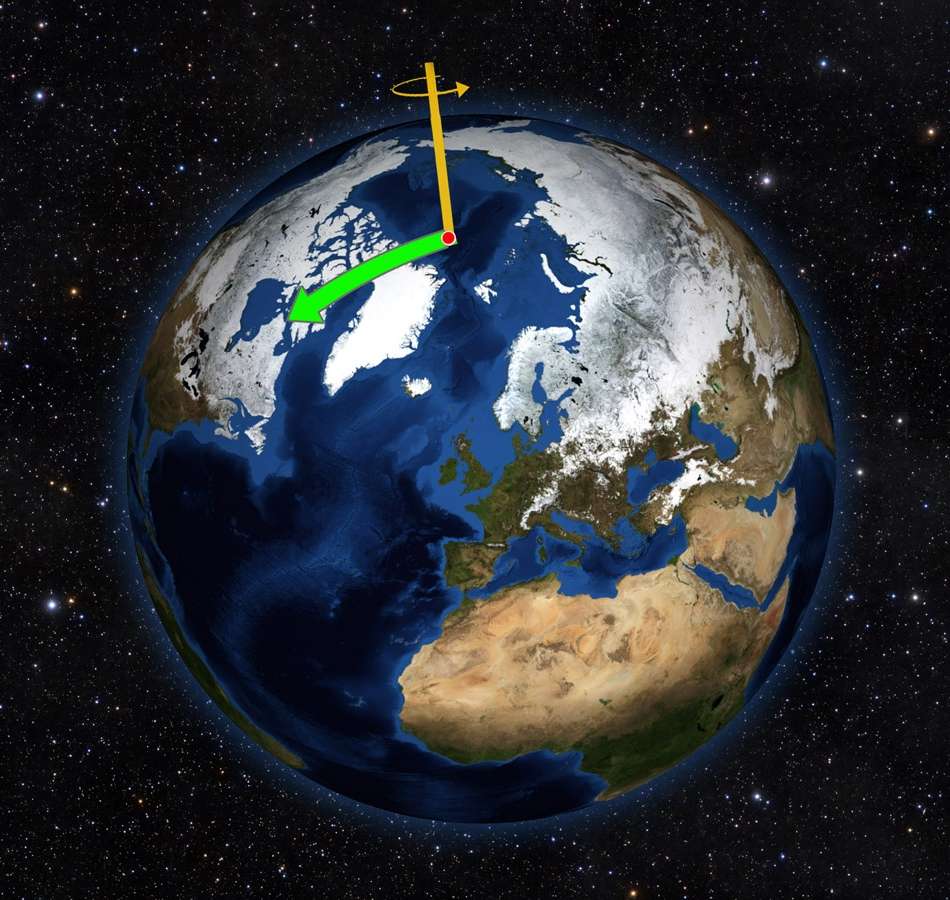
Каждый человек знает, что планета, на которой он живет, вращается вокруг своей оси, причем экваториальная плоскость Земли наклонена под углом 23˚ к плоскости эклиптики.
Как рассчитать угловую скорость вращения вокруг своей оси Земли? Для этого можно воспользоваться совершенно любой из формул, которые приведены были выше. Поскольку мы знаем, что один оборот вокруг оси происходит за 24 часа, то для расчета следует использовать выражение с периодом T. Получаем:
ω = 2×π/T = 2×3,1416/(24×3600) = 7,27×10-5 рад/с.
Здесь значение периода T было переведено в секунды. Полученное значение является небольшим.
Представляет интерес рассчитать, с какой линейной скоростью движутся точки на поверхности планеты на широте 0˚ (экватор). Экваториальный радиус Земли равен 6 378 000 м. Подставляя это значение в формулу для скорости, получим:
v = ω×r = 7,27×10-5×6 378 000 = 463,8 м/с = 1670 км/ч.
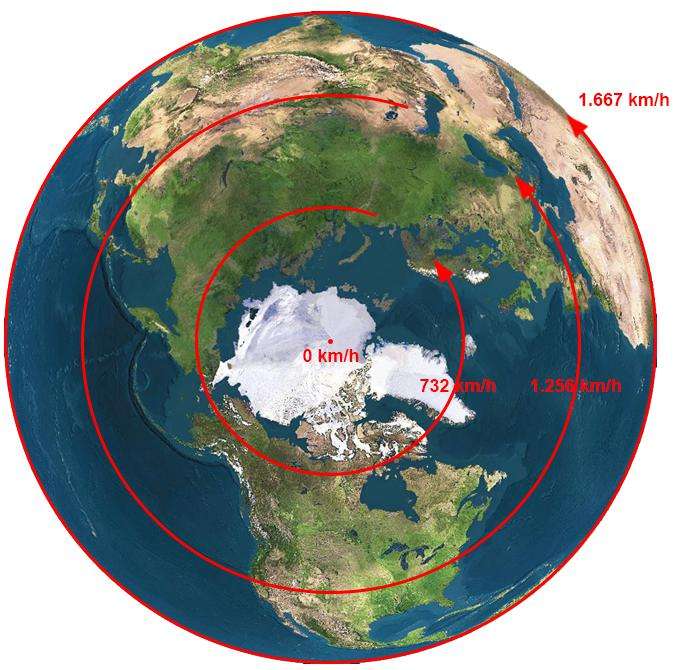
Полученное значение является большим в сравнении со скоростями, которые мы наблюдаем в жизни. Человек эту скорость не ощущает, поскольку вращается вместе с воздухом и почвой под ногами с одной скоростью, то есть он покоится относительно них.
Рассмотренное вращение Земли приводит не только к возникновению явления дня и ночи, но и к появлению так называемой силы Кориолиса, которая оказывает влияние на некоторые земные процессы, например, изменяет направление ветров.
Вращение Земли по своей орбите
Рассчитаем теперь угловую скорость вращения Земли вокруг Солнца. Для этого воспользуемся следующими данными: точное значение сидерического периода обращения нашей планеты по орбите составляет 365 дней 6 часов 9 минут и 9,7632 секунды, то есть T = 31558149,7632 секунд. Теперь можно воспользоваться формулой:
ω = 2×π/T = 2×3,1416/(31558149,7632) = 1,991×10-7 рад/с.
То есть угловая орбитальная скорость нашей планеты меньше на 1,5 порядка, чем аналогичная величина для вращения вокруг собственной оси. Вычислим линейную скорость, учитывая, что средний радиус орбиты равен 149 597 871 000 метров:
v = ω×r = 1,991×10-7×149 597 871 000 = 29784,8 м/с = 107 225 км/ч.
С этой огромной скоростью наша планета движется в космическом пространстве вокруг Солнца.
С орбитальным движением планеты и наклоном ее оси связано существование времен года в Северном и Южном полушариях.
Источник
С КАКОЙ СКОРОСТЬЮ ВРАЩАЕТСЯ ЗЕМЛЯ?
С какой скоростью вращается Земля вокруг своей оси? Не для кого не секрет, что смена дня и ночи технически вызвана вращением Земли. Но вам когда-нибудь приходило в голову с какой скоростью она вращается? И как посчитать эту скорость?
Если говорить о равномерном движении по окружности, можно выделить две скорости: угловую (ω) и линейную (v). Давайте найдем и ту, и другую для нашей прекрасной голубой планеты.
Угловая скорость вращения Земли
Угловая скорость определяет то, как быстро изменяется угол с течением в времени. Так как один полный оборот соответствует углу в 360 о или 2π, а время, за которое он совершается есть период Т, то угловую скорость можно выразить как:
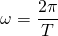
На всякий случай. Чтобы не было вопросов откуда берется 2π.
Один радиан соответствует углу с дугою равной радиусу. Соответственно чтобы посчитать количество радиан в окружности нам необходимо ее длину то есть 2πR, поделить на радиус R. R и R сокращаем и получаем 2π. Или приближенно 6.28.
Мы знаем, что в сутках 24 часа, а, следовательно, можно предположить, что период обращения Земли вокруг своей оси Т составит так же 24 часа. Но не торопитесь переводить это время в секунды и подставлять в уравнение, записанное выше. Так как Земля вращается еще вокруг солнца, то период обращения её вокруг собственной оси будет немного короче привычных нам солнечных суток и составит 23 часа 56 минут и 4 секунды. Это так называемые звездные сутки. В пересчете на секунды мы получаем: Т=86164 с.

Теперь можно найти угловую скорость:

Линейная скорость вращения Земли
Если говорить об угловой скорости, то она одинакова для любой точки нашей планеты. И не важно: пингвин в Антарктике, слон в Африке или Вы у себя дома, все будут иметь одинаковую угловую скорость. Но когда речь заходит о скорости линейной, то тут все наоборот. Она будет максимальна на экваторе и убывать к полюсам, так как напрямую зависит от радиуса окружности вращения. А это значит, что если вы залезете на табуретку вкрутить лампочку, то ваша линейная скорость увеличится. Строго говоря, линейная скорость описывает скорее не вращение Земли вокруг своей оси, она описывает вращение каких то отдельных её точек.
Рассчитать линейную скорость очень просто. По определению, скорость — это отношение пройденного пути ко времени, за которое этот путь был совершен. Если за один оборот мы проходим путь, равный длине окружности, а время движения будет ни что иное как период обращения Т, то, выразив длину окружности из известной школьной формулы: L= 2πR, мы получим уравнение для расчета линейной скорости:
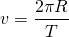
Так как угловая скорость  , то мы можем смело записать:
, то мы можем смело записать:

Радиус земли на экваторе R = 6378245 м, а значит линейная скорость там будет равна:  м/с.
м/с.
Для сравнения скорость звука в воздухе составляет 365 м/с. А это значит, что, сидя спокойно на стульчике где-нибудь в Африке или Индонезии мы будем двигаться со скоростями, превышающими звук. Если перевести эту величину в километры в час, то получится 1674 км/ч. В общем скорости сопоставимые со скоростями сверхзвуковой авиации.

Линейная скорость в зависимости от широты
Но это на экваторе. Ближе к полюсам, как я уже говорил, значение будет ниже. Так как радиус вращения будет снижаться.
Для того чтоб найти радиус вращения на той или иной широте. Необходимо косинус этой широты умножить на земной радиус.
К примеру, для Санкт-Петербурга соответствует шестидесятая северная широта. Косинус шестидесяти градусов как известно одна вторая. То есть радиус вращения будет вдвое меньше земного, а значит и линейная скорость будет так же в два раза меньше экваториальной, всего 837 км/ч.
А с какой линейной скоростью вращаетесь Вы. Ответы можете писать в комментариях, а я с Вами прощаюсь. Всего хорошего, до скорых встреч.
Источник
Скорость вращения Земли
Как известно, наша планета движется, и не только вокруг Солнца, но и вокруг своей оси. Вдобавок, мы знаем, что для любого движения характерна определённая скорость, которая может зависеть (как и само движение) от различных факторов. Следовательно, вращение Земли также имеет свою скорость.
Скорость — это векторная физическая величина, характеризующая быстроту перемещения материальной точки за любой отрезок времени относительно величины промежутка.
Скорость вращения Земли
Правда, земная скорость — вещь относительна. Так как для её расчёта нужна определённая точка отсчёта. Например, для того, чтобы вычислить с какой скоростью движется Земля вокруг своей оси, такой точкой является центр планеты.
Однако, говоря о подобном параметре земельного кружения, важно знать, что скорость разделяют на угловую и линейную.
Угловая скорость
Это величина, которая равна отношению угла тела к отрезку времени, затраченному на этот поворот. Можно сказать, что это быстрота изменения угла тела за промежуток времени. Выражается она в радианах в секунду, и для всех точек имеет постоянное значение.
Как выяснилось, на полный оборот нашей планеты вокруг своей оси требуется 23 часа 56 минут 4,09053 секунды. Проще говоря, одни звездные сутки.
Формула угловой скорости: отношение изменения угла за время.
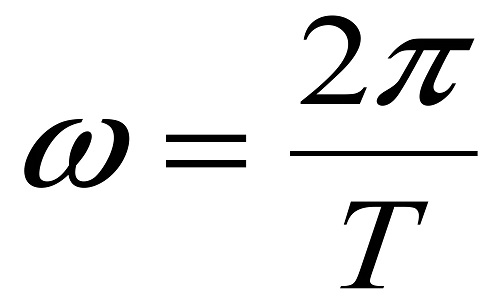 Формула угловой скорости
Формула угловой скорости
Так как земной оборот равен 360 градусов или 2π (2*3,14=6,28), а время этого оборота в секундах 86344, то угловая скорость вращения Земли вокруг своей оси приблизительно равна 7,26851851851-5с-1.
Линейная скорость
Такую характеристику применяют для того, чтобы выразить темп движения по окружности. Как известно, при круговом вращении тела его разные точки имеют разные скорости. Хотя угловая величина перемещения для них остаётся неизменной.
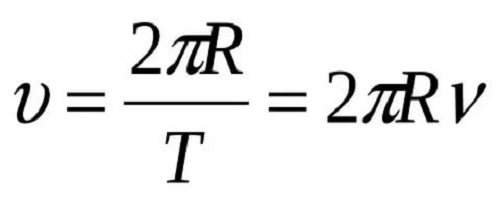 Формула линейной скорости
Формула линейной скорости
А это значит, что скорость вращения Земли равна примерно 465 м/сек. То есть расчет производится путём деления окружности на время, затраченное на весь оборот.
Однако скорость движения Земли изменяется, потому как её окружность также меняется относительно широты. Ведь радиус планеты уменьшается к полюсам. Соответственно, на разных широтах разный темп вращения. Другими словами, где меньший радиус медленнее и скорость. К примеру, на полюсах она почти нулевая, а на экваторе составляет 1674 км/час.
Для того, чтобы рассчитать скорость вращения Земли на другой широте, необходимо косинус выбранной широты умножить на экваторную скорость. Например, быстроту движения планеты на широте 30 градусов мы вычислим, если косинус 30 градусов, который равен 0,866, умножим на 1674. Таким образом, получаем 1449,7 км/час.
С какой скоростью Земля движется относительно Солнца
Поскольку наша планета, как и другие планеты звездной группы, движутся вокруг Солнца, у данного движение также есть своя скоростная величина.
На полный оборот вокруг главного светила уходит 365 дней 5 часов 48 минут и 46 секунд. Хотя мы привыкли округлять и говорить просто один год. Между прочим за каждый такой год накапливается по пять часов, так сказать, лишних. Но и им нашли место, их объединяют и каждому следующему четвертому году добавляют один день. Наверняка вы догадались, что такие года называются високосными.
 Вращение Земли вокруг Солнца
Вращение Земли вокруг Солнца
На основании данных о времени полного оборота планеты вокруг Солнца, не трудно вычислить с какой быстротой она движется относительно него. Следует учитывать, что двигаемся мы по орбите. А значит определяем с какой скоростью Земля летит именно по орбите.
Как рассчитать темп земного движения вокруг Солнца
Для этого необходимо радиус орбиты или расстояние до Солнца (≈150 млн км) умножить на 2π (23,14=6,28), что составляет 942 млн км. Все это разделим на время, затраченное на этот промежуток (365 дней 24 часа*3600 секунд=31 536 000 секунд). В итоге получаем 29,87 км в секунду.
Принято считать, что средняя скорость Земли по орбите (по окружности Солнца) равна 30 км/сек.
По данным учёных, скорость вращения Земли вокруг своей оси постепенно уменьшается. Причем наблюдаются пятилетние циклы то ускорения, то замедления движения планеты. Но объяснить по какой причине происходят такие изменения пока не получается. Поэтому за движением нашей планеты ведётся постоянное наблюдение и мониторинг. Возможно, отыщется какая-либо взаимосвязь данного явления.
Источник
Чему равна угловая скорость вращения планеты
Рассмотрите таблицу, содержащую некоторые характеристики планет Солнечной системы. Размеры и параметры орбит даны в сравнении с планетой Земля.
| Имя | Диаметр | Масса | Орбитальный
(земных суток) |
||
|---|---|---|---|---|---|
| Нептун | 3,9 | 17,2 | 30,1 | 165 | 0,67 |
| Уран | 4 | 14,6 | 19,2 | 84 | 0,72 |
| Сатурн | 9,5 | 95,2 | 9,5 | 29,5 | 0,43 |
| Юпитер | 11,2 | 318 | 5,2 | 11,9 | 0,41 |
| Марс | 0,53 | 0,11 | 1,5 | 1,9 | 1 |
| Земля | 1 | 1 | 1 | 1 | 1 |
| Венера | 0,95 | 0,82 | 0,72 | 0,62 | 243 |
| Меркурий | 0,38 | 0,06 | 0,39 | 0,24 | 58,6 |
Выберите два утверждения, которые соответствуют характеристикам планет.
1) Линейная скорость вращения по орбите у Сатурна больше, чем у Урана.
3) Угловая скорость вращения Марса относительно собственной оси вращения больше, чем у Земли.
4) Средняя плотность Венеры почти в 10 раз меньше средней плотности Сатурна.
5) Вторая космическая скорость для Нептуна больше, чем для Урана.
1) Линейная скорость планеты равна Отношение скоростей Сатурна и Урана
больше единицы. Значит, линейная скорость вращения по орбите у Сатурна больше, чем у Урана.
Утверждение 1 верно.
2) Ускорение свободного падения на планете Ускорение свободного падения на Венере по отношению к земному
И, значит,
Утверждение 2 неверно.
3) Период вращения Марса относительно собственной оси равен периоду вращения Земли (1 сутки), значит, у них одинаковые угловые скорости
Утверждение 3 неверно.
4) Средняя плотность планеты Отношение средней плотности Венеры к средней плотности Сатурна
больше единицы. Значит, средняя плотность Венеры больше средней плотности Сатурна.
Утверждение 4 неверно.
5) Вторая космическая скорость Масса Нептуна больше массы Урана, а радиус Нептуна меньше радиуса Урана, значит, вторая космическая скорость для Нептуна больше, чем для Урана.
Источник
Какова скорость вращения Земли вокруг своей оси?

Земля вращается вокруг своей оси, и доказательством этого факта является смена дня и ночи. Но какова скорость этого вращательного движения?
Линейная скорость измеряется в м/с и характеризует величину, на которую отдельная материальная точка перемещается за единицу времени. Разные точки Земли находятся на разном расстоянии от ее оси, а потому имеют разную линейную скорость. Так, Северный и Южный полюс вообще не участвуют во вращении, так как именно через них проходит земная ось. Быстрее же всего вращаются точки экватора. Их линейная скорость составляет 465 м/с, или 1674 км/ч. Это примерно в 1,4 раза больше скорости звука. На широте, соответствующей северной 60° широты (на которой располагается Санкт-Петербург), линейная скорость вращения примерно вдвое меньше.
Линейная скорость вращения Земли на разных широтах:
Различия в линейной скорости разных точек Земли порождают интересные эффекты. Дело в том, что от величины скорости зависит центробежная сила, которая направлена против силы земного тяготения. Из-за изменчивости центробежной силы наша Земля немного сплюснута у полюсов. Примечательно, что этот эффект был сначала предсказан Ньютоном, и лишь после его смерти обнаружен французом Мопертюи.
Также из-за разности линейных скоростей ускорение свободного падения на экваторе меньше, чем на полюсе. В результате ракете, стартующей с космодрома вблизи экватора, нужно меньше топлива для преодоления земной гравитации. Именно поэтому такая страна, как Франция, запускает свои спутники в космос не со своей континентальной территории, а из Гвианы, колонии в Южной Америке, располагающейся почти на экваторе.
Список использованных источников
Источник
| Угловая скорость | |
|---|---|
 |
|
| Размерность | T −1 |
| Единицы измерения | |
| СИ | рад/с |
| СГС | рад/с |
| Другие единицы |
градус/с об/с об/мин |
Углова́я ско́рость — векторная величина, характеризующая быстроту и направление вращения материальной точки или абсолютно твёрдого тела относительно оси вращения. Модуль угловой скорости для вращательного движения совпадает с мгновенной угловой частотой вращения, а направление перпендикулярно плоскости вращения и связано с направлением вращения правилом правого винта. Строго говоря, угловая скорость представляется псевдовектором (аксиальным вектором), и может быть также представлена в виде кососимметрического тензора[1].
Угловая скорость в двухмерном пространстве[править | править код]
|
|
Этот раздел статьи ещё не написан. Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (31 августа 2016) |
Векторное представление в трёхмерном пространстве[править | править код]
В трёхмерном пространстве вектор угловой скорости по величине равен углу поворота точки вокруг центра вращения за единицу времени:
а направлен по оси вращения согласно правилу буравчика, то есть в ту сторону, в которую ввинчивался бы буравчик или винт с правой резьбой, если бы вращался в эту сторону. Другой мнемонический подход для запоминания взаимной связи между направлением вращения и направлением вектора угловой скорости состоит в том, что для условного наблюдателя, находящегося на конце вектора угловой скорости, выходящего из центра вращения, само вращение выглядит происходящим против часовой стрелки.
Угловая скорость является аксиальным вектором (псевдовектором). При отражении осей системы координат компоненты обычного вектора (например, радиус-вектора точки) меняют знак. В то же время компоненты псевдовектора (в частности, угловой скорости) при таком преобразовании координат остаются прежними.
Тензорное представление[править | править код]
|
|
Этот раздел статьи ещё не написан. Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (31 августа 2016) |
Единицы измерения[править | править код]
Единица измерения угловой скорости, принятая в Международной системе единиц (СИ) и в системах СГС и МКГСС, — радиан в секунду (русское обозначение: рад/с, международное: rad/s)[2][Комм 1]. В технике также используются обороты в секунду, намного реже — градусы, минуты, секунды дуги в секунду, грады в секунду. Часто в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли просто на глаз, подсчитывая число оборотов за единицу времени.
Свойства[править | править код]


Угловая скорость (синяя стрелка) в полторы единицы по часовой стрелке

Угловая скорость (синяя стрелка) в одну единицу против часовой стрелки (вектор угловой скорости направлен навстречу направлению взгляда наблюдателя)
Вектор мгновенной скорости любой точки абсолютно твёрдого тела, вращающегося с угловой скоростью 
где 


- В случае плоского вращения, то есть когда все векторы скоростей точек тела всегда лежат в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось вращения, то есть на прямую, ортогональную плоскости вращения. В этом случае кинематика вращения сильно упрощается. Однако в общем случае угловая скорость может менять со временем направление в трёхмерном пространстве, и такая упрощенная картина не работает.
- Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю). Равномерное вращение является частным случаем плоского вращения.
- Производная угловой скорости по времени есть угловое ускорение.
- Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчёта, отличающихся положением начала отсчёта и скоростью его движения, но двигающихся равномерно прямолинейно и поступательно друг относительно друга. Однако в этих инерциальных системах отсчёта может различаться положение оси или центра вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).
- В случае движения точки в трёхмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:
где
— радиус-вектор точки (из начала координат),
— скорость этой точки,
— векторное произведение,
— скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы
подходящие по определению, по-другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как даёт разные
для каждой точки, а при вращении абсолютно твёрдого тела вектора угловой скорости вращения всех его точек совпадают). Однако в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.
- В случае равномерного вращательного движения (то есть движения с постоянным вектором угловой скорости) абсолютно твёрдого тела декартовы координаты точек вращающегося так тела совершают гармонические колебания с угловой (циклической) частотой, равной модулю вектора угловой скорости.
Связь с конечным поворотом в пространстве[править | править код]
Примечания[править | править код]
Комментарии[править | править код]
- ↑ Плоский угол, определяемый как отношение длины дуги окружности, заключённой между двумя радиусами, к длине радиуса, безразмерен, поэтому единицей измерения плоских углов является число «один», а единицей измерения угловой скорости в системе СИ — с−1. Однако, в случае плоских углов единице «один» присвоено специальное наименование «радиан» для того, чтобы в каждом конкретном случае облегчить понимание того, какая именно физическая величина имеется в виду[3].
Источники[править | править код]
- ↑ Ишлинский А. Ю. Классическая механика и силы инерции / Отв. ред. Б. В. Раушенбах. — М.: «Наука», 1987. — С. 239.
- ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 98. — 240 с. — ISBN 5-7050-0118-5.
- ↑ Units for dimensionless quantities, also called quantities of dimension one (англ.). SI Brochure: The International System of Units (SI). Международное бюро мер и весов (2006; обновлено в 2014). Дата обращения: 2016-1-29.
См. также[править | править код]
- Угловая частота
- Угловое ускорение
- Момент импульса
Литература[править | править код]
- Лурье А. И. Аналитическая механика. — М.: ГИФМЛ, 1961. — С. 100-136. — 824 с.
Содержание:
- Определение и формула угловой скорости
- Равномерное вращение
- Формула, связывающая линейную и угловую скорости
- Единицы измерения угловой скорости
- Примеры решения задач
Определение и формула угловой скорости
Определение
Круговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность
с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.
Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.
Перемещение при вращении характеризуют при помощи угла поворота
$(varphi)$ . Часто используют вектор элементарного поворота
$bar{dvarphi}$ , который равен по величине элементарному углу поворота тела
$(d varphi)$ за маленький отрезок времени dt и направлен по мгновенной оси вращения в сторону,
откуда этот поворот виден реализующимся против часовой стрелки. Надо отметить, что только элементарные угловые перемещения являются векторами.
Углы вращения на конечные величины векторами не являются.
Определение
Угловой скоростью называют скорость изменения угла поворота и обозначают ее обычно буквой
$omega$ . Математически определение угловой скорости записывают так:
$$bar{omega}=frac{d bar{varphi}}{d t}=dot{bar{varphi}}(1)$$
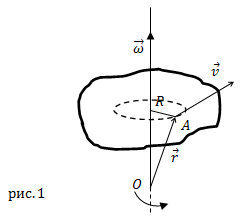
Угловая скорость – векторная величина (это аксиальный вектор). Она имеет направление вдоль мгновенной оси вращения совпадающее
с направлением поступательного правого винта, если его вращать в сторону вращения тела (рис.1).
Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости),
так и за счет поворота оси вращения в пространстве ($bar{omega}$ при этом изменяет направление).
Равномерное вращение
Если тело за равные промежутки времени поворачивается на один и тот же угол,
то такое вращение называют равномерным. При этом модуль угловой скорости находят как:
$$omega=frac{varphi}{t}(2)$$
где $(varphi)$ – угол поворота, t – время, за которое этот поворот совершён.
Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот
($Delta varphi=2 pi$). Угловая скорость связана с периодом обращения как:
$$omega=frac{2 pi}{T}(3)$$
С числом оборотов в единицу времени ($nu) угловая скорость связана формулой:
$$omega=2 pi nu(4)$$
Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения,
но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно
с данной мгновенной величиной скорости.
Формула, связывающая линейную и угловую скорости
Линейная скорость $bar{v}$ точки А (рис.1), которая расположена
на расстоянии R от оси вращения связана с вектором угловой скорости следующим векторным произведением:
$$bar{v}=[bar{omega} bar{R}](5)$$
где $bar{R}$ – перпендикулярная к оси вращения компонента радиус-вектора точки
$A (bar{r})$ (рис.1). Вектор
$bar{r}$ проводят от точки, находящейся на оси вращения к рассматриваемой точке.
Единицы измерения угловой скорости
Основной единицей измерения угловой скорости в системе СИ является: [$omega$]=рад/с
В СГС: [$omega$]=рад/с
Примеры решения задач
Пример
Задание. Движение тела с неподвижной осью задано уравнением
$varphi=2 t-4 t^{3}$,
$(varphi)$ в рад, t в сек.
Начало вращения при t=0 c. Положительным считают углы указанные направлением стрелки (рис.2). В каком направлении (
относительно часовой стрелки поворачивается тело) в момент времени t=0,5 c.
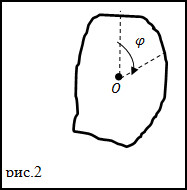
Решение. Для нахождения модуля угловой скорости применим формулу:
$$omega=frac{d varphi}{d t}(1.1)$$
Используем заданную в условии задачи функцию
$varphi(t)$, возьмем производную от нее по времени, получим функцию
$omega(t)$:
$$omega(t)=2-8 t^{2}(1.2)$$
Вычислим, чему будет равна угловая скорость в заданный момент времени (при t=0,5 c):
$$omega(t)=2-8(0,5)^{2}=0left(frac{r a d}{c}right)$$
Ответ. В заданный момент времени тело имеет угловую скорость равную нулю, следовательно, она останавливается.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Скорости вращения тела заданы системой уравнений:
$$left{begin{array}{c}bar{omega}_{1}=t^{2 bar{i}} \ bar{omega}_{2}=2 t^{2} bar{j}end{array}right.$$
где $bar{i}$ и
$bar{j}$ – единичные ортогональные векторы. На какой угол $(varphi)$ поворачивается тело за время равное 3 с?
Решение. Определим, какова функция, которая связывает модуль скорости вращения тела и время (t)
($omega(t)$). Так как вектора
$bar{i}$ и
$bar{j}$ перпендикулярны друг другу, значит:
$$omega=sqrt{omega_{1}^{2}+omega_{2}^{2}}=sqrt{left(t^{2}right)^{2}+left(2 t^{2}right)^{2}}=t^{2} sqrt{5}(2.2)$$
Модуль угловой скорости связан с углом поворота как:
$$omega=frac{d varphi}{d t}(2.3)$$
Следовательно, угол поворота найдем как:
$$varphi=int_{t_{1}}^{t_{2}} omega d t=int_{0}^{3} t^{2} sqrt{5} d t=left.sqrt{5} frac{t^{3}}{3}right|_{0} ^{3} approx 20(mathrm{rad})$$
Ответ. $varphi = 20$ рад.
Читать дальше: Формула удельного веса.

![{vec v}=[ {vec omega },{vec r} ],](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf77d103c0490cb68964169060fade3d70aeecab)



