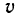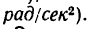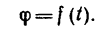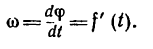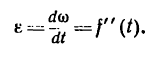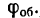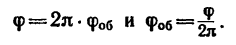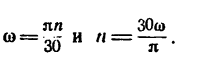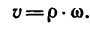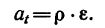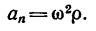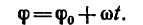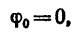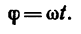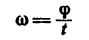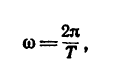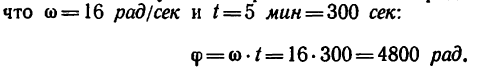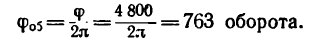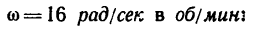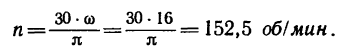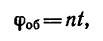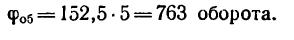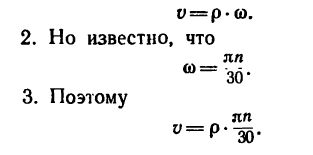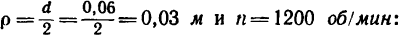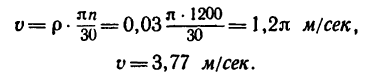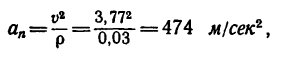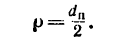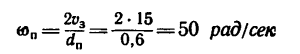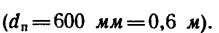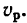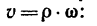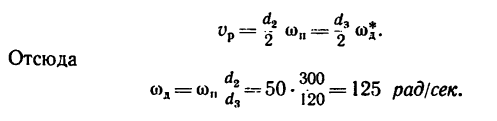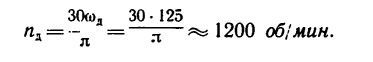АННОТАЦИЯ
Актуальность и цель. Объект исследования – ременная передача, состоящая из двух шкивов и ремня. Предмет исследования – тяговые характеристики ремня. Тяговая способность ремня и ременной передачи характеризуется экспериментальными графиками зависимостей относительного скольжения ремня и коэффициента полезного действия от коэффициента тяги передачи. Задача состоит в разработке математической модели ременной передачи, позволяющей теоретически оценивать тяговую способность ремня и рациональный режим работы в зоне упругого скольжения.
Материалы и методы. Кинематический и силовой расчет ременной передачи построен на теории упругого скольжения ремня по шкивам, разработанной Н. П. Петровым и Н. Е. Жуковским. В соответствии с этой теорией на шкивах существуют дуги упругого скольжения ремня. При этом вследствие упругого скольжения отношение скоростей точек ведомой и ведущей ветвей ремня линейно связано с относительным скольжением ремня, равным разности относительных удлинений ветвей. В статье предложена математическая модель ременной передачи, в основу которой положены новое полученное уравнение связи между скоростями точек ведущей и ведомой ветвей ремня и уравнения движения ремня как сплошной среды.
Результаты. Разработана математическая модель ременной передачи, позволяющая изучать тяговые характеристики ремня и определять рациональный режим работы. Разработана компьютерная модель, с помощью которой получены оценки тяговых характеристик.
Новизна. Предложено новое уравнение связи между скоростями точек ведущей и ведомой ветвей ремня.
Выводы. В режиме отсутствия буксования ремня эффективность ременной передачи возрастает при уменьшении коэффициента запаса сцепления. Коэффициент полезного действия достигает максимума при такой нагрузке, когда коэффициент запаса сцепления на одном из шкивов уменьшается до минимально допустимого. Чтобы поддерживать заданный коэффициент запаса сцепления, при изменении нагрузки силу натяжения ремня целесообразно регулировать.
ABSTRACT
Background. The object of research is belt transmission that consists of two pulleys and a belt. Subject of research is the traction characteristics of a belt. The challenge is to develop a mathematical model of the belt transmission, allowing in theory to evaluate the traction capacity of a belt and a rational mode of operation.
Materials and methods. Mathematical model of belt transmission is based on equation relationship between the velocities of lead and driven belt branches points and the equations of motion of the belt.
Results. The developed mathematical model of the belt transmission allows to study the belt traction characteristics and to determine a rational mode of operation. It was developed the computer model to estimate the traction experimental characteristics.
The novelty. It is proposed the new equation relationship between the speeds of points of leading and driven belt branches.
Conclusions. Belt transmission efficiency increases with decreasing safety factor of adhesion. Coefficient of efficiency reaches its maximum at this load, when the factor of adhesion on one of the pulleys is reduced to the minimum. To maintain the specified factor of adhesion, when changing the load force it is advisable to adjust the belt tension.
Введение
Кинематический и силовой расчет ременной передачи построен на теории упругого скольжения ремня по шкивам, разработанной Н. П. Петровым и Н. Е. Жуковским [2]. В соответствии с этой теорией на шкивах существуют дуги упругого скольжения ремня. При этом вследствие упругого скольжения отношение скоростей точек ведомой и ведущей ветвей ремня линейно связано с относительным скольжением ремня, равным разности относительных удлинений ветвей.
Статья посвящена разработке математической модели ременной передачи, в основу которой положены новое полученное уравнение связи между скоростями точек ведущей и ведомой ветвей ремня и уравнения движения ремня как сплошной среды.
1. Объект исследования и основные обозначения
Ременная передача – это механическая система, состоящая из ведущего шкива, ведомого шкива и соединяющего их ремня.
Введем следующие обозначения (рис. 1):
R1, R2 – радиус шкива 1 и шкива 2 соответственно, м;
L – расстояние между осями шкивов 1 и 2, м;
/Belov1%20.files/image001.png)
δ – половина толщины ремня, м;
α1, α2 – радиальный угол охвата ремнем ведущего и ведомого шкива, рад;
r1, r2 – радиус цапфы вала ведущего и ведомого шкива, м;
,
– относительное удлинение cрединного волокна ведущей и ведомой ветви ремня соответственно;
1,
2 – угловая скорость шкива 1 и шкива 2 соответственно, рад/с;
,
– скорость набегающей на шкив точки ремня ведущей и ведомой ветви соответственно, м/с;
u – передаточное отношение;
ρ – плотность ремня, кг/м3;
,
– величина силы натяжения ведущей и ведомой ветви ремня соответственно без учета веса, Н;
– начальная сила натяжения ремня без учета веса, Н;
E – модуль упругости ремня, Па;
– начальное нормальное напряжение в сечении ремня, Н;
– предел упругости ремня, Па;
f – коэффициент трения скольжения ремня со шкивом;
µ – коэффициент трения скольжения во вращательной паре “вал шкива − опора”;
M1, M2 – величина момента пары сил, приводящих в движение ведущий шкив 1, и пары сил полезного сопротивления (рабочей нагрузки), действующих на ведомый шкив 2 соответственно, Н м;
,
– величина момента силы трения во вращательной паре “вал − опора” ведущего и ведомого шкива относительно оси вращения соответствующего шкива, Н м;
P1, P2 – мощность момента M1, M2 пары сил соответственно, Вт;
η – коэффициент полезного действия ременной передачи.
2. Формулировка задачи
Тяговая способность ремня и ременной передачи характеризуется экспериментальными графиками зависимостей относительного скольжения ремня и коэффициента полезного действия от коэффициента тяги передачи [2, с. 137, 138]. Задача состоит в разработке математической модели ременной передачи, позволяющей теоретически оценивать тяговую способность ремня и рациональный режим работы в зоне упругого скольжения.
3. Кинематика ременной передачи
Рассмотрим ременную передачу с ведущим шкивом 1 и ведомым 2 при неизменной нагрузке и равномерных вращениях шкивов. В соответствии с исследованиями Н. П. Петрова и Н. Е. Жуковского дуга охвата шкива ремнем состоит из участков сцепления и скольжения [2, с. 130]. /Belov1%20.files/image014.png)
точек участка AB ведущей ветви ремня равна скорости точки A равномерно вращающегося шкива. При этом скорости точек участка BC ремня, касающегося ведущего шкива, уменьшаются до
в точке С схода, то есть участок BC ремня «отстает» от шкива из-за укорочения и скользит по нему. Аналогичные условия должны соблюдаться на дуге KE ведомого шкива. Скорость
точки K ведомой ветви ремня при набегании на шкив равна скорости точки K шкива. При этом скорости точек участка DE ремня, касающихся шкива, увеличиваются до
в точке E схода, то есть участок DE ремня «опережает» шкив из-за удлинения:
/Belov1%20.files/image015.png)
При буксовании ремня равенства (1) не соблюдаются.
Рассмотрим участок AC ремня, огибающий ведущий шкив. За время t его место займет участок AA1 длиной ведущей ветви, а участок AC займет положение CС1 длиной
ведомой ветви:
; .
. (2)
Участки AA1 и CС1 в разные моменты времени представляют один и тот же участок AC ремня и имеют длину в недеформированном состоянии. Следовательно,
;
. (3)
Подставляя выражения для ,
из равенств (3) в равенства (2) и исключая время t, придем к такому равенству:
. (4)
По определению,
или с учетом равенств (1), (4)
. (5)
Формула (5) справедлива при отсутствии буксования ремня. Она доказывает, что передаточное отношение ременной передачи равно отношению радиусов ведомого и ведущего шкивов, умноженному на коэффициент пропорциональности, который не равен единице и зависит от относительных удлинений ведущей и ведомой ветвей ремня.
4. Динамика шкива и ремня
Установим соотношения между величинами моментов M1, M2 . Вес ремня учитывать не будем. Можно доказать, что он не влияет на работу движущих сил. Примем, что при неизменной нагрузке 1) вращения шкивов равномерные; 2) движение ремня установившееся; 3) ремень находится в упругом состоянии растяжения.
/Belov1%20.files/image026.png)
,
сил натяжения ведущей и ведомой ветви соответственно; 2) равнодействующая
реакций ведущего шкива.
При неизменном сопротивлении движение ремня как сплошной среды – установившееся. Полагая, что плотности и площади поперечного сечения ведомой ветви и ремня в ненапряженном состоянии отличается незначительно, запишем уравнение сохранения масс в интегральном виде [3, с. 54]:
,
где ,
− плотности и площадь поперечного сечения ведущей ветви ремня.
Момент силы или количества движения материальной точки относительно оси шкива будем считать положительным, если при взгляде на рисунок сила или количество движения стремятся вращать шкив вокруг оси против хода стрелки часов. Уравнение моментов количества движения относительно оси O вращения шкива ремня на шкиве при установившемся движении запишем в интегральном виде [3, с. 54]:
или с учетом уравнения сохранения масс
, (6)
где – величина момента силы
относительно оси шкива.
Уравнение равномерного вращения шкива 1 представим в виде уравнения равновесия моментов сил относительно оси вращения:
.
Следовательно, уравнение (6) можно записать так:
или
. (7)
Рассматривая участок ремня, охватывающий ведомый шкив, придем к аналогичному уравнению:
. (8)
При неизменности общей длины ремня растяжение ведущей ветви «компенсируется» сжатием ведомой ветви, то есть уменьшение силы сжатия «компенсируется» увеличением силы растяжения:
(9)
или
. (10)
Найдем величины ,
моментов сил трения во вращательной паре ведущего и ведомого шкива. На ведущий шкив со стороны элемента ab ремня действует элементарная нормальная сила dN1 и элементарная сила dT1 трения сцепления, а на ведомый шкив – соответственно dN2 и dT2. На вал ведущего шкива со стороны опоры действует элементарная сила, уравновешивающая силу dN1 и элементарная сила dQ1 трения, а на вал ведомого шкива − силы dN2, dQ2 (рис. 4).
По определению,
/Belov1%20.files/image042.png)
Силы трения скольжения связаны с силами давления такими равенствами:
;
.
Следовательно, формулы (11) можно переписать так:
/Belov1%20.files/image045.png)
/Belov1%20.files/image046.png)
/Belov1%20.files/image047.png)
и
, вес, нормальная и касательная составляющие реакции шкива, элементарные равнодействующие которых равны dN и dT. Приращение
вектора
имеет проекцию
на ось касательной к окружности шкива и проекцию
на ось нормали к окружности шкива:
Расчеты показали, что касательное ускорение точек ремня, обусловленное его деформацией, приводит к изменению сил натяжения ремня менее чем на 1% и им можно пренебречь. Вес ремня не влияет на работу движущих сил, и его также не будем учитывать. Рассмотрим предельный случай, когда скорость точки элемента ремня наибольшая и давление ремня на шкив наименьшее. Уравнения движения центра масс элемента ab ремня массы на ведущем шкиве в естественном виде [1] запишем так:
/Belov1%20.files/image055.png)
Проинтегрируем обе части уравнений по всем элементам ab ремня на дуге охвата ремня по окружности шкива 1:
/Belov1%20.files/image056.png)
Формулы (12) с учетом равенств (9), а также (13) и аналогичных для ведомого шкива примут такой вид:
/Belov1%20.files/image057.png)
По определению, условие отсутствия буксования ремня на ведущем шкиве можно записать так:
или с учетом равенств (13)
(15)
Условие отсутствия буксования для ведомого шкива выводится аналогично:
(16)
Сцепление ремня с ведущим и ведомым шкивом характеризуется соответственно коэффициентом β1, β2 запаса сцепления:
/Belov1%20.files/image061.png)
Уравнения (4), (7), (8), (10) позволяют найти четыре неизвестные ,
,
,
. Они справедливы при отсутствии буксования ремня.
Отметим, что искомые неизвестные являются константами, если момент пары сил нагрузки не изменяется. Если момент пары сил изменяется и задан как функция времени, то при малом моменте сил инерции шкивов четыре неизвестные ,
,
,
определяются из тех же уравнений как функции от времени.
5. Алгоритм расчета
1. Задаем исходные данные: R1 [м]; R2 [м]; L [м]; r1 [м]; r2 [м]; s [м2]; ρ [кг/м3]; 1 [рад/с]; M2 [Н м];
[Па]; E [Па];
[Па]; f ; µ.
2. Определяем углы охвата ремней, скорость точки ведущей ветви по формуле (1), начальной силы растяжения ремня и моментов холостого хода по формулам (14).
;
;
;
;
;
.
3. Отмечаем, что три уравнения (4), (8), (10) содержат три неизвестные ,
,
. Они приводятся к кубичному уравнению относительно переменной z:
,
где ;
;
;
.
4. Находим единственный корень z кубического уравнения на отрезке [0, 1] численным методом (например, методом Ньютона) и определяем скорость точки ведомой ветви ремня: .
5. Определяем неизвестные ,
из уравнений (4), (10):
;
;
6. Определяем силы натяжения и момент пары движущих сил из уравнений (7): , Н;
, Н;
, Н м.
7. Проверяем условия (15), (16) отсутствия буксования:
;
8. Проверяем условие упругости ремня по среднему слою: .
9. При выполнении условий в п. 7, 8 определяем угловую скорость ведомого шкива по формуле (1): , рад/с.
10. Определяем передаточное отношение по формуле .
11. Определяем мощности движущих сил и сил сопротивления:
;
.
12. Оцениваем коэффициент полезного действия ременной передачи:
.
13. Оцениваем относительное скольжение ремня по формуле
.
14. Оцениваем коэффициент тяги передачи по формуле
.
15. Оцениваем коэффициенты запаса сцепления по формулам (17).
6. Анализ тяговых характеристик
Рассчитаем тяговые характеристики ременной передачи (табл. 1).
1. Исходные данные
|
R1, м |
R2, м |
L, м |
r1, мм |
r2, мм |
s, мм2 |
δ, мм |
ρ, кг/м3 |
|
M2, Н м |
|
E, МПа |
|
f |
µ |
|
0,1 |
0,2 |
0,7 |
10 |
20 |
160 |
2 |
1200 |
800 |
40 |
1,6 |
160 |
2,2 |
0,3 |
0,12 |
Расчет произведем по формулам алгоритма, полагая, что единицы измерения исходных данных приведены к системе СИ.
/Belov1%20.files/image099.png)
тяги и относительное скольжение возрастают (рис. 7, слева).
Коэффициент полезного действия передачи увеличивается с увеличением момента пары сил нагрузки от 5 до 40 Н м и увеличении коэффициента тяги (рис. 7, справа).
/Belov1%20.files/image100.png)
С увеличением нагрузки коэффициент β1 запаса сцепления ремня с ведущим шкивом и β2 с ведомым шкивом уменьшаются (рис. 8, слева).
/Belov1%20.files/image101.png) |
При уменьшении коэффициента запаса сцепления на одном из шкивов до 1 эффективность ременной передачи возрастает. Коэффициент полезного действия достигает максимума при такой нагрузке и тяге, когда коэффициент запаса сцепления на одном из шкивов уменьшится до минимально допустимого.
Чтобы поддерживать заданный коэффициент запаса сцепления, при повышении нагрузки силу натяжения ремня необходимо регулировать, увеличивая ее прямо пропорционально моменту пары сил нагрузки (рис. 8, справа).
Рассмотрим вариант модели, когда в исходных данных вместо начальной силы натяжения ремня или начального нормального напряжения в сечении ремня задано значение β коэффициента запаса сцепления
.Тогда равенство (10) с учетом (17) можно переписать так:
, (18)
где
Уравнения (4), (7), (8), (18) позволяют найти четыре неизвестные ,
,
,
. Начальная сила натяжения ремня определяется по формуле (10):
.
Как показали расчеты, если коэффициент запаса сцепления на одном из шкивов равен 1, то есть дуги упругого скольжения и охвата шкива ремнем совпадают, то справедлива формула Эйлера без учета «вклада» сил инерции, деформации и толщины ремня: .
Снижение модуля упругости ремня в процессе эксплуатации приводит к ухудшению характеристик передачи (рис. 9).
/Belov1%20.files/image107.png) |
При снижение эксплуатационных характеристик ремня дополнительное растяжение позволяет уменьшить коэффициент запаса сцепления и увеличить коэффициент полезного действия передачи.
Выводы
1. Компьютерная модель ременной передачи позволяет оценить тяговые характеристики ремня.
2. В режиме отсутствия буксования ремня эффективность ременной передачи возрастает при уменьшении коэффициента запаса сцепления. Коэффициент полезного действия достигает максимума при такой нагрузке, когда коэффициент запаса сцепления на одном из шкивов уменьшится до минимально допустимого.
3. Чтобы поддерживать заданный коэффициент запаса сцепления, при изменении нагрузки силу натяжения ремня целесообразно регулировать.
Список литературы:
1. Белов.М.И. , Пылаев Б.В. Теоретическая механика. 2-е изд., перераб. и доп. − М.: ИНФРА-М, 2016. − 336 с. / [Электронный ресурс]. – Ре-жим доступа: URL: http://znanium.com/catalog.php?bookinfo=556474 (дата обращения 12.05.2017).
2. Гузенков П. Г. Детали машин. − М.: Высшая школа, 1982. − 352 c
3. Седов Л. И. Механика сплошной среды. том II. Учебник. − М.: Наука, 1976. − 574 с.
Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.
Угловая скорость
Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.
Обозначение угловой скорости: ω (омега).
Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.
С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.
Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:
Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.
Быстрота изменения угла φ (перемещения плоскости П из положения П1 в положение П2) – это и есть угловая скорость:
Приняв вектор k как единичный орт положительного направления оси, получим:
Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.
Формулы угловой скорости
Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:
- если известно количество оборотов n за единицу времени t:
- если задан угол поворота φ за единицу времени:
- если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:
Размерности угловой скорости:
- Количество оборотов за единицу времени [об/мин], [c-1].
- Угол поворота за единицу времени [рад/с].
Определение угловой скорости
Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.
Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.
Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.
Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.
Другие примеры решения задач >
Угловое ускорение
Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:
Обозначение: ε (Эпсилон)
Единицы измерения углового ускорения: [рад/с2], [с-2]
Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.
Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).
Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:
Расчет углового ускорения
Пример: По заданному значению касательной составляющей полного ускорения aτ точки B, расположенной на расстоянии r от центра вращения колеса.
Требуется определить величину и направление углового ускорения колеса ε, если aτ = 10 м/с2, r = 50 см.
Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.
Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.
В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:
Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость
ω = 1,5 с-1 = 9,42 рад/с.
Смотрите также:
- Примеры расчета угловой скорости и ускорения
- Скорости и ускорения точек вращающегося тела
Вращательное движение твердого тела:
При поступательном движении тела все его точки движутся по одинаковым траекториям и в каждый данный момент они имеют равные скорости и равные ускорения.
Поэтому поступательное движение тела задают движением какой-либо одной точки, обычно движением центра тяжести.
Рассматривая в какой-либо задаче движение автомобиля (задача 147-29) или тепловоза , фактически рассматриваем движение их центров тяжести.
Вращательное движение тела нельзя отождествить с движением какой-либо одной его точки. Ось любого вращающегося тела (маховика дизеля, ротора электродвигателя, шпинделя станка, лопастей вентилятора и т. п.) в процессе движения занимает в пространстве относительно окружающих неподвижных тел одно и то же место.
Движение материальной точки или поступательное движение тела характеризуют в зависимости от времени линейные величины s (путь, расстояние),
Вращательное движение тела в зависимости от времени t характеризуют угловые величины: 
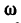
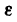
Закон вращательного движения тела выражается уравнением
Угловая скорость — величина, характеризующая быстроту вращения тела, определяется в общем случае как производная угла поворота по времени
Угловое ускорение – величина, характеризующая быстроту изменения угловой скорости, определяется как производная угловой скорости
Приступая к решению задач на вращательное движение тела, необходимо иметь в виду, что в технических расчетах и задачах, как правило, угловое перемещение выражается не в радианах 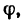
Поэтому необходимо уметь переходить от числа оборотов к ра-дианному измерению углового перемещения и наоборот.
Так как один полный оборот соответствует 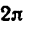
Угловая скорость в технических расчетах очень часто измеряется в оборотах, произведенных в одну минуту (об/мин), поэтому необходимо отчетливо уяснить, что 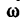
Переход от одних единиц угловой скорости к другим производится по формулам
При вращательном движении тела все его точки движутся по окружностям, центры которых расположены на одной неподвижной прямой (ось вращающегося тела). Очень важно при решении задач, приведенных в этой главе, ясно представлять зависимость между угловыми величинами 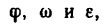
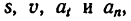
Если р- расстояние от геометрической оси вращающегося тела до какой-либо точки А (на рис. 205 р=ОА), то зависимость между 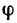
s—p-
Зависимость между угловой скоростью тела и скоростью точки в каждый данный момент выражается равенством
Касательное ускорение точки зависит от углового ускорения и определяется формулой
Нормальное ускорение точки зависит от угловой скорости тела и определяется зависимостью
При решении задачи, приведенной в этой главе, необходимо ясно понимать, что вращением называется движение твердого тела, а не точки. Отдельно взятая материальная точка не вращается, а движется но окружности — совершает криволинейное движение.
Равномерное вращательное движение
Если угловая скорость 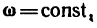
Уравнение равномерного вращения имеет вид
В частном случае, когда начальный угол поворота
Угловую скорость равномерно вращающегося тела
можно выразить и так:
где Т — период вращения тела; 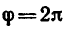
Задача №1
Маховое колесо вращается равномерно с угловой скоростью 16 рад/сек. Определить, сколько оборотов сделает колесо за 5 мин вращения.
Решение 1.
1. Находим угол поворота маховика в радианах, имея в виду,
2. Находим число оборотов маховика:
Таким образом, за 5 мин маховик сделает 763 оборота. Решение 2.
1. Переведем угловую скорость
2. Имея в виду, что уравнение равномерного вращательного движения можно представить так:
где 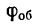
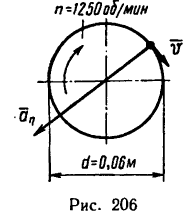
Задача №2
Вал, диаметр которого 0,06 м, вращается равномерно и делает 1200 об/мин. Определить скорость и ускорение точек вала на его поверхности (рис 206). Решение.
1. Скорость точки вращающегося тела можно найти по формуле
4 Подставим сюда
Вал вращается равномерно, значит скорость точек остается
численно неизменной. По этой же касательное ускорение.
5. Нормальное ускорение найдем из формулы
которое также в данном случае остается по модулю неизменным.
Задача №3
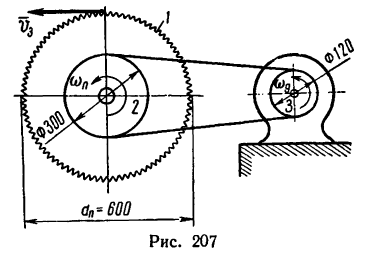
Дисковая пила 1 имеет диаметр 600 мм.
На валу пилы насажен шкив 2 диаметром 300 мм, а шкив
соединен бесконечным ремнем со шкивом двигателя 3 (рис. 207) дна» метром 120 мм. С какой угловой скоростью должен вращаться шкив двигателя, чтобы скорость зубьев пилы не превышала 15 м/сек?
Решение.
1. Так как пила 1 и шкив 2 насажены на одном валу, то они имеют одну и ту же угловую скорость <о„ и скорость зубьев пилы 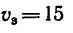
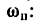
2. Находим угловую скорость шкива 2, который обеспечивает необходимую рабочую скорость зубьев пилы:
3. Теперь найдем угловую скорость юд шкива двигателя. Шкивы 2 и 3 соединены бесконечным ремнем. Полагая, что
ремень не растягивается и не проскальзывает на шкивах, можно считать, что все его точки движутся с одной и той же скоростью Ор. Это означает, что скорости точек, расположенных на поверхностях обоих шкивов, одинаковы и равны
Поэтому применим зависимость
Отсюда
4. Если перевести эту угловую скорость в об[мин, то
Таким образом, для того чтобы зубья пилы имели скорость 15 м/сек, шкив двигателя должен вращаться с угловой скоростью 125 рад/сек или 1200 об/мин.
- Равнопеременное вращательное движение
- Неравномерное вращательное движение
- Плоскопараллельное движение тела
- Определение передаточных отношений различных передач
- Равнопеременное движение точки
- Неравномерное движение точки по любой траектории
- Определение траектории, скорости и ускорения точки
- Кинематический способ определения радиуса кривизны траектории
1
Рассчитайте диаметр ведущего шкива по формуле: D1 = (510/610) · ³√(p1·w1) (1), где:
— p1 — мощность двигателя, кВт;
— w1 — угловая скорость ведущего вала, радианы в секунду. Величину мощности двигателя возьмите из технической характеристики в его паспорте. Как правило, там же указывается количество оборотов двигателя в минуту.
2
Переведите количество оборотов двигателя в минуту в радианы в секунду, умножив исходное число на коэффициент 0,1047. Подставьте найденные числовые значения в формулу (1) и вычислите диаметр ведущего шкива (узла).
3
Вычислите диаметр ведомого шкива по формуле: D2= D1·u (2), где:
— u — передаточное число;
— D1 — рассчитанный по формуле (1) диаметр ведущего узла. Передаточное число определите делением угловой скорости ведущего шкива на необходимую угловую скорость ведомого узла. И наоборот, по заданному диаметру ведомого шкива можно рассчитать его угловую скорость. Для этого вычислите отношение диаметра ведомого шкива к диаметру ведущего, затем поделите на это число величину угловой скорости ведущего узла.
4
Найдите минимальное и максимальное расстояние между осями обоих узлов по формулам: Аmin = D1+D2 (3), Аmax = 2,5·(D1+D2) (4),
где:
— Аmin — минимальное расстояние между осями;
— Аmax — максимальное расстояние;
— D1 и D2 — диаметры ведущего и ведомого шкивов. Расстояние между осями узлов не должно быть более 15 метров.
5
Рассчитайте длину ремня передачи по формуле: L = 2А+П/2·(D1+D2)+(D2-D1)²/4А (5), где:
— А — расстояние между осями ведущего и ведомого узлов,
— Π — число «пи»,
— D1 и D2 — диаметры ведущего и ведомого шкивов. При вычислении длины ремня прибавьте к получившемуся числу 10 — 30 см на его сшивку. Итак, пользуясь приведенным формулами (1-5), вы легко сможете рассчитать оптимальные величины узлов, составляющих плоскоременную передачу.
В этой статье
- История
- Устройство ременной передачи
- Открытая, перекрестная и полуперекрестная передача
- Повышающая и понижающая передача
- Как посчитать передаточное отношение для ремённой передачи
- Передаточное число
- Передаточное отношение многоступенчатой ремённой передачи
- Виды приводных ремней
- Преимущества и недостатки ремённых передач
- Определения
- Вопросы
- Задачи
- Полезное видео
История
Ремённая передача – одна из древнейших и простых механических передач, в которой используются приводные ремни и специальные колеса — шкивы. По некоторым источникам, ременная передача впервые документально описана китайским философом, поэтом и политиком Ян Сюном (53 год до н. э. – 18 год н. э.) периода империи Хань в тексте «Словарь местных выражений». Описанное устройство использовали ткачи в своей работе с шелком.
Кстати, слово «ремённая» записывается через букву «ё», на которую и нужно ставить ударение. Но в печати, например, в нашем следующем заголовке, точки над «ё» могут опускать. Это не является ошибкой, но не забудьте ставить ударение правильно.
На средневековых картинах можно увидеть механизм — самопрялку, в которой принцип ремённой передачи используется для ускорения получения пряжи. Большое развитие ремённая передача вместе с другими механизмами получила во времена английской промышленной революции (1780-1830 гг.), которая началась с изобретения в 1769 году паровой машины. Небольшие кустарные ремесленные производства начали вытесняться фабричным трудом с большим количеством машин.


На приведенной ниже картинке показаны примеры использования ремённой передачи в современных технических устройствах – от двигателя внутреннего сгорания автомобиля до 3D-принтера.

Устройство ременной передачи
Ведущее и ведомое колесо – это шкивы. Их соединяет приводной ремень. Ведущий шкив — тот, который крутит мотор или другая внешняя сила, а ведомый – следующий за ним. Часто для предотвращения соскакивания ремня на ободе шкива делают канавку или бортики.
Чтобы ремень не проскальзывал, его нужно хорошо натянуть. Кто ездил на велосипеде хорошо знает проблему, что плохо натянутая цепь так и норовит слететь со звездочки, а если перетянешь – трудно ехать и она легко порвется. Для натяжения ремня или устранения его колебаний могут использоваться натяжные и прижимные ролики.
Диаметр ведущего шкива мы обозначим английской буквой d1, а ведомого — буквой d2. Нам это понадобится при расчетах.

Ремень является самым дешевым устройством в данном механизме. Но за счет него ремённая передача обеспечивает плавность хода и снижение шума. Такая передача способна амортизировать рывки и снижать нагрузку на мотор. Так, если на циркулярном станке резко заклинит диск при распиливании дубовой доски, электромотор остановится не сразу, а с задержкой за счет упругости ремня и его проскальзывания.
Рассмотрим следующую схему.

Ведущая ветвь ремня — та, которая набегает на ведущий шкив. Она при работе передачи испытывает растяжение.
Ведомая ветвь ремня — та, которая сходит с ведущего ремня и набегает на ведомый. Она при работе сжимается и расслабляется.
Сжатие и растяжение двух ветвей компенсируется. Иначе ремень рвется. При переходе с одной ветви на другую ремень упруго сжимается или растягивается. В этих зонах на шкиве происходит упругое скольжение ремня. Из-за изменения величины упругого скольжения передаточное отношение ремённой передачи непостоянное и может увеличиваться или уменьшаться в зависимости от нагрузки. При очень большой нагрузке ремень может упруго скользить по всей поверхности шкива.
Также важно знать про угол обхвата ремнём шкива. Чем больше угол обхвата, тем больше площадь контакта, тем больше полезная сила трения. При большой разнице в диаметрах шкивов этот угол может быть очень маленьким. Ремень при этом может проскальзывать. Чтобы увеличить угол обхвата без увеличения межосевого расстояния можно использовать прижимной ролик (смотри картинку ниже). В таком случае устанавливают ролик на ведомую ветвь, которая расслаблена, иначе ведущая ветвь растянется еще сильнее и износ ремня значительно вырастет.

Открытая, перекрестная и полуперекрестная передача
- В открытой ременной передаче шкивы расположены в одной плоскости параллельно друг-другу. Такая передача не меняет направления вращения ведомого шкива.
- В перекрестной ременной передаче приводной ремень закручен восьмеркой. Большой минус такого способа изменения направления вращения – большой износ ремня из-за дополнительного трения. Этот способ можно использовать при создании моделей из образовательного конструктора, но он редко используется в промышленных устройствах.
- В полуперекрестной ременной передаче ось вращения одного из шкивов повернута на некоторый угол относительно другой оси (например, на 90 градусов).
Повышающая и понижающая передача
Рассмотрим нижнюю картинку. Зеленый шкив с помощью ручки крутит персонаж с силой F. Это ведущий шкив. Синий шкив крутится за счет ремня. Это ведомый шкив. К нему на вал подвешен груз с максимально возможной массой, которую может поднять механизм.
- В первом случае диаметр ведущего и ведомого шкивов одинаковый. Скорость и сила на выходе не поменяется.
- Во втором случае диаметр ведущего шкива меньше ведомого. Скорость на выходе упадет. Такая передача называется понижающей. Сила при этом увеличится и механизм сможет поднять груз большей массы, чем первый.
- В третьем случае диаметр ведущего шкива больше ведомого. Скорость на выходе увеличится. Такая передача называется повышающей. Сила при этом уменьшится и механизм сможет поднять груз меньшей массы, чем первый и второй.
Почему так происходит? Любой сложный механизм можно представить через простые механизмы. В данном случае ручка, за которую тянет персонаж и радиус к точке на окружности, которую толкает приводной ремень, образуют рычаг. Посмотрите на следующий рисунок.
Короче плечо рычага к нагрузке (радиус шкива) – больше сила, но меньше пройденный путь.
Длиннее плечо рычага к нагрузке (радиус шкива) – меньше сила, но больше пройденный путь.
Эти схемы с понижающей и повышающей ремённой передачей наглядно демонстрируют работу золотого правила механики — за выигрыш в силе приходится платить таким же проигрышем в расстоянии (схема 1) или за выигрыш в расстоянии приходится платить таким же проигрышем в силе (схема 2).
Как посчитать передаточное отношение для ремённой передачи
При создании ремённой передачи нужно понимать, во сколько мы выиграем или проиграем в скорости и силе, чтобы собрать устройство с нужными характеристиками.
Передаточное отношение обозначается буквой i. Оно показывает, во сколько раз снизилась скорость вращения на выходе. Согласно золотому правилу механики, во столько же раз увеличится сила (крутящий момент).
Формулу для расчета передаточного отношения можно вывести из правила рычага. Передаточное отношение для ремённой передачи рассчитывается так:

Таким же образом передаточное отношение можно посчитать через соотношения радиусов.
Узнать размеры шкивов можно с помощью линейки. Самый точный метод измерения диаметра – с помощью штангенциркуля.

Передаточное отношение удобно записывать со знаком деления в виде i = 1 : 1. Эта запись показывает, что 1 оборот на входе даст 1 оборот на выходе. Передаточное отношение i = 5 : 1 показывает, что 5 оборотов на входе дает 1 оборот на выходе, то есть скорость упала в 5 раз (передача понижающая).
Если дробь можно сократить, её сокращают. Например, i = 5 : 25 = 1 : 5 (передача повышающая).
Передаточное число
Передаточное отношение можно записать в виде числа, поделив числитель на знаменатель. Например, i = 5 : 1 = 5, или i = 1 : 4 = 0,25. В данном случае говорят о передаточном числе.
Рассмотрим разные варианты передаточных чисел:

Передаточное отношение многоступенчатой ремённой передачи
Если передача многоступенчатая (двух-, трехступенчатая и т.д.), то общее передаточное отношение будет вычисляться как произведение отдельных передаточных отношений.

Эта формула справедлива для следующего рисунка:

Передаточное отношение для шкивов, жестко закрепленных на общей оси, не считается — скорость их вращения будет всегда одинаковой!
Виды приводных ремней
Видов ремней достаточно много, так как используются они в разных условиях. Где-то нужно передать очень большую мощность так, чтобы ремень не порвался и не растянулся. Где-то ремень не должен проскальзывать. Где-то ремень должен крутиться очень-очень быстро и мало изнашиваться со временем. А где-то нужно передать вращение на большое расстояние и под углом.
Очень распространенная классификация ремней – по поперечному сечению или форме. Основные виды: 1 — плоские ремни, 2 – клиновые ремни, 3 – ремни круглого сечения (пассики), 4 – многоручьевые ремни (или поликлиновые), 5 – зубчатые ремни.

В крупной промышленной технике самые распространенные ремни – клиновые и поликлиновые. Они достаточно толстые по сечению и имеют увеличенную за счет боковой поверхности площадь сцепления со шкивами.
В небольших электронных устройствах чаще используются плоские ремни и пассики (ремни с круглым сечением).

Плоские ремни широко использовались в 19-м и начале 20 века на фабриках для передачи движения на несколько машин с одного линейного вала (англ. line shaft). Они широко применялись и применяются в лесопильных станках, молотилках, электрогенераторах.
В станках с ЧПУ (3D-принтерах, плоттерах, лазерных станках) используются зубчатые ремни, так-так они сохраняют постоянное передаточное отношение и не проскальзывают.
Преимущества и недостатки ремённых передач
Как и у любого устройства, у ремённой передачи есть свои плюсы и минусы по сравнению с другими механизмами. Выделим важные из них.
Преимущества:
- простота конструкции;
- малая стоимость:
- малая шумность;
- плавность работы;
- сглаживание ударных перегрузок за счет упругости ремня;
- возможность менять направление вращения под разным углом;
- возможность передавать вращение на большое расстояние.
Недостатки:
- большие габариты конструкции;
- плохая работа на больших скоростях (появление вибраций);
- большая нагрузка на оси (валы, подшипники);
- непостоянное передаточное отношение при разной нагрузке (из-за упругого скольжения);
- малый срок службы ремня по сравнению с зубчатыми колесами;
- биение приводного ремня при его слабом натяжении;
- необходимость в дополнительных элементах при большой длине ремня или малом угле обхвата;
- увеличение износа приводного ремня или осей при неправильном натяжении.
Определения
- Ведущая ветвь ремня — набегает на ведущий шкив. При работе передачи растягивается.
- Ведомая ветвь ремня — сходит с ведущего ремня и набегает на ведомый. При работе передачи расслабляется.
- Межосевое (межцентровое) расстояние – кратчайшее расстояние между осями шкивов.
- Натяжной ролик (леникс, от нем. lenix, lenixrolle — натяжной ролик) – элемент ремённой или цепной передачи; свободно вращающееся на оси колесо (шкив, звездочка, ролик), которое используется для регулирования натяжения ремня или цепи. Например, используется в тракторах для натяжения гусениц или в двигателе автомобиля для натяжения ремня ГРМ (газораспределительного механизма).
- Пассик (от польского pasek — ремешок) – исторически вошедшее в наш оборот название приводного ремня круглого сечения. Слово «пассик» имеет польское происхождение. Его появление в русском словаре связывают с 80-ми годах 20-го века, когда им называли соответствующий элемент в импортном польском магнитофоне. Пассик, как правило, выполнен из резины или других полимерных материалов. Пассики использовались в устройстве протяжного механизма магнитной ленты старого кассетного магнитофона – он хорошо сглаживал рывки от электромотора и предохранял от искажений звука. «Пассики» входят в комплект конструктора Lego WeDo или ресурсного набора Lego MINDSTORMS Education EV3. В общем, всякий пассик — приводной ремень, но не каждый приводной ремень – пассик.
- Приводной ремень – гибкий замкнутый элемент (ремень) для передачи вращения между двумя шкивами. Вращение передается за счет силы трения (гладкий ремень) или силы зацепления (ремень с зубчиками). Может иметь разную форму: бывают плоские ремни, зубчатые ремни, клиновидные ремни.
- Ремённая передача (англ. belt drive)– механизм, предназначенный для передачи вращательного движения с помощью силы трения или зубчатого зацепления замкнутой гибкой связи (ремня) с помощью колес (шкивов), закрепленных на входном и выходном вале.
- Угол обхвата – угол прилегания ремня к шкиву.
- Шкив – фрикционное (англ. friction — трение) колесо с ободом или канавкой по окружности. Передает или принимает движение от приводного ремня. В отличие от блока, который имеет похожую форму, шкив всегда передавет усилие с оси на ремень, либо принимает усилие с ремня на ось. Блок же всегда свободно вращается на оси и обеспечивает изменение направления движения каната/троса, а также изменяет прикладываемую силу.
Вопросы
1. Что ты можешь сказать о ремённых передачах по этим двум изображениям? В чем их отличие и из каких элементов они состоят?

Задачи
1. Мальчик Ваня измерил штангенциркулем ведущий и ведомый шкив. Диаметр первого составил 12 миллиметров, второго – 32 миллиметра. Какое передаточное отношение у этой ремённой передачи?
2. Угловая скорость вращения вала мотора – 420 оборотов в секунду. Какая угловая скорость будет у ведомого шкива, если передаточное отношение i = 12 : 1?
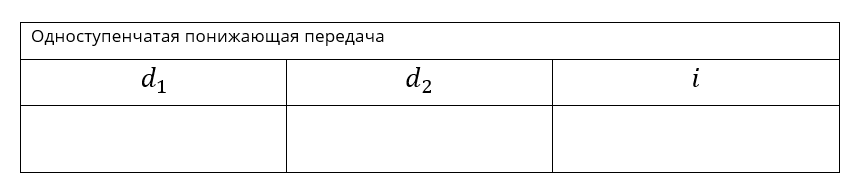
3. Собери одноступенчатую понижающую ремённую передачу из деталей Lego. В качестве шкивов можно использовать диск узкого или большого колеса и желтые втулки. На ведущую ось установи ручку, на ось ведомого шкива установи стрелку, чтобы считать обороты.
Измерь с помощью линейки или штангенциркуля диаметры шкивов.
Заполни таблицу. Проверь опытным путем полученное значение с помощью стрелки.

4. Собери двухступенчатую понижающую ремённую передачу с ручкой и стрелкой (пример — в 3 задаче). Посчитай передаточное отношение через диаметры. Проверь полученное значение опытным путем.


Полезное видео
- Э+М. Ременная передача. Урок №3
- GetAClass. Золотое правило механики
- Анимация. Прямая и перекрестная ременная передача
- Анимация. Ременная передача — работы различных механизмов с помощью ремня
/Belov1%20.files/image053.png)
/Belov1%20.files/image104.png)