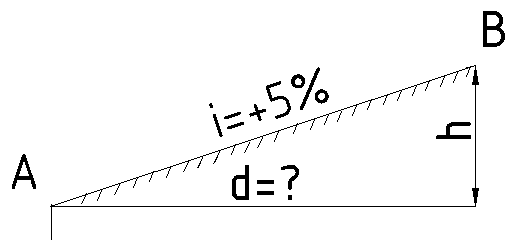7.2.1. Определение
Угол наклона
линии
– угол, отсчитываемый от горизонтальной
плоскости, проходящей через центр лимба
вертикального угломерного круга до
направления линии визирования.
Углы наклона бывают
положительные
(+ν),
отрицательные
(–ν),
могут изменяться от 0 до 90° (рис. 52).
Для измерения
углов наклона у теодолитов служит
вертикальный
угломерный круг (ВУК),
у которого имеются два конструктивных
отличия от круга горизонтального:
-
лимб жёстко
соединен с осью зрительной трубы и
вращается вместе с трубой; -
алидада неподвижна,
ее линия 0 – 180° должна совпадать с
горизонтом.
Перед каждым
отсчётом алидаду необходимо установить
в горизонтальное положение. Это положение
обеспечивается тогда, когда пузырёк
цилиндрического уровня при алидаде ВУК
находится на середине.
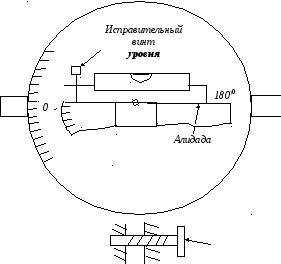
Рис. 52. Измерение
вертикальных углов
7.2.2. Место нуля вертикального круга
У теодолита с
металлическими кругами и у некоторых
оптических, цилиндрический уровень
прикреплён непосредственно к алидаде
вертикального круга (рис. 53). При вращении
микрометренного винта алидада
поворачивается, соответственно,
перемещается пузырёк цилиндрического
уровня. При изменении угла наклона
линии, перед взятием отсчёта по
вертикальному кругу, пузырёк уровня
выводят на середину (микрометренным
винтом у теодолитов с металлическими
кругами, подъёмными винтами у некоторых
оптических теодолитов). Но при этом даже
при расположении пузырька уровня на
середине линия нулей отсчётного
приспособления может составлять
некоторый угол с линией горизонта. Этот
угол называется местом
нуля вертикального круга (М0).
Место нуля –
отсчет по вертикальному кругу, когда
пузырёк уровня при алидаде находится
в нульпункте, а визирная ось зрительной
трубы занимает горизонтальное положение.
Микрометренный
винт алидады ВУК
Рис.
53. Цилиндрический уровень при алидаде
вертикального круга (TT-50,
TT-5)
7.2.3. Расчётные формулы места нуля для теодолитов с металлическими кругами
Если МО≠0, то для
приведённой на рис. 51 оцифровки лимба
получаем расчётные формулы, исходя из
следующего.
При визировании
на точку М обозначим отсчёт по вертикальному
кругу при круге право – КП (рис. 54 а), при
круге лево – КЛ (рис. 54 б). Тогда
и
,
(28, 29)
соответственно
,
(30)
.
(31)
Решая систему,
получаем:
,
.
(32, 33)
Итак, визируя на
какую-то достаточно удалённую и высоко
расположенную точку при двух положениях
вертикального круга, взяв отсчёты КП и
КЛ для определения МО и для вычисления
угла наклона, можем пользоваться
расчётными формулами:
,
(34)
,
,
(35)
.
(36)
При использовании
этих формул к отсчётам, меньшим 90°,
следует
прибавить 360°
.
7.2.4. Расчётные формулы места нуля для оптических теодолитов
Приведённые выше
расчётные формулы для определения угла
наклона получены для теодолитов с
металлическими кругами (ТТ-50; ТТ-5 и др.).
Конструктивные особенности оптических
теодолитов определяют отличие в расчётных
формулах и в способах приведения М0 к
нулю. Так, для Т30 будет:
,
,
,
.
При значениях КП
и КЛ меньшим 90°
, прибавить
360° .
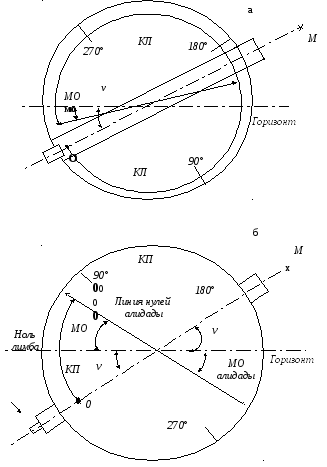
Рис. 54. Определение
места нуля вертикального угломерного
круга
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Собрание уникальных книг, учебных материалов и пособий, курсов лекций и отчетов по геодезии, литологии, картированию, строительству, бурению, вулканологии и т.д.
Библиотека собрана и рассчитана на инженеров, студентов высших учебных заведений по соответствующим специальностям. Все материалы собраны из открытых источников.
Измерение вертикальных углов.
Для измерения вертикальных углов служит вертикальный круг теодолита, жестко укрепленный на оси зрительной трубы и вращающийся вместе с ней.
В точных теодолитах соосно с вертикальным кругом крепится алидада вертикального круга с отсчетным устройством и собственным уровнем или компенсатором углов наклона, его заменяющим.
В теодолитах Т30 отсчетное устройство вертикального круга укреплено неподвижно в стойке теодолита, а его уровнем служит уровень при алидаде горизонтального круга. При измерении вертикального угла пузырек уровня приводят в нульпункт подъемными винтами подставки.
Вертикальные круги разных типов теодолитов оцифрованы различно, отчего различаются формулы вычисления вертикальных углов по полученным в ходе измерений отсчетам. Рассмотрим измерение углов наклона теодолитом Т30.
Отсчет при трубе, расположенной горизонтально, и пузырьке уровня в нульпункте называется местом нуля вертикального круга (М0).
Для измерения вертикального угла наводят трубу на визирную цель при двух положениях вертикального круга (слева и справа) и, приводя каждый раз пузырек уровня в нульпункт, берут отсчеты по вертикальному кругу: Л (лево) и П (право).
Очевидно, что угол наклона равен разности отсчетов при трубе, наведенной на цель и при трубе, расположенной горизонтально. Поэтому для круга слева напишем
ν = Л – М0. (7.1)
Аналогично, учитывая оцифровку вертикального круга Т30, где при круге справа отсчеты сопровождаются противоположным знаком (положительные углы знаком минус и наоборот), напишем
ν = М0 – П (7.2)
Из формул (7.1) и (7.2) находим формулы угла наклона и места нуля.
;
. (7.3).
В ряде случаев, определяя углы наклона, ограничиваются измерениями при одном положении вертикального круга (слева или справа). Тогда пользуются формулой (7.1) или (7.2), для чего предварительно необходимо определить место нуля, измерив какой-нибудь угол при двух положениях вертикального круга и вычислив место нуля по формуле (7.3).
Вычисления по формулам (7.1) – (7.2) упрощаются, когда М0=0. Поэтому, если место нуля велико, его исправляют. При круге слева и пузырьке уровня в нульпункте наводят трубу на точку, по которой определяли место нуля. Вращением наводящего винта трубы устанавливают на вертикальном круге отсчет, равный углу наклона n. При этом изображение точки сместится из центра сетки нитей. Действуя вертикальными исправительными винтами сетки нитей, смещают сетку так, чтобы изображение точки оказалось в центре сетки. Учитывая что теперь труба наведена на точку с углом наклона n, и отсчет по вертикальному кругу равен Л = n из равенства (7.1) видим, что место нуля стало равно нулю М0 = 0.
Закрепленные
Понравившиеся
Теория
Измерение вертикальных углов
Вертикальные углы – это углы в вертикальной плоскости, проходящей через ось вращения теодолита и визирную ось зрительной трубы (коллимационная плоскость).
Вертикальный угол между отвесной линией и линией визирования называется зенитным расстоянием Z (рис.20).
Вертикальный угол между горизонтальной линией и линией визирования называется углом наклона () (см. рис.20).
Z + = 90°.
С помощью теодолитов ТЗО, 2ТЗО которые используются при выполнении этой лабораторной работы, измеряются углы наклона,
поэтому в дальнейшем будем говорить об измерении углов наклона. Полный приём измерения угла наклона состоит из измерений в положениях «круг лево» и «круг право».
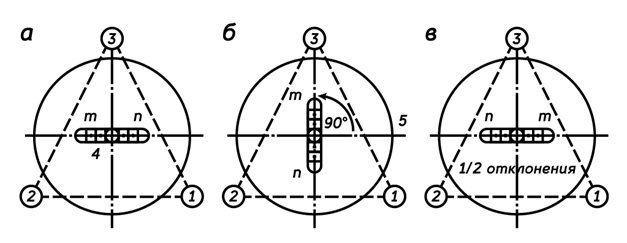
Теодолит устанавливается над заданной точкой и приводится в рабочее положение. Ослабив закрепительные винты алидады горизонтального круга и вертикального круга, выполняется наведение на визирную цель. При выполнении работы в лаборатории визирной целью является учебная марка. На рис. 21 показаны варианты наведения на различные виды марок при измерении вертикальных углов.
Наведение выполняется сначала грубо «вручную», а затем, закрутив закрепительные винты и добившись чёткого изображения визирной цели, выполняется точное наведение с помощью наводящих винтов. После этого берётся отсчёт по шкале отсчётного устройства вертикального круга теодолита.
При работе с теодолитами ТЗО, 2ТЗО перед взятием отсчёта с помощью подъёмных винтов приводится в нуль-пункт пузырёк уровня алидады горизонтального круга. Такие измерения выполняются в пол жениях «круг лево» и «круг право».
Рис. 21. Схема наведения на марки
Углы вычисляются по формулам:
для теодолита ТЗО
= (КЛ – КП -180) / 2;
= КЛ-МО; МО = (КЛ + КП +180) / 2; (11)
= МО – КП -180;
для теодолитов 2ТЗО
= (КЛ – КП) / 2;
= КЛ – МО; МО = (КЛ + КП) / 2; (12)
= МО – КП,
где КЛ – отсчёт по шкале вертикального круга, взятый в положении теодолита «круг лево»; КП – отсчет по шкале вертикального круга, взятый в положении теодолита «круг право»; МО – место нуля.
Место нуля — это отсчёт по шкале вертикального круга,
соответствующий горизонтальному положению визирной оси зрительной трубы и оси уровня вертикального круга. Для записи
результатов измерений углов наклона может использоваться журнал
измерений, приведённый в табл. 13.
Таблица 13
Журнал измерения углов наклона
Дата: 7.07.2010 Погода: облачно, тихо
Время: 8 ч 48 мин Видимость: хорошая
Теодолит:2ТЗОП № 848 Наблюдал: Иванов В.И.
| Назва-ние
или номер станции |
Назва-
ние или номер точки визиро-вания |
Положение
КЛ КП |
Отсчёты по
вертикальному кругу |
Место нуля
МО |
Угол наклона |
| о / | о / | ||||
| А | 1 | кл
кп |
+2 17,5 (1)
-2 19,0 (2) |
-0,8(3) | +2 18,2(4) |
| 2 | кл
кп |
-1 02,0 (5)
+ 1 01,0 (6) |
-0,5(7) |
-1 01,5(8) |
Примечание. Цифры в скобках указывают последовательность измерений и записей.
Контролируется качество измерения углов наклона по постоянству места нуля, Колебание места нуля не должно превышать 1′ для теодолита 2ТЗОП.
* – все приведённые в методических указаниях допуски при выполнении лабораторной работы могут быть увеличены в два раза.
Содержание
- Как вычисляется уклон рельефа?
- Калькулятор уклонов
- Онлайн калькулятор
- Посчитать уклон
- Посчитать превышение
- Посчитать расстояние
- Теория
- Как посчитать уклон
- Как посчитать превышение
- Как посчитать расстояние
- 1.3.2 Приемы определения крутизны склона
- 1.3.3 Определение географических и прямоугольных координат по топографической карте
- Билет №14. Определение уклонов и углов наклона по карте. Построение линии заданного уклона
- Практическая работа №3 Определение отметки точки по горизонталям
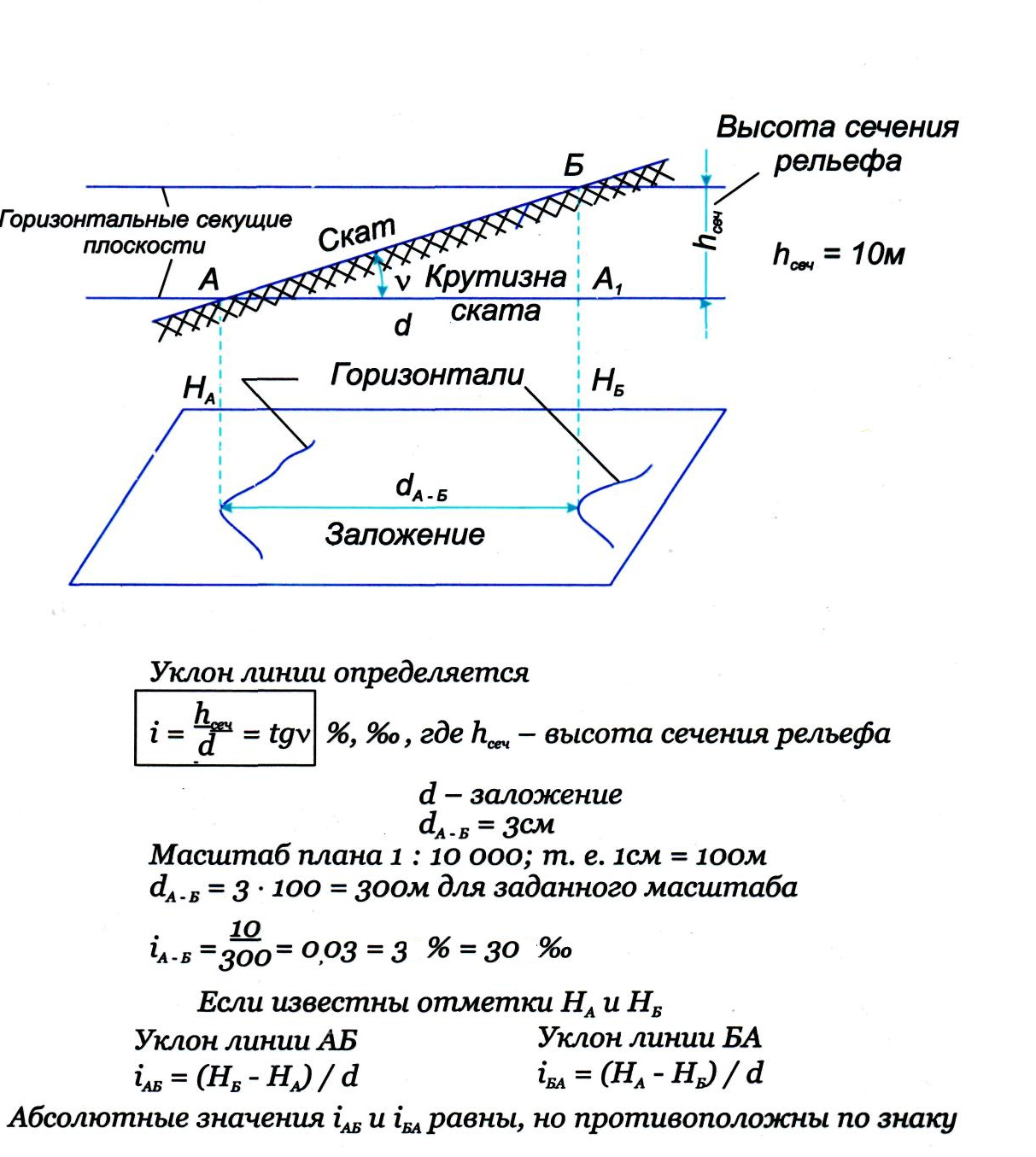
- Уклон линии. Скат. Крутизна ската
- Практическая работа №4 Определение уклона линии
Как вычисляется уклон рельефа?



Уклон является падением поверхности на единицу расстояния, выраженным в безразмерной (м / м, км / км и др.) или размерной (проценты, промилле, градус) форме.
Измерив по карте заложение а и зная высоту сечения рельефа h, можно вычислить тангенс угла наклона (уклон линии) и затем сам угол наклона ν.
Углом наклона линии называется угол между горизонтальным проложением линии и самой линией.
Иногда вместо угла наклона используют уклон местности – это тангенс угла наклона, его выражают обычно в процентах (%) или промилле (‰) (промилле – это тысячная часть целого).
Для быстрого определения угла наклона по карте пользуются специальным графиком заложений, который помещается внизу листа карты справа.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: 


Источник
Калькулятор уклонов
Онлайн калькулятор
Посчитать уклон
Расстояние L =
Превышение h =
Посчитать превышение
Уклон α =
Расстояние L =
Посчитать расстояние
Уклон α =
Превышение h =
Теория
Как посчитать уклон
Для того чтобы посчитать уклон вам, для начала, необходимо знать расстояние (L) и превышение (h). Далее следуйте формулам:
В процентах:
Уклон в % = h / L ⋅ 100
В промилле:
Уклон в ‰ = h / L ⋅ 1000
В градусах:
Уклон в ° = arctg ( h /L)
Пример
Для примера рассчитаем уклон дороги в процентах: на дистанции в L = 500 м дорога поднимается на h = 30 м:
Уклон дороги = 30/500 ⋅ 100 = 6%
Как посчитать превышение
Чтобы вычислить превышение (h), надо знать расстояние (L) и уклон (в процентах, в промилле или в градусах).
Если уклон в процентах (%):
h = L ⋅ Уклон в % /100
Если уклон в промилле (‰):
h = L ⋅ Уклон в ‰ /1000
Если уклон в градусах (°):
h = L ⋅ tg(α) , где α — уклон в градусах
Пример
Для примера найдём превышение h, если расстояние L= 5м, а угол уклона α=45°:
h = 5 ⋅ tg(45) = 5 ⋅ 1 = 5 м
Как посчитать расстояние
Для того чтобы посчитать расстояние (L) необходимо знать превышение (h) и уклон (в процентах, в промилле или в градусах).
Если уклон в процентах (%):
L = h / Уклон в % ⋅ 100
Если уклон в промилле (‰):
L = h / Уклон в ‰ ⋅ 1000
Если уклон в градусах (°):
L = h / tg(α) , где α — уклон в градусах
Пример
Для примера посчитаем расстояние (L), которое потребуется железной дороге, чтобы подняться на (h =) 6 м при угле подъёма 30‰:
Источник
1.3.2 Приемы определения крутизны склона
Расстояние между соседними горизонталями на плане или карте называется заложением склона. Заложение есть любое расстояние между соседними горизонталями, оно характеризует крутизну ската местности и обозначается d (рис. 1.8).
Вертикальный угол, образованный направлением ската с плоскостью горизонта и выраженный в угловой мере, называется углом наклона склона ν. Чем больше угол наклона, тем круче склон. (прим. В геодезии склон часто называют – скат).
Рис. 1.8 Определение угла наклона склона
Другой характеристикой крутизны служит уклон i. Уклоном линии местности называют отношение превышения к горизонтальному проложению. Из формулы следует (рис. 1.5), что уклон безразмерная величина. Его выражают в сотых долях (%) или тысячных долях – промилле (‰).
Например: i = 0,020 = 20‰ = 2%.
Если угол наклона склона до 45°, то он изображается горизонталями, если его крутизна более 45°, то рельеф обозначают специальными знаками (например, условный знак обрыва, рис. 1.1).
Для графического определения углов наклона по заданному значению заложения d, масштабу М и высоте сечения рельефа h строят график заложений (рис. 1.7, 1.9).
Вдоль прямой линии основания графика намечают точки, соответствующие значениям углов наклона. От этих точек перпендикулярно к основанию графика откладывают в масштабе карты отрезки, равные соответствующим заложениям, а именно
Концы этих отрезков соединяют плавной кривой (рис. 1.9).
Заложение линии, угол наклона которой надо определить, снимают с карты при помощи измерителя, а затем, укладывая на графике между основанием и кривой измеренный отрезок, находят соответствующее ему значение угла наклона (рис. 1.9).
Рис. 1.9 Фрагмент топографической карты и график заложения
1.3.3 Определение географических и прямоугольных координат по топографической карте
Определение географических координат
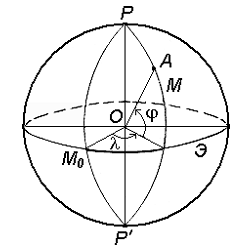
Рис. 1.10 Система географических координат
Географическая широта φ – угол, образованный отвесной линией в данной точке и экваториальной плоскостью. Географическая долгота λ – двугранный угол между плоскостью меридиана данной точки и начального меридиана (рис. 1.10).
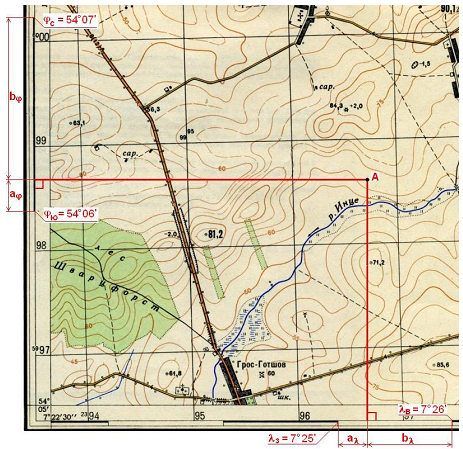
Для определения географических координат точки используют минутную рамку карты и значения долготы и широты, подписанные в углах рамки. Из данной точки к ближайшим сторонам минутной рамки с помощью прямоугольного треугольника опускают перпендикуляры (рис. 1.11) и измеряют отрезки aφ ,bφ , aλ, bλ
Рис.1.11 Определение географических координат
Широту и долготу заданной точки получают из выражений
φА= φю + 

где φю, φс – широты южной и северной параллели, проходящих через границы минутного деления рамки; aφ– расстояние, мм, от точки до южной параллели; вφ– расстояние, мм, от точки до северной параллели; λз, λв– долготы западного и восточного меридианов, проходящих через границы минутного деления рамки;aλ– расстояние, мм, от точки до западного меридиана;вλ– расстояние, мм, от точки до восточного меридиана.
На примере рис. 1.11:
Определение прямоугольных координат точек
Система прямоугольных координат представлена на карте километровой сеткой, образованной равностоящими линиями X и Y. при составлении топографических карт поверхность Земли меридианами через 6° делят на 60 зон, которые нумеруют, начиная от Гринвичского меридиана в направлении с запада на восток. Каждую зону изображают на плоскости, используя проекцию Гаусса-Крюгера, и устанавливают в ней прямоугольную систему координат, направляя ось Х на север по осевому меридиану зоны, а ось Y – на восток по экватору. Линии абсцисс Х и ординат Y на выходах за внутреннюю рамку карты подписывают значениями, выраженными в километрах (рис. 1.12). При этом у крайних линий сетки значения координат подписывают полностью – 5997 и 6006, а у промежуточных линий только две последние цифры 98, 99 и т.д.
Рис. 1.12 Определение прямоугольных координат
Прямоугольные координаты точки определяют, используя километровую сетку и оцифровку ее линий у внутренней рамки. Для этого находят координаты углов квадрата, в котором расположена точка, и измеряют кратчайшее расстояние от заданной точки до всех сторон квадрата (рис. 1.12).
Источник
Билет №14. Определение уклонов и углов наклона по карте. Построение линии заданного уклона
Определение уклонов и углов наклона. Отрезки линий на земной поверхности обычно имеют наклон, отчего начало и конец отрезка находятся на разных высотах. Разность их высот – превышение, а проекция отрезка на горизонтальную плоскость – его горизонтальное проложение.
Уклоном i линии называется отношение превышения h к горизонтальному проложению d:
Для определения по карте уклона линии на участке KL между двумя горизонталями (рис. 4.7) измеряют его горизонтальное проложение – заложение d. Поскольку концы отрезка лежат на смежных горизонталях, превышение hмежду ними равно высоте сечения рельефа, подписанному под южной рамкой карты. Воспользовавшись формулой (4.2), вычисляют уклон, который принято выражать в тысячных. Если, например, h=1 м, d=48 м , то уклон равен i =1 м / 48 м = 0,021=21‰.
 |
Рис. 4.7. Определение высоты точки M и уклона на отрезке KL |
С другой стороны, отношение превышения h к горизонтальному проложению d равно тангенсу угла n наклона линии. Поэтому
что позволяет, вычислив уклон определить по нему угол наклона.
При пользовании картой углы наклона не вычисляют, а определяют с помощью графика заложений (рис. 4.8), расположенного под южной рамкой карты. По горизонтальной оси графика отложены углы наклона, а по вертикальной — соответствующие этим углам заложения d, выраженные в масштабе карты и рассчитанные по формуле
гдеh — высота сечения рельефа, а M – знаменатель масштаба карты.
 |
Рис. 4.8. График заложений |
Для определения угла наклона отрезка KL (рис. 4.7), расположенного между горизонталями, берут его в раствор циркуля и на графике заложений (рис. 4.8) находят такой угол, над которым ордината равна раствору циркуля d. Это и есть искомый угол наклона.
При необходимости многократного определения уклонов пользуются графиком уклонов, построенным аналогично графику заложений, но с отложением по горизонтальной оси не углов наклона, а уклонов.
Проведение линии с уклоном, не превышающим заданного предельного. Необходимость решения такой задачи возникает, например, при выборе трассы для будущей дороги. Вычисляют соответствующее заданному предельному уклону iпр заложение, выраженное в масштабе карты, 
Чтобы уклон линии не превосходил iпр, ни одно заложение на ней не должно быть меньше, чем рассчитанное d. Если расстояние между горизонталями больше рассчитанного, направление линии можно выбирать произвольно. В противном случае в раствор циркуля берут отрезок, равный d, и строят ломаную линию, умещая между горизонталями рассчитанное предельное заложение (рис. 4.9).
Источник
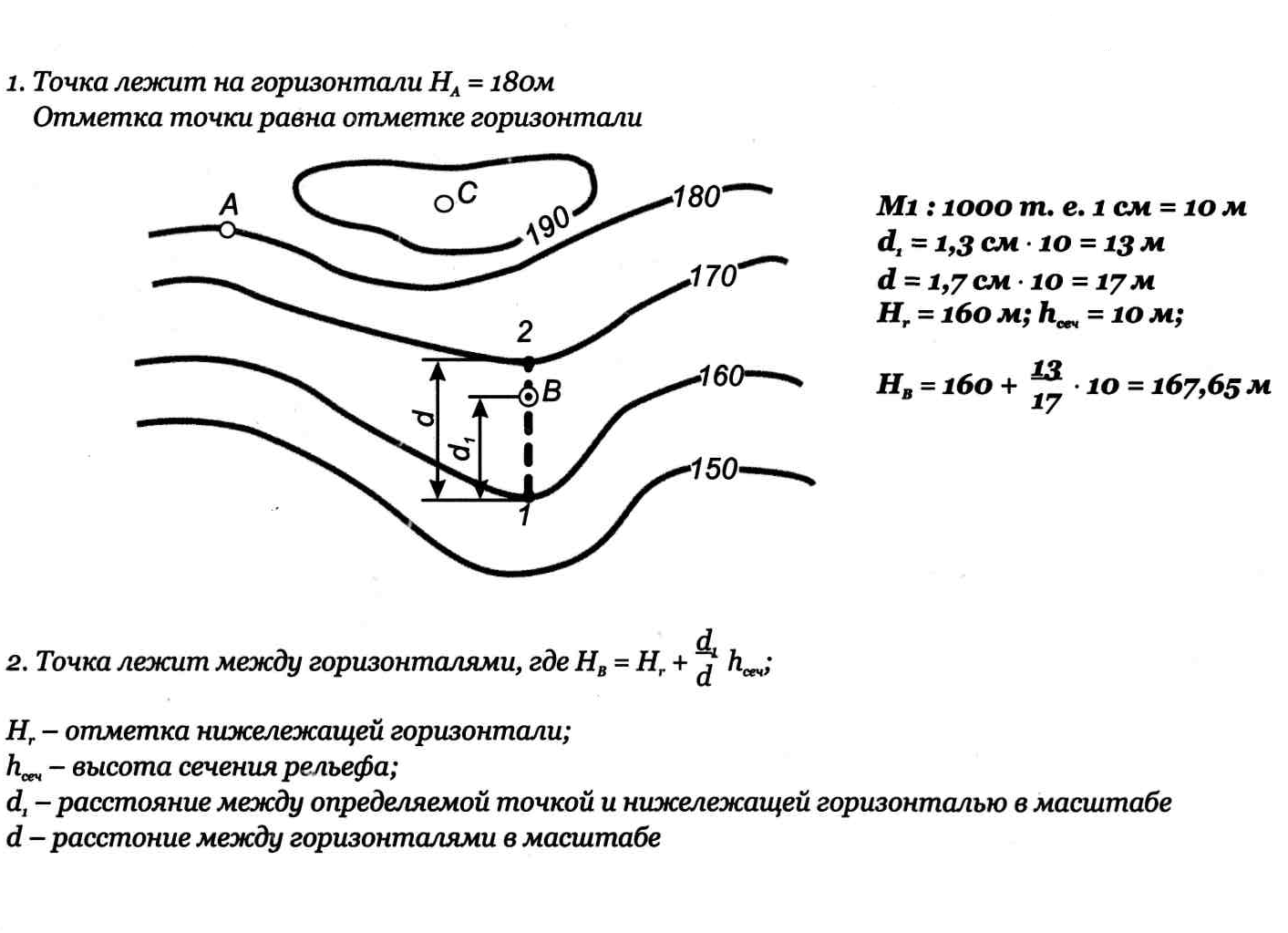
Практическая работа №3 Определение отметки точки по горизонталям
Алгоритм выполнения задания:
1. Определим форму рельефа, изображенного на рисунке.
2. Подсчитаем число горизонталей и полугоризонталей ( изображаются пунктирной линией) между точками .
3. Умножим число горизонталей на высоту сечения рельефа. К полученной цифре прибавим число полугоризонталей, умноженное на половину сечения рельефа. Полученная цифра является превышением между точками.
Рис. 26 Определение отметок местности по горизонталям
4. Высота точки, лежащей на горизонтали, равна высоте горизонтали. Для определения высоты горизонтали к высоте известной горизонтали прибавляем число горизонталей между точками, умноженное на высоту сечения рельефа.
5. Высота точки, лежащей на полугоризонтали равна высоте этой полугоризонтали. Для определения высоты точки подсчитываем число целых горизонталей и полугоризонталей. Количество целых горизонталей умножаем на высоту сечения рельефа, количество полугоризонталей умножаем на половину сечения рельефа и суммируем произведения.
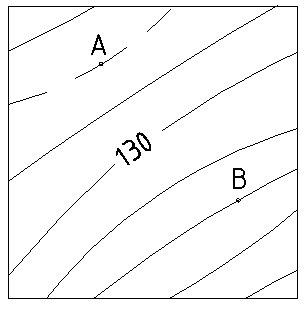
1. Определите превышение между точками А и В на плане, если высота сечения рельефа 2,5 м.
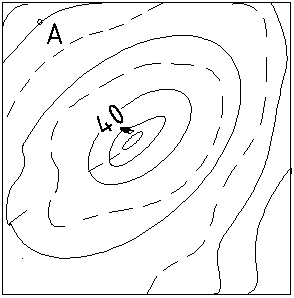
2. Определите, чему равна отметка точки А на плане с горизонталями, если высота сечения рельефа 2,5 м?
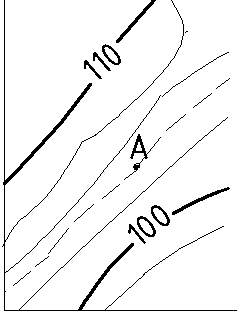
3. Чему равна отметка точки А на данном плане в горизонталях, если ho =2,5м?
Уклон линии. Скат. Крутизна ската
Уклоном линии называется превышение, которое приходится на единицу горизонтального расстояния и определяется по формуле:
Рис. 27 Уклон линии.
Заложением называется горизонтальная проекция линии ската между двумя смежными горизонталями.
Крутизна ската местности по линии АВ характеризуется углом ν , который она образует с горизонтальной плоскостью. Крутизну ската можно определить уклоном i. (Формулу вычисления уклона смотри на рисунке 26 «Уклон линии»).
Пример 1. Определить угол наклона ν и уклон ската местности ᵢ между горизонталями на плане масштаба 1:1000, если заложение d = 20 мм, высота сечения рельефа h = 1 метр.
Решение: на местности заложению будет соответствовать длина отрезка
20 мм . 1000= 20 м.
По формуле: тангенс угла наклона равняется дроби i = h / d, в числителе которой высота сечения рельефа h, а в знаменателе – заложение d.
1:20 = 0,05 = 5% = 50‰
1. Что такое крутизна ската, заложение ската ?
2. Как определить превышение между двумя точками на плане?
3. Как определить уклон линии на плане?
Практическая работа №4 Определение уклона линии
Алгоритм выполнения задания:
1. Рассмотрим прямоугольный треугольник, катетами которого являются: h – высота сечения рельефа, d – расстояние между соседними горизонталями.
2. Исходя из формулы i = h / d, определим, что d= h/ i. Подставим в формулу числа, произведем расчеты.
3.Чтобы определить уклон линии, используем формулу i = h / d. Превышение между точками h определяется как произведение высоты сечения рельефа на количество горизонталей. Разделив превышение на длину линии, получим уклон линии.
1. Определите, чему равно заложение ската АВ, если его высота h – 2,4 м , а уклон i – 5%.
2. Каков уклон линии АВ на плане М1:10000, ho =2,5м ? (Длина АВ на плане – 25м см)
Источник
Работа с теодолитом – тема настоящей инструкции. Ниже поэтапно приведена методика измерения теодолитом, аккуратное выполнение пунктов которой обеспечит получение точных результатов. Настоящая инструкция предполагает, что пользователь обладает начальными знаниями о том, как работать с теодолитом, знаком с основными узлами и принципом работы прибора.
Установка теодолита в рабочее положение
Измерение горизонтальных углов теодолитом предполагает установку прибора в вершине определяемого угла. Для этого сначала ставят штатив так, чтобы центр площадки для установки штатива был примерно над точкой, а плоскость площадки – горизонтальна. Только после этого теодолит закрепляют на штативе, центрируют и горизонтируют прибор.
Центрирование теодолита – это проецирование оси вращения алидады и лимба по отвесной линии на вершину определяемого угла с точностью для механического отвеса ± 5 мм, ± 1-2 мм для оптического отвеса. Сначала проводится центрирование штатива с помощью механического отвеса с точностью 10-15 мм. При этом необходимо установить штатив горизонтально, чтобы регулировка подъемных винтов позволила произвести горизонтирование прибора. При установке прибора на штатив, производим окончательное центрирование теодолита, передвигаем оптический теодолит, ослабив становой винт.
Горизонтирование теодолита – это последовательное горизонтирование плоскости лимба горизонтального угломерного круга (ГУК) и приведение вертикальной оси вращения в отвесное положение. Процесс горизонтирования контролируется по цилиндрическому уровню алидады ГУК и производится посредством подъёмных винтов теодолита. Поворачивая алидаду, направляют ось уровня по двум подъёмным винтам и перемещают пузырёк уровня в центр. Затем следует повернуть алидаду на 90° и, используя третий подъёмный винт, вновь перевести пузырёк в центр. Действия необходимо повторять до тех пор, пока пузырек не станет сходить с середины при всех позициях алидады горизонтального круга. Допустимое его отклонение не больше двух делений шкалы цилиндрического уровня.
Горизонтирование теодолита
Для получения достоверного результата работа с теодолитом требует соблюдения двух геометрических условий:
- ось вращения прибора находится в вертикальном положении;
- ось цилиндрического уровня – в горизонтальном положении.
Измерение горизонтального угла теодолитом
Визирование
Визирование – совмещение центра сетки нитей с точкой.
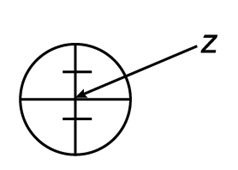
Сетка нитей – это стеклянная пластина с нанесёнными на нём линиями (характер их нанесения может быть разным). Пересечение средних линий называют центром сетки нитей Z.
Наведение центра нитей на точку
Для визирования теодолита на точку необходимо:
- Закрепить лимб.
- Открепить алидаду для того, чтобы по грубому визиру, расположенному наверху зрительной трубы, установить прибор примерно на искомую точку.
- Закрепить алидаду.
- Для наблюдения установить зрительную трубу так, чтобы сетка нитей имела резкое изображение. Эта операция называется установкой по глазу и производится вращением окулярного колена.
- Установить зрительную трубу так, чтобы точка визирования была видна наилучшим образом. Эта операция называется установкой по предмету и производится вращением кремальеры.
- Навести центр сетки нитей точно на точку визирования посредством наводящих винтов алидады и зрительной трубы. Если вертикальный круг оказывается с правой стороны от трубы, если смотреть со стороны окуляра, говорят “круг право” (КП). Если вертикальный круг оказался слева – “круг лево” (КЛ).
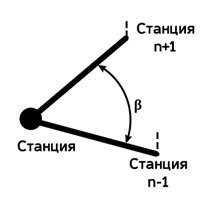
Измерение горизонтального угла β
Измерение горизонтального угла теодолитом предполагает установку прибора в вершине измеряемого горизонтального угла (т.н. станция), а рейки на станциях n+1 и n–1.
Перекрестие сетки нитей совмещают с самой нижней видимой точкой рейки так, чтобы вертикальная нить совпадала с осью рейки.
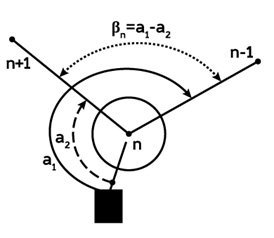
Затем выполняют следующую последовательность действий (первый полуприём):
- наводят центр сетки нитей на вершину заднего (правого) угла (n – 1) и снимают отсчёт по лимбу горизонтального круга – отсчёт а1;
- наводят на вершину переднего (левого) угла (n + 1) снимают отсчет а2;
- определяют значение угла при круге лево βкл=а1-а2.
Измерение горизонтального угла на станции n:
β – горизонтальный угол
До начала второго полуприёма (КП) разблокируют зрительную трубу и переводят через положение зенита. Затем разблокируют алидаду и поворачивают прибор на 180° , проводят измерения при КП. При втором полуприёме (КП) визирование и измерения производят аналогично, различия в значениях угла в двух полуприёмах (С) не должно превышать двойной точности прибора (t): С < 2t.
Измерение горизонтального угла β на станции n (КЛ):
n – станция
n–1 –- вершина заднего угла
n+1 – вершина переднего угла
а1 – отсчёт на вершину заднего угла
а2 – отсчёт на вершину переднего угла
Вычисление горизонтальных углов
При выполнении условия расхождения в значениях угла, полученных за два полуприёма, средний горизонтальный угол рассчитывают по формуле: βср = (βКЛ + βКП) /2.
Лимб горизонтального угломерного круга оцифрован всегда от нуля до 360? через 1?, слева направо.
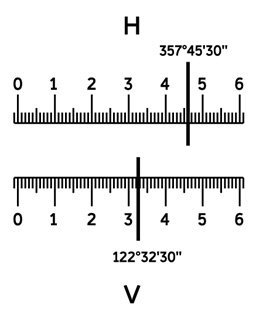
Отсчёт по горизонтальному кругу берут следующим образом:
- считывают по шкале алидады количество градусов отсчётного штриха (по рисунку – 125°);
- считывают минуты слева направо от нуля, учитывая, что цена деления на шкале ГУ – 5´ (по рисунку – 07´).
Отсчётный микроскоп теодолита RGK TO-15:
отсчёт по ГУК – “125°07´”
отсчёт по ВУК – “-0°35´”
Измерение вертикального угла теодолитом
Измеренный угол наклона может иметь как положительное, так и отрицательное значение, изменяясь от -90° до 90°.
Работа с теодолитом требует проводить горизонтирование алидады каждый раз при отсчёте. Горизонтальным считается положение, когда пузырёк цилиндрического уровня алидады или трубы расположен посередине ампулы. Однако, даже при нахождении пузырька в центре ампулы линия нулей отсчётного устройства может находиться под небольшим углом по отношению к линии горизонта, который называется место нуля вертикального круга (М0). Важной чертой измерения вертикальных углов является необходимость учёта места нуля вертикального круга. Для этого при создании съёмочного обоснования снимают отсчёты по вертикальному угломерному кругу (ВУК) при КЛ и КП, а при тахеометрической съёмке – на каждой станции перед началом работы определяют место нуля.
При измерении вертикальных углов теодолитом центр сетки нитей переводят на высоту инструмента, ранее отмеченную на рейке. Высоту инструмента определяют с помощью листа белой бумаги и рейки, приставляя её почти вплотную к окуляру. Пользователь при этом должен вести наблюдение в объектив. Лист передвигают по рейке, пока он не закроет ровно ½ поля зрения. Высоту инструмента на рейке удобно отмечать тонкой круглой резинкой.
Сначала снимают отсчёт, визируя при круге лево. Затем, переведя трубу через зенит, визируют и снимают отсчёт при круге права.
Существует несколько способов оцифровки лимба вертикального угломерного круга (ВУК). У теодолита RGK TO-15 (TO-05) оцифровка секторная, при которой ВУК разбит на 4 сектора по 90°, из которых два сектора имеют положительную оцифровку, а два других – отрицательную. Для взятия отсчёта:
- считывают количество градусов отсчётного штриха (по рисунку – “-0°”);
- считывают минуты – если вверху стоит “-0” – по отрицательной шкале от нуля до отсчётного штриха, если вверху стоит “+0” – по положительной шкале от нуля до отсчётного штриха (по рисунку – “-35?”).
Далее проводят вычисление вертикального угла. При этом отсчёты от 0° до 90° соответствуют измеряемому положительному вертикальному углу.
Вычисление вертикальных углов
После снятия отсчётов рассчитывают вертикальный угол через М0, либо по результатам двух отсчётов, полученных при визировании на цель в двух положениях зрительной трубы (КЛ и КП).
Расчётные формулы для секторной оцифровке лимба вертикального круга от нуля в обе стороны – по ходу и против хода часовой стрелки (RGK TO-05 и TO-15):
М0 = (КП + КЛ)/2; v = МО-КП; ν=КЛ−М0
При расчёте по этим формулам не обязательно добавлять 360°.
Измерение расстояний теодолитом
В этом разделе рассмотрим, как работать с теодолитом для измерения расстояний. В сетке нитей зрительной трубы теодолита имеются два дополнительных горизонтальных дальномерных штриха, расположенных по обе стороны от центра сетки нитей на равных расстояниях. Наличие этих штрихов позволяет производить измерение теодолитом расстояния D от прибора до рейки.
Для этого по рейке определяют величину дальномерного интервала n в сантиметрах, умножая полученное число на 100, затем полученное значение из сантиметров переводят в метры (дальномерный коэффициент зрительной трубы, как правило, равен 100) , т. е.
D = K*n =100*n
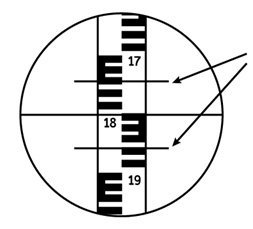
В случае, приведенном на рисунке:
- отчет по верхнему дальномерному штриху – 1747 мм;
- отчет по нижнему дальномерному штриху – 1856 мм.
Дальномерный интервал n равен разности отчетов по нижнему и верхнему дальномерным штрихам.
n = 1856-1747=109 мм = 10,9 см.
По формуле вычисляем расстояние: D = 100*10,9 см=1090 см = 10,9 м
Для измерения теодолитом расстояний при помощи нитяного дальномера относительная ошибка обычно составляет от 1/100 до 1/300.
Измерение теодолитом расстояния по дальномерным штрихам