Загрузить PDF
Загрузить PDF
Нахождение угла наклона прямой – это один из важнейших навыков в геометрии, необходимый для построения графика линейной функции или для определения координат точек пересечения прямой с осями X и Y. Угол наклона прямой определяет скорость ее роста или убывания,[1]
то есть как быстро прямая перемещается по вертикали в зависимости от движения по горизонтали. Угол наклона прямой легко вычисляется по координатам двух точек, лежащих на этой прямой.
-
1
Уясните формулу для вычисления углового коэффициента. Угловой коэффициент равен тангенсу угла наклона прямой, который она образует с осью Х, и вычисляется как отношение вертикального расстояния между двумя точками к горизонтальному расстоянию между двумя точками.
-
2
Выберите две точки и найдите их координаты. Можно выбрать любые две точки, лежащие на прямой.
-
3
Задайте порядок точек (относительно друг друга). Одна точка будет первой точкой, а другая – второй. Не имеет значения, какая точка будет первой, а какая второй – главное не перепутать их порядок в процессе вычисления.[2]
-
4
Запишите формулу для вычисления углового коэффициента. Формула:
, где VR – вертикальное расстояние, определяемое изменением координаты «у», GR – горизонтальное расстояние, определяемое изменением координаты «х».[3]
Реклама
-
1
В формулу для вычисления углового коэффициента подставьте координаты «у». Не перепутайте их с координатами «х» и убедитесь, что подставляете правильные координаты первой и второй точек.
-
2
В формулу для вычисления углового коэффициента подставьте координаты «х». Не перепутайте их с координатами «у» и убедитесь, что подставляете правильные координаты первой и второй точек.
-
3
Вычтите координаты «у». Вы найдете вертикальное расстояние.
-
4
Вычтите координаты «х». Вы найдете горизонтальное расстояние.
-
5
Если возможно, сократите дробь. Вы найдете угловой коэффициент.
-
6
Обращайте внимание на отрицательные числа. Угловой коэффициент может быть положительным или отрицательным. В случае положительного значения прямая возрастает (движется вверх слева направо); в случае отрицательного значения прямая убывает (движется вниз слева направо).
- Помните, что если и в числителе, и в знаменателе стоят отрицательные числа, то результат будет положительным.
- Если в числителе или в знаменателе стоит отрицательное число, то результат будет отрицательным.
-
7
Проверьте ответ. Для этого измерьте или посчитайте (по шкалам осей) вертикальное и горизонтальное расстояния. Если они совпали с вычисленными, то ответ правильный.
- Если измеренные или посчитанные вертикальное и горизонтальное расстояния не совпали с вычисленными, то ответ не правильный.
Реклама
Советы
Похожие статьи
Об этой статье
Эту страницу просматривали 90 201 раз.
Была ли эта статья полезной?
In this platform, you will learn about the slope of a line. The slope of a line calculates the steepness and the direction of the line. It will show how the slant line will be and how much the line rises vertically compared to the runs horizontally. In a coordinate plane predict whether the lines are parallel or perpendicular for finding the slope of the lines.
On this page, check out the 10th Grade Math concept of the slope of a line, formula, how to find the slope of a line with two points, types of slope, methods to find the slope, solved example problems, and so on.
Do Read:
- Equation of a Straight Line
- Slope of the Graph of y = mx + c
Slope of a Line Meaning & Definition
In mathematics, the slope of a line is defined as the change in the y coordinate with respect to the change in the x coordinate of that line. The net change in the y coordinate is Δy, while the net change in the x coordinate is Δx. So the change in the y coordinate with respect to the change in the x coordinate can be written as
m = change in y / change in x = Δy/Δx.
tan θ = Δy/Δx.
where tan θ, m will be the slope of the line.
It is also defined as the ratio of the rise to the run, or rise divided by the run. The slope of a line measures the tangent of the angle made by the line with the x-axis. In general, to determine a line’s slope, we need to have two different coordinates values on the line. The slope of a line image is shown below,
The slope is constant throughout a straight line. To calculate the slope of a line, the x and the y coordinates of the points lying on the line can be used. To calculate slope of a line the formula is
m = (y2 – y1)/(x2 – x1) = Δy/Δx
Where x1, x2 are the coordinates of the x-axis and y1, y2 are the coordinates of the y-axis.
Slope Between Two Points
In a straight line, there are two points by using these two points we can calculate the slope of a line. We can apply the coordinates of the two points, in a slope of line formula. The two coordinate points are,
P1 = (x1, y1)
P2 = (x2, y2)
We know that the slope of a line is the change in the y coordinate with respect to the change in the x coordinate of that line. So, substitute the values of Δy and Δx in the equation of slope, then we get
Δy = y2 – y1
Δx = x2 – x1
Now, these values in a ratio, we get
The Slope m = tan θ = (y2 – y1)/(x2 – x1)
where the slope of a line is m.
θ is the positive x-axis line angle.
Slope of a Line Formula
Using the equation of the line we will calculate the slope of a line. The slope of a line general formula is given as,
y = mx + b
Where m is the slope of a line, m = tan θ = Δy/Δx.
θ, be the angle made by the line with the positive x-axis.
Δy is the net change in the y-axis.
Δx is the net change in the x-axis.
Example: What is the equation of a line whose slope is 1, that passes through the point (-2, -6)?
Solution: Given that the slope is 1. So the value of m will be 1.
We know the general equation of a line formula, y = mx + b.
Now substitute the value of m is 1, then we get
y = x + b.
We have ‘a’ the value of one point on the line. So, we put the value of the point (-2, -6) in the equation y = x + b, and we get,
b = -4
Substituting the values of m and b in the general equation, we get the final equation y = x – 4.
Therefore, the equation of a line is y = x – 4.
How do you find the Slope of a Line?
Using the different methods we will find the slope of the line. The first method is the equation method, using this method to find the value of the slope of a line. The equation is,
m = (y2 – y1)/(x2 – x1)
where m is the slope of the line.
In other words, the change in x is run, and therefore the change in y is rise or fall. Thus, we defined a slope of a line as, m = rise/run.
How to Find Slope of a Line on Graph?
You are finding the slope of a line from the graph, one method is directly applied which is the formula method to the coordinates of two points lying on the line. If the values of the two coordinates points are not given. At this time, we have to use another method to find the slope of the line. So in this method, we have to find the tangent of the angle which is made by a line on the x-axis. The below figure shows the way how we find the slope of a line,
It has only one value. So, for finding the slopes Method1 and Method 2 will be equal. In addition, we are given the equation of a straight line. The general equation of a line is,
y = mx + b
The value of the slope line is given as m.
The following are the steps to find the slope of a line such that the coordinates of two points lying on the line are (x1, y1), (x2, y2).
Step 1: Note the coordinates of the two points lying on the line, (x2, y2), (x1, y1)
Step 2: Apply the slope of line formula, m = (y2 – y1)/(x2 – x1).
Step 3: Finally, we get the value of the given slope line.
Types of Slope
Depending upon the relationship between the two variables x and y there are different types of slopes and then the value of the gradient or slope of the line is obtained. There are 4 different types of slopes namely,
-
- Positive slope
- Negative slope
- Zero slope
- Undefined Slope
Positive Slope: A positive slope indicates that in a coordinate plane while moving from left to right the line rises, it also signifies that when x increases, the y also increases.
Negative Slope: In a negative slope, the coordinate plane is moving from left to right then the line falls, which also signifies that when x increases, then y decreases.
Zero Slope: The line in a zero slope the rise will be zero. So applying the rise over run formula we get the slope of the line as zero.
Undefined Slope: In an undefined slope, the line value of the run is zero. So, the slope of a vertical line will be undefined.
The Slope of the Horizontal Line
A horizontal line is a straight line that is parallel to the x-axis or in a coordinate plane, it will be drawn from left to right or right to left. So, the net change in the y-coordinates of the horizontal line will be zero. Then the slope of a horizontal line will be,
Slope of a horizontal line, m = Δy/Δx = zero.
The Slope of the Vertical Line
The vertical line is a straight line that is parallel to the y-axis or it is a line from top to bottom or bottom to top in a coordinate plane. Thus, the net change in the x-coordinates of the vertical line is zero. So, the slope of a vertical line is,
The Slope of a vertical line is m = Δy/Δx = undefined.
Finding Slope of the Perpendicular Lines
A set of perpendicular lines always has an angle of 90º angle between them. Suppose, if we have two perpendicular lines L1 and L2 in the coordinate plane, then the lines are inclined with the x-axis at angles θ1 and θ2 respectively. The given angles will follow the external angle theorem as, θ2 = θ1 + 90º.
Therefore, the slopes can be given as,
m1 = tan θ1
m2 = tan (θ1 + 90º) = – cot θ1
m1 × m2 = -1
So, the two perpendicular lines’ slope product is equal to -1.
Slope of Parallel Lines
A set of parallel lines always has an equal angle of inclination. Suppose we have two parallel lines L1 and L2 in a coordinate plane, then they are inclined at angles θ1 and θ2 respectively with the x-axis. So that θ2 = θ1
Then, the slopes will be
m1= m2
So, the slopes of the two parallel lines are equal.
Read More:
- Drawing Graph of y = mx + c Using Slope and y-intercept
- Problems on Plotting Points in the x-y Plane
- Conditions of Collinearity of Three Points
Slope of a Line Examples
Example 1:
The equation of a line is 2y = 6x + 7, find its slope value?
Solution:
Given that, the equation is 2y = 6x+7.
Now, we need to find out the slope of the equation.
We know that the formula of the slope is, y = mx + b
Now, try to bring the equation to this form. The coefficient of y = 1, then we get,
y = 6x/2 + 7/2 = 3x+3.5
So, the coefficient of x is found to be 3.
Hence, our slope will be the same as the coefficient of x.
Therefore, the slope of an equation line is 4.
Example 2:
If the equation of a line is given as x = 7. Find the value of the given slope of the line?
Solution:
As given in the question, the equation is x = 7.
Now, we will find the value of the slope of the given line.
Observe that y is missing from the given equation. So, we assume that the coefficient of y is 0.
Then we get, (0)y = x – 7
Now, we make the coefficient of y as 1. Let us divide both sides by Zero.
We know that if anyone is divided by zero, then the value can not be determined.
So, in this case, the coefficient of x will be divided by zero which gives us our slope. In such cases, the answer will not be defined. So we can safely say that our slope is not defined in such cases.
The Slope is not defined.
Example 3:
If the rise is 20 units, while the run is just 10 units, What is the slope of the line?
Solution:
In the given question, the run is 10 units and the rise is 20 units.
We all know that the slope of a line will be
m = Rise/Run
Now, substituting the values, we will get
m = Rise/Run = 20/10 = 2
Thus, the slope of a line is 2.
Example 4:
Find the slope of a line that is parallel to the x-axis and intersects the y – axis at y = 2.
Solution:
Given that, the y-axis is y=2.
We all know that the slope of any line is the tangent of its angle made with the x-axis.
So, if the given line is parallel to the x-axis, then the angle will be 0º. So, the tan 0º is 0.
Then the value of the slope is,
m = tan 0 = 0
Thus, the value of the slope will be Zero.
Example 5:
Determine the value of b, if the slope of a line passing through the points (b, 7) and (8, -5) is 6.
Solution:
Given that,
The points are (x1, y1)= (b,7) and (x2 , y2) = (8,-5)
The slope is m= 6.
Now, we will find the value of b.
We know that Slope (m) = (y2 – y1)/(x2 – x1)
Substitute the value in the above formula.
Then the value is 6 = (-5-7)/(8-b)
6 = (-12)/(8-b)
-2= (8-b)
-2-8 = -b
b = 10
Therefore, the value of the b is 10.
FAQ’s on Slope of a Line
1. What is the Slope of a Line?
The slope of a line, also known as the gradient is defined as the value of the steepness or the direction of a line in a coordinate plane. The slope will be calculated by using different methods, given the equation of a line or the coordinates of points lying on the straight line.
2. What is the Slope of a Line formula?
We can calculate the slope of a line directly using the slope of a line formula given the coordinates of the two points lying on the line. The formula is given as,
The slope is m = tan θ =(y2 – y1)/(x2 – x1)
3. How Does Slope Looks Like?
The slope is nothing but the measure of the tangent of the angle made with the x-axis. So, it is a measure of an angle.
4. How do you find the slope of a line?
We need to find the ratio of the difference between the y-coordinates and x-coordinates of the two points, that form the line. The resulted value is the slope of the line. It shows the rise of the line along the y-axis over the run along the x-axis.
5. How do you Show that Three Points are Collinear by Slope?
Using the slope formula we will prove the collinearity of three points. So the slope of lines AB and BC should be equal for the three given points to be collinear.
Уклон любой линии
на карте находим по формуле:
tgν
= h/d
= i, (1.8)
где
ν
– угол наклона линии к горизонту, в
градусах;
h
– разность отметок (превышение) концов
линии;
d
– горизонтальное проложение (проекция)
линии;
i
– уклон линии в тысячных долях.
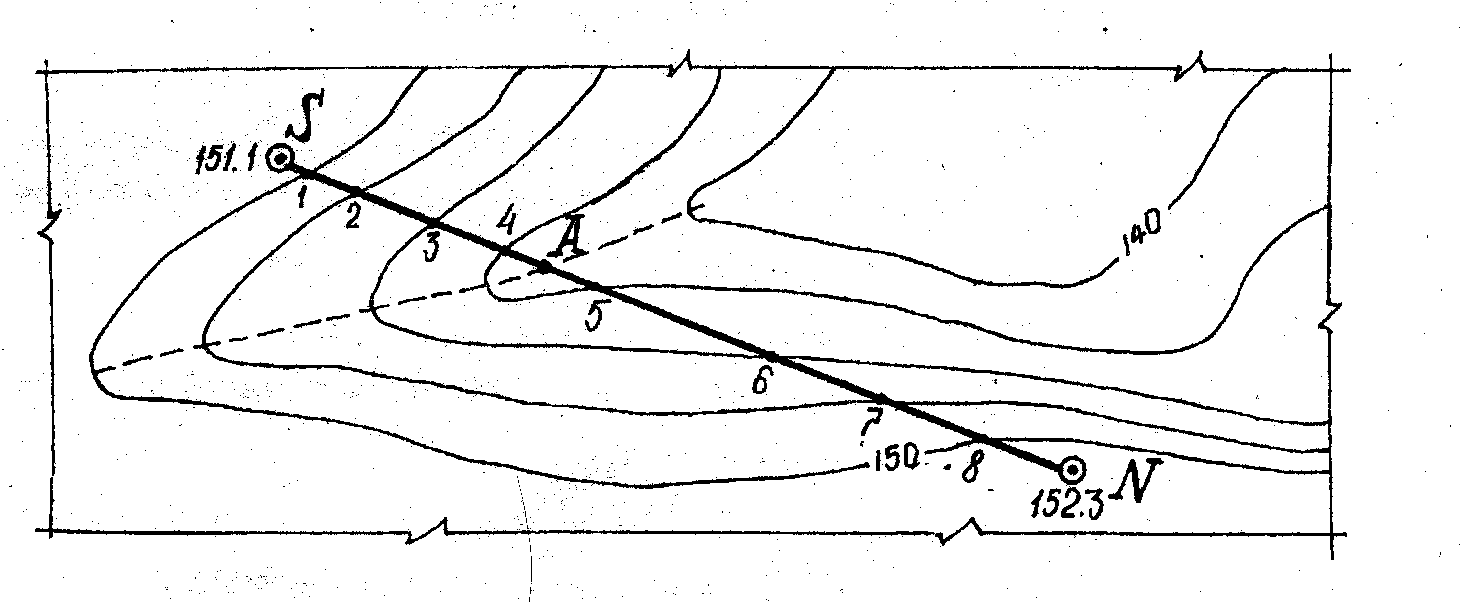
Например,
найти уклон линии между точками S
и А (рис. 1.6). Уклон линии SА
определяем так:
h
= (HA
– HS)
= 141.3 – 151.1 = 9.8 м
d
= SA
M = 3.8 x 100 = 380 м.
Здесь
SA
= 3,8 см,
М – знаменатель
масштаба, равный 100 м.
i
= tgν
= -9.8
380 = – 0.026,
ν
= 130.
Рисунок 1.6 –
Определение уклонов
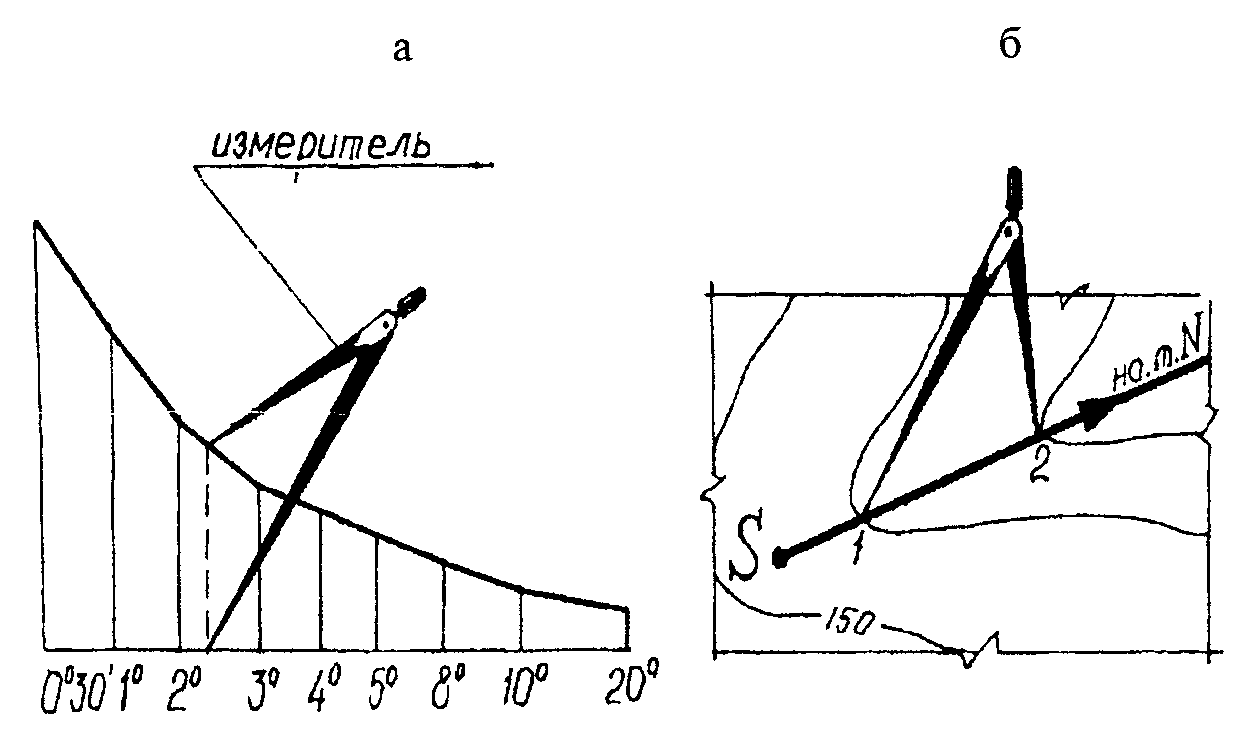
1.5.7. Измерение угла наклона линии с помощью графиков «Масштаб заложения»
Графики
масштабов заложения (рис. 1.7а) строятся
по формулам, вытекающим из выражения
(1.8):
для
определения углов наклона: d
= h
/ tg
ν;
(1.9)
для
определения уклонов: d
= h/i.
(1.10)
Пользуясь
циркулем-измерителем, по построенным
графикам масштабов заложений находят
искомые ν
и i
для отрезков заданной линии SN
(рис. 1.7б).
Рисунок
1.7 – Определение уклонов с помощью
графика масштаба заложения
1.5.8. Построение профиля местности
Профиль
местности (рис. 1.8) строят на миллиметровой
бумаге по заданной линии SN
в такой последовательности:
-
к
заданной профильной линии SN
прикладывают лист миллиметровой бумаги
и переносят на её край короткими
черточками места пересечения горизонталей
с профильной линией (выходы горизонталей); -
на
листе миллиметровой бумаги слева у
горизонтальных линий подписывают
высоты, соответствующие высотам
горизонталей на карте, приняв условно
промежутки между этими линиями за
высоту сечения; -
от
всех черточек (выходов горизонталей)
опускают перпендикуляры до пересечения
их с соответствующими по отметкам
параллельными линиями и отмечают
полученные точки пересечения; -
соединяют
точки пересечения плавной кривой,
которая и изображает профиль местности.
Длины
отрезков S
– 1, 1 – 2 и т.д. измеряют по линейному
масштабу и подписывают под профилем
(рис. 1.8).
Вертикальный
масштаб (шкала высот) принимается в
десять раз крупнее горизонтального.
Отметку условного горизонта вычисляют
по формуле
УГ = Но – К
М, (1.11)
где Но – минимальная отметка точки на
линии профиля, округлённая до значения,
кратного знаменателю вертикального
масштаба;
М – знаменатель вертикального масштаба
(м);
К – коэффициент, принимаемый равным 5
– 7.
Измеренные
и вычисленные значения отметок Н,
превышений h,
горизонтальных проложений d,
уклонов i
и углов наклона ν
для всех отрезков заданной профильной
линии SN
заносят в таблицу 1.2.
Таблица
1.2 – Расчет элементов продольного
профиля местности
|
№№ точек |
Отметка точки Н, м |
Расстояние между |
Горизонтальное |
Уклон i= h/d |
Угол наклона, ν, |
|
S |
|||||
|
1 |
|||||
|
2 |
|||||
|
….. |
|||||
|
N |
Р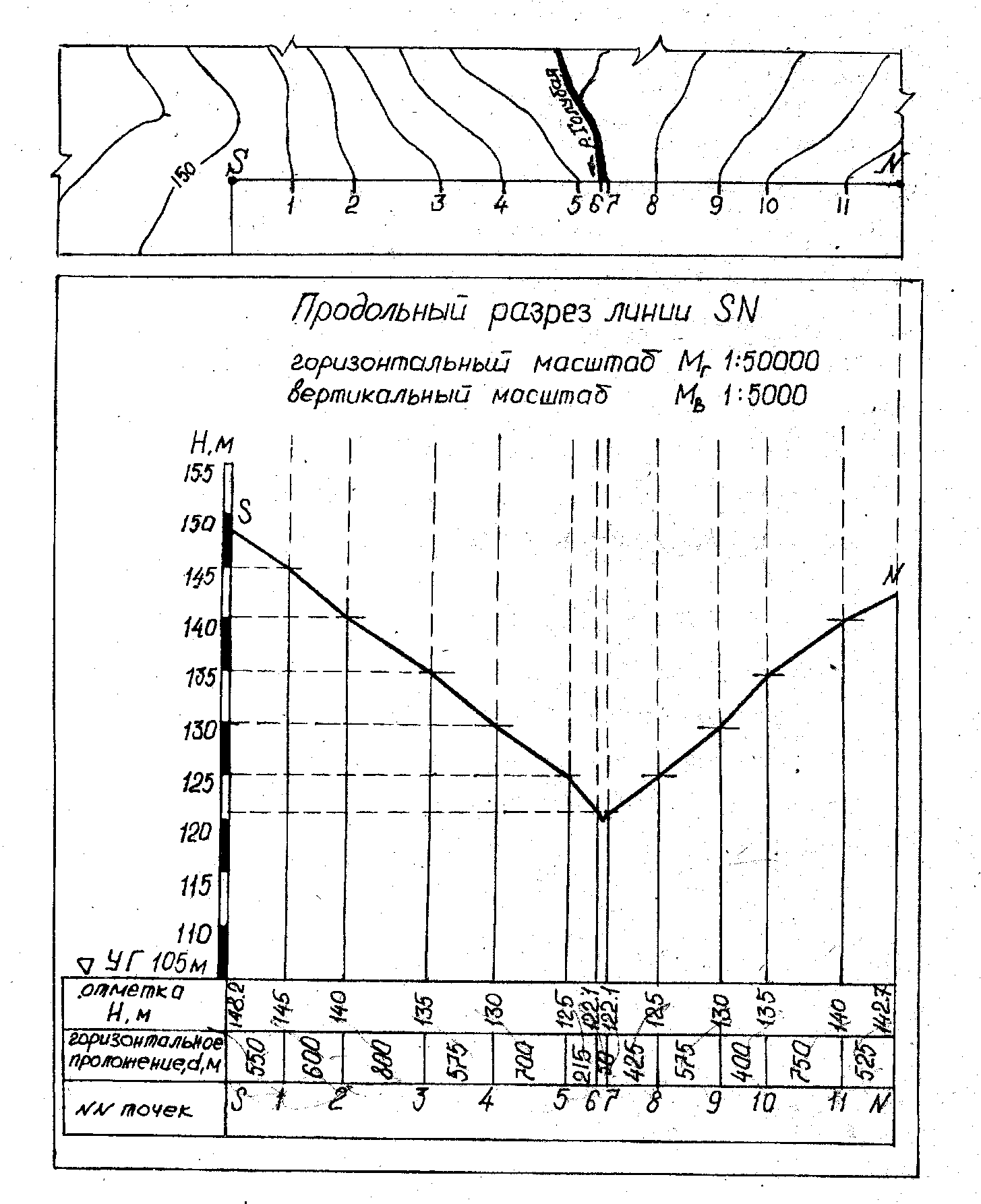
1.8 – Продольный профиль местности
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Углы наклона прямой
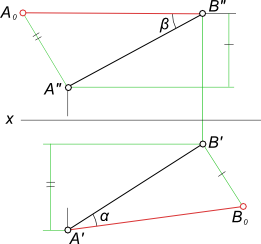
Углы наклона прямой общего положения по двум ее проекциям находятся попутно при определении действительной величины отрезка способом прямоугольного треугольника.
В отличие от отрезков прямых частного положения, проецирующихся хотя бы на одну из плоскостей проекций в натуральную величину, отрезок прямой общего положения на плоскости проекций проецируется с искажением. Для того чтобы найти его натуральную величину, необходимо провести ряд преобразований.
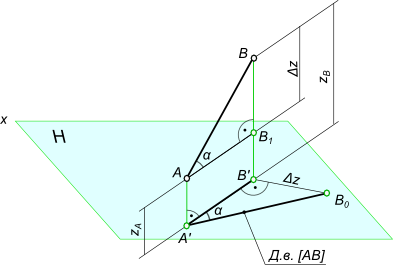
Углы наклона прямой
[
tg α = BB_1/AB_1 = (BB` – B`B_1)/AB_1 = (z_B – z_A)/A`B`
]
Возьмем прямую общего положения АВ и спроецируем ее на горизонтальную плоскость проекций . Через точку А проведем линию, параллельную плоскости . Таким образом в пространстве получим прямоугольный треугольник , один из катетов которого (AB1) равен длине проекции отрезка, а угол между отрезком и этим катетом является углом наклона заданного отрезка к плоскости проекций (рис.).
Для определения натуральной величины отрезка прямой общего положения и угла наклона ее к плоскости проекций на эпюре (КЧ) необходимо построить прямоугольный треугольник:
– первый катет этого треугольника равен проекции отрезка на плоскости проекций (обычно прямоугольный треугольник пристраивают к проекции отрезка, однако в некоторых задачах целесообразно прямоугольный треугольник строить в стороне от проекций геометрических объектов);
– из проекции любого конца отрезка под прямым углом к проекции отрезка проводится луч, на котором откладывается длина второго катета, равная разности расстояний от концов отрезка до данной плоскости проекций;
– гипотенуза полученного таким образом прямоугольного треугольника равна действительной величине заданного отрезка;
– угол наклона отрезка к той или иной плоскости проекций равен углу между гипотенузой – натуральной величиной и катетом – проекцией на эту плоскость проекций.
Углы наклона прямой, отрезка общего положения всегда будут меньше их ортогональных проекций.
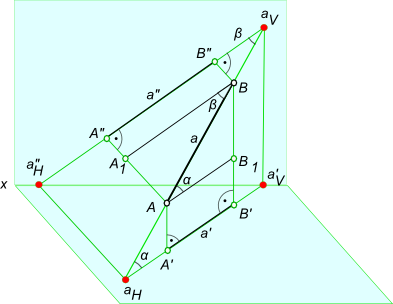
Углы наклона прямой
Для графического определения на эпюре Монжа действительной величины отрезка достаточно
построить прямоугольный треугольник, взяв за один его катет горизонтальную (фронтальную, профильную)
проекцию отрезка, а за другой катет – разность удаления концов отрезка от горизонтальной (или
соответственно фронтальной, профильной) плоскости проекции.
[
tg α = BB_1/AB_1 = (BB` – B`B_1)/AB_1 = (z_B – z_A)/A`B`
]
[
tg β = AA_1/BA_1 = (AA” – A”A_1)/BA_1 = (y_A – y_B)/A”B”
]
Графическое определение действительной величины отрезка [AB] путем построения прямоугольных треугольников
ΔA`B`B0 или ΔA”B”A0 и попутно углов его наклона:
– α к горизонтальной плоскости проекции;
– β к фронтальной плоскости проекции.
Углы наклона прямой
Углы наклона прямой к плоскости проекций проецируется на эпюре без искажений, когда она занимает положение прямой уровня, это может быть:
– Горизонтальная прямая;
– Фронтальная прямая;
– Профильная прямая
Углы наклона прямой применяются в статье графическая работа 1: Графическая работа 1
Определение углов наклона плоскости смотри также: Линия наибольшего наклона
+
Содержание
- Графическое представление
- Типы откосов
- Как рассчитывается наклон линии?
- Решенные упражнения
- – Упражнение 1
- Решение
- – Упражнение 2.
- Решение
- Примеры
- Пример 1
- Пример 2
- Ссылки
В наклон линии – тангенс угла θ, который указанная линия образует с горизонтальной осью, который обычно измеряется против часовой стрелки. Наклон любой линии всегда постоянен, поэтому это одна из важнейших ее характеристик.
Для его расчета необходимо знать две точки на прямой, координаты которых равны (x1, Y1) и (x2, Y2). Между обеими точками рисуется сегмент, принадлежащий линии, а затем сегменты, которые представляют расстояние между x.1 и х2, а между и1 и и2, как на рисунке ниже.
Три сегмента образуют прямоугольный треугольник, ноги которого: Δx = x2 – Икс1 у Δy = y2 – Y1. Они соответствуют горизонтальному и вертикальному перемещению соответственно.
Теперь мы определяем частное, называемое тангенсом угла θ и сокращенно tg θ, которое и есть наклон м прямой:
m = tg θ = Δy / Δx
Обратите внимание, что для прямой этот угол остается постоянным, независимо от точек, взятых для вычисления его касательной. В любом случае это значение дает нам меру крутизны линии.
Формула наклона по координатам выбранных точек:
т = (у – у1 ) / (Икс2 – Икс1)
Графическое представление
Ниже у нас есть несколько ситуаций, в которых актуально понятие наклона. Его значение можно легко вычислить, измерив соответствующее вертикальное и горизонтальное смещение, а затем сделав частное, указанное в начале.
Это дает нам представление о неровности или уклоне какой-либо конструкции, например, пандуса, крыши или дороги:
Наклон пандуса, показанного на рисунке 2 слева, равен m = 1/12, уклон крыши равен m = 1/3, а уклон дороги выражен в процентах. 10% означает, что на каждые 100 метров горизонтального продвижения достигается 10 метров высоты:
В этом случае наклон составляет 10/100 = 0,1, что в процентах равно 10%.
Типы откосов
Наклон линии может быть положительным, отрицательным или нулевым. Например, линия, показанная на рисунке 1, имеет положительный наклон. Мы сразу ценим это, потому что видим, что линия «поднимается», если смотреть слева направо.
Если линия спускается слева направо, то ее наклон отрицательный. А когда линия горизонтальна, ее наклон равен нулю.
Наконец, для вертикальных линий наклон не определен.
Графическое изображение каждого типа представлено ниже:
Как рассчитывается наклон линии?
Вычислить наклон очень просто, вам просто нужно найти вертикальное смещение и горизонтальное смещение, а затем сделать частное между ними.
Когда у нас есть чертеж линии в декартовой плоскости, эти смещения находятся путем выбора любых двух точек на прямой P1 И п2, определяя его координаты и применяя определение, данное в начале:
т = (у – у1 ) / (Икс2 – Икс1 )
Поскольку величина наклона не зависит от выбора P1 И п2 , мы собираемся выбрать любую точку P с координатами (x, y), принадлежащую прямой, координаты которой неизвестны, и другую точку P1 чьи координаты: (x1, Y1).
Уклон:
т = (у – у1) / (х – х1)
Мы можем очистить Y:
и и1 = m (х – х1)
Теперь предположим, что точка P1 – пересечение прямой с вертикальной осью координат (0, b). Подставив это в приведенное выше уравнение:
y – b = m (x – 0) → y = mx + b
Это выражение известно как уравнение прямой в виде Наклон перехват, поскольку прямая однозначно определяется, когда известен ее наклон и пересечение с вертикальной осью.
Знания только наклона недостаточно, чтобы охарактеризовать линию на плоскости, поскольку бесконечные линии могут иметь одинаковый наклон, что означает, что они параллельны, но проходят через другие точки.
Решенные упражнения
– Упражнение 1
Найдите наклон линии, показанной на следующем рисунке:

Решение
п1 И п2 Это две легко читаемые точки, которые будут использоваться для расчета.Обратите также внимание, что они являются соответствующими пересечениями с осями координат.
Координаты каждой точки:
п1 (4.0) и P2 (0,4)
Подставив в уравнение для наклона:
m = (4-0) / (0-4) = 4 / (- 4) = -1
Наклон отрицательный, чего и следовало ожидать, глядя на график.
– Упражнение 2.
Найдите уравнение прямой, проходящей через точку (1, -6) и параллельной прямой y = 2x – 3.
Решение
Наклон искомой прямой должен быть таким же, как у y = 2x – 3, поскольку они параллельны. Для этой линии наклон m = 2, поэтому искомая линия имеет вид:
и и1 = 2 (х – х1)
Теперь подставляем точку, через которую проходит наша линия: x1 = 1 и y1 = -6.
у – (-6) = 2 (х – 1)
Следовательно, y = 2x – 2-6 → y = 2x – 8
Примеры
Две величины могут быть связаны таким образом, что их график представляет собой прямую линию. В этом случае говорят, что величины имеют линейную зависимость, а наклон линии можно интерпретировать как скорость изменения одной переменной к другой.
Пример 1
Предположим, что бассейн наполнен водой на показатель постоянная во времени. Естественно, что чем больше времени проходит, тем больше воды сохраняется. Что ж, скорость, с которой бассейн наполняется, – это в точности наклон линии, которая связывает объем со временем:
В этом примере бассейн наполняется со скоростью 6/3 галлона в минуту или 2 галлона в минуту.
Пример 2
Когда мобильный телефон движется по прямой с постоянной скоростью, наклон графика положения как функции времени не что иное, как указанная скорость. На графике показан мобильный телефон с положительной скоростью, что означает, что он движется от начала координат.
Ссылки
- Альварес Дж. Склон шоссе. Получено с: geogebra.es.
- Карена, М. 2019. Учебное пособие по довузовской математике. Национальный университет Литорала.
- Хоффман, Дж. Выбор тем по математике. Том 4.
- Хименес, Р. 2008. Алгебра. Прентис Холл.
- Стюарт, Дж. 2006. Precalculus: математика для исчисления. 5-е. Издание. Cengage Learning.
- Зилл, Д. 1984. Алгебра и тригонометрия. Макгроу Хилл.