-
Как определить натуральную величину отрезка прямой общего положения.
Прямая, не
параллельная ни одной плоскости проекция,
называется прямой общего положения.
Натуральная
величина отрезка прямой общего положения
определяется величиной гипотенузы
прямоугольного треугольника, построенного
на одной из проекций как на катете.
Второй катет треугольника равен разности
расстояний концов отрезка до плоскости
проекций на которой взят первый катет.
-
Как определить углы наклона прямой линии к плоскостям п1 и п2.
Угол наклона
отрезка прямой к плоскости проекций –
угол, противолежащий катету треугольника,
равному разности расстояний концов
отрезка (∆y).
α – угол наклона отрезка к плоскости П2
можно определить из прямоугольного
треугольника.
Угол наклона к П1
(ниже оси х на эпюре) определяется как
угол между отрезком А1В1
и натуральной величиной этого отрезка.
Угол наклона к П2
(выше оси х на эпюре) определяется как
угол между отрезком А2В2
и натуральной величиной этого отрезка.
-
Главные линии плоскости.
1.Горизонтали h –
прямые, лежащие в данной плоскости и
параллельные горизонтальной плоскости
проекций.
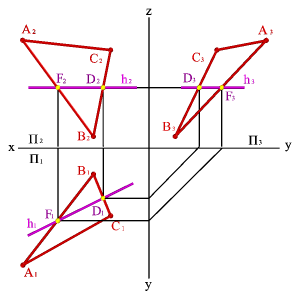
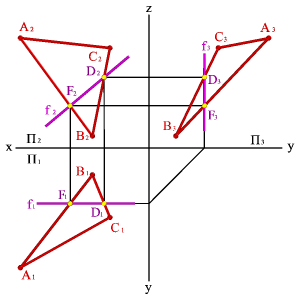
2.Фронтали f – прямые,
расположенные в плоскости и параллельные
фронтальной плоскости проекций.
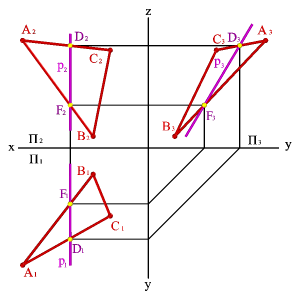
3.Профильные прямые
р – прямые, которые находятся в данной
плоскости и параллельны профильной
плоскости проекций.
4.Линия наибольшего
наклона к горизонтальной плоскости
проекций называется линией ската.

-
Проецирующие плоскости.
Плоскость частного
положения – плоскость проходящая через
проецирующие прямые, т.е. перпендикулярная
к одной или одновременно к двум основным
плоскостям проекций. Если плоскость
перпендикулярна только к одной плоскости
проекций, то она называется проецирующей
плоскостью. Существует три вида
проецирующих плоскостей:
1.Горизонтально-проецирующая
плоскость – перпендикулярна к П1.
И поэтому проецируется на нее как прямая.
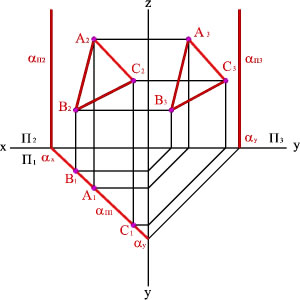
2. Фронтально-проецирующая
плоскость – перпендикулярна к П2.
И поэтому проецируется на нее как прямая.
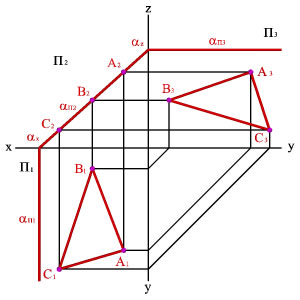
3. Профильно-проецирующая
плоскость – перпендикулярна к П3.
И поэтому проецируется на нее как прямая.
На обычном ортогональном чертеже, когда
плоскость П3
не используется, профильно-проецирующая
плоскость выглядит как плоскость общего
положения.
-
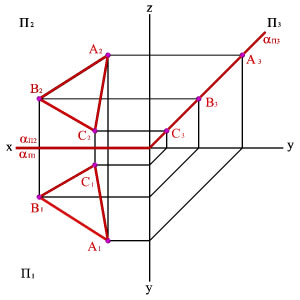
Линии уровня.
Плоскость уровня
– плоскости, параллельные плоскостям
проекций – занимают частное положение
в пространстве;
Горизонтальная
плоскость – плоскость, параллельная
горизонтальной плоскости проекций
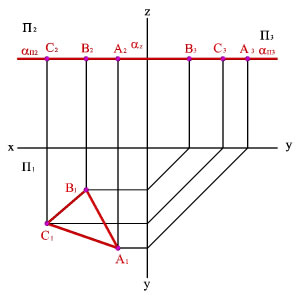
Фронтальная
плоскость – плоскость, параллельная
фронтальной плоскости проекций
Профильная плоскость
– плоскость, параллельная профильной
плоскости проекций

-
Что называется
следами плоскости и как они изображаются
на эпюре.
Следами плоскости
называются линии пересечения плоскости
с плоскостями проекций.
-
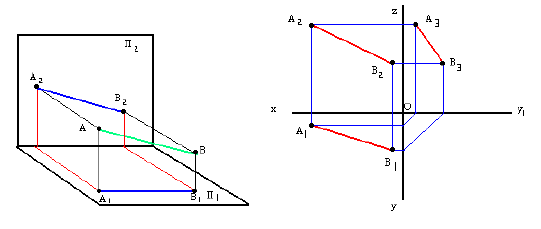
Как определяется
видимость прямой и плоскости по
конкурирующим точкам.
Точки, у которых
проекции на П1
совпадают, называют конкурирующими по
отношению к плоскости П1,
а точки, у которых проекции на П2
совпадают, называют конкурирующими по
отношению к плоскости П2.
-
Как определяется
принадлежности точки плоскости.
Точка принадлежит
плоскости, если она принадлежит прямой,
лежащей в этой плоскости.
-
Как опустить
перпендикуляр из точки к плоскости.
Расстояние от
точки до плоскости равно длине
перпендикуляра, опущенного из точки на
эту плоскость. Пусть требуется найти
расстояние от точки K до плоскости s
(АВС).
Алгоритм построения:
Строится перпендикуляр
из точки K на плоскость s (АВС) : m1 h1, m2
f2.
Находится точка
N – точка пересечения перпендикуляра m
с плоскостью s (АВС).
Определяется
расстояние от точки K до точки N с помощью
прямоугольного треугольника K1N1M0. Длина
гипотенузы N1M0 – это искомое расстояние:
|KN| = N1M0.
-
Как из точки,
принадлежащей плоскости, восстановить
перпендикуляр.
-
Как через точку
провести плоскость, параллельную
заданной плоскости.
-
Когда плоскости
параллельны.
Две плоскости
параллельны, если две пересекающиеся
прямые одной плоскости соответственно
параллельны двум пересекающимся прямым
другой плоскости.
-
В каком случае
плоскости перпендикулярны.
Две плоскости
перпендикулярны, если одна из них
проходит через перпендикуляр к другой.
-
Как изображается
на эпюре точка в проекциях с числовыми
отметками.
Прямоугольные
проекции точек на горизонтальную
плоскость проекций сопровождаемые
числами, определяющими удаление самих
точек от этой плоскости, называются
проекциями с числовыми отметками.
Точка задается
своей горизонтальной проекцией и числом
при ней(отметкой), отражающим высоту
этой точки над горизонтальной плоскостью
проекций.
-
Как изображается
прямая линия в проекциях с числовыми
отметками.
Если взять 2 точки
в пространстве и соединить их прямой,
то получим отрезок, расположенный
определенным образом относительно П0.
Проекция отрезка будет выражена отрезком
А3В5, при наличии линейного масштаба она
вполне определяет отрезок АВ в
пространстве.
-
Что такое уклон
прямой.
Уклон отрезка –
Отношение разности отметок концов к
заложению.
I = hв-hа
/ l = tg(x)
(x-угол наклона прямой к плоскости П0).
-
Что такое интервал
прямой.
Интервалом прямой
называют горизонтальное расстояние
между такими двумя точками прямой,
разность отметок которых равна 1.
L = l / hв-hф.
Если прямая задана
отметками не целых чисел, то для нахождения
точек кратных целому числу проводят
градуирование прямой, то есть находят
отметки чисел, определяют интервал
прямой.
-
Что такое
заложение прямой.
Заложение – это
горизонтальная проекция отрезка прямой
на плоскости нулевого уровня (l).
-
В каком случае
прямые в проекциях с числовыми отметками
параллельны.
Параллельные
прямые могут быть параллельными если
их проекции параллельны, интервалы
равны, уклоны равны, одинаково
ориентированы, отметки возрастают в
одном направлении.
-
В каком случае
прямые в проекциях с числовыми отметками
пересекаются, скрещиваются.
Прямые пересекающиеся
если отметки прямых в точки пересечения
одинаковы, прямые соединяющие точки с
одинаковыми отметками параллельны.
Скрещивающиеся
прямые если отметки в точке пересечения
проекций для каждой прямой разные. Линии
соединяющие точки с одинаковыми отметками
не параллельны. Если проекции скрещивающихся
прямых параллельны, то уклоны должны
быть не равными, или при равных уклонах
противоположно ориентированы.
-
Задание плоскости
в проекциях с числовыми отметками.
а) Тремя точками,
не лежащими на одной прямой, и их
отметками.
б) Прямой и точкой,
не лежащей на этой прямой, и их отметками.
в) Двумя параллельными
прямыми и их отметками.
г) Двумя пересекающимися
прямыми с отметками.
д) Топографической
поверхностью
е) Масштабом уклона
плоскости
-
Что такое масштаб
уклона плоскости.
Масштаб уклона
плоскости – проекция линии наибольшего
наклона (ската), с нанесенными на ней
интервалами.
-
Как опустить
перпендикуляр из точки к плоскости в
проекциях с числовыми отметками.
-
Задание прямой
в проекциях с числовыми отметками.
Проекция прямой
задается:
– двумя точками с
отметками при наличии линейного масштаба;
– точкой с отметкой
и стрелкой с величиной уклона, указывающей
навправление убывания отметок.
-
Как определить
угол простирания плоскости.
Угол простирания
плоскости отсчитывает против часовой
стрелки от северного конца магнитной
стрелки до направления линии простирания
плоскости.
Простиранием
плоскости называется направление
горизонтальной плоскости, указываемое
стрелкой вправо, если смотреть в сторону
возрастания отметок.
-
Как определяется
линия пересечения плоскостей в проекциях
с числовыми отметками, если плоскости
заданы двумя треугольниками.
Градуируем сторону
с наибольшей разностью отметок, проводим
главную линию (соединяем третью вершину
с соответствующей отметкой).
Аналогично со
вторым треугольником.
Ищем точки
пересечения одноименных линий. И получаем
линию пересечения двух треугольников.
-
Как определяется
линия пересечения плоскостей в проекциях
с числовыми отметками, если плоскости
заданы масштабами уклонов.
1.Градуируем
плоскость.
2.Из точек градуировки
проводим перпендикулярные прямые.
3.Одноименные
пересекающиеся прямые, проводим линию
пересечения двух плоскостей.
-
Как определить
точку пересечения прямой общего
положения с плоскостью в ортогональных
проекциях.
Если прямая не
лежит в плоскости и не параллельна ей,
она пересекает плоскость.
Задача на определение
точки пересечения прямой с плоскостью
сводится к следующему:
1) проведению
вспомогательной плоскости (Вспомогательную
плоскость рекомендуется выбирать такую,
которая даст наиболее простое графическое
решение задачи) через данную прямую;
2) нахождению линии
пересечения вспомогательной плоскости
с данной плоскостью;
3) определению
точки пересечения данной прямой с линией
пересечения плоскостей, а следовательно,
с данной плоскостью.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
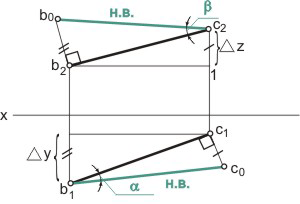
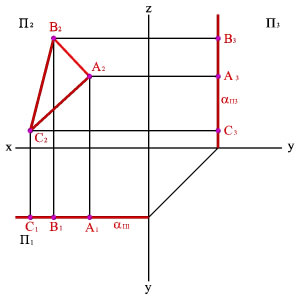
4.5. Определение длины отрезка и углов его наклона к плоскостям проекций
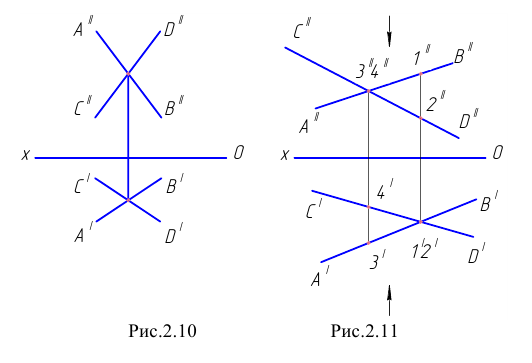
Прямая общего положения на плоскости проекций отображается с искажением (рис.4.6). Для того чтобы найти её натуральную величину, необходимо воспользоваться правилом прямоугольного треугольника, согласно которому на комплексном чертеже натуральной величиной прямой является гипотенуза прямоугольного треугольника, построенного на двух катетах. Один из этих двух катетов – это проекция рассматриваемой прямой, а вторым катетом является разность координат начала и конца этой прямой или разность координат z точек А и В (Δz = zA – zB).
Углы наклона прямой общего положения к плоскостям проекций по двум ее проекциям находят при определении действительной величины этой прямой способом прямоугольного треугольника. Если взять прямую общего положения АВ и спроецировать ее на горизонтальную плоскость проекций, а через точку А провести линию, параллельную плоскости, то в пространстве получится прямоугольный треугольник, один из катетов которого (AB’) равен длине проекции прямой АВ, а угол между прямой и этим катетом будет углом наклона заданной прямой к горизонтальной плоскости проекций (рис. 4.6), что можно подтвердить известным математическим соотношением:
tg α = BB’ / AB’ = (BB1 – B’B1) / AB’ = (zB – zA) / A1 B1.
Прямая А1В0 представляет натуральную величину прямой общего положения АВ.
Для определения натуральной величины прямой общего положения АВ и угла наклона её к плоскости проекций на эпюре (комплексном чертеже) необходимо построить прямоугольный треугольник:
– первый катет этого треугольника равен проекции прямой, на плоскости проекций;
– для построения второго катета необходимо из проекции любого конца проекции прямой линии под прямым углом к проекции провести луч, на котором отложить длину второго катета, равную разности расстояний от концов прямой до данной плоскости проекций;
– гипотенуза полученного прямоугольного треугольника будет равна действительной величине заданной прямой;
– угол наклона прямой линии к той или иной плоскости проекций равен углу между гипотенузой – натуральной величиной и катетом – проекцией прямой на эту плоскость проекций.
Углы наклона прямой линии общего положения к плоскости, всегда меньше их ортогональных проекций.
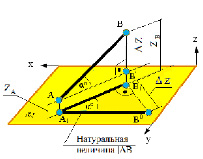
Рис. 4.6. Определение угла наклона и натуральной величины отрезка
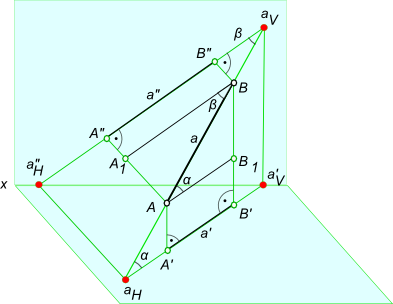
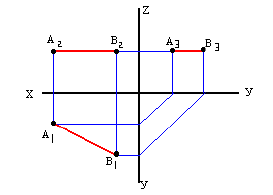
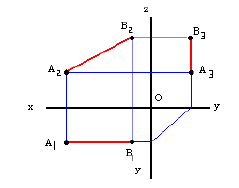
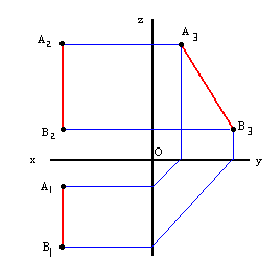
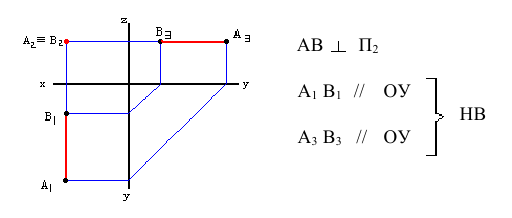
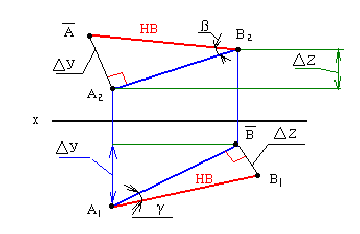
Учитывая сказанное выше и рассмотрев рис. 4.7, можно утверждать, что длина отрезка АВ равна гипотенузе треугольника, катетами которого являются фронтальная проекция отрезка А2В2 и разность координат Y точек А и В (ΔY = YB – YA). Угол этого треугольника, лежащий против катета ΔY, равен углу наклона отрезка АВ к фронтальной плоскости проекций π2 (угол β°).
По аналогии длина отрезка АВ может быть определена и как гипотенуза треугольника, катеты которого профильная проекция отрезка А3В3 и разность координат Х (Δ Х = ХА – ХВ) точек А и В. Угол γ° этого треугольника, лежащий против катета Δ Х, определяет угол наклона отрезка АВ к профильной плоскости проекций π3.
На рис. 4.8 показан пример определения натуральной (действительной) длины прямой АВ и углов её наклона к плоскостям проекций.
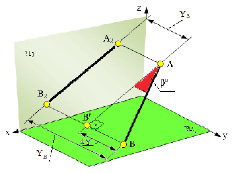
Рис. 4.7. Определение угла наклона и натуральной величины отрезка
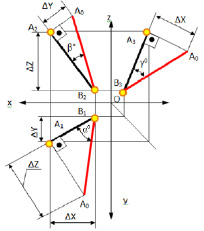
Рис. 4.8. Определение длины отрезка и углов наклона к плоскостям проекций на комплексном чертеже
Угол αº, получен при построении прямоугольного треугольника на горизонтальной проекции прямой. Углы β и γ определены с использованием фронтальной и профильной проекций прямой соответственно. Натуральная величина, указанной прямой, обозначена гипотенузами прямоугольных треугольников, построенных на трёх плоскостях проекций.
Углы наклона прямой
Углы наклона прямой общего положения по двум ее проекциям находятся попутно при определении действительной величины отрезка способом прямоугольного треугольника.
В отличие от отрезков прямых частного положения, проецирующихся хотя бы на одну из плоскостей проекций в натуральную величину, отрезок прямой общего положения на плоскости проекций проецируется с искажением. Для того чтобы найти его натуральную величину, необходимо провести ряд преобразований.
Углы наклона прямой
[
tg α = BB_1/AB_1 = (BB` – B`B_1)/AB_1 = (z_B – z_A)/A`B`
]
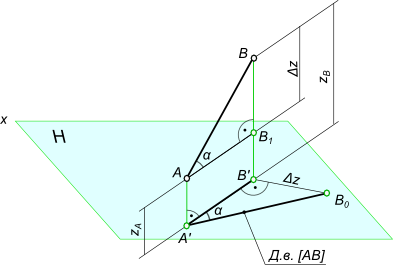
Возьмем прямую общего положения АВ и спроецируем ее на горизонтальную плоскость проекций . Через точку А проведем линию, параллельную плоскости . Таким образом в пространстве получим прямоугольный треугольник , один из катетов которого (AB1) равен длине проекции отрезка, а угол между отрезком и этим катетом является углом наклона заданного отрезка к плоскости проекций (рис.).
Для определения натуральной величины отрезка прямой общего положения и угла наклона ее к плоскости проекций на эпюре (КЧ) необходимо построить прямоугольный треугольник:
– первый катет этого треугольника равен проекции отрезка на плоскости проекций (обычно прямоугольный треугольник пристраивают к проекции отрезка, однако в некоторых задачах целесообразно прямоугольный треугольник строить в стороне от проекций геометрических объектов);
– из проекции любого конца отрезка под прямым углом к проекции отрезка проводится луч, на котором откладывается длина второго катета, равная разности расстояний от концов отрезка до данной плоскости проекций;
– гипотенуза полученного таким образом прямоугольного треугольника равна действительной величине заданного отрезка;
– угол наклона отрезка к той или иной плоскости проекций равен углу между гипотенузой – натуральной величиной и катетом – проекцией на эту плоскость проекций.
Углы наклона прямой, отрезка общего положения всегда будут меньше их ортогональных проекций.
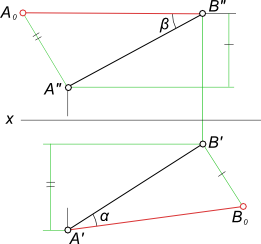
Углы наклона прямой
Для графического определения на эпюре Монжа действительной величины отрезка достаточно
построить прямоугольный треугольник, взяв за один его катет горизонтальную (фронтальную, профильную)
проекцию отрезка, а за другой катет – разность удаления концов отрезка от горизонтальной (или
соответственно фронтальной, профильной) плоскости проекции.
[
tg α = BB_1/AB_1 = (BB` – B`B_1)/AB_1 = (z_B – z_A)/A`B`
]
[
tg β = AA_1/BA_1 = (AA” – A”A_1)/BA_1 = (y_A – y_B)/A”B”
]
Графическое определение действительной величины отрезка [AB] путем построения прямоугольных треугольников
ΔA`B`B0 или ΔA”B”A0 и попутно углов его наклона:
– α к горизонтальной плоскости проекции;
– β к фронтальной плоскости проекции.
Углы наклона прямой
Углы наклона прямой к плоскости проекций проецируется на эпюре без искажений, когда она занимает положение прямой уровня, это может быть:
– Горизонтальная прямая;
– Фронтальная прямая;
– Профильная прямая
Углы наклона прямой применяются в статье графическая работа 1: Графическая работа 1
Определение углов наклона плоскости смотри также: Линия наибольшего наклона
+
Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.
Угол наклона прямой и угловой коэффициент прямой
Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси Ох с их угловым коэффициентом. Допустим, что задана декартова система координат Ох на плоскости.
Угол наклона прямой к оси Ох, расположенный в декартовой системе координат Оху на плоскости, это угол, который отсчитывается от положительного направления Ох к прямой против часовой стрелки.
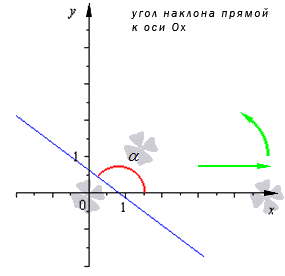
Когда прямая параллельна Ох или происходит совпадение в ней, угол наклона равен 0. Тогда угол наклона заданной прямой α определен на промежутке [0, π).
Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.
Стандартное обозначение буквой k. Из определения получим, что k=tg α. Когда прямая параллельна Ох, говорят, что угловой коэффициент не существует, так как он обращается в бесконечность.
Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.

Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.
Посчитать угловой коэффициент прямой при угле наклона равном 120°.
Решение
Из условия имеем, что α=120°. По определению необходимо вычислить угловой коэффициент. Найдем его из формулы k=tg α=120=-3.
Ответ: k=-3.
Если известен угловой коэффициент, а необходимо найти угол наклона к оси абсцисс, тогда следует учитывать значение углового коэффициента. Если k>0, тогда угол прямой острый и находится по формуле α=arctg k. Если k<0, тогда угол тупой, что дает право определить его по формуле α=π-arctgk.
Определить угол наклона заданной прямой к Ох при угловом коэффициенте равном 3.
Решение
Из условия имеем, что угловой коэффициент положительный, а это значит, что угол наклона к Ох меньше 90 градусов. Вычисления производятся по формуле α=arctg k=arctg 3.
Ответ: α=arctg 3.
Найти угол наклона прямой к оси Ох, если угловой коэффициент = -13.
Решение
Если принять за обозначение углового коэффициента букву k, тогда α является углом наклона к заданной прямой по положительному направлению Ох. Отсюда k=-13<0, тогда необходимо применить формулу α=π-arctgkПри подстановке получим выражение:
α=π-arctg-13=π-arctg 13=π-π6=5π6.
Ответ: 5π6.
Уравнение с угловым коэффициентом
Уравнение вида y=k·x+b, где k является угловым коэффициентом, а b некоторым действительным числом, называют уравнением прямой с угловым коэффициентом. Уравнение характерно для любой прямой, непараллельной оси Оу.
Если подробно рассмотреть прямую на плоскости в фиксированной системе координат, которая задана уравнением с угловым коэффициентом, который имеет вид y=k·x+b. В данном случае значит, что уравнению соответствуют координаты любой точки прямой. Если подставить координаты точки М, M1(x1, y1), в уравнениеy=k·x+b, тогда в этом случае прямая будет проходить через эту точку, иначе точка не принадлежит прямой.
Задана прямая с угловым коэффициентом y=13x-1. Вычислить, принадлежат ли точки M1(3, 0) и M2(2, -2) заданной прямой.
Решение
Необходимо подставить координаты точки M1(3, 0) в заданное уравнение, тогда получим 0=13·3-1⇔0=0. Равенство верно, значит точка принадлежит прямой.
Если подставим координаты точки M2(2, -2), тогда получим неверное равенство вида -2=13·2-1⇔-2=-13. Можно сделать вывод, что точка М2 не принадлежит прямой.
Ответ: М1 принадлежит прямой, а М2 нет.
Известно, что прямая определена уравнением y=k·x+b, проходящим через M1(0, b), при подстановке получили равенство вида b=k·0+b⇔b=b. Отсюда можно сделать вывод, что уравнение прямой с угловым коэффициентом y=k·x+b на плоскости определяет прямую, которая проходит через точку 0, b. Она образует угол αс положительным направлением оси Ох, где k=tg α.
Рассмотрим на примере прямую, определенную при помощи углового коэффициента, заданного по виду y=3·x-1. Получим, что прямая пройдет через точку с координатой 0, -1 с наклоном в α=arctg3=π3 радиан по положительному направлению оси Ох. Отсюда видно, что коэффициент равен 3.
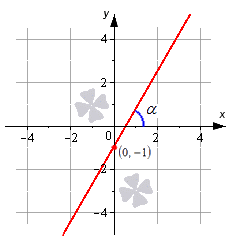
Уравнение прямой с угловым коэффициентом, проходящей через заданную точку
Необходимо решить задачу, где необходимо получить уравнение прямой с заданным угловым коэффициентом, проходящим через точку M1(x1, y1).
Равенство y1=k·x+b можно считать справедливым, так как прямая проходит через точку M1(x1, y1). Чтобы убрать число b, необходимо из левой и правой частей вычесть уравнение с угловым коэффициентом. Из этого следует, что y-y1=k·(x-x1). Данное равенство называют уравнением прямой с заданным угловым коэффициентом k, проходящая через координаты точки M1(x1, y1).
Составьте уравнение прямой, проходящей через точку М1 с координатами (4,-1), с угловым коэффициентом равным -2.
Решение
По условию имеем, что x1=4, y1=-1, k=-2. Отсюда уравнение прямой запишется таким образом y-y1=k·(x-x1)⇔y-(-1)=-2·(x-4)⇔y=-2x+7.
Ответ: y=-2x+7.
Написать уравнение прямой с угловым коэффициентом, которое проходит через точку М1 с координатами (3,5), параллельную прямой y=2x-2.
Решение
По условию имеем, что параллельные прямые имеют совпадающие углы наклона, отсюда значит, что угловые коэффициенты являются равными. Чтобы найти угловой коэффициент из данного уравнения, необходимо вспомнить его основную формулу y=2x-2, отсюда следует, что k=2. Составляем уравнение с угловым коэффициентом и получаем:
y-y1=k·(x-x1)⇔y-5=2·(x-3)⇔y=2x-1
Ответ: y=2x-1.
Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно
Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись. Для этого необходимо представлять в другом виде. Например, уравнение вида y=k·x+b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.
Можем получить каноническое уравнение прямой на плоскости, используя уравнение прямой с угловым коэффициентом. Получаем x-x1ax=y-y1ay. Необходимо слагаемое b перенести в левую часть и поделить на выражение полученного неравенства. Тогда получим уравнение вида y=k·x+b⇔y-b=k·x⇔k·xk=y-bk⇔x1=y-bk.
Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.
Привести уравнение прямой с угловым коэффициентом y=-3x+12к каноническому виду.
Решение
Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:
y=-3x+12⇔-3x=y-12⇔-3x-3=y-12-3⇔x1=y-12-3
Ответ: x1=y-12-3.
Общее уравнение прямой проще всего получить из y=k·x+b, но для этого необходимо произвести преобразования: y=k·x+b⇔k·x-y+b=0. Производится переход из общего уравнения прямой к уравнениям другого вида.
Дано уравнение прямой видаy=17x-2. Выяснить, является ли вектор с координатами a→=(-1, 7) нормальным вектором прямой?
Решение
Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:
y=17x-2⇔17x-y-2=0
Коэффициенты перед переменными являются координатами нормального вектора прямой. Запишем это так n→=17, -1, отсюда 17x-y-2=0. Понятно, что вектор a→=(-1, 7) коллинеарен вектору n→=17, -1, так как имеем справедливое соотношение a→=-7·n→. Отсюда следует, что исходный вектор a→=-1, 7 – нормальный вектор прямой 17x-y-2=0, значит, считается нормальным вектором для прямой y=17x-2.
Ответ: Является
Решим задачу обратную данной.
Необходимо перейти от общего вида уравнения Ax+By+C=0, где B≠0, к уравнению с угловым коэффициентом. для этого решаем уравнение относительно у. Получим Ax+By+C=0⇔-AB·x-CB.
Результат и является уравннием с угловым коэффициентом, который равняется -AB.
Задано уравнение прямой вида 23x-4y+1=0 . Получить уравнение данной прямой с угловым коэффициентом.
Решение
Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:
23x-4y+1=0⇔4y=23x+1⇔y=14·23x+1⇔y=16x+14.
Ответ: y=16x+14.
Аналогичным образом решается уравнение вида xa+yb=1, которое называют уравнение прямой в отрезках, или каноническое вида x-x1ax=y-y1ay. Нужно решить его относительно у, только тогда получим уравнение с угловым коэффициентом:
xa+yb=1⇔yb=1-xa⇔y=-ba·x+b.
Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:
x-x1ax=y-y1ay⇔ay·(x-x1)=ax·(y-y1)⇔⇔ax·y=ay·x-ay·x1+ax·y1⇔y=ayax·x-ayax·x1+y1
Имеется прямая, заданная уравнением x2+y-3=1. Привести к виду уравнения с угловым коэффициентом.
Решение.
Исходя из условия, необходимо преобразовать, тогда получим уравнение вида _formula_. Обе части уравнения следует умножить на -3 для того, чтобы получить необходимо уравнение с угловым коэффициентом. Преобразуя, получим:
y-3=1-x2⇔-3·y-3=-3·1-x2⇔y=32x-3.
Ответ: y=32x-3.
Уравнение прямой вида x-22=y+15 привести к виду с угловым коэффициентом.
Решение
Необходимо выражение x-22=y+15 вычислить как пропорцию. Получим, что 5·(x-2)=2·(y+1). Теперь необходимо полностью его разрешить, для этого:
5·(x-2)=2·(y+1)⇔5x-10=2y+2⇔2y=5x-12⇔y=52x
Ответ: y=52x-6.
Для решения таких заданий следует приводит параметрические уравнения прямой вида x=x1+ax·λy=y1+ay·λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.
Найти угловой коэффициент прямой, если она задана параметрическими уравнениями x=λy=-1+2·λ.
Решение
Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:
x=λy=-1+2·λ⇔λ=xλ=y+12⇔x1=y+12.
Теперь необходимо разрешить данное равенство относительно y, чтобы получить уравнение прямой с угловым коэффициентом. для этого запишем таким образом:
x1=y+12⇔2·x=1·(y+1)⇔y=2x-1
Отсюда следует, что угловой коэффициент прямой равен 2. Это записывается как k=2.
Ответ: k=2.
Содержание:
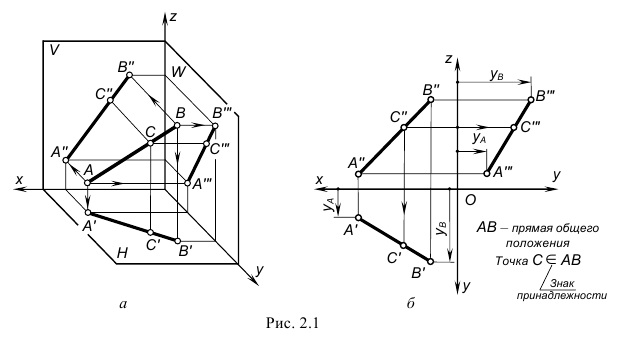
Прямая линия проецируется в виде прямой линии. В общем случае прямая линия – безгранична. Положение прямой в пространстве обычно определяется заданием двух точек. Если спроецировать эти точки на плоскость и соединить найденные проекции точек, то полученная проекция отрезка определяет проекцию всей линии, так как отрезок может быть продолжен в любую сторону на требуемое расстояние.
Общее положение прямой
Прямой общего положения называется прямая, пересекающая все плоскоcти координат.
Пусть заданы две точки 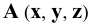
Соединяя соответствующие проекции точек прямыми линиями, получим проекции прямой, заданной отрезком 
Известно, что две проекции прямой определяют её положение в пространстве. Оценив наглядность и измеримость полученного изображения, заметим:
- – что форма проецируемого элемента – прямая линия, так как все проекции его прямые;
- – размеры проекций отрезка не равны истинной длине отрезка, так как он наклонён ко всем плоскостям проекций;
- – положение прямой относительно плоскостей координат может быть установлено по чертежу.
Отметим следующее важное обстоятельство: если точка лежит на прямой, то её проекции расположены на соответствующих проекциях прямой (точка С на Рис.2.1).
Известно, что две прямые, пересекаемые рядом параллельных прямых, рассекаются ими на пропорциональные части. Следовательно, отношение отрезков прямой равно отношению проекций этих отрезков, т.е.
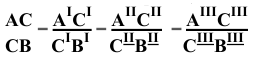
Частные случаи положения прямой
К частным случаям положения прямой относят прямые: параллельные одной из плоскостей координат, перпендикулярные к одной из плоскостей координат, лежащие в плоскости координат, совпадающие с осью координат.
Прямая, параллельная какой – либо плоскости координат, проецируется на эту плоскость в истинную величину. Это очевидно, так как 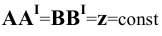 (Рис.2.2, а) и, следовательно,
(Рис.2.2, а) и, следовательно, 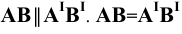 – как противоположные стороны прямоугольника.
– как противоположные стороны прямоугольника.
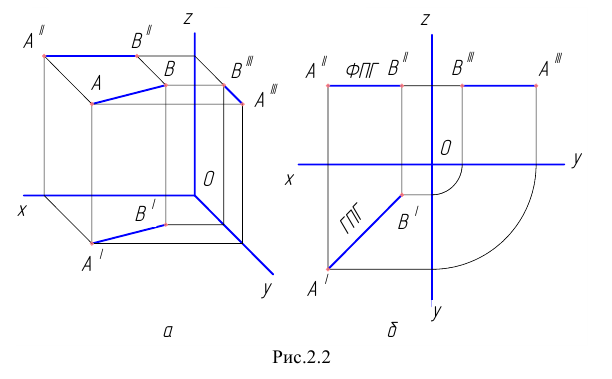
Для прямоугольных проекций прямой, параллельной плоскости  (горизонтали) (см. Рис.2.2, б), характерно, что
(горизонтали) (см. Рис.2.2, б), характерно, что 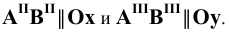 Отсюда следует: любая прямая, фронтальная проекция которой параллельна оси
Отсюда следует: любая прямая, фронтальная проекция которой параллельна оси 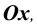 , параллельна плоскости
, параллельна плоскости  Горизонтальная проекция горизонтали (ГПГ) -истинная длина отрезка.
Горизонтальная проекция горизонтали (ГПГ) -истинная длина отрезка.
Аналогично, любая прямая 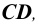 горизонтальная проекция
горизонтальная проекция 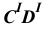 которой параллельна оси
которой параллельна оси 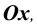 , параллельна плоскости
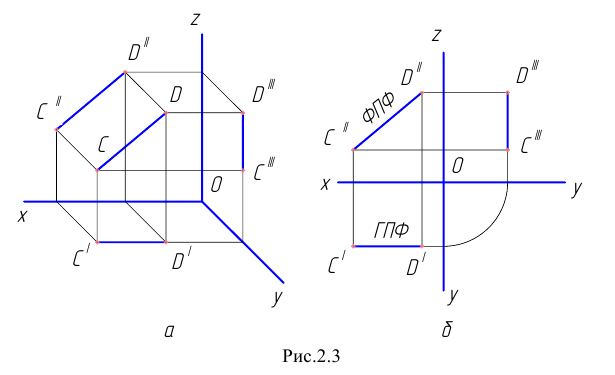
, параллельна плоскости 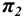 (фронталь) (Рис.2.3, а, б). Фронтальная проекция фронтали (ФПФ) – истинная длина отрезка.
(фронталь) (Рис.2.3, а, б). Фронтальная проекция фронтали (ФПФ) – истинная длина отрезка.
Прямым, параллельным плоскостям координат, принято давать общее название линий уровня.
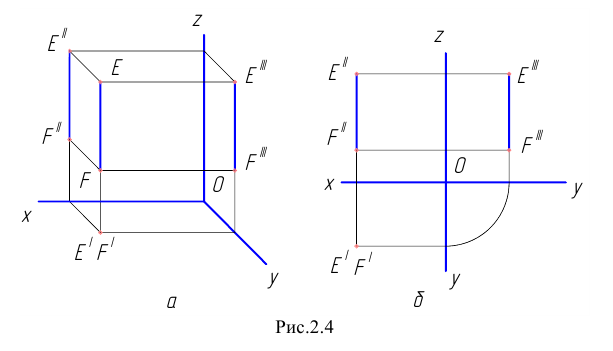
Прямая, перпендикулярная к какой-либо плоскости координат (проецирующая прямая), параллельна оси координат, перпендикулярной к этой плоскости. Например, прямая 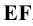 , перпендикулярная к плоскости
, перпендикулярная к плоскости 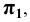 параллельна оси
параллельна оси 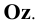 Горизонтальная проекция такой прямой (Рис.2.4, а, б) – точка. Фронтальная и профильная проекции прямой, перпендикулярной к плоскости
Горизонтальная проекция такой прямой (Рис.2.4, а, б) – точка. Фронтальная и профильная проекции прямой, перпендикулярной к плоскости 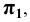 параллельны оси
параллельны оси 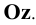
В общем случае, если прямая перпендикулярна к плоскости координат, то на эту плоскость она проецируется в виде точки, а на две другие плоскости – в истинную длину и параллельно той оси координат, которой параллельна сама прямая.
Если прямая расположена в плоскости координат, то её проекция на эту плоскость совпадает с самой прямой, а две другие проекции совпадают с осями координат.
Если прямая совпадает с осью координат, то две её проекции совпадают с самой прямой, а на плоскость, перпендикулярную этой оси, прямая спроецируется точкой в начало координат.
Определение истинной длины отрезка прямой
Пусть отрезок прямой  задан горизонтальной проекцией
задан горизонтальной проекцией  (Рис.2.5, а). Фигура
(Рис.2.5, а). Фигура 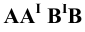 в натуре – прямоугольная трапеция, у которой углы
в натуре – прямоугольная трапеция, у которой углы 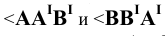 – прямые, а отрезки
– прямые, а отрезки 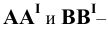 соответственно расстояния от точек
соответственно расстояния от точек  и
и 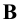 до плоскости
до плоскости 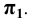 Эти отрезки численно равны координатам
Эти отрезки численно равны координатам 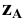 и
и 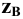 точек. Отсюда следует, что для определения истинной длины отрезка по его проекции нужно построить на этой проекции прямоугольную трапецию с параллельными сторонами, соответственно равными расстояниям от точек отрезка до плоскости. Такой способ определения длины отрезка называют способом трапеции.
точек. Отсюда следует, что для определения истинной длины отрезка по его проекции нужно построить на этой проекции прямоугольную трапецию с параллельными сторонами, соответственно равными расстояниям от точек отрезка до плоскости. Такой способ определения длины отрезка называют способом трапеции.
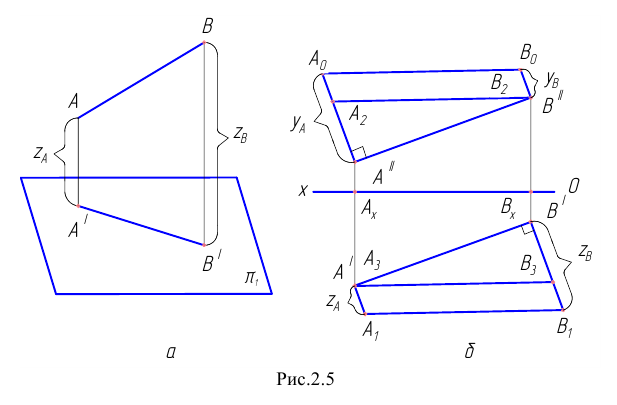
Рассмотрим пример определения истинной длины отрезка, расположенного в первом октанте. Пусть имеются проекции  (см. Рис.2.5,б).
(см. Рис.2.5,б).
Определим его истинную длину по фронтальной проекции. Для этого в точках  восстановим перпендикуляры к проекции
восстановим перпендикуляры к проекции  и отложим на них отрезки
и отложим на них отрезки 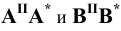 , соответственно равные расстояниям от точек
, соответственно равные расстояниям от точек 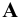 и
и 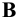 до плоскости
до плоскости  т.е. координаты
т.е. координаты 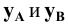 (недостающие координаты точек). Итак
(недостающие координаты точек). Итак 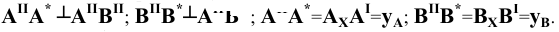
Соединяя точки 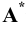 и
и 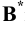 прямой, находим
прямой, находим  – истинную длину отрезка
– истинную длину отрезка 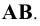
Аналогичное построение можно выполнить на горизонтальной проекции отрезка. В этом случае 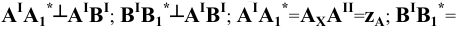
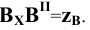 Соответственно,
Соответственно,  – истинная длина отрезка
– истинная длина отрезка 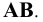
Построение можно упростить. Если отложить на перпендикуляре, восстановленном из точки 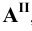 , отрезок
, отрезок 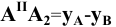 и соединить точки
и соединить точки 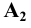 и
и 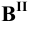
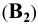 прямой. Аналогично найдём
прямой. Аналогично найдём 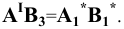 Такой приём определения истинной длины отрезка называется способом треугольника.
Такой приём определения истинной длины отрезка называется способом треугольника.
Отметим, что в способе треугольника одновременно с истинной длиной отрезка определяется угол наклона прямой к соответствующей плоскости координат:
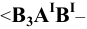 угол наклона прямой к плоскости
угол наклона прямой к плоскости 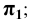
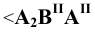 – угол наклона прямой к плоскости
– угол наклона прямой к плоскости 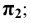
Рассмотрим пример определения истинной длины отрезка для случая, когда координаты концевых точек имеют разные знаки. Пусть, например, точка 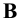 (Рис. 2.6, а) расположена над плоскостью
(Рис. 2.6, а) расположена над плоскостью 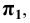 а точка
а точка  – под плоскостью
– под плоскостью  .
.
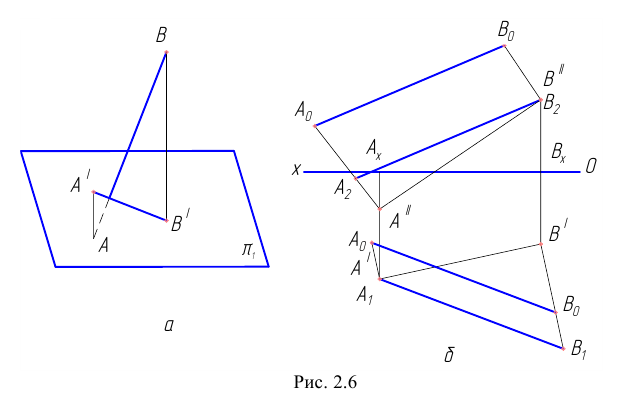
Особенностью построения в данном случае является необходимость учёта знаков недостающих координат точек, т.е. значения этих координат откладываются на перпендикулярах, восстановленных к концам проекции отрезка, в произвольные, но разные стороны (см. Рис.2.6, б). В нашем примере 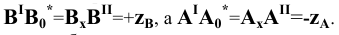
При построении способом треугольника на перпендикуляре, восстановленном из точки 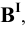 откладывается отрезок
откладывается отрезок 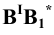 , равный алгебраической разности недостающих координат:
, равный алгебраической разности недостающих координат: 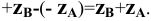 Определение истинной длины отрезка по его вертикальной проекции аналогично рассмотренному ранее примеру.
Определение истинной длины отрезка по его вертикальной проекции аналогично рассмотренному ранее примеру.
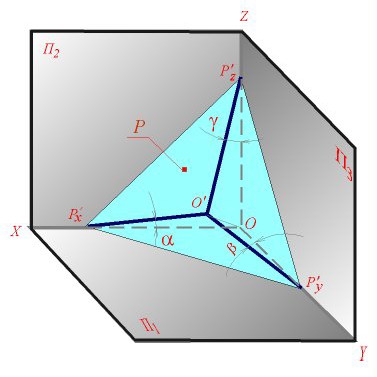
Следы прямой линии
Следом прямой линии ни данной плоскости координат называется точка пересечения (встречи) прямой с упомянутой плоскостью.
Точка пересечения прямой с плоскостью 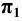 называется горизонтальным следом, с плоскостью
называется горизонтальным следом, с плоскостью 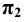 – фронтальным (вертикальным) следом и с плоскостью
– фронтальным (вертикальным) следом и с плоскостью 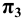 – профильным следом прямой. Следы прямой обозначаются буквами, соответственно
– профильным следом прямой. Следы прямой обозначаются буквами, соответственно 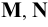 и
и 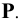
Изобразим в косоугольных проекциях (Рис.2.7) произвольный отрезок 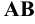 прямой общего положения и вторичные проекции этого отрезка. Построение проекций следов начнём с горизонтального следа. Согласно определению, искомая точка принадлежит прямой и, кроме того, расположена в плоскости
прямой общего положения и вторичные проекции этого отрезка. Построение проекций следов начнём с горизонтального следа. Согласно определению, искомая точка принадлежит прямой и, кроме того, расположена в плоскости 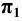 . Если точка принадлежит прямой, то её проекции лежат на соответствующих проекциях прямой. Но, с другой стороны, точка лежит в плоскости координат и, следовательно, её проекция на эту плоскость совпадает с самой точкой. Таким образом, искомое изображение горизонтального следа прямой должно быть расположено в точке пересечения изображения прямой и её горизонтальной проекции. Продолжая отрезки
. Если точка принадлежит прямой, то её проекции лежат на соответствующих проекциях прямой. Но, с другой стороны, точка лежит в плоскости координат и, следовательно, её проекция на эту плоскость совпадает с самой точкой. Таким образом, искомое изображение горизонтального следа прямой должно быть расположено в точке пересечения изображения прямой и её горизонтальной проекции. Продолжая отрезки  и
и 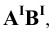 отметим точку их пересечения
отметим точку их пересечения 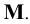
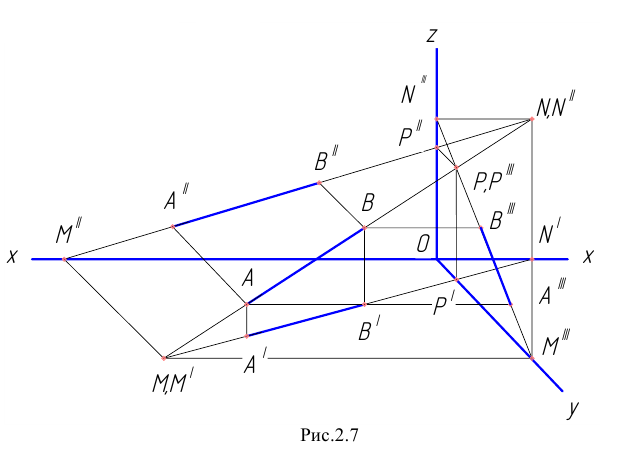
Изображение горизонтальной проекции 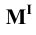 следа совпадает с изображением точки
следа совпадает с изображением точки 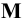 . Изображение фронтальной проекции
. Изображение фронтальной проекции 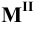 горизонтального следа найдём на оси
горизонтального следа найдём на оси  , проведя через точку
, проведя через точку 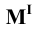 прямую, параллельную оси
прямую, параллельную оси 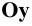 . Изображение профильной проекции
. Изображение профильной проекции 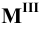 горизонтального следа получим в точке пересечения с осью
горизонтального следа получим в точке пересечения с осью 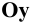 прямой, проведённой через точку
прямой, проведённой через точку 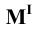 параллельно оси .
параллельно оси .
Точка  принадлежит также прямой
принадлежит также прямой 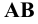 и её проекции должны находиться на соответствующих проекциях прямой. Следовательно, изображения фронтальной и профильной проекций горизонтального следа должны лежать на продолжении отрезков
и её проекции должны находиться на соответствующих проекциях прямой. Следовательно, изображения фронтальной и профильной проекций горизонтального следа должны лежать на продолжении отрезков  и
и  (в точках пересечения
(в точках пересечения 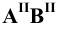 с осью
с осью 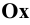 и
и 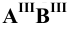 с осью
с осью 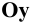 ).
).
Построение проекций фронтального  и профильного
и профильного  следов прямой осуществляется в той же последовательности.
следов прямой осуществляется в той же последовательности.
Местоположение следов прямой  и их проекций на плоскостях координат представлено в таблице:
и их проекций на плоскостях координат представлено в таблице:

Рассмотрим построение прямоугольных проекций следов прямой общего положения, заданной проекциями отрезка  (Рис.2.8). Построение начнём с нахождения проекций горизонтального следа прямой.
(Рис.2.8). Построение начнём с нахождения проекций горизонтального следа прямой.
Для этого следует найти сначала фронтальную или профильную проекции этого следа. Фронтальную проекцию 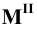 получим в точке пересечения фронтальной проекции прямой с осью
получим в точке пересечения фронтальной проекции прямой с осью  . Горизонтальную проекцию
. Горизонтальную проекцию 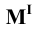 найдём в точке пересечения горизонтальной проекции прямой (продолжение отрезка
найдём в точке пересечения горизонтальной проекции прямой (продолжение отрезка  ) с перпендикуляром, восстановленным из точки
) с перпендикуляром, восстановленным из точки  к оси
к оси  . Профильная проекция
. Профильная проекция  горизонтального следа может быть получена в точке пересечения профильной проекции
горизонтального следа может быть получена в точке пересечения профильной проекции  прямой с осью
прямой с осью  или как третья проекция точки
или как третья проекция точки  по двум проекциям
по двум проекциям  и
и  . Отметим, что профильная проекция горизонтального следа должна находиться на горизонтальной оси
. Отметим, что профильная проекция горизонтального следа должна находиться на горизонтальной оси  .
.
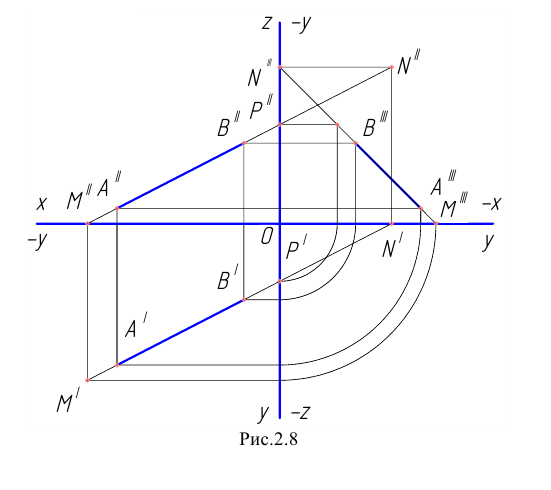
Горизонтальную проекцию  фронтального следа прямой найдём, продолжив горизонтальную проекцию прямой до пересечения с осью
фронтального следа прямой найдём, продолжив горизонтальную проекцию прямой до пересечения с осью  Фронтальную проекцию
Фронтальную проекцию 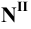 этого следа получим в точке пересечения перпендикуляра к оси
этого следа получим в точке пересечения перпендикуляра к оси 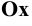 , восстановленного из точки
, восстановленного из точки 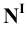 , с продолжением фронтальной проекции прямой. Профильную проекцию
, с продолжением фронтальной проекции прямой. Профильную проекцию 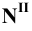 фронтального следа найдём, опустив перпендикуляр из точки
фронтального следа найдём, опустив перпендикуляр из точки 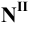 на ось
на ось 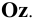 Точка
Точка 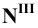 будет также в точке пересечения профильной проекции прямой с осью
будет также в точке пересечения профильной проекции прямой с осью 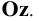
Аналогичным построением найдём проекции профильного следа.
В заключение данного раздела отметим следующее:
- – прямая, параллельная одной из плоскостей координат, имеет лишь два следа;
- – прямая, перпендикулярная к плоскости координат, имеет лишь один след;
- – два следа прямой совпадают в одной точке, если прямая пересекает ось координат;
- – три следа прямой совпадают, если прямая проходит через начало координат.
Взаимное положение прямых линий
Возможны три случая относительного положения прямых линий. Прямые могут быть взаимно параллельны, могут пересекаться друг с другом или скрещиваться.
Если прямые параллельны, то их соответствующие проекции тоже параллельны.
Пусть даны косоугольные проекции двух взаимно параллельных прямых и
и  (см. Рис.2.9, а).
(см. Рис.2.9, а).
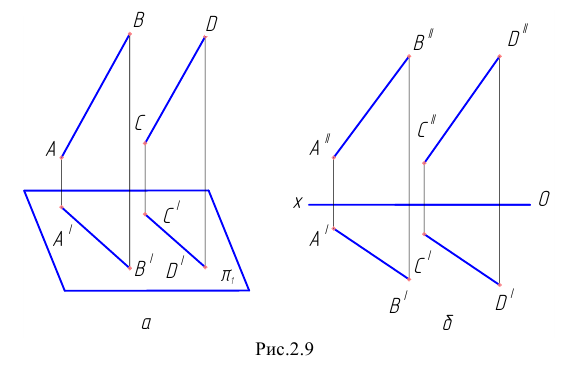
Чтобы через данную точку провести прямую, параллельную заданной, нужно через проекции этой точки провести прямые, параллельные соответствующим проекциям заданной прямой.
У пересекающихся прямых соответствующие проекции пересекаются и проекции точки пересечения связаны перпендикуляром к соответствующей оси координат. Пусть даны две пересекающиеся в точке  прямые
прямые 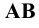 и
и 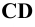 (см. Рис.2.10).
(см. Рис.2.10).
Точка 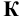 принадлежит обеим прямым. Следовательно, проекции этой точки должны лежать на проекциях обеих прямых, т.е. в точках
принадлежит обеим прямым. Следовательно, проекции этой точки должны лежать на проекциях обеих прямых, т.е. в точках  и
и  пересечения соответствующих проекций.
пересечения соответствующих проекций.
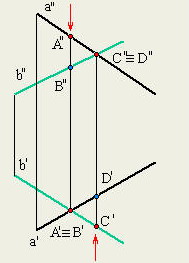
Скрещивающиеся прямые не имеют общей точки. Их проекции могут пересекаться, но точки пересечения не находятся в проекционной связи друг с другом, т. е. не лежат на перпендикуляре к соответствующей оси координат.
Изобразим прямоугольные проекции Рис.2.11) двух скрещивающихся прямых 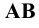 и
и 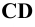 . В точку пересечения их горизонтальных проекций проецируются две точки: точка 1, принадлежащая прямой
. В точку пересечения их горизонтальных проекций проецируются две точки: точка 1, принадлежащая прямой 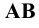 , и точка 2, принадлежащая прямой
, и точка 2, принадлежащая прямой 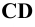 . Эти точки называются конкурирующими. С их помощью определяется взаимное положение прямых относительно плоскостей проекций (видимость проекций геометрических элементов). Так, в нашем случае, приведённом на Рис.2.11, луч, проецирующий прямые на плоскость
. Эти точки называются конкурирующими. С их помощью определяется взаимное положение прямых относительно плоскостей проекций (видимость проекций геометрических элементов). Так, в нашем случае, приведённом на Рис.2.11, луч, проецирующий прямые на плоскость  встретит раньше точку 1. Следовательно, эта часть прямой
встретит раньше точку 1. Следовательно, эта часть прямой 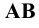 расположена выше прямой
расположена выше прямой 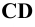 . Аналогично определим, что левая часть прямой
. Аналогично определим, что левая часть прямой 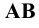 расположена дальше от плоскости
расположена дальше от плоскости  вместе с принадлежащей ей точкой 3, чем прямая
вместе с принадлежащей ей точкой 3, чем прямая 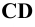 . В общем случае при определении видимости прямоугольных проекций на плоскости
. В общем случае при определении видимости прямоугольных проекций на плоскости  направление проецирующего луча принимают заданным сверху вниз, на плоскости
направление проецирующего луча принимают заданным сверху вниз, на плоскости  – снизу вверх и на плоскости
– снизу вверх и на плоскости 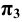 – слева направо.
– слева направо.
Проекции отрезка прямой линии
Как известно из элементарной геометрии, прямая линия определяется двумя точками, поэтому, чтобы построить проекции этой прямой, необходимо иметь проекции двух точек, принадлежащих этой прямой.
Прямую, не параллельную ни одной из плоскостей проекций, называют прямой общего положения.
На рис. 2.1 дано пространственное изображение и чертеж прямой АВ. Точки А и В находятся на разных расстояниях от каждой из плоскостей пространства, т е. прямая АВ не параллельна не одной из них. Значит, прямая АВ общего положения.
Задание и изображение на чертеже прямой общего положения
Прямая линия в пространстве определяется положением двух ее точек, например А и В. Значит, достаточно выполнить комплексный чертеж этих точек, а затем соединить одноименные проекции точек прямыми линиями, получим соответственно горизонтальную и фронтальную проекции прямой.
Прямая общего положения называется прямая не параллельная ни одной из плоскостей проекций. Прямая, параллельная или перпендикулярная одной из плоскостей проекций, называется прямой частного положения.
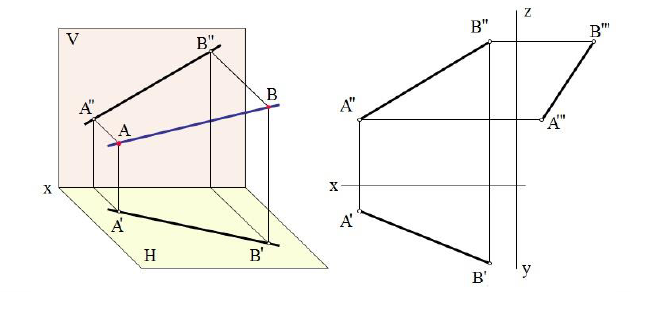
Рисунок 2.1 – Прямая общего положения
Прямые, параллельные или перпендикулярные к плоскостям проекций, называются прямыми частного положения. Прямая, параллельная какой-либо одной плоскости проекций, называется прямой уровня. Существуют три линии уровня:
- горизонтальная – прямая, параллельная горизонтальной плоскости проекций Н;
- фронтальная – прямая, параллельная фронтальной плоскости проекций V;
- профильная – прямая, параллельная профильной плоскости проекций W.
Прямые уровня
Прямая, параллельная одной из плоскостей проекций, называется прямой уровня.
Название зависит от того, какой плоскости она параллельна.
Различают: горизонтальную прямую уровня (горизонталь) h, фронтальную прямую уровня (фронталь) f, профильную прямую уровня (профиль) р.
Все точки прямых уровня имеют равные или высоты (горизонталь), или глубины (фронталь), или широты (профиль). Поэтому соответствующие проекции прямых параллельны проекциям определенных осей координат.
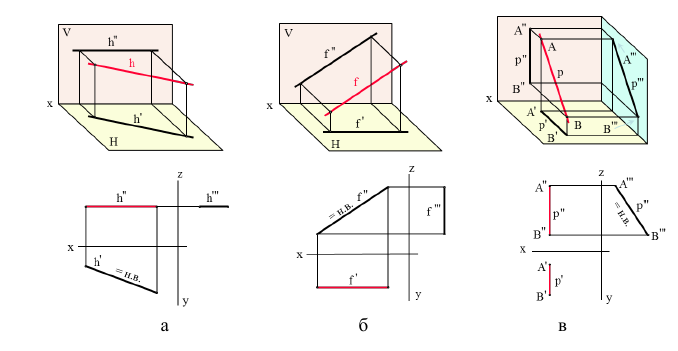 Рисунок 2.2 – Прямые уровня; а- горизонталь, б- фронталь, в- профиль Примечание: н.в. – натуральная величина прямой
Рисунок 2.2 – Прямые уровня; а- горизонталь, б- фронталь, в- профиль Примечание: н.в. – натуральная величина прямой
Проецирующие прямые
Прямая, перпендикулярная какой-либо плоскости проекции, называется проецирующей.
Различают: горизонтально проецирующую (АВ), фронтально проецирующую (CD) и профильно проецирующую (EF) (рис. 8).
У проецирующей прямой одна проекция вырождается в точку, а две другие проекции параллельны самой прямой и совпадают с направлением линии связи.
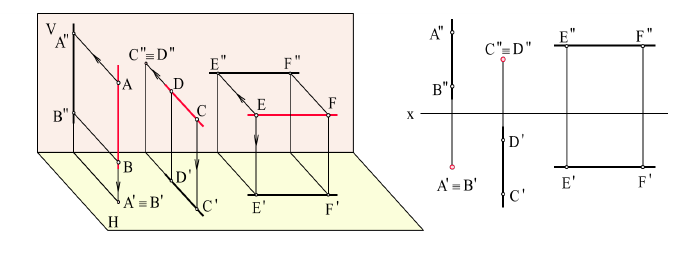
Рисунок 2.3 – Проецирующие прямые; АВ- горизонтально проецирующая CD – фронтально-проецирующая, EF-профильно-проецирующая
Следы прямой линии
Точки пересечения прямой линии с плоскостями проекции называют следами. В системе трех плоскостей проекции прямая общего положения имеет три следа – горизонтальный, профильный и фронтальный и профильный; прямая, параллельная одной из плоскостей проекции – два, и прямая, перпендикулярная к плоскости проекции – один след.
Что бы найти горизонтальный след, надо продлить фронтальную проекцию а”в” (рис. 2.4) до пересечения с осью Х (точка М”) и из этой точки восстановить перпендикуляр к оси X (линию связи) до пересечения с продолжением горизонтальной проекции a’b’.
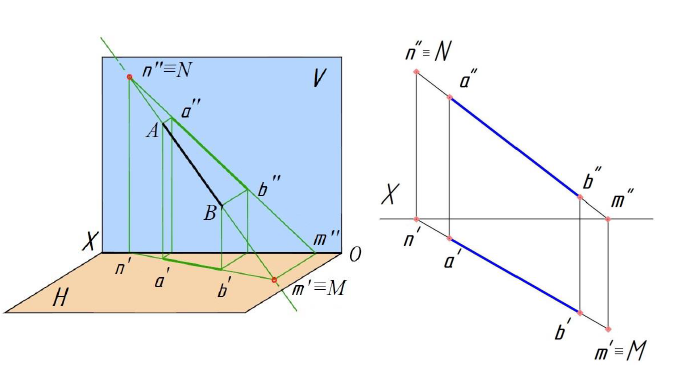
Рисунок 2.4 – Следы прямой линии
Точка м’– горизонтальная проекция горизонтального следа, которая совпадает с самим следом М.
Для нахождения фронтального следа необходимо продолжить горизонтальную проекцию а’ в’ до пересечения с осью X (точка n’) и через точку n’, которая является горизонтальной проекцией фронтального следа, провести перпендикуляр к оси X до пересечения с продолжением фронтальной проекцией а”в”. Точка n”– фронтальная проекция фронтального следа, которая совпадает с фронтальным следом N.
Отметим, что прямая не имеет следа на плоскости проекций в том случае, если она параллельна этой плоскости.
Определение натуральной величины отрезка и углов его наклона к плоскостям проекций
Возьмем отрезок АВ (рис. 2.5) и построим его ортогональную проекцию на горизонтальной плоскости проекций Н. В пространстве при этом образуется прямоугольный треугольник A’BB’, в котором одним катетом является горизонтальная проекция этого отрезка, вторым катетом разность высот точек А и В отрезка, а гипотенузой является сам отрезок.
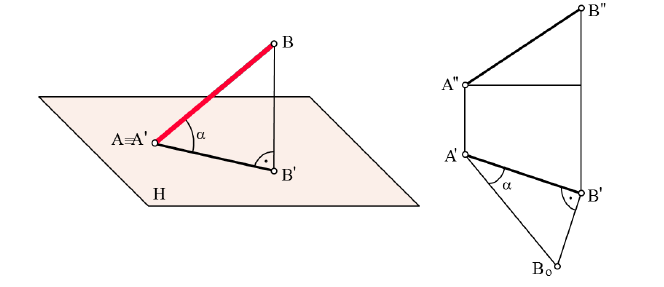
Рисунок 2.5 – Определение натуральной величины отрезка способом прямоугольного треугольника
На чертеже прямоугольный треугольник построен на горизонтальной проекции отрезка АВ, второй катет треугольника  равен разности высот точек АВ, замеренную на плоскости V, гипотенуза его и будет натуральной величиной отрезка АВ. Угол между горизонтальной проекцией А’В’ и гипотенузой
равен разности высот точек АВ, замеренную на плоскости V, гипотенуза его и будет натуральной величиной отрезка АВ. Угол между горизонтальной проекцией А’В’ и гипотенузой  треугольника
треугольника  это угол наклона данного отрезка АВ к плоскости Н.
это угол наклона данного отрезка АВ к плоскости Н.
Аналогичное построение можно сделать на фронтальной проекции отрезка, только в качестве второго катета надо взять разность глубин его концов, замеренную на плоскости Н.
Деление отрезка прямой линии
Иногда требуется разделить отрезок в данном отношении. Из свойств параллельного проецирования известно, что отношение отрезков одной и той же прямой равно отношению проекций эти отрезков.
Чтобы разделить отрезок прямой в заданном отношении, необходимо разделить в этом отношении одну из проекций этого отрезка, а затем с помощью линий связи перенести делящую точку на другие проекции.
На рис. 2.6 дан пример деления отрезка прямой линии АВ в отношение 2 : 3.
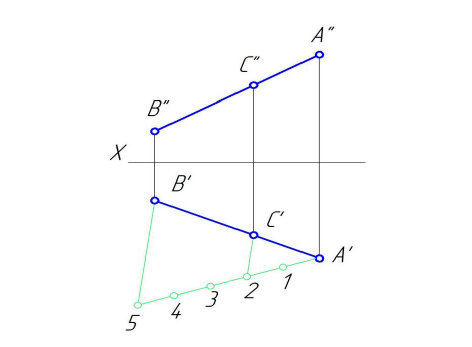
Рисунок 2.6 – Деление отрезка прямой линии
Из точки А’ проведен вспомогательный отрезок прямой, на котором отложено пять одинаковых частей произвольной длинны. Проведя отрезок В’5 и параллельно ему точку 2 прямую, получим точку С’ причем А’К’ : КБ’ = 2 : 3; затем линии связи находим точку С”. Точка С делит отрезок АВ в отношении 2 : 3.
Взаимное расположение двух прямых
- Пересекающиеся прямые. В этом случае прямые а и b имеют одну общую точку, проекции которой А’ и А” расположены на одной линии связи (рис 2.7).
- Параллельные прямые. По свойству параллельного проецирования проекции параллельных прямых на любую плоскость параллельны, т.е. если
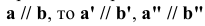 .
. - Скрещивающиеся прямые. Если две прямые скрещиваются, то их одноименные проекции могут пересекаться в точках, не лежащих на одной линии связи: две точки А и В – горизонтально конкурирующие точки, две точки С и D – фронтально конкурирующие. Как видно из чертежа, точка А расположена над точкой В; следовательно, прямая а проходит над прямой b. Точка С расположена перед (ближе к зрителю) точкой D, следовательно, прямая b проходит в этом месте впереди прямой а.
Правило определения видимости на комплексном чертеже:
из двух горизонтально конкурирующих точек на поле Н видна та точка, которая расположена выше, а из двух фронтально конкурирующих точек на поле V видна та точка, которая расположена ближе (по отношению к наблюдателю).
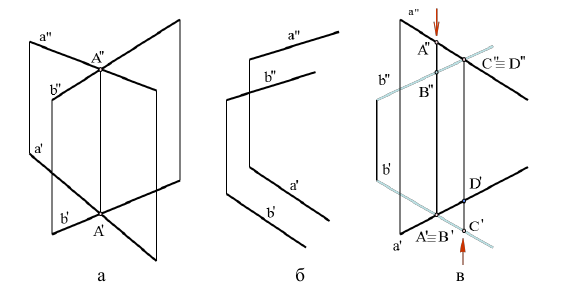
Рисунок 2.7 – Расположение двух прямых; а – пересекающиеся, б – параллельные, в – скрещивающиеся
Взаимное расположение точки и прямой
Из свойств параллельного проецирования (свойство принадлежности) известно, что если точка лежит на прямой, то ее проекции должны лежать на одноименных проекциях этой прямой.
Поэтому, из четырех точек А, В, С и D, приведенных на чертеже (рис. 2.8), лишь одна точка А лежит на прямой. Точка В находится над прямой, так как она расположена выше, чем горизонтально конкурирующая с ней точка прямой а (фронтальная проекция этой точки прямой а отмечена крестиком). Аналогично, точка С находится перед прямой а, точка D расположена ниже и дальше точки прямой а.
Определение взаимного положения точки и профильной прямой выполняется с помощью построения профильной проекции. На рис. 2.8 точка С расположена над и перед прямой АВ.
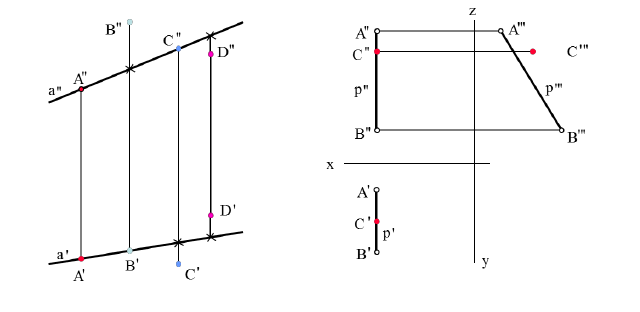
Рисунок 2.8 – Расположение точки и прямой
Взаимно перпендикулярные прямые
Для того, чтобы прямой угол проецировался без искажения, необходимо и достаточно, чтобы одна его сторона была параллельна, а другая не перпендикулярна к плоскости проекций.
Пусть сторона АВ прямого угла ABC параллельна плоскости Н. Требуется доказать, что проекция его: угол А’В’С’ равен 90.
Прямая АВ перпендикулярна плоскости, так как АВ перпендикулярна двум прямым этой плоскости ВС и ВВ’, проходящих через точку В. Прямая АВ и ее прекция А’В’ две параллельные прямые, поэтому А’В’ также перпендикулярна плоскости. Следовательно, А’В’ перпендикулярна В’С’.
Две взаимно перпендикулярные прямые (рис. 2.9) (пересекающиеся или скрещивающиеся) тогда сохраняют свою перпендикулярность в горизонтальной проекции, если одна из этих прямых является горизонталью.
Две взаимно перпендикулярные прямые сохраняют свою перпендикулярность во фронтальной проекции, если одна из них является фронталыю.
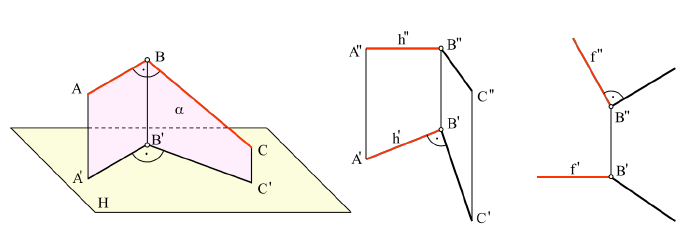
Рисунок 2.9 – Две взаимно перпендикулярные прямые (проецирование прямого угла)
Проецирование отрезка прямой
Для этого необходимо и достаточно спроецировать две конечные точки отрезка.
Положение прямой относительно плоскостей проекций
Прямая общего положения – прямая, не параллельная ни одной из плоскостей проекций.
Прямая частного положения – прямая, параллельная или перпендикулярная плоскости проекций.
Положение прямой относительно плоскостей проекций
Прямая общего положения – прямая, не параллельная ни одной из плоскостей проекций.
Прямая частного положения – прямая, параллельная или перпендикулярная плоскости проекций.
Прямые уровня
Это прямые, параллельные одной из плоскостей проекций, на которую они проецируются в натуральную величину. Они находятся на одном уровне от соответствующей плоскости.
Горизонтальная прямая – прямая, параллельная горизонтальной плоскости проекций 
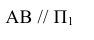
Профильная и фронтальные проекции // со ответственно осям X и У
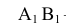 – натуральная величина (НВ) отрезка АВ
– натуральная величина (НВ) отрезка АВ
Фронтальная прямая – прямая, параллельная фронтальной плоскости проекций
Фронтальная прямая – прямая, параллельная фронтальной плоскости проекций 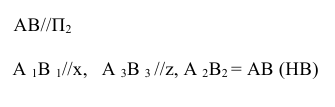
Профильная прямая – прямая, параллельная профильной плоскости проекций 
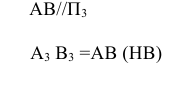
Проецирующие прямые
Это прямые, перпендикулярные одной из плоскостей проекций, на которую они проецируются в точку. Они совпадают с направлением проецирования.
Проецирующие прямые одновременно параллельны двум другим плоскостям проекций.
Горизонтально-проецирующая прямая – это прямая, перпендикулярная горизонтальной плоскости проекций 

Фронтально-проецирующая прямая – прямая, перпендикулярная фронтальной плоскости проекций 
Профильно-проецирующая прямая – прямая, перпендикулярная профильной плоскости проекций 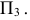
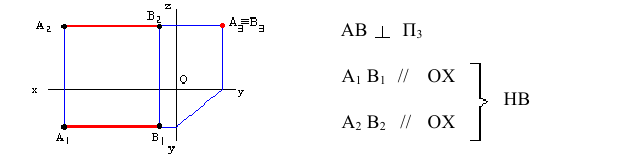
Точка на прямой
Если точка принадлежит прямой, то её проекции лежат на одноименных проекциях этой прямой.
Следы прямой
Точка пересечения прямой с плоскостями называется следом прямой.
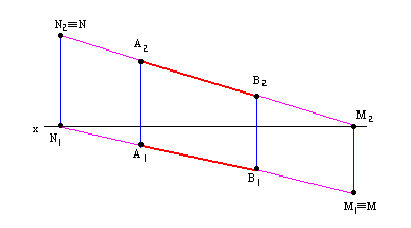
Чтобы построить горизонтальный след прямой необходимо:
- Продолжить фронтальную проекцию
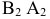 до пересечения с осью X в точке
до пересечения с осью X в точке 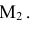
- Провести через эту точку линию связи на
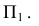
- Продолжить горизонтальную проекцию
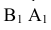 до пересечения с этой линией связи в точке
до пересечения с этой линией связи в точке 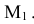
Для построения фронтального следа надо продолжить горизонтальную проекцию 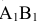 до пересечения с осью X. Из полученной точки
до пересечения с осью X. Из полученной точки 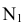 провести линию связи на
провести линию связи на 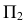 до пересечения с продолжением
до пересечения с продолжением 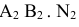 – фронтальный след прямой АВ.
– фронтальный след прямой АВ.
- М – горизонтальный след прямой
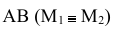
- N – фронтальный след прямой
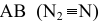
Дан отрезок общего положения. Найти горизонтальный и фронтальный следы.
Взаимное положение прямых
1 .Если в пространстве прямые параллельны, то их одноименные проекции параллельны между собой. ( Если одноименные проекции прямых общего положения параллельны на двух плоскостях проекций, то эти прямые параллельны).
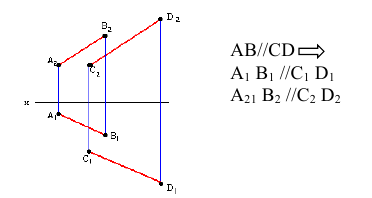
2. Если прямые пересекаются, то их одноименные проекции пересекаются между собой, а точка их пересечения лежит на одной линии связи.
Справедливо и обратное, кроме профильных прямых.
3. Если прямые не параллельны и не пересекаются, то они называются скрещивающимися.
Проецирование прямого угла
Прямой угол проецируется прямым, если одна из его сторон параллельна одной из плоскостей проекций, т.е. является фронтальной или горизонтальной прямой. (Прямой угол проецируется прямым па ту плоскость проекции, кото рои параллельна одна из его сторон, т. е. является фронтальной или горизонтальной прямой).
Определение натуральной величины отрезка прямой общего положения способом прямоугольного треугольника
Натуральная величина отрезка АВ определяется как гипотенуза прямоугольного треугольника, одним из катетов является проекция отрезка, а вторым – разница расстояний концов другой проекции до оси X 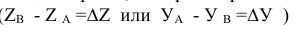
Угол между прямой линией и плоскостью проекций определяется как угол между прямой и её проекцией на эту плоскость.
Что такое прямая линия
Прямая линия в системе плоскостей проекций занимает определенное положение. Прямая может располагаться относительно плоскостей проекций произвольно или занимать некоторое частное положение – быть параллельной, перпендикулярной или принадлежать какой-либо плоскости проекций.
Способы задания прямой
- Двумя точками.
- Точкой и направлением.
- Линией пересечения двух плоскостей.
- Своими проекциями.
Классификация прямых
В зависимости от положения прямых относительно плоскостей проекций различают прямые общего положения и прямые частного положения.
Прямые общего положения
Прямая общего положения – прямая, наклоненная под произвольными углами ко всем трем плоскостям проекций (рис. 4.1, 4.2).
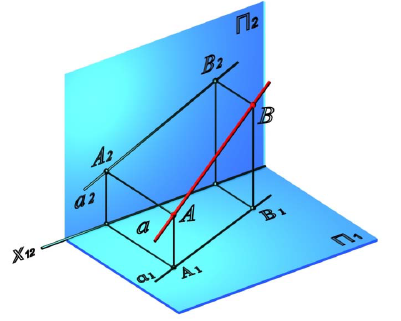
Рис. 4.1. Прямая общего положения:
a(AB) – прямая общего положения;
a1(A1B1) – горизонтальная проекция прямой a(AB);
a2(A2B2) – фронтальная проекция прямой a(AB)
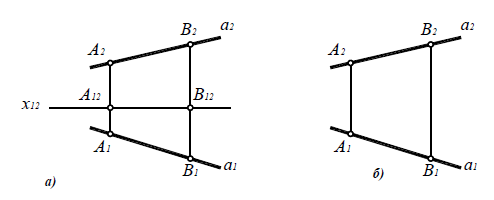
Рис. 4.2. Комплексный чертеж прямой общего положения:
а – двухкартинный комплексный чертеж; б – безосный комплексный чертеж
Прямые частного положения
Среди прямых частного положения различают линии уровня и проецирующие прямые.
Линии уровня
Прямые линии, параллельные какой-либо плоскости проекций, называются линиями уровня.
Горизонталь h – прямая, параллельная горизонтальной плоскости проекций h || П1 (рис. 4.3).
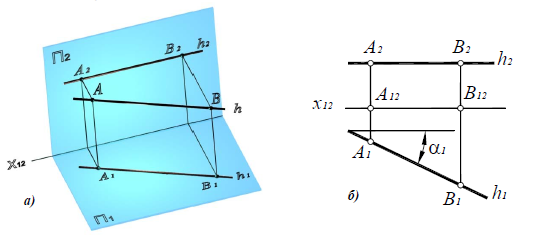
Рис. 4.3. Горизонталь:
a – наглядное изображение; б – комплексный чертеж
Поскольку высоты всех точек горизонтали равны между собой: h2 A1A 2 илиh2|| П1.
A1A 2 илиh2|| П1.
Любой отрезок горизонтали проецируется на П1 в натуральную величину:
[A1B1 ] = [AB ].
Угол наклона h к Π2 также проецируется на П1 в натуральную величину:
Фронталь  – прямая, параллельная фронтальной плоскости проекций
– прямая, параллельная фронтальной плоскости проекций  || П2 (рис. 4.4).
|| П2 (рис. 4.4).
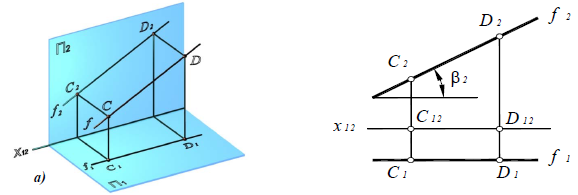
Рис. 4.4. Фронталь:
a – наглядное изображение;
б – комплексный чертеж
Поскольку глубина всех точек фронтали одинакова: 1
1 C1C2
C1C2
Отрезки фронтали и угол наклона к П1 проецируются на П1 в натуральную величину:[C2D2] =[CD]; Zβ1=Zβ=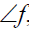 , П1.
, П1.
Профильная прямая р – прямая, параллельная профильной плоскости проекций p|| П3 (рис. 4.5).
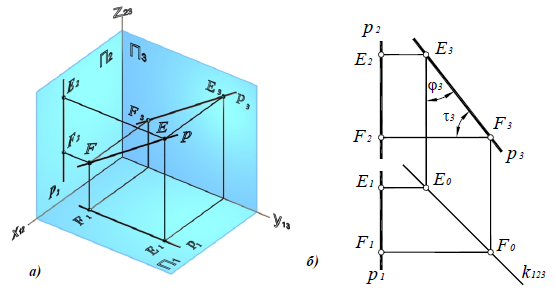
Поскольку широта всех точек профильной прямой одинакова: р2 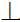 E2E1.
E2E1.
Отрезки профильной прямой и углы наклона к П1 и П2 проецируются на П3 в натуральную величину: [E3F3] =[EF]; .
.
Проецирующие прямые
Прямая линия, перпендикулярная одной из плоскостей проекций или параллельная направлению проецирования, называется проецирующей.
Горизонтально-проецирующая прямая – прямая, перпендикулярная горизонтальной плоскости проекций a 1 П1(рис. 4.6).
П1(рис. 4.6).
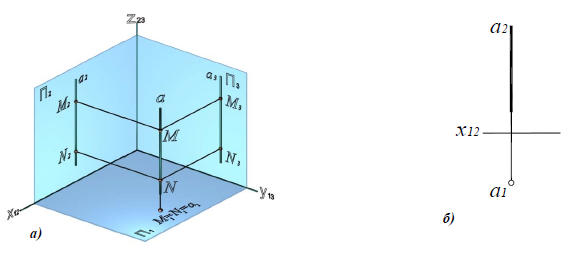
Рис. 4.6. Горизонтально-проецирующая прямая:
a – наглядное изображение;
б – комплексный чертеж
Фронтально-проецирующая прямая – прямая, перпендикулярная фронтальной плоскости проекций b 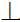 П2(рис. 4.7).
П2(рис. 4.7).
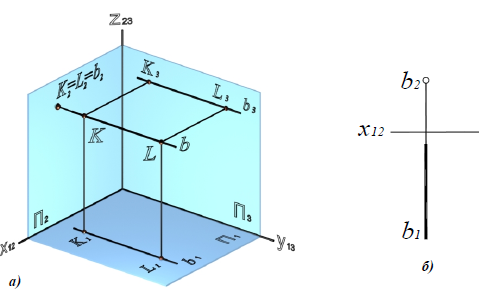
Рис. 4.7. Фронтально-проецирующая прямая:
a – наглядное изображение;
б – комплексный чертеж
Профильно-проецирующая прямая – прямая, перпендикулярная профильной плоскости проекций c  П3(рис. 4.8).
П3(рис. 4.8).
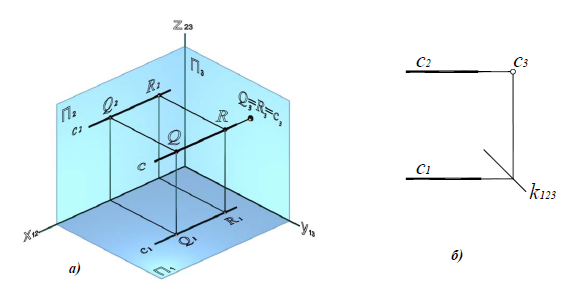
Рис. 4.8. Профильно-проецирующая прямая:
a – наглядное изображение;
б – комплексный чертеж
Взаимное положение прямых линий
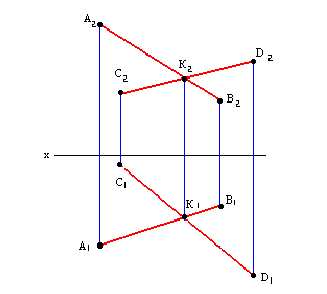
Прямые линии в пространстве могут быть параллельными, пересекающимися или скрещивающимися.
Если прямые параллельны (рис. 4.9), то их одноименные проекции параллельны: a || b  (α1|| b1) и (a2|| b2).
(α1|| b1) и (a2|| b2).
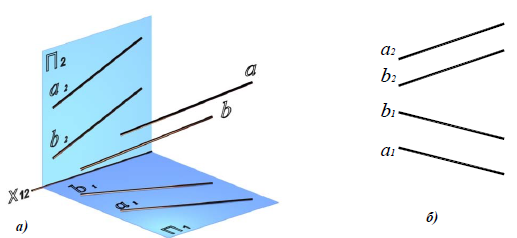
Рис. 4.9. Параллельные прямые a и b:
a – наглядное изображение; б – комплексный чертеж
Пересекающиеся прямые имеют общую точку (рис. 4.10), то есть точки пересечения их одноименных проекций лежат на общей линии связи:
c × d = K  c1 × d1 = K1 ;
c1 × d1 = K1 ;
c 2 × d2 = K2 и K 1 K 2  х12.
х12.
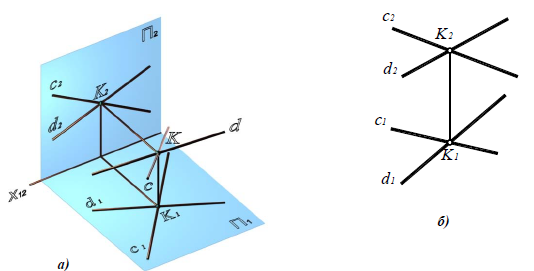
Рис. 4.10. Пересекающиеся прямые c иd:
a – наглядное изображение; б – комплексный чертеж
Прямые, не имеющие общей точки и не параллельные между собой, являются скрещивающимися (рис. 4.11, 4.12).
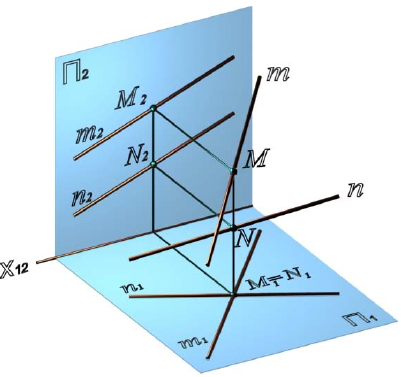
Рис. 4.11. Скрещивающиеся прямые m и n
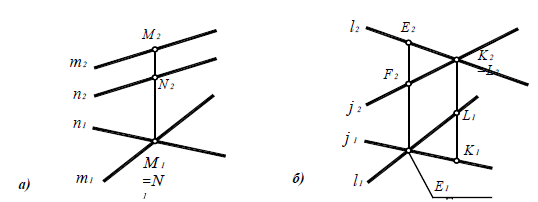
Рис. 4.12. Проекции скрещивающихся прямых:
a – скрещивающиеся прямые m иn;
б – скрещивающиеся прямые l u j
Проекции прямых пересекаются l1×j1=E1 и 12×j2=K2, но E1K2 не является общей линией связи (см. рис. 4.12,б).
Если пересекающиеся и параллельные прямые лежат в одной плоскости, то скрещивающиеся прямые лежат в двух параллельных плоскостях.
Принадлежность точки прямой линии
Точка принадлежит прямой, если ее проекции принадлежат соответствующим (одноименным) проекциям прямой (рис. 4.13).
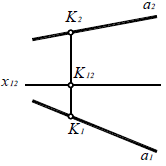
Рис. 4.13. Принадлежность точки прямой линии:
K ∈ a  K 1 ∈ a1 и K2 ∈ a2;
K 1 ∈ a1 и K2 ∈ a2;
[K1K2 ]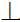 х12
х12
Определение натуральной величины отрезка. Способ треугольника
Отрезок [AB] – отрезок прямой общего положения. Ни одна из проекций отрезка не равна его натуральной величине.
На рис. 4.14 A1ABB1 – прямоугольная трапеция, наклонной стороной которой является отрезок [AB], высотой – его горизонтальная проекция [A1B1], основаниями – горизонтально-проецирующие прямые (AA1) и (BB1).
Если провести прямую (AB0) || (A1B1), то от трапеции A1ABB1 отсекается прямоугольный треугольник ABB0 с гипотенузой [AB], один катет которого [AB0 ] = [A1B1 ], другой – [BB0 ] равен разности высот точек A и B.
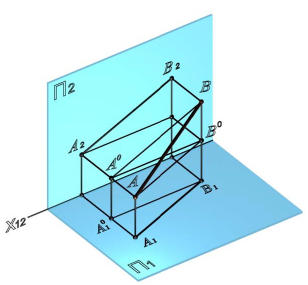
Рис. 4.14. Определение натуральной величины отрезка способом треугольника
На комплексном чертеже (рис. 4.15,а) прямоугольный треугольник строится непосредственно при горизонтальной проекции отрезка: ΔA1B1B’ = ΔABB0 . Одним катетом прямоугольного треугольника является горизонтальная проекция [A1B1 ], вторым – разность высот точек A и B (отрезок [BB0 ] = [B1B’]), гипотенуза [ A1B’] и будет равна натуральной величине отрезка [AB ].
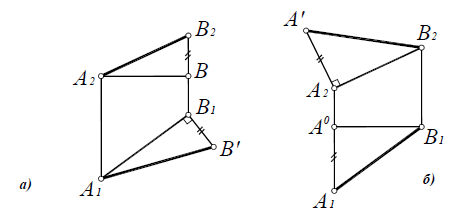
Рис. 4.15. Определение натуральной величины отрезка:
а – на горизонтальной проекции;
б – на фронтальной проекции
Аналогичные построения возможны и на фронтальной проекции (рис. 4.15,б), тогда одним катетом прямоугольного треугольника является фронтальная проекция[A2B2], а вторым – разность глубин точек A и B (отрезок [A2A’]=[A1A0]), гипотенуза [ B2A’]будет равна натуральной величине отрезка [AB ].
Таким образом, можно сформулировать общее правило:
Натуральная величина отрезка прямой определяется гипотенузой прямоугольного треугольника, одним катетом которого является одна из проекций отрезка, а вторым – разность расстояний концов другой проекции отрезка относительно друг друга.
Проекции прямой. Положение прямой относительно плоскостей проекций
Относительно плоскостей проекций H, V и W прямые линии могут занимать различные положения и имеют соответствующие наименования, а на чертежах проекции этих прямых занимают относительно осей проекций x, y и z характерные положения. Следовательно, по чертежу прямой линии можно мысленно представить ее пространственное положение относительно плоскостей проекций, т. е. научиться «читать» чертеж прямой.
Прямые общего положения – не параллельны (и соответственно не перпендикулярны) плоскостям проекций H, V и W. Следовательно, на чертеже проекции прямых общего положения не параллельны (и не перпендикулярны) осям проекций x, y и z. Отсюда проекции прямых общего положения искажают их натуральную величину.
На рис. 2.1 изображены проекции прямой общего положения АВ, фронтальная A”B” и горизонтальная A’B’ проекции которой расположены произвольно относительно оси проекций x, но не параллельны и не перпендикулярны оси x – это характерный признак прямой общего положения на чертеже! Профильная проекция A”‘B”‘ прямой общего положения также должна быть не параллельна и не перпендикулярна осям проекций z и y, что и показывает построение.
Точка на прямой. Теорема о принадлежности точки прямой: если точка принадлежит прямой, то на чертеже одноименные проекции точки лежат на одноименных проекциях прямой.
На рис. 1.4 показано построение проекций точки С, принадлежащей прямой АВ.
Прямые особого (частного) положения
Прямые уровня – прямые, параллельные одной плоскости проекций:
- – фронтальные прямые – параллельные плоскости проекций V;
- – горизонтальные прямые – параллельные плоскости проекций H;
- – профильные прямые – параллельные плоскости проекций W.
На рис. 2.2 изображены проекции фронтальной прямой АВ и принадлежащей ей точки С. Запомните характерные признаки расположения проекций фронтальной прямой на чертеже:
- – горизонтальная проекция A’B’ параллельна оси проекций x;
- – фронтальная проекция A”B” расположена к оси проекций x под углом φH, который определяет ее наклон к плоскости проекций H; фронтальная проекция A”B” определяет также натуральную величину этой прямой;
- – профильная проекция A”‘B”‘ по построению располагается параллельно оси проекций z.
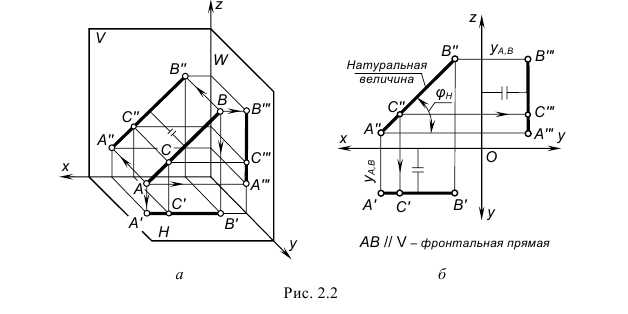
На рис. 2.3 изображены проекции горизонтальной прямой CD и принадлежащей ей точки Е. Запомните характерные признаки расположения проекций горизонтальной прямой на чертеже:
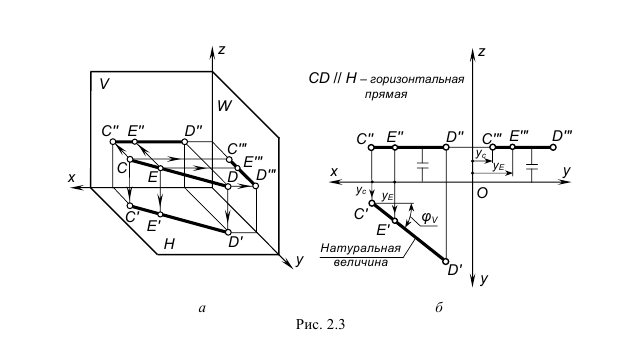
- – фронтальная проекция C”D” параллельна оси проекций x;
- – горизонтальная проекция C’D’ расположена к оси проекций x под углом φV, который определяет ее наклон к плоскости проекций V; горизонтальная проекция C’D’ определяет также натуральную величину этой прямой;
- – профильная проекция C”‘D”‘ по построению располагается горизонтально (//y).
На рис. 2.4 изображены проекции профильной прямой EF и принадлежащей ей точки N. Запомните характерные признаки расположения проекций профильной прямой на чертеже:
- – фронтальная проекция E”F” перпендикулярна оси проекций x (параллельна оси проекций z);
- – горизонтальная проекция E’F’ перпендикулярна оси проекций x;
- – профильная проекция E”‘F”‘ по построению расположена под углом φV к плоскости проекций V и под углом φH к плоскости проекций H; профильная проекция E'”F'” определяет также натуральную величину этой прямой.
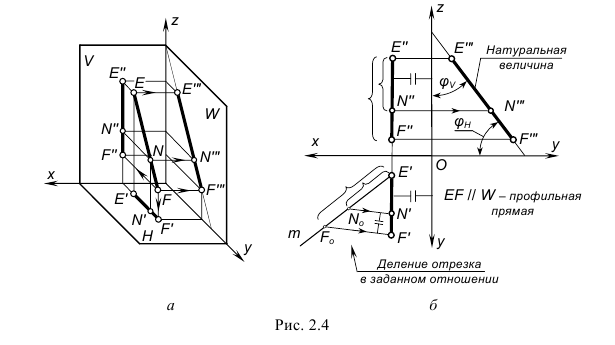
Деление отрезка в заданном отношении
На рис. 2.4 показано построение горизонтальной проекции N’ точки N, принадлежащей профильной прямой EF. Построение основано на одном из свойств параллельного проецирования: отношение отрезков прямой линии равно отношению их проекций.
Пусть точка N делит отрезок EF в каком-то отношении. Следовательно, проекции отрезка делятся в том же отношении. Если, например, дана фронтальная проекция N” точки N, принадлежащей отрезку EF, то для построения горизонтальной проекции N’ на горизонтальной проекции E’F’ отрезка нужно выполнить следующие графические действия:
- – провести произвольную прямую m из любой вершины горизонтальной проекции E’F’;
- – отложить на этой прямой два отрезка: отрезок E’Fo, равный по величине фронтальной проекции E”F”, и отрезок E’No, равный по величине E”N”;
- – соединить прямой точки Fo и F’ на горизонтальной проекции;
- – из построенной точки No провести прямую, параллельную прямой FoF’, – точка N’ и будет искомой.
Прямые проецирующие – перпендикулярные одной плоскости проекций (параллельные двум плоскостям проекций):
- – фронтально-проецирующие прямые – перпендикулярные плоскости проекций V (параллельные плоскостям проекций H и W);
- – горизонтально-проецирующие – перпендикулярные плоскости проекций H (параллельные плоскостям проекций V и W);
- – профильно-проецирующие прямые – перпендикулярные плоскости проекций W (параллельные плоскостям проекций H и V).
!!! Поскольку положение проецирующих прямых совпадает по направлению с проецирующим лучом к одной из плоскостей проекций, то одна из проекций прямых проецируется (вырождается) в точку. Говорят, что проецирующие прямые обладают «собирательным» свойством, так как их вырожденные проекции-точки «собирают», то есть представляют собой проекции всех точек, лежащих на этих прямых.
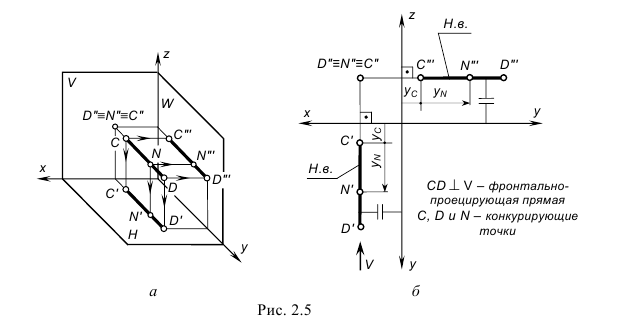
На рис. 2.5 изображены проекции фронтально-проецирующей прямой CD и принадлежащей ей точки N. Запомните характерные признаки расположения проекций фронтально-проецирующей прямой на чертеже:
- – фронтальная проекция CD(C”D”) представляет собой точку, т. е. фронтальные проекции точек C, D и N совпадают как лежащие на одном проецирующем луче к плоскости проекций V;
- – горизонтальная проекция C’D’ расположена перпендикулярно оси проекций x и определяет натуральную величину прямой;
- – профильная проекция C”‘D”‘ по построению располагается перпендикулярно оси проекций z и также определяет натуральную величину прямой.
!!! Конкурирующие точки – точки, лежащие на одном проецирующем луче, называются конкурирующими.
На рис. 2.5 точки C, D и N на прямой CD являются конкурирующими и по их расположению на прямой относительно плоскости V (по координатам y) можно определить на горизонтальной проекции порядок их «видимости»: ближе к наблюдателю и дальше от плоскости V (с наибольшей координатой y) находится точка D, затем точка N и точка C.
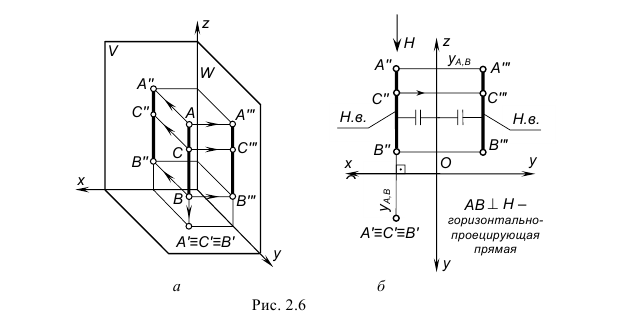
На рис. 2.6 изображены проекции горизонтально-проецирующей прямой AB и принадлежащей ей точки C. Запомните характерные признаки расположения проекций горизонтально-проецирующей прямой на чертеже:
– горизонтальная проекция AB(A’B’) представляет собой точку, т. е. горизонтальные проекции точек A, B и C совпадают как лежащие на одном проецирующем луче к плоскости проекций H;
– фронтальная проекция A”B” расположена перпендикулярно оси x и определяет натуральную величину прямой;
– профильная проекция A”‘B”‘ по построению располагается параллельно оси z и также определяет натуральную величину прямой.
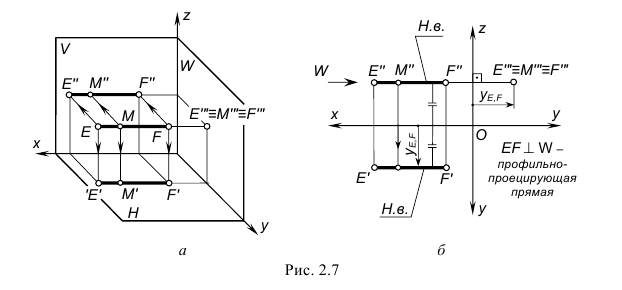
На рис. 2.7 изображены проекции профильно-проецирующей прямой EF и принадлежащей ей точки M. Запомните характерные признаки расположения проекций профильно-проецирующей прямой на чертеже:
- – профильная проекция EF(E”‘F”‘) представляет собой точку, т. е. профильные проекции точек E, F и M совпадают как лежащие на одном проецирующем луче к плоскости проекций W;
- – фронтальная проекция E”F” расположена параллельно оси x и определяет натуральную величину прямой;
- – горизонтальная проекция E’F’ по построению также располагается параллельно оси x и также определяет натуральную величину прямой.
Определение по чертежу натуральной величины отрезка прямой общего положения способом прямоугольного треугольника и углов ее наклона к плоскостям проекций H и V.
Натуральной величиной заданного на чертеже отрезка прямой общего положения является гипотенуза построенного прямоугольного треугольника, одним катетом которого может быть горизонтальная (или фронтальная) проекция отрезка, а вторым катетом этого треугольника будет разница координат ∆z (или ∆y) конечных точек этого отрезка относительно оси проекций x.
На рис. 2.8 показано построение натуральной величины заданного отрезка AB способом прямоугольного треугольника относительно фронтальной и горизонтальной его проекций, для чего выполнен следующий графический алгоритм (графические действия):
- 1-е действие. Провести перпендикулярную линию m к фронтальной проекции AB(A”B”) отрезка.
- 2-е действие. На этой прямой линии отложить отрезок A”Ao, равный разнице координат ∆y конечных точек А(А’) и В(B’) отрезка относительно оси проекций x.
- 3-е действие. Достроить гипотенузу AоB” треугольника, которая определяет искомую натуральную величину отрезка АВ.
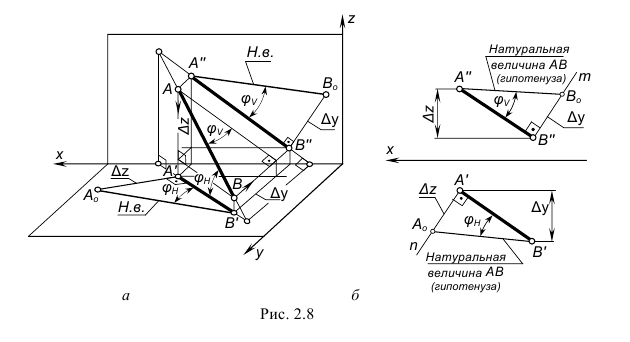
Аналогичные построения выполнены относительно горизонтальной проекции отрезка A’B’ – гипотенуза А’Bо также определяет натуральную величину заданного отрезка.
В построенных прямоугольных треугольниках углы между проекциями отрезка и гипотенузой определяют углы наклона прямой к плоскостям проекций H и V:
- – угол φV между фронтальной проекцией A”B” отрезка и гипотенузой AoB” определяет наклон отрезка к плоскости проекций V;
- – угол φH между горизонтальной проекцией A’B’ отрезка и гипотенузой A’Bо определяет наклон отрезка к плоскости проекций H.
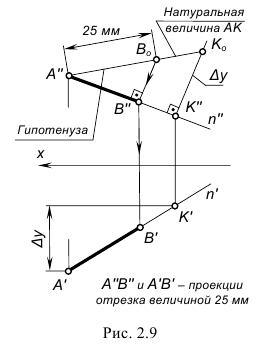
!!! В задачах по начертательной геометрии часто требуется построить на прямой общего положения, не имеющей второй конечной точки, проекции отрезка какой-либо заданной величины.
На рис. 2.9 показано построение на прямой n с одной конечной точкой A проекций отрезка AB заданной величины 25 мм, для чего выполнен следующий графический алгоритм (графические действия):
- 1-е действие. Ограничить прямую n произвольным отрезком АК(А’K’, A”K”).
- 2-е действие. Построить натуральную величину произвольного отрезка АК способом прямоугольного треугольника относительно, например, фронтальной проекции A”K” – это гипотенуза – A”Kо (см. рис. 2.9).
- 3-е действие. На построенной натуральной величине A”Ko (гипотенузе) от точки A” отложить отрезок равный 25 мм и построить точку Bо.
- 4-е действие. Из построенной точки Bо провести перпендикуляр на проекцию n” заданной прямой n и получить точку B”, т. е. построить фронтальную проекцию А”В” отрезка АВ заданной величины 25 мм; по линии связи определить горизонтальную проекцию B’ точки B, т. е. построить горизонтальную проекцию А’В’ отрезка АВ заданной величины 25 мм.
- Чертежи на заказ
Понятие о следах прямой
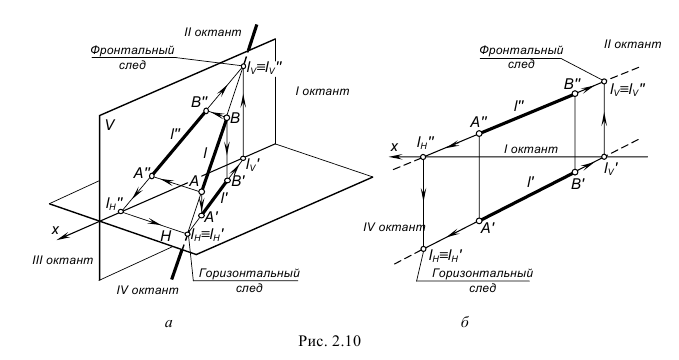
Следами прямой называются точки ее пересечения с плоскостями проекций.
На рис. 2.10 показано построение на чертеже фронтального и горизонтального следов прямой АВ и определено прохождение прямой по октантам пространства: из IV через I во II.
Взаимное положение двух прямых
Две прямые в пространстве могут быть параллельными, пересекаться или скрещиваться. Запомните характерные признаки расположения на чертеже проекций двух различно расположенных прямых.
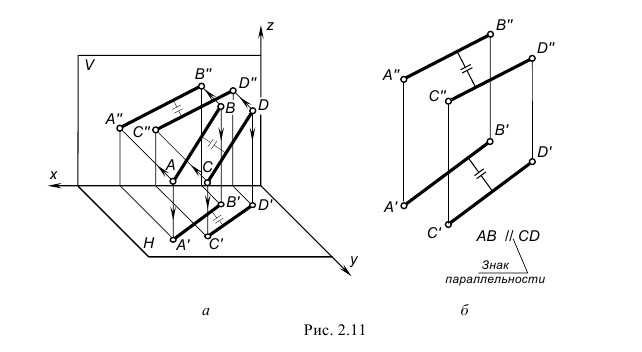
Параллельные прямые. Если прямые в пространстве параллельны, то их одноименные проекции на чертеже также параллельны.
На рис. 2.11 изображены параллельные прямые AB и CD. На чертеже фронтальные и горизонтальные проекции прямых параллельны: A”B”//C”D” и A’B’//C’D’.
Пересекающиеся прямые. Если прямые в пространстве пересекаются, то на чертеже проекции точки пересечения прямых лежат на одной линии связи.
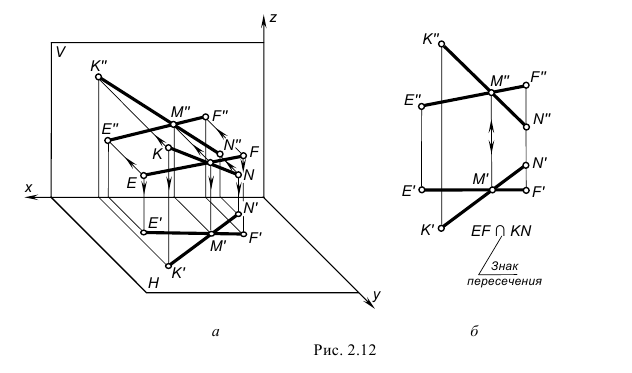
На рис. 2.12 изображены проекции пересекающихся прямых EF и KN. Проекции точки их пересечения M(M”,M’) лежат на пересечении одноименных проекций прямых и на одной линии связи.
Скрещивающиеся прямые
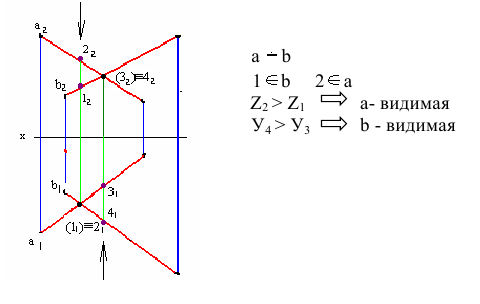
Если две прямые не параллельны и не пересекаются, то они в пространстве скрещиваются. На чертеже их проекции могут накладываться, образуя конкурирующие точки, лежащие на одном проецирующем луче.
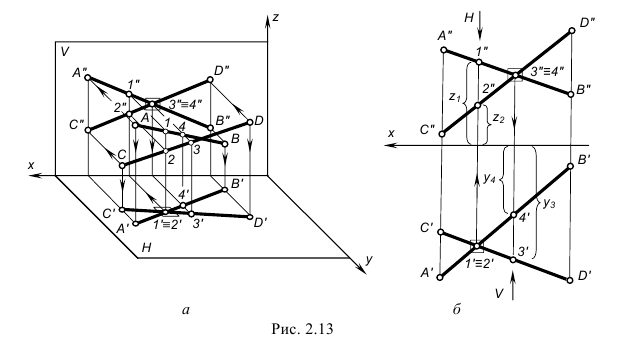
На рис. 2.13 изображены проекции двух скрещивающихся прямых АВ и CD. Их одноименные проекции накладываются и образуют четыре конкурирующие точки (2 пары):
- – конкурирующие точки 1 и 2 лежат на одном проецирующем луче, перпендикулярном плоскости проекций H, но принадлежат разным прямым: точка 1 принадлежит прямой AB, а точка 2 – прямой CD; горизонтальные проекции точек 1 и 2 совпадают;
- – конкурирующие точки 3 и 4 лежат на проецирующем луче, перпендикулярном плоскости проекций V, но принадлежат разным прямым: точка 3 принадлежит прямой CD, а точка 4 – прямой AB; фронтальные проекции точек 3 и 4 совпадают.
!!! Конкурирующие точки, как было сказано выше, позволяют наблюдателю определить по чертежу относительное расположение прямых по их удаленности от плоскостей проекций H и V:
- – по конкурирующим точкам 1 и 2 при взгляде на них сверху вниз на плоскость H (по стрелке) видно, что точка 1 расположена выше точки 2 (координата z1 больше координаты z2), т. е. на горизонтальной проекции прямая АВ расположена над прямой CD;
- – по конкурирующим точкам 3 и 4 при взгляде на них снизу вверх на плоскость V (по стрелке) видно, что точка 3 расположена ближе к наблюдателю (координата y3 больше координаты y4), т. е. на фронтальной проекции прямая CD расположена перед прямой АВ.
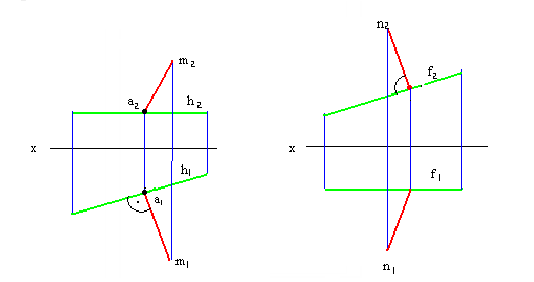
Теорема о проекции прямого угла. Частное положение прямых – перпендикулярные прямые
Пересекающиеся прямые в пространстве могут быть расположены под прямым углом, т. е. взаимно перпендикулярно. Прямой угол между перпендикулярными прямыми может проецироваться на чертеж в натуральную величину при определенном условии.
Теорема о проекции прямого угла:
- – если одна сторона прямого угла параллельна какой-либо плоскости проекций, а вторая сторона ей не перпендикулярна, то на эту плоскость проекций угол проецируется в натуральную величину, т. е. прямым (90°).
На рис. 2.14 дано изображение, поясняющее теорему о проекции прямого угла. Две перпендикулярные прямые AB и AC, образующие плоскость β, проецируются на некоторую плоскость проекций H. Прямая AС по условию параллельна этой плоскости проекций. Доказательство теоремы основано на известной из геометрии теореме о трех перпендикулярах (обратная теорема): прямая n, проведенная в плоскости H перпендикулярно наклонной прямой АВ (n AB; n // A’C’), перпендикулярна и ее проекции; следовательно, угол B’A’C’ – прямой.
AB; n // A’C’), перпендикулярна и ее проекции; следовательно, угол B’A’C’ – прямой.
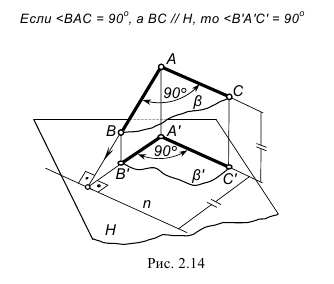
!!! Для решения многих задач начертательной геометрии требуется по условию строить проекции прямого угла.
На рис. 2.15, а, б показано построение на чертеже недостающей фронтальной проекции прямого угла KMN.
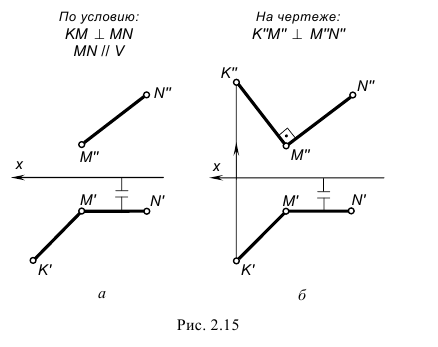
На рис. 2.15, а изображено графическое условие задачи: дана горизонтальная проекция K’M’N’ прямого угла и фронтальная проекции M”N” одной стороны этого угла.
На рис. 2.15, б показано решение задачи: так как одна сторона MN прямого угла по условию является фронтальной прямой, т. е. параллельна фронтальной плоскости проекций V, то по теореме о проекции прямого угла на плоскость V заданный прямой угол KMN должен проецироваться прямым; следовательно, фронтальную проекцию K”M” стороны KM прямого угла проводим перпендикулярно заданной фронтальной проекции стороны MN(M”N”).
На рис. 2.16, а, б показано построение на чертеже недостающей горизонтальной проекции прямого угла ECD.
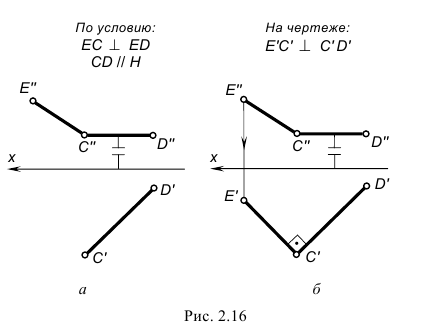
На рис. 2.16, а изображено графическое условие задачи: дана фронтальная проекция E”C”D” прямого угла и горизонтальная проекция C’D’ одной стороны этого угла.
На рис. 2.16, б показано решение задачи: так как одна сторона CD прямого угла по условию является горизонтальной прямой, т. е. параллельна горизонтальной плоскости проекций H, то по теореме о проекции прямого угла на плоскость H заданный прямой угол ECD должен проецироваться прямым; следовательно, горизонтальную проекцию E’C’ стороны угла EC проводим перпендикулярно заданной горизонтальной проекции стороны CD(C’D’).
Структуризация материала второй лекции в рассмотренном объеме схематически представлена на рис. 2.17 (лист 1). На последующих листах 2–4 компактно приведены иллюстрации к этой схеме, способствующие закреплению изученного материала и его быстрому визуальному повторению (рис. 2.18–2.20).
Проекции прямой. Положение прямой относительно плоскостей проекций. Взаимное положение прямых. Способ прямоугольного треугольника. Теорема о проекции прямого угла
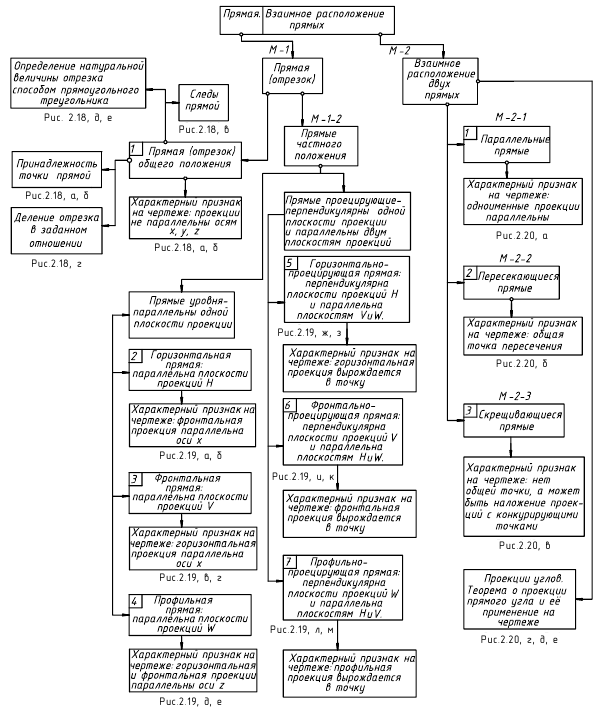
Прямые обозначают на чертеже строчными буквами латинского алфавита: а, в, m, n и т.д. Отрезки прямых обозначаются прописными буквами: АВ, MN и т.д.
- Знак пареллельности прямых: АВ // MN.
- Знак пересечения прямых: АВ ∩ MN.
- Знак скрещивающихся прямых: АВ
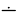 MN.
MN.
Прямая общего положения
Прямая общего положения и её проекции
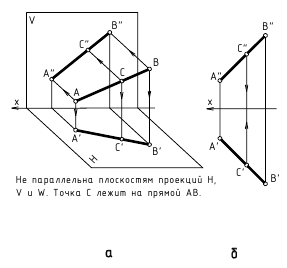
Следы прямой
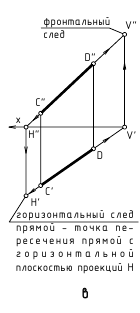
Деление отрезка в заданном отношении (например, 1:3)
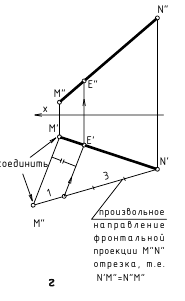
Теорема о принадлежности точки прямой: если точка принадлежит прямой, то на чертеже одноимённые проекции точки лежат на одноимённых проекциях прямой (см. рис. 2.1а, б; 2.4б).
Определение натуральной величины отрезка способом прямоугольного треугольника на чертеже
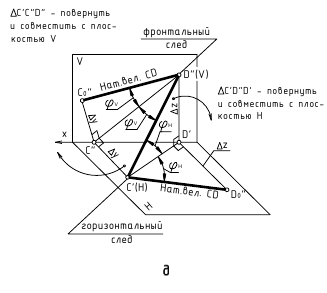
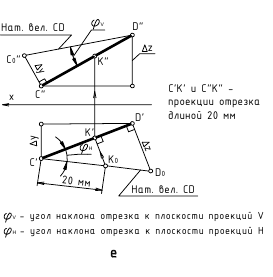
Прямые частного положения
Горизонтальная прямая уровня: //H
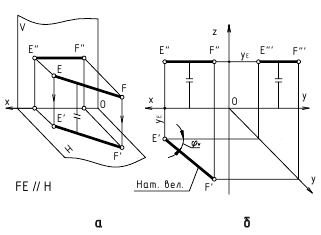
Фронтальная прямая уровня: //V
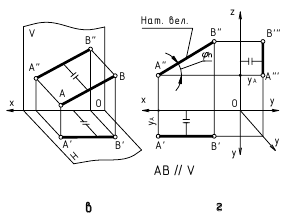
Профильная прямая уровня: //W
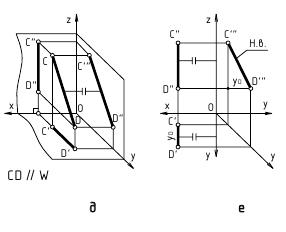
Горизонтально-проецирующая прямая:  H
H
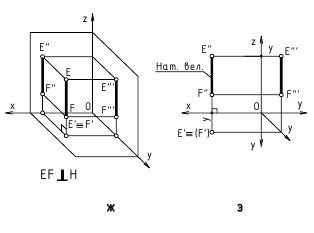
Фронтально-проецирующая прямая:  V
V
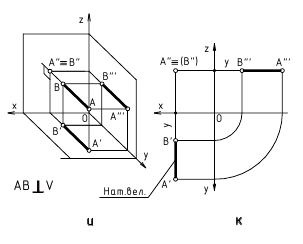
Профильно-проецирующая прямая:  W
W
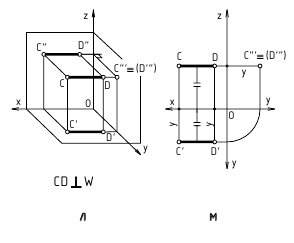
Взаимное расположение прямых
Параллельные прямые
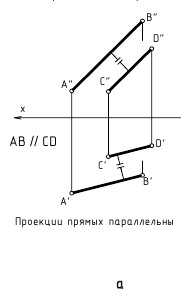
Пересекающиеся прямые
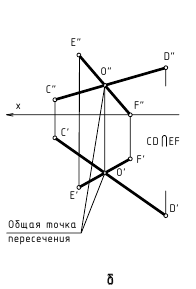
Скрещивающиеся прямые
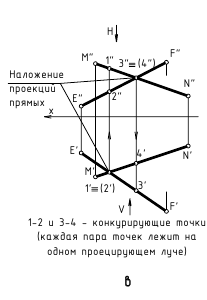
Теорема о проекции прямого угла
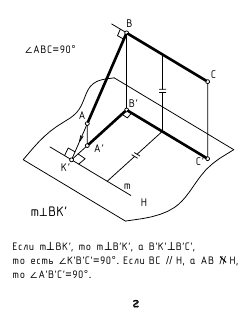
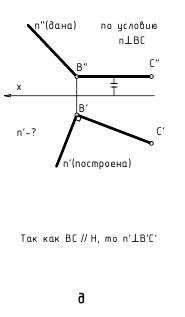
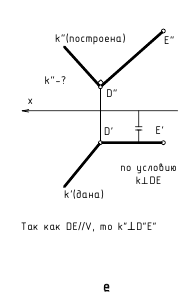
Теорема о проекции прямого угла: если одна сторона прямого угла пареллельна плоскости проекций (а вторая не параллельна и не перпендикулярна этой плоскости), то на эту плоскость проекций прямой угол проецируется в виде прямого угла.
Знак перпендикулярности элементов: 
Задание прямой
Положение прямой линии в пространстве определяется двумя точками или точкой и направлением. Поэтому на эпюре прямую можно задать проекциями ее отрезка (рис. 2.1), проекциями некоторой произвольной части прямой, не указывая концевых точек этой части (рис. 2.2), или указывая одну точку этой прямой (рис. 2.3).
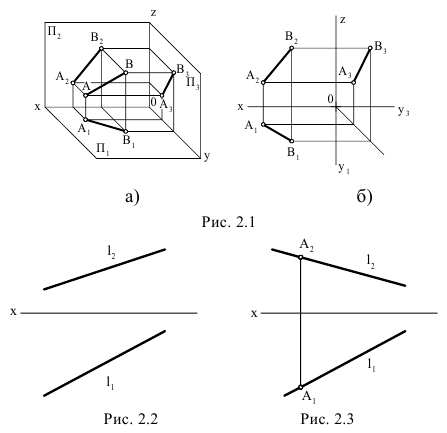
Прямая общего положения
Прямая общего положения не параллельна и не перпендикулярна ни одной из плоскостей проекций.
На эпюре проекции прямой общего положения составляют с осями проекций произвольные углы, поэтому величина каждой проекции меньше истинной величины самой прямой (см. рис. 2.1).
Прямые частного положения
Прямые, параллельные или перпендикулярные плоскостям проекций, называют прямыми частного положения.
Прямая, параллельная какой-либо плоскости проекций, а с двумя другими плоскостями образующая произвольные углы, называется прямой уровня. Различают три линии уровня:
- прямую, параллельную горизонтальной плоскости проекций; называют горизонтальной или горизонталью
- прямую, параллельную фронтальной плоскости проекций; называют фронтальной или фронталью
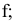
- прямую, параллельную профильной плоскости проекций; называют профильной
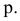
Каждая линия уровня будет проецироваться в натуральную величину на ту плоскость проекций, которой она параллельна, углы наклона 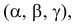 которые эта прямая образует с двумя другими плоскостями проекций, также будут проецироваться на эту плоскость без искажения (рис. 2.4 – 2.6).
которые эта прямая образует с двумя другими плоскостями проекций, также будут проецироваться на эту плоскость без искажения (рис. 2.4 – 2.6).
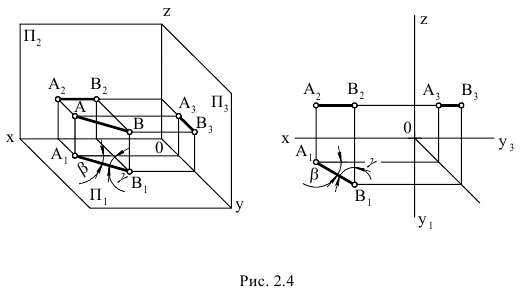
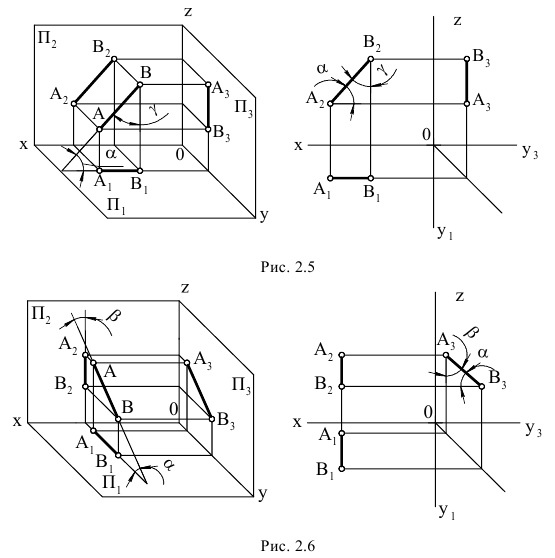
На рис. 2.4 видно, что все точки горизонтальной прямой 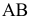 удалены на одинаковые расстояния от плоскости
удалены на одинаковые расстояния от плоскости 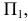 поэтому фронтальная проекция любой горизонтали параллельна оси
поэтому фронтальная проекция любой горизонтали параллельна оси 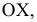 а профильная проекция параллельна оси
а профильная проекция параллельна оси 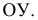 Величины фронтальной и профильной проекций будут меньше натуральной величины самой прямой.
Величины фронтальной и профильной проекций будут меньше натуральной величины самой прямой.
Эти отличительные особенности характерны и для фронтальной и профильной прямых.
Прямые уровня могут принадлежать плоскостям проекций. Такие прямые называют нулевой горизонталью и нулевой фронталью (рис. 2.7).
Прямые, перпендикулярные одной из плоскостей проекций, а двум другим параллельные, называются проецирующими:
- горизонтально-проецирующая – прямая, перпендикулярная горизонтальной плоскости проекций (рис. 2.8);
- фронтально-проецирующая – прямая, перпендикулярная фронтальной плоскости проекций (рис. 2.9);
- профильно-проецирующая – прямая, перпендикулярная профильной плоскости проекций (рис. 2.10).
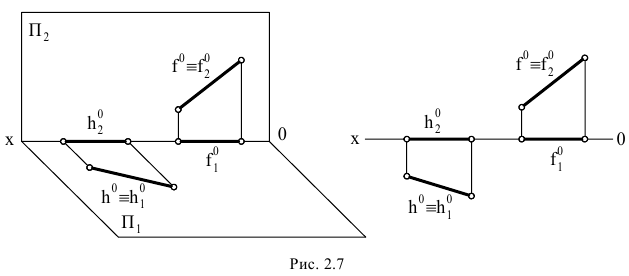
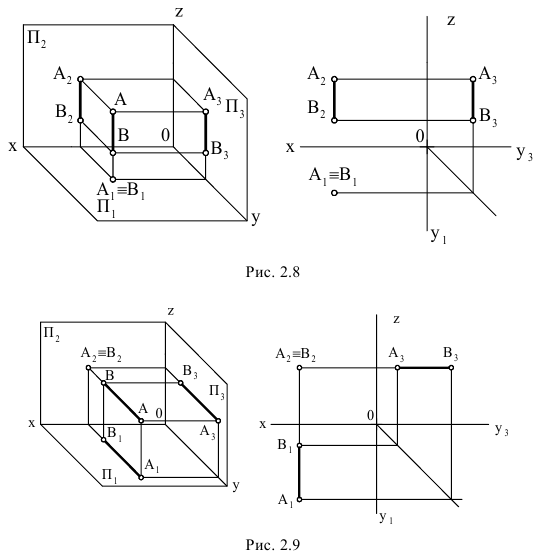
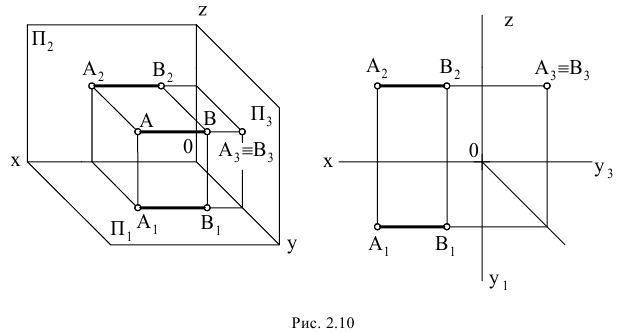
На рис. 2.8 – 2.10 видно, что проекции прямых, перпендикулярных плоскостям проекций, на этих плоскостях представляют собой точки, а на тех плоскостях, которым прямые параллельны, проекции прямых будут перпендикулярны осям и равны по величине самим прямым.
Принадлежность точки прямой. Деление отрезка прямой линии в данном отношении
Если точка лежит на прямой, то ее проекции будут лежать на одноименных проекциях этой прямой.
На рис. 2.11 изображена прямая и три точки: 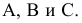 Точка
Точка 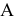 принадлежит прямой
принадлежит прямой  точки
точки  – не принадлежат, т.к.
– не принадлежат, т.к. 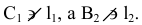
На рис. 2.12 показано построение точки  принадлежащей профильной прямой
принадлежащей профильной прямой  если известна фронтальная проекция точки
если известна фронтальная проекция точки  Для построения неизвестной горизонтальной проекции используется профильная проекция
Для построения неизвестной горизонтальной проекции используется профильная проекция 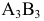 отрезка прямой
отрезка прямой 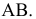
Чтобы разделить отрезок прямой в данном отношении, достаточно разделить в этом отношении одну из проекции заданного отрезка, а потом с помощью линии связи перенести делящую точку на другие проекции отрезка.
На рис. 2.13 точка  делит отрезок
делит отрезок 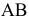 в отношении
в отношении 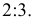 Для этого из точки
Для этого из точки  проведена вспомогательная прямая, на которой отложено 5 равных отрезков произвольной длины.
проведена вспомогательная прямая, на которой отложено 5 равных отрезков произвольной длины.
Если необходимо разделить отрезок профильной прямой  точкой
точкой 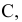 заданной фронтальной проекцией
заданной фронтальной проекцией 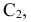 то выполняют следующие построения: из точки
то выполняют следующие построения: из точки 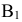 проводят произвольную вспомогательную прямую, откладывают на ней
проводят произвольную вспомогательную прямую, откладывают на ней 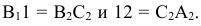 Соединяют точки
Соединяют точки 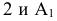 и параллельно прямой
и параллельно прямой 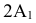 через точку 1 проводят прямую до пересечения с
через точку 1 проводят прямую до пересечения с 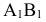 в точке
в точке 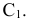 Это и будет недостающая проекция точки
Это и будет недостающая проекция точки 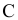 (рис. 2.14).
(рис. 2.14).
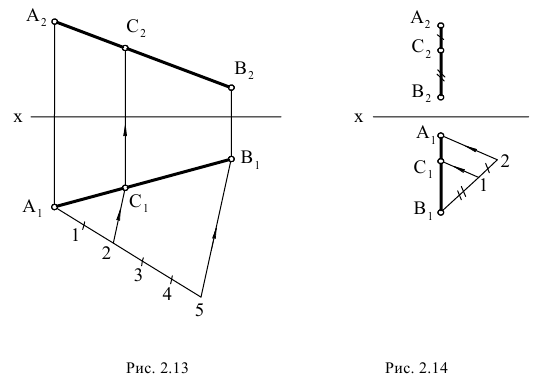
Определение длины отрезка прямой общего положения и углов наклона прямой к плоскостям проекций
Для определения натуральной величины отрезка прямой общего положения необходимо построить на чертеже прямоугольный треугольник, одним катетом которого является проекция отрезка на какую-либо плоскость проекций, а величина другого катета равна разности расстояний концов отрезка от плоскости проекций, на которой взяли первый катет. Натуральная величина отрезка прямой будет равна гипотенузе этого треугольника. Угол между катетом-проекцией и гипотенузой равен углу наклона отрезка к этой плоскости проекций.
На рис. 2.15 показано проецирование отрезка 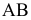 на горизонтальную плоскость
на горизонтальную плоскость  Через точку
Через точку 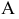 проведена прямая
проведена прямая 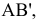 параллельная горизонтальной проекции отрезка
параллельная горизонтальной проекции отрезка  В полученном прямоугольном треугольнике
В полученном прямоугольном треугольнике 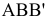 катет
катет 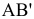 равен проекции
равен проекции 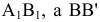 равен разности расстояний концов отрезка от плоскости проекций
равен разности расстояний концов отрезка от плоскости проекций 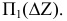 Гипотенуза этого треугольника равна длине отрезка
Гипотенуза этого треугольника равна длине отрезка 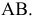 Угол
Угол 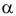 в треугольнике
в треугольнике 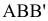 является углом наклона отрезка прямой
является углом наклона отрезка прямой 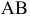 к плоскости
к плоскости 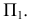
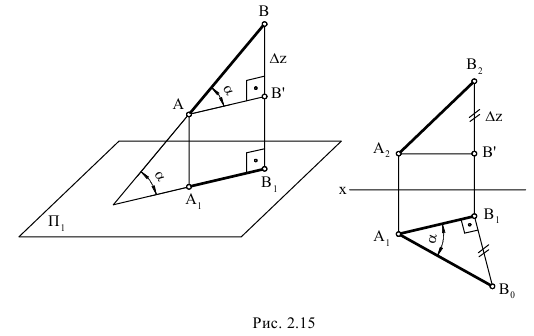
Для определения угла наклона отрезка прямой  на фронтальной плоскости проекций
на фронтальной плоскости проекций  строят прямоугольный треугольник аналогичным путем: через точку
строят прямоугольный треугольник аналогичным путем: через точку  проводят прямую
проводят прямую 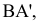 параллельную
параллельную 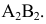 Катет
Катет 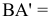
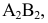 а второй катет
а второй катет 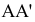 равен
равен 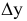 – разности расстояний точек
– разности расстояний точек 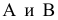 от плоскости
от плоскости 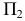 (рис. 2.16).
(рис. 2.16).
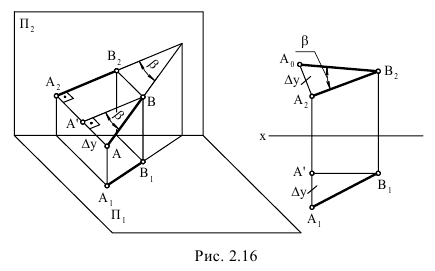
Угол  в этом же треугольнике
в этом же треугольнике  является углом наклона прямой
является углом наклона прямой  к плоскости
к плоскости 
Следы прямой линии
Прямая общего положения пересекает все плоскости проекций. Точки пересечения прямой линии с плоскостями проекций называют следами прямой. Точка  – горизонтальный след прямой, точка
– горизонтальный след прямой, точка  – фронтальный. Горизонтальная проекция
– фронтальный. Горизонтальная проекция  горизонтального следа прямой совпадает с самим следом – точкой
горизонтального следа прямой совпадает с самим следом – точкой 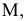 а фронтальная проекция этого следа
а фронтальная проекция этого следа 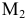 лежит на оси
лежит на оси  (рис. 2.17). Фронтальная проекция
(рис. 2.17). Фронтальная проекция  фронтального следа прямой совпадает с точкой
фронтального следа прямой совпадает с точкой  а горизонтальная проекция
а горизонтальная проекция  лежит на оси
лежит на оси 
Для построения горизонтального следа  прямой необходимо продолжить фронтальную проекцию прямой до пересечения с осью
прямой необходимо продолжить фронтальную проекцию прямой до пересечения с осью  и в этой точке восстановить перпендикуляр до пересечения с горизонтальной проекцией прямой.
и в этой точке восстановить перпендикуляр до пересечения с горизонтальной проекцией прямой.
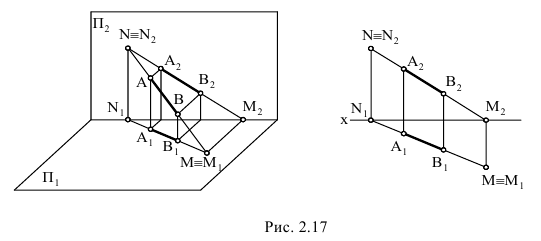
Для построения фронтального следа прямой продолжаем горизонтальную проекцию прямой до пересечения с осью  и восстанавливаем перпендикуляр к оси до пересечения с фронтальной проекцией прямой. С помощью этих правил на рис. 2.18 и рис. 2.19 построены следы прямых
и восстанавливаем перпендикуляр к оси до пересечения с фронтальной проекцией прямой. С помощью этих правил на рис. 2.18 и рис. 2.19 построены следы прямых 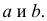
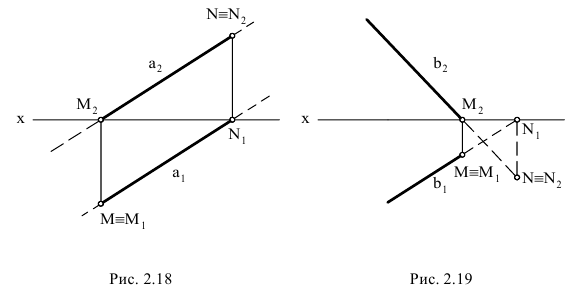
Так как следы прямых – точки, в которых прямая переходит из одной четверти в другую, то они позволяют определить видимость этой прямой. Та часть прямой, которая расположена в пределах первого октанта, будет видимой. Проекции видимой части прямой изображаются сплошными линиями, а невидимой – штриховыми.
На рис. 2.20 показано построение следов прямой 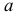 в системе трех плоскостей проекций.
в системе трех плоскостей проекций.
Построение горизонтального и фронтального следов выполняют по правилам, указанным выше, профильный след 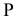 находят как точку пересечения прямой
находят как точку пересечения прямой 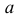 с профильной плоскостью проекций. Профильная проекция профильного следа прямой совпадает с самим следом, горизонтальная проекция этого следа
с профильной плоскостью проекций. Профильная проекция профильного следа прямой совпадает с самим следом, горизонтальная проекция этого следа 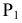 лежит на оси
лежит на оси  фронтальная проекция
фронтальная проекция  лежит на оси
лежит на оси  Чтобы построить профильный след прямой, продолжают фронтальную проекцию прямой
Чтобы построить профильный след прямой, продолжают фронтальную проекцию прямой 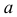 до пересечения с осью
до пересечения с осью  Отмечают точку
Отмечают точку  и из этой точки проводят перпендикуляр к оси
и из этой точки проводят перпендикуляр к оси  до пересечения с профильной проекцией прямой. Эта точка и будет искомым следом
до пересечения с профильной проекцией прямой. Эта точка и будет искомым следом  с которым совпадает
с которым совпадает  Горизонтальная проекция
Горизонтальная проекция  определяется как пересечение горизонтальной проекции прямой с осью
определяется как пересечение горизонтальной проекции прямой с осью  (рис. 2.21).
(рис. 2.21).
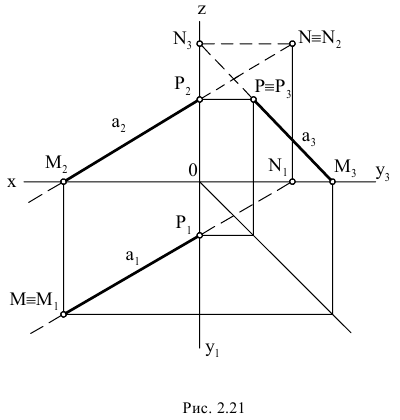
Взаимное положение прямых
Прямые в пространстве могут занимать различное взаимное положение. Они могут быть параллельными, пересекающимися и скрещивающимися.
Если прямые в пространстве пересекаются, то на эпюре их одноименные проекции пересекаются, и точки пересечения проекций этих прямых лежат на одной линии связи (рис. 2.22).
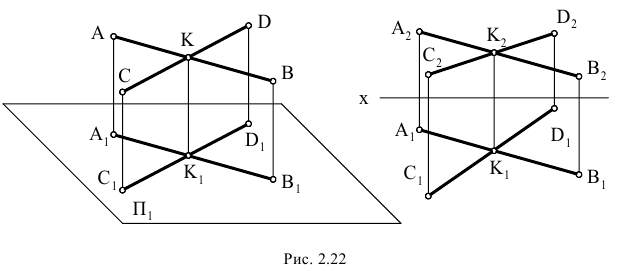
Если прямые в пространстве параллельны, то на эпюре их одноименные проекции параллельны. На рис. 2.23 изображены прямые общего положения  их горизонтальные и фронтальные проекции параллельны между собой. Можно утверждать, что и в пространстве эти прямые параллельны. Но для профильных прямых этого условия недостаточно. Для определения их взаимного положения необходимо построить профильные проекции прямых. На рис. 2.24 горизонтальные и фронтальные проекции прямых
их горизонтальные и фронтальные проекции параллельны между собой. Можно утверждать, что и в пространстве эти прямые параллельны. Но для профильных прямых этого условия недостаточно. Для определения их взаимного положения необходимо построить профильные проекции прямых. На рис. 2.24 горизонтальные и фронтальные проекции прямых 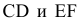 параллельны, но эти прямые не параллельны, что следует из взаимного положения их профильных проекций.
параллельны, но эти прямые не параллельны, что следует из взаимного положения их профильных проекций.
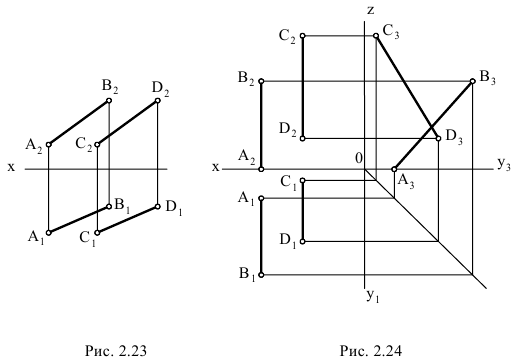
Если прямые в пространстве не пересекаются и не параллельны между собой, то такие прямые называются скрещивающимися. На эпюре точки пересечения одноименных проекций скрещивающихся прямых не лежат на одной линии связи. Эти точки не являются общими для прямых (рис. 2.25). Точка пересечения одноименных проекций скрещивающихся прямых является на эпюре проекцией двух конкурирующих точек, принадлежащих заданным прямым.
Конкурирующие точки – это точки, лежащие на одном перпендикуляре к плоскости проекций. На эпюре (см. рис. 2.25) горизонтальные проекции конкурирующих точек  совпадают, но точка 1 принадлежит прямой
совпадают, но точка 1 принадлежит прямой  а точка 2 – прямой
а точка 2 – прямой 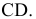
Из чертежа видно, что расстояния от плоскости  до точек 1 и 2 различны. Фронтальная проекция перпендикуляра, обозначенная стрелкой, позволяет определить, какая из точек расположена ниже. В данном примере точка 2, лежащая на прямой
до точек 1 и 2 различны. Фронтальная проекция перпендикуляра, обозначенная стрелкой, позволяет определить, какая из точек расположена ниже. В данном примере точка 2, лежащая на прямой  расположена ниже, чем точка 1, лежащая на прямой
расположена ниже, чем точка 1, лежащая на прямой  Следовательно, прямая
Следовательно, прямая 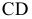 проходит под прямой
проходит под прямой 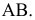
Точке пересечения фронтальных проекций соответствуют точки 3 и 4, расположенные на прямых 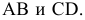 Горизонтальная проекция перпендикуляра, отмеченная стрелкой, позволяет определить, какая из этих точек ближе к наблюдателю. Из чертежа видно, что точка 3 расположена ближе к наблюдателю, чем точка 4. Поэтому прямая
Горизонтальная проекция перпендикуляра, отмеченная стрелкой, позволяет определить, какая из этих точек ближе к наблюдателю. Из чертежа видно, что точка 3 расположена ближе к наблюдателю, чем точка 4. Поэтому прямая 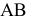 проходит перед
проходит перед 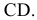
Проекции плоских углов
Плоский угол проецируется на плоскость проекций в натуральную величину, если его стороны параллельны этой плоскости проекций.
Для того чтобы прямой угол проецировался на плоскость в натуральную величину, необходимо и достаточно, чтобы одна из его сторон была параллельна, а другая не перпендикулярна плоскости проекций. Изображенный на рис. 2.26 угол 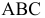 – прямой, одна его сторона
– прямой, одна его сторона 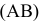 параллельна плоскости проекций
параллельна плоскости проекций 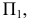 поэтому на эту плоскость он спроецировался в виде прямого угла, т.е. в натуральную величину.
поэтому на эту плоскость он спроецировался в виде прямого угла, т.е. в натуральную величину.
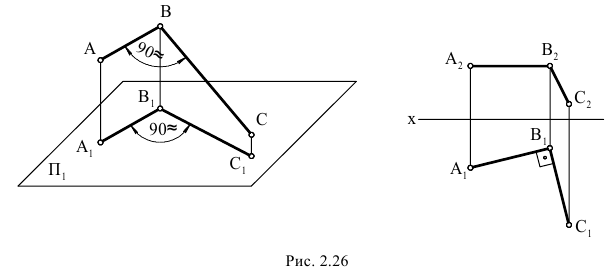
- Плоскость
- Поверхности
- Изображения и обозначения на чертежах
- Отображение пространственных объектов на плоскость
- Метод проекций
- Методы проецирования
- Образование проекций
- Точка и прямая
