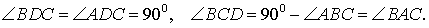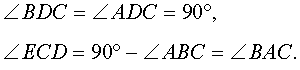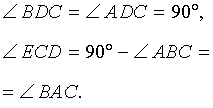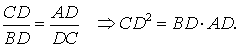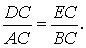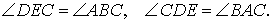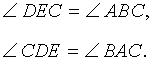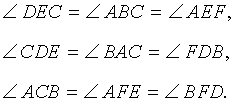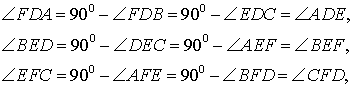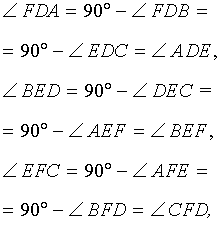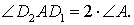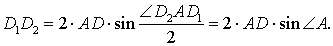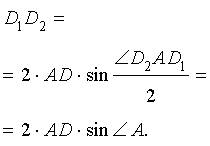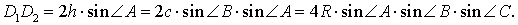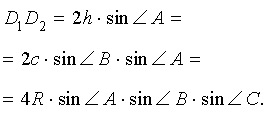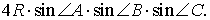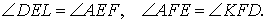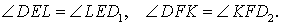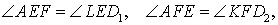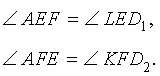СВОЙСТВА ОРТОЦЕНТРИЧЕСКИХ ТРЕУГОЛЬНИКОВ
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Метшина А.Р. 1
1МБОУ “СОШ№ 11” г. Нижнекамск
Морозова Т.Н. 1
1МБОУ “СОШ№ 11”, 11 А
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Предметом нашего исследования являются ортоцентрические треугольники и их свойства.
Цель – изучение свойств ортоцентрических треугольников и исследование путей их использования для решения задач.
Задачи:
1) выяснить, что такое ортотреугольник;
2) изучить и проанализировать свойства ортотреугольников;
3) рассмотреть возможное применение
этих свойств для решения задач.
4) подвести итоги.
Во время выполнения поставленных задач нами был использован описательный метод исследования, изучение и обобщение.
Практическая значимость: результаты проведенного исследования могут стать опорой для решения олимпиадных задач, задач ЕГЭ и ОГЭ с использованием свойств отроцентрических треугольников.
ОСНОВНАЯ ЧАСТЬ
Глава 1. Исторические сведения и свойства
§ 1. Что такое ортоцентрический треугольник?
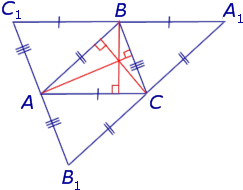
Ортотреуго́льник (ортоцентрический треугольник) — это треугольник ΔA1B1C1, вершины которого являются основаниями высот треугольника ∆ABC. Для ортотреуго́льника (для ортоцентрического треугольника) ΔA1B1C1 сам треугольник ∆ABC является треугольником трёх внешних биссектрис. То есть отрезки AB, BC и CA являются тремя внешними биссектрисами треугольника ΔA1B1C1.
§ 2. Исторические сведения
В начале 18 века итальянский инженер и математик Фаньяно дей Тоски поставил перед собой такую задачу: вписать в остроугольный треугольник АВС треугольник наименьшего периметра так, чтобы на каждой из сторон данного треугольника лежала одна вершина вписанного. Аналитическое решение этой задачи было опубликовано в 1755 году. Было доказано, что существует единственный треугольник наименьшего периметра KMN, его вершина K – основание высоты CK. Искомым треугольником всегда будет ортотреугольник KMN.
§ 3.Свойства ортотреугольников
1.Теорема о подобии треугольников. Ортотреугольник отсекает треугольники, подобные данному.
Доказательство:
В остроугольном треугольнике проведены высоты , . Найдем углы треугольника , если , а .
Прямоугольные треугольники и имеют общий угол при вершине С, они подобны, поэтому .
Из этого равенства следует, что в треугольниках и стороны, прилежащие к общему углу при вершине С, пропорциональны. Следовательно, по второму признаку подобия треугольников подобен . В подобных треугольниках против соответственных сторон лежат равные углы, поэтому угол , .
Аналогично можно доказать подобие треугольников и ; и , если провести высоту CC1. При этом , и .
Как следствие данной теоремы, верно следующее утверждение:
Две смежные стороны ортотреугольника образуют равные углы с соответствующей стороной исходного треугольника.
Среди всех треугольников, вписанных в данный треугольник, только ортотреугольник обладает указанным свойством.
І. Ортоцентрический треугольник H1H2H3 В остроугольном треугольнике ABC соединим отрезками основания высот H1,H2,H3 (рис. 1). Получим
треугольник H1H2H3. Рассмотрим некоторые свойства этого треугольника, которые используют при решении задач.
Свойство 1. Стороны ортоцентрического треугольника H1H2H3 антипараллельны сторонам треугольника ABC.
Доказательство. Обозначим точку H — точку пересечения высот треугольника ABC (ортоцентр). Опишем окружность около четырёхугольника AH2HH3. Тогда ∠AH2H3 = ∠AHH3 = ∠ABC, значит, сторона H2H3 антипараллельна стороне BC. Аналогично доказывается антипараллельность двух других сторон треугольника
H1H2H3.
Свойство 2. Высоты треугольника ABC являются биссектрисами внутренних углов треугольника H1H2H3.
Доказательство. Действительно, поскольку ∠H3H1B = ∠H2H1C = ∠A, то ∠H3H1A= ∠AH1H2.
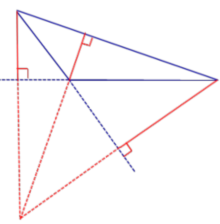
Свойство 3. Отрезок OA перпендикулярен отрезку H2H3.
Доказательство. Действительно, если описать окружность около треугольника H1H2H3, дуги, на которые опираются углы ∠H2H1A и ∠AH1H3, равны, а значит, OA⊥H2H3 (рис. 2).
Свойство 4. Вершины треугольника ABC являются центрами вневписанных окружностей ортоцентрического треугольника H1H2H3 (рис. 3).
Доказательство. Поскольку отрезок AH2 перпендикулярен биссектрисе H2B, а AH3⊥CH3, то пересечение отрезков AH2 и AH3, – точка A есть центр вневписанной окружности, касающейся стороны H2H3.
Свойство 5. Имеет место формула pH = hasinA, где pH — полупериметр треугольника H1H2H3, ha — высота AH1.
Доказательство. Из точки A опустим перпендикуляр AF на прямую H1H3 (рис.3). Поскольку∠H1AF = ∠H3H1B (углы с взаимно перпендикулярными сторонами), то ∠HAF = ∠A и H1F = hasinA (из треугольника H A1 F), или pH = hasinA.
Свойство 6. Имеет место формула S = RpH, где S — площадь треугольника ABC, R — радиус окружности, описанной около треугольника ABC.
Доказательство. Действительно, поскольку pH = hasinA, то
pH= sinA, и S = RpH(a — длина стороны BC).
Свойство 7. Окружность Леонарда Эйлера.
Доказательство. Опишем окружность около треугольника H1H2H3. Докажем, что окружности (обозначим её γe), кроме точек H1, H2, H3, принадлежат середины отрезков AH, BH, CH (их называют точками Эйлера и обозначают E1, E2, E3), ещё три точки M1, M2, M3 — середины сторон BC, AC, AB. Начнём с точек Эйлера. Заметим, что доказательство нестандартно (рис. 4).
Поскольку прямая H H1 (рис. 4) принадлежит биссектрисе угла ∠H2H1H3, то точка её пересечения с окружностью γe, описанной
около треугольника H1H2H3, будет серединой дуги H2H3, то есть точкой W1 треугольника H1H2H3, а точка A — центром вневписанной
окружности (свойство 4).
По теореме Мансиона ( IW1 = W1Ia = W1B = W1C): AE1 = E1H. Значит, точка совпадает с серединой отрезка IW1 для треугольника H1H2H3 с точкой E1. Поскольку точки B и C также центры вневписанных окружностей, то утверждение относительно середин отрезков AH, BH и CH доказано. Докажем, что середины AC, BC и AB (точки M1, M2, M3) принадлежат окружности γe.
Воспользуемся свойством вневписанных окружностей с центрами Ib и Ic. Пусть W1A— точка, диаметрально противоположная точке W1. Тогда W1A— середина отрезка IbIc. Пусть окружность γe пересекает сторону BC в точке X (рис. 4). Поскольку ∠E1H1X1 = 90°, то точки X и E1 диаметрально противоположны, а поскольку точка E1 есть точкой W1 окружности, то точка X совпадает с серединой отрезка BC (точки B и C — центры вневписанных окружностей). Теорема об окружности Эйлера для треугольника ABC доказана новым способом.
ІІ. Ортоудвоенный треугольник
Высоты AH1, BH2, CH3 продолжим до пересечения с описанной окружностью (рис. 5).
Получим треугольник N1N2N3, который назовём ортоудвоенным. Поскольку HH1 = H1N1, HH2 = H2N2, HH3 = H3N3, то этот треугольник гомотетичен треугольнику H1H2H3 с центром гомотетии — серединой отрезка OE ( E — центр окружности Эйлера) и коэффициентом гомотетии k =
Свойство 1. Вершины треугольника ABC делят дуги N2N3, N3N1, N1N2 пополам.
Доказательство. Действительно, ∠ N2N1A = ∠ N3N1A.
Свойство 2. Высоты треугольника ABC принадлежат биссектрисам внутренних углов треугольника N1N2N3.
Доказательство. Действительно, это следует из свойства 1.
Свойство 3. Радиус OA перпендикулярен отрезкам N2N3 и H2H3.
Доказательство. Действительно, это следует из свойства 1.
Свойство 4. Точка, симметричная ортоцентру H относительно середины M1 отрезка BC принадлежит окружности, описанной около треугольника
ABC.
Доказательство. Проведём диаметр AA1 (рис.6) и найдём точку X, гомотетичную точке A1. Поскольку A1X = XH, то отрезок OX — средняя линия треугольника
AA1H. Значит, он параллелен AH и равен
AH, то есть OX = OM1 и точка X совпадает с точкой M1 — серединой отрезка BC.
Свойство 5. Прямая Эйлера. Центроид M треугольника ABC принадлежит отрезку OH.
Доказательство. Проведём отрезок AM1 (рис. 6). Он пересечёт OH в точке Y. Поскольку то M1M : AM = 1 : 2, а значит, точка Y совпадает с точкой M1.
Окружность девяти точек
Около треугольника H1H2H3 опишем окружность γe. Её центр делит пополам отрезок OH (точка E). Середины отрезков AH, BH, CH (точки E1, E2, E3) гомотетичны точкам A, B и C и принадлежат окружности γe.
Докажем, что точки M1, M2, M3 принадлежат окружности γe.
Доказательство. Действительно, точки A1 и H симметричны относительно точки B. Кроме того, точки A1 и M1 гомотетичны, а значит, точка M1 принадлежит окружности γe.
ІІІ. Ортоцентрический треугольник Q1Q2Q3
треугольника W1W2W3
Опишем окружность около треугольника ABC и построим точки W1,W2, W3 (середины дуг BC, AC, AB) (рис. 7).
Точку пересечения хорд W2W3 и AW1 обозначим Q1. Аналогично получим точки Q1 и Q3. По теореме «листа трилистника» имеем: IW1 = W1C. Поскольку ∪ AW2 = ∪ W2C, то
∠ Q3W1C = ∪ QW1I и W1Q3 ⊥ IC,
а значит, треугольник Q1Q2Q3 — ортоцентрический треугольник треугольника W1W2W3. В равнобедренном треугольнике IW1C IQ3 = Q3C. Аналогично, IQ1 = Q1A, следовательно, стороны треугольника Q1Q2Q3 вдвое меньше соответственных сторон треугольника ABC. Поэтому (применяем формулу S = RpH ) площадь треугольника W1W2W3 . (1°)
Девять середин треугольника W1W2W3
Поскольку окружность, описанная около треугольника Q1Q2Q3, есть окружность Эйлера треугольника W1W2W3, то девять точек принадлежат одной окружности: середины отрезков W1W3, W2W3, W1W2, IW1, IW2, IW3, IA, IB, IC.
ІV. Ортоцентрический треугольник ABC Рассмотрим треугольник, вершины которого — центры вневписанных окружностей Ia, Ib, Ic (рис.8).
Ортоцентрическим треугольником этого
треугольника будет треугольник ABC, так как
каждая из его вершин есть пересечение внутренней и внешней биссектрис. Поскольку радиус окружности, описанной около треугольника ABC будет R, то радиус окружности, описанной около треугольника IaIbIc будет 2R, а площадь SIaIbIc=2R⋅p.
Окружность Эйлера треугольника IaIbIc
Поскольку окружность, описанная около треугольника ABC, является окружностью Эйлера треугольника IaIbIc, то девять точек принадлежат одной окружности: вершины треугольника ABC, точки W1, W2, W3, середины
отрезков IaIb, IaIc, IbIc (окружность шести середин).
V. Треугольник, подобный ортоцентрическому треугольнику H1H2H3
Через вершины A, B и C проведём касательные к окружности, описанной около треугольника ABC. Получим треугольник T1T2T3 (рис. 9).
Поскольку OA⊥H2H3 и OA⊥T1T2, то T1T2||H2H3, а треугольник T1T2T3 подобен треугольнику H2H3H1. Заметим, что площадь ST треугольника T1T2T3 (его называют
тангенциальным) вычисляют по формуле:
ST=R⋅pT, где R — радиус окружности, вписанной в треугольник T1T2T3.
Глава 2. Применение.
§ 1 Применение свойств ортотреугольника для решения задач
Задача 1.
Пусть и – высоты треугольника АВС. Докажите, что треугольник подобен треугольнику АВС. Чему равен коэффициент подобия?
Решение:
подобен треугольнику АВС по теореме 1. Коэффициент подобия . В прямоугольных треугольниках и , . Значит, .
Ответ: .
Следствием данной задачи будет следующее утверждение: каждая сторона ортотреугольника равна произведению противолежащей стороны на косинус противолежащего угла исходного треугольника.
Задача 2.
Треугольник АВС остроугольный, и угол ВАС равен α. На стороне ВС как на диаметре построена полуокружность, пересекающая стороны АВ и АС в точках Р и Q соответственно. Найдите отношение площадей треугольников АВС и APQ.
Решение:
Поскольку и – высоты треугольника , треугольник подобен с коэффициентом подобия , поэтому
Задача 3
В остроугольном треугольнике АВС проведены высоты АD, ВЕ и СF. Докажите, что pR=Pr, где p-периметр треугольника EDF, Р – периметр треугольника АВС.
Решение(без применения свойств):
1. Т.к. и согласно задаче 1 , то . ,
, поэтому .
-
Пусть О – центр описанной окружности , R – ее радиус. Тогда Т.к. по т. синусов , то после подстановки, получаем .
-
Аналогично и , т.е. . Поскольку и , то , что и требовалось доказать.
Решение(без применения свойств):
-
По свойству 6 . , тогда , что и требовалось доказать.
Задача 4
Треугольник АВС остроугольный, и . Определите углы высотного треугольника.
Решение:
1. Строим высоты , , .
подобен .
подобен .
2.-высотный.
; .
Ответ: ; ; .
Задача 5.
В равнобедренном треугольнике ABCс основанием AC = 4 и боковой стороной AB = 8проведены высоты AA1,BB1,CC1.Найти периметр треугольника A1B1C1и длину высоты CC1.
Решение:
-
Т.к. – равнобедренный, то – высота, медиана, биссектриса ;.
-
Т.к. подобен , то .
3. .
4. Т.к. подобен , то; .
5. ||, а это значит, что подобен .
6. .
7. По т. Пифагора .
Ответ: ; .
Задача 6
В равнобедренном треугольнике ABC(AB = BC)проведены высоты AA1,
BB1,CC1.Известно, чтоAC = 9,
A1C1 = 7. Найти периметр треугольника ABC.
Решение:
-
Т.к. подобен , то и (1)
-
по гипотенузе и острому углу, т.к рассматриваемые треугольники прямоугольные, .
-
Т.к. и , отсекая пропорциональные отрезки, то ||.
-
подобен , т.е. .
-
Пусть , тогда , .
Известно, что , , поэтому, подставив данные в (1), получим ,
т.е. .
Ответ: .
Глава 3. Анкетирование учащихся
Всем ученикам 10 и 11 классов я задала по 4 вопроса:
-
Знаете ли вы об ортоцентрических треугольниках?
-
Применяли ли вы свойства ортоцентрических треугольников при решении задач?
-
Как вы считаете, можно ли облегчить решение задач, используя эти свойства?
-
Хотели бы вы научиться решать задачи на применение свойств ортоцентрических треугольников?
Подсчитав ответы «да», я получила следующие результаты:
|
Класс |
Кол-во детей на момент опроса |
1 вопрос |
2 вопрос |
3 вопрос |
4 вопрос |
|
10а |
19 |
1 |
1 |
1 |
13 |
|
11а |
20 |
3 |
2 |
2 |
17 |
Заключение.
Итак, в ходе работы по данной теме мы узнали, что такое ортоцентрические треугольники, какими свойствами они обладают. Все поставленные перед началом работы цели были достигнуты.
Знания, полученные в ходе выполнения данной работы пригодятся при подготовке к ЕГЭ и вступительным испытаниям в ВУЗы страны. Данная работа может быть полезна и для других ребят, готовящихся к олимпиадам и экзаменам по математике.
Список используемой литературы
1. Журнал «Математика. Все для учителя» №4, 2016, 12-17 стр.
2. Смирнова И.М., Смирнов В.А., «Геометрия на профильном уровне обучения», М., Педагогический университет «Первое сентября», 2006.
3. http://ppt4web.ru/geometrija/ortotreugolnik-i-ego-svojjstva.html
4.Ортотреугольник:[Электронный ресурс]//Википедия. URL: https://ru.wikipedia.org/wiki/Ортотреугольник
5. http://www.itmathrepetitor.ru/spravochnik-olimpiadnika-planimetri-2
Просмотров работы: 5929
Ортотреуго́льник (или ортоцентрический треугольник) — треугольник 





Свойства[править | править код]
- Задача Фаньяно: ортотреугольник остроугольного треугольника
обладает наименьшим периметром из всех вписанных треугольников.
- Окружность девяти точек: окружность, описанная вокруг ортотреугольника остроугольного треугольника
, проходит через середины сторон треугольника Δ
и через середины отрезков, соединяющих ортоцентр с вершинами треугольника
. Радиус этой окружности равен половине радиуса окружности, описанной вокруг треугольника Δ
.
- Высоты остроугольного треугольника являются биссектрисами углов его ортотреугольника.
- Стороны треугольника являются тремя внешними биссектрисами его ортотреугольника, таким образом треугольник является треугольником трёх внешних биссектрис своего ортотреугольника.
- Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.
- Если точки
,
и
на сторонах соответственно
,
и
остроугольного треугольника Δ
таковы, что
,
и
, то
— ортотреугольник треугольника
.
- Ортотреугольник треугольника Δ
отсекает при вершинах
,
и
треугольники, подобные треугольнику Δ
с коэффициентами подобия соответственно
,
,
.
- Окружности, описанные вокруг отсекаемых ортотреугольником треугольников, проходят через ортоцентр, и их центры лежат на серединах отрезков, соединяющих ортоцентр исходного треугольника с вершинами исходного треугольника.
- Если вокруг остроугольного треугольника описать окружность и в трех вершинах треугольника провести прямые, касательные к окружности, то пересечение этих прямых образует треугольник, который называют тангенциальным треугольником по отношению к исходному треугольнику, и стороны которого параллельны сторонам ортотреугольника исходного треугольника.
Свойства подобия родственных треугольников[править | править код]
- Ортотреугольник и тангенциальный треугольник подобны (Зетель, следствие 1, § 66, с. 81).
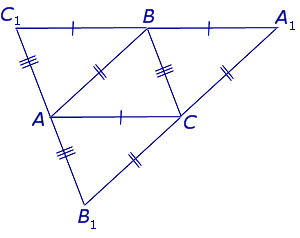
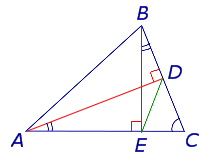
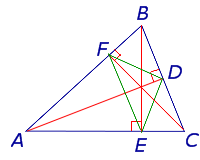
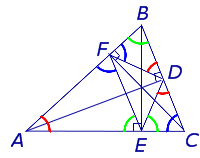
- Треугольник Жергонна ортотреугольника и исходный треугольник подобны (см. рисунок).
- Треугольник трёх внешних биссектрис треугольника трех внешних биссектрис и исходный треугольник подобны.
- Ортотреугольник треугольника Жергонна и исходный треугольник подобны.
- Выше указанные свойства подобия родственных треугольников являются следствием ниже перечисленных свойств параллельности (антипараллельности) сторон родственных треугольников.
Свойства параллельности (антипараллельности) сторон родственных треугольников[править | править код]
- Стороны данного остроугольного треугольника антипараллельны соответствующим сторонам ортотреугольника, против которых они лежат.
- Стороны тангенциального треугольника антипараллельны соответствующим противоположным сторонам данного треугольника (по свойству антипараллельности касательных к окружности).
- Стороны тангенциального треугольника параллельны соответствующим сторонам ортотреугольника.
- Если точки касания вписанной в данный треугольник окружности соединены отрезками, то получится треугольник Жергонна. Пусть в полученном треугольнике проведены высоты. Тогда прямые, соединяющие основания этих высот, параллельны сторонам исходного треугольника. Следовательно, ортотреугольник треугольника Жергонна и исходный треугольник подобны.
Другие свойства[править | править код]
- Площадь ортотреугольника равна:
где 

- Окружность, описанная около ортотреугольника Δabc, для самого треугольника ΔABC является окружностью Эйлера (окружностью 9 точек), то есть одновременно проходит, через 3 основания медиан последнего. Заметим, что эти 3 основания медиан являются вершинами дополнительного треугольника для треугольника ΔABC.
- Радиусы окружности, описанной около данного треугольника ΔABC, проведенные через его вершины, перпендикулярны соответственным сторонам ортотреугольника Δabc (Зетель, следствие 2, § 66, с. 81).
Литература[править | править код]
- Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 38-39. — ISBN 5-94057-170-0.
- Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.:Учпедгиз, 1962. 153 с.
Это обычное степенное уравнение
6^x=t t>0
t+1/t-2>0
(t^2-2t+1)/t>0 умножаеи на t право лево так как t>0
(t-1)^2>0
выполняется при любых t
и значит решение любое число х
Ответ:
(x;y)=(0;-2)
Объяснение:
1) 1-4а+4а²-6а+9=4а²-10а+10
2) а²+аб-2а+ба+б²-2б+2а+2б-4-2аб-4=а²+б²-8
(b+2)(b+4)=b^2+4b+2b+8=b^2+6b+8
(b+3)^2=b^2+6b+9
В первом +8, а во втором +9…
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
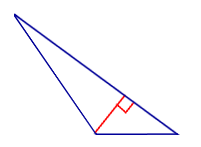
Точки A1, B1, C1 — основания высот треугольника ABC, проведённые из соответствующих вершин. Решите задачи по данным рисунков.
2
Точки A1, B1, C1 — основания высот треугольника ABC, проведённые из соответствующих вершин. Решите задачи по данным рисунков.
3
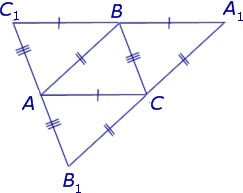
Точки A1, B1, C1 — основания высот треугольника ABC, проведённые из соответствующих вершин. Решите задачи по данным рисунков.
4
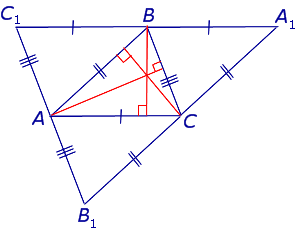
Точки A1, B1, C1 — основания высот треугольника ABC, проведённые из соответствующих вершин. Решите задачи по данным рисунков.
5
Точки A1, B1, C1 — основания высот треугольника ABC, проведённые из соответствующих вершин. Решите задачи по данным рисунков.
Пройти тестирование по этим заданиям
Ортоцентрический треугольник и его свойства
Предметом нашего исследования являются ортоцентрические треугольники и их свойства.
Цель – изучение свойств ортоцентрических треугольников и исследование путей их использования для решения задач.
1) выяснить, что такое ортотреугольник;
2) изучить и проанализировать свойства ортотреугольников;
3) рассмотреть возможное применение
этих свойств для решения задач.
4) подвести итоги.
Во время выполнения поставленных задач нами был использован описательный метод исследования, изучение и обобщение.
Практическая значимость: результаты проведенного исследования могут стать опорой для решения олимпиадных задач, задач ЕГЭ и ОГЭ с использованием свойств отроцентрических треугольников.
Глава 1. Исторические сведения и свойства
§ 1. Что такое ортоцентрический треугольник?
Ортотреуго́льник (ортоцентрический треугольник) — это треугольник ΔA1B1C1, вершины которого являются основаниями высот треугольника ∆ABC. Для ортотреуго́льника (для ортоцентрического треугольника) ΔA1B1C1 сам треугольник ∆ABC является треугольником трёх внешних биссектрис. То есть отрезки AB, BC и CA являются тремя внешними биссектрисами треугольника ΔA1B1C1.
§ 2. Исторические сведения
В начале 18 века итальянский инженер и математик Фаньяно дей Тоски поставил перед собой такую задачу: вписать в остроугольный треугольник АВС треугольник наименьшего периметра так, чтобы на каждой из сторон данного треугольника лежала одна вершина вписанного. Аналитическое решение этой задачи было опубликовано в 1755 году. Было доказано, что существует единственный треугольник наименьшего периметра KMN, его вершина K – основание высоты CK. Искомым треугольником всегда будет ортотреугольник KMN.
§ 3.Свойства ортотреугольников
1.Теорема о подобии треугольников. Ортотреугольник отсекает треугольники, подобные данному.
В остроугольном треугольнике проведены высоты , . Найдем углы треугольника , если , а .
Прямоугольные треугольники и имеют общий угол при вершине С, они подобны, поэтому .
Из этого равенства следует, что в треугольниках и стороны, прилежащие к общему углу при вершине С, пропорциональны. Следовательно, по второму признаку подобия треугольников подобен . В подобных треугольниках против соответственных сторон лежат равные углы, поэтому угол , .
Аналогично можно доказать подобие треугольников и ; и , если провести высоту CC1. При этом , и .
Как следствие данной теоремы, верно следующее утверждение:
Две смежные стороны ортотреугольника образуют равные углы с соответствующей стороной исходного треугольника.
Среди всех треугольников, вписанных в данный треугольник, только ортотреугольник обладает указанным свойством.
І. Ортоцентрический треугольник H1H2H3 В остроугольном треугольнике ABC соединим отрезками основания высот H1,H2,H3 (рис. 1). Получим
треугольник H1H2H3. Рассмотрим некоторые свойства этого треугольника, которые используют при решении задач.
Свойство 1. Стороны ортоцентрического треугольника H1H2H3 антипараллельны сторонам треугольника ABC.
Доказательство. Обозначим точку H — точку пересечения высот треугольника ABC (ортоцентр). Опишем окружность около четырёхугольника AH2HH3. Тогда ∠AH2H3 = ∠AHH3 = ∠ABC, значит, сторона H2H3 антипараллельна стороне BC. Аналогично доказывается антипараллельность двух других сторон треугольника
Свойство 2. Высоты треугольника ABC являются биссектрисами внутренних углов треугольника H1H2H3.
Свойство 3. Отрезок OA перпендикулярен отрезку H2H3.
Доказательство. Действительно, если описать окружность около треугольника H1H2H3, дуги, на которые опираются углы ∠H2H1A и ∠AH1H3, равны, а значит, OA⊥H2H3 (рис. 2).
Свойство 4. Вершины треугольника ABC являются центрами вневписанных окружностей ортоцентрического треугольника H1H2H3 (рис. 3).
Доказательство. Поскольку отрезок AH2 перпендикулярен биссектрисе H2B, а AH3⊥CH3, то пересечение отрезков AH2 и AH3, – точка A есть центр вневписанной окружности, касающейся стороны H2H3.
Свойство 5. Имеет место формула pH = hasinA, где pH — полупериметр треугольника H1H2H3, ha — высота AH1.
Доказательство. Из точки A опустим перпендикуляр AF на прямую H1H3 (рис.3). Поскольку∠H1AF = ∠H3H1B (углы с взаимно перпендикулярными сторонами), то ∠HAF = ∠A и H1F = hasinA (из треугольника H A1 F), или pH = hasinA.
Свойство 6. Имеет место формула S = RpH, где S — площадь треугольника ABC, R — радиус окружности, описанной около треугольника ABC.
Доказательство. Действительно, поскольку pH = hasinA, то
pH= sinA, и S = RpH(a — длина стороны BC).
Свойство 7. Окружность Леонарда Эйлера.
Доказательство. Опишем окружность около треугольника H1H2H3. Докажем, что окружности (обозначим её γe), кроме точек H1, H2, H3, принадлежат середины отрезков AH, BH, CH (их называют точками Эйлера и обозначают E1, E2, E3), ещё три точки M1, M2, M3 — середины сторон BC, AC, AB. Начнём с точек Эйлера. Заметим, что доказательство нестандартно (рис. 4).
Поскольку прямая H H1 (рис. 4) принадлежит биссектрисе угла ∠H2H1H3, то точка её пересечения с окружностью γe, описанной
около треугольника H1H2H3, будет серединой дуги H2H3, то есть точкой W1 треугольника H1H2H3, а точка A — центром вневписанной
окружности (свойство 4).
По теореме Мансиона ( IW1 = W1Ia = W1B = W1C): AE1 = E1H. Значит, точка совпадает с серединой отрезка IW1 для треугольника H1H2H3 с точкой E1. Поскольку точки B и C также центры вневписанных окружностей, то утверждение относительно середин отрезков AH, BH и CH доказано. Докажем, что середины AC, BC и AB (точки M1, M2, M3) принадлежат окружности γe.
Воспользуемся свойством вневписанных окружностей с центрами Ib и Ic. Пусть W1 A — точка, диаметрально противоположная точке W1. Тогда W1 A — середина отрезка IbIc. Пусть окружность γe пересекает сторону BC в точке X (рис. 4). Поскольку ∠E1H1X1 = 90°, то точки X и E1 диаметрально противоположны, а поскольку точка E1 есть точкой W1 окружности, то точка X совпадает с серединой отрезка BC (точки B и C — центры вневписанных окружностей). Теорема об окружности Эйлера для треугольника ABC доказана новым способом.
ІІ. Ортоудвоенный треугольник
Высоты AH1, BH2, CH3 продолжим до пересечения с описанной окружностью (рис. 5).
Получим треугольник N1N2N3, который назовём ортоудвоенным. Поскольку HH1 = H1N1, HH2 = H2N2, HH3 = H3N3, то этот треугольник гомотетичен треугольнику H1H2H3 с центром гомотетии — серединой отрезка OE ( E — центр окружности Эйлера) и коэффициентом гомотетии k =
Свойство 1. Вершины треугольника ABC делят дуги N2N3, N3N1, N1N2 пополам.
Доказательство. Действительно, ∠ N2N1A = ∠ N3N1A.
Свойство 2. Высоты треугольника ABC принадлежат биссектрисам внутренних углов треугольника N1N2N3.
Доказательство. Действительно, это следует из свойства 1.
Свойство 3. Радиус OA перпендикулярен отрезкам N2N3 и H2H3.
Доказательство. Действительно, это следует из свойства 1.
Свойство 4. Точка, симметричная ортоцентру H относительно середины M1 отрезка BC принадлежит окружности, описанной около треугольника
Доказательство. Проведём диаметр AA1 (рис.6) и найдём точку X, гомотетичную точке A1. Поскольку A1X = XH, то отрезок OX — средняя линия треугольника
AA1H. Значит, он параллелен AH и равен
AH, то есть OX = OM1 и точка X совпадает с точкой M1 — серединой отрезка BC.
Свойство 5. Прямая Эйлера. Центроид M треугольника ABC принадлежит отрезку OH.
Доказательство. Проведём отрезок AM1 (рис. 6). Он пересечёт OH в точке Y. Поскольку то M1M : AM = 1 : 2, а значит, точка Y совпадает с точкой M1.
Окружность девяти точек
Около треугольника H1H2H3 опишем окружность γe. Её центр делит пополам отрезок OH (точка E). Середины отрезков AH, BH, CH (точки E1, E2, E3) гомотетичны точкам A, B и C и принадлежат окружности γe.
Докажем, что точки M1, M2, M3 принадлежат окружности γe.
Доказательство. Действительно, точки A1 и H симметричны относительно точки B. Кроме того, точки A1 и M1 гомотетичны, а значит, точка M1 принадлежит окружности γe.
ІІІ. Ортоцентрический треугольник Q1Q2Q3
Опишем окружность около треугольника ABC и построим точки W1,W2, W3 (середины дуг BC, AC, AB) (рис. 7).
Точку пересечения хорд W2W3 и AW1 обозначим Q1. Аналогично получим точки Q1 и Q3. По теореме «листа трилистника» имеем: IW1 = W1C. Поскольку ∪ AW2 = ∪ W2C, то
а значит, треугольник Q1Q2Q3 — ортоцентрический треугольник треугольника W1W2W3. В равнобедренном треугольнике IW1C IQ3 = Q3C. Аналогично, IQ1 = Q1A, следовательно, стороны треугольника Q1Q2Q3 вдвое меньше соответственных сторон треугольника ABC. Поэтому (применяем формулу S = RpH ) площадь треугольника W1W2W3 . (1°)
Поскольку окружность, описанная около треугольника Q1Q2Q3, есть окружность Эйлера треугольника W1W2W3, то девять точек принадлежат одной окружности: середины отрезков W1W3, W2W3, W1W2, IW1, IW2, IW3, IA, IB, IC.
ІV. Ортоцентрический треугольник ABC Рассмотрим треугольник, вершины которого — центры вневписанных окружностей Ia, Ib, Ic (рис.8).
Ортоцентрическим треугольником этого
треугольника будет треугольник ABC, так как
каждая из его вершин есть пересечение внутренней и внешней биссектрис. Поскольку радиус окружности, описанной около треугольника ABC будет R, то радиус окружности, описанной около треугольника IaIbIc будет 2R, а площадь SIaIbIc=2R⋅p.
Поскольку окружность, описанная около треугольника ABC, является окружностью Эйлера треугольника IaIbIc, то девять точек принадлежат одной окружности: вершины треугольника ABC, точки W1, W2, W3, середины
V. Треугольник, подобный ортоцентрическому треугольнику H1H2H3
Через вершины A, B и C проведём касательные к окружности, описанной около треугольника ABC. Получим треугольник T1T2T3 (рис. 9).
тангенциальным) вычисляют по формуле:
ST=R⋅pT, где R — радиус окружности, вписанной в треугольник T1T2T3.
Глава 2. Применение.
§ 1 Применение свойств ортотреугольника для решения задач
Задача 1.
Пусть и – высоты треугольника АВС. Докажите, что треугольник подобен треугольнику АВС. Чему равен коэффициент подобия?
подобен треугольнику АВС по теореме 1. Коэффициент подобия . В прямоугольных треугольниках и , . Значит, .
Следствием данной задачи будет следующее утверждение: каждая сторона ортотреугольника равна произведению противолежащей стороны на косинус противолежащего угла исходного треугольника.
Задача 2.
Треугольник АВС остроугольный, и угол ВАС равен α. На стороне ВС как на диаметре построена полуокружность, пересекающая стороны АВ и АС в точках Р и Q соответственно. Найдите отношение площадей треугольников АВС и APQ.
Поскольку и – высоты треугольника , треугольник подобен с коэффициентом подобия , поэтому
Задача 3
В остроугольном треугольнике АВС проведены высоты АD, ВЕ и СF. Докажите, что pR=Pr, где p-периметр треугольника EDF, Р – периметр треугольника АВС.
Решение(без применения свойств):
1. Т.к. и согласно задаче 1 , то . ,
Пусть О – центр описанной окружности , R – ее радиус. Тогда Т.к. по т. синусов , то после подстановки, получаем .
Аналогично и , т.е. . Поскольку и , то , что и требовалось доказать.
Решение(без применения свойств):
По свойству 6 . , тогда , что и требовалось доказать.
Задача 4
Треугольник АВС остроугольный, и . Определите углы высотного треугольника.
1. Строим высоты , , .
Задача 5.
Т.к. – равнобедренный, то – высота, медиана, биссектриса ;.
4. Т.к. подобен , то; .
5. ||, а это значит, что подобен .
7. По т. Пифагора .
Задача 6
В равнобедренном треугольнике ABC(AB = BC)проведены высоты AA1,
Т.к. подобен , то и (1)
по гипотенузе и острому углу, т.к рассматриваемые треугольники прямоугольные, .
Т.к. и , отсекая пропорциональные отрезки, то ||.
Известно, что , , поэтому, подставив данные в (1), получим ,
Глава 3. Анкетирование учащихся
Всем ученикам 10 и 11 классов я задала по 4 вопроса:
Знаете ли вы об ортоцентрических треугольниках?
Применяли ли вы свойства ортоцентрических треугольников при решении задач?
Как вы считаете, можно ли облегчить решение задач, используя эти свойства?
Хотели бы вы научиться решать задачи на применение свойств ортоцентрических треугольников?
Подсчитав ответы «да», я получила следующие результаты:
Высота треугольника. Задача Фаньяно
Высота треугольника. Свойство высоты прямоугольного треугольника
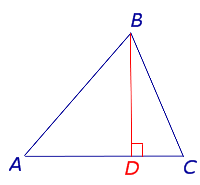
Определение 1 . Высотой треугольника называют перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону треугольника. Основанием высоты называют основание этого перпендикуляра (рис.1).
На рисунке 1 изображена высота BD , проведённая из вершины B треугольника ABC . Точка D – основание высоты.
Для высоты прямоугольного треугольника, проведённой из вершины прямого угла, справедливо следующее утверждение.
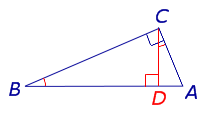
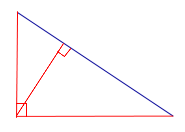
Утверждение . Длина высоты прямоугольного треугольника, опущенной на гипотенузу, является средним геометрическим между длинами отрезков, на которые основание высоты делит гипотенузу (рис.2).
Доказательство . Углы треугольников BCD и ACD (рис.2) удовлетворяют соотношениям
Таким образом, длина отрезка CD является средним геометрическим между длинами отрезков BD и AD , что и требовалось доказать.
Высоты можно провести из каждой вершины треугольника, однако у треугольников различных типов высоты располагаются по-разному, как показано в следующей таблице.
Расположение высот у треугольников различных типов
| Фигура | Рисунок | Описание |
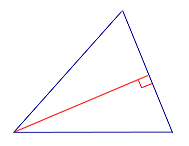
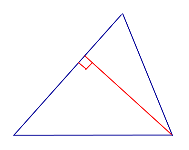
| Остроугольный треугольник | 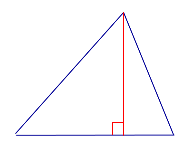 |
Все высоты остроугольного треугольника лежат внутри треугольника. |
 |
||
 |
||
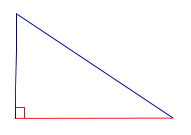
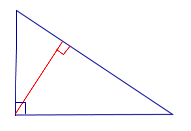
| Прямоугольный треугольник | 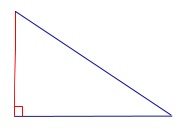 |
Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника |
 |
||
 |
||
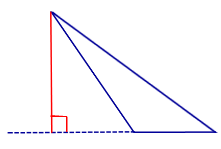
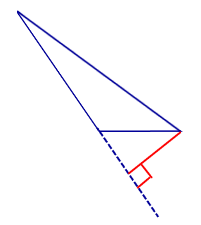
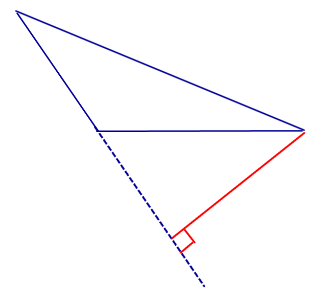
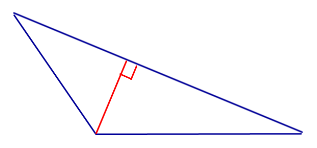
| Тупоугольный треугольник | 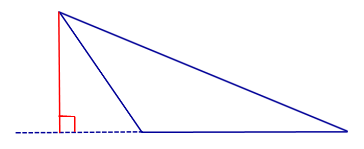 |
Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника |
 |
||
 |
| Остроугольный треугольник | ||
 |
 |
 |
| Все высоты остроугольного треугольника лежат внутри треугольника. | ||
| Прямоугольный треугольник | ||
 |
 |
 |
| Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника | ||
| Тупоугольный треугольник | ||
 |
 |
 |
| Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника |
Все высоты остроугольного треугольника лежат внутри треугольника.
Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника
Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника
Ортоцентр треугольника
Теорема 1 . Высоты треугольника (или их продолжения) пересекаются в одной точке.
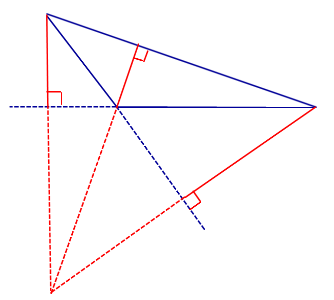
Доказательство . Рассмотрим произвольный треугольник ABC и проведём через каждую из его вершин прямую, параллельную противолежащей стороне (рис.3).
Обозначим точки пересечения этих прямых символами A1 , B1 и C1 , как показано на рисунке 3.
Следовательно, точка B является серединой стороны C1A1 .
Следовательно, точка A является серединой стороны C1B1 .
Следовательно, точка C является серединой стороны B1A1 .
и в силу теоремы о серединных перпендикулярах пересекаются в одной точке.
Теорема 1 доказана.
Определение 2 . Точку пересечения высот треугольника (или их продолжений) называют ортоцентром треугольника.
У треугольников различных типов ортоцентры располагаются по-разному, как показано в следующей таблице.
Расположение ортоцентров у треугольников различных типов
Ортоцентр остроугольного треугольника лежит внутри треугольника.
Ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла
Ортоцентр тупоугольного треугольника лежит вне треугольника.
В ортоцентре тупоугольного треугольника пересекаются не высоты, а продолжения высот треугольника.
Ортоцентр остроугольного треугольника лежит внутри треугольника.
Ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла
Ортоцентр тупоугольного треугольника лежит вне треугольника.
В ортоцентре тупоугольного треугольника пересекаются не высоты, а продолжения высот треугольника.
Ортоцентрический треугольник
Решим следующую задачу.
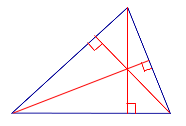
Задача . В остроугольном треугольнике ABC проведены высоты AD и BE (рис.5). Доказать, что треугольник DCE подобен треугольнику ABC .
Решение . Рассмотрим треугольники ADC и BEC . Эти треугольники подобны в силу признака подобия прямоугольных треугольников с равными острыми углами (угол C общий). Следовательно, справедливо равенство
Это равенство, а также наличие общего угла C позволяют на основании признака подобия треугольников заключить, что и треугольники DCE и ABC подобны. Решение задачи завершено.
Определение 3 . Ортоцентрическим треугольником (ортотреугольником) называют треугольник, вершинами которого служат основания высот исходного треугольника (рис 6).
Из определения 3 и следствия 1 вытекает следствие 2.
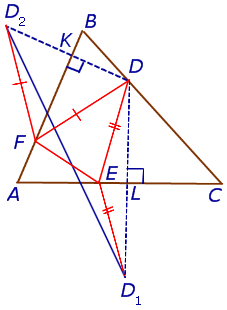
Следствие 2 . Пусть FDE – ортоцентрический треугольник с вершинами в основаниях высот остроугольного треугольника ABC (рис 7).
Тогда справедливы равенства
Из следствия 2 вытекает теорема 2.
Теорема 2 . Высоты остроугольного треугольника являются биссектрисами углов его ортоцентрического треугольника (рис.7).
Доказательство . Воспользовавшись следствием 2, получаем:
что и требовалось доказать.
Задача Фаньяно
Задача Фаньяно . Рассматриваются всевозможные треугольники DEF , вершины D, E и F которых лежат на сторонах BC, AC и AB остроугольного треугольника ABC соответственно. Доказать, что из всех треугольников DEF наименьшим периметром обладает ортоцентрический треугольник треугольника ABC .
Решение . Пусть DEF – один из рассматриваемых треугольников. Обозначим символом D1 точку, симметричную точке D относительно прямой AC , и обозначим символом D2 точку, симметричную точке D относительно прямой AB (рис.8).
Поскольку отрезок прямой – кратчайшее расстояние между двумя точками, то периметр треугольника DEF оказывается не меньшим, чем длина отрезка D1D2 . Отсюда вытекает, что при фиксированной точке D наименьшим периметром обладает такой треугольник DEF , вершины F и E которого являются точками пересечения прямой D1D2 с прямыми AB и AC соответственно. Периметр этого треугольника равен длине отрезка D1D2 (рис.9).
Заметим также, что выполнено равенство
Кроме того, выполнено равенство
Отсюда вытекает, что длина отрезка D1D2 будет наименьшей тогда, когда длина отрезка AD будет наименьшей, т.е. в том случае, когда отрезок AD является высотой треугольника ABC . Другими словами, наименьшим периметром обладает такой треугольник DEF , у которого вершина D является основанием высоты треугольника ABC , проведённой из вершины A , а вершины E и F построены по описанной выше схеме. Таким образом, среди всевозможных треугольников DEF треугольник с наименьшим периметром является единственным.
Если обозначить длину высоты, проведённой из вершины A , длину стороны AB и радиус описанной около треугольника ABC окружности буквами h, c и R соответственно, то, воспользовавшись теоремой синусов, получим:
Следовательно, наименьший периметр рассматриваемых треугольников DEF равен
Теперь докажем, что ортоцентрический треугольник и является треугольником с наименьшим периметром. Для этого воспользуемся следующей леммой.
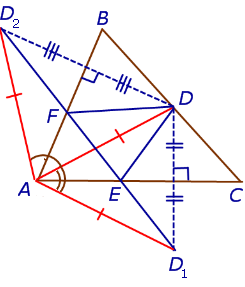
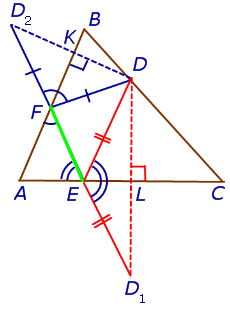
Лемма . Пусть DEF – ортоцентрический треугольник треугольника ABC (рис.10).
В этом случае отрезок D1D2 проходит через точки F и E .
Доказательство . Заметим, что в силу следствия 2 выполняются равенства:
Кроме того, в силу равенства треугольников DFK и KFD2 , а также в силу равенства треугольников DEL и LED1 выполняются равенства:
откуда вытекает, что углы AEF и D1EL , а также AFE и D2FK являются вертикальными углами. Это означает, что точки D1 , F, E , D2 лежат на одной прямой. Лемма доказана.
Доказательство леммы и завершает решение задачи Фаньяно.
Свойства высот треугольника. Ортоцентр
Схема 1. В треугольнике АВС проведены высоты АМ и СК.
Н – точка пересечения высот треугольника (ортоцентр), Н=АМ∩СК
Запомните этот рисунок. Перед вами – схема, из которой можно получить сразу несколько полезных фактов.
1. Треугольники МВК и △АВС, подобны, причем коэффициент подобия
, если 

- Четырехугольник АКМС можно вписать в окружность. Эта вспомогательная окружность поможет решить множество задач.
- Четырехугольник ВКМН также можно вписать в окружность.
- Радиусы окружностей, описанных вокруг треугольников АВС, АНС, ВНС и АВН, равны.
- ,где R – радиус описанной окружности .
Докажем эти факты по порядку.
1) Заметим, что на рисунке есть подобные треугольники. Это АВМ и СВК, прямоугольные треугольники с общим углом В, и они подобны по двум углам
Мы получили, что в треугольниках МВК и АВС стороны, прилежащие к углу В, пропорциональны. Получаем, что по углу и двум сторонам.
2) Докажем, что вокруг четырехугольника АКМС можно описать окружность. Для этого необходимо и достаточно, чтобы суммы противоположных углов четырехугольника АКМС были равны .
Пусть ∠ACB=∠BKM=γ (поскольку треугольники МВК и АВС подобны), тогда
– как смежный с углом ВКМ. Получили, что , и это значит, что четырехугольник AKMC можно вписать в окружность.
3) Рассмотрим четырехугольник KBMH. Его противоположные углы ВКН и ВМН – прямые, их сумма равна , и значит, четырехугольник КВМН можно вписать в окружность.
4) По теореме синусов, радиус окружности, описанной вокруг треугольника АВС,
Радиус окружности, описанной вокруг треугольника АНС,
Мы помним, что . Значит, синусы углов АВС и АНС равны, и радиусы окружностей, описанных вокруг треугольников АВС и АНС равны.
5) Докажем, что ,где R – радиус описанной окружности . Поскольку четырехугольник КВМН можно вписать в окружность и углы ВКН и ВМН – прямые, отрезок ВН является диаметром этой окружности. Треугольник МВК также вписан в эту окружность, и по теореме синусов, .
Диаметр окружности, описанной вокруг треугольника АВС, равен Поскольку треугольники МВК и АВС подобны, отношение диаметров описанных вокруг них окружностей равно . Получили, что
Задача ЕГЭ по теме «Высоты треугольника» (Профильный уровень, №16)
2. В остроугольном треугольнике KMN проведены высоты KB и NA.
а) Докажите, что угол ABK равен углу ANK.
б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и
а) Докажем, что
(по двум углам). Запишем отношение сходственных сторон:
Но это значит, что (по углу и двум сторонам), причем .
– смежный с углом ,
,
,четырехугольник ABNK можно вписать в окружность.
(опираются на одну дугу).
[spoiler title=”источники:”]
http://www.resolventa.ru/uslugi/ege/egebase2.htm
http://ege-study.ru/materialy-ege/svojstva-vysot-treugolnika-ortocentr/
[/spoiler]