Как найти углы поворота колес

МАШИНОСТРОЕНИЕ И ТРАНСПОРТ: ТЕОРИЯ, ТЕХНОЛОГИИ, ПРОИЗВОДСТВО

УДК 629.33

В.В. Беляков1, Ю.В. Палутин2, А.В. Тумасов1, Д.А. Бутин1, А.П. Трусов1

РАСЧЕТ УГЛОВ ПОВОРОТА УПРАВЛЯЕМЫХ КОЛЕС АВТОМОБИЛЯ

С УЧЕТОМ УВОДА

Нижегородский государственный технический университет им. Р.Е. Алексеева1 Нижегородская государственная сельскохозяйственная академия2

Представлен способ расчета углов поворота управляемых колес автомобиля, учитывающий угол увода шин управляемой оси. Различные известные теории на практике почти не используются в связи со сложностью вычислений, при этом геометрия рулевого управления основывается на опыте и анализе существующих автомобилей. Выявлено, что теория поворота управляемых колес Фиала наиболее адекватно описывает физические процессы, протекающие в контакте пневматической шины с опорной поверхностью. Предложенная методика отличается от ранее используемых значительным упрощением расчетов. В качестве данных, требуемых для расчета углов поворота управляемых колес, используются колесная база, высоты ЦТ, ширина колеи, масса на оси, коэффициент увода шин, боковое ускорение, радиус движения. Приведенный расчет зависимости поворота управляемых колес может быть использован на стадии проектирования автомобиля.

Ключевые слова: углы поворота управляемых колес, соотношение углов поворота направляющих колес, управляемые колеса, геометрия рулевого управления, схождение.

Введение

Зависимость поворота управляемых колес автомобиля влияет на износ шин, а также на управляемость и устойчивость движения в повороте. В различные периоды развития автомобилестроения выдвигались те или иные теории поворота управляемых колес с целью уменьшения износа шин и улучшения показателей управляемости при движении в поворот. На основании анализа работ П.В. Аксенова, Д.А. Антонова, С.В. Бахмутова, Л.Л. Гинцбурга, А. Дика, Р.П. Кушвида, Э.И. Григолюка, Н.Т. Катанаева, В.Н. Кравца, К.С. Колесникова, А.А. Полунгяна, В.Ф. Платонова, В.А. Петрушова, Д.Р. Эллиса, Е.О. Рыкова, Ю.В. Шемякина, Г.П. Антипова, Н.А. Алфутова, М.В. Гурьянова, В.М. Семенова, В.И. Кольцова, Я.Е. Фа-робина, W.F. Milliken, D.L. Millken, H.B. Pacejka [1-14] можно выделить четыре наиболее распространенные теории поворота управляемых колес:

• параллелограммная – углы поворота управляемых колес всегда равны друг другу;

• геометрическая – соотношение углов поворота определяется по условию Аккер-мана;

• система по Гауфу и Ширеру – углы бокового увода обоих передних колес должны быть по возможности малыми, что достигается при одинаковой величине их углов бокового увода;

• система Фиала [12,13] – соотношения уводов пропорционально перераспределенной нагрузке;

• система по Хассельгруберу [7,8] – мощность бокового трения, т.е. производная боковой силы при уводе и компонента скорости, перепендикулярной к плоскости вращения шины, должны быть одинаковыми для обоих передних колес.

© Беляков В.В., Палутин Ю.В., Тумасов А.В., Бутин Д.А., Трусов А.П.

Для выявления наиболее оптимальной концепции необходимо представление в теории движения автомобиля и работы пневматической шины. При движении в повороте у автомобиля происходит перераспределение нормальных реакций колес. Под действием бокового ускорения на центр тяжести, нагрузка на внешнее колесо увеличиваются, а на внутреннем – снижается, что представлено на схеме (рис. 1). Рулевое управление – так же, как и подвеска – должно обеспечивать оптимальное положение пневматических шин относительно опорной поверхности во время движения. Для определения оптимальных режимов работы пневматических шин передней оси необходимы данные о качении шины с уводом. На рис. 2. представлены графики, характеризующие качение шины с уводом для различных вертикальных нагрузок. Следует обратить внимание, как изменяется зависимость боковой силы от угла уводы при различных вертикальных силах. При уменьшении вертикальной силы уменьшается максимальная боковая сила, развиваемая колесом, пропорционально боковой силе снижается угол увода, при котором достигается максимальное ее значение. Из графиков видно, что при изменении вертикальной силы характеристика шины на линейном участке остается неизменной.

Ру Ру

внешн внутр

Рис. 1. Схема распределения сил Рис. 2. Диаграмма боковой силы

в управляемых колесах от угла увода

На основании данных о движении автомобиля в повороте и работы пневматической шины можно сделать выводы о теориях поворота управляемых колес. Так, теория закона Ак-кермана подходит для жестких не пневматических колес, катящихся без увода; система по Га-уфу и Ширеру неприемлема в связи с тем, что углы увода у внешнего и внутреннего колеса будут разными из-за различных вертикальных сил; система по Хассельгруберга также не состоятельна в связи с тем, что не возможно на шинах развивать одинаковое боковое усилие, при том, что у них различные вертикальные силы; по этому самой объективной и учитывающий работу пневматической шины является система Фиала.

Расчет распределения вертикальной силы между колесами управляемой оси

Распределение вертикальных сил на управляемых колесах от действия бокового ускорения, действующего при движении автомобиля в повороте, рассчитывается по формулам (1), (2). При таком подходе перераспределения нагрузок на передней оси не учитываются многие факторы: угловая жесткость подвесок, жесткость кузова на кручение. Также эти формулы подходят только для равномерного движения без продольного ускорения.

^внутр _ ^9,81Мрсь^ ^

¿твнешн _ ^9,81Мос^ | ^ДуЯцт^

г-»внутр гвнешн

где , ^2внешн – сила вертикальная на управляемом колесе внутреннем и внешнем соответственно, Н; Мось – масса на управляемой оси, кг; ау – боковое ускорение, м/с2; Нцт – высота центра тяжести, м; В – ширина колеи, м.

Боковые силы

Суммарная боковая сила, действующая на шины управляемой оси, рассчитывается по формуле (3). При этом расчете не учитываются переходный процесс установления кругового движения.

1 = Мось ■ . (3)

Боковые силы между внутренним и внешним колесом будут распределяться пропорционально вертикальным силам, согласно закону силы трения. Расчет боковых сил на внутреннем и внешнем колесе производится по формулам (4), (5).

внутр

рвнутр = I р • __(4)

У 9,81-Мось’ (4)

рвнешн

гв™ = I • -, (5)

^ У 9,81 •Мось’ 4 ‘

где /^шутр, /увнешн – сила боковая на управляемом колесе внутреннем и внешнем соответственно, Н.

Характеристика качения колеса с уводом

Характеристику качения шины с уводом можно описать формулой любого из авторов теории шин Пасейки, Щадрин, Эллис, Фуфаев и других. Как правило, это функции боковой силы от угла увода, но для решения нашей задачи необходима обратная функция угла увода от боковой силы. Поскольку вывод угла увода из функции не всегда возможен или затруднен для решения данной задачи, примем, что шина работает только в зоне упругой деформации. Допущение, что при небольших углах увода шин зависимость линейна, имеется у многих авторов и часто используется при решении задач. Это допущение сильно упрощает расчетную формулу, при этом погрешность остается в рамках допустимого на режимах качения шин без жесткого скольжения. Режим жесткого скольжения в рамках оптимизации поворота управляемых колес не рассматривается. Представив зависимость угла увода от боковой силы в виде линейной зависимости выражение примет элементарный вид (6), (7):

внутр

авнУтр= _У-, (6)

^увода

рвнешн

квнешн= -, (7)

^увода

где авнугр, авнешн – угол увода внутреннего и внешнего колеса, град; кувод – коэффициент увода шины от боковой силы, Н/град.

Поворот управляемых колес

На первом этапе рассчитывается угол поворота управляемых колес по закону Аккер-мана, потому что по этой траектории будут двигаться центры управляемых колес. Схема идеального поворота управляемых колес по закону Аккермана представлена на рис. 3

Рис. 3. Схема поворота управляемых колес

Расчет углов поворота по Аккерману производится без учета угла увода колес задней оси, а также радиус движения принимается до центра задней оси, приняв, что радиус движения ЦТ отличается не сильно, расчетные формулы (8) и (9).

0,

внутр идеал

идеал

= arctg (

—),

Я+(Б/2)/’

(8)

(9)

Действительные углы поворота управляемых колес вычисляются по сумме идеальных углов поворота и углов увода, представлены в формулах (10) и (11).

лвнУ’Р = лвнУ’Р .^внутр ^действ ^идеал ‘

двнешн _ двнешн I -„.внешн

^действ ^идеал

(10) (11)

Результаты

В качестве примера был проведен расчет оптимальных углов поворота колес по теории Фиала. Расчет был проведен для автомобиля с параметрами, представленными в табл. 1.

Таблица 1

Параметры автомобиля

Параметр Значение

Колесная база, м 3,145

Высота ЦТ, м 0,85

Ширина колеи передней оси, м 1,75

Масса на передней оси, кг 1273

Коэффициент увода шин, Н/град 1250

В результате расчета были получены углы поворота управляемых колес. Для наглядности зависимости поворота колес от параметров движения в повороте в табл. 2 приведены значения расхождения колес.

Таблица2

Расхождения углов поворота управляемых колес

Расхождение управляемых колес, град

Радиус движения, м Боковое ускорения, м/с2

1 2 3 4 5 6

10 3,41993 3,11739 2,61316 1,90723 0,99962 -0,1097

20 0,70897 0,40643 -0,0978 -0,80373 -1,7113 -2,8207

30 0,25372 -0,04882 -0,55305 -1,25897 -2,1666 -3,2759

40 0,09756 -0,20498 -0,70921 -1,41513 -2,3228 -3,4321

50 0,02583 -0,27671 -0,78094 -1,48687 -2,3945 -3,5038

По результатам расчета оптимальных углов поворота управляемых колес выявлено две зависимости: с уменьшением радиуса движения увеличивается расхождение колес; с увеличением бокового ускорения расхождение колес уменьшается.

Исследования А.С. Добрина выявили, что при эксплуатации среднестатистического автомобиля на дорогах общего пользования боковые ускорения не превышают 3 м/с2. Этот порог называют «порогом неприятных ощущений»: он вызывает чувства дискомфорта и опасности. Если принять этот фактор во внимание и сопоставить с результатами расчета оптимального расхождения колес, то видно, что от 0 до 3 м/с2 угол расхождения колес крайне мал и увеличивается лишь при маневрировании и движениями с радиусами менее 20 м. Если рассматривать режимы движения с ограниченным боковым ускорением и исключить режим маневрирования, оптимальные углы поворота колес настолько близки по значениям, что зависимость поворота колес можно принять параллельной.

Если в эксплуатации автомобиля значительную часть составляет маневрирование с минимальными радиусами поворота, то наиболее адекватным теоретической конструкцией является закон поворота управляемых колес по Аккерману. Данный расчет также подтверждает правильность использования в спортивных автомобилях класса «Формула 1» и «Формула 3» кинематики рулевого управления с зависимостью Анти-Аккермана. Автомобили, двигающиеся с большими боковыми ускорениями, при определенных конструктивных параметрах имеют оптимальные углы поворота управляемых колес в положительном схождении.

Вывод

В результате анализа теорий оптимального поворота управляемых колес в качестве наиболее адекватно описывающей физические процессы, протекающие в контакте пневматической шины с опорой поверхностью, была определена теория Фиала. Основанный на ней способ расчета оптимальных углов поворота, в силу ряда допущений (линейная зависимость

увода от боковой силы, увод колес задней оси) был сведен к инженерным формулам. Полученные результаты могут быть сопоставлены с геометриями рулевых управлений, используемых на автомобилях различных эксплуатаций. Приведенный расчет зависимости поворота управляемых колес может быть использован на стадии проектирования автомобиля.

Анализ рассчитанных величин углов поворота колес показывает, что для автомобилей, двигающихся с небольшими боковыми ускорениями до 1 м/с2, геометрия поворота управляемых колес схожа с геометрической теорией Аккермана, а при движении с боковыми ускорениями, близкими к потери динамической устойчивости, зависимость может быть описана по теории Анти-Аккермана.

Исследования выполнены при финансовой поддержке Министерства образования и науки РФ по договору № 02.G25.31.0193 от 27.04.2016 г. (постановление Правительства Российской Федерации от 9 апреля 2010 года № 218).

Экспериментальные исследования выполнены с использованием оборудования Центра коллективного пользования НГТУ «Транспортные системы».

Библиографический список

1. Чудаков, Е.А. О рациональной форме рулевой трапеции // Доклады АН СССР. – М.: Изд-во АН СССР. – 1952. – Т. 88. – № 4.

2. Фрикционный износ резин / Сборник статей под ред. д.т.н. В.Ф. Евстратова. – М.: Химия, 1964, -271 с.

3. Фаробин, Я.Е. О рациональной форме рулевой трапеции // Автомобильная промышленность. – Т. 2. – 1959. – С. 15-17.

4. Фаробин, Я.Е. Теория поворота транспортных машин / Я.Е. Фаробин. – М.: Машиностроение, 1970, – 176 с.

5. Стефанович, Ю.Г. Исследование рулевой трапеции автомобилей / Ю.Г. Стефанович: Дис. … канд. техн. наук. – М., 1954. – 147 с.

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

6. Кушвид, Р.П. Исследование рулевого управления автомобиля (оптимизация по критерию минимума износа шин) / Р.П. Кушвид. – дисс. …канд. техн. наук. – М., 1978, – 202 с.

7. Hasselgruber, H. Veerhaiten eines Kraftfahrzeuges bei Kurveenfahrt Automobilitechn Z / H. Has-selgruber. – №7. – 1965.

8. Hasselgruber, H. Zweckmäbige Auslegung van Krafttahrzeugienkungen in Hinbick auf Kurven vehaiten ung Reifengchonung / H. Hasselgruber // Automob. Ind., – № 3 (1). – 1964.

9. Добрин, A.C. Исследование движения автомобиля по заданной траектории / А.С. Добрин. – М.: НАМИ, 1966. – С. 35-65.

10. Добрин, A.C. Устойчивость и управляемость автомобиля при неустановившемся движении // Автомобильная промышленность. 1968. – № 9. – С.29-35.

11.Schallamach, A. The theori of dynamie rubber friction / А. Schallamach. – Wear. – 1963. – v.6. – № 5.

12.Fiala, E. Kraftkorrigierte Lenkanggeometrie / E. Fiala // ATZ. – 1959. – № 2.

13.Fiala E. Zur Fahrdunamik des Stressenfahrzeges unter Berück gichtigung der Lenkwngelastizitet / E. Fiala // ATZ. – № 3. – 1960.

14.Тумасов, А.В. Способ расчета интенсивности износа шин для различных режимов движения автомобиля / А.В. Тумасов, Д.А. Бутин, А.А. Васильев // Беспилотные транспортные средства: проблемы и перспективы. Сборник материалов 94 международной научно-технической конференции Ассоциации автомобильных инженеров. – Н. Новгород: НГТУ им. Р.Е. Алексеева, 2016. – С. 123-129.

Дата поступления

в редакцию: 07.03.2019

V.V. Belyakov, Y.V. Palutin, A.V. Tumasov, D.A. Butin, A.P. Trusov

CALCULATION STEETING GEOMETRY OF THE CAR TAKING INTO ACCOUNT THE SLIP ANGLE TIRE

Nizhny Novgorod State Technical University n.a. R.E. Alekseev

Purpose: method for calculating the steering angle of the directive wheels of a car. Design/methodology/approach: The calculation is presented in the form of engineering formulas. Findings: The calculation results are comparable with the geometry of the steering controls of existing cars. Research limitations/implications: In calculating the slip of the tires of the driven axes adopted linear, and the slip of tires of the rear axle not included.

Originality/value: for the first time the theory of geometry of steering control of the car of the Fiala theory is presented in a simple mathematical form.

Key words: steering angles, steering angle difference, steering geometry, slip angle, toe in.

Соотношение углов поворота управляемых колес



При повороте автомобиля его управляемые колеса должны катиться в плоскости своего вращения без бокового скольжения. Для обеспечения этого условия векторы скоростей центров всех колес должны быть перпендикулярны радиусам, проведенным из центра поворота (рис. 1).

У автомобиля, имеющего жесткие в поперечном направлении шины, векторы скоростей совпадают со средними плоскостями колес, и центр поворота О находится на продолжении оси заднего моста. Соотношение между углами поворота θ_н и θ_в соответственно наружного и внутреннего колес определяется из треугольников ОАВ и ОСД:

ctg θ_н – ctg θ_в = (ОС – ОА)/L = L_шк/L, (1)

где L_шк – расстояние между центрами шкворней, равное приблизительно колее управляемых колес.

Из равенства (1) следует, что внутреннее колесо относительно центра поворота должно быть повернуто на больший угол, чем внешнее.

Чтобы обеспечить требуемое соотношение между углами поворота управляемых колес их соединяют рулевой трапецией.
Однако точного выполнения равенства (1) рулевая трапеция не обеспечивает. Поэтому при проектировании трапеций считают достаточным, если при значениях θ_н от 5 до 8 градусов расхождение между теоретическим и действительными значениями θ_н не превышает 12…15‘, а при θ_в от 25 до 30 градусов – не более 3 градусов.

При углах поворота до 15 градусов зависимость θ_н = f(θ_в) близка к линейной, что позволяет вместо углов θ_н и θ_в использовать расчетный средний угол θ, равный их полусумме.

Так как на автомобилях устанавливаются эластичные шины, то векторы скоростей центров колес вследствие их увода не совпадают со средними плоскостями колес.
Изменится также и соотношение углов поворота управляемых колес, которое будет зависеть от скорости движения, а так как учитывать этот фактор конструктивно сложно, то им пренебрегают.
Следовательно, автомобиль на эластичных шинах при совершении поворота движется с боковым проскальзыванием управляемых колес, и величина этого проскальзывания будет зависеть от скорости движения.

***



Колебания управляемых колес

Управляемые колеса, передний мост, подвеска и рулевое управление представляют собой упругую операционную систему, которая при наличии возмущающих импульсов может приходить в колебательное движение, сопровождающееся вилянием управляемых колес.

Так, передний мост вследствие упругой деформации рессор может перемещаться относительно продольной оси автомобиля (точка О на рис. 2, а) на угол ψ, а колеса вследствие упругой деформации привода управления – на угол φ относительно оси шкворня (точка δ на рис. 2, б).

Наезд одним из колес переднего моста на неровность дороги вызовет поворот управляемых колес относительно шкворней, который в свою очередь будет стремиться увеличить наклон колес. Таким образом, перекос переднего моста в результате наезда на неровность вызовет угловые колебания колес, которые в свою очередь усилят перекос моста. Колебания будут продолжаться и после того, как колесо съехало с неровности.
Такие колебания называются собственными. Они зависят только от характеристик упругих элементов подвески, моментов инерции и масс отдельных деталей.

Но бывают и вынужденные колебания колес автомобиля, если в системе управляемых колес имеется какой-нибудь постоянный источник возмущающих сил. Такая система будет иметь незатухающие колебания.

Источником незатухающих колебаний может являться, например, неуравновешенность (дисбаланс) колес. Например вентиль создает центробежную силу С (рис.3, а). При диаметральном расположении вентилей (рис. 3, б) возникает знакопеременный возмущающий момент, который и будет источником автоколебаний.
Дисбаланс колес может быть вызван неравномерностью распределения весовых элементов шины, дефектами колесных дисков и другими факторами. Наиболее эффективным методом борьбы с дисбалансом колес является их балансировка на специальном оборудовании.

При скорости движения автомобиля более 70 км/ч колеса могут создавать 6…8 колебаний в секунду со значительной амплитудой. Это может сопровождаться периодическим отрывом колес от дороги, вследствие чего возможна потеря управления автомобилем.

Способом борьбы с возникновением колебаний управляемых колес является устранение дисбаланса колес, а также применение независимых подвесок. Независимая подвеска не должна позволять управляемым колесам совершать угловые перемещения в плоскости дороги.
На рис. 5 показаны схемы независимых подвесок автомобиля. Подвески а, б и в позволяют колесам перемещаться только поступательно.

Подвески г и д позволяют колесам совершать угловые перемещения в вертикальной плоскости, т. е. могут явиться причиной возникновения колебаний колес. При этом подвеска д лучше подвески г, поскольку ее амплитуда колебаний будет меньше, чем подвески г.

***

Стабилизация управляемых колес



Управляемые колеса
автомобиля имеют развал и схождение.

Развал
– это отклонение
центральной плоскости вращения колеса
от вертикали. Величина развала
характеризуется углом развала (рис. 75)

Рис. 75. Реакции опорной
поверхности при развале

Если
верхняя часть колеса наклонена наружу,
то угол развала (_р)
считается положительным,
если в противоположную сторону – то
отрицательным.
У автомобилей положительный развал
управляемых колес предусматривают для
того, чтобы компенсировать выбор зазоров
в подшипниках ступицы, величина которых
нарастает по мере их износа, а также
упругие деформации. Угол развала на
передних колесах легковых автомобилей
выбирают таким образом, чтобы при
нагрузке, равной 2 – 3 чел, был небольшой
положительный развал _р
= +5′ – +10′. Меньшие значение приводят к
повышенному износу внутренней части
беговой дорожки шины, а большие – наружной.

Схождение
– это отклонение
центральных плоскостей вращения
управляемых колес от продольной оси
автомобиля (рис. 76).

Рис. 76. Cхождение колес

Величину
схождения оценивают разницей расстояний
В и
С, т.е.

L_с
= В
– С. (274)

Расстояния
В и С измеряются между точками, лежащими
в одной горизонтальной плоскости на
высоте центров колес и на заданном
удалении от центров. Угол схождения
колес ()
рассчитывается по формуле:

 

,
(275)

где Д – расстояние
между линиями замера.

Наименьший
износ шины происходит при параллельности
центральных плоскостей вращения
управляемых колес продольной оси
автомобиля. Для того, чтобы обеспечить
указанное положение в движении,
необходимо, чтобы в статическом положении
было
небольшое схождение колес. Это объясняется
следующим. При движении на левом и на
правом колесе образуются касательные
реакции R_хл
и R_хп,
которые создают моменты относительно
осей вращения поворотных цапф. Указанные
моменты слегка разворачивают колеса и
они становятся параллельными друг
другу. При этом разворот колес объясняется
главным образом наличием зазоров в
сочленениях и их податливостью (особенно
в опорах рычагов). Для легковых автомобилей
классической компоновки достаточно
схожде­ния колес в 2 – 3 мм.

У
переднеприводных автомобилей касательные
реакции направлены в противоположную
сторону, т.е. вперед, поэтому для них
предпочтительно отрицательное схождение
колес.

11.8. Маневренность автотранспортных средств

Под
маневренностью
автомобиля понимают
его способность передвигаться в условиях
ограниченного по длине и ширине
пространства.

Для
количественной оценки маневренности
используется ряд геометрических и
силовых показателей /2/.

К
основным геометрическим
показателям маневренности относятся:

1) радиусы поворота
по следу колес;

2) ширина полосы
движения по следу колес;

3) радиусы поворота
по габаритам;

4) ширина полосы
движения по габаритам;

5) угол горизонтальной
гибкости (для автопоездов).

К
силовым
показателям маневренности можно отнести:

1) усилие на рулевом
колесе при повороте управляемых колес
на месте;

2) удельное
сопротивление повороту.

Радиусы
поворота по
следу колес
– это расстояния от центра поворота
автомобиля, осуществляемого с минимальной
скоростью при максимальном повороте
управляемых колес, до траектории
движения переднего наружного (R_пнmin)
и заднего внутреннего колеса (R_звmin)
(рис. 77).

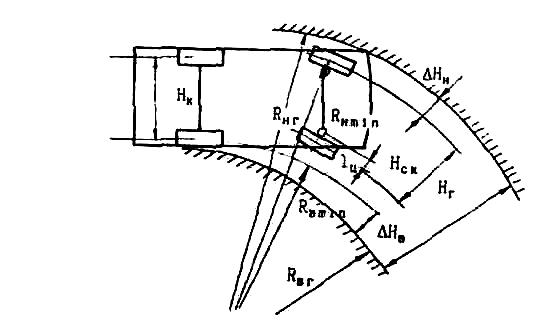
Рис. 77. Геометрические
показатели маневренности

По
своему физическому смыслу данные
показатели выражают минимальные
радиусы кривых, по которым возможно
движение переднего наружного и заднего
внутреннего колеса при совершении
автомоби­лем поворотов в предельно
стесненных условиях маневрирования.
Радиусы поворотов по следу колес можно
найти и расчетным путем по формулам:

R_нmin
=

,
(276)

R_вmin
=

.
(277)

где
_нmax,
_вmax
-максимальный угол поворота наружного
и внутреннего управляемых колес
автомобиля.

Как следует из
формул (276) и (277), радиусы поворота тем
меньше, чем больше углы поворота
управляемых колес.

Ширина
полосы движения по следу колес
(Н_ск)
– это ширина полосы, в пределах которой
размещаются колеса автотранспортного
средства в процессе его криволинейного
движения с минимальной скоростью и при
максимальном повороте управляемых
колес (рис. 77).

Ширину
указанной полосы движения можно
определить экспериментальным путем
посредством замера расстояния между
следами соответствующих колес или по
формуле:

Н_ск
= R_пнmin
– R_звmin.
(278)

Заметим,
что при уменьшении угла поворота
управляемых колес радиусы поворота по
следу колес возрастают, но ширина полосы
движения при этом уменьшается, достигая
минимума (Н_ск^min
= Н_к)
при _н
= _в
= 0, т.е. при прямолинейном движении.

Радиусы
поворота по габаритам
представляют собой расстояния от оси
поворота до траекторий движения
соответственно наиболее удаленной
(R_нг)
и наиболее близкой (R_вг)
к оси поворота точки корпуса автомобиля
при максимальном повороте управляемых
колес и движении с минимальной скоростью
(рис. 77).

R_нг
= R_пнmin
+ H_н,;
(279)

R_вг
= R_звmin
– H_в,
(280)

где
H_н,
H_в
– величина свеса корпуса автомобиля за
траекторию

движения
соответственно переднего наружного и
заднего внутреннего колеса.

Численные
значения показателей R_нг
и R_вг
определяют ширину полосы движения по
габаритам.

Ширина
полосы движения
по габаритам
(Н_г
= R_нг
– R_вг)
– это ширина полосы движения, в пределах
которой корпус автотранспортного
средства совершает поворот при
максимальном повороте управляемых
колес и движении с минимальной скоростью.

Обеспечение высокой маневренности
особенно актуально для автопоездов.
Это связано не только с их большой
габаритной длиной, но и с тем, что при
повороте траектория движения прицепа
(или полуприцепа) смещается к центру,
что ведет к увеличению габаритной ширины
полосы движения (рис. 78).

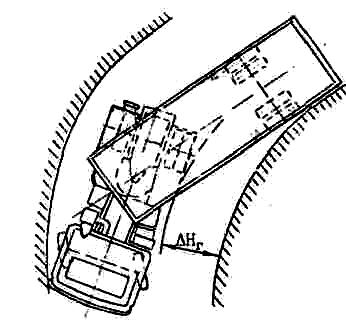
Рис. 78. Поворот
седельного автопоезда

Особенно значительно
смещение колеи у седельных автопоездов
при использовании длиннобазных
полуприцепов.

У
прицепных автопоездов значительное
увеличение габаритной ширины вызывает
удлинение дышла и базы прицепа. Однако
при одинаковой грузоподъемности такие
автопоезда гораздо маневреннее, нежели
седельные.

При
выполнении различных маневров, особенно
при установке автопоезда под погрузку
или выгрузку, либо на место хранения,
важное значение имеет так называемый
угол
горизонтальной
гибкости
().
Применительно к прицепному автопоезду
он определяет предельное отклонение
оси

дышла
прицепа от продольной оси автотягача,
а для седельного – предельное отклонение
оси полуприцепа (рис. 79).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Как видно из выражения (1), разность котангенсов
углов поворота внешнего и внутреннего управляемых колес должна быть всегда величиной
постоянной. Только при соблюдении этого условия колеса автомобиля на повороте
будут двигаться без скольжения т. е. иметь чистое качение. Поэтому часто выражение
(1) называют условием отсутствия скольжения колес на повороте.

Теоретическая (идеальная) зависимость a_н и a_в, определяемая по формуле
(1), представлена на рис. 12 (кривая 1).

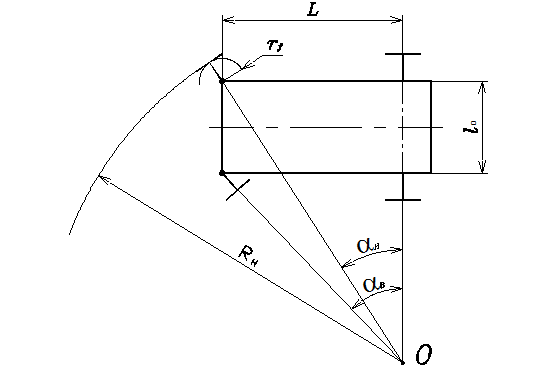
Рис. 11. Схема поворота автомобиля

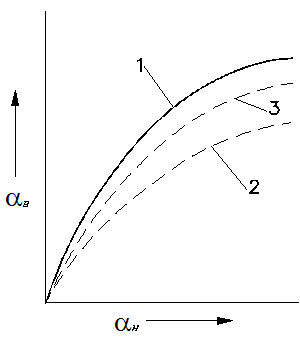
Рис. 12. Зависимость углов поворота управляемых колес:

1 – теоретическая (идеальная) зависимость; 2, 3 – зависимости,
полученные при различных конструктивных вариантах трапеции

Максимальные углы поворота управляемых колес определяется
как

;

,

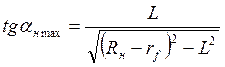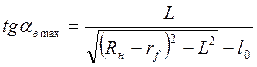где	Rн	– радиус поворота по колее переднего наружного колеса (Rн = (1,8…2,4)L – для неполноприводных автомобилей; Rн = (2,7…2,9)L – для полноприводных автомобилей);
	rf	– плечо обкатки.

Подбор параметров рулевой
трапеции (рис. 13) начинается с определения угла  наклона боковых рычагов
трапеции. Они располагаются таким образом, чтобы х = (0,7…0,8) при заднем и
х = (0,8…1) при переднем расположении попёречной тяги.

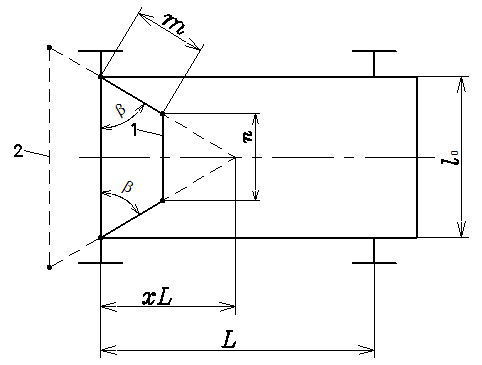
Рис.
13. Схема расположения задней (1) и передней (2) рулевых трапеций

Угол b
может быть найден как:

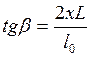
или по графикам, показанным
на рис. 14.

Для выполненных конструкций b = 66…74°,  отношение
m/n =
0,12…0,16, длина поперечной тяги определяется таким образом:

.

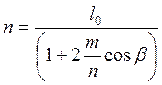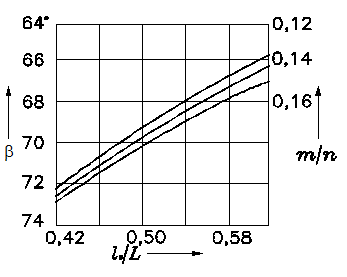
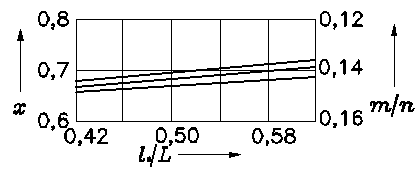
Рис. 14. Наивыгоднейшие соотношения размеров рулевой трапеции и
автомобиля

После определения предварительных размеров трапеции
проверяют правильность её кинематики, т. е. находят действительные углы поворота
колес. Эта проверка осуществляется графически следующим образом. Вычерчивается
в масштабе трапеция (рис. 15), соответствующая прямолинейному движению колес
(нейтральное положение). Из т. “А” с интервалом (примерно 5°), соответствующим углу поворота внутреннего
колеса, от  до  проводятся
лучи. Затем, циркулем из т. “А” на лучах откладываются отрезки, соответствующие
длине левой боковой тяги рулевой трапеции, и делаются засечки. Из полученных
точек циркулем откладываются расстояния, равные поперечной тяге рулевой
трапеции, и делаются засечки. А из точки “В” делаются засечки на расстоянии,
равном длине правой боковой тяги рулевой трапеции. Полученные точки соединяют и
находят положение поперечной и правой боковой тяги рулевой трапеции. Замеряя
полученные отклонения правой боковой тяги, получают углы поворота наружного
колеса a_н. Полученная
таким образом графическая зависимость  наносится
на теоретическую (идеальную) кривую (см. рис. 12, кривая 2) и, если разница
между полученными значениями и идеальными превышает 5 %, изменяются параметры m, n или b и снова, теперь уже с откорректированными
размерами, вычерчивается в масштабе рулевая трапеция и заново графически
определяются углы поворота колес a_н
и a_в и зависимость  (см. рис. 12, кривая 3). Если же в этом
случае разница между полученными значениями и идеальными превышает 5 %,
операцию повторяют.

Рис. 15. Схема графического определения действительных углов поворота
управляемых колес автомобиля

При независимой подвеске передних колес поперечную
рулевую тягу выполняют разрезной, состоящей из двух или трех звеньев (рис. 16).
Включение в рулевую трапецию каждого дополнительного звена с шарнирами
усложняет кинематическую схему и влечет за собой увеличение отклонений зависимости
между углами поворота управляемых колес от теоретической (идеальной)
зависимости . Отклонение будет меньше, если звенья
поперечной тяги располагаются на одной прямой (трапеция симметрична
относительно продольной оси автомобиля, а сошка и маятниковый рычаг
параллельны).

После определения размеров трапеции определяется общее
кинематическое передаточное число рулевого управления.

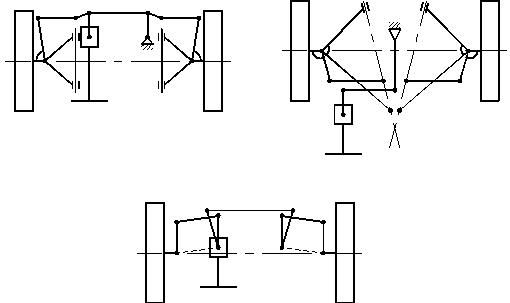
Рис. 16. Схемы разрезных рулевых трапеций при независимой подвеске
управляемых колес:

а – трехзвенная поперечная тяга (трапеция образована поворотными
рычагами); б – двухзвенная поперечная тяга (трапеция образована поворотными
рычагами); в – трехзвенная поперечная тяга (трапеция образована сошкой и
маятниковым рычагом)

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание – внизу страницы.

Угла – поворот – колесо

Cтраница 1

Углы поворота колес можно найти по формуле Виллиса, в которой вместо угловых скоростей используем пропорциональные им углы поворота.
 [1]

После этого находим результирующие углы поворота колес как сумму углов поворота в обоих этапах движения.
 [3]

Как только значение какого-либо угла поворота колеса qn превзойдет значение я, так полученная формула ( 11) теряет свой смысл, так как ошибка колеса имеет линейный или нарастающий характер изменения только в пределах половины окружности.
 [4]

Разность Э – а всегда равна углу поворота колеса zd за один цикл механизма.
 [5]

Открытая часть пропорциональна ходу штока или углу поворота ручного колеса.
 [6]

Упорные болты 6 в задней оси ограничивают углы поворота колес.
 [8]

При этом появляется и угловая скорость разворота, пропорциональная углу поворота колес.
 [9]

Момент М уз растет с увеличением скорости движения автомобиля и угла поворота колес, но лишь до начала частичного бокового проскальзывания шины.
 [11]

Под графиками изменения теоретической и фактической действующей ошибок в зависимости от угла поворота колеса построены графики дополнительных ускорений, соответствующие каждой из этих ошибок. Из этих графиков видно, что кривые изменения ошибок не очень резко отличаются между собой и максимумы их совпадают, но кривые изменения ускорений отличаются значительно. Поскольку динамические явления, возникающие при работе неточного механизма, оцениваются по величинам ускорений, то становится очевидным, что расчет динамических усилий дает отличающиеся результаты в зависимости от того, будет ли принята во внимание теоретическая или фактическая действующая ошибка.
 [12]

Углы развала передних колес, поперечного и продольного накдонов шкворней поворотных цапф и углы поворота колес измеряют переносным ручным прибором ГАРО модели 2142 для легковых и модели 2183 для грузовых автомобилей. В комплект каждого из этих приборов входят ( рис. 85) жидкостный прибор, два измерителя углов поворота колес и приспособление для облегчения поворота колес.
 [14]

Страницы:  

   1

   2

   3

   4