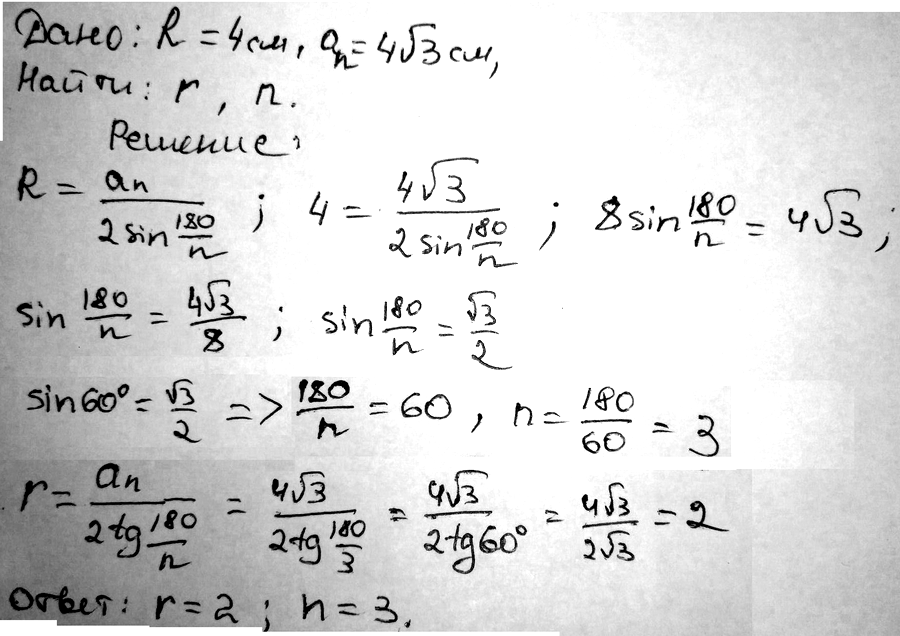Геометрия 9 Контрольная 2 (Мерзляк) с ответами. Контрольная работа по геометрии в 9 классе «Правильные многоугольники» для УМК Мерзляк, Полонский, Якир из 4-х вариантов. Методическое пособие для учителей и родителей.
Геометрия 9 класс (УМК Мерзляк)
Контрольная работа № 2
Тема: Правильные многоугольники
К-2 Вариант 1 (задания)
К-2 Вариант 2 (задания)
- Найдите углы правильного сорокапятиугольника.
- Найдите площадь круга, вписанного в правильный шестиугольник со стороной 10 см.
- Около окружности описан правильный треугольник со стороной 18 см. Найдите сторону квадрата, вписанного в эту окружность.
- Радиус окружности, вписанной в правильный многоугольник, равен 5 см, а сторона многоугольника – 10 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.
- Сторона треугольника равна 8√2 см, а прилежащие к ней углы равны 35° и 100°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.
- Углы квадрата со стороной 8 см срезали так, что получили правильный восьмиугольник. Найдите сторону образовавшегося восьмиугольника.
К-2 Вариант 3 (задания)
- Найдите углы правильного тридцатишестиугольника.
- Найдите длину окружности, описанной около правильного треугольника со стороной 9 см.
- В окружность вписан правильный шестиугольник со стороной 9 см. Найдите сторону правильного треугольника, описанного около этой окружности.
- Радиус окружности, описанной около правильного многоугольника, равен 8√2 см, а радиус вписанной в него окружности – 8 см. Найдите: 1) сторону многоугольника; 2) количество сторон многоугольника.
- Сторона треугольника равна 5 см, а прилежащие к ней углы равны 45° и 105°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.
- Углы правильного треугольника срезали так, что получили правильный шестиугольник со стороной 8 см. Найдите сторону данного треугольника.
К-2 Вариант 4 (задания)
- Найдите углы правильного тридцатиугольника.
- Найдите площадь круга, описанного около квадрата со стороной 16 см.
- Около окружности описан квадрат со стороной 36 см. Найдите сторону правильного треугольника, вписанного в эту окружность.
- Радиус окружности, вписанной в правильный многоугольник, равен 12 см, а сторона многоугольника – 8√3 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.
- Сторона треугольника равна 10√3 см, а прилежащие к ней углы равны 10° и 50°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.
- Углы квадрата срезали так, что получили правильный восьмиугольник со стороной 4 см. Найдите сторону данного квадрата.
Ответы на контрольную работу № 2
ОТВЕТЫ на Вариант 1
№ 1. Найдите углы правильного сорокаугольника.
Решение: Сумма углов многоугольника равна 180°×(n-2). Так как у правильного многоугольника все углы равны, то величину угла можно вычислить как 180°×(n-2)/n. Для п = 40 угол равен 180° × 38/40 = 171°.
ОТВЕТ: 171°.
№ 2. Найдите длину окружности, вписанной в правильный треугольник со стороной 12 см.
ОТВЕТ: 4π√3 см.
№ 3. В окружность вписан квадрат со стороной 8 см. Найдите сторону правильного шестиугольника, описанного около этой окружности.
ОТВЕТ: (8√6)/3 см.
№ 4. Радиус окружности, описанной около правильного многоугольника, равен 4 см, а сторона многоугольника – 4√3 см. Найдите: 1) радиус окружности, вписанной в многоугольник; 2) количество сторон многоугольника.
ОТВЕТ: 1) 2 см; 2) 3 стороны.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
№ 5. Сторона треугольника равна 6√3 см, а прилежащие к ней углы равны 40° и 80°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.
Решение: Третий угол = 180 – 40 – 80 = 60⁰. Вписанные углы равны половине дуг, на которые они опираются, т.е. 80⁰, 160⁰ и 120⁰.
Радиус описанной окр. R = (6√3) / (2 sin 60°) = (6√3) / (√3) = 6 см.
Длина всей окружности l = 2πR = 12π (см)
Дуги: (80/360)*12π = 8π/3 (см)
(160/360)*12π = 16π/3 (см)
(120/360)*12π = 4π (см)
ОТВЕТ: 8π/3 см, 16π/3 см, 4π см.
№ 6. Углы правильного треугольника со стороной 6 см срезали так, что получили правильный шестиугольник. Найдите сторону образовавшегося шестиугольника.
ОТВЕТ: 2 см.
Подсказка: Так как отрезанные части углов — это тоже правильные треугольники, то их боковые стороны равны стороне правильного шестиугольника. Отсюда получаем, что сторона исходного треугольника разделена на 3 части. Следовательно, сторона образовавшегося шестиугольника равна 6/3 = 2 (см).
ОТВЕТЫ на Вариант 2
№ 1. Найдите углы правильного сорокапятиугольника.
Решение: Сумма углов многоугольника равна 180°×(n-2). Так как у правильного многоугольника все углы равны, то величину угла можно вычислить как 180°×(n-2)/n. Для п = 45 угол равен 180°×43/45 = 172°.
ОТВЕТ: 172°.
№ 2. Найдите площадь круга, вписанного в правильный шестиугольник со стороной 10 см.
ОТВЕТ: 75π см2.
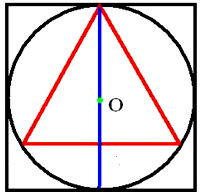
№ 3. Около окружности описан правильный треугольник со стороной 18 см. Найдите сторону квадрата, вписанного в эту окружность.
ОТВЕТ: 3√6 см.
№ 4. Радиус окружности, вписанной в правильный многоугольник, равен 5 см, а сторона многоугольника – 10 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.
Дано: r = 5 см; an = 10 см;
Найти: 1) R; 2) n – ?
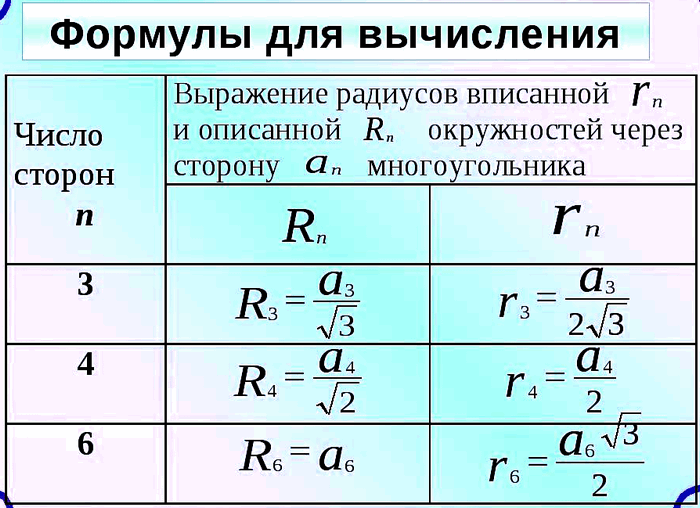
Решение: 1) an = 2r tg (180°/n)
10 = 2 • 5 • tg (180°/n) ⇒ 1 = tg (180°/n).
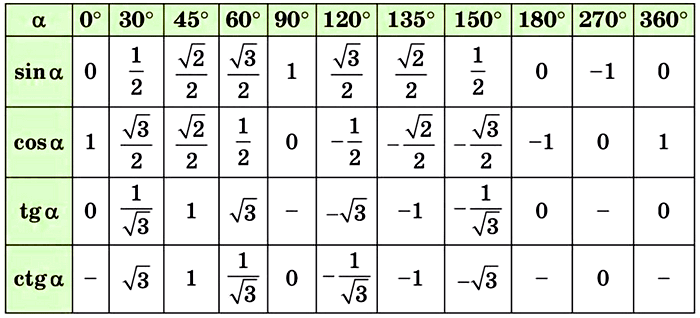
По таблице находим 1 = tg 45°
==> 180°/n = 45° ⇒ n = 4 (квадрат).
2) an = 2R sin (180°/n)
10 = 2R sin 45° ⇒ R = 5/sin45° = 5•2/√2 = 5√2 (см).
ОТВЕТ: 1) 5√2 см; 2) 4 стороны.
№ 5. Сторона треугольника равна 8√2 см, а прилежащие к ней углы равны 35° и 100°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.
Решение: Третий угол = 180 – 100 – 35 = 45⁰. Вписанные углы равны половине дуг, на которые они опираются, т.е. 90⁰, 70⁰ и 200⁰.
Радиус описанной окр. R = (8√2)/(2sin45⁰) = (8√2)/√2 = 8 (см)
Длина всей окружности l = 2πR = 16π (см)
Дуги: (90/360)*16π = 4π (см)
(70/360)*16π = 28π/9 (см)
(200/360)*16π = 80π/9 (см).
ОТВЕТ: 80π/9 см; 28π/9 см; 4π см.
№ 6. Углы квадрата со стороной 8 см срезали так, что получили правильный восьмиугольник. Найдите сторону образовавшегося восьмиугольника.
ОТВЕТ: ≈ 3,3137 см.
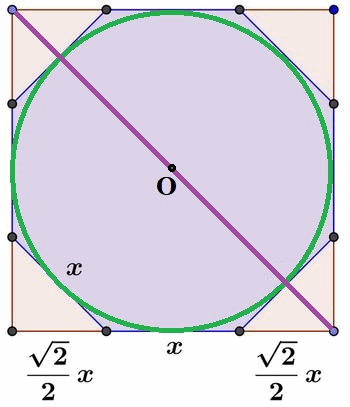
Возможный вариант решения: Радиус вписанной окружности и для квадрата и для восьмиугольника = 4 см. Диагональ квадрата = 8√2 см. Половина диагонали квадрата (расстояние из центра вписанной окружности до угла квадрата) = 4√2 см. Срезанный уголок — это равнобедренный прямоугольный треугольник, высота которого = 4√2 — 4 (половина диагонали квадрата минус радиус окружности). Гипотенуза равнобедренного прямоугольного треугольника равна удвоенной высоте к гипотенузе, это и есть сторона образовавшегося восьмиугольника
х = 2 * (4√2 — 4) = 8√2 — 8 = 3,3137 (см)
Другой вариант решения: х = 8 / (√2 + 1) = 3,3137 (см) Смотри рисунок ниже.
ОТВЕТЫ на Вариант 3
№ 1. Найдите углы правильного тридцатишестиугольника.
Решение: Сумма углов многоугольника равна 180°×(n-2). Так как у правильного многоугольника все углы равны, то величину угла можно вычислить как 180°×(n-2)/n. Для п = 36 угол равен 180°×34/36 = 170°.
ОТВЕТ: 170°.
№ 2. Найдите длину окружности, описанной около правильного треугольника со стороной 9 см.
ОТВЕТ: 6π√3 см.
№ 3. В окружность вписан правильный шестиугольник со стороной 9 см. Найдите сторону правильного треугольника, описанного около этой окружности.
ОТВЕТ: 18√3 см.
№ 4. Радиус окружности, описанной около правильного многоугольника, равен 8√2 см, а радиус вписанной в него окружности – 8 см. Найдите: 1) сторону многоугольника; 2) количество сторон многоугольника.
Дано: R = 8√2 см; r = 8 см;
Найти: 1) an; 2) n – ?
Решение: 1) r = R cos (180°/n)
8 = 8√2 cos (180°/n) ⇒ cos (180°/n) = 8/8√2 = √2/2.
По таблице находим √2/2 = cos 45°
⇒ 180°/n = 45° ⇒ n = 4 (квадрат).
2) an = 2R sin (180°/n) = 2 • 8√2 • sin 45° = 16√2 • √2/2 = 16 (см).
ОТВЕТ: 1) 16 см; 2) 4 стороны.
№ 5. Сторона треугольника равна 5 см, а прилежащие к ней углы равны 45° и 105°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.
Решение: Третий угол = 180 – 45 – 105 = 30⁰. Вписанные углы равны половине дуг, на которые они опираются, т.е. 90⁰, 210⁰ и 60⁰.
Радиус описанной окр. R = 5 / (2 sin 30°) = 5 / (2 • 1/2) = 5 см.
Длина всей окружности l = 2πR = 10π (см)
Дуги: (90/360)*10π = 2,5π (см)
(210/360)*10π = 35π/6 (см)
(60/360)*10π = 5π/3 (см)
ОТВЕТ: 2,5π см; 35π/6 см; 5π/3 см.
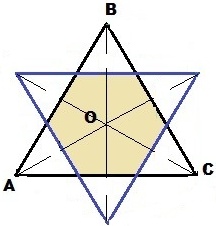
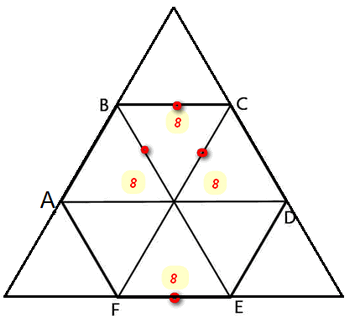
№ 6. Углы правильного треугольника срезали так, что получили правильный шестиугольник со стороной 8 см. Найдите сторону данного треугольника.
ОТВЕТ: 24 см.
Указание к решению: Проведем диагонали правильного шестиугольника ABCDEF, получим шесть РАВНОСТОРОННИХ треугольников (на чертеже отмечено). Диагональ правильного шестиугольника в два раза больше его стороны, т.е. 16 см. Срезанные углы треугольника тоже равносторонние треугольники. Следовательно сторона первоначального правильного треугольника равна 8 * 3 = 24 (см).
ОТВЕТЫ на Вариант 4
№ 1. Найдите углы правильного тридцатиугольника.
Решение: Сумма углов многоугольника равна 180°×(n-2). Так как у правильного многоугольника все углы равны, то величину угла можно вычислить как 180°×(n-2)/n. Для п = 30 угол равен 180°×28/30 = 168°.
ОТВЕТ: 168°.
№ 2. Найдите площадь круга, описанного около квадрата со стороной 16 см.
Решение: S = R2π. R = d/2 = a√2/2.
S = (16√2/2)2π = (8√2)2π = 82*2π = 2*64π = 128π (см2)
ОТВЕТ: 128π см2.
№ 3. Около окружности описан квадрат со стороной 36 см. Найдите сторону правильного треугольника, вписанного в эту окружность.
Решение: Радиус вписанной в квадрат окружности R = 36 : 2 = 18(см). Это же радиус описанной окружности около треугольника. Сторону правильного треугольника находим по формуле а = R√3 = 18√3 (см).
ОТВЕТ: 18√3 см.
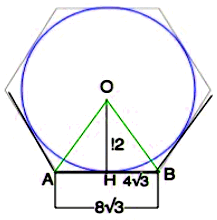
№ 4. Радиус окружности, вписанной в правильный многоугольник, равен 12 см, а сторона многоугольника – 8√3 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.
Решение: Центр вписанной в угол окружности лежит на биссектрисе.
Окружности, вписанной в правильный многоугольник — в точке пересечения биссектрис его углов. На рисунке АВ — сторона, АО = ВО — биссектрисы углов правильного многоугольника. ОН — радиус вписанной окружности,
tg∠ОВН = ОН : ВН = √3.
Следовательно, ∠ОВН = 60°, угол многоугольника 120°, смежный с ним внешний угол равен 60°. Сумма внешних углов многоугольника 360°. Количество внешних углов, взятых по одному при вершинах, равно числу сторон многоугольника.
Число сторон 360° : 60° = 6.
Радиус описанной около правильного шестиугольника окружности равен его стороне R6 = a6 = 8√3.
ОТВЕТ: 1) 8√3 см; 2) 6 сторон.
№ 5. Сторона треугольника равна 10√3 см, а прилежащие к ней углы равны 10° и 50°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.
Решение: Третий угол = 180 – 10 – 50 = 120⁰. Вписанные углы равны половине дуг, на которые они опираются, т.е. 20⁰, 100⁰ и 240⁰.
Радиус описанной окр. R = 10√3 / (2 sin 120°) = 10√3 / √3 = 10 см.
Длина всей окружности l = 2πR = 20π (см)
Дуги: (20/360) • 20π = 10π/9 (см)
(100/360) • 20π = 50π/9 (см)
(240/360) • 20π = 40π/3 (см).
ОТВЕТ: 10π/9 см; 50π/9 см; 40π/3 см.
№ 6. Углы квадрата срезали так, что получили правильный восьмиугольник со стороной 4 см. Найдите сторону данного квадрата.
ОТВЕТ: 4 (√2 + 1) ≈ 9,67 см.
Вы смотрели: Геометрия 9 Контрольная 2 (Мерзляк). Контрольная работа по геометрии в 9 классе «Решение треугольников» для УМК Мерзляк, Полонский, Якир в 4-х вариантах. Методическое пособие.
Смотреть аналогичную контрольную № 2 с решениями (2 варианта)
Вернуться к Списку контрольных работ из Методички (по 4 варианта)
Цитаты из пособия «Геометрия 9 класс. Методическое пособие / Е.В. Буцко и др.» использованы в учебных целях.
Контрольная работа № 2 по теме “Правильные многоугольники” (9 класс, Мерзляк А.Г. и др.)
Даны четыре варианта контрольной работы, удобно вносить изменения и печатать.
Просмотр содержимого документа
«Контрольная работа № 2 по теме “Правильные многоугольники” (9 класс, Мерзляк А.Г. и др.)»
Контрольная работа № 2 по теме «Правильные многоугольники»
1. Найдите углы правильного сорокаугольника.
2. Найдите длину окружности, вписанной в правильный треугольник со стороной 12 см.
3. В окружность вписан квадрат со стороной 8 см. Найдите сторону правильного шестиугольника, описанного около этой окружности.
4. Радиус окружности, описанной около правильного многоугольника, равен 4 см, а сторона многоугольника — 4 
см. Найдите: 1) радиус окружности, вписанной в многоугольник; 2) количество сторон многоугольника.
5. Сторона треугольника равна 6 см, а прилежащие к ней углы равны 40° и 80°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.
6. Углы правильного треугольника со стороной 6 см срезали так, что получили правильный шестиугольник. Найдите сторону образовавшегося шестиугольника.
1. Найдите углы правильного сорокапятиугольника.
2. Найдите площадь круга, вписанного в правильный шестиугольник со стороной 10 см.
3. Около окружности описан правильный треугольник со стороной 18 см. Найдите сторону квадрата, вписанного в эту окружность.
4. Радиус окружности, вписанной в правильный многоугольник, равен 5 см, а сторона многоугольника — 10 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.
5. Сторона треугольника равна 8 
см, а прилежащие к ней углы равны 35° и 100°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.
6. Углы квадрата со стороной 8 см срезали так, что получили правильный восьмиугольник. Найдите сторону образовавшегося восьмиугольника.
1. Найдите углы правильного тридцатишестиугольника.
2. Найдите длину окружности, описанной около правильного треугольника со стороной 9 см.
3. В окружность вписан правильный шестиугольник со стороной 9 см. Найдите сторону правильного треугольника, описанного около этой окружности.
4. Радиус окружности, описанной около правильного многоугольника, равен 8 см, а радиус вписанной в него окружности — 8 см. Найдите: 1) сторону многоугольника; 2) количество сторон многоугольника. 5. Сторона треугольника равна 5 см, а прилежащие к ней углы равны 45° и 105°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.
6. Углы правильного треугольника срезали так, что получили правильный шестиугольник со стороной 8 см. Найдите сторону данного треугольника.
1. Найдите углы правильного тридцатиугольника.
2. Найдите площадь круга, описанного около квадрата со стороной 16 см.
3. Около окружности описан квадрат со стороной 36 см. Найдите сторону правильного треугольника, вписанного в эту окружность.
4. Радиус окружности, вписанной в правильный многоугольник, равен 12 см, а сторона многоугольника — 8 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.
5. Сторона треугольника равна 10 см, а прилежащие к ней углы равны 10° и 50°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.
6. Углы квадрата срезали так, что получили правильный восьмиугольник со стороной 4 см. Найдите сторону данного квадрата.
ГДЗ по геометрии 9 класс Мерзляк дидактические материалы контрольная работа вариант №1 – 2
Авторы: Мерзляк А.Г. , Полонский В.Б. , Рабинович Е.М. , Якир М.С. .
Издательства: Просвещение, Вентана-граф 2017-2021
Тип: Дидактические материалы, Алгоритм успеха
Подробный решебник (ГДЗ) по Геометрии за 9 (девятый) класс дидактические материалы – готовый ответ контрольная работа вариант №1 – 2. Авторы учебника: Мерзляк, Полонский, Рабинович, Якир. Издательство: Вентана-граф 2017-2021.
Похожие ГДЗ
ГДЗ учебник геометрия 9 класс А.Г. Мерзляк
ГДЗ Самостоятельные и контрольные работы геометрия 9 класс Мерзляк А.Г. углубленный уровень
ГДЗ учебник геометрия 9 класс Мерзляк А.Г. углубленный уровень
ГДЗ Математические диктанты, Контрольные работы (Методическое пособие) геометрия 9 класс Буцко Е.В.
ГДЗ Рабочая тетрадь геометрия 9 класс Мерзляк А.Г.
1. Найдите углы правильного 60-угольника. 2. Найдите длину окружности, описанной около квадрата со стороной 8 см. 3. Сторона правильного треугольника, вписанного в окружность, равна 5√3 см. Найдите сторону правильного шестиугольника, описанного около этой окружности. Контрольные работы 4. Радиус окружности, описанной около правильного многоугольника, равен 2√3 см, а радиус окружности, вписанной в него, — 3 см. Найдите: 1) сторону многоугольника; 2) количество сторон многоугольника. 5. Сторона треугольника равна 4ч/2 см, а прилежащие к ней углы равны 80° и 55°. Найдите длины дуг, на которые делят окружность, описанную около треугольника, его вершины. 6. В правильном шестиугольнике ABCDEF соединили середины сторон АВ, CD и EF. Найдите сторону правильного треугольника, образовавшегося при этом, если АВ = а.
Найдите углы 36-угольника, если известно, что все они равны.
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,279
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,949
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
[spoiler title=”источники:”]
http://megaresheba.ru/gdz/geometriya/9-klass/didakticheskie-materiali-merzlyak/1-kr-2
http://www.soloby.ru/702920/%D0%BD%D0%B0%D0%B9%D0%B4%D0%B8%D1%82%D0%B5-%D1%83%D0%B3%D0%BB%D1%8B-36-%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%B0-%D0%B5%D1%81%D0%BB%D0%B8-%D0%B8%D0%B7%D0%B2%D0%B5%D1%81%D1%82%D0%BD%D0%BE-%D1%87%D1%82%D0%BE-%D0%B2%D1%81%D0%B5-%D0%BE%D0%BD%D0%B8-%D1%80%D0%B0%D0%B2%D0%BD%D1%8B
[/spoiler]
ntunoul24
Вопрос по геометрии:
Найдите углы правильного 36 угольника
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
gurtolesthab
Α=180(n-2)/n
α=180(36-2)/36=170°
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,653 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,926 -
разное
16,901
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Правильный многоугольник
Угол
Многоугольник представляет плоскую замкнутую геометрическую фигуру, у которой может быть три, четыре и более сторон, пересекающихся в трех, четырех и более точках, называющихся вершинами. Называются они в соответствии с количеством сторон или вершин. Например, многоугольник с пятью сторонами называется пятиугольник, с шестью — шестиугольник и т. д. Правильным называют многоугольник с равными углами и сторонами. Например, квадрат. Если в задании известна одна из этих величин, несложно узнать остальные. В равностороннем n-угольнике, сумма всех углов рассчитывается как:
(n — 2) 180°
а сумма всех его сторон будет равна:
P = na
P — периметр;
а — сторона;
n — количество сторон.
Определяем угол правильного n-угольника:
А = (n — 2) / n х 180°
Если в задании имеется радиус вписанной окружности ®, тогда сторону (а) правильного n-угольника определяет по формуле:
a = 2r · tg · 180° / n
a = 2r · tg · π / n
Если задан радиус ® описанной окружности, то находим сторону по формуле:
a = 2 R · sin · 180° / n
a = 2 R · sin · π / n
Соответственно, если известна сторона правильного n-угольника, находим r вписанной окружности:
r = a / (2 tg · 180° / n)
r = a / (2 tg · π / n)
и R описанной окружности n-угольника по его стороне:
R= a / (2 sin · 180° / n)
R= a / (2 sin · π / n)
Онлайн калькулятор поможет вам быстро и правильно определить число и величину сторон правильного многоугольника, размер его внешнего и внутреннего углов, а также другие показатели.
