Как найти углы при основании равнобедренной трапеции

Как найти углы при основании равнобедренной трапеции

Утверждение.

(Свойство равнобедренной трапеции)

Углы при основании равнобедренной трапеции равны.

uglyi pri osnovanii ravnobedrennoy trapetsii

    [angle A = angle D]

    [angle B = angle C]

uglyi pri osnovanii ravnobedrennoy trapetsii ravnyiДано: ABCD — трапеция,

AD ∥ BC,AB=CD.

Доказать:∠A=∠D, ∠B=∠C.

Доказательство:

uglyi ravnobedrennoy trapetsii1) Проведем из вершин тупых углов высоты BF и CK:

    [BF bot AD,BF bot BC,]

    [CK bot AD,CK bot BC.]

2) Рассмотрим треугольники ABF и DCK.

∠AFB=90º, ∠DKC=90º (так как BF и CK — высоты трапеции).

AB=CD (по условию),

BF=CK (как высоты трапеции).

Отсюда следует, что треугольники ABF и DCK равны (по катету и гипотенузе).

3) Из равенства треугольников следует равенство соответствующих углов: ∠A=∠D.

4) ∠A+∠ABC=180º (как внутренние односторонние при AD ∥ BC и секущей AB).

Отсюда, ∠ABC=180º-∠A.

Аналогично, ∠D+∠DCB — внутренние односторонние при AD ∥ BC и секущей CD, и ∠DCB=180º-∠D.

Так как ∠A=∠D, то и ∠ABC=∠DCB.

Что и требовалось доказать.

Источник

Трапеция —  геометрическая фигура представляет собой выпуклый четырехугольник с параллельными
противоположными сторонами. Они называются основаниями. Две другие стороны — боковые.
Трапеция, у которой они одинакового размера, называется равнобедренной. Если одна из боковых сторон
образует у основания угол в 90 градусов-прямоугольной.

Прямая линия, проведенная от одного основания
к другому, именуется высотой трапеции. Величина ее высчитывается делением суммы оснований на 2.
Диагонали — это отрезки, соединяющие противоположные углы фигуры. У равнобедренной трапеции
они равны по длине. Средняя линия-прямая, делящая пополам боковые стороны.

  • Угол трапеции при основании через высоту и прилегающую
    боковую сторону
  • Угол трапеции через нижнее основание, боковую сторону и
    диагональ
  • Угол равнобедренной трапеции через нижнее основание,
    среднию линию и боковую сторону
  • Угол равнобедренной трапеции через среднию линию, верхнее
    основание и боковую сторону
  • Острый угол при нижнем основании прямоугольной трапеции
    через высоту и два основания
  • Острый угол при нижнем основании прямоугольной трапеции
    через два основания и боковую сторону

Угол трапеции при основании через высоту и прилегающую боковую сторону

Рис 1

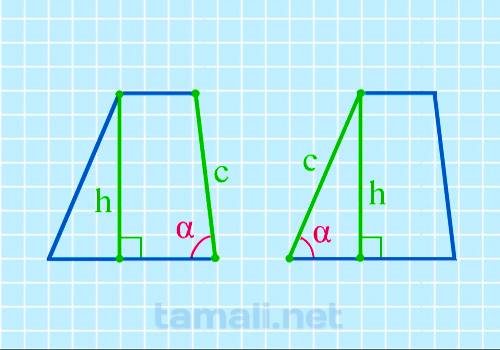
Введем обозначения: h-высота, с — боковая сторона. Угол трапеции α при основании вычисляется с
помощью формулы

sin α = h/с

где: h — высота трапеции, c — боковая сторона.

Цифр после
запятой:

Результат в:

Пример. Заменим буквенные обозначения условными цифрами. Пример: если высота равна
9см, боковая сторона-11см, получим: sin α = 9 / 11 = 0,818 , отсюда α =
55º. Указанное значение находим в таблице синусов. Данный показатель синуса угла соответствует
величине 55 градусов.

Через нижнее основание, среднию линию и боковую сторону в равнобедренной трапеции

Рис 3

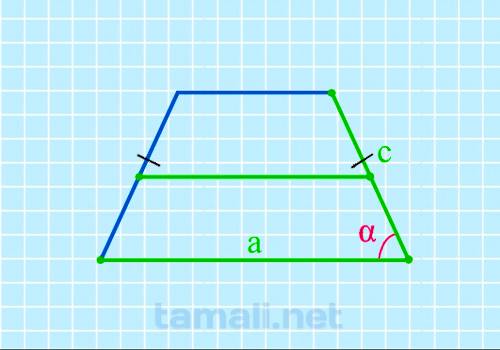
Угол равнобедренной трапеции через нижнее основание, среднюю линию и боковую сторону находится по
формуле:

cos α = (2a-2m) / 2c

где а — нижнее основание, m — средняя линия, с — боковая сторона.

Цифр после
запятой:

Результат в:

Пример.Заменим буквы условными цифровыми значениями. Если нижнее основание равно 8
см, средняя линия-6, а боковая сторона-4,8 см, то косинус угла равен 0,41666, что соответствует 65
градусам. cos α = (2 * 8 — 2 * 6) / 2 * 4,8 = 0, 41666, отсюда α =
65º. Равнобедренная трапеция — геометрическая фигура с нижними острыми углами. Это ее
особенность.

Угол трапеции, зная размер нижнего основания, боковой стороны и диагонали

Рис 2

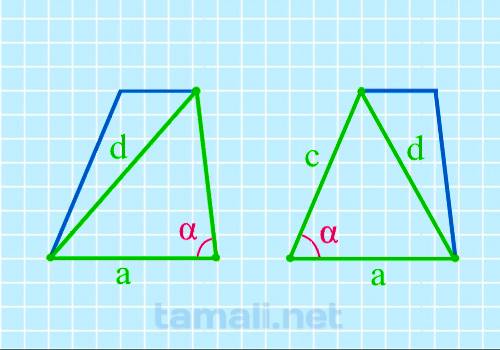
Если известны эти величины, воспользуемся формулой:

cos α= (a²+c²-d²) / 2ac

где а-нижнее основание, d-диагональ, с-боковая сторона.

Цифр после
запятой:

Результат в:

Пример. При условной величине нижнего основания 4 см, диагонали — 5.7 см,
боковой стороны — 4,4 см косинус равняется 0,081534, что соответствует углу 85 градусов по
таблице функций. cos α= (4² + 4,4² — 5,7²) / 2*4*4,4 = 0,081534,
отсюда α = 85º.

Через среднюю линию, верхнее основание и боковую сторону в равнобедренной трапеции

Рис 4

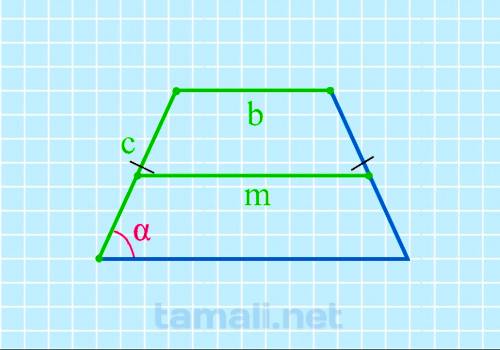
Нахождение угла равнобедренной трапеции через среднюю линию, верхнее основание и боковую сторону
выполняется по предложенной формуле:

cos α = (2m-2b) / 2c

где m — средняя линия, b — верхнее основание, c — боковая сторона.

Цифр после
запятой:

Результат в:

Пример. Введем условные цифровые значения. Допустим, что у равнобедренной трапеции
верхнее основание равно 4 см, средняя линия-6, боковая сторона-4 см. Косинус составляет 0,5.
Значение соответствует 60 градусам по таблице Брадиса. cos α = (2 * 6 — 2 * 4) / 2 * 4 = 0,5,
отсюда α = 60º

Вычисление острого угла при нижнем основании, если известны величины обоих оснований и боковой
стороны в прямоугольной трапеции

Рис 6

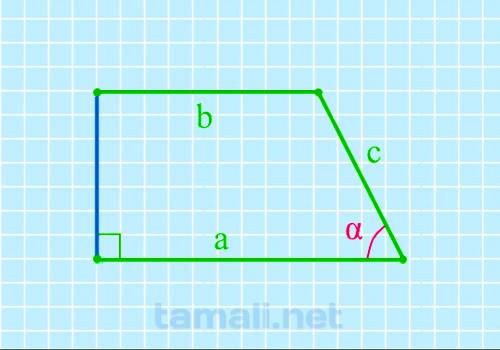
Находится по формуле

cos α = (a — b) / c

где a,b — основания, c — боковая сторона.

Цифр после
запятой:

Результат в:

Пример. Если буквенные выражения заменить условными цифровыми, получится наглядный
пример вычисления. Допустим, длина нижнего основания а 8 см, верхнего b-5,8 см, размер боковой
стороны с-4,8. Подставив в формулу цифровые значения, получим итог: косинус равен 0,45833.
Сравниваем показатель с таблицей вычисления Брадиса: он соответствует углу 63 градуса. cos α=(8 — 5,8) / 4,8 = 0,45833, отсюда α = 63º

Острый угол при нижнем основании, зная высоту и размеры двух оснований прямоугольной трапеции

Рис 5

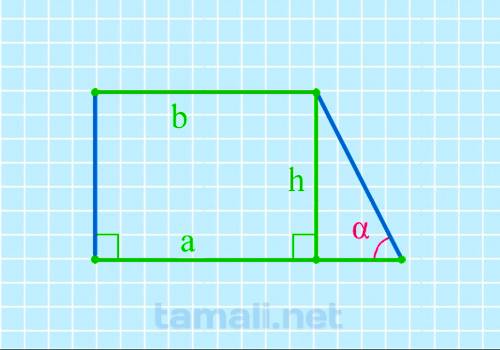
При известных указанных величинах воспользуемся следующей формулой:

tg(α) = h / (a-b)

где h — высота, a,b — верхнее и нижнее основания.

Цифр после
запятой:

Результат в:

Пример. Введя условные цифровые значения h = 15, a = 11, b = 10 получим tg(α) = 15 / (11-10) = 15. При вычислении получим значение тангенса: 15.
По таблице функций показатель соответствует 86 градусам.

Следует знать несколько закономерностей данной геометрической конструкции. У трапеции четыре угла,
общая сумма которых составляет 360 градусов.

Равнобедренная отличается двумя равными острыми, прилегающими к нижнему основанию, и тупыми
одинаковой величины-к верхнему. У прямоугольной трапеции два угла по 90 градусов, другие —
острый и тупой. Если он прилегает к нижнему основанию, величина такого угла определяется делением
высоты на разность между нижним и верхним основаниями. Угол трапеции при основании равен отношению
высоты к боковой стороне.

Источник

chet

   Углы равнобедренной трапеции. Здравствуйте! В этой статье речь пойдёт о решении задач с трапецией. Данная группа заданий входит в состав экзамена, задачки простые. Будем вычислять углы трапеции, основания и высоты. Решение ряда задач сводится к решению прямоугольного треугольника, как говориться: куда мы без теоремы Пифагора, синуса и косинуса?

Работать будем с равнобедренной трапецией. У неё равны боковые стороны и углы при основаниях. О трапеции есть статья на блоге, посмотрите.

1

Отметим небольшой и важный нюанс, который в процессе решения самих заданий подробно расписывать не будем. Посмотрите, если у нас дано два основания, то большее основание высотами, опущенными к нему, разбивается на три отрезка – один равен меньшему основанию (это противолежащие стороны прямоугольника), два других равны друг другу (это катеты равных прямоугольных треугольников):

2

Простой пример: дано два основания равнобедренной трапеции 25 и 65. Большее основание разбивается на отрезки следующим образом:

3

*И ещё! В задачах не введены буквенные обозначения. Это сделано умышленно, чтобы не перегружать решение алгебраическими изысками. Согласен, что это математически неграмотно, но цель донести суть. А обозначения вершин и прочих элементов вы всегда можете сделать сами и записать математически корректное решение.

Рассмотрим задачи:

zadacha

27439. Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.

Для того чтобы найти угол необходимо построить высоты. На эскизе обозначим данные в условии величины. Нижнее основание равно 65, высотами оно разбивается на отрезки 7, 51 и 7:

4

В прямоугольном треугольнике нам известна гипотенуза и катет, можем найти второй катет (высоту трапеции) и далее уже вычислить синус угла.

По теореме Пифагора указанный катет равен:

5

Таким образом:

6

Ответ: 0,96

zadacha

27440. Основания равнобедренной трапеции равны 43 и 73. Косинус острого угла трапеции равен 5/7. Найдите боковую сторону.

Построим высоты и отметим данные в условии величины, нижнее основание разбивается на отрезки 15, 43 и 15:

7

Ответ: 21

zadacha

27441. Большее основание равнобедренной трапеции равно 34. Боковая сторона равна 14. Синус острого угла равен (2√10)/7. Найдите меньшее основание.

Построим высоты. Для того чтобы найти меньшее основание нам необходимо найти чему равен отрезок являющийся катетом в прямоугольном треугольнике (обозначен синим):

8

Можем вычислить высоту  трапеции, а затем найти катет:

9

По теореме Пифагора вычисляем катет:

10

Таким образом, меньшее основание равно:

11

Ответ: 22

zadacha

27442. Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен 5/11. Найдите высоту трапеции.

Построим высоты и отметим данные в условии величины. Нижнее  основание разбивается на отрезки:

1010

Что делать? Выражаем тангенс известного нам угла при основании в прямоугольном треугольнике:

1011

Ответ: 10

zadacha

27443. Меньшее основание равнобедренной трапеции равно 23. Высота трапеции равна 39. Тангенс острого угла равен 13/8. Найдите большее основание.

Строим высоты и вычисляем чему равен катет:

12

Таким образом большее основание будет равно:

13

Ответ: 71

zadacha

27444. Основания равнобедренной трапеции равны 17 и 87. Высота трапеции равна 14. Найдите тангенс острого угла.

Строим высоты и отмечаем известные величины на эскизе. Нижнее основание разбивается на отрезки 35, 17, 35:

14

По определению тангенса:

15

Ответ: 0,4

zadacha

77152. Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону.

Построим эскиз, построим высоты и отметим известные величины, большее основание разбивается на отрезки 3, 6 и 3:

16

Выразим гипотенузу обозначенную как х через косинус:

17

Из основного тригонометрического тождества найдём cosα

18

Таким образом:

19

Ответ: 5

zadacha

27818. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 500? Ответ дайте в градусах.

20

Из курса геометрии нам известно, что если имеем две параллельные прямые и секущую, что сумма внутренних односторонних углов равна 1800.  В нашем случае это

21

C условии сказано, что разность противолежащих углов равна 500, то есть

22

Так как у равнобедренной трапеции углы  при основании равны, то есть угол А равен углу В, то можем записать

23

Имеем два уравнения с двумя  неизвестными, можем решить систему:

24

*Конечно, эту задачу можно было легко решить просто перебирая пары углов )

zadacha

27833. В равнобедренной трапеции большее основание равно 25, боковая сторона равна 10, угол между ними 600. Найдите меньшее основание.

25

Построим высоты DE и CF:

27

Меньшее основание равно отрезку EF, так как DC и EF это противолежащие стороны прямоугольника. Отрезок EF мы можем найти если вычислим АЕ. Выразим этот катет прямоугольного треугольника ADE через функцию косинуса:

26

Так как AE=FB=5, то EF=25–5–5=15. Следовательно и DC=15.

Ответ: 15

zadacha

27837. Основания равнобедренной трапеции равны 15 и 9, один из углов равен 450. Найдите высоту трапеции.

28

Из точек D и C опустим две высоты:

29

Как уже сказано выше они разбивают большее основание на три отрезка: один равен меньшему основанию, два других равны друг другу.

В данном случае они равны 3, 9 и 3 (в сумме 15). Кроме того, отметим что высотами отсекаются прямоугольные треугольники, причём они являются равнобедренными, так как углы при основании равны по 450. Отсюда следует, что высота трапеции будет равна 3.

Ответ: 3

На этом всё! Успеха вам!

С уважением, Александр.

P.S: Расскажите о сайте в социальных сетях!

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 12 декабря 2021 года; проверки требуют 4 правки.

Равнобедренная трапеция
Isosceles trapezoid.svg
Тип четырёхугольник, трапеция
Рёбра 4
Вид симметрии Dih2, [ ], (*), порядок 2
Двойственный многоугольник дельтоид
Свойства
выпуклый, вписанный

В евклидовой геометрии равнобедренная трапеция — это выпуклый четырёхугольник с осью симметрии, проходящей через середины двух противоположных сторон. Этот четырёхугольник является частным случаем трапеций. В любой равнобедренной трапеции две противоположные стороны (основания) параллельны, а две другие стороны (боковые) имеют одинаковые длины (свойство, которому удовлетворяет также параллелограмм). Диагонали также имеют одинаковые длины. Углы при каждом основании равны и углы при разных основаниях являются смежными (в сумме дающие 180º).

Специальные случаи[править | править код]

Прямоугольники и квадраты обычно рассматриваются как специальные случаи равнобедренных трапеций, хотя в некоторых источниках они таковыми не считаются.

Другим специальным случаем является трапеция с 3 равными сторонами. В англоязычной литературе её называют trilateral trapezoid (трёхсторонняя трапеция) [1], trisosceles trapezoid (триравнобедренная трапеция) [2] или, реже, symtra [3]. Такую трапецию можно рассматривать как отсечение 4 последовательных вершин от правильного многоугольника, имеющего 5 или более сторон.

Самопересечения[править | править код]

Любой несамопересекающийся четырёхугольник с единственной осью симметрии должен быть либо равнобедренной трапецией, либо дельтоидом[3]. Однако, если разрешить самопересечение, множество симметричных четырёхугольников нужно расширить включением в него самопересекающиеся равнобедренные трапеции, в которых пересекающиеся стороны равны, а две другие стороны параллельны, и антипараллелограммы, у которых противоположные стороны имеют равные длины.

У любого антипараллелограмма выпуклая оболочка является равнобедренной трапецией и антипараллелограмм может быть получен из диагоналей равнобедренной трапеции[4].

Isosceles trapezoid example.png Crossed isosceles trapezoid.png Antiparallelogram.svg
Выпуклая равнобедренная
трапеция 		Самопересекающаяся
равнобедренная трапеция 		Антипараллелограмм

Свойства[править | править код]

Если четырёхугольник является трапецией, не обязательно проверять, равны ли боковые стороны (и недостаточно, поскольку ромбы, являющиеся специальными случаями трапеций с боковыми сторонами равной длины, но у него нет осевой симметрии через середины оснований). Любое из следующих свойств выделяет равнобедренную трапецию от других трапеций:

  • Диагонали имеют одинаковую длину.
  • Углы при основании равны.
  • Отрезок, соединяющий середины параллельных сторон, перпендикулярен им.
  • Противоположные углы дополнительны (до 180º), из чего, в свою очередь, следует, что равнобедренные трапеции являются вписанными четырёхугольниками.
  • Диагонали делятся точкой пересечения на попарно равные отрезки. В терминах рисунка ниже, AE = DE, BE = CE (и AE ≠ CE, если хотят исключить прямоугольники).

Если прямоугольники включаются в класс трапеций, то можно определить равнобедренную трапецию как “вписанный четырёхугольник с равными диагоналями” [5], как “вписанный четырёхугольник с парой параллельных сторон”, или как “выпуклый четырёхугольник с осью симметрии, проходящей через середины противоположных сторон”.

Углы[править | править код]

В равнобедренной трапеции углы при основаниях попарно равны. На рисунке ниже углы ∠ABC и ∠DCB являются одинаковыми тупыми углами, а углы ∠BAD и ∠CDA являются одинаковыми острыми углами.

Поскольку прямые AD и BC параллельны, углы, принадлежащие противоположным основаниям, являются дополнительными, то есть ∠ABC + ∠BAD = 180°.

Диагонали и высота[править | править код]

Другая равнобедренная трапеция.

Диагонали равнобедренной трапеции равны. То есть любая равнобедренная трапеция является равнодиагональным четырёхугольником. Однако диагонали равнобедренной трапеции делятся в одной и той же пропорции. На рисунке диагонали AC и BD имеют одинаковую длину (AC = BD) и делят друг друга на отрезки той же длины (AE = DE и BE = CE).

Отношение, в котором делятся диагонали, равно отношению длин параллельных сторон, то есть

{displaystyle {frac {AE}{EC}}={frac {DE}{EB}}={frac {AD}{BC}}.}

Длина каждой диагонали, согласно следствию из теоремы Птолемея, задаётся формулой

{displaystyle p={sqrt {ab+c^{2}}}},

где a и b — длины параллельных сторон AD и BC, а c — длина каждой боковой стороны AB и CD.

Высота, согласно теореме Пифагора, задаётся формулой

{displaystyle h={sqrt {p^{2}-left({frac {a+b}{2}}right)^{2}}}={tfrac {1}{2}}{sqrt {4c^{2}-(a-b)^{2}}}.}

Расстояние от точки E до основания AD задаётся формулой

{displaystyle d={frac {ah}{a+b}}},

где a и b — длины оснований AD и BC, а h — высота трапеции.

Площадь[править | править код]

Площадь равнобедренной (а также любой) трапеции равна половине произведения суммы оснований на высоту. На рисунке, если мы примем AD = a, BC = b, а высота h равна длине отрезка между прямыми AD и BC (перпендикулярного им), то площадь K задаётся формулой:

{displaystyle K={frac {h}{2}}left(a+bright).}

Если вместо высоты трапеции известны длины боковых сторон AB =CD = c, то площадь можно вычислить по формуле Брахмагупты площади вписанных четырёхугольников. Равенство двух боковых сторон упрощает формулу до

{displaystyle K={sqrt {(s-a)(s-b)(s-c)^{2}}},}

где {displaystyle s={tfrac {1}{2}}(a+b+2c)} — полупериметр трапеции. Эта формула аналогична формуле Герона вычисления площади треугольника. Эту же формулу можно переписать в виде

{displaystyle K={frac {1}{4}}{sqrt {(a+b)^{2}(a-b+2c)(b-a+2c)}}.}

Радиус описанной окружности[править | править код]

Радиус описанной окружности задаётся формулой[6]

{displaystyle R=c{sqrt {frac {ab+c^{2}}{4c^{2}-(a-b)^{2}}}}.}

Для прямоугольника, в котором a = b, формула упрощается до {displaystyle R={tfrac {1}{2}}{sqrt {a^{2}+c^{2}}}}.

См. также[править | править код]

  • Равнобедренная описанная трапеция

Литература[править | править код]

  • George Bruce Halsted. Elementary Synthetic Geometry. — J. Wiley & sons, 1896..
  • William Dwight Whitney, Benjamin Eli Smith. The Century Dictionary and Cyclopedia. — The Century co., 1911..

Примечания[править | править код]

  1. ↑ Michael de Villiers, Hierarchical Quadrilateral Tree [1] Архивная копия от 22 декабря 2014 на Wayback Machine
  2. ↑ isosceles trapezoid. Дата обращения: 25 сентября 2016. Архивировано 26 августа 2016 года.
  3. ↑ 1 2 Halsted, 1896, с. 49–53.
  4. ↑ Whitney, Smith, 1911, с. 1547.
  5. ↑ Mzone.mweb.co.za. Дата обращения: 25 сентября 2016. Архивировано 19 июля 2011 года.
  6. ↑ Trapezoid at Math24.net: Formulas and Tables [2] Архивная копия от 28 июня 2018 на Wayback Machine Accessed 1 July 2014.

Ссылки[править | править код]

  • Some engineering formulas involving isosceles trapezoids
Источник

3. Геометрия на плоскости (планиметрия). Часть I


1. Вспоминай формулы по каждой теме


2. Решай новые задачи каждый день


3. Вдумчиво разбирай решения

Признаки и свойства равнобедренной трапеции

(blacktriangleright) Равнобедренная трапеция – трапеция, у которой боковые стороны равны.

Свойства равнобедренной трапеции:

(blacktriangleright) Углы при каждом основании равны;

(blacktriangleright) Диагонали равны;

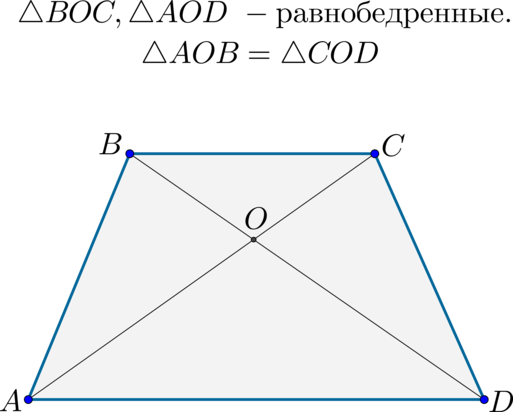
(blacktriangleright) Два треугольника, образованные диагоналями и одним из оснований, являются равнобедренными;

(blacktriangleright) Два треугольника, образованные диагоналями и боковой стороной, равны.


Задание
1

#296

Уровень задания: Равен ЕГЭ

В трапеции (ABCD): (AB = CD), (angle C – angle A = 80^{circ}). Найдите (angle D + angle B – angle C). Ответ дайте в градусах.

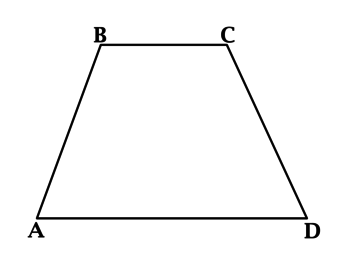
У равнобедренной трапеции углы при одном основании равны, тогда (angle B = angle C) и, следовательно, (angle D + angle B – angle C = angle D = angle A).

У равнобедренной трапеции сумма противоположных углов равна (180^{circ}) (так как (angle C = angle B), а (angle A + angle B = 180^{circ}), как сумма односторонних при параллельных прямых и секущей).

(angle A + angle C = 180^{circ}),

(angle C – angle A = 80^{circ})
тогда, вычитая из верхнего равенства нижнее, получаем (2cdot angle A = 100^{circ}). В итоге имеем: (angle D + angle B – angle C = angle A = 50^{circ}).

Ответ: 50


Задание
2

#1699

Уровень задания: Равен ЕГЭ

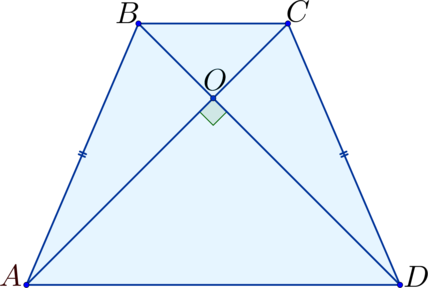
Диагонали в равнобедренной трапеции (ABCD) перпендикулярны. Найдите площадь трапеции, если диагональ (AC) равна (2).

В равнобедренной трапеции диагонали равны, поэтому (AC = BD = 2). Пускай (O) – точка пересечения диагоналей.

[begin{gathered}
S_{ABCD} = S_{triangle ABC} + S_{triangle CDA} = frac{1}{2}cdot AC cdot BO + frac{1}{2}cdot AC cdot OD =\ =frac{1}{2}cdot AC cdot(BO + OD) = frac{1}{2}cdot AC cdot BD = frac{1}{2} cdot 2 cdot 2 = 2end{gathered}]

Ответ: 2


Задание
3

#1789

Уровень задания: Равен ЕГЭ

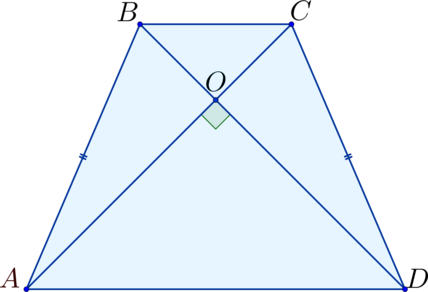
Найдите диагонали равнобедренной трапеции, если они перпендикулярны, а площадь трапеции равна (8).

Пусть (ABCD) — трапеция с диагоналями (AC) и (BD), (O) – точка их пересечения, тогда
(S_{ABCD} = S_{triangle ABC} + S_{triangle CDA} = frac{1}{2}cdot AC cdot BO + frac{1}{2}cdot AC cdot OD = )
(frac{1}{2}cdot AC cdot(BO + OD) = frac{1}{2}cdot AC cdot BD =
frac{1}{2}cdot AC^2 = 8) (Rightarrow) (AC = 4).

Ответ: 4


Задание
4

#1704

Уровень задания: Равен ЕГЭ

В равнобедренной трапеции (ABCD) основание (AD) вдвое длиннее основания (BC) и боковой стороны. Найдите острый угол трапеции.

Если опустить высоты (BH) и (CK) на основание (AD), то они отсекут равные отрезки (AH) и (KD), причем (AB = BC = HK) (Rightarrow) (AH = frac{AD – HK}{2} = frac{HK}{2} = frac{AB}{2}) (Rightarrow) (angle ABH = 30^circ), как угол в прямоугольном треугольнике, противолежащий катету, равному половине гипотенузы (Rightarrow) (angle BAK = 90^circ – 30^circ = 60^circ).

Ответ: 60


Задание
5

#295

Уровень задания: Равен ЕГЭ

(ABCD) – трапеция с основаниями (AD) и (BC). При этом (AB = CD = 6), (BC = 4), один из углов трапеции (ABCD) равен (60^{circ}). Найдите (AD).

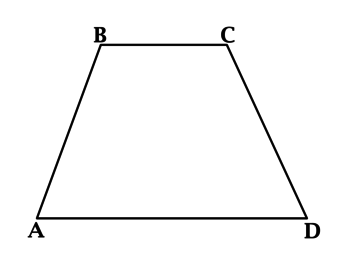
Пусть (angle A = 60^{circ}), (BE) – высота в треугольнике (ABD). (angle ABE = 90^{circ} – 60^{circ} = 30^{circ}). Катет, лежащий против угла в (30^{circ}), равен половине гипотенузы, тогда (AE = 0,5cdot 6 = 3).

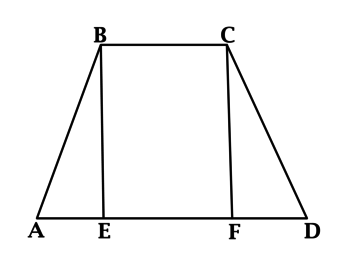
У равнобедренной трапеции углы при одном основании равны, тогда (angle D = 60^{circ}). Пусть (CF) – высота в треугольнике (ACD), тогда аналогично тому, как находили (AE), находим, что (FD = 3). (EF = BC), так как (BCFE) – прямоугольник. Тогда (AD = AE + EF + FD = 3 + 4 + 3 = 10).

Ответ: 10


Задание
6

#1700

Уровень задания: Равен ЕГЭ

Диагонали в равнобедренной трапеции (ABCD) перпендикулярны. (O) – точка пересечения диагоналей, причем (AO:OC = 7:1). Найдите периметр трапеции, если меньшее основание равно (1).

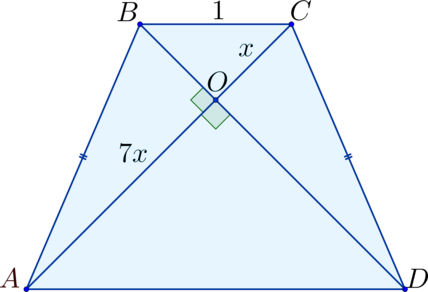
(BC) – меньшее основание, треугольники (triangle BOC) и (triangle AOD) подобны и их стороны относятся как (1:7) (Rightarrow) (BC:AD = 1:7) (Rightarrow) (AD = 7); (OB = OC), (OB^2 + OC^2 = 1^2) (Rightarrow) (OB = OC = frac{1}{sqrt2}) (Rightarrow) (AO = frac{7}{sqrt2}). В (triangle ABO): (AO^2 + OB^2 = AB^2) (Rightarrow) (AB = 5). Тогда (P_{ABCD} = AB + BC + CD + AD = 1 + 7 + 5 + 5 = 18).

Ответ: 18


Задание
7

#1702

Уровень задания: Равен ЕГЭ

В равнобедренной трапеции (ABCD) биссектриса (angle ABC) параллельна боковой стороне (CD) и пересекает основание (AD) в точке (K), которая делит (AD) в отношении (AK:KD = 1:2). Найдите периметр трапеции, если меньшее основание равно (4).

(BCDK) – параллелограмм, т.к. противоположные стороны попарно параллельны; (angle AKB = angle KBC), т.к. накрест лежащие при параллельных (BC) и (AD); (angle BAK = angle CDK = angle KBC) (Rightarrow) (triangle ABK) – равносторонний треугольник. (BC = KD = 4) (Rightarrow) (AK = 2 = AB = CD) (Rightarrow) (P_{ABCD} = AB + BC + CD + KD + AK = 2 + 4 + 2 + 4 + 2 = 14).

Ответ: 14

Учащимся старших классов, которые готовятся сдавать ЕГЭ по математике, в обязательном порядке стоит повторить тему «Равнобедренная трапеция» и освежить в памяти ее основные свойства и признаки. Многолетняя практика показывает, что подобные задания ежегодно встречаются в программе аттестационного испытания. Поэтому, если вы хотите успешно решить задачи ЕГЭ на применение основных свойств диагоналей или углов равнобедренной трапеции, вам непременно стоит разобраться в этой теме.

Образовательный портал «Школково» предлагает новый подход к подготовке к аттестационному испытанию. Наш ресурс позволяет учащимся определить наиболее сложные темы и ликвидировать имеющиеся пробелы в знаниях. Специалисты «Школково» подготовили и изложили весь материал в максимально доступной форме.

Чтобы выпускники могли успешно справляться с геометрическими задачами, мы рекомендуем вспомнить определение равнобедренной трапеции, свойства ее сторон, углов и диагоналей, а также формулу для вычисления площади. Эта информация представлена в разделе «Теоретическая справка».

Вспомнив основные свойства углов, диагоналей и сторон равнобедренной трапеции, учащиеся имеют возможность закрепить усвоенный материал, выполнив практические задания. Упражнения различного уровня сложности представлены в разделе «Каталог». В каждом из них вы найдете подробный алгоритм решения и правильный ответ.

Практиковаться в выполнении заданий по теме «Трапеция» при подготовке к ЕГЭ выпускники могут в режиме онлайн, находясь не только в Москве, но и в любом другом городе России. В случае необходимости любое упражнение можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.

УСТАЛ? Просто отдохни

Источник

Добавить комментарий