Как найти углы ромба если известен периметр

chansedefat209

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!

Как написать хороший ответ?

Ромб – это параллелограмм, у которого все стороны равны.

• “Чтоб Выучить, распознать нечто стоящее – узнать его в движении, при изменениях”
• Ромб провернем на 180 градусов вокруг точки пересечения диагоналей – ромб совместится с самим собой. Симметрия.
• Отразим ромб зеркально по диагонали – новый ромб совпадет с прежним. Симметрия.

Замечание: Если “зряче видим” центральную и осевые симметрии ромба, то все его свойства у нас “в кармане”.

Свойства ромба:

• Ромб симметричен относительно точки O – пересечения диагоналей.      O – центр симметрии.
• Ромб симметричен относительно любой из диагоналей.       Диагональ – ось симметрии.
• У ромба, по определению, Стороны   равны     $AB=BC=CD=DA=a$.
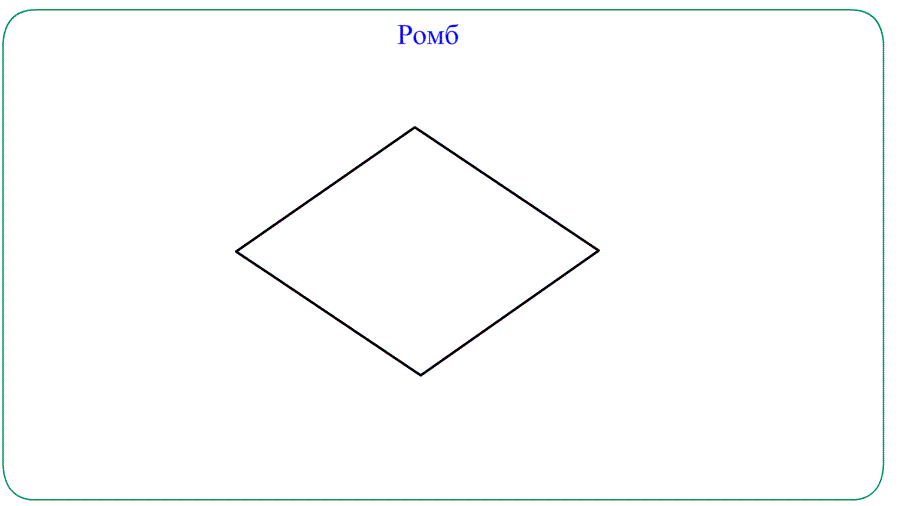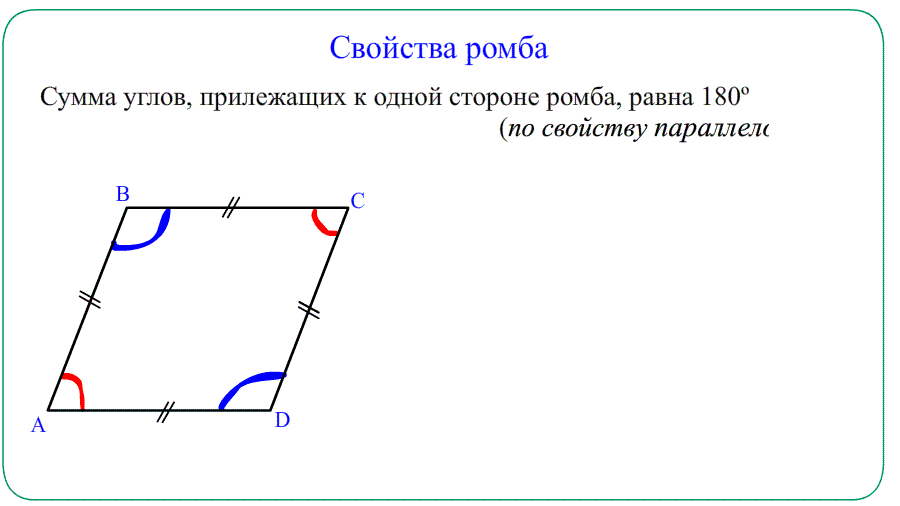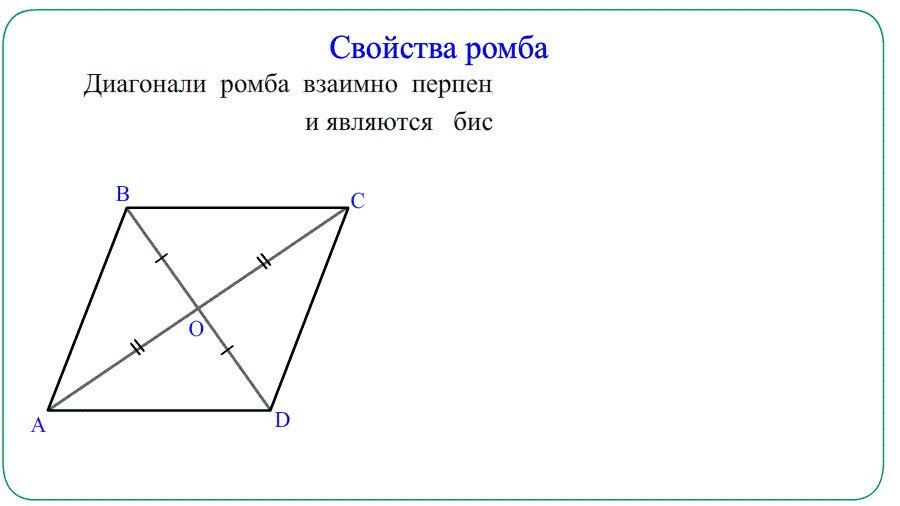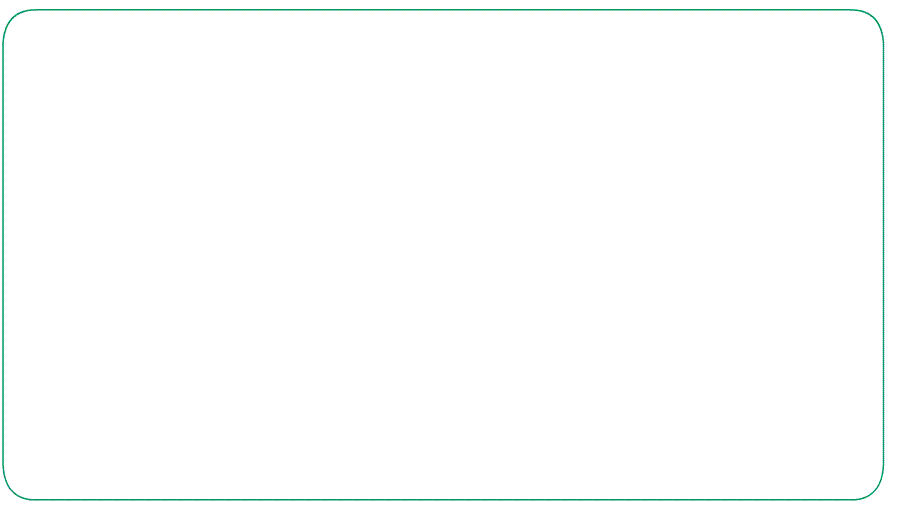
• Противолежащие углы    равны   $angle A=angle C$ ,   $angle B=angle D$ . Прилежащие       $angle A+angle B=180^o$   ,    $angle A+angle D=180^o$.
• Диагонали ромба пересекаются и точкой пересечения делятся пополам      $AO=OC=frac{AC}{2}$     и     $BO=OD=frac{BD}{2}$.
• Диагонали ромба взаимно перпендикулярны    и   образуют   прямоугольные   $bigtriangleup$ треугольники.
• Диагонали ромба со сторонами ромба образуют равнобедренные   $bigtriangleup$ треугольники.
• Диагонали ромба являются    биссектрисами углов – делят углы пополам.
• Диагонали ромба со сторонами образуют равные    накрест лежащие углы.
• Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.
• Меньшая диагональ   $AC^2=a^2+b^2-2cdot acdot bcdotcos D$     ,      большая –   $BD^2=a^2+b^2+2cdot acdot bcdotcos D$ .
• Сумма   {Цвет:Red квадратов диагоналей ромба равна    $AC^2+BD^2=4cdot a^2$     четырежды квадрат стороны.
• Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.

Формулы Площади ромба:

• Площадь   ромба   равна    произведению   основания на высоту      $S_{ABCD}=ADcdot CH$ , $S=acdot h$ ;
• Площадь   ромба   равна   через синус угла:        $S=a^2cdotsin A$     ,          квадрат стороны на синус .
• Площадь   ромба   через диагонали:    $S=frac{ACcdot BD}{2}$ .      – половина произведения диагоналей

Вписанная окружность в ромб:

• В четырехугольник   можно   вписать   окружность только если … суммы противоположных сторон   равны.
• Вписать окружность можно в ромб и квадрат, ;
• Если   вписывается, то площадь     $S=pcdot r$,     $p=2cdot a$       $S=2cdot a cdot r$.
• Центр Вписанной окружности находится на пересечении диагоналей. Диагонали – суть биссектрисы углов.

Задача 1:        Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен $45^o$.

• Решение:      “Односторонние углы”:     В параллелограмме   сумма углов, прилежащих к одной стороне, равна   $180^o$    .       
• Противоположные стороны ромба параллельны, их пересекает диагональ (секущая). Какие накрест лежащие углы равны?
• Как найти все углы ромба. Кем является Диагональ в ромбе для угла?     Ответ:     $22^o30’$   ,   $67^o30’$

Задача 2:         Найти площадь ромба   $ABCD$,   если его высота   $EB=12$   , а меньшая диагональ $BD=13$.

• Решение:          Проведем высоту   из той же вершины, из которой   проведена   меньшая диагональ.       
• Получили прямоугольный треугольник $BED$ .    Он   подобен тем треугольникам, на которые ромб делится диагоналями:     
• $bigtriangleup BED sim bigtriangleup AOD=bigtriangleup AOB=bigtriangleup COB=bigtriangleup COD$    . Все прямоугольные и есть равные углы.
• например   $alpha$.     Для нахождения площади нам нужно найти или сторону ромба, или его вторую диагональ.
• Для угла   $alpha$   в   $bigtriangleup EBD$   мы знаем гипотенузу и противолежащий катет   $Rightarrow$     $sinalpha=frac{BE}{BD}=frac{12}{13}$
• Перейдем к   $bigtriangleup OCD$ : в нем прилежащий катет    $OD=frac{1}{2}BD=6,5$.    Чтобы найти второй катет, нам нужен тангенс,
• а чтобы найти   гипотенузу, т. е. сторону ромба, – косинус. Найдем их через основное тригонометрическое тождество :
• $sin^2alpha+cos^2alpha=1$ .   Тогда косинус:   $cosalpha=pmsqrt{1-sin^2alpha}=pmsqrt{1-frac{144}{169}}=pmsqrt{frac{25}{169}}=pmfrac{5}{13}$
• Угол   $alpha$   острый,   так как он входит в прямоугольный треугольник,   т. е. принадлежит первой четверти.
• Следовательно, косинус положительный и мы останавливаемся на одном значении:   $cosalpha = frac{5}{13}$
• Тогда:   $frac{DO}{DC}=frac{6,5}{DC}=cosalpha=frac{5}{13}$             $Rightarrow$        $DC=frac{6,5cdot13}{5}=frac{13cdot13}{10}=16,9$
• Площадь ромба равна произведению основания на высоту:    Ответ:    $S=16,9cdot12=202,8$

Задача 3:          В Ромбе   $ABCD$    точка $K$ делит сторону   $CD$ в соотношении   $2:7$, а    $M$ делит   $1:3$ сторону   $BC$.       $MN$   параллельна   $AB$,   $O$ – пересечение $MN$ и   $BK$.    Найти площадь трапеции   $ABON$, если площадь   $ABCD=420$.

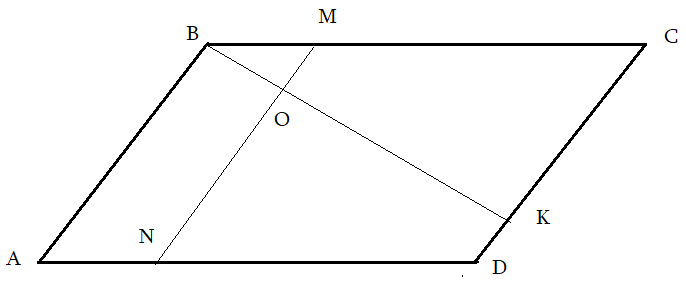
Решение:    пробa    Анализ рисунка:    

• $AB$, $MN$,   $CD$ – параллельные.   Какие углы равные?
• Треугольники   $BMO$ и    $BKC$ подобные.   Коэффициент подобия   $1:3$.
• Отношение площадей    $BMO$   и   $BKC$ равен    $1:9$ – квадрату коэффициента подобия.
• (по формулам) Площади   $BKC$   и    $BCD$ относятся как    $CK$ и   $CD$, т.е.   $5:7$.
• Площадь   $BCD$   равен половине площади   $ABCD$,   т.е. $S_{BCD}=210$.
• $S_{ABMN}:S_{ABCD}=1:3$        $Rightarrow$       $S_{ABMN}=140$ .   
• Из складываемости площадей:     площадь $ABON$ =   разности   площадей   $ABMN$   и    $BOM$.

Упражнения:

Ромб – это параллелограмм, у которого все стороны равны.

• “Чтоб Выучить, распознать нечто стоящее – узнать его в движении, при изменениях”
• Ромб провернем на 180 градусов вокруг точки пересечения диагоналей – ромб совместится с самим собой. Симметрия.
• Отразим ромб зеркально по диагонали – новый ромб совпадет с прежним. Симметрия.
• Отразим ромб зеркально по другой диагонали – ромб совпадает с самим собой. Симметрия.

Замечание: Если “зряче видим” центральную и осевые симметрии ромба, то все его свойства у нас “в кармане”.

Свойства ромба:

• Ромб симметричен относительно точки O – пересечения диагоналей.      O – центр симметрии.
• Ромб симметричен относительно любой из диагоналей.       Диагональ – ось симметрии.
• У ромба, по определению, Стороны   равны     $AB=BC=CD=DA=a$.
• Противолежащие углы    равны   $angle A=angle C$ ,   $angle B=angle D$ . Прилежащие       $angle A+angle B=180^o$   ,    $angle A+angle D=180^o$.
• Диагонали ромба пересекаются и точкой пересечения делятся пополам      $AO=OC=frac{AC}{2}$     и     $BO=OD=frac{BD}{2}$.
• Диагонали ромба взаимно перпендикулярны    и   образуют   прямоугольные   $bigtriangleup$ треугольники.
• Диагонали ромба со сторонами ромба образуют равнобедренные   $bigtriangleup$ треугольники.
• Диагонали ромба являются    биссектрисами углов – делят углы пополам.
• Диагонали ромба со сторанами образуют равные    накрест лежащие углы.
• Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.
• Меньшая диагональ   $AC^2=a^2+b^2-2cdot acdot bcdotcos D$     ,      большая –   $BD^2=a^2+b^2+2cdot acdot bcdotcos D$ .
• Сумма   {Цвет:Red квадратов диагоналей ромба равна    $AC^2+BD^2=4cdot a^2$     четырежды квадрат стороны.
• Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.

Формулы Площади ромба:

• Площадь   ромба   равна    произведению   основания на высоту      $S_{ABCD}=ADcdot CH$ , $S=acdot h$ ;
• Площадь   ромба   равна   через синус угла:        $S=a^2cdotsin A$     ,          квадрат стороны на синус .
• Площадь   ромба   через диагонали:    $S=frac{ACcdot BD}{2}$ .      – половина произведения диагоналей

Вписанная окружность в ромб:

• В четырехугольник   можно   вписать   окружность только если … суммы противоположных сторон   равны.
• Вписать окружность можно в ромб и квадрат, ;
• Если   вписывается, то площадь     $S=pcdot r$,     $p=2cdot a$       $S=2cdot a cdot r$.
• Центр Вписанной окружности находится на пересечении диагоналей. Диагонали – суть биссектрисы углов.

Задача 1:        Найти периметр ромба   $ABCD$, в котором    $angle C=60^o$ , а меньшая диагональ равна    $10,5$ см.

• Решение:          Рассмотрим   $bigtriangleup BCD$. Что в нём равного? $Rightarrow$ каков   данный   треугольник?             
• По условию,   угол $bigtriangleup BCD$ у вершине   $angle B=60^o$   , тогда как два других угла?
• Каков все-таки этот   треугольник?   Чему равны стороны ромба. А сумма сторон? Ответ:     $p=42$ см.

Задача 2:        Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен $45^o$.

• Решение:      “Односторонние углы”:     В параллелограмме   сумма углов, прилежащих к одной стороне, равна   $180^o$    .       
• Противоположные стороны ромба параллельны, их пересекает диагональ (секущая). Какие накрест лежащие углы равны?
• Как найти все углы ромба. Кем является Диагональ в ромбе для угла?     Ответ:     $22^o30’$   ,   $67^o30’$

Задача 3:         Найти площадь ромба   $ABCD$,   если его высота   $EB=12$   , а меньшая диагональ $BD=13$.

• Решение:          Проведем высоту   из той же вершины, из которой   проведена   меньшая диагональ.       
• Получили прямоугольный треугольник $BED$ .    Он   подобен тем треугольникам, на которые ромб делится диагоналями:     
• $bigtriangleup BED sim bigtriangleup AOD=bigtriangleup AOB=bigtriangleup COB=bigtriangleup COD$    . Все прямоугольные и есть равные углы.
• например   $alpha$.     Для нахождения площади нам нужно найти или сторону ромба, или его вторую диагональ.
• Для угла   $alpha$   в   $bigtriangleup EBD$   мы знаем гипотенузу и противолежащий катет   $Rightarrow$     $sinalpha=frac{BE}{BD}=frac{12}{13}$
• Перейдем к   $bigtriangleup OCD$ : в нем прилежащий катет    $OD=frac{1}{2}BD=6,5$.    Чтобы найти второй катет, нам нужен тангенс,
• а чтобы найти   гипотенузу, т. е. сторону ромба, – косинус. Найдем их через основное тригонометрическое тождество :
• $sin^2alpha+cos^2alpha=1$ .   Тогда косинус:   $cosalpha=pmsqrt{1-sin^2alpha}=pmsqrt{1-frac{144}{169}}=pmsqrt{frac{25}{169}}=pmfrac{5}{13}$
• Угол   $alpha$   острый,   так как он входит в прямоугольный треугольник,   т. е. принадлежит первой четверти.
• Следовательно, косинус положительный и мы останавливаемся на одном значении:   $cosalpha = frac{5}{13}$
• Тогда:   $frac{DO}{DC}=frac{6,5}{DC}=cosalpha=frac{5}{13}$             $Rightarrow$        $DC=frac{6,5cdot13}{5}=frac{13cdot13}{10}=16,9$
• Площадь ромба равна произведению основания на высоту:    Ответ:    $S=16,9cdot12=202,8$

Задача 4:          В Ромбе   $ABCD$    точка $K$ делит сторону   $CD$ в соотношении   $2:7$, а    $M$ делит   $1:3$ сторону   $BC$.       $MN$   параллельна   $AB$,   $O$ – пересечение $MN$ и   $BK$.    Найти площадь трапеции   $ABON$, если площадь   $ABCD=420$.

Решение:    пробa    Анализ рисунка:    

• $AB$, $MN$,   $CD$ – параллельные.   Какие углы равные?
• Треугольники   $BMO$ и    $BKC$ подобные.   Коэффициент подобия   $1:3$.
• Отношение площадей    $BMO$   и   $BKC$ равен    $1:9$ – квадрату коэффициента подобия.
• (по формулам) Площади   $BKC$   и    $BCD$ относятся как    $CK$ и   $CD$, т.е.   $5:7$.
• Площадь   $BCD$   равен половине площади   $ABCD$,   т.е. $S_{BCD}=210$.
• $S_{ABMN}:S_{ABCD}=1:3$        $Rightarrow$       $S_{ABMN}=140$ .   
• Из складываемости площадей:     площадь $ABON$ =   разности   площадей   $ABMN$   и    $BOM$.

Упражнения:

Ромб – это параллелограмм, у которого все стороны равны.

• “Чтоб Выучить, распознать нечто неподвижное – узнать его в движении, при изменениях”
• Ромб провернем на 180 градусов вокруг точки пересечения диагоналей – ромб совместится с самим собой. Симметрия.
• Отразим ромб зеркально по диагонали – новый ромб совпадет с прежним. Симметрия.
• Отразим ромб зеркально по другой диагонали – ромб совпадает с самим собой. Симметрия.

Замечание: Если “зряче видим” центральную и осевые симметрии ромба, то все его свойства у нас “в кармане”.

Свойства ромба:

• Ромб симметричен относительно точки O – пересечения диагоналей.      O – центр симметрии.
• Ромб симметричен относительно любой из диагоналей.       Диагональ – ось симметрии.
• У ромба, по определению, Стороны   равны     $AB=BC=CD=DA=a$.
• Противолежащие углы    равны   $angle A=angle C$ ,   $angle B=angle D$ . Прилежащие       $angle A+angle B=180^o$   ,    $angle A+angle D=180^o$.
• Диагонали ромба пересекаются и точкой пересечения делятся пополам      $AO=OC=frac{AC}{2}$     и     $BO=OD=frac{BD}{2}$.
• Диагонали ромба взаимно перпендикулярны    и   образуют   прямоугольные   $bigtriangleup$ треугольники.
• Диагонали ромба со сторонами ромба образуют равнобедренные   $bigtriangleup$ треугольники.
• Диагонали ромба являются    биссектрисами углов – делят углы пополам.
• Диагонали ромба со сторонами образуют равные    накрест лежащие углы.
• Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.

Квадрат – одновременно прямоугольник, ромб, параллелограмм. Диагонали квадрата    равны между собой и делятся пополам.

Задача 1:        Найти периметр ромба   $ABCD$, в котором    $angle C=60^o$ , а меньшая диагональ равна    $10,5$ см.

• Решение:          Рассмотрим   $bigtriangleup BCD$. Что в нём равного? $Rightarrow$ каков   данный   треугольник?             
• По условию,   угол $bigtriangleup BCD$ у вершины   $angle B=60^o$   , тогда как два других угла?
• Каков все-таки этот   треугольник?   Чему равны стороны ромба. А сумма сторон? Ответ:     $p=42$ см.

Задача 2:        Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен $45^o$.

• Решение:      “Односторонние углы”:     В параллелограмме   сумма углов, прилежащих к одной стороне, равна   $180^o$    .       
• Противоположные стороны ромба параллельны, их пересекает диагональ (секущая). Какие накрест лежащие углы равны?
• Как найти все углы ромба. Кем является Диагональ в ромбе для угла?     Ответ:     $22^o30’$   ,   $67^o30’$

• Полезные напоминания: “В равностороннем треугольнике все углы равны    60    градусов.
• Если в равнобренном треугольнике один из углов 60, то это равносторонный треугольник – стороны равны, углы тоже.
• В прямоугольном треугольнике катет напротив угла 30 градусов равен половине гипотенузы.

Упражнения:

Задачи из сайта https://resh.edu.ru :

Задача 11: В ромбе АВСD ∠А = 140°, диагонали пересекаются в точке O. Найдите угол CBO.

Задача 12:    В ромбе ABCD ∠С = 50°. Точка O – точка пересечения диагоналей ромба. Найдите угол OBC.

Задача 13: Одна из диагоналей ромба образует с его стороной угол 65°. Найдите больший угол ромба.

Задача 14: ???? В любом ромбе равны…      Противолежащие углы равны, сумма соседних углов равна 180 градусов:(?) Ромб, у которого все углы равны, это… (?)    Диагонали пересекаются и точкой пересечения делятся пополам. (?)   Диагонали взаимно перпендикулярны. (?)

Задача 15: Отрезки AB и CD пересекаются в их общей середине. В образовавшемся четырёхугольнике ∠CAD = ∠ADB. Найдите ∠BCA.

Задача 16: На диагонали квадрата как на стороне построен новый квадрат. Чему равна его диагональ, если сторона исходного квадрата равна 6 см?

Задача 17: Одна из диагоналей ромба образует с его стороной угол 65°. Найдите больший угол ромба.