Как найти углы ромба если известна площадь

Углы ромба онлайн

С помощю этого онлайн калькулятора ромба можно найти углы ромба по известным элементам. Для нахождения углов ромба введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть смотрите ниже.

Открыть онлайн калькулятор

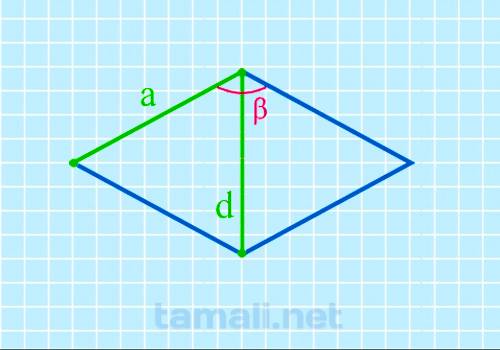
1. Углы ромба через сторону и высоту

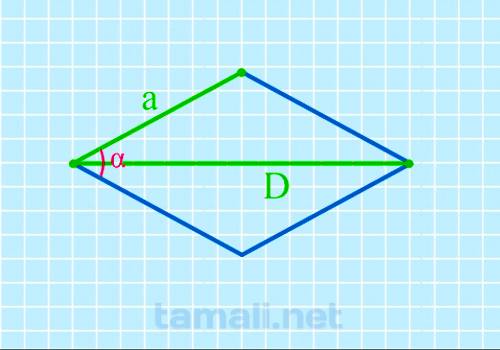
Пусть известны сторона и высота ромба (Рис.1).

Покажем, что углы ромба через сторону и высоту вычисляются по формулам

( small alpha= mathrmfrac<large h> <large a>)

(1)

( small beta= 180°-alpha )

(2)

(small frac<large h><large sin alpha>=frac<large a><large sin 90°>.)

(3)

(small sin alpha=frac<large h><large a>)

(4)

(small alpha=mathrmfrac<large h><large a>)

(5)

Поскольку сумма соседних углов ромба равна 180° (свойство 4 статьи Ромб), то угол β вычисляется из формулы (2).

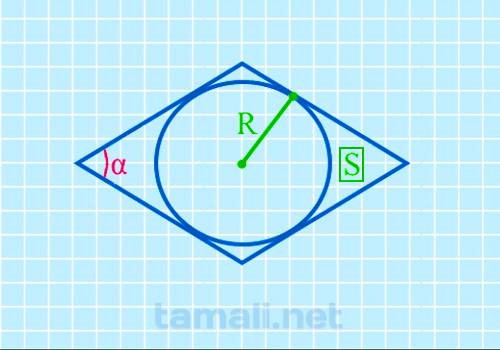
2. Углы ромба ромба через площадь и высоту

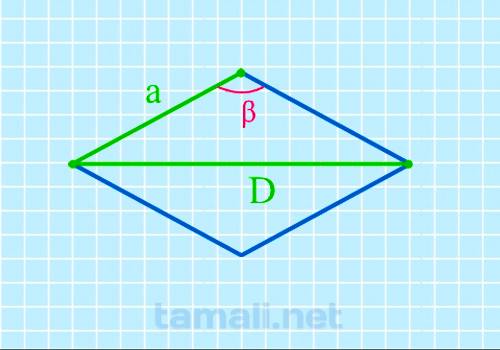
Рассмотрим ромб с высотой h и площадью S (Рис.2).

Покажем, что углы ромба через площадь и высоту вычисляются по формулам:

( small alpha= mathrmfrac<large h^2><large S>, )

(6)

( small beta= 180°-alpha . )

(7)

Площадь ромба через сторону и высоту вычисляется из формулы:

( small S=a cdot h. )

(8)

Найдем a из формулы (8) и подставим в (1):

( small alpha= mathrmfrac<large h><large a>=mathrmfrac<large h><large frac> ) ( small =mathrmfrac<large h^2> <large S>)

(9)

Как отметили в параграфе 1, соседний угол β вычисляется по формуле (7).

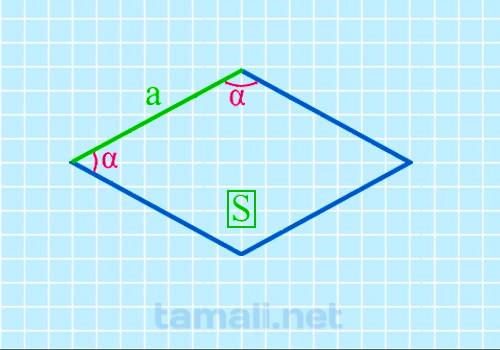
3. Углы ромба через площадь и сторону

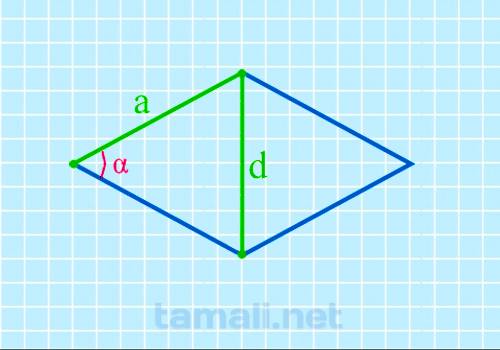
Пусть известны площадь и сторона ромба (Рис.3).

Чтобы найти формулу углов ромба через площадь и сторону, из формулы (8) найдем h и подставим в (1):

Следовательно угол α ромба через площадь и сторону вычисляется из формулы:

( small alpha =mathrmfrac<large S><large a^2>. )

(10)

Как отметили выше, соседний угол β вычисляется по формуле (7).

4. Углы ромба через диагонали

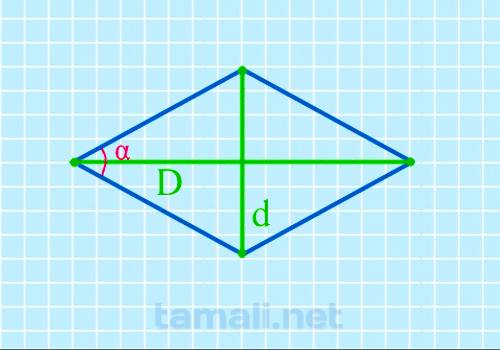
Пусть известны диагонали d₁ и d₂ ромба (Рис.4). Выведем формулу вычисления углов α и β ромба.

(small h=frac<large d_1d_2><large sqrt>.)

(11)

(small a=frac<large sqrt><large 2>.)

(12)

Подставляя (11) и (12) в (4), получим:

(small sin alpha=frac<large h><large a>) ( small =frac<frac<large d_1d_2><large sqrt>><frac<large sqrt><large 2>> ) ( small =frac<large 2d_1d_2> <large d_1^2+d_2^2>.)

(13)

(small alpha=mathrm frac<large 2d_1d_2> <large d_1^2+d_2^2>.)

(14)

Как отметили выше, соседний угол β вычисляется по формуле (7).

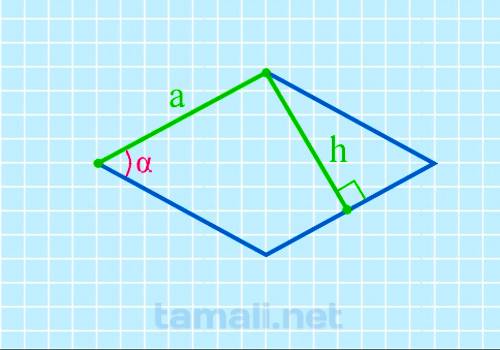
5. Углы ромба через сторону и диагональ

Пусть известны сторона a=AB ромба и диагональ d=AC (Рис.5).

Найдем углы ромба. Учитывая свойства 5, 6 и 7 ромба, получаем, что треугольник AOB прямоугольный и ( small angle ABO =frac<alpha> <2>.) Тогда для треугольника AOB имеют места следующие равненства:

(small frac<large AO><large a>=sin frac<alpha><2>,)

(small frac<large AO><large a>=cos frac<beta><2>)

(small sin frac<alpha><2>=frac<large d><large 2a>)

(15)

(small cos frac<beta><2>=frac<large d><large 2a >.)

(16)

Формулы половинного угла для синуса и косинуса имеют следующий вид:

(small sin frac<alpha><2>=±sqrt<frac<large 1-cos alpha><large 2 >>,)

(17)

(small cosfrac<beta><2>=±sqrt<frac<large 1+cos beta><large 2 >>.)

(18)

Найдем из формул (17),(18) ( small cos alpha ) и ( small cos beta: )

(small cos alpha=1-2cdot sin^2 frac<alpha><2>,)

(19)

(small cos beta=2cdot sin^2 frac<beta><2>-1,)

(20)

Подставляя (15),(16) в (19),(20), получим формулы углов ромба через сторону и диагональ:

(small cos alpha=1- frac<large d^2><large 2a^2>,)

(21)

(small cos beta=frac<large d^2><large 2a^2>-1.)

(22)

(small alpha=mathrm left(1- frac<large d^2> <large 2a^2>right),)

(23)

(small beta=mathrm left( frac<large d^2><large 2a^2>-1 right).)

(24)

Отметим, что полученный угол α находится напротив диагонали d, а угол β делится диагональю d на две равные части.

6. Углы ромба через сторону и радиус вписанной окружности

Пусть известны сторона ромба и радиус вписанной окружности (Рис.6). Найдем углы ромба.

В статье Высота ромба мы вывели формулу высоты ромба через радиус вписанной октужности:

(small h=2 cdot r.)

(25)

Подставляя (25) в (4) и (5) параграфа 1 данной статьи, получим:

(small sin alpha=frac<large 2 cdot r><large a>)

(26)

(small alpha=mathrmfrac<large 2 cdot r><large a>)

(27)

Как отметили выше, соседний угол β ромба вычисляется по формуле:

Геометрические фигуры. Ромб. Углы ромба. Как найти угол ромба.

Углы ромба, нахождение:

1. Сумма 4-х внутренних углов ромба равняется 360°, точно так же как и у всякого четырехугольника. Противоположные углы ромба имеют одинаковую величину, причем, всегда в 1-ой паре равных углов — углы острые, во второй – тупые. 2 угла, которые прилегают к 1-ной стороне в сумме составляют развернутый угол.

Ромбы с равным размером стороны могут внешне довольно сильно отличаться друг от друга. Это разница объясняется различной величиной внутренних углов. То есть, для определения угла ромба не хватит знать лишь длину его стороны.

2. Для вычисления величины углов ромба хватит знать длины диагоналей ромба. После построения диагоналей ромб разбивается на 4 треугольника. Диагонали ромба располагаются под прямым углом, то есть, треугольники, которые образовались, оказываются прямоугольными.

Ромб — симметричная фигура, его диагонали есть в одно время и осями симметрии, вот почему каждый внутренний треугольник равен остальным. Острые углы треугольников, которые образованы диагоналями ромба, равняются ½ искомых углов ромба.

3. Тангенс острого угла прямоугольного треугольника соответствует отношению противолежащего катета к прилежащему. ½ любой из диагоналей ромба оказывается катетом прямоугольного треугольника.

Обозначим большую и малую диагонали ромба как d₁ и d₂, а углы ромба — А (острый) и В (тупой), теперь из соотношения сторон в прямоугольных треугольниках внутри ромба находим:

4. Из формулы двойного угла tg (2α) = 2/(сtg α – tg α) находим тангенсы углов ромба:

По тригонометрическим таблицам находят углы, которые соответствуют полученным значениям тангенсов.

Острый угол ромба равен 60 градусам.

Когда острый угол ромба = 60°, значит, диагональ равняется стороне ромба и делит его на 2 одинаковых равносторонних треугольника.

∆ ABD и ∆ BCD — равносторонние,

1) Изучим треугольник ABD.

Т.к. AB=AD (так как являются сторонами ромба), значит, ∆ ABD является равнобедренным треугольником с основанием BD.

Углы при основании равнобедренного треугольника:

Так как каждый угол треугольника ABD равен 60 градусов, значит, ∆ ABD является равносторонним треугольником. Значит, BD=AB.

2) Треугольники ABD и BCD одинаковы по трем сторонам (AB=BC=CD=AD (как стороны ромба), BD=AB (из доказанного)).

То есть, ∆ BCD оказывается равносторонним треугольником.

Что и требовалось доказать.

Т.к. сумма углов ромба, которые прилежат к одной стороне, равна 180º, когда острый угол ромба равен 60º, его тупой угол равен 120º. Таким образом:

Когда тупой угол ромба равен 120 градусам, значит диагональ равняется стороне ромба и делит его на 2 равных равносторонних треугольника.

Ромб с прямыми углами называется квадратом.

Ромб. Формулы, признаки и свойства ромба

Признаки ромба

∠BAC = ∠CAD или ∠BDA = ∠BDC

Δ ABO = Δ BCO = Δ CDO = Δ ADO

Основные свойства ромба

∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC

AC 2 + BD 2 = 4AB 2

Сторона ромба

Формулы определения длины стороны ромба:

1. Формула стороны ромба через площадь и высоту:

2. Формула стороны ромба через площадь и синус угла:

3. Формула стороны ромба через площадь и радиус вписанной окружности:

4. Формула стороны ромба через две диагонали:

5. Формула стороны ромба через диагональ и косинус острого угла ( cos α ) или косинус тупого угла ( cos β ):

6. Формула стороны ромба через большую диагональ и половинный угол:

7. Формула стороны ромба через малую диагональ и половинный угол:

8. Формула стороны ромба через периметр:

Диагонали ромба

Формулы определения длины диагонали ромба:

d ₁ = a √ 2 + 2 · cosα

d ₁ = a √ 2 – 2 · cosβ

d ₂ = a √ 2 + 2 · cosβ

d ₂ = a √ 2 – 2 · cosα

d ₁ = 2 a · cos ( α /2)

d ₁ = 2 a · sin ( β /2)

d ₂ = 2 a · sin ( α /2)

d ₂ = 2 a · cos ( β /2)

7. Формулы диагоналей через площадь и другую диагональ:

8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:

Периметр ромба

Периметром ромба называется сумма длин всех сторон ромба.

Длину стороны ромба можно найти за формулами указанными выше.

Формула определения длины периметра ромба:

Площадь ромба

Формулы определения площади ромба:

4. Формула площади ромба через две диагонали:

5. Формула площади ромба через синус угла и радиус вписанной окружности:

6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):

S =	1	d 1 2 · tg ( α /2)
2

S =	1	d 2 2 · tg ( β /2)
2

Окружность вписанная в ромб

Формулы определения радиуса круга вписанного в ромб:

1. Формула радиуса круга вписанного в ромб через высоту ромба:

2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:

3. Формула радиуса круга вписанного в ромб через площадь и синус угла:

4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:

5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:

6. Формула радиуса круга вписанного в ромб через две диагонали:

r =	d 1 · d 2
2√ d 1 2 + d 2 2

7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

[spoiler title=”источники:”]

http://www.calc.ru/Geometricheskiye-Figury-Romb-Ugly-Romba-Kak-Nayti-Ugol-Romba.html

http://ru.onlinemschool.com/math/formula/rhombus/

[/spoiler]

Ромб – геометрическая фигура, представляющая собой отдельную разновидность параллелограмма. Все
имеющееся стороны равны между собой. Геометрическая фигура представляет собой отдельную
разновидность параллелограмма. Все имеющееся стороны равны между собой. Чтобы исключить риски
недопонимания, а также освоить принципы расчетов, рекомендуется ознакомиться с некоторыми
особенностями подробней.

Острый угол ромба через длинную диагональ и сторону

Для проведения расчетов используется формула:

cos α = D² / 2a² — 1

где D — длинная диагональ, a — сторона.

Пример. Предположим, что длинная диагональ 25 мм, сторона – 15 мм. Отталкиваясь от
полученных сведений, результат получается следующим: cos α = 25² / 2 х 15² — 1 = 67.11º

Тупой угол ромба через длинную диагональ и сторону

Имея достоверные данные о значение длинной диагонали (D) и стороне (a), порядок вычисления не
предполагает под собой каких-либо сложностей с определением. Для этого в геометрии предлагается
воспользоваться следующей формулой:

cos β =  D² / 2a² — 1

Пример. Предположим, D = 60 мм, a = 90 мм. Исходя из полученных сведений, расчет по
имеющейся формуле имеет вид: cos β =  60² / 2 х 90² — 1. В таком
случае cos β = 141.05. При условии, что D>a, решение не представляется возможным.

Острый угол ромба через короткую диагональ и сторону

Для проведения интересующегося расчета требуется знать данные о короткой диагонали (d) и стороне (a).
При условии наличия используемая формула имеет следующий вид:

cos α = 1 – d² / 2a²

где d — короткая диагональ, a — сторона.

Пример. Из представленной формулы следует, что инициировать получение интересующих
данных не вызывает сложностей. Чтобы удостовериться в этом, достаточно рассмотреть пример. Допустим,
что d = 40 мм, a = 25 мм. В таком случае определение результата осуществляется следующим образом:
cos α = 1 – 40² / 2 х 25².

Используя калькулятор, становится известно,
что cos α = 106.26. Подтвердить подлинность результата можно в режиме онлайн через
специализированный сервис вычислений.

Острый угол ромба через диагонали

Представленный параметр расчета по праву считается одним из наиболее сложных. Чтобы исключить риски
допущения ошибок и недопонимания, рекомендуется ответственно подходить к организации вычислений.
Чтобы узнать информацию, чему равняется sin α, достаточно воспользоваться следующей формулой:

sin α = (2 · Dd)/ (D² + d²)

где D является длинной диагональю,  d — короткой.

Во время определения sin α оптимальным решением станет использование стандартных математических
правил. Они предполагают первичное умножение, после чего деление. Суммирование осуществляется на
завершающем этапе определения значения.

Пример. Предположим, D = 85 мм, d = 15 мм. Имеющиеся значения требуется подставить в
формулу. В итоге получается: sin α = (2 · 85)/85² + 15². Используя
автоматизированный калькулятор для геометрии, получается, что sin α = 20.01

Тупой угол ромба через короткую диагональ и сторону

Порядок вычисления предполагает использование соответствующей формулы. Чтобы инициировать расчет
требуется знать точные данные относительно короткой диагонали (d) и стороне (a). В таком случае
расчет проходит следующим образом:

cos β = 1 — d² / 2a²

где d — короткая диагональ, a — сторона ромба.

Пример. Предположим, что d = 27 мм, a = 65 мм. Используя имеющуюся формулу,
вычисление проходит по следующей процедуре: cos β = 1 — 27²/2х65².

Используя стандартные принципы
вычисления либо специализированный онлайн калькулятор, cos β = 23.98. Чтобы гарантировать
достоверность вычислений настоятельно рекомендуется выполнять проверку полученных данных несколькими
способами.

Острый угол ромба через радиус вписанной окружности в ромб и площадь ромба

Принципы определения интересующей величины предполагают необходимость использования следующей
формулы:

sin(α) = 4R²/S

где R – радиус, S – заявленная площадь геометрической фигуры.

Пример. Предположим, что радиус составляет 2 см, заявленная площадь 20 мм² .
Подставив имеющиеся значения в формулу, имеем следующий вид: sin(α) = 4 х 2²/20 = 53º.

Угол ромба через площадь и сторону

Представленный метод часто используется, чтобы узнать интересующий параметр. Главное условие –
наличие известных величин из формулы, которая имеет следующий вид:

sin(α) = S/a²

где S является площадью ромба, a — стороной.

Рассмотрим порядок определения неизвестной величины на конкретном примере. Допустим, что S = 65 мм² ,
a – 12 мм. В таком случае, получается: sin(α) = 65/12³ = 26,83º.

Острый угол ромба через высоту и сторону

Для определения синуса предполагается использование следующей несложной формулы:

sin(α) = h / a

где h – заявленные показатели высоты, a — сторона.

Пример. Допустим, что высота составляет 9, сторона – 15. Следовательно, вычисления
осуществляются следующим образом: sin(α) = 9/15 = 36.86 градусов.

Половинный угол ромба через высоту и диагональ

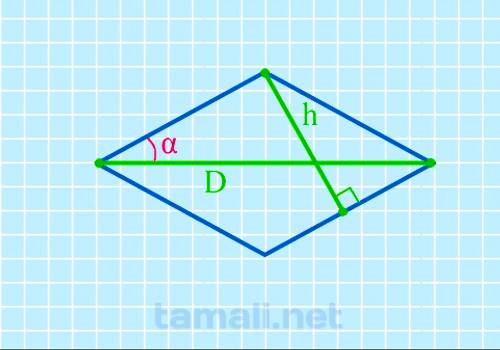
Чтобы отыскать интересующий синус, требуется воспользоваться следующим правилом определения
величины:

sin( α/2 ) = h/D

где h – имеющаяся высота, D – заявленная длина диагонали.

Пример. Высота 43, диагональ 76. Следовательно, sin( α/2 ) = 43/76 = 34.4.

Половинный тупой угол ромба через диагонали

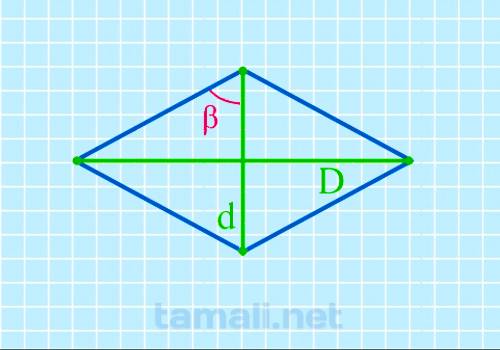
Использование рассматриваемого метода не предполагает под собой существенных сложностей. Достаточно
воспользоваться специально разработанной формулой, которая имеет следующий вид:

tg( β/2 ) = D / d

где D выступает длинной диагональю, d — короткой.

Пример. Достаточно подставить для вычисления имеющиеся данные, чтобы в конечном
итоге получить искомый результат. К примеру, D = 80 мм, d = 35 мм. Используя стандартные принципы
вычисления получается: tg( β/2 ) = 80/35 = 66.37

Половинный острый угол ромба через диагонали

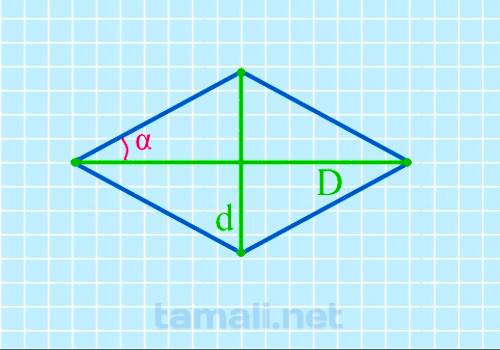
Проведение расчетов с помощью представленной методики требует наличия всех переменных, среди которых
короткая и длинная диагонали. Если все необходимые параметры известны, вычисление осуществляется по
представленной формуле:

tg( α/2 ) = d / D

где D,d – заявленная длина диагоналей.

Пример. Предположим, что D = 15 мм, d = 50 мм. Подставим имеющие значения в формулу,
имеем вид: tg( α/2 ) = 50 /15 С помощью несложных подсчетов получается, что tg( α/2 ) = 73.3
градуса.

Ромб представляет собой параллелограмм, который имеем равные стороны. При наличии исключительно
прямых углов – квадрат.

Дополнительно выделяют следующие признаки:

• имеющиеся диагонали ромба перпендикулярны;
• диагонали ромба выступают биссектрисами его углов;
• сумма квадратов всех диагоналей приравнивается к квадраты стороны, которая умножается на 4.

Чтобы параллелограмм считался ромбом, крайне важно соблюдение одного из нескольких условий, к которым
принято относить:

• все имеющиеся стороны геометрической фигуры равны между собой;
• диагонали пересекаются исключительно под прямым углом;
• диагонали геометрической фигуры выступают биссектрисами углов.

Найти углы ромба, зная только его сторону, нельзя: существуют ромбы, имеющие разные углы, но одинаковые стороны. На пальцах: сделайте ромб из проволоки, “сплющите” его — он останется ромбом, стороны будут те же, углы изменятся.

Значит, чтобы найти углы ромба нужно знать что-то ещё (или что-то другое). Например, зная сторону и диагональ, найти угол можно по теореме косинусов: если x — сторона, d — диагональ, a — угол напротив диагонали, то условие теоремы косинуов — d^2 = x^2 + x^2 – 2 * x^2 * cos(a), из него следует a = arccos((2x^2 – d^2)/2x^2). (Я говорю “найти угол”, а не “найти углы”, потому что если мы знаем один угол, остальные находятся тривиально: если один угол равен а градусов, то угол напротив него тоже а, остальные два — по 180-а).

Есть и другие варианты: через сторону и площадь (пользуясь тем, что площадь — это квадрат стороны умножить на синус угла), через две диагонали (мы знаем, что диагонали в ромбе пересекаются под прямым углом и делятся точкой пересечения пополам — отсюда следует, что тангенс половины угла ромба равен отношению диагоналей, просто по определнию тангенса; зная сторону и диагональ, кстати, тоже можно искать угол примерно таким способом, вместо теоремы косинусов) и так далее.

Информация по назначению калькулятора

Ромб – это четырехугольник (плоская фигура, замкнутая форма, четыре стороны) с четырьмя сторонами равной длины и противоположными сторонами, параллельными друг другу. Все ромбы являются параллелограммами, но не все параллелограммы являются ромбами. Все квадраты являются ромбами, но не все ромбы являются квадратами. Противоположные внутренние углы ромбов совпадают. Диагонали ромба всегда делят пополам друг друга под прямым углом.

Четыре внутренних угла ромба всегда составляют в сумме 360°, а его диагонали всегда перпендикулярны друг другу

Одной из двух характеристик, которые делают ромб уникальным, является то, что его четыре стороны равны по длине или конгруэнтны. Другое идентифицирующее свойство состоит в том, что противоположные стороны параллельны.

Онлайн калькулятор предназначен для нахождения параметров ромба, таких как:

• Длины сторон

– равны между собой (AB=BC=CD=DA)

• Высота

– что бы найти высоту ромба, необходимо его площадь поделить на сторону (h=S/AB)

• Периметр

– равен сумме всех сторон, или стороне ромба умноженной на 4 (P=AB+BC+CD+DA=AB*4)

• Площадь

– равна произведению стороны и высоты (S=AB*h)

• Диагонали

– всегда перпендикулярны

• Углы

– всегда составляют в сумме 360°

• Радиус Вписанной окружности
• Диаметр Вписанной окружности
• Длина Вписанной окружности
• Площадь Вписанной окружности

Введите данные:

Округление:

* – обязательно заполнить