Примечание: дробные числа записывайте
через точку, а не запятую.
Округлять до -го знака после запятой.
Решение треугольников онлайн
С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Решение треугольника по трем сторонам
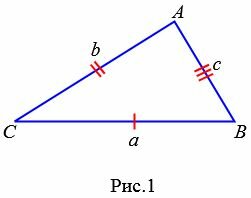
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем  .
.
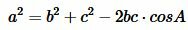
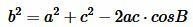
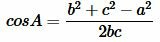 |
(1) |
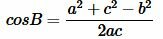 |
(2) |
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения
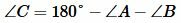 .
.
Пример 1. Известны стороны треугольника ABC: 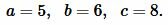 Найти
Найти  (Рис.1).
(Рис.1).
Решение. Из формул (1) и (2) находим:
И, наконец, находим угол C:
Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
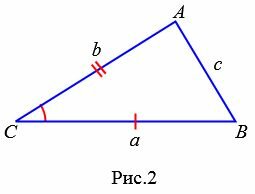
Найдем сторону c используя теорему косинусов:
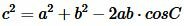 .
.
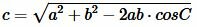 .
.
Далее, из формулы
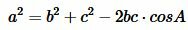 .
.
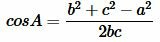 . . |
(3) |
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:
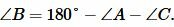 .
.
Пример 2. Известны две стороны треугольника ABC: 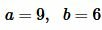 и
и 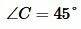 (Рис.2). Найти сторону c и углы A и B.
(Рис.2). Найти сторону c и углы A и B.
Решение. Иcпользуя теорму косинусов найдем сторону c:
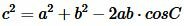 ,
,
Из формулы (3) найдем cosA:
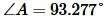 .
.
Поскольку уже нам известны два угла то находим третий:
Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
Так как, уже известны два угла, то можно найти третий:
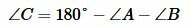 .
.
Далее, для находждения сторон b и c воспользуемся тероемой синусов:
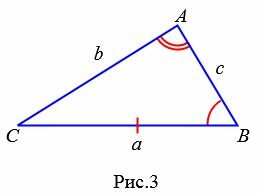
Пример 3. Известна одна сторона треугольника ABC: 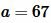 и углы
и углы 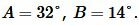 (Рис.3). Найти стороны b и c и угол С.
(Рис.3). Найти стороны b и c и угол С.
Решение. Поскольку известны два угла, то легко можно найти третий угол С:
Найдем сторону b. Из теоремы синусов имеем:
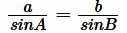
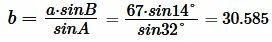
Найдем сторону с. Из теоремы синусов имеем:
Нахождение углов треугольника по заданным сторонам
Нахождение углов треугольника по заданным сторонам с использованием теоремы косинусов.
От нашего пользователя поступил запрос на создание калькулятора, рассчитывающего углы треугольника по заданным сторонам — Расчет углов треугольника.
Для треугольника, в отличие от, скажем, четырехугольника, эта задача имеет решение, ибо треугольник можно однозначно определить по трем сторонам (а также по двум сторонам и углу между ними, и по стороне и двум прилежащим углам).
Стороны в треугольнике, кстати сказать, должны следовать неравенству треугольника, то есть, сумма любых двух сторон должна быть больше третьей стороны.
Математически (см. рисунок) это выражается системой
c” />
a” />
b” />
В случае невыполнения хотя бы одного из условий треугольник называют вырожденным. Собственно, это и не треугольник уже.
Идем дальше — при известных сторонах углы проще всего определить, пользуясь теоремой косинусов, частным случаем которой является теорема Пифагора (см. рисунок)
Калькулятор ниже рассчитывает углы по введенным длинам сторон. Если треугольник вырожденный, то в результате будут нули.
[spoiler title=”источники:”]
http://matworld.ru/geometry/reshenie-treugolnikov.php
http://planetcalc.ru/534/
[/spoiler]
Исторический термин «решение треугольников» (лат. solutio triangulorum) обозначает решение следующей тригонометрической задачи: найти остальные стороны и/или углы треугольника по уже известным[1]. Существуют также обобщения этой задачи на случай, когда заданы другие элементы треугольника (например, медианы, биссектрисы, высоты, площадь и т. д.), а также на случай, когда треугольник располагается не на евклидовой плоскости, а на сфере (сферический треугольник), на гиперболической плоскости (гиперболический треугольник) и т. п. Данная задача часто встречается в тригонометрических приложениях — например, в геодезии, астрономии, строительстве, навигации.
Решение плоских треугольников[править | править код]

У треугольника[2] общего вида имеется 6 основных элементов: 3 линейные (длины сторон 

Алгоритм решения задачи зависит от того, какие именно характеристики треугольника считаются известными. Поскольку вариант «заданы три угла» исключён из рассмотрения, остаются 5 различных вариантов[4]:
- три стороны;
- две стороны и угол между ними;
- две стороны и угол напротив одной из них;
- сторона и два прилежащих угла;
- сторона, противолежащий угол и один из прилежащих.
Основные теоремы[править | править код]
Стандартным методом решения задачи является использование нескольких фундаментальных соотношений, выполняющихся для всех плоских треугольников[5]:
- Теорема косинусов
- Теорема синусов
- Сумма углов треугольника
Из других иногда полезных на практике универсальных соотношений следует упомянуть теорему тангенсов, теорему котангенсов, теорему о проекциях и формулы Мольвейде.
Замечания[править | править код]
- Для нахождения неизвестного угла надёжнее использовать теорему косинусов, а не синусов, потому что значение синуса угла при вершине треугольника не определяет однозначно самого угла, поскольку смежные углы имеют один и тот же синус[6]. Например, если
то угол
может быть как
, так и
, потому что синусы этих углов совпадают. Исключением является случай, когда заранее известно, что в данном треугольнике тупых углов быть не может — например, если треугольник прямоугольный. С косинусом такие проблемы не возникают: в интервале от
до
значение косинуса определяет угол однозначно.
- При построении треугольников важно помнить, что зеркальное отражение построенного треугольника тоже будет решением задачи. Например, три стороны однозначно определяют треугольник с точностью до отражения.
- Все треугольники подразумеваются невырожденными, то есть длина стороны не может быть нулевой, а величина угла — положительное число, меньшее, чем
.

Три стороны[править | править код]
Пусть заданы длины всех трёх сторон 
Чтобы найти углы 
Третий угол сразу находится из правила, что сумма всех трёх углов должна быть равна 
Не рекомендуется второй угол находить по теореме синусов, потому что, как указано в замечании 1, существует опасность спутать тупой угол с острым. Этой опасности не возникнет, если первым определить, по теореме косинусов, наибольший угол (он лежит против наибольшей из сторон) — два других угла точно являются острыми, и применение к ним теоремы синусов безопасно.
Ещё один метод вычисления углов по известным сторонам — использование теоремы котангенсов.

Две стороны и угол между ними[править | править код]
Пусть для определённости известны длины сторон 


Фактически задача сведена к предыдущему случаю. Далее ещё раз применяется теорема косинусов для нахождения второго угла:
Третий угол находится из теоремы о сумме углов треугольника: 

Две стороны и угол напротив одной из них[править | править код]
В этом случае решений может быть два, одно или ни одного. Пусть известны две стороны 


Для краткости обозначим 
- Задача не имеет решения (сторона
«не достаёт» до линии
) в двух случаях: если
или если угол
и при этом
- Если
существует единственное решение, причём треугольник прямоугольный:
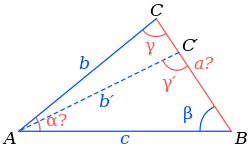
- Если
то возможны 2 варианта.
- Если
, то угол
имеет два возможных значения: острый угол
и тупой угол
. На рисунке справа первому значению соответствуют точка
, сторона
и угол
, а второму значению — точка
, сторона
и угол
.
- Если
, то
(большей стороне треугольника соответствует больший противолежащий угол). Поскольку в треугольнике не может быть двух тупых углов, тупой угол для
исключён и решение
единственно.
- Если
Третий угол определяется по формуле 

Сторона и два угла[править | править код]
Пусть задана сторона 

Вначале определяется третий угол. Например, если даны углы 

Решение прямоугольных треугольников[править | править код]

Прямоугольный треугольник
В этом случае известен один из углов — он равен 90°. Необходимо знать ещё два элемента, хотя бы один из которых — сторона. Возможны следующие случаи:
- два катета;
- катет и гипотенуза;
- катет и прилежащий острый угол;
- катет и противолежащий острый угол;
- гипотенуза и острый угол.
Вершину прямого угла традиционно обозначают буквой 





Расчётные формулы существенно упрощаются, так как вместо теорем синусов и косинусов можно использовать более простые соотношения — теорему Пифагора:
и определения основных тригонометрических функций:
Ясно также, что углы 


При корректной постановке задачи (если заданы гипотенуза и катет, то катет должен быть меньше гипотенузы; если задан один из двух непрямых углов, то он должен быть острый) решение всегда существует и единственно.
Два катета[править | править код]
Гипотенуза находится по теореме Пифагора:
Углы могут быть найдены с использованием функции арктангенса:
или же по только что найденной гипотенузе:
Катет и гипотенуза[править | править код]
Пусть известны катет 


После этого углы определяются аналогично предыдущему случаю.
Катет и прилежащий острый угол[править | править код]
Пусть известны катет 

Гипотенуза 
Катет 
Острый угол 
Катет и противолежащий острый угол[править | править код]
Пусть известны катет 

Гипотенуза 
Катет 

Гипотенуза и острый угол[править | править код]
Пусть известны гипотенуза 

Острый угол 
Катеты определяются из соотношений
Решение сферических треугольников[править | править код]


Стороны сферического треугольника 
Сферический треугольник общего вида полностью определяется тремя из шести своих характеристик (3 стороны и 3 угла). Стороны сферического треугольника 
Решение треугольников в сферической геометрии имеет ряд отличий от плоского случая. Например, сумма трёх углов 
Из других соотношений могут оказаться полезными формулы аналогии Непера[13] и формула половины стороны[14].

Три стороны[править | править код]
Если даны (в угловых единицах) стороны 
,
,
,

Две стороны и угол между ними[править | править код]
Пусть заданы стороны 


Углы 

Две стороны и угол не между ними[править | править код]
Пусть заданы стороны 

Угол 
Здесь, аналогично плоскому случаю, при 


Остальные величины можно найти из формул аналогии Непера[16]:
,
.

Сторона и прилежащие углы[править | править код]
В этом варианте задана сторона 


Две неизвестные стороны получаются из формул аналогии Непера:
или, если использовать вычисленный угол 

Два угла и сторона не между ними[править | править код]
В отличие от плоского аналога данная задача может иметь несколько решений.
Пусть заданы сторона 


Если угол для стороны 

Остальные величины определяются из формул аналогии Непера:

Три угла[править | править код]
Если заданы три угла, стороны находятся по теореме косинусов:
,
,
.
Другой вариант: использование формулы половины угла[19].
Решение прямоугольных сферических треугольников[править | править код]
Изложенные алгоритмы значительно упрощаются, если известно, что один из углов треугольника (например, угол 
Вариации и обобщения[править | править код]
Во многих практически важных задачах вместо сторон треугольника задаются другие его характеристики — например, длина медианы, высоты, биссектрисы, радиус вписанного или описанного круга и т. д. Аналогично вместо углов при вершинах треугольника в задаче могут фигурировать иные углы. Алгоритмы решения подобных задач чаще всего комбинируются из рассмотренных выше теорем тригонометрии.
Примеры:
Примеры практического применения[править | править код]
Триангуляция[править | править код]
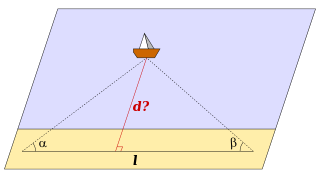
Чтобы определить расстояние 



Этот метод используется в каботажном судоходстве. Углы 

Другой пример: требуется измерить высоту 


Расстояние между двумя точками на поверхности земного шара[править | править код]

Надо вычислить расстояние между двумя точками на земном шаре[25]:
- Точка
: широта
долгота
- Точка
: широта
долгота
Для сферического треугольника 

Это случай «две стороны и угол между ними». Из приведенных выше формул получается:
,
где 
История[править | править код]
Зачатки тригонометрических знаний можно найти в математических рукописях Древнего Египта, Вавилона и Древнего Китая. Главным достижением этого периода стало соотношение, позже получившее имя теоремы Пифагора; Ван дер Варден считает, что вавилоняне открыли его между 2000 и 1786 годами до н. э.[26]
Общая постановка задачи решения треугольников (как плоских, так и сферических) появилась в древнегреческой геометрии[27]. Во второй книге «Начал» Евклида теорема 12 представляет собой словесный аналог теоремы косинусов для тупоугольных треугольников[28]:
В тупоугольных треугольниках квадрат на стороне, стягивающей тупой угол, больше [суммы] квадратов на сторонах, содержащих тупой угол, на дважды взятый прямоугольник, заключённый между одной из сторон при тупом угле, на которую падает перпендикуляр, и отсекаемым этим перпендикуляром снаружи отрезком при тупом угле.
Следующая за ней теорема 13 — вариант теоремы косинусов для остроугольных треугольников. Аналога теоремы синусов у греков не было, это важнейшее открытие было сделано гораздо позднее[29]: древнейшее из дошедших до нас доказательств теоремы синусов на плоскости описано в книге Насир ад-Дин Ат-Туси «Трактат о полном четырёхстороннике», написанной в XIII веке[30].
Первые тригонометрические таблицы составил, вероятно, Гиппарх в середине II века до н. э. для астрономических расчётов. Позднее астроном II века Клавдий Птолемей в «Альмагесте» дополнил результаты Гиппарха. Первая книга «Альмагеста» — самая значимая тригонометрическая работа всей античности. В частности, «Альмагест» содержит обширные тригонометрические таблицы хорд для острых и тупых углов, с шагом 30 угловых минут. В таблицах Птолемей приводит значение длин хорд с точностью до трех шестидесятиричных знаков[31]. Такая точность примерно соответствует пятизначной десятичной таблице синусов с шагом 15 угловых минут[1].
Птолемей явно не формулирует теорему синусов и косинусов для треугольников. Тем не менее он всегда справляется с задачей решения треугольников, разбивая треугольник на два прямоугольных[32].
Параллельно с развитием тригонометрии плоскости греки, под влиянием астрономии, далеко продвинули сферическую тригонометрию[33]. Решающим этапом в развитии теории стала монография «Сферика» в трёх книгах, которую написал Менелай Александрийский (около 100 года н. э.). В первой книге он изложил теоремы о сферических треугольниках, аналогичные теоремам Евклида о плоских треугольниках (см. I книгу «Начал»). По сообщению Паппа, Менелай первым ввёл понятие сферического треугольника как фигуры, образованной отрезками больших кругов[34]. Несколько десятилетий спустя Клавдий Птолемей в своих трудах «География», «Аналемма» и «Планисферий» даёт подробное изложение тригонометрических приложений к картографии, астрономии и механике.
В IV веке, после упадка античной науки, центр развития математики переместился в Индию. Сочинения индийских математиков (сиддханты) показывают, что их авторы были хорошо знакомы с трудами греческих астрономов и геометров[35]. Чистой геометрией индийцы интересовались мало, но их вклад в прикладную астрономию и расчётные аспекты тригонометрии очень значителен. В частности, индийцы первыми ввели в использование косинус[36]. Кроме того, индийцы знали формулы для кратных углов 


В VIII веке учёные стран Ближнего и Среднего Востока познакомились с трудами древнегреческих и индийских математиков и астрономов. Их астрономические трактаты, аналогичные индийским сиддхантам, назывались «зиджи»; типичный зидж представлял собой сборник астрономических и тригонометрических таблиц, снабжённый руководством по их использованию и (не всегда) изложением общей теории[38]. Сравнение зиджей периода VIII—XIII веков показывает быструю эволюцию тригонометрических знаний. Самые ранние из сохранившихся трудов принадлежат ал-Хорезми и ал-Марвази (IX век), которые рассмотрели, наряду с известными ещё индийцам синусом и косинусом, новые тригонометрические функции: тангенс, котангенс, секанс и косеканс[36].
Сабит ибн Курра (IX век) и ал-Баттани (X век) первыми открыли фундаментальную теорему синусов для частного случая прямоугольного сферического треугольника. Для произвольного сферического треугольника доказательство было найдено (разными способами и, вероятно, независимо друг от друга) Абу-л-Вафой, ал-Худжанди и ибн Ираком в конце X века[29]. В другом трактате ибн Ирака сформулирована и доказана теорема синусов для плоского треугольника[39]. Сферическая теорема косинусов в общем виде сформулирована в странах ислама не была, однако в трудах Сабита ибн Курры, ал-Баттани и других астрономов имеются эквивалентные ей утверждения[40].
Фундаментальное изложение тригонометрии как самостоятельной науки (как плоской, так и сферической) дал персидский математик и астроном Насир ад-Дин ат-Туси в 1260 году[41]. Его «Трактат о полном четырёхстороннике» содержит практические способы решения типичных задач, в том числе труднейших, решенных самим ат-Туси — например, построение сторон сферического треугольника по заданным трём углам[42]. Таким образом, к концу XIII века были открыты базовые теоремы, необходимые для эффективного решения треугольников.
В Европе развитие тригонометрической теории стало чрезвычайно важным в Новое время, в первую очередь для артиллерии, оптики и навигации при дальних морских путешествиях. В 1551 году появились 15-значные тригонометрические таблицы Ретика, ученика Коперника, с шагом 10″[43]. Потребность в сложных тригонометрических расчётах вызвала в начале XVII века открытие логарифмов, причём первые логарифмические таблицы Джона Непера содержали только логарифмы тригонометрических функций. Среди других открытий Непера — эффективный алгоритм решения сферических треугольников, получивший название «формулы аналогии Непера»[44]. Алгебраизация тригонометрии, начатая Франсуа Виетом, была завершена Леонардом Эйлером в XVIII веке, после чего алгоритмы решения треугольников приобрели современный вид.
См. также[править | править код]
- Признаки подобия треугольников
- Площадь треугольника
- Сферическая тригонометрия
- Сферический треугольник
- Триангуляция
- Тригонометрические тождества
- Тригонометрические функции
- Формулы Мольвейде
Примечания[править | править код]
- ↑ 1 2 Выгодский М. Я., 1978, с. 266—268.
- ↑ Плоский треугольник иногда называют прямолинейным.
- ↑ Элементарная математика, 1976, с. 487.
- ↑ Solving Triangles. Maths is Fun. Дата обращения: 23 Jule 2012. Архивировано 30 июня 2019 года.
- ↑ Элементарная математика, 1976, с. 488.
- ↑ Степанов Н. Н., 1948, с. 133.
- ↑ Solving SSS Triangles. Maths is Fun. Дата обращения: 23 Jule 2012. Архивировано 30 сентября 2012 года.
- ↑ Solving SAS Triangles. Maths is Fun. Дата обращения: 24 Jule 2012. Архивировано 30 сентября 2012 года.
- ↑ Solving SSA Triangles. Maths is Fun. Дата обращения: 24 Jule 2012). Архивировано 30 сентября 2012 года.
- ↑ Выгодский М. Я., 1978, с. 294.
- ↑ Элементарная математика, 1976, с. 493—496.
- ↑ Solving ASA Triangles. Maths is Fun. Дата обращения: 24 Jule 2012. Архивировано 30 сентября 2012 года.
- ↑ Степанов Н. Н., 1948, с. 87—90.
- ↑ Степанов Н. Н., 1948, с. 102—104.
- ↑ 1 2 Энциклопедия элементарной математики, 1963, с. 545.
- ↑ Степанов Н. Н., 1948, с. 121—128.
- ↑ Степанов Н. Н., 1948, с. 115—121.
- ↑ Степанов Н. Н., 1948, с. 128—133.
- ↑ Степанов Н. Н., 1948, с. 104—108.
- ↑ Основные формулы физики, 1957, с. 14—15.
- ↑ Цейтен Г. Г., 1932, с. 223—224.
- ↑ Цейтен Г. Г., 1938, с. 126—127.
- ↑ 1 2 Геометрия: 7—9 классы, 2009, с. 260—261.
- ↑ Геометрия: 7—9 классы, 2009, с. 260.
- ↑ Степанов Н. Н., 1948, с. 136—137.
- ↑ van der Waerden, Bartel Leendert. Geometry and Algebra in Ancient Civilizations. — Springer, 1983. — ISBN 3-540-12159-5.
- ↑ Глейзер Г. И., 1982, с. 77.
- ↑ Глейзер Г. И., 1982, с. 94—95.
- ↑ 1 2 Матвиевская Г. П., 2012, с. 92—96.
- ↑ Berggren, J. Lennart. Mathematics in Medieval Islam // The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook (англ.). — Princeton University Press, 2007. — P. 518. — ISBN 9780691114859.
- ↑ История математики, том I, 1970, с. 143.
- ↑ Ван дер Варден. Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции. — М.: Наука, 1959. — С. 366. — 456 с.
- ↑ Матвиевская Г. П., 2012, с. 25—27.
- ↑ Матвиевская Г. П., 2012, с. 33—36.
- ↑ Матвиевская Г. П., 2012, с. 40—44.
- ↑ 1 2 Сираждинов С. Х., Матвиевская Г. П., 1978, с. 79.
- ↑ Юшкевич А. П. История математики в Средние века. — М.: ГИФМЛ, 1961. — С. 160. — 448 с.
- ↑ Матвиевская Г. П., 2012, с. 51—55.
- ↑ Матвиевская Г. П., 2012, с. 111.
- ↑ Матвиевская Г. П., 2012, с. 96—98.
- ↑ Туси Насирэддин. Трактат о полном четырёхстороннике. Баку, Изд. АН АзССР, 1952.
- ↑ Рыбников К. А., 1960, с. 105.
- ↑ История математики, том I, 1970, с. 320.
- ↑ Степанов Н. Н. § 42. Формулы «аналогии Непера» // Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — С. 87—90. — 154 с.
Литература[править | править код]
- Теория и алгоритмы
- Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б., Позняк Э. Г., Юдина И. И. Геометрия: 7—9 классы. Учебник для общеобразовательных учреждений. — 19-е изд. — М.: Просвещение, 2009. — 384 с. — ISBN 978-5-09-021136-9.
- Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Гельфанд И. М., Львовский С. М., Тоом А. Л. Тригонометрия, учебник для 10 класса. — М.: МЦНМО, 2002. — ISBN 5-94057-050-X.
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
- Мензел Д. (ред.). Основные формулы физики. Глава 1. Основные математические формулы. — М.: Изд. иностранной литературы, 1957. — 658 с.
- Основные понятия сферической геометрии и тригонометрии // Энциклопедия элементарной математики (в 5 томах). — М.: Физматгиз, 1963. — Т. 4. — С. 518—557. — 568 с.
- Степанов Н. Н. Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948.
- История
- Глейзер Г. И. История математики в школе. VII-VIII классы. Пособие для учителей. — М.: Просвещение, 1982. — С. 76—95. — 240 с.
- Глейзер Г. И. История математики в школе. IX-X классы. Пособие для учителей. — М.: Просвещение, 1983. — 352 с.
- История математики под редакцией А. П. Юшкевича в трёх томах, М.: Наука.
- История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I.
- Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
- Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
- Матвиевская Г. П. Очерки истории тригонометрии: Древняя Греция. Средневековый Восток. Позднее Средневековье. — Изд. 2-е. — М.: Либроком, 2012. — 160 с. — (Физико-математическое наследие: математика (история математики)). — ISBN 978-5-397-02777-9.
- Рыбников К. А. История математики в двух томах. — М.: Изд. МГУ, 1960. — Т. I.
- Сираждинов С. Х., Матвиевская Г. П. Абу Райхан Беруни и его математические труды. Пособие для учащихся. — М.: Просвещение, 1978. — 95 с. — (Люди науки).
- Цейтен Г. Г. История математики в древности и в средние века. — М.—Л.: ГТТИ, 1932. — 230 с.
- Цейтен Г. Г. История математики в XVI и XVII веках. — М.—Л.: ОНТИ, 1938. — 456 с.
Решить треугольник Онлайн по координатам
Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
По сторонам треугольника найти его углы
Чтобы по сторонам треугольника найти его углы, нужно применить теорему косинусов.

Рассмотрим треугольник ABC.
Обозначим BC=a, AC=b, AB=c,
∠A=α, ∠B=β, ∠C=γ.
По теореме косинусов
![]()
![]()
откуда
![]()
Аналогично как следствие из теоремы косинусов находятся косинусы других углов треугольника:
![]()
и
![]()
![]()
и
![]()
Прежде чем рассмотреть на конкретных примерах, как по сторонам треугольника найти его углы, выясним, как по таблицам Брадиса по значению синуса или косинуса определить угол.
2.9. Типовая задача с треугольником
Многие помнят из школы признаки равенства треугольников, признаки подобия треугольников и мучительное заучивание доказательств теорем. Как в
сердцАх сказал один мой одноклассник, «не понимаю, на### доказывать равенство треугольников, если и так видно, что они одинаковые». Мы тоже не
будем ничего доказывать, поскольку аналитическая геометрия рассматривает треугольник совсем с другой стороны.
Типовая задача, как правило, формулируется так: Даны три вершины треугольника. Требуется найти… много чего требуется
найти…. Повезёт, если будет пункта 3-4, но чаще всего их 5-6 и даже больше. И вам повезло – разберём всё! Или почти всё:
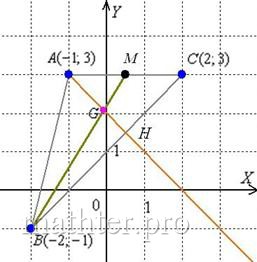
Задача 95
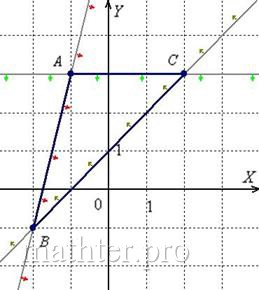
Даны вершины треугольника ![]() . Требуется:
. Требуется:
1) составить уравнения сторон ![]() и найти их угловые коэффициенты;
и найти их угловые коэффициенты;
2) найти длину стороны ![]() ;
;
3) найти ![]() ;
;
4) составить прямой ![]() , проходящей через точку
, проходящей через точку ![]() параллельно прямой
параллельно прямой ![]() ;
;
5) составить уравнение высоты ![]() и найти её длину;
и найти её длину;
6) вычислить площадь треугольника ![]() ;
;
7) составить уравнение медианы ![]() ;
;
8) найти точку пересечения ![]() .
.
и для особо опасных энтузиастов:
9) найти уравнение биссектрисы ![]() ;
;
10) найти центр тяжести ![]() треугольника;
треугольника;
11) составить систему линейных неравенств, определяющих треугольник.
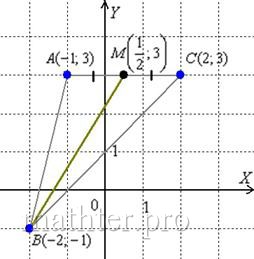
С чего начать решение? Начать целесообразно с выполнения чертежа. По условию этого можно не делать, но для самоконтроля и
самопроверки всегда строим чертёж на черновике, не устану это рекомендовать:
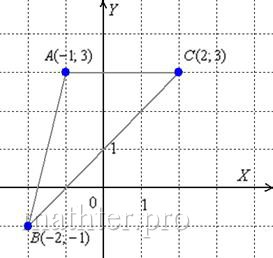
Ещё раз напоминаю, что самый выгодный масштаб 1 единица = 1
см (2 тетрадные клетки). Всё хорошо видно, и расстояния удобно измерять линейкой.
Вперёд без страха и сомнений:
1) Составим уравнения сторон ![]() и найдём их угловые
и найдём их угловые
коэффициенты.
Поскольку известны вершины треугольника, то уравнения каждой стороны составим по двум
точкам.
Составим уравнение стороны ![]() по точкам
по точкам ![]() :
:
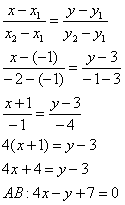
Для проверки мысленно либо на черновике подставляем координаты каждой точки в полученное уравнение.
Теперь
найдём угловой коэффициент. Для этого перепишем общее уравнение в виде уравнения с угловым коэффициентом:
![]()
Таким образом, угловой коэффициент: ![]()
Самостоятельно разбираемся со сторонами ![]() и сверяемся, что
и сверяемся, что
получилось:
![]()
2) Найдём длину стороны ![]() . Используем соответствующую формулу для точек
. Используем соответствующую формулу для точек ![]() :
:
![]()
Сторону легко измерить обычной линейкой, хотя это не сильно строгая проверка 🙂
3) Найдём ![]() . Это Задача 31, повторим:
. Это Задача 31, повторим:
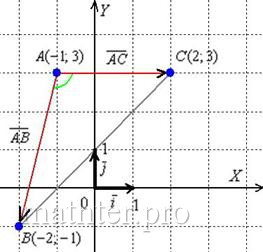
Используем формулу 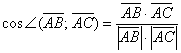 .
.
Найдём векторы:
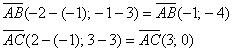
Таким образом:
![]()
![]() , и сам угол:
, и сам угол:
![]() , ну что же, похоже на правду, желающие могут приложить транспортир, у кого
, ну что же, похоже на правду, желающие могут приложить транспортир, у кого
он есть.
Внимание! При выполнении этого пункта лучше не использовать формулы ориентированного угла
между прямыми, так как они всегда дают острый угол.
4) Составим уравнение прямой ![]() , проходящей через точку
, проходящей через точку ![]() параллельно прямой
параллельно прямой ![]() . Это стандартная задача, и мы ленимся отработать её вновь!
. Это стандартная задача, и мы ленимся отработать её вновь!
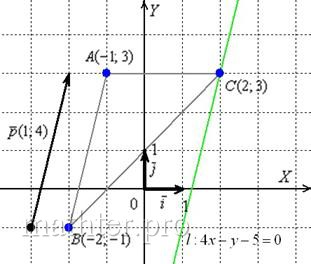
Из общего уравнения прямой ![]() вытащим направляющий вектор
вытащим направляющий вектор ![]() .
.
Составим уравнение прямой ![]() по точке
по точке ![]() и направляющему вектору
и направляющему вектору ![]() :
:
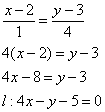
5) Составим уравнение высоты ![]() и найдём её длину.
и найдём её длину.
Первую часть задания мы тоже решали:
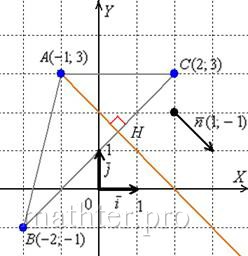
Из уравнения стороны ![]() снимаем вектор нормали
снимаем вектор нормали ![]() . Уравнение высоты
. Уравнение высоты
![]() составим по точке
составим по точке ![]() и направляющему вектору
и направляющему вектору ![]() :
:
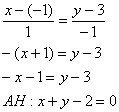
Обратите внимание, что координаты точки ![]() нам не известны.
нам не известны.
Иногда уравнение высоты находят из соотношения угловых коэффициентов перпендикулярных прямых: ![]() . В данном случае
. В данном случае ![]() , тогда:
, тогда: ![]() . Уравнение высоты
. Уравнение высоты ![]() составим по точке
составим по точке ![]() и угловому коэффициенту
и угловому коэффициенту ![]() :
:
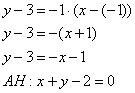
Длину высоты можно найти двумя способами.
Существует окольный путь:
а) находим ![]() – точку
– точку
пересечения высоты и стороны ![]() ;
;
б) находим длину отрезка ![]() по двум
по двум
известным точкам.
Но зачем? – ведь есть удобная формула расстояния от точки ![]() до прямой
до прямой ![]() :
:
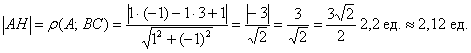
6) Вычислим площадь треугольника. Используем «школьную» формулу:
![]()
7) Уравнение медианы ![]() составим в два шага:
составим в два шага:
а) Найдём точку ![]() – середину стороны
– середину стороны ![]() . Используем формулы координат середины отрезка.
. Используем формулы координат середины отрезка.
Известны концы ![]() , и тогда середина:
, и тогда середина:
![]()
б) Уравнение медианы ![]() составим по точкам
составим по точкам ![]() :
:
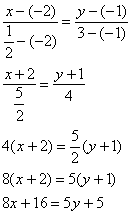
![]() – для проверки подставим координаты точек
– для проверки подставим координаты точек ![]() .
.
8) Найдём точку пересечения ![]() высоты и медианы:
высоты и медианы:
![]() в
в
Первое уравнение умножили на 5, складываем их почленно:
![]() – подставим в первое уравнение:
– подставим в первое уравнение:
![]()
![]()
9) Биссектриса делит угол пополам:
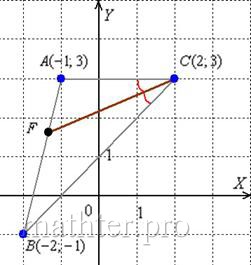
Из свойств биссектрисы внутреннего угла следует соотношение длин следующих отрезков:
![]()
Длины сторон уже найдены в предыдущих пунктах: ![]() .
.
Таким образом, ![]() . Координаты точки
. Координаты точки ![]() найдём по формулам деления отрезка в данном отношении. Да,
найдём по формулам деления отрезка в данном отношении. Да,
параметр «лямбда» получился просто сказочным, ну а кому сейчас легко? Точки ![]() известны и понеслась нелёгкая:
известны и понеслась нелёгкая:
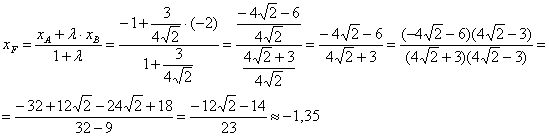
Примечание: на последнем шаге я умножил числитель и знаменатель на сопряжённое выражение ![]() – чтобы использовать формулу
– чтобы использовать формулу ![]() и
и
избавиться от иррациональности в знаменателе.
Разбираемся со второй координатой:
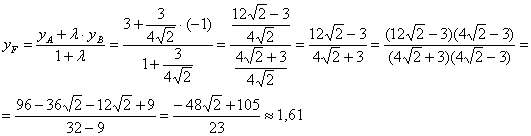
аким образом: 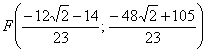
И предчувствие вас не обмануло, уравнение биссектрисы ![]() составим по точкам
составим по точкам 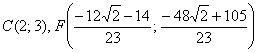 по формуле
по формуле ![]() :
:
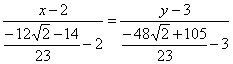
обратите внимание на технику упрощений:
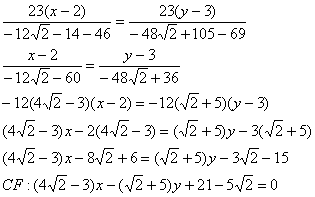
Проверил, всё сходится. На практике, конечно, вычисления почти всегда будут проще. Никого не хотел запугать, так уж получилось =)
10) Найдём центр тяжести треугольника.
Но сначала поймём, что такое центр тяжести плоской фигуры. Мысленно вырежьте из тонкого однородного картона любую фигуру. …Почему-то фигура зайца
в голову пришла. Так вот: если слегка насадить данную фигуру центром тяжести (какой же я изверг =)) на вертикально расположенную иголку, то
теоретически фигура не должна свалиться.
Центром тяжести треугольника является точка пересечения его медиан. В треугольнике три медианы и пересекаются они в одной точке.
Из пункта 7 нам уже известна одна из медиан: ![]() . Как решить задачу?
. Как решить задачу?
Напрашивается очевидный алгоритм: можно найти уравнение второй медианы (любой из двух оставшихся) и точку пересечения этих медиан. Но есть путь
короче! Нужно только знать полезное свойство:
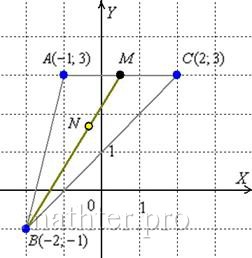
Точка пересечения медиан делит каждую из медиан в
отношении ![]() , считая от вершины треугольника. Поэтому справедливо
, считая от вершины треугольника. Поэтому справедливо
отношение ![]()
Нам известны концы отрезка – точки ![]() и
и ![]() .
.
По формулам деления отрезка в данном отношении:
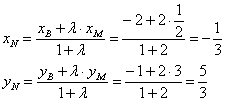
Таким образом, центр тяжести треугольника: ![]()
И заключительный пункт задачи, для освоения которого нужно уметь решать недавно разобранные линейные
неравенства:
11) Составим систему линейных неравенств, определяющих треугольник.
Для удобства я перепишу найденные уравнения сторон:
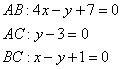
Рассмотрим прямую ![]() . Треугольник лежит в полуплоскости, где находится
. Треугольник лежит в полуплоскости, где находится
вершина ![]() . Составим вспомогательный многочлен
. Составим вспомогательный многочлен ![]() и вычислим его значение в точке
и вычислим его значение в точке ![]() :
: ![]() . Поскольку сторона
. Поскольку сторона ![]() принадлежит треугольнику, то неравенство будет нестрогим:
принадлежит треугольнику, то неравенство будет нестрогим: ![]()
Внимание! Если вам не понятен этот алгоритм, то обратитесь к
Задаче 90.
Рассмотрим прямую ![]() . Треугольник расположен ниже данной прямой, поэтому
. Треугольник расположен ниже данной прямой, поэтому
очевидно неравенство ![]() .
.
И, наконец, для ![]() составим многочлен
составим многочлен ![]() , в который подставим координаты точки
, в который подставим координаты точки ![]() :
: ![]() .
.
Таким образом, получаем третье неравенство: ![]() .
.
Итак, треугольник ![]() определяется следующей системой линейных
определяется следующей системой линейных
неравенств:
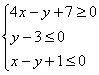
Готово.
Какой можно сделать вывод?
Многие задачи аналитической геометрии прозрачны и просты,
главное, не допустить вычислительных ошибок.
Следует отметить, что по настоящему трудные задачи в аналитической геометрии встречаются редко, и вы справитесь практически с любой из них!
Главное, придерживаться методики решения и проявить маломальское упорство.
Ну что, может ещё задачку? Да ладно, не надо стесняться, я же по глазам вижу, что хотите =)
Но сейчас на очереди другая увлекательная тема, продолжаем изучать геометрию плоскости:
 3.1. Алгебраическая линия и её порядок
3.1. Алгебраическая линия и её порядок
 2.8. Как научиться решать задачи по геометрии?
2.8. Как научиться решать задачи по геометрии?
| Оглавление |
Автор: Aлeксaндр Eмeлин

























































